Phylogeographic and population genetic structure of bighorn sheep ( Ovis canadensis ) in North American deserts

Abstract

Fossil data are ambiguous regarding the evolutionary origin of contemporary desert bighorn sheep ( Ovis canadensis subspecies). To address this uncertainty, we conducted phylogeographic and population genetic analyses on bighorn sheep subspecies found in southwestern North America. We analyzed 515 base pairs of mtDNA control region sequence and 39 microsatellites in 804 individuals from 58 locations. Phylogenetic analyses revealed 2 highly divergent clades concordant with Sierra Nevada ( O. c. sierrae ) and Rocky Mountain ( O. c. canadensis ) bighorn and showed that these 2 subspecies both diverged from desert bighorn prior to or during the Illinoian glaciation (~315–94 thousand years ago [kya]). Desert bighorn comprised several more recently diverged haplogroups concordant with the putative Nelson ( O. c. nelsoni ), Mexican ( O. c. mexicana ), and Peninsular ( O. c. cremnobates ) subspecies. Corresponding estimates of effective splitting times (~17–3 kya), and haplogroup ages (~85–72 kya) placed the most likely timeframe for divergence among desert bighorn subspecies somewhere within the last glacial maximum. Median-joining haplotype network and Bayesian skyline analyses both indicated that desert bighorn collectively comprised a historically large and haplotype-diverse population, which subsequently lost much of its diversity through demographic decline. Using microsatellite data, discriminant analysis of principle components (DAPC) and Bayesian clustering analyses both indicated genetic structure concordant with the geographic distribution of 3 desert subspecies. Likewise, microsatellite and mitochondrial-based F_ST comparisons revealed significant fixation indices among the desert bighorn genetic clusters. We conclude these desert subspecies represent ancient lineages likely descended from separate Pleistocene refugial populations and should therefore be managed as distinct taxa to preserve maximal biodiversity.

Los datos de fósiles sobre el origen evolutivo de las ovejas del desierto ( Ovis canadensis subespecies) contemporáneas son ambiguos. Para dilucidar esta incertidumbre, llevamos a cabo análisis filogeográficos y de genética de poblaciones entre cinco subespecies de ovejas del suroccidente de Norteamérica. Analizamos 515 pb de secuencia de la región control del ADN mitocondrial y 39 microsatélites en 804 ovejas de 58 localidades. Los análisis filogenéticos revelaron 2 clados altamente divergentes concordantes con ovejas de la Sierra Nevada ( O. c. sierrae ) y de las Montañas Rocosas ( O. c. canadensis ), y demostraron que estas dos subespecies divergieron antes o durante la glaciación de Illinois (315,000–94,000 años). Las ovejas del desierto formaron varios haplogrupos recientemente derivados concordantes con las subespecies de Nelson ( O. c. nelsoni ), México ( O. c. mexicana ) y peninsular ( O. c. cremnobates ). Las estimaciones correspondientes al tiempo de separación efectiva (17,000–3,000 años) y edades de haplogrupos (85,000–72,000 años) son los plazos más probables para las divergencias entre subespecies de ovejas del desierto dentro de la última glaciación máxima. Análisis de redes de haplotipos de unión de medias y análisis bayesianos de líneas de horizonte indicaron que las ovejas del desierto formaron una población históricamente grande y diversa en términos de haplotipos, que luego perdieron gran parte de su diversidad a través de un descenso demográfico. Utilizando datos de microsatélites los análisis DAPC y TESS indicaron agrupamiento genético concordante con la distribución geográfica actual de las tres subespecies. Asimismo, comparaciones de F_ST con datos de microsatélites y mitocondriales revelaron índices de fijación significativos entre los grupos genéticos de ovejas del desierto. Concluimos que estas subespecies de ovejas del desierto representan linajes antiguos que probablemente descienden de poblaciones de distintos refugios del Pleistoceno, y que por lo tanto deben ser manejadas como taxones distintos para preservar su biodiversidad máxima.

Bighorn sheep ( Ovis canadensis Shaw, 1804) are native to the deserts of southwestern North America (hereafter, desert southwest), as well as the adjacent and climatically distinct alpine zones of the Sierra Nevada and Rocky Mountain ranges. Once abundant, bighorn sheep suffered widespread local extinction following European settlement as a result of overharvest, livestock-transmitted disease, and habitat loss and fragmentation ( Seton 1929 ; Buechner 1960 ; Valdez and Krausman 1999 ). Ongoing efforts to restore bighorn sheep throughout their native range, particularly in the desert southwest, have relied heavily on translocations ( Rowland and Schmidt 1981 ; Bleich et al. 1990 ; Singer et al. 2000 ; Boyce et al. 2011 ). However, such actions require thorough understanding of both the taxonomy and phylogeographic structure among populations ( Weeks et al. 2011 ).

Significant taxonomic revision of O. canadensis at the subspecific level has occurred during the past several decades, yet phylogenetic relationships have not been adequately tested with modern molecular methods. Currently recognized subspecies include California ( O. c. californiana ; not considered in this study), Rocky Mountain ( O. c. canadensis ), and Sierra Nevada ( O. c. sierrae ) bighorn, as well as disputed subspecies designations among desert populations. Reference texts ( Wilson and Reader 2005 ) continue to use the morphology-based designations of Cowan (1940) , recognizing 4 desert subspecies: Nelson ( O. c. nelsoni ), Mexican ( O. c. mexicana ), Peninsular ( O. c. cremnobates ), and Weems ( O. c. weemsi ) bighorn. However, subsequent morphometric studies questioned these subspecies as artifacts of small sample size and age-related size differences ( Bradley and Baker 1967 ; Wehausen and Ramey 1993 ). Further, a restriction fragment length polymorphism (RFLP) study of mitochondrial DNA (mtDNA) failed to resolve these subspecies ( Ramey 1995 ). As a result, Wehausen and Ramey (1993) proposed desert bighorn be synonymized to a single taxon ( O. c. nelsoni ).

Lack of a consistent taxonomy has created confusion among managers and conservation biologists. For instance, Peninsular bighorn sheep were designated threatened by the State of California in 1984 as O. c. crembobates . Since then, Peninsular bighorn have been provisionally synonymized with O. c. nelsoni ( Wehausen and Ramey 1993 ) and were listed under the Endangered Species Act in 1999 (63 FR 13134), yet are protected as a distinct population segment. Ultimately, subspecies designations are valuable to conservation if they serve as commonly understood indicators of significant genetic variation and potential local adaptation that could be lost if mismanaged (i.e., translocated) as a single taxon. An updated genetic characterization of bighorn sheep occupying the desert southwest should therefore help inform taxonomy and management by examining how patterns of genetic variation compare with competing hypotheses regarding subspecies.

Achieving clarity regarding the phylogenetic history, and ultimately taxonomy, of desert bighorn sheep requires a basic understanding of the evolutionary history of the taxon. Unfortunately, the fossil record is somewhat ambiguous regarding the origin of contemporary desert bighorn in the desert southwest. Fossil evidence indicates Ovis continuously occupied at least 2 late Pleistocene glacial refugia in southern North America: 1 in the current Mojave Desert, established ~300 thousand years ago (kya), prior to the Illinoian glaciation ( Jefferson 1991 ), and another in the north near Natural Trap Cave, Wyoming ( Martin and Gilbert 1978 ; Wang 1988 ), established during the Sangamon interglacial (~100 kya). However, competing hypotheses regarding the origins of desert bighorn sheep relative to these refugial populations cannot be eliminated based on fossil geochronology ( Geist 1985 ). The 1st hypothesis proposes that Ovis from the northern refugium spread south, ultimately joining or displacing sheep from the Mojave refugium to give rise to contemporary desert populations. The 2nd hypothesis proposes that the northern colonizers were outcompeted and replaced by Ovis expanding from the Mojave refugium. These hypotheses provide clear alternatives that are testable using phylogenetic methods. Predictions following from the 1st hypothesis include: 1) contemporary desert bighorn populations should exhibit haplotypes recently diverged from contemporary Rocky Mountain bighorn haplotypes—i.e., since the last glacial maximum (LGM); 2) these derived desert haplotypes should represent only a subset of the lineages (i.e., founder effect) reflected in the Rocky Mountain population, and 3) these northern-derived desert haplotypes potentially occur in association with more deeply divergent (pre-Illinoian) haplotypes originating from the Mojave refugium. Predictions following from the 2nd hypothesis include: 1) all haplotypes in contemporary desert bighorn populations belong to 1 or more lineages that are deeply divergent (pre-Illinoian) from those occurring in Rocky Mountain bighorn populations, and 2) the existence of more than 1 such lineage would provide evidence that multiple southern refugia contributed to colonization of the desert southwest.

In this study, we characterized the phylogeographic and genetic structure of bighorn sheep occupying the desert southwest. We utilized a large number of samples from previously under represented areas of the native range of desert bighorn sheep. For clarity, we utilized the disputed desert subspecies designations of Cowan (1940) , as this taxonomy recognizes the greatest number of taxonomic units among which genetic variation could be compared. Our objectives were to 1) use mtDNA control region sequences and nuclear microsatellites to characterize phylogeographic and population genetic variation both within desert bighorn and in relation to the Sierra Nevada and Rocky Mountain subspecies, 2) estimate splitting times among subspecies to test fossil record-based hypotheses regarding colonization of the desert southwest, 3) reconstruct historical demography to estimate the timeframe of population declines, and 4) use these results to evaluate genetic support for competing desert subspecies designations.

M aterials and M ethods

Sample collection.

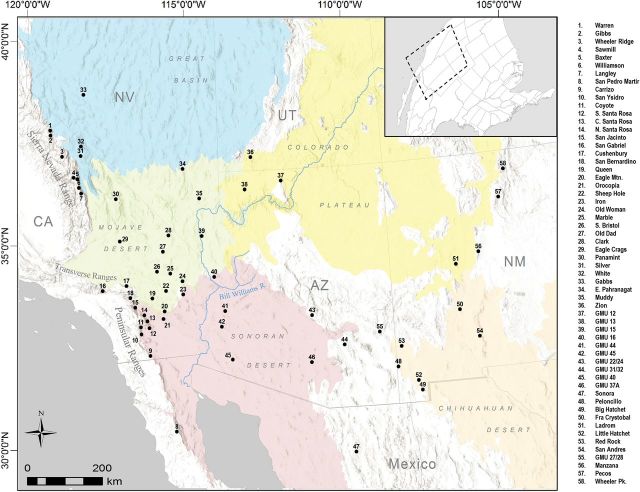
We used a total of 804 adult bighorn sheep ( n = 437 F, 353M, 14 unknown sex) captured by biologists from state agencies or harvested by hunters from 58 locations across the southwestern United States and northern Mexico, as well as 2 locations in Canada, during 1992–2013 ( Fig. 1 ; Supplementary Data ). Desert bighorn samples ( n = 655) were assigned to their geographic regions of origin, including the Peninsular Ranges, Transverse Ranges, Mojave, Sonoran, and Chihuahuan Deserts, Great Basin, and Colorado Plateau. This scheme allowed us to test the genetic evidence for competing subspecies designations within desert bighorn sheep without a priori assumptions regarding group membership. In addition to the desert bighorn sheep composing the core of our sample, we also included 52 endemic Sierra Nevada bighorn sheep, as well as 97 Rocky Mountain bighorn sheep from either Canada or (re)introduced populations in northern New Mexico and eastern Arizona ( Fig. 1 ; Supplementary Data ). No samples of California or Weems bighorn sheep were available for inclusion in this study.

Fig. 1.

Study area within the southwestern United States and northern Mexico, including 58 locations from which bighorn sheep ( Ovis canadensis ) subspecies were sampled. Significant geographic features are depicted as they relate to subspecies ranges. For locations, GMU refers to game management units as defined by the Arizona Game and Fish Department.

Laboratory methods.

Total genomic DNA was extracted from blood, muscle, or skin tissue using Qiagen DNeasy Blood and Tissue kits (Qiagen Inc., Valencia, California) following the manufacturer’s protocol. Each sample was genotyped at 39 microsatellite loci described in Buchalski et al. (2015) . Sex was confirmed via amplification of the Amelogenin marker described in Weikard et al. (2006) . To estimate genotyping error, we randomly selected 30 samples, along with positive and negative controls, to blindly regenotype. We estimated the average error rate per locus as the ratio between the number of single-locus genotypes including at least 1 allelic mismatch and the number of replicated single-locus genotypes ( Pompanon et al. 2005 ).

A fragment of the mitochondrial control region was amplified following the protocol described by Epps et al. (2005) . Cycle sequencing was performed bidirectionally using BigDye 3.1 and an ABI 3730 Genetic Analyzer (Applied Biosystems, Foster City, California). Forward sequences were verified with the sequence of the reverse strand using Sequencher 5.1 (Gene Codes Corp.) and incomplete sequences, or those with discrepancies, were reamplified and resequenced. We aligned the sequences in MEGA 6 ( Tamura et al. 2013 ) using the ClustalW algorithm ( Thompson et al. 1994 ) under default settings, at which time we discovered a 75 base pair (bp) repetitive sequence (RS) localized in the left domain near the tRNA ^Pro gene. All individuals examined had at least 2 copies of the RS, with a limited number (~5%) displaying 3 copies. We normalized the sequences by manually removing the extra RS from those haplotypes that had it and limited our analyses to the 515bp fragment common to all individuals (see Supplementary Data for a full description). Sequences for each novel haplotype were deposited into GenBank (accession nos. KU363638–KU363690).

We used a basic local alignment search tool ( BLAST — Altschul et al. 1997 ) to search the nucleotide database in GenBank for all unique haplotypes present in our data, finding 35 homologous sequences for desert bighorn sheep, including accession nos. AF076911–AF076917 ( Boyce et al. 1999 ), AY903993–AY904017 ( Epps et al. 2005 ), KP688366–KP688368 ( Buchalski et al. 2015 ), and AY116621–AY116623 (unpublished sequences for 2 Mexican and 1 Weems bighorn). We downloaded the archived sequences, preserving the original haplotype names, for inclusion in our phylogenetic analyses.

Range-wide population genetic structure.

We used discriminant analysis of principle components (DAPC— Jombart et al. 2010 ) to identify population structure among microsatellite genotypes. This method entails no assumptions regarding the cause of structure (i.e., island model versus isolation-by-distance [IBD]) and, in contrast to other clustering approaches (i.e., Pritchard et al. 2000 ), does not assume Hardy–Weinberg or gametic equilibrium. Analysis was implemented in R 3.0.2 ( R Development Core Team 2015 ) using the package adegenet 1.4-2 ( Jombart 2008 ). The optimal number of genetic clusters ( K ), was estimated by conducting 10 independent runs of the find.clusters function with the diffNgroup option selected. The number of principal components as predictors for the discriminant analysis was set to 7 following alpha-score optimization (i.e., trade-off between power of discrimination and overfitting; Supplementary Data ). Scatterplots of microsatellite genotypes in relation to discriminant functions were created in adegenet .

We then used TESS 2.3.1 ( Chen et al. 2007 ) to evaluate structure among microsatellite genotypes in a spatially explicit context. Program TESS accounts for spatial autocorrelation in allele frequencies due to IBD by treating sample location coordinates as prior information during estimation of admixture proportions. This allows for differentiation between clinal transitions and abrupt breaks (i.e., contact zones versus barriers) between discrete genetic groups or clusters ( Durand et al. 2009 ; Francois and Durand 2010 ). We first ran the no-admixture model with 200,000 iterations, of which the initial 100,000 were excluded as burn-in, to test the number of clusters ( K ) from 2 to 10, with 10 replicates each. A plot of the deviance information criterion (DIC) against K was used to identify the most likely number of clusters. This value was then used in 100 replicate runs of the admixture model, using the same number of iterations as above. Individual cluster memberships from the 10 runs having the highest likelihoods were averaged using CLUMPP 1.1.2 ( Jakobsson and Rosenberg 2007 ) and visualized using DISTRUCT 1.1 ( Rosenberg 2004 ). Predictive maps of each genetic cluster were generated using custom R scripts provided with the TESS software download ( http://www-timc.imag.fr/Olivier.Francois/TESS_Plot.html ).

We used nested hierarchical analysis of molecular variance (AMOVA— Excoffier et al. 1992 ) to examine the distribution of genetic variation associated with competing desert subspecies designations. In our 1st set of analyses, the Sierra Nevada and Rocky Mountain subspecies were compared to a varying number of groups within desert bighorn sheep. Desert bighorn grouping schemes included 1) the Peninsular, Nelson, and Mexican subspecies of Cowan (1940 ; K = 5), 2) Peninsular and Nelson bighorn pooled together as suggested by Wehausen and Ramey (1993 ; K = 4), and 3) all desert bighorn pooled together as implied by Ramey (1995 ; K = 3). To allow for lesser divergence within desert bighorn sheep in relation to the Sierra Nevada and Rocky Mountain subspecies, we conducted a 2nd set of analyses using desert bighorn only. We tested grouping schemes 1 and 2 based on the rationale above. This analytical design was applied to both microsatellite allele and control region haplotype frequency data in Arlequin 3.5.1.2 ( Excoffier and Lischer 2010 ). Significance was determined from 10,000 permutations of the data.

We then evaluated pairwise differentiation between each genetic cluster identified above. Pairwise F_ST values based on microsatellite allele and control region haplotype frequencies were estimated following Weir and Cockerham (1984) , as implemented in Arlequin. Ten thousand random permutations were used to test significance, and α for each test was adjusted for multiple comparisons using the modified false discovery rate (FDR) method ( Benjamini and Yekutieli 2001 ).

We wished to quantify the spatial scale of IBD among desert bighorn sheep herds, while avoiding potential biases resulting from past translocations. Therefore, we identified native herds within our sample ( n = 23) as those with no history of translocation (i.e., according to Bleich et al. 1990 ; Cox and Cummings 2005 ). Geographic distances among native herd locations were calculated in ArcGIS (ESRI, Redlands, California), ln transformed, and converted to a matrix. We then estimated group genetic distances as F_ST /(1 − F_ST ) according to Slatkin (1995) for both microsatellite allele and control region haplotype frequencies in Arlequin. Correlations between genetic and geographic distances were determined using Mantel tests in the R package Ecodist ( Goslee and Urban 2007 ). To better visualize the scale over which genetic marker frequencies were spatially autocorrelated, we created Mantel correlograms using distance class sizes of 20 km and the Vegan package ( Oksanen et al. 2015 ). For all tests, correlations were determined using permutation tests with 1,000 randomizations.

Genetic diversity indices.

Indices of population genetic diversity were estimated for each genetic cluster identified above. We used Fisher’s exact test ( Guo and Thompson 1992 ) as implemented in Genepop 4.2 ( Rousset 2008 ) to test for departures from Hardy–Weinberg proportions and genotypic linkage equilibrium using 10,000 dememorization steps, 20 batches, and 5,000 iterations per batch. Test results were adjusted for multiple pairwise comparisons using FDR correction. Estimates of the number of alleles per locus ( N_A ), expected ( H_E ) and observed ( H_O ) heterozygosity, and the inbreeding coefficient ( F_IS ) were generated in GenAlex ( Peakall and Smouse 2012 ). Allelic richness ( A_r ) was calculated using the methods of Mousadik and Petit (1996) as implemented in the PopGenReport package ( Adamack and Gruber 2014 ) for R. The number of polymorphic sites, nucleotide diversity (π), number of haplotypes ( H_n ), and haplotype diversity ( H_d ) were calculated for mtDNA control region sequences using DNAsp 5.10 ( Librado and Rozas 2009 ).

Phylogeographic analyses.

We constructed a phylogenetic tree of unique haplotype sequences in MEGA 6 using the maximum likelihood (ML) algorithm, with support at the nodes calculated from 1,000 bootstrap replicates. Evolutionary distances (i.e., branch lengths) were computed under the Hasegawa–Kishino–Yano (HKY) model of nucleotide substitution ( Hasegawa et al. 1985 ), proportion of invariable sites, and gamma distribution shape (HKY+I+Γ model), as this was determined to be the best-fitting model according to the Bayesian information criteria (BIC) in MEGA 6. All positions containing alignment gaps and missing data were eliminated from the data set for tree construction (complete deletion option). We used the Snow sheep ( Ovis nivicola ; GenBank accession no. DQ249894) indigenous to Asia as the outgroup.

Phylogenetic relationships among haplotypes were also inferred using median-joining network analysis in Network 4.6.1.3 ( Bandelt et al. 1999 ). Within Network, we used the average number of mutations (rho) separating ancestral and descendent haplotypes ( Forster et al. 1996 ; Saillard et al. 2000 ) to estimate haplogroup ages within desert bighorn, as well as the time to most recent common ancestor (TMRCA) between desert bighorn and both the Sierra Nevada and Rocky Mountain lineages.

To estimate effective splitting times between subspecies, we modeled the demographic history of bighorn by coalescent simulation in IMa2 ( Hey 2010a , 2010b ). We computed estimates and associated 95% highest posterior density (HPD) intervals, in terms of mutational accumulation under the HKY mutation model. We estimated only “effective” splitting times (i.e., as if no postdivergence gene flow occurred), rather than testing models that incorporated gene flow, because of the large number of pairwise comparisons and computational time that would have been required. Therefore, if our assumptions regarding gene flow were incorrect, the resulting estimates would be conservative (i.e., erring toward more recent divergence). We performed replicate runs with different random number seeds for all comparisons to confirm consistency. Validity of results was evaluated based on unimodality of posterior distributions and their tendency to approach zero on both ends, stationarity of parameter estimates and model likelihoods, and the cumulative consistency of numerical estimates with one another and in relation to empirical estimates of net sequence divergence ( Nei and Li 1979 ), which provided an intuitive qualitative check on simulation results.

We also constructed Bayesian skyline plots to infer changes in population size through time for each desert subspecies using BEAST 1.8.2 ( Drummond et al. 2005 ; Drummond and Rambaut 2007 ). We used a HKY+Γ model of nucleotide substitution with default (constant) settings and 10 skyline groups. Because our focus was on the intraspecific (evolutionarily recent) divergence among bighorn, we assumed a strict clock throughout ( Brown and Yang 2011 ).

We translated mutation-scaled estimates of time into absolute estimates by multiplying by the expected number of years per mutation event. Previous estimates of mitochondrial mutation rates for Ovis spp. have varied due to different assumptions underlying the external calibrations. The divergence of bighorn sheep from other Ovis spp. was initially assumed to be 5.63 million years ago (My— Hiendleder et al. 1998 ), yet more recently was estimated to be as recent as 2.42 My ( Rezaei et al. 2010 ), resulting in a 2.33-fold difference in the mutation rate implied for mtDNA. Although we used the control region in this study, cytochrome b ( Cytb ) has been found to mutate close to 2% per million years (Ma) for a range of large-bodied terrestrial mammals, including bovids ( Nabholz et al. 2008 ). We reviewed the Cytb data available for Ovis spp. ( Bunch et al. 2006 ; Rezaei et al. 2010 ), which suggested the more recent calibration resulted in a rate close to the expected 2% per Ma. The corresponding mutation rate if recalibrated to the more ancient date would be < 1% per Ma, which we found unrealistic. Therefore, we adopted the more recent date and recalibrated the control region estimates from Hiendleder et al. (1998) . Specifically, we estimated the mutation rate and associated variance by averaging (and computing a confidence interval for) the 4 most recent Ovis nodes provided by Hiendleder et al. (2002 , n = 4 from table 2, therein). These calculations resulted in an estimate of 6.1%, 95% CI 4.2–7.9% per Ma. Our use of this more recent calibration resulted in more conservative (recent) divergence estimates. All estimates and confidence limits presented here can be recalibrated to the lower (less conservative) rate by multiplying by 2.33 (the ratio of the 2 external calibration points, 5.63Ma/2.42 Ma).

R esults

Population genetic structure.

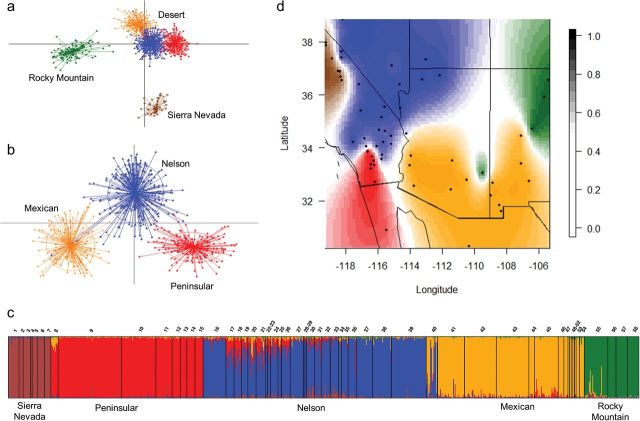
We obtained unique multilocus microsatellite genotypes for 804 individuals and observed agreement between 1,135 of the 1,170 single-locus genotypes analyzed twice, indicating a genotyping error rate of 3%. The diffNgroups option for the DAPC differentiated microsatellite genotypes into 5 genetic clusters ( K = 5) in 8 out of 10 runs. The scatterplot of individual genotypes using 4 discriminant functions indicated the Sierra Nevada and Rocky Mountain subspecies were highly discriminated from desert bighorn and one another, with strong separation visible along the first 2 principle component axes ( Fig. 2a ). The scatter plot also suggested the presence of hierarchical structure, with apparent substructure among desert bighorn. To further investigate this substructure, we conducted a 2nd DAPC using only desert bighorn genotypes ( n = 655). The 3 clusters identified in the 1st DAPC were well discriminated along both axes with no overlap of 95% inertia ellipses ( Fig. 2b ). The TESS analysis further supported the results of DAPC. Mean DIC values indicated K = 5 as the best clustering option for our data (i.e., piecewise change in function shape at this value; Supplementary Data ). Individual admixture proportions ( Fig. 2c ) for each cluster indicated clear geographic structure among Sierra Nevada and Rocky Mountain bighorn, as well as desert clusters concordant with the subspecies designations of Cowan (1940) , including 1) Peninsular bighorn from the Peninsular Ranges ( n = 288), 2) Nelson bighorn from the Transverse Ranges, Mojave Desert, southern Great Basin, and Colorado Plateau ( n = 180), and 3) Mexican bighorn from the Sonoran and Chihuahuan Deserts ( n = 187; Fig. 2d ).

Fig. 2.

a) Scatterplot of the first 2 principal components of the DAPC suggests microsatellite genotypes form 5 genetic clusters, as well as hierarchical structure among bighorn sheep ( Ovis canadensis ) within the study area. Each point represents 1 individual and ellipses around clusters represent 95% confidence. b) Scatterplot of the first 2 principal components of the DAPC used to identify genetic structure within desert bighorn only. c) Posterior estimates of individual admixture proportions among genetic clusters ( K = 5) as determined by TESS. Each bar represents an individual, and the height of the bar represents the relative probability of belonging to a given cluster. Sample locations are indicated above the chart, subspecies below. d) Sample locations overlaid with predictive boundaries for each genetic cluster identified by TESS. Boundaries are based on simple kriging of the posterior probability of cluster membership at each location.

Both TESS and DAPC indicated intermingled Nelson and Mexican bighorn genotypes associated with the northern Sonora Desert, north of the Bill Williams River in Arizona (i.e., location 40; Figs. 1 and 2 ). The TESS analysis also indicated low-level admixture between the Peninsular and Nelson genetic clusters in the southern Mojave Desert in California (locations 17–26; Fig. 2c ). Interestingly, admixture proportions indicated an absence of introgression between Sierra Nevada genotypes and desert bighorn immediately to the east. As expected, Rocky Mountain genotypes occurred at sites of known (re)introduction for this subspecies, both within (eastern Arizona) and adjacent to (northern New Mexico) the native range of desert bighorn sheep ( Figs. 2c and d ). Admixture proportions indicated introgression of desert bighorn into the Rocky Mountain population in eastern Arizona (location 55), with no evidence of the reverse in adjacent desert bighorn herds ( Fig. 2c ).

The AMOVAs produced results similar to the DAPC, indicating significant variance among Sierra Nevada, Rocky Mountain, and desert bighorn, with substructure apparent in the latter. For the AMOVA including all samples, outcomes were similar for both mtDNA and microsatellite data ( Table 1 ). Among-group variance was maximized at K = 3, with groups consisting of 1) Sierra Nevada, 2) Peninsular, Nelson, and Mexican, and 3) Rocky Mountain bighorn sheep—with significant ( P < 0.001) among-group fixation indices ( F_CT ) of 0.22 for mtDNA and 0.16 for microsatellites. However, significant F_CT estimates for the alternative formulations of population structure ( K = 4 pooling Peninsular and Nelson bighorn, and K = 5 considering each desert subspecies separately) suggested the presence of substructure. The desert bighorn only AMOVAs also supported the presence of substructure, with F_CT estimates significant ( P < 0.001) and of similar magnitude at K = 2 and K = 3 for microsatellite and mtDNA data sets ( Table 1 ).

Table 1.

Analysis of molecular variance results for different configurations of population genetic structure among 1) all bighorn samples and 2) desert bighorn samples only, using mtDNA and microsatellite data sets. The number of inferred genetic populations for each test is indicated by K . Letters (A–E) indicate membership of a subspecies to a genetic population under a specific test.

Subspecies	All samples						Desert samples
	mtDNA			Microsatellites			mtDNA		Microsatellites
	K = 3	K = 4	K = 5	K = 3	K = 4	K = 5	K = 2	K = 3	K = 2	K = 3
Sierra Nevada	A	A	A	A	A	A
Peninsular	B	B	B	B	B	B	B	B	B	B
Nelson	B	B	C	B	B	C	B	C	B	C
Mexican	B	C	D	B	C	D	C	D	C	D
Rocky Mountain	C	D	E	C	D	E
F CT a	0.22	0.15	0.16	0.16	0.12	0.13	0.11	0.08	0.06	0.08

^a All estimates were statistically significant at P < 0.001.

Pairwise F_ST estimates based on mtDNA data indicated significant differentiation among all clusters ( Table 2 ). We found the lowest estimates among the desert clusters (0.11–0.18), which is consistent with low discrimination as indicated by the DAPC scatterplot ( Fig. 2a ). Comparisons between the desert clusters and the Sierra Nevada (0.43–0.50) and Rocky Mountain subspecies (0.17–0.25) indicated higher genetic differentiation. This pattern was also reflected in the microsatellite data. Pairwise F_ST values among the desert clusters were lower (0.08–0.14; Table 2 ) than those comparisons to the Sierra Nevada (0.19–0.26) or Rocky Mountain (0.15–0.25) subspecies.

Table 2.

Pairwise F_ST estimates based on 39 microsatellite loci (below diagonal) and 515 base pairs of mtDNA control region sequence (above diagonal) for bighorn sheep ( Ovis canadensis ) genetic clusters, approximating subspecies. All estimates were statistically significant following false detection rate (FDR) correction.

Genetic cluster	Sierra Nevada	Peninsular	Nelson	Mexican	Rocky Mountain
Sierra Nevada		0.50	0.43	0.43	0.57
Peninsular	0.26		0.18	0.16	0.25
Nelson	0.19	0.09		0.11	0.19
Mexican	0.26	0.14	0.08		0.17
Rocky Mountain	0.33	0.25	0.15	0.20

The Mantel test based on microsatellite data found a strong positive correlation between ( ln ) geographic distance and genetic distance ( r = 0.51; P < 0.001; Supplementary Data ), while the Mantel correlogram suggested genotype frequencies were spatially autocorrelated, with significant positive r -values between 0 and 60 km. The Mantel test using mtDNA data resulted in a lower correlation between geographic and genetic distance ( r = 0.26; P = 0.034), and the correlogram indicated spatial autocorrelation in haplotype frequencies between 0 and 40 km.

Genetic diversity.

We observed substantial genetic diversity within each cluster identified ( Table 3 ), with all 39 microsatellite loci polymorphic in each cluster. Average allelic richness ranged from 2.7 to 8.2 and observed heterozygosity was generally high, ranging from 0.37 to 0.58. We observed statistically significant deviations from HWE in all clusters except for the Sierra Nevada subspecies, suggesting the presence of substructure in the remaining 4. This finding is not surprising given the spatial scale of our sampling, existing evidence of regional genetic structure among desert bighorn herds ( Epps et al. 2010 ; Buchalski et al. 2015 ), and our results for IBD tests.

Table 3.

Indices of genetic diversity (averages) for bighorn sheep ( Ovis canadensis ) genetic clusters, approximating subspecies, for both microsatellites (left) and mitochondrial DNA (right). The diversity indices used are as follows: A = alleles per locus; A_R = allelic richness; H_E = expected heterozygosity; H_O = observed heterozygosity; F_IS = inbreeding coefficient; H_n = number of haplotypes; H_{d =} haplotype diversity; π = nucleotide diversity.

Genetic cluster	Microsatellites						mtDNA
	N	A	A R	H E	H O	F IS	n	H n	H d	π
Sierra Nevada	52	2.4	2.7	0.39	0.37	0.03	47	1	0	0
Peninsular	187	4.7	4.9	0.54	0.50	0.09 a	175	10	0.76	0.0128
Nelson	288	8.4	8.2	0.68	0.53	0.21 a	279	30	0.87	0.0126
Mexican	180	6.2	6.3	0.60	0.53	0.13 a	170	25	0.91	0.0119
Rocky Mountain	97	6.4	6.8	0.64	0.58	0.10 a	87	10	0.73	0.0073

^a Deviation from Hardy–Weinberg equilibrium (homozygote excess) indicated by P ≤ 0.001.

Normalization of the control region sequence data required the removal of RS 2 from 36% of Rocky Mountain, < 1% of desert, and 0% of Sierra Nevada samples. Thus, RS 2 was relatively common in Rocky Mountain bighorn as compared to the other subspecies. Data normalization resulted in 515bp sequences with minimal missing data from 758 samples. Of the aligned nucleotide positions, 81 sites (16%) were variable and 70 sites (14%) were parsimony-informative. We discovered 74 distinct haplotypes, of which 24 were previously described in GenBank. We also identified 12 haplotypes in GenBank that were not present in our data and retained these for phylogenetic analyses. Accession numbers of all haplotypes analyzed are listed in Supplementary Data . Haplotypes were frequently restricted to a single location or had localized distributions limited to neighboring mountain ranges. The number of mtDNA haplotypes corresponding to each genetic cluster ranged from 1 to 25 ( Table 3 ). The Sierra Nevada sample exhibited only a single haplotype. Excluding this population, haplotype and nucleotide diversity were high ( H_d = 0.73–0.91, π = 0.0073–0.0128).

Phylogeographic analyses.

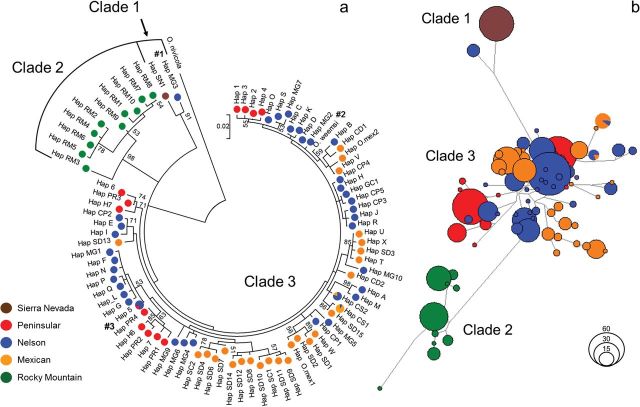
Phylogenetic inference by building a ML tree indicated the presence of 3 distinct clades, 2 of which exhibited bootstrap support > 90% ( Fig. 3a ). The 3 clades corresponded approximately to Sierra Nevada, Rocky Mountain, and desert bighorn and composed a polytomy indicating no support for any specific divergence pattern. The ML tree also represented desert bighorn as a polyphyletic group. Clade 1 consisted of the single Sierra Nevada haplotype and desert bighorn haplotype MG3 ( Fig. 3a , #1). Haplotype MG3 was found in 8 individuals from the Panamint Range and 1 individual from Eagle Crags, both in the northern Mojave Desert in California ( Fig. 1 ; Supplementary Data ). Clade 2 consisted of Rocky Mountain haplotypes, both from within the native range for that subspecies (i.e., Alberta and British Columbia) and (re)introduced populations in Arizona and New Mexico. Clade 3 was not well supported statistically, but represented the most basal portion of the tree and consisted entirely of desert bighorn. Within Clade 3, subclades were largely concordant with the desert subspecies designations of Cowan (1940) and only occasionally polyphyletic. Finally, the haplotype for Weems bighorn sheep obtained from GenBank did not cluster with haplotypes from Peninsular bighorn sheep ( Fig. 3a , #2), even though both are endemic to Baja California.

Fig. 3.

a) Rooted maximum likelihood tree based on 515 base pairs of the mtDNA control region illustrating 3 main bighorn sheep lineages. Branch lengths are scaled to evolutionary distances and bootstrap values > 50, based on 1,000 replicates, are shown next to the branches. Haplotype names correspond to those in Supplementary Data and colors to genetic clusters indicated in Figure 2 . #1—Desert haplotype representing ancient gene flow event or incomplete lineage sorting with Sierra Nevada bighorn. #2—Position of Weems bighorn haplotype obtained from GenBank. #3—For the purpose of illustration, frequencies for Hap 5 include the findings of Boyce et al. (1999) and Epps et al. (2010) , to depict all published evidence of haplotype sharing between Peninsular and Nelson bighorn. b) Unrooted median-joining network illustrating the 3 lineages. Branch lengths are proportional to the number of substitutions, and node sizes to the number of individuals represented.

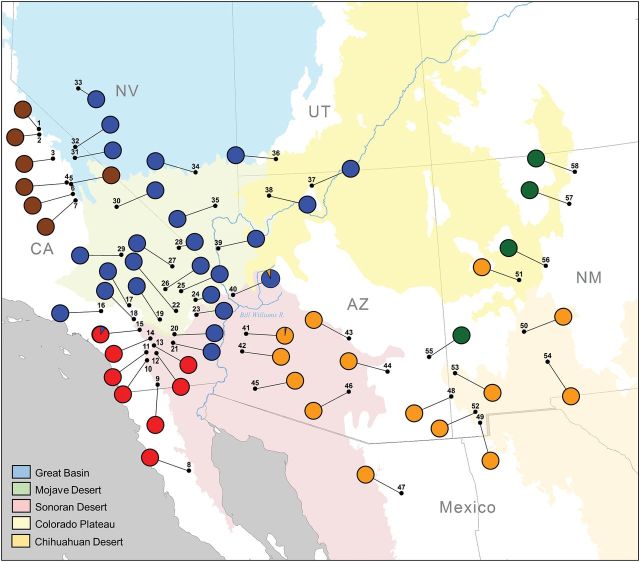
The unrooted, median-joining haplotype network also recognized 3 clades corresponding to Sierra Nevada, Rocky Mountain, and desert bighorn ( Fig. 3b ). We estimated TMRCA for the Rocky Mountain clade and desert bighorn at 680±130 kya, and the Sierra Nevada clade and desert bighorn at 640±120 kya. In addition, we estimated TMRCA between the single Sierra Nevada haplotype and haplotype MG3 at 150±60 kya. Within the desert clade ( Supplementary Data ), the network was sparse with a center consisting of several inferred but unsampled haplotypes. There was little haplotype sharing among subspecies, and the geographic areas where haplotype sharing was observed ( Fig. 4 ) coincided with zones of subspecies intergradation originally identified by Cowan (1940 : 574), including the northern Sonoran Desert (locations 40 and 41), as well as the northern Peninsular Ranges (location 15). The network also indicated several endemic haplogroups within the Peninsular and Mexican subspecies with ages predating the LGM—103 to 56 kya for Peninsular bighorn and 160 to 9 kya for Mexican bighorn sheep ( Supplementary Data ).

Fig. 4.

Geographic distribution of mtDNA control region haplogroups among sampled herds of Ovis canadensis subspecies, shown as pie diagrams. Locations are numbered as in Figure 1 . For the purpose of illustration, haplotype frequencies for the San Jacinto population (15) include our results and the findings of Boyce et al. (1999) , demonstrating a shared haplotype between the northern Peninsular Ranges and southern Mojave Desert.

The IMa2 analyses estimated pairwise effective splitting times for Sierra Nevada, Rocky Mountain, and desert bighorn at the mid- to late Pleistocene (315–94 kya), although our pairwise estimates were incomplete ( Table 4 ). Due to the presence of only a single haplotype in contemporary Sierra Nevada bighorn, and its close relationship to a desert bighorn haplotype, we did not estimate splitting times between these taxa ( Table 4 ). Pairwise estimates among desert bighorn were considerably more recent (9–6 kya) than those with Rocky Mountain bighorn, with the exception of the Peninsular and Mexican populations (122 kya). Further, splitting time estimates from IMa2 generally increased with net sequence divergence following a saturating curve ( Supplementary Data ), except for a single outlier representing the Mexican versus Penninsular bighorn comparison. One of the assumptions of IMa2 is that no intervening populations are missing from the analysis, which was clearly violated in this case and potentially responsible for the unreasonably high estimate. We therefore conducted a 3 population analysis in IMa2, which constrained the splitting times among these 3 populations to be tree like (rooted to O. nivicola as an outgroup). These results estimated that Mexican bighorn split from Nelson and Penninsular bighorn 17 kya (95% HPD: 37–3 kya) and that the latter 2 populations separated 3 kya (95% HPD: 8–0.5 kya). Because our analyses assumed no gene flow since divergence, the effect of any subsequent gene flow would be to render our splitting time estimates too recent. Therefore, these estimates were conservative, particularly for desert subspecies where historical gene flow was most likely.

Table 4.

IMa2 estimates of splitting times (× 1,000 years) based on control region sequences (above diagonal). The 95% highest posterior density of the estimates are indicated in parentheses. Average pairwise sequence divergence (Dxy) is indicated below the diagonal. Diagonal contains average sequence divergence within a taxon. Net sequence divergence (Da) is calculated by subtracting average within taxon sequence divergence from Dxy.

	Sierra Nevada	Peninsular	Nelson	Mexican	Rocky Mountain	Snow sheep
Sierra Nevada	0.0000				315 (114–532)
Peninsular	0.0370	0.0127	6 (0–17)	122 (59–190) a	273 (67–442)
Nelson	0.0350	0.0160	0.0141	9 (1–21)	94 (9–185)
Mexican	0.0370	0.0160	0.0150	0.0119	299 (116–484)
Rocky Mountain	0.0440	0.0360	0.0330	0.0370	0.0073
Snow sheep	0.0580	0.0640	0.0630	0.0610	0.0710

^a Inconsistency between the splitting time estimate and net sequence divergence.

Estimates of historical demography via Bayesian skyline plots suggested Nelson bighorn had the largest historical population size, followed by Mexican bighorn, with Peninsular bighorn having the smallest historical size ( Fig. 5 ). The Bayesian skyline plots were generally parallel for all 3 populations suggesting expansion during the Sangamon interglacial period, followed by large declines following the LGM. However, 95% highest posterior density intervals were insufficiently narrow to distinguish whether declines occurred during the late Pleistocene or Holocene ( Supplementary Data ). Population decline apparently began the earliest and was the most pronounced (~5×) in Nelson bighorn, whereas the Peninsular population appears to have declined more recently.

Fig. 5.

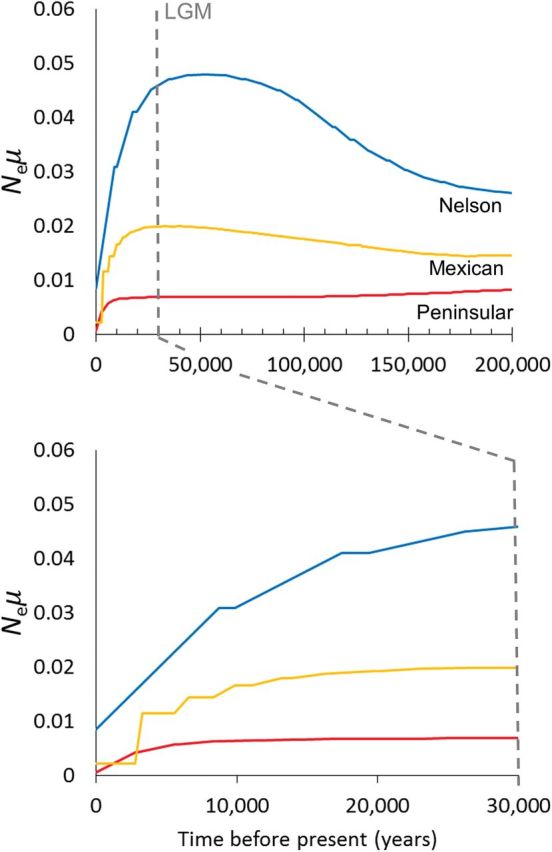
Estimated changes in size ( N_e μ) through time for 3 desert bighorn sheep populations based on Bayesian skyline reconstruction from mtDNA control region sequences. Plots illustrate recent declines in all populations ranging from the last glacial maximum (LGM) to the late Holocene (assuming 6.1% per Ma substitution rate). Estimates indicate that Nelson bighorn sheep, followed by Mexican bighorn sheep, had the historically largest population sizes, whereas Peninsular bighorn sheep had the smallest population which declined most recently.

D iscussion

Genetic divergence among Sierra Nevada, Rocky Mountain, and desert bighorn sheep.

This study provides the most extensive characterization to date of genetic differentiation and structure among bighorn populations in the desert southwest. Phylogenetic analyses of mtDNA identified 2 well-supported clades associated with Sierra Nevada and Rocky Mountain bighorn. Desert bighorn haplotypes were basal to these clades, but were shallowly differentiated from one another. Population genetic analyses were consistent with this phylogenetic structure. The DAPC showed strong discrimination among all 3 major lineages (i.e., the 2 clades and desert bighorn) and the AMOVAs indicated among-group variance was maximized at K = 3.

The deep divergence among geographically endemic bighorn clades implied long-term isolation ( Avise 2000 ). Rho estimates suggested that TMRCA of desert bighorn and both the Rocky Mountain and Sierra Nevada lineages dates prior to the Illinoian Glaciation. Further, our estimates of splitting times among these lineages suggest divergence during the late Pleistocene and appear comparable to other phylogenetic data for the subgenus Pachyceros (i.e., North American wild sheep, including O. canadensis and Dall sheep [ O. dalli ], as well as their Asian counterpart O. nivicola ). Loehr et al. (2006) estimated divergence between Nelson and Rocky Mountain bighorn at ~380 kya, which is generally consistent with our IMa2 estimates recalibrated to the 2.6% per Ma mutation rate (see “Materials and Methods”). Studies using Cytb and nuclear sequences estimated the divergence between O. nivicola and North American Pachyceriforms at 2.3–1.6 My, and the divergence between O. canadensis and O. dalli at 1.4–0.95 My ( Bunch et al. 2006 ; Rezaei et al. 2010 ).

Our divergence estimates help to further resolve the origins of desert bighorn, as well as colonization of the desert southwest. The fossil record indicates Ovis continuously inhabited the Mojave region since ~300 kya ( Jefferson 1991 ), as well as a more recent refugium located further north in Wyoming, with a fossil record of continuous Ovis presence since ~100 kya ( Martin and Gilbert 1978 ; Wang 1988 ). Our data suggest these refugia were the result of separate colonization events from a Beringian source predating the Illinoian glaciation (i.e., on the order of 300 kya) during periods when ice-free corridors between Laurentide and Cordilleran ice sheets were present. Such a deep divergence between the Wyoming and Mojave refugial populations elevates the evolutionary significance of their relationships to contemporary desert bighorn. The geochronology of fossils suggests that bighorn first expanded from Wyoming into Nevada (beginning ~18 kya) and progressively further south, followed by later expansions from the Mojave refugium (~12 kya), rendering the fossil record somewhat ambiguous with respect to the origins of contemporary desert bighorn ( Geist 1985 ). On the basis of phylogenetic positioning, our data clearly support a scenario where colonists from the Mojave refugium displaced the earlier northern colonists and strongly refute the possibility of northern colonists partially giving rise to contemporary desert bighorn.

Geist (1985) proposed that northern expansion from the Mojave refugium during the early Holocene (~12 kya) resulted in establishment of the Sierra Nevada subspecies (synonymous with California bighorn at the time of Geist’s writing). Based on our findings, this seems unlikely. Net sequence divergence between the single Sierra Nevada haplotype and all 3 desert subspecies (~2.3%) corresponds to an estimated splitting time of approximately 125 kya ( Supplementary Data ). Further, the Nelson bighorn haplotype that formed a clade with the single Sierra Nevada haplotype was sufficiently divergent to suggest the last contact between these 2 lineages predated the LGM (150±60 kya). The polyphyletic nature of desert bighorn relative to Sierra Nevada bighorn could reflect either secondary contact between the lineages or incomplete lineage sorting. Despite the possibility of ancient gene flow, we found no evidence of contemporary gene flow between desert and Sierra Nevada bighorn based on microsatellite genotypes. Given that the Sierra Nevada Range is separated from desert bighorn occupied ranges by as little as 10 km in some areas, this finding suggests the possibility of nongeographic behavioral barriers or other forms of reproductive isolation between these subspecies.

Genetic relationships within desert bighorn sheep.

Our results indicated the desert subspecies defined by Cowan (1940 ; excluding Weems bighorn sheep) diverged from one another more recently ( Fig. 3a ). Estimated splitting times based on the 3 population coalescent simulation suggested Mexican bighorn may have diverged as early as the late Pleistocene (37–3 kya), with the 2 other populations separating in the Holocene (8–0.5 kya). However, 2 observations suggest the possibility that splits among these subspecies could be considerably older. First, our assumption of no genetic exchange among desert subspecies since they diverged is conservative, and any actual gene flow would put estimates further back in time. Second, the haplotype network revealed several endemic haplogroups with ages significantly predating the LGM ( Supplementary Data ). For Peninsular bighorn, all but 1 of its 13 haplotypes occurred in 3 endemic haplogroups, estimated on average to reflect derivation from their ancestral haplotypes ~85 kya ( Fig. 3a ). Mexican bighorn also showed isolation from Nelson bighorn populations, as the majority of its 25 haplotypes occurred in endemic haplogroups dating to a similar timeframe (~72 kya). All shared haplotypes occurred in areas recognized by Cowan (1940) as zones of intergradation between desert subspecies (i.e., the northern Peninsular Ranges and the northern Sonora Desert in the vicinity of the Bill Williams River; Fig. 4 ). Regardless of whether these shared haplotypes reflected ancient shared ancestry or recent gene flow, the matrilineal diversity of Peninsular and Mexican bighorn was significantly divergent from the Nelson subspecies.

Both the Bayesian skyline plots and haplotype network suggested that modern desert bighorn reflect a small fragmented subset of a once massive population. The network was sparse, with a large number of missing intermediate haplotypes. The Bayesian skyline analyses also suggested a large ancestral desert bighorn population that expanded during the Sangamon interglacial, followed by demographic decline since the LGM. Ramey’s (1995) study using a much more slowly mutating mtDNA marker found a widespread desert haplotype, which sat at the center of a star-like phylogeny, consistent with a population expansion. Putting our findings and his findings together suggests an expansion across the southwest dating well before the Pleistocene–Holocene boundary as proposed by Geist (1985) . Based on the estimated ages for several of the endemic desert haplogroups, we suggest Ovis persisted in multiple southern refugia during the LGM, as originally proposed by Ramey (1995) , rather than a single Mojave refugium. Following deglaciation, changes in the distribution of habitat may have allowed for secondary contact among these populations, resulting in the more recent splitting time estimates we observed. Ultimately, all refugial populations experienced fragmentation and demographic decline during the Holocene.

Analyses of population genetic structure based on microsatellite and mtDNA also supported significant differentiation among desert subspecies. Both the DAPC and TESS analyses indicated genetic clustering concordant with Cowan’s subspecies distributions. Likewise, AMOVA among desert subspecies produced significant fixation index estimates among groups ( F_CT ), regardless of the underlying model of population structure. Microsatellite and mitochondrial DNA-based F_ST comparisons among the desert bighorn genetic clusters were statistically significant and indicated that desert bighorn do not form a single genetic population.

The TESS analysis indicated low-level admixture between the Peninsular and Nelson subspecies in the southern Mojave Desert (locations 17–26; Fig. 2c ). This pattern of admixture was inconsistent with clinal variation indicative of an active contact zone ( Durand et al. 2009 ), but rather appears to represent relict gene flow between the 2 lineages. We interpret this as evidence of secondary contact following postglacial expansion of the Peninsular and Nelson refugial populations. However, the degraded nature of the contact (i.e., low-level admixture versus a clinal transition) suggests a subsequent disruption of gene flow, possibly by contemporary anthropogenic barriers or range contraction of the Peninsular population during the last century. Quite importantly, the geographic location of these admixed genotypes matches the findings of previous morphometric analyses. Wehausen and Ramey (1993) used univariate and PC analyses to demonstrate major overlap in skull morphology characters between Peninsular and southern Mojave herds, both of which differed significantly from herds in the northern Mojave and Great Basin. This overlap was used to justify synonymizing Peninsular bighorn ( O. c. cremnobates ) with Nelson bighorn ( O. c. nelsoni ). Our genetic data suggest these morphological similarities may actually be the result of a relatively recent (i.e., Holocene) contact between the lineages. Further, TESS analyses showed no evidence of clinal variation between Nelson and Mexican bighorn, but rather intermingled genotypes in the northern Sonora Desert (i.e., location 40; Fig. 2 ). These findings suggest the Nelson and Mexican lineages may have only recently come into contact in eastern Arizona, possibly as a result of successful recovery and expansion. Additional sampling at a finer spatial scale would be necessary to precisely delineate the boundary between these 2 populations.

Mantel test and correlogram results indicated IBD was also a source of genetic structure among bighorn herds within desert subspecies. Lower correlation between genetic and geographic distances and the smaller spatial scale of genetic autocorrelation for the mtDNA relative to the nuclear markers was consistent with ewe philopatry ( Krausman et al. 1999 ). This pattern of IBD indicates dispersal is negatively correlated with geographic distance between neighboring habitat patches (i.e., mountain ranges), reaching an asymptote at a distance beyond which dispersal is unlikely to occur (> 60 km). These findings agree with previous landscape genetics models for bighorn in the Mojave Desert that estimated the maximum effective dispersal distance of rams at 16.4 km-cost-units (corresponding to 16.4 km of flat terrain or 164 km of sloped terrain— Epps et al. 2007 ) and ewes at 10.0 km-cost-units ( Creech et al. 2014 ). The scale of spatial autocorrelation we observed is reasonable for each marker type, considering that the distance between our sampling locations often covered both flat and mountainous terrain. Our results provide additional support for metapopulation structure in desert bighorn ( Bleich et al. 1996 ), with genetic connectivity among mountain ranges occurring via a stepping-stone model of gene flow.

Genetic diversity of bighorn sheep populations.

Using the numerically largest and geographically broadest set of desert bighorn sheep samples analyzed to date, we found substantial genetic diversity throughout the native range. Observed heterozygosity and allelic richness were comparable or higher than other studies ( Gutierrez-Espeleta et al. 2001 ; Epps et al. 2005 , 2006 ; Buchalski et al. 2015 ) and suggest desert bighorn retained substantial range-wide genetic diversity despite demographic declines and loss of population connectivity. The federally endangered Sierra Nevada population had low genetic diversity, consistent with recent bottlenecks and small size. Low allelic richness and expected heterozygosity were comparable to the finding of Johnson et al. (2011) , while mtDNA haplotype diversity (the presence of a single haplotype) had not previously been published for this population. Genetic diversity indices for the San Gabriel population in the Transverse Ranges ( Fig. 1 , location 16; A_R = 3.3, H_E = 0.40, H_d = 0) were considerably lower than averages for Nelson bighorn ( A_R = 8.2, H_E = 0.68, H_d = 0.87) and were comparable to the Sierra Nevada population. Highway infrastructure associated with Los Angeles separates the San Gabriel population from others within the Transverse Ranges, suggesting that this population is largely isolated and may continue to lose genetic diversity via drift. Additional sampling to better characterize genetic diversity is necessary to fully evaluate the status of this population.

Conservation of desert bighorn sheep genetic diversity.

In this study, we provide evidence of genetic structure highly concordant with the desert subspecies proposed by Cowan (1940) . However, full characterization of the phylogenetic history of desert bighorn would require additional analyses utilizing more conserved regions of the mitochondrial genome and potentially nuclear sequence data to more accurately estimate divergence dates. Ultimately, conflicts between subspecies designations based on morphological versus genetic data may prove difficult to resolve and are somewhat peripheral to the more practical challenge of identifying and conserving important biological diversity.

The 3 desert bighorn sheep lineages identified in this study occupy desert biomes that vary significantly in climate ( Laity 2009 ), suggesting exposure to different selection regimes. Hence, local adaptation is expected to have shaped some of the genomic diversity among desert bighorn sheep. Functional differences among herds have been documented, which are assumed to have a genetic basis—including horn size and lambing period ( Wehausen 1991 , 2005 ). Identifying conservation units that recognize adaptive differences may prove essential for continued recovery, especially in response to increasing threats from disease outbreak and prolonged drought resulting from climate change. For example, evolutionary significant units (ESUs) place an emphasis on adaptive variation and evolutionary potential ( Ryder 1986 ; Waples 1991 ; Moritz 1994 ; Crandall et al. 2000 ), with precedence for granting ESUs legal protection under the Endangered Species Act. We recommend the delineation of conservation units be guided by a landscape genomics approach (sensu— Funk et al. 2012 ), utilizing neutral loci and loci under selection to characterize adaptive differences among herds.

Translocations and reintroductions have been critical in helping bighorn sheep populations recover across western North America ( Krausman 2000 ). While largely conducted to increase abundance and distribution, successful genetic management of bighorn sheep may also require translocations that increase heterozygosity and facilitate genetic rescue. Reintroduced herds typically have low genetic diversity resulting from founder events and subsequent drift ( Hedrick et al. 2001 ; Whittaker et al. 2004 ; Hedrick 2014 ). While herd supplementation with unrelated animals can result in genetic rescue, both in terms of increased genetic diversity and higher fitness among hybrids ( Hogg et al. 2006 ; Miller et al. 2012 ; Olson et al. 2012 ), outbreeding depression can also occur in crosses between populations within a species (i.e., between subspecies— Edmands 2007 ). Our data indicate desert subspecies became isolated during the LGM, or potentially earlier, in some cases with minimal secondary contact. For this reason, we feel translocations among Peninsular, Nelson, and Mexican bighorn are not advised. Our data suggest the maintenance of viable levels of genetic diversity should be attainable through translocations among herds within each of the 3 desert lineages. Whenever genetic rescue is contemplated, guidelines such as those proposed by Hedrick and Fredrickson (2010) should be consulted to evaluate the costs and benefits. In the absence of adequate data, managers should adopt the “local is best” translocation strategy, as proposed by Ramey (1995) , as the most reliable means for preserving local adaptation.

S upporting I nformation

The Supporting Information documents are linked to this manuscript and are available at Journal of Mammalogy online ( Supplementary Data ). The materials consist of data provided by the author that are published to benefit the reader. The posted materials are not copyedited. The contents of all supporting data are the sole responsibility of the authors. Questions or messages regarding errors should be addressed to the author.

Supplementary Data .—Bighorn sheep ( Ovis canadensis ) samples used in this study organized by location.

Supplementary Data .—Methods and rationale for alignment of mtDNA control region sequences.

Supplementary Data .—(a) Spline interpolation of the optimal a-score (i.e., proportion of successful reassignments corrected for the number of retained PCs from the DAPC. (b) Mean values of the DIC, averaged over 10 runs, estimated by TESS for models with the number of genetic clusters ( K ) ranging from 2 to 10. Dashed lines were inserted to indicate a piecewise change in the function at K = 5. (c) Bayesian information criteria (BIC) for different numbers of genetic clusters. The chosen number of clusters ( K = 5), based on 8 out of 10 independent runs of the diffNgroups algorithm in the package adegenet, is the minimum number after which the decrease in BIC becomes negligible.

Supplementary Data .—Results of isolation-by-distance (IBD) tests among native herds ( n = 23) of desert bighorn sheep. Graphs are shown for microsatellites (top row) and mtDNA haplotypes (bottom row). Scatter plots of genetic distance ( F_ST /(1 − F_ST ) plotted against ln geographic distance (left) and Mantel correlograms illustrating the scale of spatial autocorrelation in allele/haplotype frequencies (right). For correlograms, closed squares indicate a significant Mantel correlation coefficient based on 1,000 permutations.

Supplementary Data .—Unrooted median-joining network illustrating the phylogenetic relationships of mtDNA haplotypes within desert bighorn sheep. Haplotype names correspond to those in Supplementary Data and colors to genetic clusters indicated in Fig. 2 . Node sizes scale to indicate the number of individuals within each haplotype. Shaded areas denote distinct haplogroups and dates represent estimated haplogroup ages (rho ± SD ). For the purpose of illustration, frequencies for haplotype 5 include our results and the findings of Boyce et al. (1999) and Epps et al. (2010) , to depict all published evidence of haplotype sharing between Peninsular and Nelson bighorn.

Supplementary Data .—Relationship between pairwise net sequence divergence (Da) and IMa2 estimates of divergence (in years before present), illustrating the outlier estimate for Peninsular versus Mexican bighorn (open circle).

Supplementary Data .—Bayesian skyline plots generated from mtDNA control region sequences showing the historical demographic trends of Nelson (a), Mexican (b), and Peninsular (c) bighorn sheep in the desert southwest (assuming 6.1% per Ma substitution rate). The black line is the median size ( N_e μ) estimate, and the gray lines represent the upper and lower 95% highest posterior density interval.