Irrigation as a Potential Driver for Anomalous Glacier Behavior in High Mountain Asia

Abstract

Many glaciers in the northwest of High Mountain Asia (HMA) show an almost zero or positive mass balance, despite the global trend of melting glaciers. This phenomenon is often referred to as the “Karakoram anomaly,” although strongest positive mass balances can be found in the Kunlun Shan mountain range, northeast of the Karakoram. Using a regional climate model, in combination with a moisture‐tracking model, we show that the increase in irrigation intensity in the lowlands surrounding HMA, particularly in the Tarim basin, can locally counter the effects of global warming on glaciers in Kunlun Shan, and parts of Pamir and northern Tibet, through an increase in summer snowfall and decrease in net radiance. Irrigation can thus affect the regional climate in a way that favors glacier growth, and future projections of glacier melt, which may impact millions of inhabitants surrounding HMA, will need to take into account predicted changes in irrigation intensity.

Key Points

• We test whether irrigation in South Asia can explain the growth of glaciers in High Mountain Asia

• Intensifying irrigation in South Asia causes an increase in summer snowfall and decrease in net radiation over Kunlun Shan, Pamir, and Tibet

• The source of the increase in snowfall over Kunlun Shan lies in the irrigated areas in the Tarim basin

1. Introduction

Meltwater from snow and glaciers in High Mountain Asia (HMA) provides a major source of water for millions of inhabitants in the downstream low lying plains. For the future livelihood of these people, it is therefore important to understand how the glaciers in HMA will respond to global warming (Immerzeel et al., 2010; Kaser et al., 2010; Lutz et al., 2014). Like many glaciers worldwide, the glaciers in HMA have generally been losing mass over the past decades, but a subset of glaciers in the region have been stable or even growing. This peculiar behavior, often called the “Karakoram anomaly” (Hewitt, 2005), has been demonstrated in the Karakoram and Pamir mountains in northwest HMA (Bolch et al., 2012, 2017; Gardelle et al., 2013; Zhou et al., 2017). Recent work shows even more positive mass balances toward the northeast of the Karakoram, in the Kunlun Shan region, as well as very negative mass balances in Spiti Lahaul, just south of the Karakoram (Brun et al., 2017; Gardelle et al., 2013, 2012; Kääb et al., 2015; Lin et al., 2017). Although these three regions are relatively close geographically, their glaciers clearly behave very differently, which suggests that either the glaciers themselves respond inherently different to a similar climatic change (Scherler et al., 2011) or that the climatic change is different on a smaller scale than that of the synoptic weather patterns (e.g., those that have previously been invoked to explain the Karakoram anomaly (Forsythe et al., 2017; Kapnick et al., 2014). In this study, we evaluate the latter scenario and we hypothesize that increases of irrigation in the regions surrounding HMA surrounding may alter the regional climate in favor of glacier growth.

The lowlands surrounding HMA host some of the largest, most intensely irrigated areas in the world. Studies with global and regional circulation models show that irrigation can regionally have a cooling and wetting effect, caused by the increase of evapotranspiration (Boucher et al., 2004; Kueppers et al., 2007; Puma & Cook, 2010; Sacks et al., 2009; Tuinenburg et al., 2014). These effects can also influence the larger scale circulation, for example, by decreasing the temperature contrasts between land and ocean (Douglas et al., 2009; Lee et al., 2011). The amount of water used for irrigation in South and East Asia has steadily increased over the last half century (Cook et al., 2015; Lobell et al., 2008; Puma & Cook, 2010; Wada et al., 2014), and hence, it might be expected that there is an increase in evapotranspiration in the region, associated with near‐surface cooling and an increase in atmospheric moisture.

We used the regional climate model WRF (Skamarock & Klemp, 2008) to establish whether the irrigation intensification influences mountain climate in HMA in ways that favors glacier growth. The glacier mass balance is the resultant of accumulation and ablation. Snowfall is the most important accumulation component and because of its high albedo it also reduces the net shortwave radiation that could be used for melting. The total energy balance largely controls glacier ablation and changes in net radiation particularly directly impact the glacier mass balance (Brock et al., 2010; Reid & Brock, 2010). Sensible and latent heat fluxes also contribute to the energy balance of glaciers, but are generally smaller terms (Collier et al., 2013; Zhu et al., 2017), and are more difficult to assess using a regional atmospheric model in which the glaciers are not explicitly modeled. Hence, we focus specifically on modeled changes in net radiation, that is, the sum of the incoming and (negative) outgoing shortwave and longwave radiation at the surface, near‐surface air temperature and snowfall as a result of intensified irrigation.

2. Methods

2.1. WRF Modeling

We apply the WRF model (Skamarock & Klemp, 2008) using a single domain, spanning roughly 12–46°N and 60–100°E, consisting of a 200 × 200 grid with a resolution of 20 × 20 km, and 50 vertical layers up to 50 hPa. Settings are almost identical to those of previous work (Collier & Immerzeel, 2015) (see supporting information for details). The irrigation was represented as a continuous light rain that was added to the surface, with the amounts described below. We forced WRF with different irrigation patterns and intensities and different levels of greenhouse gas (GHG) concentrations, yet identical boundary conditions, and assess the corresponding difference in model outcomes. We have performed runs with increases of both irrigation and GHG concentrations, as well as increases in only irrigation or GHG to separate the two effects. We simulated 7 years, from 1 October 2009 to 1 October 2016, using boundary and initial conditions from ERA‐INTERIM (Dee et al., 2011). These multiple years were used to obtain a reasonable sample of the interannual variability to be able to assess the significance of our results and to increase the significance for systematic patterns. Note that it was not our goal to model these specific years as accurately as possible but to show the effects of irrigation using identical external forcing. We found that some important surface quantities from the standard ERA‐INTERIM initialization contained large and obvious artifacts with unrealistic values, so we used GLDAS (Rodell et al., 2004) monthly mean values to initialize soil moisture, soil temperatures, and skin temperatures. We initialized and ran summer (kharif) periods (May–September) and winter (rabi) periods (October–April) separately, with separate irrigation patterns and without the use of nudging. Snow heights over Karakoram are known to be overestimated when WRF is initialized by ERA‐INTERIM (Collier & Immerzeel, 2015). We checked this and with our initializations in spring and autumn, Karakoram snow heights are not as extreme (roughly 5 m at most). Since we are looking at differences between model runs with identical initial conditions, we did not apply a correction for the snow height. To initiate the atmosphere, we applied a 10 day spin‐up period for each season, which was disregarded in the further analysis.

We focus here on two cases: the ΔHIST case, which represents the difference between WRF runs that have modern‐day irrigation and GHG gas concentrations and runs with no irrigation and GHG concentrations from the period around 1900, and the ΔDEC case, which represents the recent change (2000–2010) in irrigation patterns and intensities and a decade increase in GHG concentrations. We changed both the irrigation amount and the GHG concentrations simultaneously to more realistically simulate climatic changes and to assess whether the effect of irrigation is significant compared to the increasing greenhouse effect. Separate tests, where either the irrigation amounts or the GHG concentrations are changed, are also performed to see which effect is more dominant. For the ΔDEC case, we increased the concentrations of CO₂ by 20 ppm, CH₄ by 80 ppb, and N₂O by 8 ppb to represent a decade of increase in GHG concentrations. For the ΔHIST case we used concentrations of CO₂ of 300 ppm, CH₄ of 800 ppb, and N₂O of 280 ppb for the concentrations around the year 1900. Except the irrigation amounts, we used identical boundary conditions for all ΔHIST and ΔDEC simulations, so our approach allows us to directly assess the impact of irrigation and GHG changes at the synoptic scale within the domain considered.

We performed short tests with different cumulus schemes and different integration times and, although there were significant differences (e.g., in rainfall intensity over India), the changes between two runs with the same settings, but with different irrigation scenarios, were qualitatively very similar over HMA. We performed further tests at a 4 × 4 km resolution without any cumulus parameterization to assess the effect of the smoothed orography and the cumulus scheme. This domain was centered around Karakoram, spanning roughly 32.5–39°N and 71–80°N, and was forced at the boundaries by the results of the 20 × 20 km domain. These higher‐resolution results were very similar to the results presented above when averaged over larger regions, both qualitatively and quantitatively, and are therefore not presented in this paper.

2.2. Irrigation Patterns

The amount of irrigation applied to the summer and winter periods for the years 2000 and 2010 was derived from the hydrological model PCR‐GLOBWB (van Beek & Bierkens, 2008). Monthly irrigation demands were calculated as in previous work (van Beek et al., 2011; Wada et al., 2011), on a 0.5° × 0.5° grid but updated to include the years 1970–2010 (Van der Esch et al., 2017; Wada et al., 2014). For each grid point, we determined the month with the largest demand for each year in the period 2000–2010 and fitted a linear trend for these months. The intersections of this line with the years 2000 and 2010 were taken as our monthly irrigation gift for each 0.5° × 0.5° grid point. In practice, this means that in months of low demand, the irrigation gift can be larger than the evapotranspiration, but in extreme years and months, the irrigation gift is smaller than the evapotranspiration.

The irrigation pattern applied in WRF is based on the high‐resolution map of area equipped for irrigation around 2005 (Siebert et al., 2010), interpolated to the 20 × 20 km WRF. For each 0.5° × 0.5° area, we multiply this pattern by an irrigation rate, such that the total monthly water gift matches the monthly demand in that area from PCR‐GLOBWB. The resulting maps are shown in the supporting information. During the period 2000–2010, the largest increases in irrigation extend and intensity can be found in Myanmar, the Tarim basin, Northern India, and the lower Indus basin.

We assumed the percentage of the WRF grid classified as irrigated cropland to equal the percentage of land equipped with irrigation and scale the default values of other WRF land use classifications such that the total of land use percentages per grid cell adds up to 100%. For the zero‐irrigation scenario, we replaced the irrigated cropland with mixed grass/shrubland in WRF.

2.3. Significance Testing

We assess the significance of our results by applying a Wilcoxon signed‐rank test (Wilcoxon, 1945), which tests whether the difference between two paired sets of data is symmetric around zero for generically distributed data. For many of the variables such a test is appropriate in our case, since we apply identical external forcing to WRF, and hence, the variable values between two different irrigation scenarios are highly correlated. However, for snowfall, timing offsets for large discrete events can cause large differences in individual time steps, whereas the total snowfall (distribution) is similar. Hence, we also apply a Mann‐Whitney U test (Mann & Whitney, 1947) for snowfall, which considers the two distributions as a whole. Furthermore, in all cases where we test bins or regions, we also apply a field significance criterion (Wilks, 2016) to control the rate of false positives due to multiple hypothesis testing. This criterion requires the P value of the Wilcoxon or Mann‐ Whitney U test for a single point, sorted by P value, to be smaller than α _FDR⋅i/N, where N is the total number of points tested, and i the P value rank. We take α _FDR to be 0.02 (twice the threshold value for the individual points (Wilks, 2016)) for our presented results.

For binning per mountain region, we consider only grid points whose centers lie within 10 km of a glacier that is larger than 2 km² in size, according to the Randolph Glacier Inventory 5.0 (Pfeffer et al., 2014).

2.4. Atmospheric Moisture Tracking

We used a water trajectory model (Dirmeyer & Brubaker, 1999, 2007; Tuinenburg et al., 2012) that tracks parcels of moisture to estimate atmospheric moisture transport and source evaporation locations of snowfall in Kunlun Shan. A moisture parcel is released four times every modeled hour at a random location within each considered WRF grid cell in Kunlun Shan, at a random height. The method assumes that the vertical snowfall distribution is proportional to the vertical water vapor distribution, and hence, a parcel has a larger chance to be released lower in the atmosphere, where specific humidity is generally larger. The parcel is advected backward in time using linear interpolation of the three‐dimensional WRF wind field, which is updated every 0.25 h time step. During every time step in this trajectory, we assume that surface evapotranspiration contributes to the specific humidity in the atmospheric column at a rate proportional to the total amount of precipitable water in the atmospheric column. Therefore, the amount of evaporation A (mm), at a given location x,y and time step t, that contributes to the snow in the target location can be described by

$$A_{x,y,t}={\mathrm{ET}}_{x,y,t}\frac{W_{\text{parcel},t}{S}_{\text{target},t}}{{\mathrm{TPW}}_{x,y,t}},$$ (1)

where ET is WRF evapotranspiration in mm, W _parcel is the amount of water in the tracked parcel in mm, S _target the fraction of water in the parcel that evaporated from the source, and TPW is the WRF total precipitable water in the atmospheric column in mm. Every time step, the amount of water in the parcel is updated based on WRF precipitation (rainfall and snowfall) P that is added the parcel, and WRF evapotranspiration removed from the parcel:

$$W_{\text{parcel},t-1}=W_{\text{parcel},t}+\left(P_{x,y,t-1}-{\mathrm{ET}}_{x,y,t-1}\right)\frac{W_{\text{parcel},t}}{{\mathrm{TPW}}_{x,y,t-1}}$$ (2)

The fraction of water in the parcel that has snowed out over a Kunlun Shan grid cell is then updated as

$$S_{\text{target},t-1}=\frac{S_{\text{target},t}{W}_{\text{parcel},t}-A_{x,y,t-1}}{W_{\text{parcel},t-1}}$$ (3)

We track the decreasing amount of water from Kunlun Shan until either less than 1% of its original amount was left in the atmosphere, the tracking time was more than 30 days, or it leaves the WRF domain. This procedure was repeated for each moisture parcel, and the resulting S _target maps were averaged over the seven model summers.

3. Results

The most obvious effect of intensified irrigation is the strong rise in evapotranspiration, and the associated decrease in daytime summer surface temperature and increase in atmospheric moisture over the heavily irrigated areas (Figures 1 and S3), which is consistent with previous work (Cook et al., 2015; Douglas et al., 2009; Kueppers et al., 2007; Lee et al., 2011; Puma & Cook, 2010; Sacks et al., 2009). The regions with a high irrigation demand show a very strong increase in net radiation (Figure 2b for the ΔHIST case), which is dominated by the longwave radiation and is related to the large increase in atmospheric moisture and decrease in surface temperature (Figures 1 and S3). Since we focus on HMA, the results for the regions surrounding HMA are not discussed in detail here.

Figure 1.

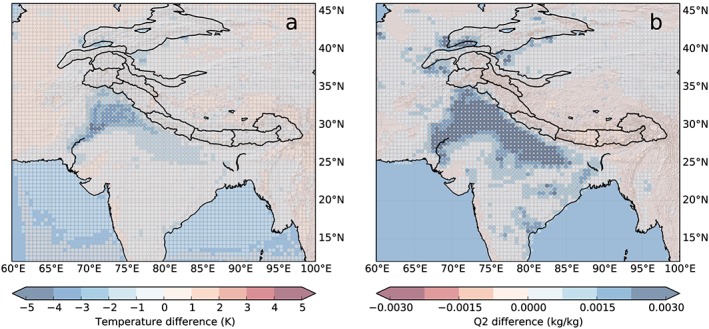
Summer daytime T_2m differences (a) and summer water vapor mass mixing ratio at 2 m differences for the ΔHIST case (b). Only 0.5° × 0.5° bins are shown where P < 0.01, including field significance, and where temperature differences are larger than 0.1 K.

Figure 2.

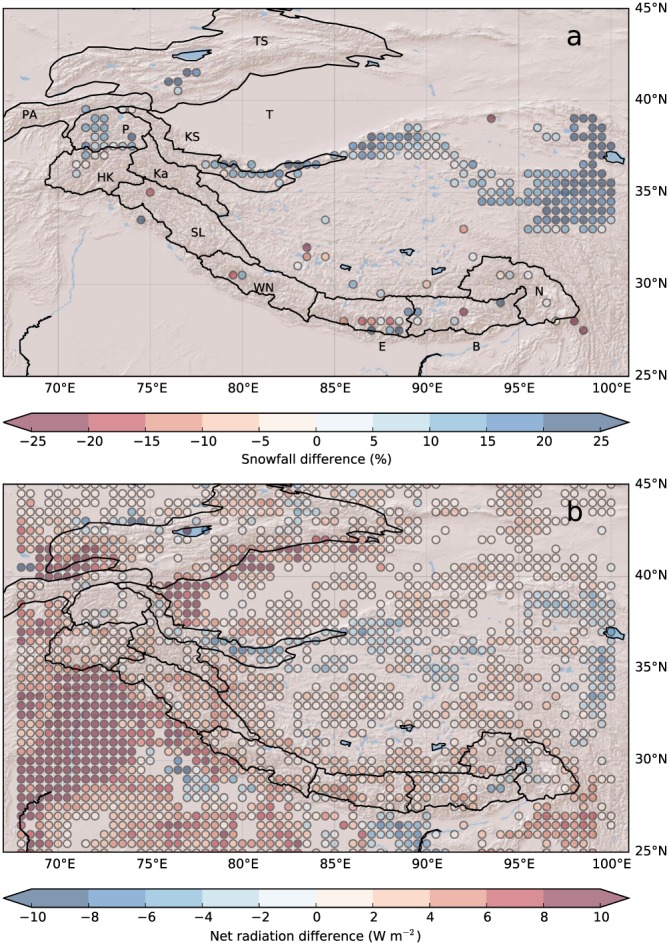
Changes in summer snowfall (a) and summer net radiation (b) for the ΔHIST case. Data are averaged in 0.5 × 0.5° bins, and only differences with low P values (P < 0.01, including field significance) are plotted. Mountain ranges and the Tarim basin are indicated (TS = Tien Shan; PA = Pamir Alay; P = Pamir; KS = Kunlun Shan; Ka = Karakoram; HK = Hindu Kush; SL = Spiti Lahaul; WN = West Nepal; E = Everest; B = Bhutan; N = Nyaingentangla; T = Tarim).

For most regions in HMA, the invoked changes in irrigation cause a relatively small shift in the location of snow events. Especially in winter, where much of the snowfall occurs in relatively few events (so‐called westerly disturbances (Dimri et al., 2015)), the differences in snowfall for the different irrigation cases show very high variability in both space and time. This is most apparent for the ranges that face the plains on the west and southwest of HMA (e.g., Spiti Lahaul and West Nepal), whose snowfall distributions are more tilted toward larger events than the mountain ranges downwind of the prevailing westerlies (e.g., Karakoram). Relatively large and significant increases in summer snowfall due to irrigation are apparent for Kunlun Shan, Pamir, and northeast Tibet. The increase is largest for the ΔHIST case, where results are significant even on a small scale (see Figure 2a). Note that care must be taken when interpreting the eastern edge of the Tibetan Plateau, since the model domain boundary is located there. When aggregated over all glaciarized grid points in the region, the increase in summer snow fall is 11% for Kunlun Shan and 9% for Pamir. The increase in absolute snowfall in Kunlun Shan is roughly twice that of Pamir, and the total precipitation increase is roughly three times that of Pamir (see Figure S6). Tests that change only the GHG concentration and only the irrigation amount show that irrigation is the main driver of these changes (see Figure S4). For the ΔDEC case, the summer snowfall shows a weaker, but qualitatively identical behavior for Kunlun Shan and Pamir, and the increase in summer snowfall is highly significant (P ≪ 0.01) when aggregated over the region, with a mean increase of summer snowfall of 2 and 5%, respectively. The large variability prevented us from obtaining statistically robust results on snowfall for the rest of HMA and for winter.

Kunlun Shan and northern Tibet also stand out as a region of decreasing summer net radiation in the ΔHIST case, despite a large increase in greenhouse effect (see Figure 2b). This is in stark contrast to the rest of HMA, which shows an overall increase in net radiation. The decrease in net radiation in Kunlun Shan is caused by both a decrease in incoming shortwave radiation due to increased cloud cover (see Figure S5), as well as an increasing albedo as a result of the additional snowfall. This negative net shortwave radiation (an average of −7.3 W m⁻² over glaciarized grid points) counters an increase in the modeled net longwave radiation (+4.7 W m⁻²) in Kunlun Shan. In contrast, when only GHG concentrations are increased to modern levels in a zero‐irrigation scenario, there is a relatively uniform increase in net radiation of +0.5–1.0 W m⁻² for the entire HMA, showing that the irrigation is the main driver for this negative net radiation in Kunlun Shan (see Figure S4). Spiti Lahaul and the southwestern tip of Karakoram show the largest increase in net radiation in the ΔHIST case, with both shortwave and longwave radiation contributing to the positive difference and with a mean increase of +1.8 W m⁻² for Spiti Lahaul and +1.1 W m⁻² for Karakoram. For the ΔDEC case, the effect is again smaller but qualitatively very similar, with a mean decrease of −0.9 W m⁻² for glaciarized grid points in Kunlun Shan and an increase of +1.0 and +0.4 W m⁻² for Karakoram and Spiti Lahaul, respectively. Pamir also has an average decrease in net radiation of −0.6 and −0.7 W m⁻² for the ΔHIST and ΔDEC cases, respectively.

Irrigation generally has a slight cooling effect over the entire HMA in summer, with Kunlun Shan showing the largest cooling of T_2m of −0.3 K for the ΔHIST case (see Figure 1). For the ΔDEC case mean changes in T_2m are less than 0.05 K over glaciarized areas. The increase in irrigation also causes changes to the large‐scale circulation by lowering the geopotential height and increasing cyclonic motion over northwest HMA (see Figure S7), although the lack of feedback with the circulation outside our limited domain means that exact positions of the cyclones are likely associated with a relatively large error.

We applied a backward moisture tracking model on our WRF output to further test our hypothesis that an increase in irrigation causes the increase in summer snowfall in Kunlun Shan and identify specific source regions. Results show that most moisture for summer snowfall in Kunlun Shan originates from the Tarim basin and its surrounding mountains (Figure 3a). For reference, roughly 2.5% of the moisture originates from the irrigated Yarkant region, roughly centered around 38.5°N, 77.5°E. Figures 3b and 3c also show that the additional Kunlun Shan snowfall in the ΔHIST and ΔDEC cases originates almost exclusively from the increased irrigation in the Tarim agricultural areas. Hence, there is a direct link between the intensifying irrigation in the Tarim agricultural areas, and the increase in summer snowfall in Kunlun Shan. Furthermore, Figure 3 shows that the additional snow originates from an increase in evapotranspiration and not from a change of source region due to a changing wind field. We confirm the prominent role of the Tarim irrigation for Kunlun Shan snowfall by performing WRF runs where only the irrigation in the Tarim basin is either zero or at the 2010 level and where the rest of the domain has irrigation applied at the 2010 level. Compared to the case with zero irrigation in the Tarim basin, the irrigated case shows a decrease in net radiation (−0.4 W m⁻², P ≪ 0.01) and an increase in snowfall (+1.5%, P ≈ 0.01) over Kunlun Shan, which is qualitatively comparable to the ΔHIST and ΔDEC cases. In contrast, the net radiation increased by +0.6 W m⁻² (P ≪ 0.01) and the summer snowfall decreased by −10% (P ≈ 0.01) in Spiti Lahaul when Tarim irrigation is applied, again showing a similar response as for the ΔHIST and ΔDEC cases.

Figure 3.

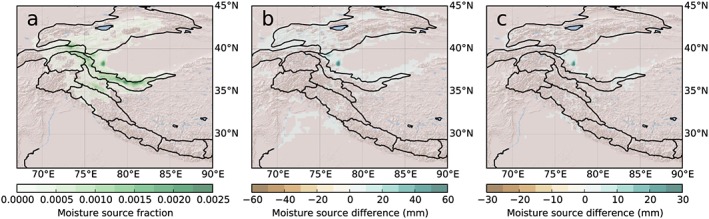
Moisture sources for Kunlun Shan summer snowfall. Fractions of the snowfall that originates from a certain grid point for summers that have 2010‐level irrigation applied (a), and the difference in amount of moisture originated from a certain pixel for the ΔHIST case (b), and the ΔDEC case (c).

4. Discussion and Conclusion

Despite the commonly used name, the largest anomaly in glacier mass balances is not actually found in the Karakoram but in the Kunlun Shan region (Brun et al., 2017; Kääb et al., 2015; Lin et al., 2017). For the Karakoram itself we found large spatial and temporal variability in snowfall, temperature, and radiation differences. We do find that the snow height from WRF at the end of the summer is higher in central Karakoram when irrigation is increased in the ΔHIST (+6 cm) and ΔDEC cases (+1 cm), due to an increase in snowfall in September (+10% of total September snowfall, P > 0.01 for ΔHIST; +17%, P ≪ 0.01 for ΔDEC). However, these effects are relatively small in terms of total snow quantities, and results on snow height on a specific date have low significances due to the very limited sample size of 7 years. More work is needed to clarify the role of irrigation on glaciers in the Karakoram.

Our results do suggest that changing patterns of irrigation around HMA, most notably the rapid intensification of irrigation in the Tarim basin, cause changes in summer snowfall and net radiation that can reduce glacier melt in Kunlun Shan, while increasing glacier melt in most of HMA, in line with observed glacier mass balances (Brun et al., 2017; Kääb et al., 2015; Lin et al., 2017). Parts of Pamir also show an increase in snowfall and a decrease in net radiance. However, unlike Kunlun Shan, most snow in Pamir falls in winter, not summer (Maussion et al., 2014). Furthermore, the effect of irrigation is weaker than for Kunlun Shan, which might explain the less prominent growth of glaciers in parts of Pamir. Although the mass balances of the small glaciers in northeastern Tibet are not well studied, our results are consistent with the observed positive trend in precipitation over the northeastern part of the Tibetan Plateau (Yang et al., 2016) A decrease in summer melt in Kunlun Shan is consistent with the observed decrease in runoff in, for example, Hotan, at the southern edge of the Tarim basin, where water flows from the Kunlun Shan mountains (Amuti & Luo, 2014). Furthermore, our results are consistent with the observed increase of atmospheric moisture and cloudiness in the Tarim basin in summer (Peng & Zhou, 2017), an increase of cyclonic motion in the middle troposphere over northwest HMA in summer (Forsythe et al., 2017), and with the observed cooling in Xinjiang (Han & Yang, 2013). We could not fully assess the effects of increasing irrigation on large‐scale circulation due to the limited domain size in this study. However, there are some suggestions that winter precipitation in northwest HMA is increasing as a result of global warming (Cannon et al., 2014; Kapnick et al., 2014; Madhura et al., 2014; Ridley et al., 2013). Together with trends in the cyclonic motion over northwest HMA (Forsythe et al., 2017), these large‐scale effects could further increase the mass of the glaciers in northwest HMA.

The increasing irrigation demand in South Asia has led to a rapid increase in groundwater stress (Tiwari et al., 2009) as well as negative ecological impacts in arid regions such as the Tarim basin (Shen et al., 2013). It is therefore questionable whether the rapid increase in irrigation in recent decades is sustainable in the near future. A future stabilization or decrease in irrigation might thus mean that the anomalous glacier mass balance in Kunlun Shan is of temporary nature, although large‐scale effects that can increase snowfall in the region, such as an increase in strength of westerly disturbances, might counteract the effect of decreasing irrigation in parts of HMA. Our results also imply that water management and policy can potentially affect the local climate in HMA and hence glacier mass balances, which in term affects water availability in the region, making the problem of water availability even more complex.

Supporting information

Supporting Information S1

de Kok, R. J. , Tuinenburg, O. A. , Bonekamp, P. N. J. , & Immerzeel, W. W. (2018). Irrigation as a potential driver for anomalous glacier behavior in High Mountain Asia. Geophysical Research Letters, 45, 2047–2054. https://doi.org/10.1002/2017GL076158