Age Affects Reinforcement Learning through Dopamine-based Learning Imbalance and High Decision Noise — not through Parkinsonian Mechanisms

Abstract

Probabilistic reinforcement learning declines in healthy cognitive aging. While some findings suggest impairments are especially conspicuous in learning from rewards, resembling deficits in Parkinson’s disease, others also show impairments in learning from punishments. To reconcile these findings, we tested 252 adults from three age groups on a probabilistic reinforcement learning task, analyzed trial-by-trial performance with a Q-reinforcement learning model, and correlated both fitted model parameters and behavior to polymorphisms in dopamine-related genes. Analyses revealed that learning from both positive and negative feedback declines with age, but through different mechanisms: When learning from negative feedback, older adults were slower due to noisy decision-making; when learning from positive feedback, they tended to settle for a non-optimal solution due to an imbalance in learning from positive and negative prediction errors. The imbalance was associated with polymorphisms in the DARPP-32 gene and appeared to arise from mechanisms different from those previously attributed to Parkinson’s disease. Moreover, this imbalance predicted previous findings on aging using the Probabilistic Selection Task, which were misattributed to Parkinsonian mechanisms.

1. Introduction

Cognitive abilities such as reasoning, perceptual speed, and memory decline in healthy cognitive aging (Lindenberger and Baltes, 1997; Murray et al., 2015; Salthouse, 1996), impairing the way people use information from previous experiences to make everyday decisions. Learning from probabilistic feedback, in particular, slows with age (Eppinger and Kray, 2011; Samanez-Larkin et al., 2014) and predicts real life debt and asset accumulation (Knutson et al., 2011). Yet, the mechanisms driving this age-related change remain poorly understood.

Probabilistic reinforcement learning occurs when unreliable “feedback” (positive, negative, or absent altogether), received in response to actions, informs future decision-making, and learning from such feedback requires approximating the value of stimulus-response relationships in face of environmental uncertainty. These value updates are hypothesized to be largely based on phasic bursts and dips in striatal dopamine levels, corresponding to unexpected positive and negative outcomes (“prediction errors”), respectively (see Schultz, 2002, for extensive review).

One possible implication of this mechanism is that chronically low striatal dopamine, as seen in Parkinson’s disease (PD) (Lotharius and Brundin, 2002), could impair reward learning and facilitate punishment learning. This has been confirmed by several behavioral studies (Bodi et al., 2009; Frank et al., 2004; Rutledge et al., 2009). For instance, both unmedicated and never-medicated PD patients are impaired in learning from probabilistic rewards and better at learning from probabilistic punishments compared to healthy controls, presumably because of sustained declines in baseline striatal dopamine (Bodi et al., 2009). The opposite pattern emerges when these patients are put on medication that increases baseline levels of striatal dopamine (Bodi et al., 2009; Frank et al., 2004).

Since healthy aging is associated with striatal dopaminergic denervation and decline (Backman et al., 2006; Bohnen et al., 2009; Gunning-Dixon et al., 1998; van Dyck et al., 2002; Volkow et al., 1996), some have suggested that PD might be a good model of accelerated age-related changes in reinforcement learning (Collier et al., 2011). Indeed, several studies have presented data consistent with this view (Frank and Kong, 2008; Kovalchik et al., 2005; Marschner et al., 2005; Mell et al., 2005; Simon et al., 2010; Wood et al., 2005). For example, Frank and Kong (2008) and Simon and colleagues (2005) used the Probabilistic Selection Task to report an age-related “negative learning bias”, indicating an inclination to learn more from punishment than reward. Such effects seem to suggest that age leads to harm-avoidant tendencies where attention during learning is given primarily to punishment, a finding that resembles results from PD patients using the same task (Frank et al., 2004).

Nevertheless, other findings challenge this view, demonstrating significant impairments in both reward and punishment learning due to aging (Eppinger and Kray, 2011; Lighthall et al., 2013; Samanez-Larkin et al., 2014). One explanation for the inconsistencies is that different methodologies have been used to evaluate reinforcement learning (Frank and Kong, 2008; Marschner et al., 2005; Mell et al., 2005; Simon et al., 2010), with some experiments not sufficiently differentiating learning from positive and negative reinforcement (Frank and Kong, 2008; Kovalchik et al., 2005; Marschner et al., 2005; Mell et al., 2005; Simon et al., 2010; Wood et al., 2005) and others possibly using insufficient numbers of trials (Eppinger and Kray, 2011; Samanez-Larkin et al., 2014). Alternatively, PD may not be a good model for the effects of aging on probabilistic reinforcement learning. Many studies were, at least partly, motivated by the neurobiological evidence for age-related declines in the dopamine system, but may not have sufficiently considered the relative effects of other broad, and equally well documented, age-related cognitive changes that influence reinforcement learning, including deficits in memory, attention and motivation (Lindenberger and Baltes, 1997; Murray et al., 2015; Salthouse, 1996) in addition to the complexity of the dopamine system itself (Karrer et al., 2017). Such changes could have confounded results, affecting the translatability of PD findings to reinforcement learning in aging.

To clarify the mechanisms contributing to these inconsistencies, we tested 252 adults from three different age groups on a well-established task (referred to here as the “Quarters” task) that distinguishes between learning from positive and negative reinforcement (Bodi et al., 2009; Mattfeld et al., 2011; Moustafa et al., 2015a; Moustafa et al., 2015b; Myers et al., 2013; Tomer et al., 2014). We analyzed both average performance and distributions of scores across individuals to identify different learning patterns. Then, we used a Q-reinforcement learning model to fit four interpretable learning parameters to the individual data of each participant and thus identify age-related cognitive changes that could explain our behavioral results. The same parameters were then used in a simulation of the Probabilistic Selection Task to explain the “negative learning bias” found in previous work (Frank et al., 2004; Rutledge et al., 2009), adding additional validity to the model we used. Finally, to clarify the potential effects of dopamine on our results, we tested the relationship between the model parameters and participants’ polymorphisms in four dopamine-related genes. Using this approach, we show that age affects positive and negative reinforcement learning through at least two different mechanisms, and these mechanisms might explain previous inconsistencies in the literature.

2. Materials and Methods

2.1 Participants

Ninety-eight younger (M = 20.0, SD = 1.5, range: 18–25 years), 94 middle-age (M = 62.5, SD = 4.6, range: 53–69 years), and 60 older (M = 77.1, SD = 5.3, range: 70–89 years) adults were recruited between January 2012 and May 2015 and compensated $15 per hour for their participation. Younger adults were recruited via fliers posted on Rutgers University—Newark and St. Olaf College campuses. Middle-aged and older age adults were recruited through advertisements posted at the City Hall and Jewish Community Center in Nutley, NJ and at churches and senior centers in Newark and the greater Newark area.

All participants gave written informed consent and underwent screening, consisting of the Dvorine colorblindness test, BDI-II Questionnaire, and a Health Screening form. Participants who failed the color discrimination test or had neurological disorders diagnosed by a physician such as Parkinson’s Disease (PD), Huntington’s Disease, and depression, or who indicated suicidal thoughts or wishes were not enrolled in the study. In addition to the computer task, a battery of neuropsychological assessments was also administered, which included the Mini Mental State Examination (MMSE), Frontal Assessment Battery (FAB), WAIS IV Digit Span, and Logical Memory I & II. Both the demographic and neuropsychological assessment data for our participants can be found in Table S1.

2.2 Experimental Task (“Quarters”)

On each trial, participants were presented with one of four abstract images, described as cards that can predict the weather (Fig. 1). Through trial and error, their goal was to correctly identify whether the image predicted Rain or Sun. After each response, participants either received or did not receive feedback, depending on the trial’s condition and accuracy of the response, before the next trial began. Trials belonged to one of two types of conditions: “positive feedback,” in which correct responses yield positive feedback and incorrect responses no feedback, and “negative feedback,” in which correct responses yield no feedback and incorrect responses negative feedback. Hence, the value of receiving no feedback was ambiguous until participants formed stimulus-response relationships.

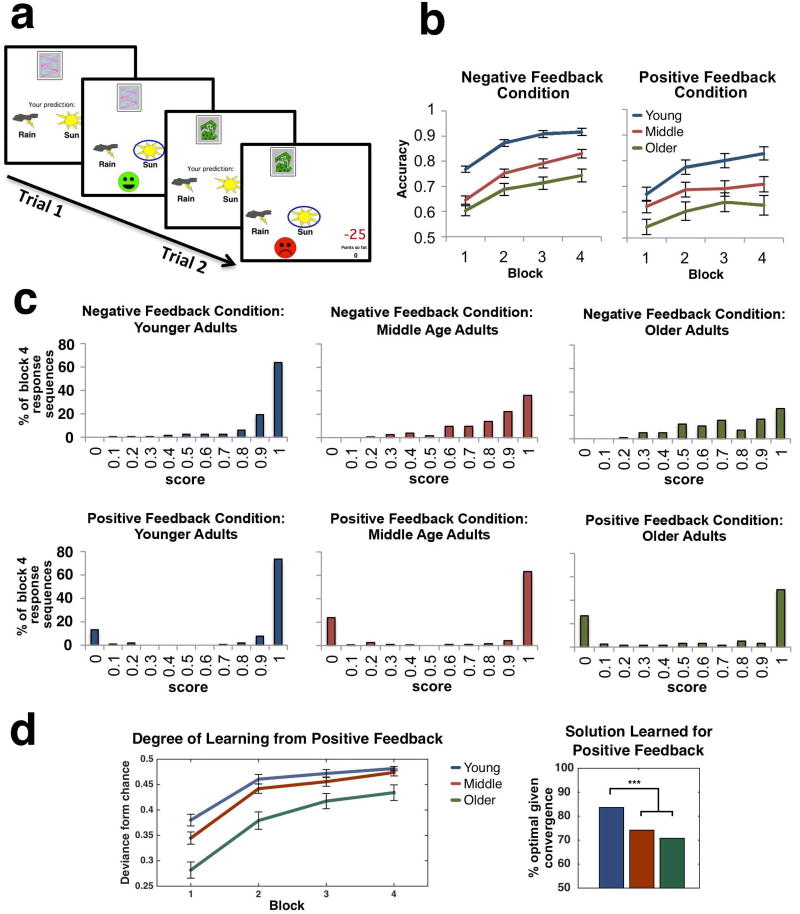
Fig. 1.

Stimuli and Feedback Conditions.

Feedback was reliable on 90% of trials. For example, in the positive feedback condition, for a particular stimulus, one response was rewarded on 90% of trials and yielded no feedback on the other 10%, whereas the other response was rewarded on 10% of trials and yielded no feedback on the other 90%. The task was run for 160 trials, comprised of 4 blocks of 40 trials. Within each block, stimulus presentation order was randomized, but always consisted of exactly 10 trials for each stimulus, out of which exactly 9 trials were reliable, making the distribution of trial type (i.e. positive feedback or negative feedback condition) uniform across blocks. Within each feedback condition, the optimal response for one stimulus was “Rain” and the other “Sun”, and these probabilistic stimulus-response contingencies were held constant for the duration of the 160 trials. Participants were not made aware of any of this structuring of trials, and they were allowed to complete the task at a pace they were comfortable with.

2.3 Procedure

The task was programmed using the SuperCard 4.6 programming language and run in full screen mode on a 13” MacBook computer. Participants were seated in an isolated testing room at a comfortable viewing distance from the screen. Before beginning the task, they received thorough instruction and were advised of the probabilistic nature of the task, that even after learning the appropriate stimulus-response associations, responses would not always yield the expected outcome. Participants were then given 4 sample trials using 2 stimuli (different from the 4 stimuli used in the task), demonstrating the possible outcomes in the task and introducing a running total of points on the bottom right hand of the screen, which was initialized to 0 for the actual task (Fig. 1). Responses were given by pressing one of two keys on the laptop computer, clearly marked as “SUN” and “RAIN;” all other keys were covered with a cardboard mask. After a response was given, the answer choice was circled in blue on the screen and feedback (if any) was given. If the response yielded negative feedback, a red frowning face appeared and red text was displayed to indicate a deduction of 25 points from the running total. If the response yielded positive feedback, a green smiling face appeared and green text was displayed to indicate an addition of 25 points to the running total. If the response yielded no feedback, nothing additional was displayed. All feedback, including “no feedback”, remained for 2 seconds before the next stimulus was presented.

2.4 Behavioral Data Analysis

For statistical analyses, “optimal” answers for each image were defined as the response that predominantly yielded the feedback with the higher value for that image (i.e. choices that led to reward on 90% of trials in the positive feedback condition and those that led to no feedback on 90% of trials for the negative feedback condition). Mean optimal accuracy scores were calculated for each participant in each of the 4 blocks of each feedback condition. Those scores were then subject to a repeated measures Analysis of Variance (ANOVA) with Age as a between-subjects factor and Block and Feedback as within-subject factors. Details of these analysis and follow up analyses are described in Results. All statistical analysis was performed using the SPSS 20 software.

2.5 Model-Based Data Analysis

Behavioral results were analyzed using a Q-learning reinforcement model, which has been established as a sound model of behavior in similar tasks used to study reinforcement learning in humans (Frank et al., 2007; Moustafa et al., 2015b; Myers et al., 2013). The model assumes that participants represent and maintain an expected value for each response (r) given a stimulus (s) and that they update these expected values after getting feedback on each trial. These expected outcome values, denoted by Q[r,s], were initialized to 0 for the first trial (of the 160). For each new trial, t+1, after a response was made to a stimulus and feedback was given, the value was updated using the following Q-learning rule:

$$Q{[r,s]}^{t+1}=Q{[r,s]}^t+\alpha ·(R-Q{[r,s]}^t)$$ (2)

where t denotes the trial number, R the reinforcement value based on feedback given at that trial, and α the learning rate. The learning rate was dependent on the prediction error term: R − Q[r, s]: if the prediction error was positive, a “positive prediction error learning rate” (α⁺) was used, and if it was negative, a “negative prediction error learning rate” was used (α⁻). The feedback value, R, was set to +1 for reward and −1 for punishment. For no-feedback, R was set to R₀, a free parameter for each participant. On each trial, the probability of choosing one of the categories, e.g. Pr(Rain), for a given stimulus, s, was calculated based on the expectancy values for each of the two possible responses to that stimulus using a softmax function:

$$\text{Pr}(\mathit{\text{Rain}})=\frac{e^{Q[\mathit{\text{Rain}},s]/\beta }}{e^{Q[\mathit{\text{Rain}},s]/\beta }+e^{Q[\mathit{\text{Sun}},s]/\beta }}$$ (3)

Here, β is the “noise” parameter of the decision, quantifying the tendency to choose the response with the higher expected value (the higher the β, the lower the tendency). Thus, this noise value reflects to what degree information gained about the expected values can be utilized in producing appropriate responses. It is also sometimes interpreted as capturing an exploration mechanism (Frank et al., 2007; Moustafa et al., 2015a).

Model based analyses were conducted by fitting four free parameters to each participant’s trial-to-trial stimulus-response sequence: positive prediction error learning rate, negative prediction error learning rate, noise in the decision process, and the reinforcement value attributed to no feedback (R₀). The last parameter represents the individual tendency to view the absence of feedback as rewarding or not (in contrast to positive and negative feedback, which, as mentioned above, supplied fixed positive and negative reinforcement values, respectively). Fitting was conducted using a maximum likelihood approach: for a given participant and a given set of these four parameter values, the log likelihood of each response for each trial was computed while updating the expected values. The sum of these log likelihoods over all trials represented the log likelihood estimate of this set of parameters:

$$\mathit{\text{LLE}}=\sum _{t=1}^{160}\mathit{\text{log}}(\text{Pr}(r,t))$$ (4)

We used grid search to fit the parameters, with α⁺, α⁻, β each ranging between [0, 1] in steps of 0.05, and R0 ranging between [−1, 1] in steps of 0.1 (following Myers et al., 2013). For each participant, the set of parameters yielding the maximum log likelihood across all 160 trials was chosen as the representative reinforcement learning profile of that participant (similar results were achieved using finer grid searches and when using gradient-based methods such as the Neldar-Mead algorithm implemented in Matlab’s fminsearch function). After finding the parameter profile for each participant, we analyzed the difference in the average and the distribution of those parameter values for each age group, as detailed in the Results section. All model-based analyses were carried out with MATLAB 2015a software.

2.6 Analysis of Probabilistic Selection Task

The Probabilistic Selection Task was modeled following the exact procedure administered to real participants, (Frank and Kong, 2008; Frank et al., 2004; Frank et al., 2007; Simon et al., 2010) but using the individual learning parameters we fit to the behavioral data collected from our experiment. On each trial, the same Q-reinforcement model described above was presented with two “stimuli” and tasked with choosing the one yielding the higher amount of reward (or lower amount of punishment). The model chose based on the stimuli’s expected outcome values Q[r,s] (initialized to 0 as before) using the softmax function (Equation 3). One of three possible pairs were used on each trial: For the AB pair, picking A yielded reward 80% of the time and punishment 20% of the time (whereas picking B yielded reward and punishment with the complementary frequency). Similarly, for the CD pair, reward-punishment frequencies for C were 70–30, and for the EF pair, the frequencies for E were 60–40. The appropriate Q[r,s] value was updated after the model’s response using Equation 2, with rewards yielding feedback value of 1 and punishments a value of −1, consistent with the way we applied the Q-reinforcement learning model to our task. No neutral trials exist in the Probabilistic Selection Task. Training continued in blocks of 60 trials (20 trials per stimulus pair) and was terminated when performance exceeded a designated threshold for each of the pair types (65% accuracy for the AB pair, 60% for the CD pair, and 50% for the EF pair; see Frank and Kong, 2008 and Kovalchik et al., 2005), or after 6 blocks. We then extracted several performance measures corresponding to the ones regularly reported in this task. For training performance, “win-stay” is computed as the probability of choosing the same response that yielded a reward in the previous trial; “lose-shift” is computed as the probability of shifting responses after it yielded punishment in the previous trial. Both measures were calculated only for the first block (see Kovalchik et al., 2005; Simon et al, 2010). Learning bias was computed in accordance with the “test” phase in the human experiments, by examining the probability of the model’s softmax choices when responding to novel pairs based on the Q values it reached at the end of training (with no further learning or feedback). ‘Choose A’ is defined as the average probability of choosing ‘A’ in pairs AC, AD, AE, AF. ‘Avoid B’ is defined as the average probability of not choosing ‘B’ in pairs BC, BD, BE, BF. The learning bias is computed as ‘Avoid B’ subtracted from ‘Choose A’. The simulated experiment was carried out for each of our participants using their individual learning profile (positive and negative prediction error learning rates, and decision noise; R₀ is not used in this task) previously fit to our Quarters task. These simulations were repeated 10 times and performance measures were averaged over the 10 runs.

2.7 Analysis of Genetic Polymorphism

We genotyped DNA from 212 of 252 participants (almost all remaining samples were discarded because of contamination during hurricane flooding, and a couple due to mislabeling or participants opting out). Each participant contributed 2 milliliters of saliva after completing the testing battery (approximately 2 hours), as to minimize sample contamination from prior meals. The saliva collection itself was done using the Oragene Discover (OGR-500) kit (i.e. test tubes), purchased from DNA genoTek. The advertised median DNA yield is 110 micrograms and stability spans years at room temperature. We took extra precaution and refrigerated these samples below room temperature, and genotyped the samples within 6 months from extraction. Genotyping occurred at the Environmental and Occupational Health Sciences Institute at Rutgers University—New Brunswick, where samples were screened via routine PCR or southern blots for polymorphisms in four genes that are implicated in regulating dopamine at the neural and molecular levels: DARPP-32, COMT, DRD2 and DAT1. Following previous reports, we concentrated on SNPs in genes previously shown to modulate reinforcement learning (Frank and Fossella, 2011; Frank et al., 2009): rs907094 for DARPP-32, rs6277 for DRD2, rs4680 for COMT, and VNTR for DAT1. SNPs of a few individuals could not be determined, and several others included rare alleles or variations and were excluded from further analysis. The final sample included participants with either AA, AG or GG alleles in the DARPP-32, COMT and DRD2 SNPs (212 participants for DARPP-32, 211 participants for each of the other two genes), and either 10/10 tandem repeat, 9/9 tandem repeat, or 9/10 for DAT1 SNP (189 participants). For each gene, we grouped participants based on the frequency of one of the alleles (e.g., for DAT1, homozygous 9/9 was 0, heterozygous 9/10 was 0.5, and homozygous 10/10 was 1) so as to detect gene dose effects. These frequencies were correlated to behavioral and model-related parameters as discussed in Results. See Supplementary Information for additional notes concerning group differences in allelic frequencies.

3. Results

3.1 Basic Learning

Participants learned to classify four stimuli into one of two categories through probabilistic feedback (Fig. 2a). Two stimuli yielded rewards for correct answers, and no feedback for incorrect ones (“positive feedback condition”); the remaining two yielded no feedback for correct answers, and punishments for incorrect ones (“negative feedback condition”). No-feedback was therefore ambiguous until stimulus-feedback associations were learned.

Fig. 2.

Behavioral Task and Results for the 252 paricipants. (a) Experimental task. Participants learned to classify 4 stimuli to one of two arbitrary categories (Rain or Sun) by trial and error using probabilistic feedback. Two stimuli yielded positive feedback (smiling face and positive points) on 90% of the trials and no feedback on 10% of the trials. The other two stimuli yielded negative feedback (frowning face and negative points) on 90% of the trials and no feedback on 10% of the trials. Two example trials are presented. (b) Learning curves for the positive and negative feedback conditions. Error bars illustrate standard errors of the means (see Supplementary Information for additional analyses). (c) Distributions of scores on Block 4 for the different age groups. y-axis represents the percent of individual response-sequences within an age group and the x-axis marks each decile of performance score. The scores for stimulus A and stimulus B of each feedback condition were computed and counted separately to avoid the score of one interfering with the other (for example, when one stimulus receives a perfect score and the other zero, they average to a misleading “random chance” score of 0.5). (d) Left, deviance from chance performance, indicating the degree of learning a solution irrespective of the type of solution. Right, percent of optimal solutions given convergence to any solution. Convergence to a solution was defined as at least three consecutive blocks with accuracy reaching higher than 0.9, or lower than 0.1, for the optimal and non-optimal solutions, respectively). *** p<0.0001.

Mean accuracy scores for all individuals were submitted to a 3 (Age: Younger, Middle-aged, Older) × 2 (Feedback: Positive, Negative) × 4 (Block: 1–4) analysis of variance (ANOVA), with Age as a between subjects factor and Feedback and Block as within-subjects factors. The analysis revealed main effects of Age [F(2,249)=26.675, p<0.0005], Block [F(3,747)=133.489, p<0.0005], and Feedback [F(1,249) = 25.303, p<0.0005], as well as interactions of Block × Feedback [F(3,747)=3.305, p<0.020] and, at a trend level, Feedback × Block × Age [F(6,747)=1.915, p=0.076]. No other interactions were significant.

Examining each of the two feedback conditions separately (Fig. 2b), the main effects of Age and Block were again significant (negative feedback: [F(2,249)=39.269, p<0.0005] and [F(1,249)=183.1, p<0.005], respectively; positive feedback: [F(2,249)=8.482, p<0.0005] and [F(3,747)=37.597, p<0.0005], respectively). Bonferroni-corrected pairwise comparisons showed that in both conditions younger adults outperformed the middle-aged (p<0.0005, p=0.038 for negative and positive feedback conditions, respectively) and older adults (both p’s<0.0006). With negative feedback, middle-aged adults also outperformed the older adults (p=0.005). The Age × Block interaction approached significance only for positive feedback [F(6,747)=2.027, p=0.060], indicating that the three age groups may have learned at different rates.

To follow up on the (marginal) Age × Block interaction for positive feedback, we analyzed this condition separately for each age group. A one-way ANOVA showed a significant effect of Block in the younger, middle-aged, and older adults ([F(3, 291)=28.434, p<0.0005], [F(3, 279)=11.550, p<0.0005], [F(3, 177)=5.409, p<0.001], respectively). Bonferroni-corrected pairwise comparisons between blocks showed that while learning for the younger adults continued from Block 1 to Block 3 (all p’s<0.05), middle-aged adults only differed significantly between Block 1 and each of the rest (all p’s<0.001) and for older adults, only between Blocks 1 and 3 (p<0.034).

In sum, we found a strong main effect of age on reinforcement learning deficits for both positive and negative feedback conditions, with some weaker indication that learning in the positive feedback condition continuing into later blocks only for younger adults.

3.2 Cognitive Strategies

While average performance can be useful for studying group differences, it may overlook meaningful individual learning differences. One way to address this issue is to examine the distribution of accuracy scores. Fig. 2c plots the distributions of block 4 stimuli accuracy scores organized by Feedback and Age. For negative feedback (upper row), accuracy scores generally ranged between 50% (chance) and 100%, with the distribution of participants skewed towards the latter. This was not the case for positive feedback (Fig. 2c, lower row), where the majority of participants performed either near 0% or 100%. That is, some participants learned to avoid feedback for at least one of the positive feedback condition stimuli, indicating a non-optimal behavior of settling for no feedback. This striking difference in distributions suggests a key distinction in the way age may affect performance in the positive and negative feedback conditions: for negative feedback, age seems to slow down learning, whereas for positive feedback, age increases the likelihood of compromising on a non-optimal solution, opting for no feedback.

To mathematically confirm our observation for positive feedback, we attempted to disentangle to what degree a solution was learned in this condition (irrespective of whether it was optimal, i.e. learning the rewarded response, or non-optimal, i.e. learning the no-feedback response), from the type of solution that was learned (i.e. optimal or not optimal).

To express the degree of learning, we computed the absolute value of the deviation from chance performance (defined as a 0.5 score), a measure that ignores whether a participant learned the optimal or non-optimal solution. These scores were subject to a 2-way ANOVA with Block and Age as the within and between-subject factors (Fig. 2d, left). The analysis revealed main effects of Block [F(1,249)=130.924, p<0.0005] and Age [F(2, 249)=18.131, p<0.0005], but no interaction [p=0.11]. Bonferroni-corrected pairwise comparisons showed that the older group learned to a lesser degree than each of the other two age groups (both p’s<0.005), but there was no difference between the middle-aged and younger adults. That is, performance differences between the younger and middle-aged adults were unlikely to be explained by the degree of learning a solution (regardless of the type of solution).

To analyze the type of solution that was learned irrespective of learning degree, we took a subset of the data, discarding slow- or non-learned stimuli. We defined “convergence” to a solution as scores that, for at least the last three blocks, remained equal or below 0.1, or equal or above 0.9, for the non-optimal and optimal solutions, respectively. This amounted to 84.2%, 78.2% and 54.2% of stimuli in the younger, middle and older groups. We then compared the frequencies of optimal versus non-optimal learned solution using a chi-square test of independence with Age (Younger, Middle-age, Older) and Solution (Optimal/Non-optimal) as factors (Fig. 2d, right). The analysis revealed a significant effect (χ(2)=6.231, p<0.05). Follow-up chi-square tests, partitioning the data to older vs. middle-age, and younger vs. older & middle-age combined, showed that younger adults tended to converge to the optimal solution more than the other age groups (χ(1)=5.933 p<0.02), but there was no difference between the middle-age and older groups (χ(1)=0.262, p=0.6087).

To summarize, older adults learned from positive feedback to a lesser degree than the remaining groups, whereas middle-age adults learned from positive feedback to approximately the same degree as younger participants. However, younger age adults were more likely to converge to the optimal solution than middle age adults, resulting in a higher group performance.

3.3 Reinforcement Learning Model Analysis

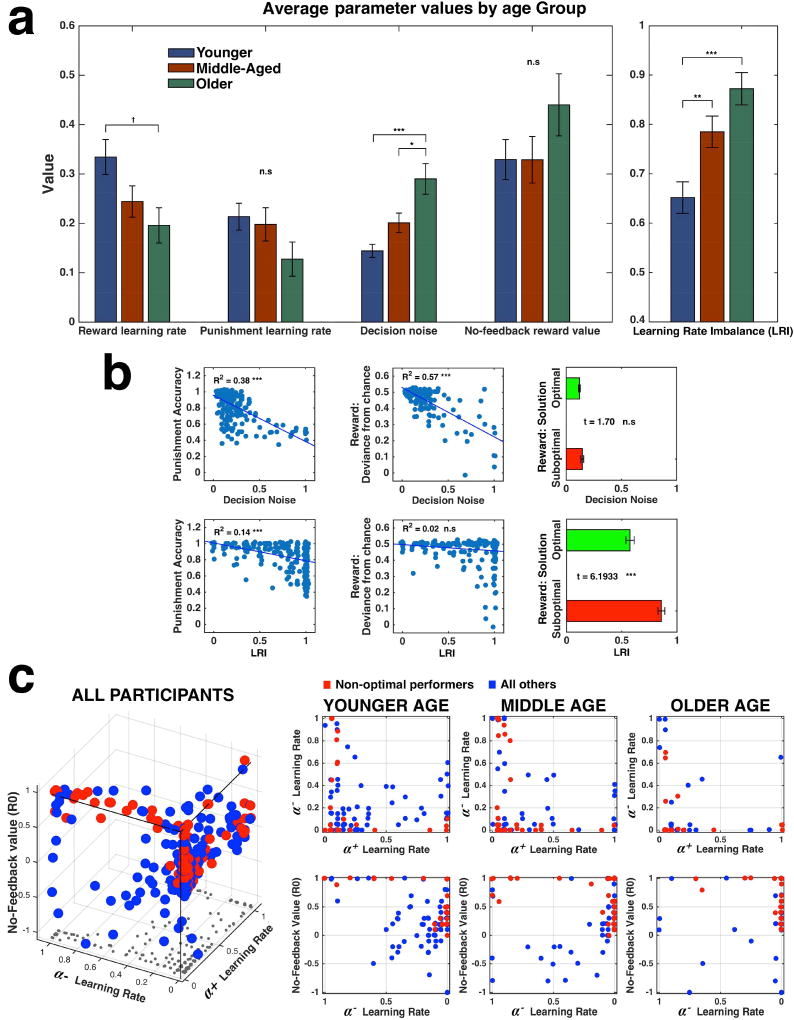
To identify mechanisms responsible for the differences in learning between the age groups, we fit four parameters to each participant’s trial-to-trial sequence according to a Q-Reinforcement learning model (see Materials and Methods): the rate of learning from positive prediction errors (α⁺), the rate of learning from negative prediction errors (α⁻), the valence assigned to no-feedback (R₀), and decision noise (β), reflecting the likelihood of choosing a response that doesn’t correspond to its expected value. Average values of these parameters for the three age groups are plotted in Fig. 3a, left¹.

Fig. 3.

Analysis of fitted parameters (for 250 participants). (a) Left, average values of the four parameters fit to the model, by age group. Right, average Learning Rate Imbalance measure, by age group. * - p < 0.02; ** - p < 0.008; *** - p < 0.0001; † - trend; n.s - not significant. Error bars illustrate standard errors of the means. (b) Correlations of behavioral performance meaasures with Decision Noise (top row) and Learning Rate Imbalance (bottom row) across all participants. Small amount of gaussian noise (SD = 0.01) was added to the scatter plots’ datapoints to improve visualisation. *** - p < 0.0001; n.s - not significant. (c) Left, 3D Scatter of three individually-fit parameters: α⁺, α⁻ and R₀, for all participants in the study. Each dot represents one participant. Projection of each dot on the X–Y plane is marked by a small grey dot to allow easier understanding of the 3D scatter. Right, 2D projections of the 3D scatter plot, on two different planes, separately for each age group. Red: Participants that learned a non-optimal solution for at least one of the positive-feedback stimuli (‘Non-optimal performers’). Blue: rest of participants. Small amount of gaussian noise (SD=0.01) was added to the datapoints to improve visualisation.

Four separate one-way ANOVAs of each parameter, Bonferroni-corrected for multiple comparisons, showed a significant difference between the groups only for the average decision noise [F(2, 247)=11.82, p<0.0001]. Pairwise comparisons indicated the effect stemmed from older adults having higher values than both the middle-aged and younger adults (p=0.012; p<0.0001, respectively). No other difference in parameter values reached significance, though α⁺ showed a trend (p<0.09).

We then determined how well decision noise accounts for each of the age-sensitive performance measures (Fig. 3b, upper row). We found that decision noise was strongly correlated with average scores for block 4 in the negative feedback condition (r(248) = −0.62, p<0.0001), as well as with the deviance from chance for block 4 in the positive feedback condition (r(248) = −0.76, p<0.0001; see also Fig. S1). For both measures, performance deteriorated as noise increased. However, noise did not distinguish optimal and non-optimal learning: considering only participants who reached convergence (defined earlier and in Fig. 2d) on at least one of the positive feedback stimuli, there was no difference in noise levels between participants who converged to the optimal solution on both stimuli (‘optimal performers’) and those who converged to the non-optimal solution on at least one of the stimuli (‘non-optimal performers’) (p=0.246).

To determine whether the difference in learning optimal and non-optimal solutions can be revealed by more in-depth model analyses, we studied the joint distribution between the other three model parameters (α⁺, α⁻, R₀). A 3D scatter plot of these parameter values for all participants illustrates several clear characteristics that distinguish non-optimal performers from the rest (Fig. 3c, left): first, almost all non-optimal- performers had at least one learning rate parameter (either α⁺, α⁻, or both) with a value near 0. Second, participants who had a low α⁺ tended to have a high R₀ value (i.e., they evaluated no feedback as very positive). Third, participants that had R₀ values below 0 (that is, they tended to see no feedback as negative) were almost never non-optimal performers.

To assess whether these patterns can characterize the three age groups, we plotted the projection of the 3D individual parameter values for each age group, on 2 planes: the α⁺ − α⁻, plane (Fig. 3c, right, upper row), and the α⁻ − R₀ plane (Fig. 3c, right, lower row). Comparing the graphs, the degree of scatter on the α⁺ − α⁻ plane tended to decrease with age, suggesting that a near-0 value on either axis is not only indicative of non-optimal performance, but also differentiates the groups. On the other hand, the tendency to treat no-feedback as highly positive did not help distinguish the age groups further.

These qualitative observations suggest that older age may be associated with a tendency towards one of two different learning strategies: (1) a ‘reward-seeking’ strategy, where learning from negative prediction errors is highly diminished, or (2) a ‘harm-avoidant’ strategy where learning from positive prediction errors is diminished. Younger adults, on the other hand, seem to be more balanced, on average, in their positive-negative learning rates. To formalize this hypothesis, we introduce a new index, the ‘Learning Rate Imbalance’ (LRI), calculated by computing the difference between the learning rates divided by their sum (termed here ‘Learning Rate Disparity’; LRD) and then taking the absolute value:

$$\mathit{\text{LRI}}=\mathit{\text{abs}}(\mathit{\text{LRD}})=\left|\frac{({\alpha }^{+}-{\alpha }^{-})}{({\alpha }^{+}+{\alpha }^{-})}\right|$$ (1)

This index ranges from 0, when the learning rates are identical, to 1, when one of the learning rates is infinitely larger than the other, thus capturing the relevant proximity to the axes in Fig. 3c.

A one-way ANOVA confirmed our qualitative observations, showing a highly significant difference in LRI between the age groups F(2, 247)=10.71, p<0.0001; Fig. 3a, right). Bonferroni-corrected pairwise comparisons showed that the younger adults had lower LRI than both the middle-aged and older adults (p = 0.007 and p<0.0001, respectively), but there was no difference between middle-aged and older adults (p=0.2158).

Next, we examined how well LRI accounts for the performance measures by repeating the same analysis previously conducted for decision noise (Fig. 3b, lower row). The results were nearly a mirror-image of the previous effects: LRI did not correlate with the deviance from chance on block 4 in the positive feedback condition (p=0.232), and while it did correlate with the average scores on block 4 of the negative feedback condition (r(248) = −0.38, p<0.0001), it explained far less of the variance compared to decision noise (R²=0.14 vs. R²=0.38). Most important, unlike decision noise, LRI significantly distinguished between optimal and non-optimal performers in the positive feedback condition (t(167)=6.19, p<0.0001).

In summary, decision noise captured differences in overall speed of learning any solution for both negative and positive feedback; LRI, in contrast, distinguished individuals who converged to the optimal solution on the positive feedback condition from those who did not, but was less predictive of how quickly this convergence occurred. Since both measures differed between age groups, these results point to the existence of two orthogonal factors through which age affects learning from probabilistic feedback.

3.4 Model Reproduces Reported Age-Related Differences in the Probabilistic Selection Task

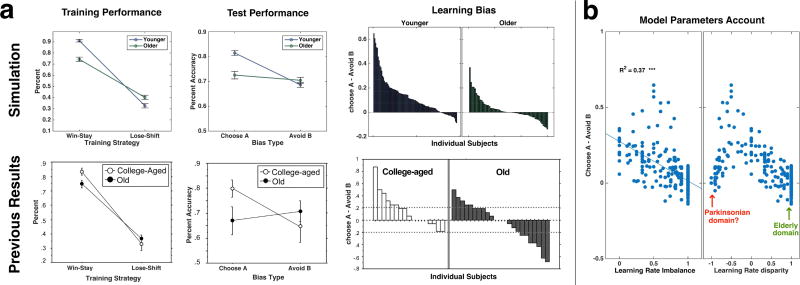
Using the fitted parameters, our model can explain previous findings based on the Probabilistic Selection Task —specifically, the widely cited “negative learning bias” used to support the analogy between striatal and behavioral changes in PD and those of healthy cognitive aging (Frank and Kong, 2008; Simon et al., 2010). In this task, participants are first trained to distinguish between stimuli differing in the probability of yielding reward versus punishment. Three different pairs are used, each with unique reward-punishment probabilities (e.g. 80%–20%, 70%–30%, etc.). Participants are then tested without feedback on novel pairings including high conflict stimuli (e.g., those that previously yielded reward on 80% vs. 70% of trials, or on 20% vs. 30% of trials). Results show that compared to younger, older adults fair worse with novel pairings of stimuli that were previously mostly rewarded, but similar or even better than younger adults on novel pairings of stimuli that were previously mostly punished.

We simulated the exact procedure of the Probabilistic Selection Task (Frank and Kong, 2008; Frank et al., 2004; Frank et al., 2007; Simon et al., 2010), with each of our individual participants represented by the parameters fit to the data collected using our Quarters task (see Material & Methods for details). We found that the relative age-dependent “negative learning bias” is closely replicated in both trend and magnitude without any need for additional model tuning (Fig. 4a; for visual clarity, middle-aged group, whose values were in between the young and old in all measures, is not displayed. See Fig. S2 for full results). However, rather than supporting the view of aging leading to harm-avoidant tendencies, the bias was highly correlated to LRI, meaning that an imbalance favoring learning from either positive or negative prediction errors can yield a negative bias (Fig. 4b, left).

Fig. 4.

Simulation of the Probabilistic Selection Task using our learned parameters and model (for 250 participants). (a) Simulation results of the Probabilistic Selection Task (upper row) compared to human results (lower row, reprinted from [20] with permission). Error bars illustrate standard errors of the means. Only the younger and older simulated groups are displayed for easier comparison (see Fig. S2 for full plots). Left, average difference during training on block 1 between the probability of re-selecting the response that was rewarded on the preceding trial, compared to the probability of shifting the response from the one punished on the preceding trial. Younger adults showed higher difference than older adults (Age × Preference: [F(2,247)=13.199, p<0.0001]; pairwise comparisons for younger vs. older: p<0.0001). Middle, Learning Bias changes. Average performance at test on novel pairings of stimuli that were previously mostly rewarded (‘Choose A’) compared to novel pairings of stimuli that were previously mostly punished (‘Avoid B’). Younger adults had a higher difference between the two than older adults (Age X Preference: [F(2,247)=14.257, p<0.0001]; pairwise comparisons for younger vs. older: p<0.04). Right, learning biases (defined as the difference between ‘Choose A’ and ‘Avoid B’) for all participants, ordered by bias values. Whereas younger adults had many more individuals with a positive learning bias than negative learning bias, the numbers were more evenly distributed in the older group. (b) Left, learning bias as a function of the Learning Rate Imbalance, showing a strong negative correlation (r(248)=0.61, p<0.0001). Right, learning bias as a function of the learning rate disparity, showing an inverted U-shape. Low learning bias is achieved either with very low disparity values (in line with ‘harm avoidant’ learning pattern previously hypothesized to characterize PD patients) or with very high disparity values (in line with ‘reward-seeking’ learning pattern, which most older adults in our study actually belonged to; see Fig. 3c).

Importantly, when plotting the learning bias against the Learning Rate Disparity (Equation 1 without taking the absolute value), we found an inverted-U shape function in which most of our aged participants were on the high α⁺ end rather than the high α⁻ end (Fig. 4b, right; see also Fig. 3c). This suggests that: (1) counterintuitively, it is possible to get a “negative bias” in the Probabilistic Selection Task with learning that strongly favors updates from positive prediction errors over negative prediction errors, and (2) in contrast to previous hypotheses, older adults lean towards reward-seeking rather than the harm-avoidant learning pattern attributed to PD patients.

Thus, our results imply that the similarity of effects found in older individuals and PD patients using the Probabilistic Selection Task may mask the fact that the mechanisms contributing to these effects are almost opposite, one heavily influenced by positive prediction errors and the other by negative prediction errors.

3.5 Genotype Analysis

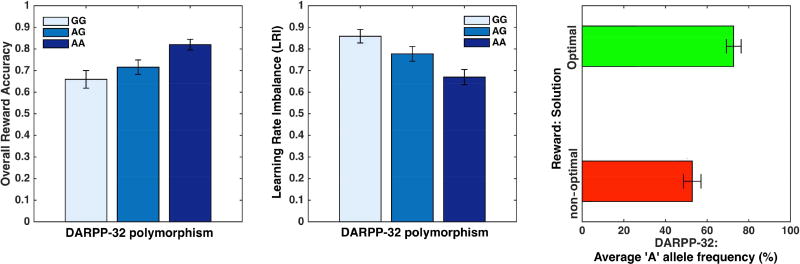
Finally, we determined whether polymorphisms in four dopamine-related genes previously implicated in reinforcement learning (Frank et al., 2007), DARPP-32, COMT, DRD2 and DAT1, predict our behavioral and modeling results. Each individual was characterized by the frequency of a specific allele for each gene (see Materials & Methods), and these frequencies were correlated across participants to each of the nine behavioral performance measures and model parameters previously investigated. Significance values for each of the correlations are displayed in Table 1 Taking a highly conservative approach and using Bonferroni-correction for the 36 multiple comparisons, we found that DARPP-32 modulated both the overall reward accuracy and the choice of learned solution, as well as the LRI (all p’s<0.02 after Bonferroni correction). The more frequent the ‘A’ allele was, the higher were the reward accuracy and probability of choosing the optimal solution, and the lower was the LRI (Fig. 5). COMT was also correlated to LRI at a trend level (p<0.06). No other parameter was associated with any genotype.

Table 1.

Relationship between genetic polymorphism and behavior

	Behavioral parameters				Model parameters
Measure Gene	Punishment accuracy	Reward accuracy	Reward: deviance	Reward: Solution	Positive learning rate	Negative learning rate	Decision noise	R0	LRI
DARPP32	0.0444	0.0007	0.0174	0.0011	0.6203	0.7193	0.0142	0.3836	0.0005
COMT	0.0198	0.1515	0.5261	0.0513	0.2145	0.2163	0.0158	0.5527	0.0017
DRD2	0.7999	0.1810	0.1034	0.0834	0.7336	0.5446	0.2701	0.3025	0.1330
DAT1	0.5396	0.8899	0.8825	0.4262	0.3283	0.1826	0.9814	0.8130	0.2381

Uncorrected p values of the correlations between genetic polymorphism in 4 dopamine-related genes, and behavioral and model parameters. Significant p values after Bonferroni correction are marked in bold.

Fig. 5.

Effects of DARPP-32 polymorphisms on reward learning and Learning Rate Imbalance (LRI) for 212 participants whose genetic data was available. Error bars illustrate standard errors of the means.

4. Discussion

Previous studies of reinforcement learning in healthy aging reported conflicting findings. Some found impairments to be specific to reward learning, possibly resulting from striatal deficits similar to PD patients, while others reported deficits in punishment learning as well. By combining behavioral, genetic and modeling methods, our work confirms that age impairs both reward and punishment learning, but these effects stem from two very different mechanisms.

4.1 Age Affects Two Distinct Cognitive Processes During Reinforcement Learning

First, we discovered that a strong predictor of age-related reinforcement learning deficits, regardless of feedback condition, is noise in the decision-making process. Decision noise decreases the likelihood of responding to stimuli in accordance with accumulated information about the stimulus-response relationships. The higher the noise, the larger the required margins between values of conflicting choices to consistently make optimal decisions. Since accumulating larger margins requires accumulating more reinforcement, this amounts to slower learning. Unlike reinforcement learning rates, decision-noise is often understood as representing the effects of global phenomena, such as cortical changes that affect memory and inhibitory control, or a tendency towards exploratory behavior (Frank et al., 2009; Moustafa et al., 2015a). Indeed, previous studies using electrophysiological and imaging during reinforcement learning showed that age-dependent performance is modulated by both striatal and non-striatal areas (Marschner et al., 2005) and existing evidence shows substantial alterations to frontal regions during aging (Coffey et al., 1992; Raz et al., 1993; Samanez-Larkin et al., 2012). Nevertheless, because the noise parameter captures information about how likely a subject is to act out of line with the expected Q-value, an alternative interpretation of this parameter is that it simply represents a poor model fit to the studied behavior rather than decision noise. Whether this is the case or whether the noise parameter actually has particular neural correlates needs to be studied in future experimental work combined with a comparison between several possible models.

Second, we showed that impairments in learning from positive feedback are not a simple reflection of rewards having a smaller impact on evaluations of actions; rather, impairments are best predicted by considering the relative influences of positive and negative learning rates. One possible mechanism may be that similar positive and negative learning rates yield a non-biased accumulation of evidence regarding the reinforcement value of a stimulus, whereas more distinct learning rates lead to early value evaluations being over-dominated by either positive or negative feedback, pushing decisions into non-optimal solutions which are then difficult to reverse. In the case of the Probabilistic Selection Task, our simulations showed that either of the overly positive or negative learning rate imbalances could recover the so-called “negative learning bias” in reinforcement learning studies. The fact that most of the age-related imbalance in our data was due to higher positive compared to negative learning rates echoes recent findings showing older age does not affect the rate of learning from good news, but reduces the rate of learning from bad news (Sharot and Garret, 2016). Moreover, because the imbalance measure was also highly correlated to DARPP-32 allelic frequency, it likely reflects dopamine system changes in the striatum during aging. Indeed, previous work has already confirmed that learning in our task recruits different subregions of the striatum depending on the feedback type (Mattfeld et al., 2011), and is sensitive to dopamine signaling (Tomer et al., 2014). Notably, the disparity between the learning rates predicted performance according to an “inverted-U” function, consistent with a long-held view of the effects of dopamine on cognitive performance (Cools and D’Esposito, 2011; see also Fig. S3).

4.2 DARPP-32 and Reinforcement Learning

While we did not reproduce reported correlations between behavior and COMT, DRD2 and DAT1 polymorphisms, those effects are not always replicated and might be task-specific or limited to specific cognitive processes (Frank and Fossella, 2011). The DARPP-32 gene, in contrast, may be more directly involved in reinforcement learning, with multiple pieces of evidence suggesting it is specifically involved in reward-learning (Calabresi et al., 2000; Frank et al., 2009; Stipanovich et al., 2008). DARPP-32 is known to modulate synaptic plasticity of striatal cells and is regulated by D1 dopamine receptors. Since the D1 signaling pathway is often conceived as reflecting positive prediction errors, it is commonly assumed that DARPP-32 affects reward learning through this pathway (Cavanagh et al., 2014). Nevertheless, the exact process is anything but clear. There is neurobiological evidence that D2-receptors, often associated with negative prediction error (Kravitz, et al., 2012), modulate DARPP-32 as well, countering the effects of D1 receptors (Svenningsson et al., 2004). In addition, somewhat paradoxically, it was found that increased frequency of ‘A’ alleles in the rs907094 SNP is associated with a positive learning bias but a smaller reward learning rate in a model similar to ours (Frank et al. 2007). The authors explained this finding as resulting from the possible benefits gained by slow accumulation of information. However, unlike our results, these findings were based on merging ‘AG’ heterozygotes with ‘GG’ homozygotes (thus not showing a dosage effect) and the model parameters were not fit to trial-by-trial data. In fact, when trial-by-trial fitting was attempted, no association of learning rate to DARPP-32 was evident (Frank et al. 2007) (cf. Table 1). Our results suggest an alternative mechanism: given that the ‘A’ allele expression in DARPP-32 was strongly associated with the LRI, it is possible that DARPP-32 plays a homeostatic role that maintains a balance between positive and negative learning updates. In other words, it may be that both the D1-pathway and the D2-pathway modulate DARPP-32 expression in opposite ways, and this modulation, in turn, increases or decreases plasticity of the same circuits, thus enforcing stability. By this account, DARPP-32 ‘A’ alleles improve reward learning by contributing to balanced learning from positive and negative prediction errors rather than by directly influencing the magnitude of updates following positive prediction errors alone.

5. Conclusions

In this study, we have shown that age has at least two distinct effects on the ability to learn from probabilistic feedback, both potentially different than the ones observed in Parkinson’s disease. In addition, we showed through simulations that the well-known Probabilistic Selection Task actually distinguishes between balanced and non-balanced learning rates rather than reward and punishment learning. Our model-derived LRI index, which was highly successful in explaining behavioral results in both our Quarters task and the Probabilistic Selection Task, may prove to be a better characterization of striatal learning than either reward or punishment-related parameters separately.

Beyond its relevance to aging research, our work has implications for studies of human reinforcement learning in general. Even after collecting data from large samples of participants, the standard ANOVAs on our behavioral data only showed weak interactions between age and feedback condition. However, after using a reinforcement learning model to formalize the learning process, we revealed specific mechanisms that distinguish behavior under different types of reinforcement. A possible reason for why the standard ANOVAs were not able to fully capture age-dependent differences between positive and negative feedback conditions could be the different distributions of performance scores for the feedback conditions (a bimodal distribution for positive feedback compared to a unimodal skewed distribution for negative feedback), highlighting the limitations of over-reliance on average performance measures in characterizing learning. One implication of the bimodal distribution is that, in principle, some participants are unlikely to ever learn the optimal solution, even if they are given an indefinite opportunity to train. This contrasts what is expected from a unimodal learning profile, where further learning should eventually lead to perfect performance as the distribution’s variance is reduced to a minimum. The current work shows that models can, in fact, capture these differences, emphasizing the importance of such approaches in analyzing human behavioral data.

That said, the model-based analyses presented here are just a first step in the direction of computational formalization of theories in aging and reinforcement learning. Future work may incorporate additional statistical techniques for parameter estimation, including hierarchical Bayesian methods and others, which may reveal further insights into the behavioral data and the underlying mechanisms.

Highlights.

Deficits in feedback learning characterizing healthy aging sometimes resemble those found in Parkinson’s disease (PD). Since both healthy aging and PD are characterized by striatal dopamine depletion, some have suggested similar mechanisms are in play; yet other studies question this view. Employing behavioral, computational and genetic methods in a large cohort of 252 healthy subjects from three different age groups, we show that age-related feedback learning impairments stem from two distinct mechanisms, one related to decision noise and the other to dopamine-dependent imbalance in learning from positive and negative feedback, and neither is similar to the typical PD impairments. We replicate past results using our model and demonstrate the importance of analyzing performance score distributions rather than just averages.