Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2019 Aug 1.
Published in final edited form as: Neurobiol Aging. 2018 Apr 24;68:151–158. doi: 10.1016/j.neurobiolaging.2018.04.009

Classifying Alzheimer’s disease with brain imaging and genetic data using a neural network framework

Kaida Ning a,b, Bo Chen c, Fengzhu Sun b, Zachary Hobel a, Lu Zhao a, Will Matloff a,d; For the Alzheimer’s Disease Neuroimaging Initiative1, Arthur W Toga a,*
PMCID: PMC5993633  NIHMSID: NIHMS963227  PMID: 29784544

Abstract

A long-standing question is how to best use brain morphometric and genetic data to distinguish AD patients from cognitively normal (CN) subjects and to predict those who will progress from mild cognitive impairment (MCI) to AD. Here we use a neural network (NN) framework on both magnetic resonance imaging-derived quantitative structural brain measures and genetic data to address this question. We tested the effectiveness of NN models in classifying and predicting AD. We further performed a novel analysis of the NN model to gain insight into the most predictive imaging and genetics features, and to identify possible interactions between features that affect AD risk. Data was obtained from the Alzheimer's Disease Neuroimaging Initiative (ADNI) cohort and included baseline structural MRI data and single nucleotide polymorphism (SNP) data for 138 AD patients, 225 CN subjects, and 358 MCI patients. We found that NN models with both brain and SNP features as predictors perform significantly better than models with either alone in classifying AD and CN subjects, with an area under the receiver operating characteristic curve (AUC) of 0.992, and in predicting the progression from MCI to AD (AUC=0.835). The most important predictors in the NN model were the left middle temporal gyrus volume, the left hippocampus volume, the right entorhinal cortex volume, and the APOE ε4 risk allele. Further, we identified interactions between the right parahippocampal gyrus and the right lateral occipital gyrus, the right banks of the superior temporal sulcus and the left posterior cingulate, and SNP rs10838725 and the left lateral occipital gyrus. Our work shows the ability of NN models to not only classify and predict AD occurrence, but also to identify important AD risk factors and interactions among them.

Keywords: Alzheimer’s disease, Mild cognitive impairment, Brain imaging, Genetics, Neural network, Understanding neural network

1. Introduction

Alzheimer disease (AD) is characterized by specific brain structural changes and genetic risk factors (Lambert et al., 2013; Weiner et al., 2015; Weiner et al., 2013). Measurements of structural changes based on brain magnetic resonance imaging (MRI) scans have previously been used to classify AD patients versus cognitively normal (CN) subjects and to predict the risk of progression from mild cognitive impairment (MCI) to AD. Statistical classification models, such as support vector machines (Aguilar et al., 2013; Da et al., 2014; Davatzikos et al., 2011; Davatzikos et al., 2009; Orru et al., 2012; Wolz et al., 2011), linear discriminant analysis (Eskildsen et al., 2015; Wolz et al., 2011), and regression models (Desikan et al., 2009; Liu et al., 2013; Young et al., 2013), etc., have been successfully trained for that. On the other hand, AD risk is also affected by genetic variants an individual carries, which can be measured accurately from birth (Lambert et al., 2013). Previous studies have also used genome-wide genetic information alone to predict AD occurrence with a logistic regression (LR) model (Ebbert et al., 2014; Escott-Price et al., 2015). With the growing availability of data that includes both brain imaging and genetic data for AD and CN subjects, researchers have combined the structural imaging data and genetic data for these AD classification and prediction tasks (Da et al., 2014; Kong et al., 2015; Zhang et al., 2014). Existing studies in AD classification and prediction have relied on statistical models that primarily include additive effects of the included structural imaging and genetic features. However, the estimation of AD risk may be more accurate if interactions among brain and genetic features are also included in these models (Delbeuck et al., 2003; Ebbert et al., 2014; Montembeault et al., 2016). To the best of our knowledge, no research study has systematically investigated these interactions while building statistical models for classifying AD subjects.

To capture the joint effects of brain and genetic features in AD risks as well as the interactions among them, we chose neural network (NN) as our modeling tool (Hinton and Salakhutdinov, 2006). NNs have led to critical breakthroughs in modern artificial intelligence problems such as visual recognition and speech recognition (Hinton and Salakhutdinov, 2006; Krizhevsky et al., 2012; LeCun et al., 2015; Silver et al., 2016). Critical to their success is the NN’s ability to extract complex interactions from data through transformation functions in the layers of nodes connected within the NNs (Gunther et al., 2009; LeCun et al., 2015). For this reason, NNs are well suited for investigating diseases with multifactorial pathophysiology and etiology, like AD, especially as datasets of neuroimaging and genetic data grow in volume.

While NN models have been exceptionally successful at making predictions, they are typically applied as "black-box" tools and not used to reveal the reasoning behind the decisions. As a result, although NNs have been applied to predict AD risks (Aguilar et al., 2013; Sankari and Adeli, 2011), the important brain and genetic features and their interactions captured by the models remain elusive. Recent advances in methods for interpretation of NN models allow researchers to identify these salient and interacting features(Ribeiro et al., 2016; Sundararajan et al., 2017; Tsang et al., 2017; Zeiler and Fergus, 2014). We take advantage of similar methods to not only train a NN model for AD classification, but also to investigate this model to identify the important predictors and interactions in the model.

In this study, we trained NN models using structural MRI and genetic data from the Alzheimer's Disease Neuroimaging Initiative (ADNI) AD patients and CN subjects. We then applied the trained models to MCI patients for predicting the risk of progression to AD and assessed the performance of the models. We then further investigated the trained NN model to identify important features and interactions among these features.

2. Materials and Methods

2.1. Description of ADNI subjects in the study

We used brain imaging and genetic data from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database (http://adni.loni.usc.edu), a large dataset established in 2004 to measure the progression of healthy and cognitively impaired participants with brain scans, biological markers, and neuropsychological assessments (Petersen et al., 2010). A goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD).

In total, 138 AD patients, 225 CN subjects, and 358 MCI patients who had quality-controlled quantitative brain structural data and genetic data were included. AD subjects were included if they maintained AD diagnosis throughout their follow-ups. Similarly, healthy control subjects were included if they maintained healthy control diagnosis throughout their follow-ups. We did not require 24 months of follow-up for the AD and healthy control subjects. Only MCI subjects who stayed as MCI or progressed to AD were considered. MCI subjects who reverted to a healthy control diagnosis were excluded. Among the 358 MCI patients, 166 progressed from MCI to AD during follow-up; 192 did not progress during at least 24 months of follow-up. Demographic information of the subjects used in our study is summarized in Table 1.

Table 1.

Demographic characteristics of Alzheimer’s disease, mild cognitive impairment, and healthy control subjects.

Diagnostic Number Female|Male Age (median[min-max])
Cognitively Normal 225 113|112 74[56–90]
Alzheimer's Disease 138 60|78 75[56–91]
Mild Cognitive Impairment 358 148|210 73[55–88]
Open in a new tab

2.2. MRI brain imaging data and genotype data

Baseline imaging data was obtained using 1.5T or 3T MRI. Cortical reconstruction and volumetric segmentation was performed using FreeSurfer (Fischl, 2012; Miriam Hartig, 2014) and obtained from the ADNI database. Subjects who had good overall segmentation and passed a visual quality control process were used in our analyses. Based on prior knowledge of brain regions affected by AD(Weiner et al., 2015; Weiner et al., 2013), we included volume measurements for the following 16 regions as potential predictors in our models: hippocampus, entorhinal cortex, parahippocampal gyrus, superior temporal gyrus, middle temporal gyrus, inferior temporal gyrus, amygdala, precuneus, inferior lateral ventricle, fusiform, posterior cingulate, superior parietal lobe, inferior parietal lobe, caudate, banks of superior temporal sulcus, lateral occipital gyrus.

ADNI subjects were genotyped on three different platforms (i.e., Illumina Human 610-Quad, Illumina Human Omni Express and Illumina Omni 2.5M). We merged the genotype data from the three platforms. Quality control ensured that 1) all subjects were of European ancestry and had genotyping rate greater than 0.95; 2) all SNPs had missing rate less than 0.05 and passed Hardy-Weinberg exact test (i.e., p-value >= 1E-6). We further extracted the genotype of APOE ε4 risk allele and 19 SNPs reported to be significantly associated with AD in a previous genome-wide association study (Lambert et al., 2013). Missing genotypes of AD-associated SNPs were imputed with IMPUTE2 using 1000 genome as reference panel (Howie et al., 2011; Howie et al., 2009).

2.3. Neural network and logistic regression models

We trained NN and LR models to classify AD versus healthy control subjects given brain and SNP features as predictors. After training the models, we applied them to MCI subjects to predict each MCI subject's risk of progression to AD.

A LR model assumes that each predictor contributes additively to the subject’s log odds of AD, (see Equation 1).

logp1−p=β0+∑i=0mβixi (1)

Here p is the probability that a subject has disease; β0 is a bias term; βi is the weight of input feature xi, reflecting the strength and directionality of xi in affecting p, and m is the number of input features.

A NN is a network whose nodes (or “artificial neurons”) encode information with their activation level (a real-valued number). We will refrain from referring to these nodes as artificial neurons to avoid confusion with biological neurons. In a NN, nodes are organized in multiple layers: an input layer, one or more hidden layers and an output layer. Nodes in the input layer represent the brain and SNP features as predictors, nodes in the second and third layers allow interactions among the predictors in the first layer, and the output layer contains a single node that represents the disease risk (Figure 1).

Figure 1.

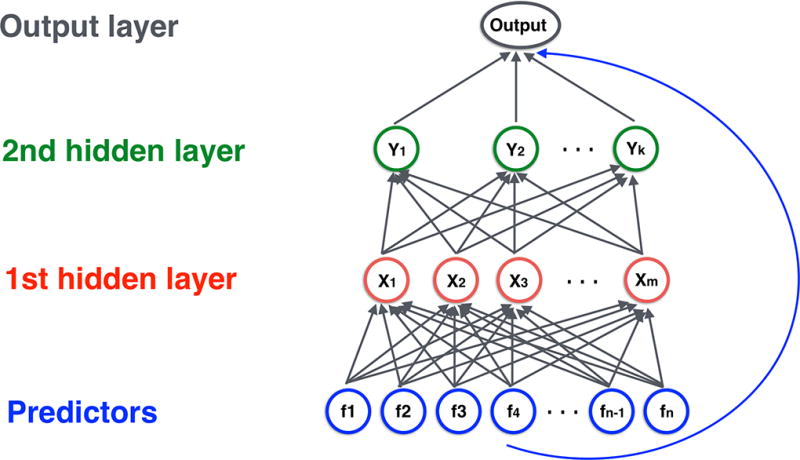
Figure 1

Open in a new tab

Structure of neural network model with two hidden layers. Neurons in the input layer holds the brain and SNP features, neurons in the second and third layers allowed interactions among the features in the first layer, and the output layer contains a single neuron that represents the disease risk. Adjacent layers are fully connected. All neurons in the input layer are connected directly to the output layer.

More specifically, in a NN with L layers, let hil denote the activation level of a node j in the l-th hidden layer, and ml denote the number of hidden units in this layer. We overload this notation to use hi0 to represent the input features xi. Each hidden unit activation is computed as the weighted sum of the nodes’ activations from the layer below followed by a non-linear transformation function f(x) (see Equation 2).

hjl=f(bjl+∑i=1ml−1hil−1wijl),l=1,…,L−1 (2)

Here wijl is the weight of the connection from hil−1, the i -th node in layer l-1, to hjl, the (j -th node in layer l. bjl is a bias term that regulates the overall activation level for node j. The non-linear function f in our model is the rectified linear function (ReLU): f(x) = max(0, x).

In the output layer, the NN predicts the log odds of AD using a weighted sum of the hidden layer features, (see Equation 3)

logp1−p=bL+∑i=1mL−1hiL−1wiL (3)

where bL and wiL are the corresponding bias and weights for the output layer. The weights and biases for all layers are learned from the training data (LeCun et al., 2015).

Contrasting Equation 3 with Equation 1, we see that the last layer of a NN is identical to a LR model except that the "features" are replaced with hidden activations at layer L-1, which are highly nonlinear functions of the input.

2.3.1. Shortcut connections

We additionally employ shortcut connections that connect all nodes in the input layer directly to the output layer (He et al., 2015; Ripley, 1996). This connectivity structure can be considered as a hybrid between LR and NN, which allows our network to not waste resources modeling additive effects in the input features and reserve the NN for complex interactions only. To prevent over-fitting we used L1 regularization on the weights and early stopping for both NN and LR models (Tibshirani, 1996). We trained both NN and LR models using MatConvNet package (Vedaldi and Lenc, 2015) with identical training protocols, which allowed fair comparison of the two models.

2.4. Procedures for model training and testing

2.4.1. Predictors in the models

We included brain and genetic features described in section 2.2 as predictors in the models. We adjusted for age, gender, education and first three principal components derived from the genetic data by including them as predictors. All predictors were normalized to have a mean of zero and a variance of 1 across subjects.

2.4.2. Random sampling and model training

We used a random selection of 80% of the AD and healthy control subjects for training models, and 20% of the remaining subjects for internal validation (i.e., for selecting the number of training iterations of NN and LR models). This random selection of samples was repeated 100 times for each model in order to take into account variations in the data. After training the models, we applied them to the MCI subjects to test their ability to predict progression to AD.

2.4.3. Hyper-parameters in the NN and LR models

The hyper-parameters explored include learning rate (ranging from 1E-3 to 1E-1) and weight decay (ranging from 1E-5 to 1). We also explored the number of hidden nodes in the two hidden layers for NN model (ranging from 2, 4, 8, up to 64 nodes in each layer). In total, we assessed 100 NN models with different hyper-parameter combinations, where the hyper-parameters were randomly selected from the afore-mentioned ranges. For each NN model with a specific hyper-parameter combination, we trained a corresponding LR model with the same learning rate and weight decay parameter values. Therefore, we trained 100 NN models, along with their corresponding LR models, where each model was trained and validated using 100 sets of randomly selected AD and healthy control subjects.

2.4.4. Model evaluation

Accuracy of models was evaluated using receiver operating characteristic curve (ROC). Since a model with a specific hyper parameter combination was trained and validated using data of 100 subsets of random AD and healthy control subjects, 100 “sub-models” (i.e., each sub-model has its own estimations of the weight parameters) were obtained for that model. Thus, we used median area under the ROC curve (AUC) of these 100 sub-models to represent a model's accuracy when applying it to the internal validation data and the testing data.

2.5. Identifying important brain and SNP features

After training the NN models where both brain and SNP features were used as predictors, we assessed the NN model with the highest accuracy in the testing data and identified brain and SNP features that were important in the model. Within a trained NN model, the importance of a feature is estimated with partial derivatives method (Gevrey et al., 2003): for each predictor xi, we took the derivative of the predicted log likelihood ratio of a subject s having AD with respect to xi and then averaged the derivative over all subjects: the importance score of xi=Es(∂ log(ps/(1−ps))∂xi), where ps is the predicted AD risk of subject s. The importance score is computed over all 100 rounds of the best-performance model, and the magnitude of the median score is used to represent the importance of predictor xi.

The same definition of importance predictors could be applied to the LR models. For LR models whose log likelihood ratio is given by Equation (1), the importance score of xi evaluates to βi. In other words, the importance of a feature is given by the corresponding regression coefficient. This is consistent with how LR has been used to assess predictor importance. We also note that since the predictors were normalized to have mean of zero and variance of 1, the importance score of the predictors we report is not dependent on scale and is comparable to each other.

2.6. Identifying interactions among features

We identified pairwise interactions among brain and SNP features by investigating the best-performing NN and LR models on the test set. Within a trained model, the pair-wise interaction between features xi and xj is defined as Iij=Es(∂2 log(ps/(1−ps))∂xi∂xj), where ps is the predicted probability that subject s has AD. Note that for LR, the interaction above has a closed-form solution, which is Iij = 0 for all xi and xj. This serves as a sanity check that LR does not model pair-wise interactions among its predictors.

For NNs, Iij does not admit a closed-form solution and must be computed numerically, which may introduce estimation errors. Leveraging the fact that the theoretical interaction scores for LR models are always 0, we apply the same numerical procedure to estimate the interaction scores for both NN and LR models, and quantify the significance of an interaction in NN by testing how significantly its score differs from the corresponding score in a LR model. In particular, we calculated pair-wise interactions in the 100 NN sub-models of the best-performing NN model. We also calculated pair-wise interactions in the LR model that had the same hyper-parameters as the best-performing NN model. For a given pair of features, we compared their interaction in the 100 NN sub-models and in the 100 LR sub-models using Wilcoxon test, then reported the interaction strength as −log(p-value).

3. Results

3.1. Models’ performance in classifying AD and in predicting progression from MCI to AD

Models that included both brain morphometric and genetic data performed significantly better than those that included either alone. Our analyses showed that when both brain and SNP features were included as predictors, the 100 sub-models of the best-performing NN model had a median AUC of 0.835 in predicting MCI progression. When only SNP features or brain features were used as predictors, the best-performing NN model had a median AUC of 0.689 and 0.820, respectively. Performance of the 100 NN sub-models with both brain and SNP features as predictors were significantly higher than that of the 100 NN sub-models with only SNP features or only brain features as predictors (t-test p-value <2E-16 for both comparisons).

Further, the best-performing NN model had a moderately, significantly higher AUC than the best-performing LR model where both brain and SNP features were included as predictors (the 100 sub-models of the best-performing LR model had a median AUC of 0.824 in predicting MCI progression; t-test p-value <2E-16), indicating that NN captured interactions among brain and SNP features which improved the model's performance. Figure 2 shows the AUC of the 100 sub-models of the best-performing NN and LR models where only SNP features or only brain features were used as predictors and where both features were used as predictors. We also note that random sampling of the training and validation data affected the models' performance: the 100 sub-models of the best NN model had an AUC between 0.811 and 0.846 in predicting MCI progression.

Figure 2.

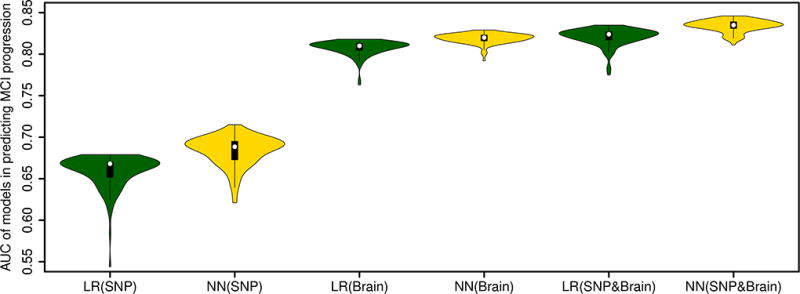
Figure 2

Open in a new tab

Accuracy (measured as area under the receiver operating characteristic curves, or AUC) of the best-performing neural network and logistic regression models in predicting progression from mild cognitive impairment to Alzheimer’s disease. Three types of models are compared: 1) models with only SNP feature predictors; 2) models with only brain feature predictors; 3) models with both SNP and brain feature predictors.

Both NN and LR models had high accuracy in classifying AD and CN subjects. According to the internal validation data, the best-performing NN model with both brain and SNP predictors had a median AUC of 0.948 while the best-performing LR model with both brain and SNP predictors had a median AUC of 0.945.

3.2. Important brain and SNP features used by NN model

Examination of the NN model with the highest AUC in the testing data revealed brain and SNP features that were important in the model. The volume of the left middle temporal gyrus, the left hippocampus, the right entorhinal cortex, the left inferior lateral ventricle and the right inferior parietal lobe were the five most important brain features in the model (i.e., these features had the largest absolute weights). As for genetic features, the APOE ε4 risk allele dosage, a major AD genetic risk factor (Lambert et al., 2013; Saunders et al., 1993), had the highest weight in the NN model. Other genetic features did not have weight as large as the aforementioned features. Table 2 lists the weight of the 5 most important brain and genetic features in the best-performing NN model. Supplementary Table 1 lists the weight of all the brain and genetic features in the best-performing NN model.

Table 2.

Weight of important features for classifying AD patients and CN subjects in the neural network model. The gene labels of the SNPs are based on the labels reported by Lambert et al. (Lambert et al., 2013).

Brain features Weight Genetic features Weight
Left Middle Temporal Gyrus 0.60 APOE ε4 dosage 0.86
Left Hippocampus 0.56 rs10948363 (CD2AP) 0.29
Right Entorhinal Cortex 0.52 rs7274581 (CASS4) 0.29
Left Inferior Lateral Ventricle 0.48 rs17125944 (FERMT2) 0.24
Right Inferior Parietal Lobule 0.40 rs4147929 (ABCA7) 0.22
Open in a new tab

3.3. Interactions among brain and genetic features captured by NN model

Our analyses of interactions within the best-performing NN model revealed that both brain and genetic features were involved in strong interactions. For example, the strongest interaction captured by NN model was between the right parahippocampal gyrus and the right lateral occipital gyrus. The second strongest interaction was between the right banks of the superior temporal sulcus and the left posterior cingulate. The interaction between the SNP rs10838725 and the left lateral occipital gyrus was the third strongest interaction. Figure 3 shows the pairwise interaction among all the brain and genetic features used in the NN model. More details of the interaction strengths are listed in Supplementary Table 2.

Figure 3.

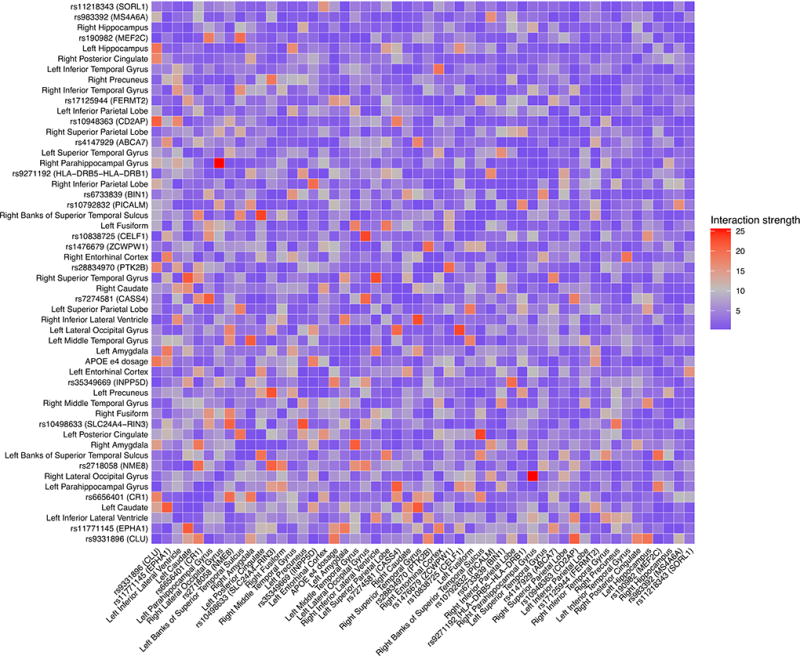
Figure 3

Open in a new tab

Strength of pairwise interactions among all the brain and genetic features used in the neural network model. The gene labels of the SNPs are based on the labels reported by Lambert et al. (Lambert et al., 2013).

4. Discussion

In this study, we systematically employed NN models for classifying AD patients and CN subjects and then investigated the ability of the trained NN models to identify important predictors and interactions in the models.

We found that including both brain and genetic features as model predictors increased the models' performance compared with only including either brain or SNP features in the models. Genetic features were important for predicting MCI progression: a random prediction usually yields an AUC around 0.5, while using genetic features as predictors increased the median AUC of the best-performing NN models to 0.689. In comparison, the best-performing NN models with brain features alone as predictors had better performance in predicting MCI progression, with a median AUC of 0.820. Including both brain and SNP features as predictors in the models further increased the models’ prediction accuracy by a moderate amount: median AUC of the best-performing NN models reached 0.835. Although the combined brain and SNP features achieves a higher AUC, it is worth noting that while the SNP features are available at birth, the brain features may not reflect the neurodegenerative changes associated with AD risks for subjects at a younger age (Jack et al., 2015; Jack et al., 2014).

Analyses of the trained NN models indicated that measurements of the middle temporal gyrus, the hippocampus and the entorhinal cortex were the most important brain features for predicting AD risks. The hippocampus plays an important role in memory formation and is well known to be affected by AD (Scheltens et al., 1992; Weiner et al., 2015; Weiner et al., 2013). Further, a previous study reported that these three structures were among the ones with the largest effect size on MCI progression (Risacher et al., 2009). As for genetic features, APOE ε4 risk allele dosage had the highest weight in the NN model. While GWAS had identified other genetic loci significantly associated with AD risks (Lambert et al., 2013), the weights of those features were lower than those of the aforementioned brain features in the model.

While the NN model performed significantly better than the LR model (p-value <2e-16), the performance increase is modest. The median AUC of the best-performing LR model was 0.824, while median AUC of the best-performing NN model was 0.835. Over all, the interaction effects were subtle compared to the additive effects. However, this modest performance increase, which is likely a result of the NN modeling interactions among predictors, provides evidence that there do exist interactions among the brain and genetic features. Beyond building the NN models for classification and prediction, there is important knowledge about disease pathophysiology to be gained in studying the interactions within them. Existing NN models of AD risk have all been treated as a black-box and not further investigated. For the first time in the field of imaging genetics, we use very recently developed NN analysis techniques to investigate the NN models and identify the important interactions among the brain and genetic features in affecting AD risk.

Our novel analysis of the trained NN model revealed three strong interactions of AD risk factors, each of which are biologically plausible, provide insight into the pathophysiology of AD, and warrant further study. First, the NN identified a strong interaction between the right parahippocampal gyrus and the right lateral occipital gyrus. A relevant finding was reported by Sommer et al. (Sommer et al., 2005), who observed correlated activity in the occipital and the parahippocampal cortex during encoding and the resulting memory trace. We would therefore expect AD patients to have aberrant connectivity between these two regions, either structurally or functionally as measured by diffusion weighted MRI or functional MRI. Second, the NN identified an interaction between the right banks of the superior temporal sulcus and the left posterior cingulate. The posterior cingulate cortex is a central part of the default mode network in the brain and is known to have prominent projections to the superior temporal sulcus (Leech and Sharp, 2014). Third, the NN found an interaction between the SNP rs10838725 and the left lateral occipital gyrus. Recent evidence suggests that the functional gene of this SNP with respect to AD is the SPI1 gene, which plays a role in myeloid cell function (Huang et al., 2017). Neuroinflammation in AD, which is mediated by myeloid cells, is known to occur in the occipital cortex (Kreisl et al., 2013). The mechanism of interactions among such brain and genetic features require further study.

Our study has some limitations. First, there are different ways to define MCI progression versus non-progression. Longer follow-up time may allow us to observe more MCI patients progressing to AD. The models’ accuracy in predicting MCI progression may change when different definitions of progression are used and when observations from longer follow-up are used. Second, as more GWAS are carried out, our understanding of the SNPs and genes associated with AD will get updated. Therefore, the importance score of the predictors and the predictor interactions should be interpreted with that in mind and would need further validation. Third, since NN models have more parameters than LR models, more data points are needed to train the NN models (Geman et al., 1992). It is possible that with a larger sample size, NN may have a more significant advantage compared to LR models. Also, our findings on the important predictors and interactions among predictors may get refined and updated as the sample size increases. Fourth, the NN models with different structures may have different performance. In our analyses, we used a structure with two hidden layers and a direct connection between the input layer and the output layer. As a comparison, in the previous studies using NN models for classifying AD, only two hidden layers were used, and no direct connection was built between the input layer and the output layer (Aguilar et al., 2013; Sankari and Adeli, 2011). Finally, interpreting NN models remains an open research topic. Our definition of important predictors and interactions was based on derivatives of the log likelihood of disease risk, while alternative definitions (Gevrey et al., 2003; Olden et al., 2004; Tsang et al., 2017; Zeiler and Fergus, 2014) may reveal other insights into the model.

To summarize, we trained NN models for classifying AD and CN subjects, yielding models with good performance on the task of classifying and predicting AD. Our novel analyses of the trained NN models led to findings of important brain and genetic features and interactions among them that affect AD risk, which can guide future research on AD etiology. Our approach of training and investigating NN models can be particularly valuable for understanding etiology of diseases that have multiple, interacting risk factors.

Supplementary Material

1

Supplementray Table 1. Weight of brain and genetic features for classifying AD patients and CN subjects in the neural network model.

2

Supplementray Table 2. Pairwise interaction strength among brain and genetic features in the neural network model.

Highlights.

Neural networks perform well in classifying AD and predicting MCI progression.

Combining brain and genetic data is optimal for classification and prediction of AD.

Analyzing neural networks reveals important features and feature interactions.

Acknowledgments

This work was supported by grants P41EB015922, U54EB020406 and R01MH094343 of the National Institutes of Health.

Data collection and sharing for this project was funded by the Alzheimer's Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Therapeutic Research Institute at the University of Southern California. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Aguilar C, Westman E, Muehlboeck JS, Mecocci P, Vellas B, Tsolaki M, Kloszewska I, Soininen H, Lovestone S, Spenger C, Simmons A, Wahlund LO. Different multivariate techniques for automated classification of MRI data in Alzheimer's disease and mild cognitive impairment. Psychiatry Res. 2013;212(2):89–98. doi: 10.1016/j.pscychresns.2012.11.005. [DOI] [PubMed] [Google Scholar]
  2. Da X, Toledo JB, Zee J, Wolk DA, Xie SX, Ou Y, Shacklett A, Parmpi P, Shaw L, Trojanowski JQ, Davatzikos C, Alzheimer's Neuroimaging, I Integration and relative value of biomarkers for prediction of MCI to AD progression: spatial patterns of brain atrophy, cognitive scores, APOE genotype and CSF biomarkers. Neuroimage Clin. 2014;4:164–173. doi: 10.1016/j.nicl.2013.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Davatzikos C, Bhatt P, Shaw LM, Batmanghelich KN, Trojanowski JQ. Prediction of MCI to AD conversion, via MRI, CSF biomarkers, and pattern classification. Neurobiology of aging. 2011;32(12):2322, e2319–2327. doi: 10.1016/j.neurobiolaging.2010.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Davatzikos C, Xu F, An Y, Fan Y, Resnick SM. Longitudinal progression of Alzheimer's-like patterns of atrophy in normal older adults: the SPARE-AD index. Brain. 2009;132(Pt 8):2026–2035. doi: 10.1093/brain/awp091. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Delbeuck X, Van der Linden M, Collette F. Alzheimer's disease as a disconnection syndrome? Neuropsychol Rev. 2003;13(2):79–92. doi: 10.1023/a:1023832305702. [DOI] [PubMed] [Google Scholar]
  6. Desikan RS, Cabral HJ, Hess CP, Dillon WP, Glastonbury CM, Weiner MW, Schmansky NJ, Greve DN, Salat DH, Buckner RL, Fischl B, Alzheimer's Disease Neuroimaging, I Automated MRI measures identify individuals with mild cognitive impairment and Alzheimer's disease. Brain. 2009;132(Pt 8):2048–2057. doi: 10.1093/brain/awp123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Ebbert MT, Ridge PG, Wilson AR, Sharp AR, Bailey M, Norton MC, Tschanz JT, Munger RG, Corcoran CD, Kauwe JS. Population-based analysis of Alzheimer's disease risk alleles implicates genetic interactions. Biol Psychiatry. 2014;75(9):732–737. doi: 10.1016/j.biopsych.2013.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Escott-Price V, Sims R, Bannister C, Harold D, Vronskaya M, Majounie E, Badarinarayan N, Gerad/Perades, consortia I, Morgan K, Passmore P, Holmes C, Powell J, Brayne C, Gill M, Mead S, Goate A, Cruchaga C, Lambert JC, van Duijn C, Maier W, Ramirez A, Holmans P, Jones L, Hardy J, Seshadri S, Schellenberg GD, Amouyel P, Williams J. Common polygenic variation enhances risk prediction for Alzheimer's disease. Brain. 2015;138(Pt 12):3673–3684. doi: 10.1093/brain/awv268. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Eskildsen SF, Coupe P, Fonov VS, Pruessner JC, Collins DL, Alzheimer's Disease Neuroimaging, I Structural imaging biomarkers of Alzheimer's disease: predicting disease progression. Neurobiology of aging. 2015;36(Suppl 1):S23–31. doi: 10.1016/j.neurobiolaging.2014.04.034. [DOI] [PubMed] [Google Scholar]
  10. Fischl B. FreeSurfer. Neuroimage. 2012;62(2):774–781. doi: 10.1016/j.neuroimage.2012.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Geman S, Bienenstock E, Doursat R. Neural networks and the bias/variance dilemma. Neural computation 1992 [Google Scholar]
  12. Gevrey M, Dimopoulos I, Lek S. Review and comparison of methods to study the contribution of variables in artificial neural network models. Ecological modelling. 2003;160(3):249–264. [Google Scholar]
  13. Gunther F, Wawro N, Bammann K. Neural networks for modeling gene-gene interactions in association studies. BMC Genet. 2009;10:87. doi: 10.1186/1471-2156-10-87. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. He K, Zhang X, Ren S, Sun J. Deep Residual Learning for Image Recognition. arXiv:1512.03385 2015 [Google Scholar]
  15. Hinton GE, Salakhutdinov RR. Reducing the dimensionality of data with neural networks. Science. 2006;313(5786):504–507. doi: 10.1126/science.1127647. [DOI] [PubMed] [Google Scholar]
  16. Howie B, Marchini J, Stephens M. Genotype imputation with thousands of genomes. G3 (Bethesda) 2011;1(6):457–470. doi: 10.1534/g3.111.001198. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Howie BN, Donnelly P, Marchini J. A flexible and accurate genotype imputation method for the next generation of genome-wide association studies. PLoS Genet. 2009;5(6):e1000529. doi: 10.1371/journal.pgen.1000529. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Huang KL, Marcora E, Pimenova AA, Di Narzo AF, Kapoor M, Jin SC, Harari O, Bertelsen S, Fairfax BP, Czajkowski J, Chouraki V, Grenier-Boley B, Bellenguez C, Deming Y, McKenzie A, Raj T, Renton AE, Budde J, Smith A, Fitzpatrick A, Bis JC, DeStefano A, Adams HHH, Ikram MA, van der Lee S, Del-Aguila JL, Fernandez MV, Ibanez L, International Genomics of Alzheimer's, P., Alzheimer's Disease Neuroimaging, I. Sims R, Escott-Price V, Mayeux R, Haines JL, Farrer LA, Pericak-Vance MA, Lambert JC, van Duijn C, Launer L, Seshadri S, Williams J, Amouyel P, Schellenberg GD, Zhang B, Borecki I, Kauwe JSK, Cruchaga C, Hao K, Goate AM. A common haplotype lowers PU.1 expression in myeloid cells and delays onset of Alzheimer's disease. Nat Neurosci. 2017;20(8):1052–1061. doi: 10.1038/nn.4587. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Jack CR, Jr, Wiste HJ, Weigand SD, Knopman DS, Vemuri P, Mielke MM, Lowe V, Senjem ML, Gunter JL, Machulda MM, Gregg BE, Pankratz VS, Rocca WA, Petersen RC. Age, Sex, and APOE epsilon4 Effects on Memory, Brain Structure, and beta-Amyloid Across the Adult Life Span. JAMA Neurol. 2015;72(5):511–519. doi: 10.1001/jamaneurol.2014.4821. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Jack CR, Jr, Wiste HJ, Weigand SD, Rocca WA, Knopman DS, Mielke MM, Lowe VJ, Senjem ML, Gunter JL, Preboske GM, Pankratz VS, Vemuri P, Petersen RC. Age-specific population frequencies of cerebral betaamyloidosis and neurodegeneration among people with normal cognitive function aged 50–89 years: a cross-sectional study. Lancet Neurol. 2014;13(10):997–1005. doi: 10.1016/S1474-4422(14)70194-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kong D, Giovanello KS, Wang Y, Lin W, Lee E, Fan Y, Murali Doraiswamy P, Zhu H. Predicting Alzheimer's Disease Using Combined Imaging-Whole Genome SNP Data. J Alzheimers Dis. 2015;46(3):695–702. doi: 10.3233/JAD-150164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kreisl WC, Lyoo CH, McGwier M, Snow J, Jenko KJ, Kimura N, Corona W, Morse CL, Zoghbi SS, Pike VW, McMahon FJ, Turner RS, Innis RB, Biomarkers Consortium, P.E.T.R.P.T In vivo radioligand binding to translocator protein correlates with severity of Alzheimer's disease. Brain. 2013;136(Pt 7):2228–2238. doi: 10.1093/brain/awt145. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks 2012 [Google Scholar]
  24. Lambert JC, Ibrahim-Verbaas CA, Harold D, Naj AC, Sims R, Bellenguez C, DeStafano AL, Bis JC, Beecham GW, Grenier-Boley B, Russo G, Thorton-Wells TA, Jones N, Smith AV, Chouraki V, Thomas C, Ikram MA, Zelenika D, Vardarajan BN, Kamatani Y, Lin CF, Gerrish A, Schmidt H, Kunkle B, Dunstan ML, Ruiz A, Bihoreau MT, Choi SH, Reitz C, Pasquier F, Cruchaga C, Craig D, Amin N, Berr C, Lopez OL, De Jager PL, Deramecourt V, Johnston JA, Evans D, Lovestone S, Letenneur L, Moron FJ, Rubinsztein DC, Eiriksdottir G, Sleegers K, Goate AM, Fievet N, Huentelman MW, Gill M, Brown K, Kamboh MI, Keller L, Barberger-Gateau P, McGuiness B, Larson EB, Green R, Myers AJ, Dufouil C, Todd S, Wallon D, Love S, Rogaeva E, Gallacher J, St George-Hyslop P, Clarimon J, Lleo A, Bayer A, Tsuang DW, Yu L, Tsolaki M, Bossu P, Spalletta G, Proitsi P, Collinge J, Sorbi S, Sanchez-Garcia F, Fox NC, Hardy J, Deniz Naranjo MC, Bosco P, Clarke R, Brayne C, Galimberti D, Mancuso M, Matthews F, European Alzheimer's Disease, I., Genetic, Environmental Risk in Alzheimer's, D., Alzheimer's Disease Genetic, C., Cohorts for, H., Aging Research in Genomic, E. Moebus S, Mecocci P, Del Zompo M, Maier W, Hampel H, Pilotto A, Bullido M, Panza F, Caffarra P, Nacmias B, Gilbert JR, Mayhaus M, Lannefelt L, Hakonarson H, Pichler S, Carrasquillo MM, Ingelsson M, Beekly D, Alvarez V, Zou F, Valladares O, Younkin SG, Coto E, Hamilton-Nelson KL, Gu W, Razquin C, Pastor P, Mateo I, Owen MJ, Faber KM, Jonsson PV, Combarros O, O'Donovan MC, Cantwell LB, Soininen H, Blacker D, Mead S, Mosley TH, Jr, Bennett DA, Harris TB, Fratiglioni L, Holmes C, de Bruijn RF, Passmore P, Montine TJ, Bettens K, Rotter JI, Brice A, Morgan K, Foroud TM, Kukull WA, Hannequin D, Powell JF, Nalls MA, Ritchie K, Lunetta KL, Kauwe JS, Boerwinkle E, Riemenschneider M, Boada M, Hiltuenen M, Martin ER, Schmidt R, Rujescu D, Wang LS, Dartigues JF, Mayeux R, Tzourio C, Hofman A, Nothen MM, Graff C, Psaty BM, Jones L, Haines JL, Holmans PA, Lathrop M, Pericak-Vance MA, Launer LJ, Farrer LA, van Duijn CM, Van Broeckhoven C, Moskvina V, Seshadri S, Williams J, Schellenberg GD, Amouyel P. Meta-analysis of 74,046 individuals identifies 11 new susceptibility loci for Alzheimer's disease. Nat Genet. 2013;45(12):1452–1458. doi: 10.1038/ng.2802. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521(7553):436–444. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
  26. Leech R, Sharp DJ. The role of the posterior cingulate cortex in cognition and disease. Brain. 2014;137(Pt 1):12–32. doi: 10.1093/brain/awt162. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Liu X, Tosun D, Weiner MW, Schuff N, Alzheimer's Disease Neuroimaging, I Locally linear embedding (LLE) for MRI based Alzheimer's disease classification. Neuroimage. 2013;83:148–157. doi: 10.1016/j.neuroimage.2013.06.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Miriam Hartig DT-S. Sky Raptentsetsang, Alix Simonson, Adam Mezher, Norbert Schuff, Michael Weiner, 2014. UCSF FreeSurfer Methods [Google Scholar]
  29. Montembeault M, Rouleau I, Provost JS, Brambati SM, Alzheimer's Disease Neuroimaging, I Altered Gray Matter Structural Covariance Networks in Early Stages of Alzheimer's Disease. Cereb Cortex. 2016;26(6):2650–2662. doi: 10.1093/cercor/bhv105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Olden JD, Joy MK, Death RG. An accurate comparison of methods for quantifying variable importance in artificial neural networks using simulated data. Ecological Modelling. 2004;178(3–4):389–397. [Google Scholar]
  31. Orru G, Pettersson-Yeo W, Marquand AF, Sartori G, Mechelli A. Using Support Vector Machine to identify imaging biomarkers of neurological and psychiatric disease: a critical review. Neurosci Biobehav Rev. 2012;36(4):1140–1152. doi: 10.1016/j.neubiorev.2012.01.004. [DOI] [PubMed] [Google Scholar]
  32. Petersen RC, Aisen PS, Beckett LA, Donohue MC, Gamst AC, Harvey DJ, Jack CR, Jr, Jagust WJ, Shaw LM, Toga AW, Trojanowski JQ, Weiner MW. Alzheimer's Disease Neuroimaging Initiative (ADNI): clinical characterization. Neurology. 2010;74(3):201–209. doi: 10.1212/WNL.0b013e3181cb3e25. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Ribeiro MT, Singh S, Guestrin C. Why should i trust you?: Explaining the predictions of any classifier; Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; 2016. pp. 1135–1144. [Google Scholar]
  34. Ripley BD. Pattern recognition and neural networks. Cambridge university press; 1996. [Google Scholar]
  35. Risacher SL, Saykin AJ, West JD, Shen L, Firpi HA, McDonald BC, Alzheimer's Disease Neuroimaging, I Baseline MRI predictors of conversion from MCI to probable AD in the ADNI cohort. Curr Alzheimer Res. 2009;6(4):347–361. doi: 10.2174/156720509788929273. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Sankari Z, Adeli H. Probabilistic neural networks for diagnosis of Alzheimer's disease using conventional and wavelet coherence. J Neurosci Methods. 2011;197(1):165–170. doi: 10.1016/j.jneumeth.2011.01.027. [DOI] [PubMed] [Google Scholar]
  37. Saunders AM, Strittmatter WJ, Schmechel D, George-Hyslop PH, Pericak-Vance MA, Joo SH, Rosi BL, Gusella JF, Crapper-MacLachlan DR, Alberts MJ, et al. Association of apolipoprotein E allele epsilon 4 with late-onset familial and sporadic Alzheimer's disease. Neurology. 1993;43(8):1467–1472. doi: 10.1212/wnl.43.8.1467. [DOI] [PubMed] [Google Scholar]
  38. Scheltens P, Leys D, Barkhof F, Huglo D, Weinstein HC, Vermersch P, Kuiper M, Steinling M, Wolters EC, Valk J. Atrophy of medial temporal lobes on MRI in "probable" Alzheimer's disease and normal ageing: diagnostic value and neuropsychological correlates. J Neurol Neurosurg Psychiatry. 1992;55(10):967–972. doi: 10.1136/jnnp.55.10.967. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Silver D, Huang A, Maddison CJ, Guez A, Sifre L, van den Driessche G, Schrittwieser J, Antonoglou I, Panneershelvam V, Lanctot M, Dieleman S, Grewe D, Nham J, Kalchbrenner N, Sutskever I, Lillicrap T, Leach M, Kavukcuoglu K, Graepel T, Hassabis D. Mastering the game of Go with deep neural networks and tree search. Nature. 2016;529(7587):484–489. doi: 10.1038/nature16961. [DOI] [PubMed] [Google Scholar]
  40. Sommer T, Rose M, Weiller C, Buchel C. Contributions of occipital, parietal and parahippocampal cortex to encoding of object-location associations. Neuropsychologia. 2005;43(5):732–743. doi: 10.1016/j.neuropsychologia.2004.08.002. [DOI] [PubMed] [Google Scholar]
  41. Sundararajan M, Taly A, Yan Q. Axiomatic attribution for deep networks. arXiv:1703.01365 2017 [Google Scholar]
  42. Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B. 1996;58(1):267–288. [Google Scholar]
  43. Tsang M, Cheng D, Liu Y. Detecting Statistical Interactions from Neural Network Weights. arXiv:1705.04977 2017 [Google Scholar]
  44. Vedaldi A, Lenc K. MatConvNet: Convolutional neural networks for MATLAB. Proceeding of the ACM Int. Conf. on Multimedia 2015 [Google Scholar]
  45. Weiner MW, Veitch DP, Aisen PS, Beckett LA, Cairns NJ, Cedarbaum J, Green RC, Harvey D, Jack CR, Jagust W, Luthman J, Morris JC, Petersen RC, Saykin AJ, Shaw L, Shen L, Schwarz A, Toga AW, Trojanowski JQ, Alzheimer's Disease Neuroimaging, I 2014 Update of the Alzheimer's Disease Neuroimaging Initiative: A review of papers published since its inception. Alzheimers Dement. 2015;11(6):e1–120. doi: 10.1016/j.jalz.2014.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Weiner MW, Veitch DP, Aisen PS, Beckett LA, Cairns NJ, Green RC, Harvey D, Jack CR, Jagust W, Liu E, Morris JC, Petersen RC, Saykin AJ, Schmidt ME, Shaw L, Shen L, Siuciak JA, Soares H, Toga AW, Trojanowski JQ, Alzheimer's Disease Neuroimaging, I The Alzheimer's Disease Neuroimaging Initiative: a review of papers published since its inception. Alzheimers Dement. 2013;9(5):e111–194. doi: 10.1016/j.jalz.2013.05.1769. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Wolz R, Julkunen V, Koikkalainen J, Niskanen E, Zhang DP, Rueckert D, Soininen H, Lotjonen J, Alzheimer's Disease Neuroimaging, I Multi-method analysis of MRI images in early diagnostics of Alzheimer's disease. PLoS One. 2011;6(10):e25446. doi: 10.1371/journal.pone.0025446. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Young J, Modat M, Cardoso MJ, Mendelson A, Cash D, Ourselin S, Alzheimer's Disease Neuroimaging, I Accurate multimodal probabilistic prediction of conversion to Alzheimer's disease in patients with mild cognitive impairment. Neuroimage Clin. 2013;2:735–745. doi: 10.1016/j.nicl.2013.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Zeiler MD, Fergus R. Visualizing and understanding convolutional networks. European conference on computer vision. 2014:818–833. [Google Scholar]
  50. Zhang Z, Huang H, Shen D, Alzheimer's Disease Neuroimaging, I Integrative analysis of multi-dimensional imaging genomics data for Alzheimer's disease prediction. Front Aging Neurosci. 2014;6:260. doi: 10.3389/fnagi.2014.00260. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1

Supplementray Table 1. Weight of brain and genetic features for classifying AD patients and CN subjects in the neural network model.

NIHMS963227-supplement-1.xlsx (9.6KB, xlsx)
2

Supplementray Table 2. Pairwise interaction strength among brain and genetic features in the neural network model.

NIHMS963227-supplement-2.xlsx (72.5KB, xlsx)

RESOURCES