Kinetics and Fidelity of the Repair of Cas9-Induced Double-Strand DNA Breaks

Summary

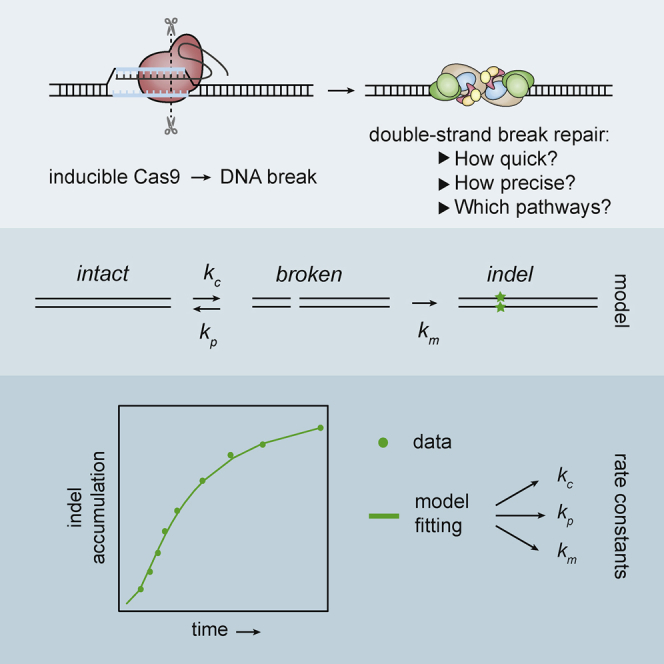
The RNA-guided DNA endonuclease Cas9 is a powerful tool for genome editing. Little is known about the kinetics and fidelity of the double-strand break (DSB) repair process that follows a Cas9 cutting event in living cells. Here, we developed a strategy to measure the kinetics of DSB repair for single loci in human cells. Quantitative modeling of repaired DNA in time series after Cas9 activation reveals variable and often slow repair rates, with half-life times up to ∼10 hr. Furthermore, repair of the DSBs tends to be error prone. Both classical and microhomology-mediated end joining pathways contribute to the erroneous repair. Estimation of their individual rate constants indicates that the balance between these two pathways changes over time and can be altered by additional ionizing radiation. Our approach provides quantitative insights into DSB repair kinetics and fidelity in single loci and indicates that Cas9-induced DSBs are repaired in an unusual manner.

Graphical Abstract

Highlights

• •Approach to measure single-locus DSB repair kinetics after Cas9-induced breaks
• •Multiple repair pathways can act on a single locus with distinct kinetics
• •Repair tends to be slow and error prone, although this depends on the locus

Brinkman et al. report a strategy to determine the rate and fidelity of double-strand break repair at single loci cut by Cas9. They also infer the contributions from different repair pathways. Cas9-induced breaks are repaired at variable but often slow rates, and the repair tends to be error prone.

Introduction

The CRISPR-Cas9 nuclease system is a powerful tool for genome editing due to its efficient targeting of specific sequences in the genome (Sander and Joung, 2014). Cas9 endonuclease is directed by a guide RNA to a specific target site in the genome, where it induces a single double-strand break (DSB) (Cong et al., 2013, Jinek et al., 2013, Mali et al., 2013). The break is subsequently repaired by the cellular DNA repair mechanisms that can introduce mutations in the target sequence (Jasin and Haber, 2016). This application of Cas9 has become widely popular to generate mutant alleles of genes and regulatory elements of interest. Despite the broad application, the process of repair of Cas9-induced DSBs has been only partially characterized. For example, it is not known how long it takes before an individual Cas9-induced DSB is repaired and how error prone this process is.

Eukaryotic cells have two main pathways for DSB repair: classical non-homologous end joining (C-NHEJ) and homologous recombination (HR) (Jasin and Haber, 2016). A large proportion of DSBs is repaired by C-NHEJ, which directly rejoins the two DNA ends. This type of repair is thought to be mostly perfect but may lead to insertions or deletions (indels) at the break site (Lieber, 2010). However, estimates of the frequency at which these indels occur are a matter of debate. The accuracy of rejoining is subject of debate and is thought to depend on the nature of the damaging agent and the end structures of the formed DSBs (Bétermier et al., 2014, Lieber, 2010). In contrast, HR is highly precise because it utilizes a homologous template sequence to restore the DNA sequences around the DSB (Greene, 2016). Apart from these two main pathways, there are alternative end joining (A-EJ) pathways that are thought to be highly mutagenic. One of these is microhomology-mediated end joining (MMEJ), which uses short sequence homologies near the two ends, leading to characteristic small deletions (McVey and Lee, 2008). Current evidence indicates that multiple pathways can contribute to the repair of Cas9-induced DSBs (Bothmer et al., 2017, van Overbeek et al., 2016), but the interplay and the relative contributions have remained largely uncharacterized. Moreover, the fidelity of these pathways in the context of Cas9-induced breaks is still largely unclear.

Related to this, it is still unknown how quickly a Cas9-induced break is repaired. DSBs have been measured by comet assays (Wang et al., 2013) or pulsed-field gel electrophoresis, typically (DiBiase et al., 2000) after exposure to high doses of ionizing radiation that cause hundreds of DSBs per cell. Time courses of such bulk measurements in mammalian cells have consistently shown that DSBs are generally repaired with a half-life of 10–60 min (DiBiase et al., 2000, Metzger and Iliakis, 1991, Núñez et al., 1995, Schwartz et al., 1988, Stenerlöw et al., 2003, Wang et al., 2006). Computational modeling of such datasets has indicated that a small sub-fraction of DSBs is rejoined more slowly, over several hours (Cucinotta et al., 2008, Metzger and Iliakis, 1991, Núñez et al., 1995, Woods and Barnes, 2016). A-EJ pathways are thought to be largely responsible for this population of more slowly repaired DSBs (Sharma et al., 2015, Wang et al., 2003). However, such bulk measurements of DSBs lack the sensitivity that is required to follow DSB repair at single loci.

Repair rates have also been inferred from immunofluorescent labeling of DSB markers, such as γH2A.X, which form transient foci at DSBs (Forment et al., 2012, Shibata et al., 2011). In irradiated mammalian cells, clearance of such foci typically takes 1–3 hr (Leatherbarrow et al., 2006, Shibata et al., 2011, Woodbine et al., 2015). Note that marker proteins at foci may linger at the DSB site after rejoining of the two DNA ends; hence, the actual repair may be quicker, as is strongly suggested by the direct DSB measurements mentioned above. So far, the rate of repair of individual Cas9-induced DSBs has remained unknown due to limitations of the available methods.

In principle, accumulation of mutations over time can be used to infer repair rates. A crude estimate based on indel detection suggested that about 15 hr were necessary to repair the majority of the Cas9-induced lesions (Kim et al., 2014). However, precise quantitative kinetics of actual rejoining of DNA ends after the induction of a DSB at a single defined genomic location are missing. One challenge is that perfectly repaired junctions are indistinguishable from DNA that was never broken, which may lead to systematic errors in the rate constants. Furthermore, when sequence-specific nucleases are used to create a break, indels may only arise after multiple cycles of breaking and perfect repair, and thus, the final mutation rate may grossly overestimate the error rate of individual repair events (Bétermier et al., 2014). Finally, with such nucleases, the accumulation of indels is also dependent on the cutting rate. Here, we tackle these problems by a combination of mathematical modeling and highly accurate measurements of indel accumulation, focusing on Cas9-induced DSBs.

Results

A Kinetic Model of DSB Repair

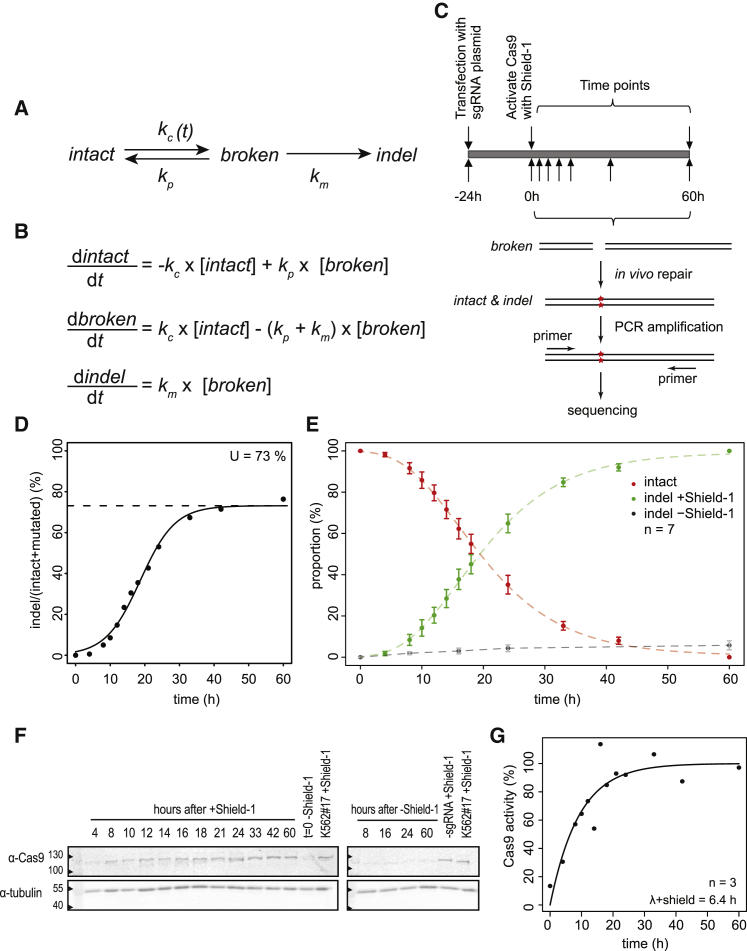
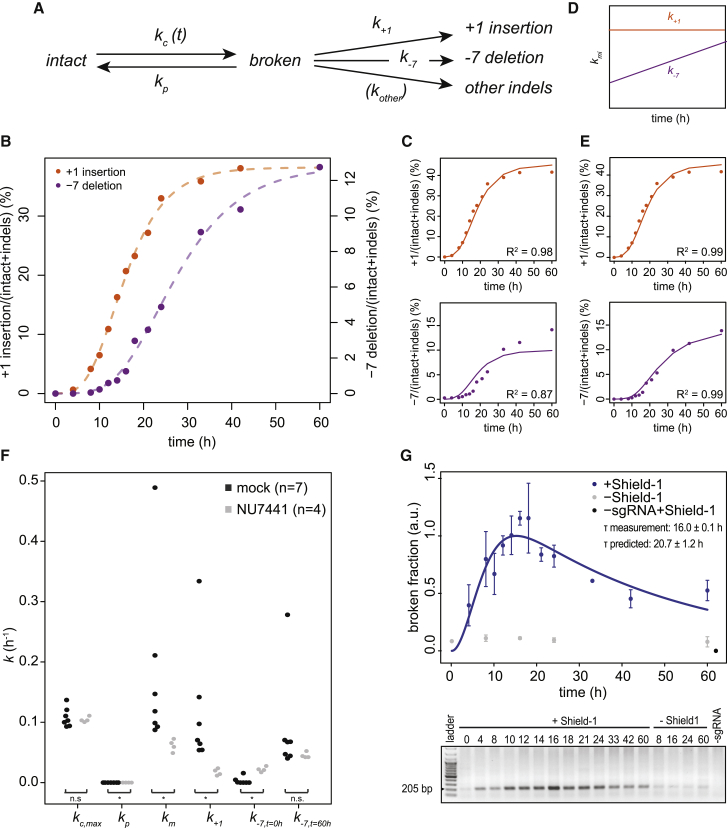
We approached the process of repair of a Cas9-induced DSB as a simple three-state model (Figure 1A). In this model, the “intact” state is the original unbroken DNA sequence that can be recognized by the complex of Cas9 and single guide RNA (sgRNA) (Cas9•sgRNA) complex. After introduction of a DSB by this complex, the DNA enters a reversible “broken” state. This state may be repaired perfectly, after which the DNA is susceptible to another round of cutting. Alternatively, an error-prone repair mechanism may introduce a small indel at the break site. The latter results in an irreversible “indel” state that can no longer be recognized properly by the sgRNA and therefore cannot be cut again by Cas9 (see below for validation of this assumption). Hence, in this model, there are three reaction steps: cutting; perfect repair; and mutagenic repair, each having a specific rate constant that we refer to as k_c, k_p, and k_m, respectively (Figure 1A).

Figure 1.

Quantitative Analysis of Cas9-Induced DSBs

(A) Proposed model of DSB repair based on stochastic transitions between intact, broken, and indel states. k_p and k_m are rate constants of perfect and mutagenic repair, respectively; k_c is the rate constant of cutting by Cas9. The latter depends on Cas9 activation and is therefore denoted as k_c(t).

(B) ODEs describing the three reaction steps, with rate constants as parameters.

(C) Outline of the experimental strategy; see main text.

(D) Representative time course experiment, showing gradual accumulation of indels. A sigmoid curve was fitted to the data to determine the plateau level at late time points (dashed line), which reflects the transfection efficiency.

(E) Relative proportions of intact (red) and indel (green) fractions at the LBR2 locus over time. The data points are normalized on to the total indel fraction to correct for the variation in transfection efficiency. Indel fraction in absence of Shield-1 is shown in gray. Average of 7 independent experiments is shown; error bars represent the SD, and the dashed lines show fitted sigmoid curves.

(F) Western blot analysis of Cas9 presence as a function of time. Tubulin was used as loading control.

(G) The intensities of Cas9 antibody signal were determined by densitometry from time points of 3 individual western blots and normalized to a sample incubated for 60 hr with Shield-1 (lanes labeled “K562#17+Shield-1” in F). An ODE fit was performed to determine the activity score of Cas9 in time.

Our aim was to determine these key descriptors of the repair process for individual Cas9•sgRNA target loci. For this purpose, we captured the model in a set of ordinary differential equations (ODEs) describing the three reaction steps, with the rate constants as parameters (Figure 1B). With this ODE model, it is possible to simulate the relative abundance of the three states over time in a pool of cells after activation of Cas9. Such simulations show that activation of Cas9 generally leads to a gradual loss of intact DNA, a transient increase in the broken DNA state, and a gradual increase in the indel state until virtually all DNA is converted to the latter. However, the shape of each curve is determined by the rate constants (Figures S1A–S1C). We reasoned that it should therefore be possible to determine the rate constants by fitting the ODE model to actual time series measurements of one or all three states after Cas9 induction.

Quantification of Cas9 Cutting and Repair Rates

We set out to measure the accumulation of indels in cells in which a specific DSB was introduced by Cas9. To control the timing of DSB formation, we established a clonal K562 cell line (K562 no.17) with a stably integrated construct that encodes a tightly controlled inducible Cas9 nuclease. To switch Cas9 activity on and off, we fused a ligand-responsive destabilizing domain (Banaszynski et al., 2006) to Cas9. With the small ligand Shield-1, Cas9 can then be reversibly stabilized for transient DSB induction. K562 cells are capable of activating DNA damage response upon DSBs, although the G1 checkpoint is affected due to a mutated TP53 gene (Law et al., 1993).

We transiently transfected K562 no. 17 with a plasmid encoding a sgRNA targeting the LBR gene (sgRNA-LBR2). We previously found that this sgRNA effectively induces indels (Brinkman et al., 2014). Twenty-four hours after transfection, we stabilized Cas9 by adding Shield-1. Flow cytometry analysis showed that cells 16 hr after damage had an ∼10% increase in G2 population, suggesting a modest check point activation (Figure S5). We collected cells at various time points up to 60 hr after Cas9 induction, amplified a ∼300-bp region around the sgRNA target site by PCR, and subjected the products to high-throughput sequencing to determine the intact and indel fractions (Figure 1C).

The results show a gradual accumulation of indels over time (Figure 1D), indicating that DSBs were introduced and repaired imperfectly. Toward the end of the time course, the indel frequency reached a plateau of ∼70%. This value corresponds approximately to the mean transfection efficiency (mean ± SD = 67.6% ± 11.9%; n = 7), determined as the proportion of cells that express GFP after transfection with a GFP-expressing plasmid (Figures S1D and S1E). We therefore assumed that the plateau value of ∼70% is good representation of the total proportion of cells that received the sgRNA and underwent DSB induction and repair. After normalization for this transfection efficiency, the data were highly reproducible over 7 independent replicate experiments (Figure 1E). Indel accumulation was dependent on stabilization of Cas9 by Shield-1 (Figure 1E).

The sigmoid appearance of the measured indel time curves suggested a delayed onset of indel accumulation. This may be explained by delayed activation of Cas9 at the beginning of the time series, as indicated by western blot analysis of Cas9 (Figure 1F). Assuming that the cutting activity of Cas9 is proportional to its abundance, we modified the computational model to incorporate the gradual increase of Cas9 levels as determined from the western blot signals (Figure 1G). We assume that the transfected cells continuously express sgRNA over the duration of the time courses, because after transfection with a GFP-expressing vector, the proportion of GFP-positive cells did not decline for at least 120 hr (Figure S1F).

Cutting and Repair Rate Constants in the LBR Gene

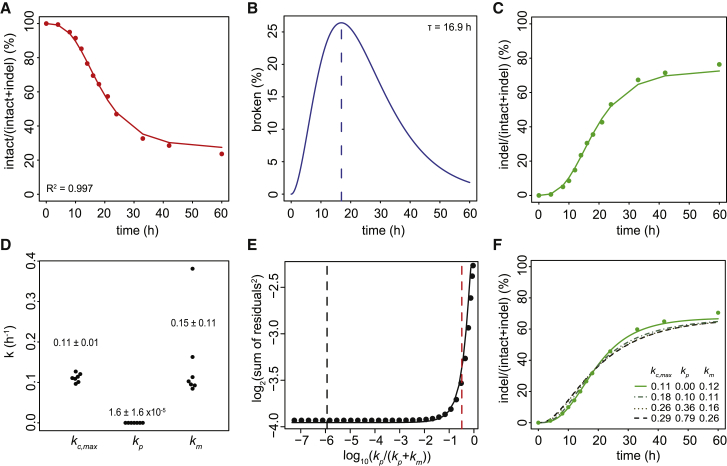
Next, we fitted the set of ODEs to the measured indel curves for sgRNA-LBR2 (Figures 2A–2D). Based on 7 independent replicate experiments, this yielded a cutting rate k_c = 0.11 ± 0.01 hr⁻¹ at maximum Cas9 expression. This corresponds to a cutting half-life (i.e., the time that would be required to cut 50% of the available target sequences in the absence of repair) of ∼6 hr. Cutting by Cas9•sgRNA-LBR2 in our system is thus a rather slow process.

Figure 2.

Estimation of Cutting and Repair Rates

(A–C) Representative time series traces of the intact (A), broken (B), and indel (C) fractions. Measured data (dots) are overlaid with the ODE model fit (solid lines). The percentage of intact and indel traces are relative to the total. The broken fraction is estimated by the model on the basis of the intact and indel measurements. τ indicates time of the largest amount of broken DNA.

(D) Distributions of rate constants from 7 independent experiments (values indicate mean ± SD).

(E) Estimate of the upper confidence bound of the proportion of perfect repair. Fitting residual errors are shown for various fixed k_p/(k_p+k_m) ratios (7 combined time series). Black dashed line marks the optimal fit; red dashed line marks the k_p/(k_p+k_m) ratio above which the fit becomes significantly worse than the optimal fit (p < 0.1; one-sided F-test). This corresponds to k_p/(k_p+k_m) = 0.28. For each k_p/(k_p+k_m) ratio, k_c,max and k_m were adjusted to produce the best fit.

(F) Examples of model fitting with various combinations of k_p and k_m forced to values that would correspond to models of rapid cycling of cutting and perfect repair (dashed curves). Green dots are measured values; green curve shows unrestrained optimal fit.

Our model fit estimated the rate constant for imperfect repair to be k_m = 0.15 ± 0.11 hr⁻¹. This corresponds to a half-life of broken DNA of 4.6 hr. Surprisingly, the rate constant for perfect repair was estimated to be k_p = 1.6 ± 1.6 × 10⁻⁵ hr⁻¹, which is about ten thousand times slower than imperfect repair. This suggests that virtually all repair events at this locus result in the formation of indels, whereas perfect repair is very rare.

Robustness of the Model

On average, the goodness of fit between the model and the measured data was R² = 0.995. We considered that the parameter estimates could be strongly influenced by the modeling of the Cas9 induction. To test this, we also modeled a simple step function with various time delays of Cas9 activation. Although the results were quantitatively slightly different (Figures S1G–S1J), the main conclusion remained that repair at this locus is slow and error prone.

Whereas these results point to robustness of the modeling, we were surprised to find the extremely low rate of perfect repair. To check whether the model with the low perfect repair rate is indeed the most optimal fit to the data, we conducted a “parameter sweep” survey, in which we imposed different fixed perfect/mutagenic repair ratios. Analysis of the fitting residuals indicated that low k_p/(k_p+k_m) ratios (∼10⁻⁶) indeed yield the best fit (Figures 2E and 2F). However, the difference with higher ratios was rather minor, and statistical testing revealed that, only at k_p/(k_p+k_m) ratios >0.28, the fit became significantly poorer (p < 0.1; F-test) than at the initially estimated ratio of 10⁻⁶. We therefore conservatively conclude that the contribution of perfect repair at this locus can be at most 28%, although lower ratios are more likely to be correct. The other parameter values (k_c, k_m, and the predicted broken fraction) showed only minor variation within this range (Figures S2A–S2E), further attesting to the robustness of the model.

From this parameter sweep analysis follows that the indel accumulation curve is not compatible with a very rapid cycle of cutting and perfect repair with only occasional imperfect repair. In such a scenario, k_p/(k_p+k_m) would be close to 1. As mentioned above, according to the F-test, this yields a significantly poorer fit compared to lower k_p/(k_p+k_m) ratios (Figures 2E and 2F). Increased cutting rates also lead to poorer fits (Figure S2F).

Experimental Validation

We validated the underlying assumptions and results of the modeling with several independent biological assays. First, we tested our assumption that the reverse reaction from the indel state to the broken state cannot occur (Figure 1A). For this purpose, we isolated several clonal cell lines that had acquired one or more indels in the target site and lacked wild-type sequences (Figure S4A). We then re-transfected 3 of these cell clones with sgRNA-LBR2 and again activated Cas9. Despite prolonged re-exposure to Cas9•sgRNA-LBR2, we could not detect any change in the indels present in each clone (Figure S4B). We conclude that the target site, once it has acquired an indel, is not recognized again by the same sgRNA.

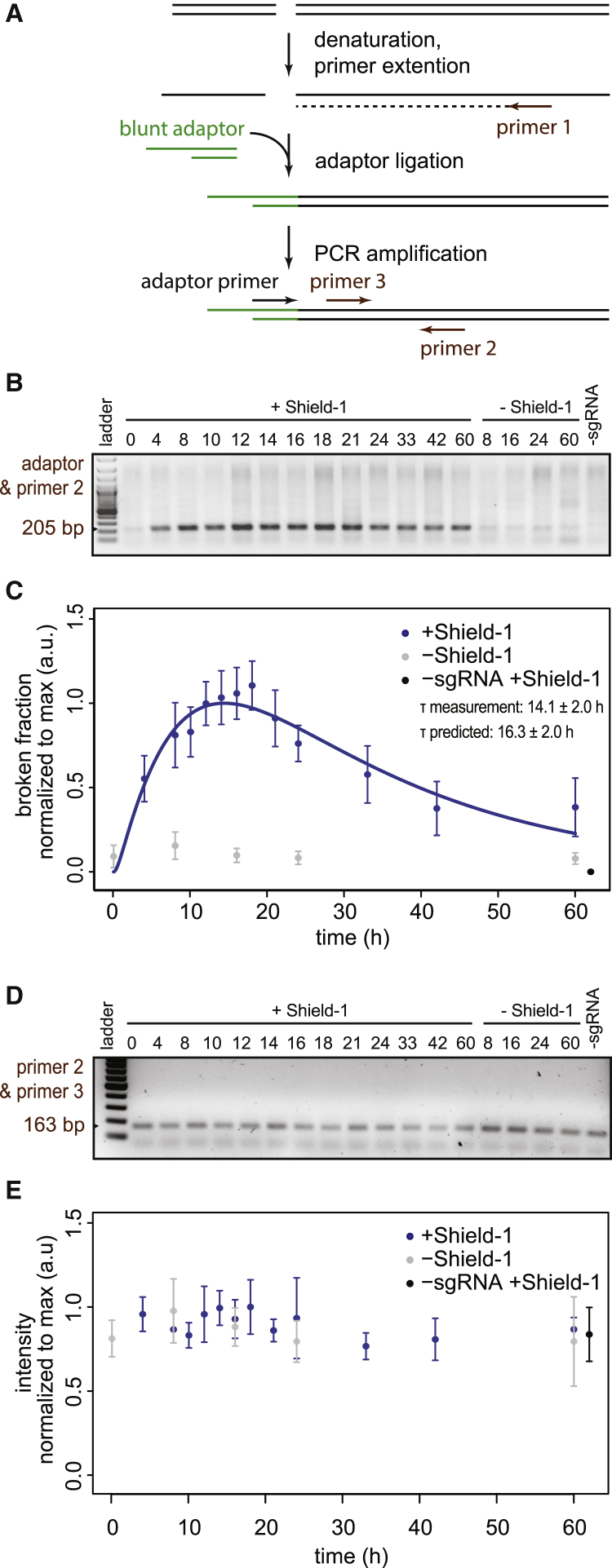
Second, we verified the kinetics of the broken state as predicted by the computational model (which was based on intact and indel frequencies only). The model predicts that the broken fraction peaks at 16.4 ± 1.7 hr, with a maximum of 19.9% ± 6.7% broken DNA (mean ± SD; n = 7; Figure 2B). To verify this, we established a variant of the ligation-mediated PCR assay for the quantification of DNA breaks at a defined location (Dai et al., 2000, Garrity and Wold, 1992). In this assay, we first denature the DNA and subject it to a primer extension reaction using a primer near the break site. This ensures that all cleavage sites are converted into blunt ends, even if resection of the broken ends has occurred. Next, an adaptor is ligated to the blunted DNA end, followed by PCR with one primer near the break site and a second primer that is complementary to the adaptor sequence (Figure 3A). When analyzed on agarose gels, the samples from cells treated with sgRNA and Shield-1 yielded a band of the expected size (Figure 3B), and the band intensity was sufficiently linear with input across the measured range (Figure S3F). Analysis of several time series showed that the band intensity increased until 14.1 ± 2.0 hr (mean ± SD; n = 4) after Cas9 induction and then decreased again (Figures 3B and 3C). This is in agreement with the peak time of the broken state as predicted by the model fitting (cf. Figure 2B). As expected, a control primer pair not spanning the break site showed stable signals over the time course (Figures 3D, 3E, and S3G). We obtained similar results when probing the other end of the same DSB (15.6 ± 2.2 hr; n = 3; Figures S3B–S3E, S3H, and S3I).

Figure 3.

Measurement of Broken Fraction

(A) Schematic view of the ligation mediated (LM)-PCR assay to detect the broken ends after DSB induction. See text for explanation.

(B) Representative agarose gel of the LM-PCR products of a time series. The expected product is 205 bp in size.

(C) The broken fraction measured as band intensities (data from 8 LM-PCR experiments from 4 independent time series; values are a.u.; mean ± SD). Solid blue line shows an ODE curve fit to the LM-PCR data to determine τ (blue shading, mean ± SD).

(D and E) Same as (B) and (C) but with primers 2 and 3 that do not span the break site. The expected product is 163 bp in size. Values are in a.u., mean ± SD, based on 7 PCR experiments from 3 independent time series.

Furthermore, the parameter sweep shows that, when k_p/(k_p+k_m) approaches 1, the predicted amount of broken DNA at peak time becomes so low (<1%) that we would be unable to measure it by ligation-mediated PCR (Figure S2D). Thus, a model consisting of a very rapid cycle of cutting and perfect repair with only occasional imperfect repair is not compatible with our ability to detect broken DNA.

Two Repair Pathways Active at One Locus

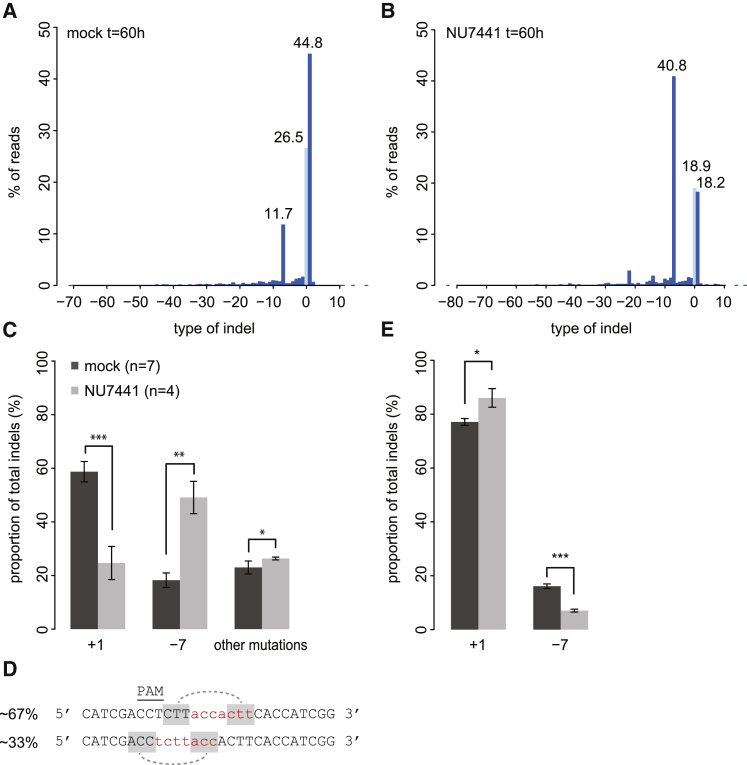
Next, we took a closer look at the indels that were generated. Repair of Cas9-induced DSBs produces non-random indel patterns that are specific for the sgRNA (Brinkman et al., 2014, van Overbeek et al., 2016). In our experiments, sgRNA-LBR2 yielded predominantly a deletion of 7 bp or an insertion of 1 bp (Figure 4A). After 60 hr of Cas9 induction, the +1 insertions reached a frequency of 59.6% ± 4.2%, whereas the −7 deletions accumulated to 18.0% ± 2.3% of the total indel pool (Figure 4C). Analysis of 20 clonal lines derived from single cells in which Cas9•sgRNA-LBR2 had been transiently active indicated that the +1 insertion is the predominant mutation but can co-occur with the −7 deletion on other alleles in the same cell (Figure S4A).

Figure 4.

Multiple Repair Pathways Active at One Locus

(A and B) The spectrum of indels and their frequencies at the LBR2 locus at time point t = 60 hr in cells cultured without (A) or with (B) 1 μM NU7441. A representative experiment is shown. Light-blue bar, wild-type sequence; dark-blue bars, indels.

(C) Frequencies of −7 and +1 indels in the presence (black, n = 7) and absence (gray, n = 4) of NU7441. All series are normalized to the total indel fraction. Asterisks indicate p values according to Student’s t test: ^∗p < 0.05; ^∗∗p < 0.005; ^∗∗∗p < 0.0005.

(D) The −7 deletions consist of two types; red nucleotides mark the deleted DNA. Shaded nucleotides show possible models for microhomology-mediated repair. Percentages indicate the proportion of observed −7 sequence reads.

(E) TIDE analysis of +1 insertion and −7 deletion indels after exposure of the cells to 10 Gy of IR at the time of Cas9 induction. Asterisks indicate p values according to Student’s t test: ^∗p < 0.05; ^∗∗p < 0.005; ^∗∗∗p < 0.0005.

Different indels can be the result of different repair pathways, e.g., C-NHEJ or MMEJ (Hicks et al., 2010, van Overbeek et al., 2016). To explore whether this may be the case for the −7 and +1 indels, we added an inhibitor of DNA-dependent protein kinase, catalytic subunit (DNA-PKcs) (NU7441) to the cells. DNA-PKcs plays an essential role in the C-NHEJ pathway, but not in MMEJ (Perrault et al., 2004). We found that, in the presence of 1 μM NU7441, the proportion of the −7 deletion events increased by 3-fold whereas the +1 insertion diminished by about 2-fold (Figures 4A–4C). The presence of NU7441 inhibitor did not affect cell viability (Figure S4C). These results indicate that the +1 insertion is the result of C-NHEJ, whereas the −7 deletion is not.

MMEJ makes use of microhomologies near the broken ends (Guirouilh-Barbat et al., 2007, Wang et al., 2006). Sequence analysis revealed that the −7 deletion fraction consists of two types of deletions that occur in an approximate ratio of 1:2 (Figure 4D). Both types can be explained by recombination through 3-nucleotide microhomologies, which strongly points to MMEJ as the responsible pathway for the formation of the −7 indel. We conclude that at least two different repair pathways are active and lead to distinct types of mutations at one specific break site.

Interestingly, we found that the ratio between the +1 and −7 indels changes in favor of the +1 insertion when 10 Gy of ionizing radiation (IR) damage was administered just prior to Cas9 induction. In particular, the −7 deletion fraction decreased about 2-fold (Figure 4E). Cell viability did not differ between the control and irradiated sample (Figure S4D). The shift in pathway utilization can be either due to additional breaks elsewhere in genome (which may sequester components of the MMEJ pathway), a cell cycle arrest, or a combination thereof.

Delayed Activity of MMEJ

Having established that two types of indels are largely the result of separate pathways, we decided to study the kinetics of these pathways in more detail by tracking the +1 and −7 indel frequencies over time. We modified the ODE model by incorporating separate k_m rate constants for each type of indel (Figure 5A). We then fitted this model to the +1 and −7 indel time series data. This yielded a good fit of the +1 curve (mean R² = 0.99) but a poorer fit of the −7 curve (mean R² = 0.93; Figure 5C). The deviation of the fitted curve is mostly due to a delay in the −7 indel appearance (Figure 5B). As a consequence, our estimate of the k_m for the −7 indel is less accurate, but we can conclude that the MMEJ pathway exhibits a delayed onset compared to C-NHEJ. Thus, the k_-7 rate appears to increase over time rather than be constant. Possibly the MMEJ pathway is only activated when C-NHEJ fails to be repair a DSB, as has been proposed previously (DiBiase et al., 2000, Guirouilh-Barbat et al., 2007, Wang et al., 2003).

Figure 5.

MMEJ Has Slower Repair Kinetics Than C-NHEJ

(A) Kinetic model of Cas9-induced DSB repair assuming that each type of indel is generated with a specific repair rate.

(B) +1 insertion and −7 deletion accumulation in a representative time series. Dashed lines show a Gompertz sigmoid fit.

(C) Same measurements as in (B) with the multi-indel ODE model fit (solid lines) for the +1 (top) and −7 (bottom) indels.

(D) Cartoon representation of hypothesized time dependency of the k₊₁ and k₋₇ rates added to the fitted model in (E).

(E) Time-dependent ODE model fit of the +1 insertion (top) and −7 deletion (bottom) as proposed in (D).

(F) Rate constants without (black) and with (gray) NU7441. The total mutagenic repair rate is represented by k_m; rate constant for the +1 insertion is k₊₁ and rate constants for the −7 deletion are k_{−7,t = 0hr} and k_{−7,t = 60hr} at the start and end of the time series, respectively. n indicates the number of time series. Asterisks indicate p values according to Wilcoxon test: ^∗p < 0.05; ^∗∗p < 0.005; ^∗∗∗p < 0.0005.

(G) Broken fraction measurements in presence of NU7441 of 2 independent time series, similar to Figures 3B and 3C.

We then tested whether the model could be improved by explicitly including such a delayed onset. For simplicity, we assumed a linear increase in the production rate of the −7 deletion over time, starting with a rate k_{−7,t = 0hr} immediately after Cas9 induction and increasing to k_{−7,t = 60hr} at the end of the time course (Figure 5D). Indeed, a better fit of the −7 indel curve (mean R² = 0.99) was obtained (Figure 5E). The model fitting estimates k₋₇ to be nearly zero at the onset of Cas9 induction, whereas at the end of the time course, it is 0.09 ± 0.09 hr⁻¹, which approaches the activity of the +1 indel repair (0.12 ± 0.10 hr⁻¹; Figure 5F). These results strongly suggest gradual activation of MMEJ over time.

Interplay between C-NHEJ and MMEJ

We wondered whether this gradual increase in MMEJ rate is somehow due to competition with the C-NHEJ pathway. To test this, we performed time course experiments in the presence of NU7441 and repeated the computational modeling. As expected, in the presence of the inhibitor, k₊₁ is reduced dramatically (∼6-fold; Figure 5F; Table S3), whereas the cutting rate k_c as well as the perfect repair rate k_p are virtually unaltered. Strikingly, in the presence of NU7441, k_{−7,t = 0hr} became about 7-fold higher than in the absence of the inhibitor, whereas k_{−7,t = 60hr} remained largely unaffected. Thus, inhibition of DNA-PKcs leads to a more rapid engagement of MMEJ soon after the DSB is introduced.

However, in the presence of NU7441, MMEJ does not fully compensate for the loss of C-NHEJ. The total repair rate is lower, as k_m is reduced and k_p remains close to zero (Figure 5F). A logical prediction is that it takes more time for DSBs to be repaired. The model as well as actual measurements show that, in the presence of NU7441, the peak time of DSBs is delayed (compare Figures 3C and 5G), although this is not statistically significant for the measured data.

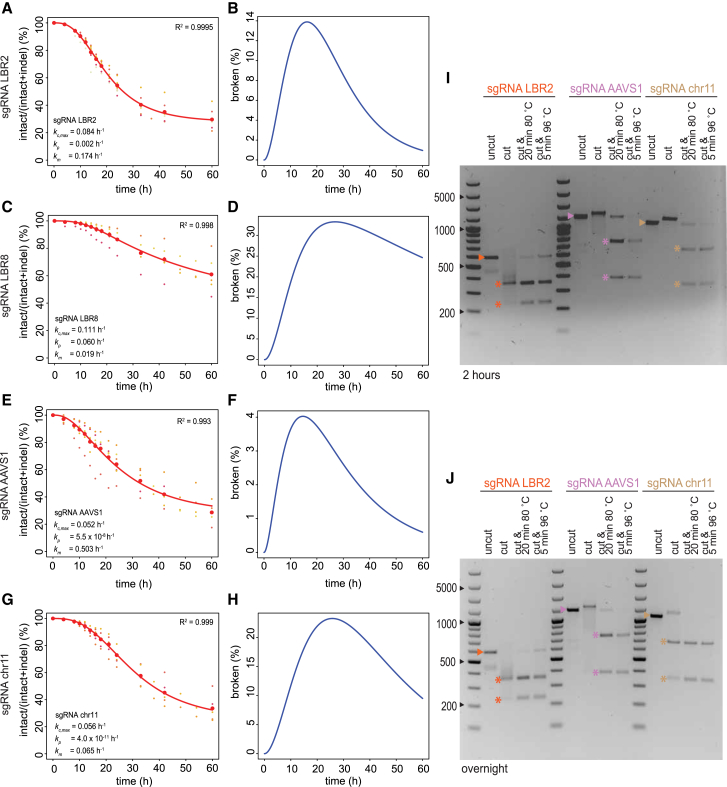
Cutting and Repair Rates in Three Other Loci

To investigate whether the rate constants are locus specific, we performed kinetics experiments for three additional loci. We designed a sgRNA (sgRNA-LBR8) targeting another sequence in the LBR gene that is 169 bp upstream of sgRNA-LBR2, a previously reported sgRNA to target the AAVS1 gene (Mali et al., 2013), and a sgRNA that targets an intergenic locus on chromosome 11 (chr11). Each target locus shows a different indel spectrum after 60 hr (Figures S6B, S6H, and S6K). For each sgRNA, we conducted multiple time series measurements (Figures 6A–6H).

Figure 6.

ODE Modeling of DSBs at Additional Loci; Cas9 Remains Bound to Broken Ends

(A–H) Time series of Cas9 cutting and repair at four loci (LBR2, A and B; LBR8, C and D; AAVS1, E and F; intergenic region on chromosome 11, G and H).

(A, C, E, and G) Intact fraction abundance of all individual replicates is shown in small dots where each replicate has a unique color. The mean of each time point is shown as big red dots. Fitted models are shown as red curves.

(B, D, F, and H) Predicted broken fraction curves.

(I and J) In vitro digestion of DNA fragments by Cas9 and one of the sgRNAs targeting LBR (orange), AAVS1 (purple), or intergenic region on chromosome 11 (brown), respectively. DNA was incubated for either 2 hr (I) or overnight (J) in the absence (uncut) or presence (cut) of Cas9 and sgRNA (Cas9•sgRNA). In some samples, Cas9 was subsequently denatured by two different heat treatment protocols as indicated. The expected band for the intact DNA is marked by an arrowhead, and the expected digestion products are marked by asterisks.

For the three new loci, the indel frequency did not fully reach a plateau at the end of the time course (Figures 6C, 6E, and 6G). This compromised the robustness of the rate constant estimates, because our algorithm used this plateau to estimate the transfection efficiency of individual experiments. We therefore employed a slightly modified computational strategy. We combined the data of all replicate experiments and performed parameter fitting in two iterations. In the first iteration, we conducted a parameter sweep for the transfection efficiency. We chose the efficiency that yielded the lowest residuals (see STAR Methods). In the second iteration, we used this value and applied a standard 1,000-fold bootstrapping approach in order to estimate confidence intervals for each parameter of the kinetic model. The results are summarized in Figures 6A–6H and Table S4.

The confidence intervals of the fitted rate constants are relatively large, and hence, the results should be interpreted with some caution. Nevertheless, for the LBR2 locus, this alternative computational strategy yielded parameter estimates that were similar to those from the original strategy. Across the four loci, the estimated cutting rates (k_c) varied only about 2-fold. The overall repair rates (perfect and imperfect repair combined) vary over an ∼8-fold range and correspond to half-lives of approximately 8.8 hr (LBR8), 1.4 hr (AAVS1), and 10.7 hr (chr11), as compared to 3.9 hr for the LBR2 locus. These values indicate that repair rates of Cas9-induced DSBs are variable and often slow.

Like for LBR2, the estimated rates of perfect repair (k_p) are very low for AAVS1 and chr11. In contrast, perfect repair in locus LBR8 is frequent, making up 76% of all repair events. For LBR8, the fitted models predicted a slower clearance of broken DNA compared to LBR2 (Figures 6B and 6D). Directly measured time courses of the LBR8 broken state are in agreement with this, with a τ of 28.9 ± 17.8 hr for LBR8 compared to 14.7 ± 2.1 hr for LBR2 (mean ± SD; measurements for both ends combined; p = 0.005; Wilcoxon test; Figures S6D–S6F). Together, these results indicate that the error rate of the repair of Cas9-induced DSBs is locus dependent and often high.

Tight Binding of Cas9 after Cutting May Explain Erroneous and Slow Repair

We sought an explanation for the relatively erroneous and slow repair that we observed. It was reported that the Cas9 can remain attached to the broken DNA ends after cutting in vitro (Sternberg et al., 2014), but it is not known how general this behavior is. We therefore tested this directly for three DNA loci for which we had determined the kinetic rate constants. By PCR, we first produced double-stranded DNA fragments of 600–1,000 bp, consisting of precisely the same sequences as the three loci. We then incubated each fragment in vitro with the respective Cas9•sgRNA complex to induce DSBs and investigated the reaction products by agarose electrophoresis (Figures 6I and 6J).

The PCR product treated with Cas9•sgRNA-LBR2 showed the expected digestion products, but the smallest fragment was underrepresented whereas a broad smear indicated aberrant migration of the DNA. After heat denaturation of Cas9•sgRNA, the smear disappeared and the smaller digestion product became clearly visible. For sgRNA-AAVS1 and sgRNA-chr11, even more pronounced effects were observed: without denaturation, the digested DNA appeared largely unbroken and the bands were shifted upward, but after heat treatment, it became clear that most of the DNA was in fact correctly digested. Together, these results indicate that the Cas9•sgRNA complex remains bound to the DNA ends after cutting, even when incubated overnight (Figure 6J). In the case of sgRNA-LBR2, it appears that this binding occurs primarily at one DSB end, whereas for the other two sgRNAs, Cas9 remains bound to both ends. As has been suggested (Richardson et al., 2016) post-cutting adherence of Cas9 to the DNA ends may impair the repair process, which could explain the slow and erroneous repair.

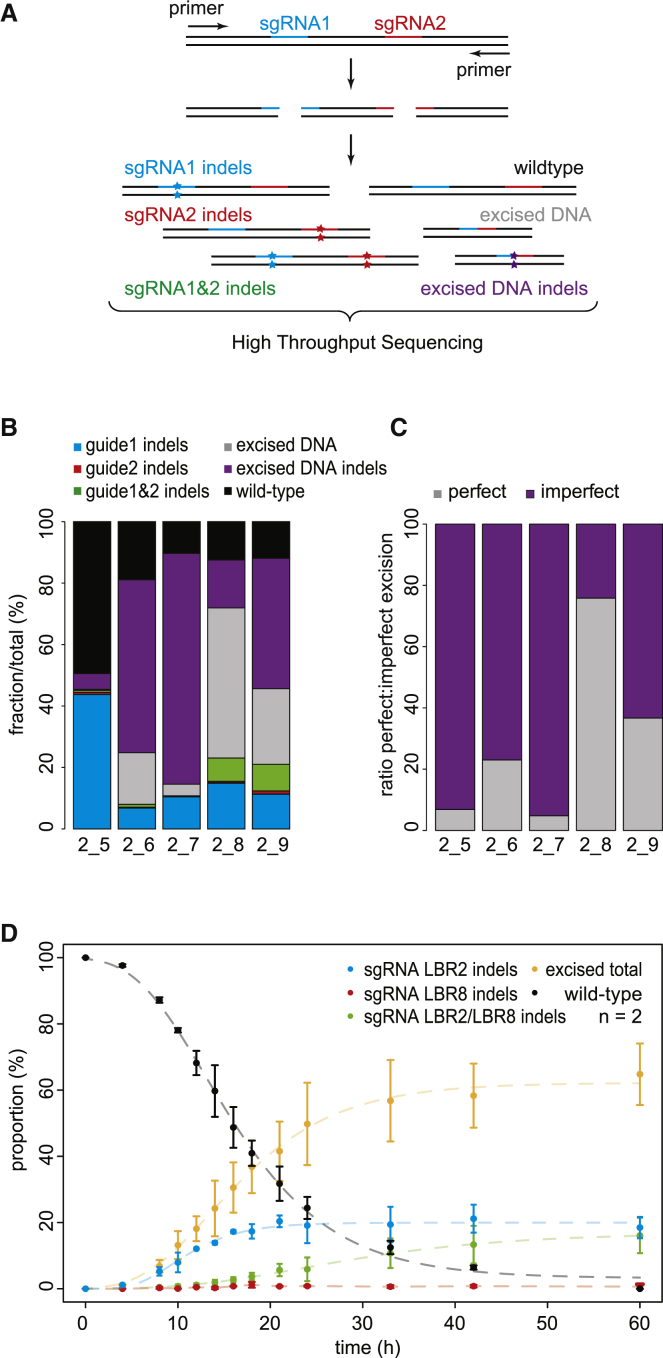
Repair Fidelity after Double Cutting

Finally, we investigated the fidelity of DSB repair upon induction of Cas9 in combination with two co-transfected sgRNAs that target adjacent sequences. If the two cuts are made simultaneously, then the intermediate fragment may be lost, after which the two remaining ends are joined by the DSB repair machinery. We amplified the resulting junctions by PCR and sequenced them in order to determine the error rate of the repair process, i.e., the frequency at which indels occur at the junction. Such a double-cut strategy has been used previously in combination with I-SceI (Guirouilh-Barbat et al., 2007, Mao et al., 2008). Importantly, once the two ends are joined perfectly, they cannot be cut again because the new junction is not recognized by either of the two sgRNAs. This assay therefore complements our kinetic modeling of single-cut repair, in which cycles of repeated cutting and perfect repair were theoretically possible.

We designed five sgRNAs targeting a second DSB site ∼110–300 bp upstream or downstream of the sgRNA-LBR2 target site. One of these was sgRNA-LBR8. We co-transfected each sgRNA together with sgRNA-LBR2, induced Cas9 expression, and harvested cells after 60 hr. PCR amplification followed by high-throughput sequencing uncovered all intermediates and end products that could be expected, such as junctions resulting from excision events as well as indels at one or both of the two cutting sites (Figures 7A and 7B).

Figure 7.

DSB Repair Fidelity after Double Cutting

(A) Repair products that may result from Cas9 in combination with two sgRNAs that target adjacent sequences. All products are amplified by PCR and detected by high-throughput sequencing.

(B) Quantification of the various repair products 60 hr after Cas9 induction in the presence of sgRNA-LBR2 and one of 5 sgRNAs (labeled 5 through 9) that target a sequence within 110–300 bp from the LBR2 site.

(C) Same as (B) but highlighting the relative proportions of perfect and imperfect junctions among the repaired excision events.

(D) Relative proportions of indels at sgRNA-LBR2 target site (blue), indels at sgRNA-LBR8 target site (red), indels at both sgRNA-LBR2 and sgRNA-LBR8 target sites (green), excised DNA (yellow), and wild-type (black) fractions over time. The data points are normalized to the total mutation fraction to correct for the variation in transfection efficiency. Average of 2 independent experiments is shown; error bars represent the SD. Dashed lines show fitted sigmoid curves.

In those DNA molecules in which excision was successfully followed by repair, rejoining had occurred with highly varying degrees of fidelity. Depending on the combination of sgRNAs tested, we found that 25%–95% of these junctions were imperfect (Figure 7C), as indicated by the occurrence of indels that ranged from 1 to ∼20 bp in size. In 4 out of 5 tested double-cut combinations, we detected at least 2-fold more excised fragments than indels at single break sites (Figure 7B). This implies that the second cut typically occurred before the first cut had been repaired. This is in agreement with our modeling results, indicating that repair of Cas9-induced breaks is often a relatively slow process.

Because the combination sgRNA-LBR2 and sgRNA-LBR8 yielded an exceptionally high frequency of perfect excisions (∼75%), we studied these repair events in more detail by generating time course data (Figure 7D). This revealed that accumulation of excisions took approximately 15 hr to reach 50% of the plateau level. This underscores again that repair of breaks induced by Cas9 at these sites is slow. Furthermore, indels at the LBR8 site alone were virtually undetectable throughout the time course, whereas indels at both sites or at the LBR2 site alone did accumulate. In part, this may be explained by the relatively high frequency of perfect repair that we estimated for LBR8 in the single-cut kinetics experiments. Another not mutually exclusive explanation may be that repair of the LBR2 site is quicker than at the LBR8 site, which is also consistent with our parameter estimates based on single cuts (Table S4).

Discussion

DNA Repair Kinetics

Our measurements and modeling of the kinetics of rejoining of broken DNA ends after a Cas9-induced lesion indicate that the rate of DSB repair is variable and relatively slow. Moreover, our results indicate that the repair process tends to be error prone. A recent study using a novel inducible Cas9 system also reported diverse kinetics profiles but did not determine rate constants (Rose et al., 2017).

Across the four tested loci, we observed repair half-life times of 1.4, 3.9, 8.8, and 10.7 hr. The latter three of these estimates are much slower than previous estimates based on bulk detection of DSBs after ionizing irradiation, which rarely exceeded 1 hr (see Introduction). Most of these previous studies were performed after a pulse of ionizing radiation ranging from 1 to 40 Gy, which creates dozens to hundreds of DSBs. Here, we introduce only a few DSBs per cell. We cannot rule out that large numbers of simultaneous DSBs accelerate the repair process. However, this seems not very likely because, in the presence of 10 Gy IR damage in addition to the Cas9-induced DSB, we see only a small shift in repair pathway choice toward the faster C-NHEJ pathway.

Another factor that could contribute to the difference in repair rates is the possible adherence of Cas9 to the DNA ends after cleavage, which could prevent access by the repair machinery (Richardson et al., 2016). In accordance with previous studies (Richardson et al., 2016, Shibata et al., 2017, Sternberg et al., 2014) our in vitro data show that Cas9 remains tightly bound to one or both DNA ends after cutting and detachment could only be achieved by protein denaturation. In vivo, catalytically inactive Cas9 was also found to tightly bind to its target DNA (Knight et al., 2015), with a dwell time of about 2 hr (Ma et al., 2016).

DNA Repair Fidelity

It has been suggested that the genome in a human cell may be hit by as many as 10–50 DSBs per day (Lieber, 2010, Vilenchik and Knudson, 2003). Yet, in the genome of skin cells of a 55-year-old individual, only about 2,000 small indels were detected by deep sequencing (Martincorena et al., 2015). In yeast and fly genomes, indels accumulate at frequencies of roughly 10⁻¹¹/base/generation (Keightley et al., 2009, Zhu et al., 2014). These data suggest that repair of naturally occurring DSBs is highly precise. Ligation of mammalian V(D)J recombination junctions has also been found to have low error rates (Bétermier et al., 2014, Schatz and Swanson, 2011). In this light, our estimated error rates in the range of 20%–100% per break event seem rather high. This raises the possibility that repair of Cas9-induced DSBs is not representative for naturally occurring DSBs.

Repair fidelity could be affected by the adherence of Cas9 to broken ends but also by the structure of the DNA ends themselves. High precision of C-NHEJ was found when DNA breaks were introduced by the I-SceI nuclease (Guirouilh-Barbat et al., 2007). I-SceI makes a staggered cut and leaves a 3′ overhang, whereas Cas9 generates blunt ends (Cong et al., 2013, Jinek et al., 2013, Mali et al., 2013). Blunt ends were shown in vitro and in wild-type yeast to be preferentially joined imprecisely (Boulton and Jackson, 1996, Schär et al., 1997). Variants of Cas9 protein that generate DSBs with different overhangs (the nickases N863A and D10A) also resulted in differences in repair (Bothmer et al., 2017, Vriend et al., 2016). Thus, the high rates of imperfect repair that we observe may in part be related to the blunt ends created by Cas9. Furthermore, the local chromatin environment of the targeted loci may affect the repair outcome, because recruitment of repair factors is dependent on the chromatin environment (Kalousi and Soutoglou, 2016).

The low rates of perfect repair that we observed also imply that HR plays only a minor role in the repair of Cas9-induced breaks, even though K562 cells are proficient in HR (Voit et al., 2014). HR frequencies in combination with Cas9 have been estimated to be up to 4%–15% (Bothmer et al., 2017, Vriend et al., 2016), but these frequencies are likely to represent an overestimate because they were measured in the presence of a donor template that was either closely linked in cis or provided in excess by transient transfection. This also indicates that the accuracy of our broken fraction assay is unlikely to be compromised by substantial amounts of extensively resected ends that could escape detection in this assay.

Repair Fidelity at Double DSBs

The proportion of perfect junctions in our double-cut assays was also variable and depending on the precise combination of sgRNAs used. In combination with sgRNA-LBR2, we observed the lowest error rate for sgRNA-LBR8, which also triggers mostly perfect repair when used in a single-cut kinetics assay. We note that repair of two nearby breaks may be more complex than of a single break. For example, the first break may trigger local chromatin changes, such as phosphorylation of H2A.X, which may in turn alter events at the second site, such as cutting rate and the recruitment of specific repair complexes. Furthermore, Cas9 may linger on one or both of the ends that are to be joined. This may depend on the orientation of the protospacer adjacent motif (PAM) sites or on other sequence features of the sgRNA used, but we have not been able to identify a predictive feature in the pairs of sgRNAs that we tested. Others have observed that sgRNA pairs resulted in high levels of precision repair (Canver et al., 2017, Geisinger et al., 2016), although Geisinger et al. considered some single-nucleotide indels as perfect repair and may have underestimated error rates.

Different Repair Pathways

We found that, at one single genomic location (LBR2), both C-NHEJ and MMEJ can repair DSBs with different kinetics. Overall, MMEJ operates with lower rates than C-NHEJ. This is in agreement with previous findings that indicate that C-NHEJ is the primary repair pathway (Chiruvella et al., 2013). We observe that the lower rate is mainly because MMEJ exhibits a delayed onset compared to C-NHEJ rather than a reduced activity. Possibly, the C-NHEJ system initially prevents access of the MMEJ pathway to the DSB; only after several hours, if C-NHEJ has failed to repair the break, the MMEJ pathway is allowed to engage. In contrast, upon inhibition of DNA-PKcs, the MMEJ has immediate access and an increased rate of activity. These results are consistent with a previously proposed model, in which MMEJ acts as a backup system for C-NHEJ (DiBiase et al., 2000, Guirouilh-Barbat et al., 2007, Wang et al., 2003).

Modeling of DSB Repair Kinetics and Fidelity: Outlook

Our methodology to determine rate constants may be improved further. We found that activation of Cas9 was relatively slow. We accommodated this by taking the gradual accumulation of Cas9 activity into account, but instant activation of Cas9 would simplify and improve the modeling. A recently reported chemically inducible variant of Cas9 (Rose et al., 2017) may serve this purpose. Stable integration of a sgRNA-expressing vector, rather than transient transfection, would ensure that 100% of the cells express the sgRNA, thus removing the need to include transfection efficiency as a fitting parameter. This would also circumvent any dilution of intranuclear plasmids due to cell division, ensuring that the expression level of the sgRNA remains stable over prolonged time course experiments. However, stable transfection will only be feasible with an inducible sgRNA expression system with very low background activity; otherwise, indels may accumulate before the start of the time course measurements.

Our measurements and modeling did not include possible differences in pathway activity over the cell cycle. The modeling also did not take into account that cells with a DSB undergo a transient cell cycle arrest, although it seems unlikely that this has a major impact on the estimates of the kinetic parameters (see STAR Methods). Certainly, we did not sample the full diversity of sequence contexts and chromatin environments, and it will be interesting to investigate the repair kinetics and fidelity of many more loci in the genome.

STAR★Methods

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Cas9 Monoclonal Antibody (7A9)	Thermo Fisher Scientific	MA5-23519
Monoclonal Anti-γ-Tubulin Clone GTU-88	Sigma Aldrich	T6557
IRDye 800CW goat anti-mouse IgG	Li-Cor	926-32210
Bacterial and Virus Strains
Escherichia coli α-Select Silver Competent Cell	Bioline	BIO-85026
Lenti virus	N/A	N/A
Biological Samples
K-562 Homo sapiens bone marrow chronic myelogenous leukemia (CML)	ATCC	CCL-243
Chemicals, Peptides, and Recombinant Proteins
Shield-1	Aobious	AOB1848
NU7441	Cayman Chemical	503468-95-9
T4 ligase 5 U/μL	Roche	10799009001
Phusion High Fidelity DNA polymerase	Thermo Fisher Scientific	F530
MyTaq Red mix	Bioline	BIO-25043
Cas9 Nuclease, S. pyogenes	NEB	M0386S
Critical Commercial Assays
CellTiter-Blue Cell Viability Assay	Promega	G8080
Isolate II Genomic DNA Kit	Bioline	BIO-52067
Isolate II PCR and Gel Kit	Bioline	BIO-52060
MEGAclear Transcription Clean-Up Kit	Thermo Fisher Scientific	AM1908
RiboMAX	Promega	P1300
Pierce BCA protein assay	Thermo Fisher Scientific	23225
Deposited Data
Raw Imaging Files	This study, Mendeley Data	http://dx.doi.org/10.17632/wg4ssg7pfw.1
Sequence files	This study, GEO	https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE113129
Experimental Models: Cell Lines
K562#17	This study	N/A
Oligonucleotides
sgRNA oligos (see Table S1 for sequences)	IDT/Invitrogen	N/A
Primers (see Table S2 for sequences)	IDT/Invitrogen	N/A
dsDamID adaptor	Vogel et al., 2007	N/A
Recombinant DNA
pX330-U6-Chimeric_BB-CBh-hSpCas9	Cong et al., 2013	Addgene 42230
pLenti-Cas9-T2A-Neo	Prahallad et al., 2015	gift of Dr. B. Evers, NKI
pPTuner IRES2	Clontech	632168
DD-Cas9	This study	N/A
pBlue-sgRNA	This study	N/A
Software and Algorithms
R Studio- Open source edition	Rstudio	https://www.rstudio.com/
Sequence data analyses	This paper	https://github.com/vansteensellab/DSB_Repair_Kinetics
Kinetics modeling	This paper	https://github.com/vansteensellab/DSB_Repair_Kinetics
TIDE software	https://tide.nki.nl	N/A
Other
Cs source Gammacell 40 Exactor	Best Theratronics	N/A
ChemiDoc Imaging Systems	BioRad	N/A
BD FACSCalibur	BD Biosciences	N/A
Odyssey scanner	Li-Cor	N/A

Contact for Reagent and Resource Sharing

Further information and requests for reagents should be directed to Lead Contact Bas van Steensel (b.v.steensel@nki.nl).

Experimental Model and Subject Details

Cell culture and transfection

We established K562#17, which is a clonal cell line of the female K562 cells (American Type Culture Collection) stably expressing DD-Cas9. K562#17 cells were cultured in RPMI 1640 (Life Technologies) supplemented with 10% fetal bovine serum (FBS, HyClone), 1% penicillin/streptomycin. Mycoplasma tests were negative. For transient transfection, 6x10⁶ K562 cells were resuspended in self-made transfection buffer (100 mM KH₂PO₄, 15 mM NaHCO₃, 12 mM MgCl₂, 8 mM ATP, 2 mM glucose (pH 7.4)) (Hendel et al., 2014). After addition of 3.0 μg plasmid DNA, the cells were electroporated in an Amaxa 2D Nucleofector using program T-016. DD-Cas9 was induced with a final concentration of 500 nM Shield-1 (Aobious).

For kinetics experiments, 18x10⁶ cells were transfected and divided over 12-well plates, one well for each time point and each well carrying 1x10⁶ cells. Cas9 was activated 24h after nucleofection and cells were collected at the indicated time points after Cas9 induction. As controls, cells without Shield-1 were collected at various time points.

DNA-PKcs inhibitor NU7441 (Cayman) (final concentration 1 μM) or DMSO (control) was added to K562#17 at the same time when the cells were supplemented with Shield-1 to induce DD-Cas9. 10 Gy of IR was administered by Cs source Gammacell 40 Exactor (Best Theratronics).

Method Details

Constructs

The sgRNA oligos (Table S1) were cloned into expression vector pBluescript with the sgRNA cassette of PX330 (Addgene plasmid 42230) and transfected into K562#17. The sgRNAs were designed using CHOPCHOP (Montague et al., 2014). The pLenti-Cas9-T2A-Neo expression vector (Prahallad et al., 2015) was a kind gift of Dr. B. Evers, NKI. In the expression vector, the ubiquitin promoter was exchanged for the hPGK promoter and a destabilization domain (DD) (Banaszynski et al., 2006) was added at the N terminus of the Cas9 gene, to generate DD-Cas9.

Cell viability

Cell viability was measured using a CellTiter-Blue Cell Viability Assay (Promega). CellTiter-Blue Reagent was 1:5 diluted in RPMI 1640 (Life Technologies) supplemented with 10% fetal bovine serum, 20 μL of this diluted CellTiter-Blue Reagent was added to 100 μL cell suspension. After a 3 hour incubation at 37°C in a 96 well tissue culture plate, fluorescence (560_Ex/590_Em) was measured on an EnVision Multilabel Plate Reader (Perkin Elmer). Results of one CellTiter-Blue Cell Viability Assay per experiment are shown. Cell viability was measured 45 hours after Shield-1.

High Throughput Sequencing

Cells were collected by centrifugation (300xg, 5 min) and the genomic DNA was isolated using the Isolate II Genomic DNA Kit (Bioline). PCR was performed in two steps; PCR1 with ∼100 ng genomic DNA and site specific barcoded primers (see Table S2). PCR2 used 2 μL of each PCR1 product with Illumina PCR Index Primers Sequences 1–12. Each sample was generated with a unique combination of a barcode and index. Both PCR reactions were carried out with 25 μL MyTaq Red mix (Bioline), 4 μM of each primer and 50 μL final volume in a 96 well plate. PCR conditions were 1 min at 95°C, followed by 15 s at 95 °C, 15 s at 58 °C and 1 min at 72 ° (15x). 20 μL of 8 samples were pooled and 100 μL was loaded onto a 1% agarose gel. PCR product was cut from gel to remove the primer dimers and cleaned with PCR Isolate II PCR and Gel Kit (Bioline). The isolated samples were sequenced by Illumina MiSeq. In this study, we only amplified the sgRNA on-target sequences. The effect of possible off-target activity of Cas9/sgRNA was ignored and is considered to be equal between the different experiments.

LM-PCR

Genomic DNA (350 ng, determined by Qubit assay, Thermo Fisher Scientific) was incubated with 0.1 μM extension primer (EB479 or EB551) (see Table S2) and Phusion High Fidelity DNA polymerase (Thermo Fisher Scientific) for 5 min at 95 °C, 30 s at 55°C and 30 s at 72 °C, to extend the non-blunt DNA ends near the break site. Subsequently, 0.16 μM dsDamID adaptor (Vogel et al., 2007) was ligated to the blunted broken ends at 16 °C overnight using T4 ligase (5 U/μL, Roche). Ligase was heat inactivated for 20 minutes at 65°C. To detect broken DNA a PCR was performed on the adaptor-broken DNA ligation product with 3 μM adaptor primer, EB486 and broken primer (EB487 or EB553). Note that this assay may not detect a fraction of the broken ends that have undergone large resection near the break site to prepare for HR. In parallel an internal standard PCR was performed with the same samples using 3 μM primers EB488 and EB487 or EB555 and EB553 that are both located downstream of the sgRNA break site. PCR conditions were 4 min at 95 °C, followed by 33 cycles of 10 s at 95°C, 10 s at 58 °C, and 10 s at 72°C. During preparation the samples were always kept at 4°C. The PCR products were analyzed on a 1.5% agarose gel and imaged with ChemiDoc Imaging Systems (BioRad). A box with a fixed volume was set over the appropriate LM-PCR band for each sample and the intensities within each box were determined in arbitrary units. The signal without sgRNA was considered background and was subtracted from all other time point samples. To correct for the arbitrary intensity values between different time series, each sample was divided by the sum of all values in one experiment. Subsequently the data was scaled to the maximum value within the time series. For the input PCR two boxes where set with similar volume at and under the PCR band for each sample. These values were subtracted to correct for background signal, divided by the sum of all values in one experiment and scaled to the maximum value within the time series. The mean of biological replicates is shown ± standard deviation (SD). The peak time (τ), when the broken fraction reaches a maximum, is determined by fitting the band intensity values of the time points with the expected curve shape from the three-state Ordinary Differential Equations (ODE) model.

TIDE method

The TIDE method was performed as described in (Brinkman et al., 2014). Briefly, PCR reactions were carried out with ∼100 ng genomic DNA in MyTaq Red mix (Bioline) and purified using the PCR Isolate II PCR and Gel Kit (Bioline). About 100-200 ng DNA from purified PCR samples was prepared for sequencing using BigDye terminator v3.1. Samples were analyzed by an Applied Biosystems 3730x1 DNA Analyzer. The data obtained was analyzed using the TIDE software (https://tide.nki.nl). The decomposition window used for TIDE was set to indels of size 0-10 bp.

In vitro digestion with Cas9

PCR fragments of the target regions were amplified with myTaq (Bioline) according to manufacturer’s instructions. See Table S2 for the used primers. In vitro transcribed sgRNA was generated by T7 promoter driven transcription using the Ribomax kit (Promega) and the RNA was purified with the MEGAclear kit (Life Technologies). 1.5 μL Cas9 (NEB), 50 μg sgRNA and 200 ng PCR fragment were incubated for 2 hours or overnight at 37°C. For denaturation of the Cas9, samples were either incubated for 20 minutes at 80°C or for 3 minutes at 96°C and slowly cooled down to 20°C (1°C/min).

Flow cytometry

K562#17 cells were collected 1 day after nucleofection and directly analyzed for fluorescence using a BD FACSCalibur. Viable cells were gated on size and shape using forward and side scatter.

For cell cycle profiles, cells were fixed with 5 mL of 70% ethanol at 4°C overnight. After fixation, cells were washed with PBS and then incubated in PBS containing propidium iodide (PI) and RNase for 30 minutes at 37°C in the dark. GFP & PI expression were measured using a 488 nm laser for excitation.

Western blotting

Whole-cell extracts of ∼0.5x10⁶ cells were prepared by washing cultures in PBS and lysing with 50 μL lysis buffer (Tris pH 7.6, 10% SDS, Roche proteinase inhibitor). Samples were pulse sonicated for 2 minutes and protein concentrations were determined using the Pierce BCA protein assay (Thermo Fisher Scientific). Samples containing 40 μg of total protein were separated by SDS-PAGE on 8% acrylamide gels and transferred to a nitrocellulose membrane through electroblotting. The membranes were blocked for 1 hour in PBS/Tween-20 0.1% containing 5% low fat milk. After washing twice with PBS/Tween20 0.1% the membranes were incubated with 1:2,000 α-Cas9 7A9 (Thermo Fisher Scientific) or γ-tubulin (T6557, Sigma) for 2 hours at room temperature with mild shaking. Subsequently, the membranes were washed again and incubated with a secondary antibody, 1:10,000 α-mouse IR800 (Li-Cor) at 37°C for 1 hour with shaking. The antibody was detected by Odyssey scanner. The gel was analyzed by setting boxes with a fixed volume over the signals in each sample. The intensity within a set box was determined by Image Studio Version 2.0. Sample t = 60 h was loaded on every gel and used to normalize for the intensity of the signal in the different gels. The mean of three biological replicates is shown ± standard deviation (SD).

The relative activity of CRISPR-Cas9 is calculated by fitting the DD-Cas9 protein abundance from the quantified signals. The model employed for fitting describes stabilization of DD-Cas9 upon introduction of Shield-1, with the unit-less relative activity:

$$\mathit{R}\left(\mathit{t}\right)=1-2^{-\frac{\mathit{t}}{\mathit{hl}}}$$ (1)

where hl is the protein half-life of DD-Cas9 with Shield-1 determined as 6.4 hours, and t is time after introduction of Shield-1. The model assumes that DD-Cas9 is very unstable without Shield-1, which is confirmed by the virtual absence of indel accumulation in the absence of stabilization (Figure 1E).

Quantification and Statistical Analyses

NGS data analysis

In each sequence read, the distance between a fixed sequence at the start and at the end are determined and used to calculate a score, defined as the difference between the measured distance in the read and the expected distance in a wild-type sequence. Insertions and deletions have score > 0 and < 0, respectively. A point mutation has score = 0, but some bases in the sgRNA target site differ from the wild-type sequence. The intact type specifies reads identical to wild-type sequences.

Per time point, the ratio of each type over the total of reads is calculated. We observed only 2 - 6.5% sequence reads in which we could not find a match with the constant parts and we discarded these reads in subsequent analyses. The called point mutations (score = 0) showed a very similar kinetic profile as the intact sequence (wild-type), indicating that they are mostly sequencing errors. We therefore assigned them as intact sequence in the analysis. Insertion and deletion levels at time point t = 0 h were considered as background and subtracted from all time points.

In the double-cut assays, paired end sequencing was performed. The forward and reverse read were matched by the unique sequence ID of a pair of reads. The deletion events were divided into two types: (i) perfectly excised DNA, and (ii) excised DNA with an indel when the deletion was larger than the expected excised product or up to 5 nucleotides smaller.

To determine the untransfected fraction, a standard sigmoid fit was applied to the time lapse curve of intact sequences according to the following equation.

$$\mathit{y}\left(\mathit{t}\right)=1-\frac{\mathit{U}}{1+{\mathit{e}}^{-\mathit{a}\left(\mathit{t}-\mathit{b}\right)}}$$ (2)

Where a, b and U are parameters that determine the shape of the curve. The fitting is done by the nls package of R by minimization of the Gaussian dispersion. U describes the asymptotic plateau, that is, the untransfected fraction.

Mathematical modeling

I. Modeling the kinetics of total indels

The three fractions of intact (P), broken (B) and total indels (M) of a locus at any given time (t) after cutting by CRISPR-Cas9 must adhere to the principle of conservation

$$\mathit{P}\left(\mathit{t}\right)+\mathit{B}\left(\mathit{t}\right)+\mathit{M}\left(\mathit{t}\right)=1$$ (3)

We assumed the cutting and repair kinetics is of first-order and the overall activity of CRISPR-Cas9 is proportional to the abundance of Cas9 that is modeled in Equation (1). As shown in the diagram (Figure 1A) and taking Equation (3) into account, the kinetics of the intact fraction (P) and the total indels (M) is determined by a nonlinear ODE

$$\{\begin{array}{c}\frac{\mathit{dP}\left(\mathit{t}\right)}{\mathit{dt}}=-{\mathit{k}}_{\mathit{c}}R\left(\mathit{t}\right)P\left(\mathit{t}\right)+{\mathit{k}}_{\mathit{p}}B\left(\mathit{t}\right)=-{\mathit{k}}_{\mathit{c}}R\left(\mathit{t}\right)P\left(\mathit{t}\right)+{\mathit{k}}_{\mathit{p}}\left(1-P\left(\mathit{t}\right)-M\left(\mathit{t}\right)\right)\\ \frac{\mathit{dM}\left(\mathit{t}\right)}{\mathit{dt}}={\mathit{k}}_{\mathit{m}}B\left(\mathit{t}\right)={\mathit{k}}_{\mathit{m}}\left(1-\mathit{P}\left(\mathit{t}\right)-\mathit{M}\left(\mathit{t}\right)\right)\end{array}$$ (4)

whereby $k_c$ stands for the maximal Cas9 cutting rate, $k_p$ for perfect repair rate and $k_m$ for mutagenic repair rate that gives rise to indels, all of which are in h^-1.

Because broken DNA is not detected in amplicons across the break site, the measured intact fraction (P_r) is the ratio between the abundance of intact sequences and the sum of the abundance of intact and indel sequences. Including the untransfected fraction (U) from Equation (2) as a part in the intact fraction, the measured intact fraction is

$${\mathit{P}}_{\mathit{r}}\left(\mathit{t}\right)=\frac{\mathit{U}+\mathit{P}\left(\mathit{t}\right)}{\mathit{U}+\mathit{P}\left(\mathit{t}\right)+\mathit{M}\left(\mathit{t}\right)}$$ (5)

Taking Equations (1), (2), and (4) together and a set of randomly chosen initial values for k_c, k_p, k_m the P(t), B(t) and M(t) were modeled. P_r(t) was calculated with Equation (5), to demonstrate simulation outcomes as shown in Figure S1. Then, we estimated the optimal values of kinetic parameters by minimizing the difference between the modeled P_r(t) and experimentally measured intact fraction using the Levenberg-Marquardt algorithm (LMA) using Package FME in R. The estimated rates were used to deduce the P(t), B(t) and M(t) fractions according to Equation (3). The time point of the highest value of B(t) is τ.

The time course spans multiple cell divisions. Because cells with broken DNA may enter a transient cell cycle arrest, this could lead to under-representation of the broken fraction, as is provides cells without broken DNA with a relative growth advantage in the cell pool. However, because of three reasons combined, we believe that the impact of this bias on our parameter estimates is minor. First, we found that the percentage of arrested cells is no more than ∼10% at 16 h after Cas9 activation, and even less at earlier and later time points (Figure S5). Second, because K562 cells are approximately tetraploid (Figure S4), arrested cells are likely to also harbor intact or indel DNA; hence a cell cycle arrest will not only reduce the broken fraction, but also the intact and indel fractions. Third, our kinetic modeling is based on the measured indel / (indel+intact) ratios, not on measurements of broken DNA. A modest underrepresentation of broken DNA in the cell pool does not significantly affect this ratio.

For Figure 6, we performed the fitting for each sgRNA, using the measurements from all time series combined. We first inferred the transfection efficiency from these data by conducting a series of model fits while varying the transfection efficiency value from 60 to 90% in steps of 1%. The transfection efficiency value that yielded the lowest sum of residuals squared was chosen. For LBR2, LBR8 and chr11 this resulted in estimated transfection efficiencies of 72%%, 69% and 75%, respectively, which is in close agreement with efficiencies observed by flow cytometry analysis (see Results). For AAVS1 this value was ∼85% but the residual errors did not converge to a clear minimum; we therefore decided to use the average estimate of the other three loci, i.e., 72%. Next, the model fitting was carried out on the data points of all replicates combined, using a standard 1,000-fold bootstrapping by random sampling of the data with replacement.

II. Testing the robustness of the modeled perfect repair rate at LBR2

For the parameter sweep analysis testing the robustness of the rate of perfect repair $k_p$ (Figure 2E, corresponding text), we restricted the ratio of $k_p$ to the total repair rate $\left(k_p+k_m\right)$ as a sweeping factor

$$\mathbf{V}\left(\mathbf{i}\right)=\frac{{\mathit{k}}_{\mathit{p}}}{{\mathit{k}}_{\mathit{p}}+{\mathit{k}}_{\mathit{m}}}=\frac{\mathbf{i}{\mathbf{W}}_0}{\mathbf{i}{\mathbf{W}}_0+\left(1-{\mathbf{W}}_0\right)2^{\mathbf{i}-1}}$$ (6)

varying from ${\text{W}}_0=0.75$ downward by i times from 1 to 32, spanning 10 orders of magnitude. The incentive of introducing $i$ as a term of multiplication is to test more carefully at high $k_p$ and a broad dynamic range with virtually equal step size at the low end. Therefore, we can represent $k_p$ as

$${\mathit{k}}_{\mathit{p}}=\frac{{\mathit{k}}_{\mathit{m}}\mathbf{V}\left(\mathbf{i}\right)}{1-\mathbf{V}\left(\mathbf{i}\right)}=\frac{\mathbf{i}{2}^{1-\mathbf{i}}{\mathbf{W}}_0{\mathit{k}}_{\mathit{m}}}{\left(1-{\mathbf{W}}_0\right)}$$ (7)

Taking Equations (1), (2), (4), (5), and (7) together, we performed the model fitting with LMA.

Given a fixed ratio V(i) of perfect repair, the F-test was applied to examine the statistical significance for the difference in performance between restricted and optimal fittings, by the standard approach that takes the degree of freedom, which is the number of time points of the experiment minus 2 (the number of parameters in the model) and the fold difference in the deviance of fittings. A cutoff at p = 0.1 is applied to determine the upper bound of deviance and thereafter the upper bound of the ratio of perfect repair (V) is calculated accordingly (Figure 2E).

Taking a similar approach of parameter sweep, we tested the robustness of $k_c$, and calculated the corresponding deviation of model fit (Figure S2F).

III. Modeling the kinetics of individual indels

To model +1 $\left(M_{+1}\right)$ and −7 $\left(M_{-7}\right)$ indels individually, we introduced the kinetic terms $k_{+1}$ and $k_{-7}$ correspondingly for each mutant. As shown in the diagram (Figure 5A), the kinetics of individual indels can be written as

$$\{\begin{array}{c}\frac{\mathit{d}{\mathit{M}}_{+1}\left(\mathit{t}\right)}{\mathit{dt}}={\mathit{k}}_{+1}B\left(\mathit{t}\right)={\mathit{k}}_{+1}\left(1-\mathit{P}\left(\mathit{t}\right)-\mathit{M}\left(\mathit{t}\right)\right)\\ \frac{\mathit{d}{\mathit{M}}_{-7}\left(\mathit{t}\right)}{\mathit{dt}}={\mathit{k}}_{-7}B\left(\mathit{t}\right)={\mathit{k}}_{-7}\left(1-\mathit{P}\left(\mathit{t}\right)-\mathit{M}\left(\mathit{t}\right)\right)\end{array}$$ (8)

Similar to the measured intact fraction $\left(P_r\right)$,the measured fraction of individual indels $\left(M_{r,+1},M_{r,-7}\right)$ can be represented as

$$\{\begin{array}{c}{\mathit{M}}_{\mathit{r},+1}\left(t\right)=\frac{{\mathit{M}}_{+1}\left(\mathit{t}\right)}{\mathit{U}+\mathit{P}\left(\mathit{t}\right)+\mathit{M}\left(\mathit{t}\right)}\\ {\mathit{M}}_{\mathit{r},-7}\left(t\right)=\frac{{\mathit{M}}_{-7}\left(\mathit{t}\right)}{\mathit{U}+\mathit{P}\left(\mathit{t}\right)+\mathit{M}\left(\mathit{t}\right)}\end{array}$$ (9)

Taking Equations (1), (2), (4), (5), and (8) together, we estimated the kinetic parameters by minimizing a gradient of differences between the modeled ${\text{P}}_{\text{r}}\left(\text{t}\right)$, $M_{r,+1}\left(t\right)$ and $M_{r,-7}\left(t\right)$ and experimentally measured sequence data of the intact, +1 and −7 fraction by LMA.

IV. Adjustment of the modeling of the −7 indel kinetics

Following the modeling of individual indels, we discovered inconsistency between the fitted curve of the −7 indel and the experimental data (Figure 5C), suggesting the repair rate for the −7 indel is not a constant. Assuming a linear change of −7 repair rate over time, we adjusted the model by introducing a starting rate $\left(k_{-7,t=0h}\right)$ and an end rate $\left(k_{-7,t=60h}\right)$ (Figure 5D), and the non-constant −7 repair rate can be described as

$${\mathit{k}}_{-7}\left(\mathbf{t}\right)={\mathit{k}}_{-7,\mathit{t}=0\mathit{h}}+\frac{{\mathit{k}}_{-7,\mathit{t}=60\mathit{h}}-{\mathit{k}}_{-7,\mathit{t}=0\mathit{h}}}{\mathit{T}}$$ (10)

whereby $T$ is 60 hours, the duration of experiment.

Adjusting Equation (8) by Equation (10), we have

$$\{\begin{array}{c}\frac{\mathit{d}{\mathit{M}}_{+1}\left(\mathit{t}\right)}{\mathit{dt}}={\mathit{k}}_{+1}\left(1-\mathit{P}\left(\mathit{t}\right)-\mathit{M}\left(\mathit{t}\right)\right)\\ \frac{\mathit{d}{\mathit{M}}_{-7}\left(\mathit{t}\right)}{\mathit{dt}}=\left({\mathit{k}}_{-7,\mathit{t}=0\mathit{h}}+\frac{{\mathit{k}}_{-7,\mathit{t}=60\mathit{h}}-{\mathit{k}}_{-7,\mathit{t}=0\mathit{h}}}{\mathit{T}}t\right)\left(1-\mathit{P}\left(\mathit{t}\right)-\mathit{M}\left(\mathit{t}\right)\right)\end{array}$$ (11)

Taking Equations (1), (2), (4), (5), (9), and (11) together, we performed the model fitting with LMA.

Data and Software Availability

Raw image files are deposited on Mendeley Data (http://dx.doi.org/10.17632/wg4ssg7pfw.1).

The accession number for the sequence files reported in this paper is NCBI GEO: GSE113129 (https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE113129).

Code is provided at https://github.com/vansteensellab/DSB_Repair_Kinetics.

Published: May 24, 2018