Abstract
Purpose
The quality of dedicated cone‐beam breast CT (CBBCT) imaging is fundamentally limited by x‐ray scatter contamination due to the large irradiation volume. In this paper, we propose a scatter correction method for CBBCT using a novel forward‐projection model with high correction efficacy and reliability.
Method
We first coarsely segment the uncorrected, first‐pass, reconstructed CBBCT images into binary‐object maps and assign the segmented fibroglandular and adipose tissue with the correct attenuation coefficients based on the mean x‐ray energy. The modified CBBCT are treated as the prior images toward scatter correction. Primary signals are first estimated via forward projection on the modified CBBCT. To avoid errors caused by inaccurate segmentation, only sparse samples of estimated primary are selected for scatter estimation. A Fourier‐Transform based algorithm, herein referred to as local filtration hereafter, is developed to efficiently estimate the global scatter distribution on the detector. The scatter‐corrected images are obtained by removing the estimated scatter distribution from measured projection data.
Results
We evaluate the method performance on six patients with different breast sizes and shapes representing the general population. The results show that the proposed method effectively reduces the image spatial non‐uniformity from 8.27 to 1.91% for coronal views and from 6.50 to 3.00% for sagittal views. The contrast‐to‐deviation ratio is improved by an average factor of 1.41. Comparisons on the image details reveal that the proposed scatter correction successfully preserves fine structures of fibroglandular tissues that are lost in the segmentation process.
Conclusion
We propose a highly practical and efficient scatter correction algorithm for CBBCT via a forward‐projection model. The method is attractive in clinical CBBCT imaging as it is readily implementable on a clinical system without modifications in current imaging protocols or system hardware.
Keywords: computed tomography, cone‐beam breast CT , scatter correction, shading correction
1. Introduction
Breast cancer can be masked in projection‐based mammography due to tissue superposition, especially in women with dense breasts.1 This drawback can be fundamentally overcome by dedicated cone‐beam breast CT (CBBCT),1, 2 which provides three‐dimensional images without physical compression as used in mammography or in digital breast tomosynthesis, and therefore it potentially improves the clinical performance.3, 4, 5, 6 However, the image quality of CBBCT is limited by scatter contamination due to the large irradiation volume.7, 8 In this paper, we propose a scatter correction method for CBBCT using a novel forward‐projection model with high correction efficacy and reliability.
The scatter‐induced artifacts on CBBCT images manifest themselves as reduced signal intensities especially around the object center as well as degraded image contrast.7, 8, 9, 10 These CBBCT imaging errors cause inaccurate quantitative assessment in clinical tasks11 and reduce sensitivity in calcification and lesion detection.10 Scatter correction methods for cone beam CT (CBCT) in general has been extensively investigated over the past decades, and this research topic continues to be active due to the increasing demands of CBCT in different clinical applications. Comprehensive reviews of scatter correction methods can be found in Refs.12, 13. Among existing approaches, measurement‐based scatter correction is most commonly used in current CBBCT imaging. Typical implementations include inserting a beam‐pass or beam‐stop arrays to sparsely sample the primary or scatter signals on the detector. The scatter distribution is subsequently obtained by interpolation or low‐pass filtration, based on the fact the scatter signals contain predominantly low‐frequency components.14, 15 These methods, however, are considered unfavorable on clinical systems due to the insertion of the beam blocker. As signal loss is inevitable in scatter measurement, an extra scan with additional dose to breast is needed, which also prolongs the scan time and increases the potential motion artifacts. Scatter in projections can be estimated conveniently without modifying the imaging geometry or hardware by analytical modeling of the relationship between primary and scatter signals.16, 17, 18, 19, 20 At the expense of substantially increased computation complexity, Monte Carlo (MC) simulation methods achieve more accurate scatter estimation via tracking the trajectory of each photon event.21, 22, 23, 24, 25 In practice, simplified MC simulation or hybrid methods26, 27 are often used to optimally balance the tradeoff between scatter correction efficacy and computation cost. In current CBBCT imaging, it has been reported that scatter estimates can be obtained via MC simulation within a clinically relevant processing time on a standard computer by assuming a semi‐ellipsoidal and uniform breast.21
In this paper, we propose a new effective and efficient modeling method for scatter correction on CBBCT images with no assumptions on the breast shape and composition. The main idea of this work is inspired by Ref.15, where a planning CT (pCT) based scatter correction approach is proposed for reducing scatter artifacts on CBCT images to improve accuracy of radiation therapy treatment. pCT is commonly available in current radiation therapy and therefore can be used as prior patient information. The basic principle of pCT‐based scatter correction is to estimate the primary signals of CBCT projections via forward projection of the registered pCT images, which are considered to be of high quality with negligible scatter contamination. Then, the low‐frequency scatter in CBCT raw projections is obtained by subtracting the estimated primary signals and low‐pass filtering. The previously proposed pCT‐based correction cannot be directly used for scatter removal in diagnostic CBBCT imaging where pCT is unavailable. In our published studies,15, 28 we find that the pCT‐based scatter correction is accurate even in the area where pCT registration has large errors. On the other hand, breast CT images have approximately binary‐object (i.e., fibroglandular and adipose tissue) distributions and existing algorithms have achieved accurate binary segmentation on CBBCT images.29 We therefore propose to first coarsely segment the first‐pass uncorrected CBBCT images into binary‐object maps and assign the segmented fibroglandular and adipose tissue with the correct attenuation coefficients based on the mean x‐ray energy. The modified CBBCT are treated as the prior images, in lieu of pCT, in our previously developed algorithm toward scatter correction. Primary signals are first estimated via forward projection on the modified CBBCT. To avoid errors caused by inaccurate segmentation, only sparse samples of estimated primary are selected for scatter estimation. A Fourier‐Transform based algorithm, referred to as local filtration, is developed to efficiently estimate the global scatter distribution on detector. The scatter‐corrected images are obtained by removing the estimated scatter distribution from measured projection data. The proposed method is evaluated on six patients with large variation in breast shapes.
2. Methods and materials
2.A. First‐pass estimation of scatter signals
We first generate the uncorrected CBBCT images from scatter contaminated projections. In all the presented patient studies, an empirical thresholding method is used to coarsely segment the breast region into adipose and fibroglandular tissues. Voxels with values between 0.1 and 0.24 per cm are considered as adipose tissue and assigned a uniform value of 0.23 per cm, and voxels with values above 0.24 per cm are considered as fibroglandular tissue and assigned a uniform value of 0.28 per cm. The assigned attenuation coefficients (i.e., ) are empirically tuned based on the calculated effective mean energy (i.e., 30.4 keV) of the x‐ray spectrum (49 kVp with a HVL of 1.39 mm Al) used in the clinical CBBCT system. It is critical to set correct values for successful scatter correction using the proposed algorithm. Values too high or too low will result in under or over correction of scatter. However, we find that these values can be fixed for all the patient studies presented in this paper. Therefore, parameter tweaking of does not reduce the practicality of our method. The resultant image is considered as prior CT, on which forward projection via Siddon's ray tracing algorithm30 is used to simulate primary projections, i.e., scatter‐free line integrals. The estimated line integrals are converted to raw projection (in unit of detector count) using x‐ray flat field intensity (I 0 ), which is determined by taking the average value of a 200 × 200 unattenuated pixel region on the measured projection data. An initial estimate of the scatter distribution, denoted as S 0 hereafter, is finally obtained by subtracting the simulated primary projection in unit of photon numbers from the measured projection.
2.B. Removal of scatter estimation errors and local filtration
The resulting S 0 includes both low‐frequency scatter distribution, denoted as S t , and the scatter estimation errors, denoted as S e , stemming mostly from the difference between the prior CT image generated by coarse segmentation and the true scatter‐free CBBCT image. To reduce the impact of S e on estimation of S t , we aim to use S 0 only in the area, , where S e is expected to be small, and then generate a whole‐field estimation of S t using low‐pass filtration and interpolation. Toward this goal, we first obtain as the area with positive and smooth , i.e.,:
| (1) |
where is the pixel index on the detector, calculates the image gradient distribution, and is the threshold of the gradient magnitude of S 0 , set at 50 detector counts in our studies.
An estimate of the whole‐field scatter distribution, , is obtained via weighted summation of available sparse samples in as:
| (2) |
where the is the Gaussian smooth kernel defined as:
| (3) |
The kernel width is set to be 4 pixels in all the presented studies.
The calculation of Eq. (2) is equivalent to signal smoothing inside and interpolation outside. To accelerate the computation, we define an indicator function, , with the same size of the projection image as:
It can be easily verified that Eq. (2) has an equivalent form using convolution:
| (4) |
Equation (4) can be efficiently implemented via fast Fourier Transform. We refer to the above technique (Eq. (4)) as local filtration in this paper.
is finally removed from the CBBCT raw projections for scatter correction.
2.C. Workflow
The workflow of the proposed scatter correction method on CBCT is summarized in Fig. 1, with the following steps:
Step 1: Reconstruct the uncorrected CBBCT images using raw projection data.
Step 2: Segment fibroglandular and adipose tissues and assign uniform linear attenuation coefficient values.
Step 3: Forward project the image obtained in Step 2 to simulate primary projection.
Step 4: Subtract the simulated primary projection from the raw projection to acquire a first‐pass scatter estimate, .
Step 5: Obtain sparse samples of via magnitude and gradient thresholding (Eq. (1)).
Step 6: Determine the final scatter distribution from the sparse sampled of in Step 5 using local filtration (Eq. (4)). Subtract the final scatter estimate from the raw projection to obtain the scatter‐corrected projection.
Step 7: Reconstruct to obtain the scatter‐corrected CBBCT images.
Figure 1.
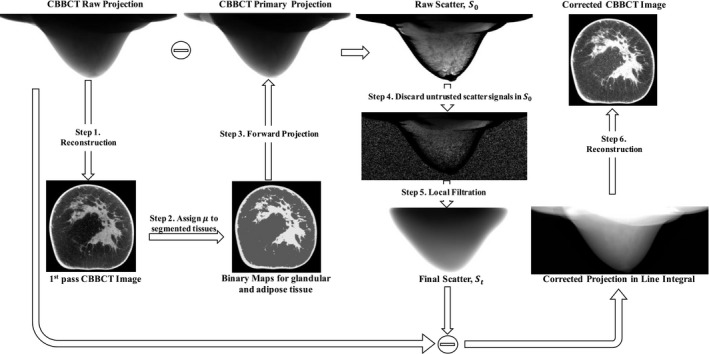
Workflow of scatter correction for CBBCT using the proposed forward‐projection model.
2.D. Evaluation
We evaluate the performance of the proposed scatter correction using a forward‐projection model on six patients in a retrospective study. These patient data were acquired during a clinical research study under a protocol that was approved by the institutional review boards of the University of Rochester Medical Center and the University of Massachusetts Medical School. The selected six cases were highly suspicious for malignancy and were assigned category 4 or 5 according to the Breast Imaging‐Reporting and Data System (BI‐RADS) of the American College of Radiology.
The clinical research CBBCT prototype system (Koning Corporation, West Henrietta, NY, USA) used for patient data acquisition has a 49 kVp tungsten anode spectrum and a first half‐value layer of 1.39 mm Al, which gives a mean energy of 30.4 keV.31 The tungsten target x‐ray tube (RAD71SP, Varian Medical Systems, Salt Lake City, UT) is powered by a high frequency generator (Sedecal, USA) and the detector is a thallium‐doped Cesium Iodine (CsI:Tl) flat‐panel detector (PaxScan® 4030CB, Varian Medical Systems, Salt Lake City, UT). The source to axis distance (SAD) is 65 cm and the source to detector distance (SDD) is 89.8 cm. Each CBBCT scan acquires 300 projections over 360°, and each projection has a size of 1024 × 768 pixels. The reconstructed CBBCT images have an isotropic voxel size of 0.273 mm.
In this paper, all the data are processed on a 1.6 GHz 64‐bit Windows 7 workstation with NVIDIA Quadro 620 GPU. It takes an average of 40 seconds and 3.5 min to perform forward projection and FDK reconstruction, respectively, on a CBBCT volume with a size of 1024 × 1024 × 450. The time for reconstruction slightly varies depending on the breast size. The step of scatter correction in projection domain takes about 10 s in total for each patient dataset with 300 projections.
In all of the evaluation studies, we use spatial non‐uniformity (SNU) and contrast‐to‐deviation ratio (CDR) as image quality metrics.21 Five regions of interest (ROI) within adipose tissue, each with 25 × 25 pixels, are manually selected from the center and the periphery of the CBBCT image for calculating SNU. SNU is defined as:
| (5) |
where and are the maximum and the minimum of the mean linear attenuation coefficients of all five ROIs, and is the average of the mean linear attenuation coefficients of all 5 ROIs. The SNU quantitates the global imaging non‐uniformity.
The CDR is calculated as:
| (6) |
where and are the mean linear attenuation coefficients of the segmented fibroglandular and adipose tissues. is the standard deviation (STD) of the linear attenuation coefficients in the segmented area of adipose tissue. Note that, is different from conventional statistical image noise since it includes the effect of existing image artifacts and small background structures. As such, the definition of CDR is slightly different from that of contrast‐to‐noise ratio.21
3. Results
3.A. Scatter correction on patient cases
Figure 2 shows one example of the uncorrected and corrected projections and the estimated scatter distribution. Figure 3 compares the uncorrected and the corrected CBBCT images in coronal and sagittal views for four patients. It is observed the proposed method substantially improve the image quality. For all six patients, the quantitative analysis on both coronal and sagittal views of the uncorrected and the corrected images is summarized in Table 1. For coronal view, the proposed correction reduces the SNU from 8.27 to 1.91% on average and increase the CDR by an average factor of 1.38. For sagittal view, the SNU is reduced from 6.50 to 3.00% on average and the CDR is increased by a factor of 1.44.
Figure 2.

Example of the raw projection, the estimated scatter and the scatter‐corrected projection. Display window: (a) and (c): [min max], (b) [100 2000] detector counts.
Figure 3.
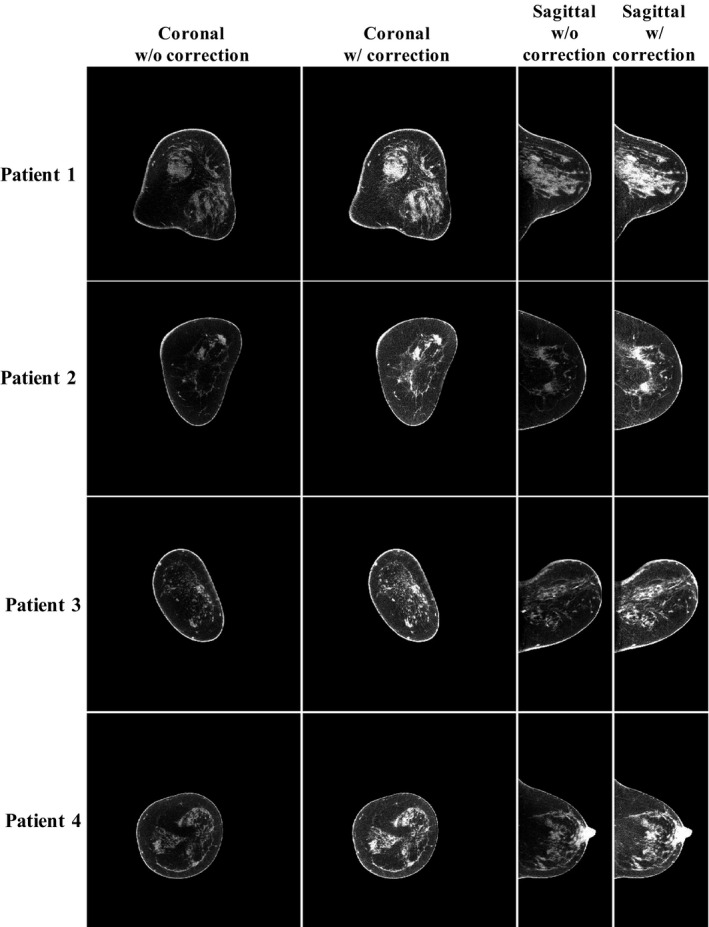
Scatter correction results for four patients with different breast shapes. Display window: [0.2 0.3] cm−1.
Table 1.
Comparison of SNU, contrast, , CDR and CDR increase ratios on the uncorrected image and the corrected images using the proposed method for six patients
| Patient # | SNU (%) (Before/After) | Contrast (cm−1) (Before/After) | (cm−1) (Before/After) | CDR (Before/After) | CDR Increase ratio | ||||
|---|---|---|---|---|---|---|---|---|---|
| Coronal view | |||||||||
| 1 | 9.32 | 2.45 | 0.034 | 0.050 | 0.010 | 0.010 | 3.44 | 5.00 | 1.45 |
| 2 | 6.50 | 1.47 | 0.045 | 0.071 | 0.007 | 0.009 | 6.09 | 7.63 | 1.25 |
| 3 | 3.89 | 0.85 | 0.032 | 0.046 | 0.006 | 0.008 | 5.17 | 6.10 | 1.18 |
| 4 | 7.08 | 2.06 | 0.032 | 0.049 | 0.007 | 0.007 | 4.65 | 6.88 | 1.48 |
| 5 | 13.70 | 3.40 | 0.035 | 0.041 | 0.009 | 0.009 | 3.90 | 4.70 | 1.21 |
| 6 | 9.10 | 1.20 | 0.037 | 0.066 | 0.010 | 0.010 | 3.80 | 6.50 | 1.71 |
| Average | 8.27 | 1.91 | 0.036 | 0.054 | 0.008 | 0.009 | 4.51 | 6.14 | 1.38 |
| Sagittal view | |||||||||
| 1 | 8.96 | 3.96 | 0.061 | 0.073 | 0.031 | 0.026 | 2.00 | 2.79 | 1.40 |
| 2 | 4.45 | 3.08 | 0.041 | 0.067 | 0.016 | 0.017 | 2.58 | 4.03 | 1.56 |
| 3 | 3.35 | 2.74 | 0.031 | 0.045 | 0.006 | 0.007 | 5.41 | 6.33 | 1.17 |
| 4 | 6.66 | 2.90 | 0.038 | 0.040 | 0.010 | 0.009 | 3.70 | 4.44 | 1.20 |
| 5 | 9.50 | 3.80 | 0.039 | 0.046 | 0.008 | 0.009 | 4.60 | 5.10 | 1.11 |
| 6 | 6.10 | 1.50 | 0.048 | 0.070 | 0.016 | 0.011 | 3.00 | 6.60 | 2.20 |
| Average | 6.50 | 3.00 | 0.043 | 0.057 | 0.015 | 0.013 | 3.55 | 4.88 | 1.44 |
3.B. Potential errors induced by inaccurate segmentation
A particular concern regarding the proposed method is that CBBCT generated from coarse segmentation is treated as the prior images and therefore segmentation errors may result in errors for scatter correction. In particular, inaccurate segmentation may potentially alter the anatomical information of CBBCT after scatter correction. Nonetheless, the removal of scatter estimates with large expected errors and the local filtration technique guarantee that the success of the proposed method does not heavily rely on accurate segmentation. To support our argument, we present two more patient studies with large segmentation errors, shown as patient 5 and 6 in Fig. 4. In the comparison of the uncorrected image and the image generate via segmentation, it is obvious that the latter loses many fine structures of fibroglandular tissue. After the proposed scatter correction, it is seen that the image uniformities for the two patients are substantially improved without structure alteration (see the comparison of zoom‐in images).
Figure 4.
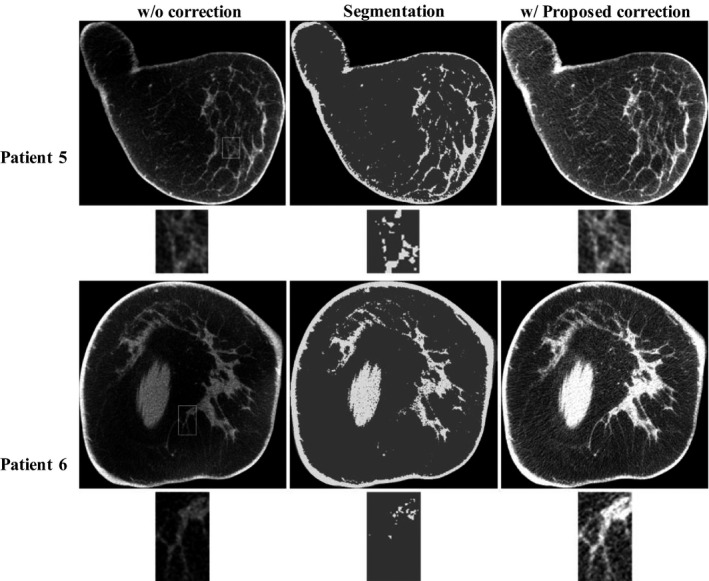
The effect of segmentation errors on the performance of the proposed correction method. For each patient, the images on the top panel are the uncorrected image, the corresponding tissue segmentation and the corrected image using proposed method. The bottom panel shows the zoom‐in views of the selected ROI (marked as white squares in the top panel) on the corresponding image above. Display window: [0.2 0.3] cm−1.
3.C. Effect of values on the method performance
One merit of the proposed method is that it estimates the whole‐field scatter distribution using only sparse samples. As shown in Eq. (1), the gradient threshold, is the only algorithm parameter in the selection of sparse samples. In this paper, we empirically chose a value of 50 detector counts to perform scatter estimation for all the patient cases. To investigate the effect of on the method performance, we compare the corrected images on Patient 6 of Fig. 4 using different values (i.e., 10, 30, 80, and 110) in the proposed algorithm, shown in Fig. 5. It is seen that a value either too large or too small degrades the quality of the resultant image and = 50 achieves a minimum image SNU of 2.6%. However, the effect of different values is not obvious on the scatter‐corrected CBBCT images, and the image SNU remains under 3.0% for a large range of values from 30 to 70.
Figure 5.
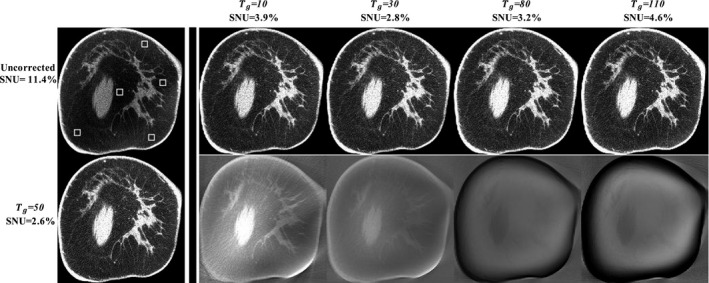
Demonstration of the effect of T g values on the performance of the proposed method. The first column shows the uncorrected image (upper) and the corrected image(bottom) using T g = 50. The rest of upper row: images corrected using different T g values. Display window: [0.2 0.3] cm−1. The rest of bottom row: difference images compared with the result using T g = 50. Display window: [−0.01 0.01] cm−1.
3.D. Comparison with the system‐embedded scatter correction
To further evaluate the performance of proposed method, we compare the corrected images with those corrected by the software embedded on the Koning CBBCT system. Figure 6 shows two representative results of comparison on patient 1 and 3, where scatter correction is particularly challenging due to the irregular breast shapes. Table 2 demonstrates the quantitative comparison of the images in Fig. 6. It shows that the proposed method outperforms the system correction in both SNU and CDR increase ratio.
Figure 6.
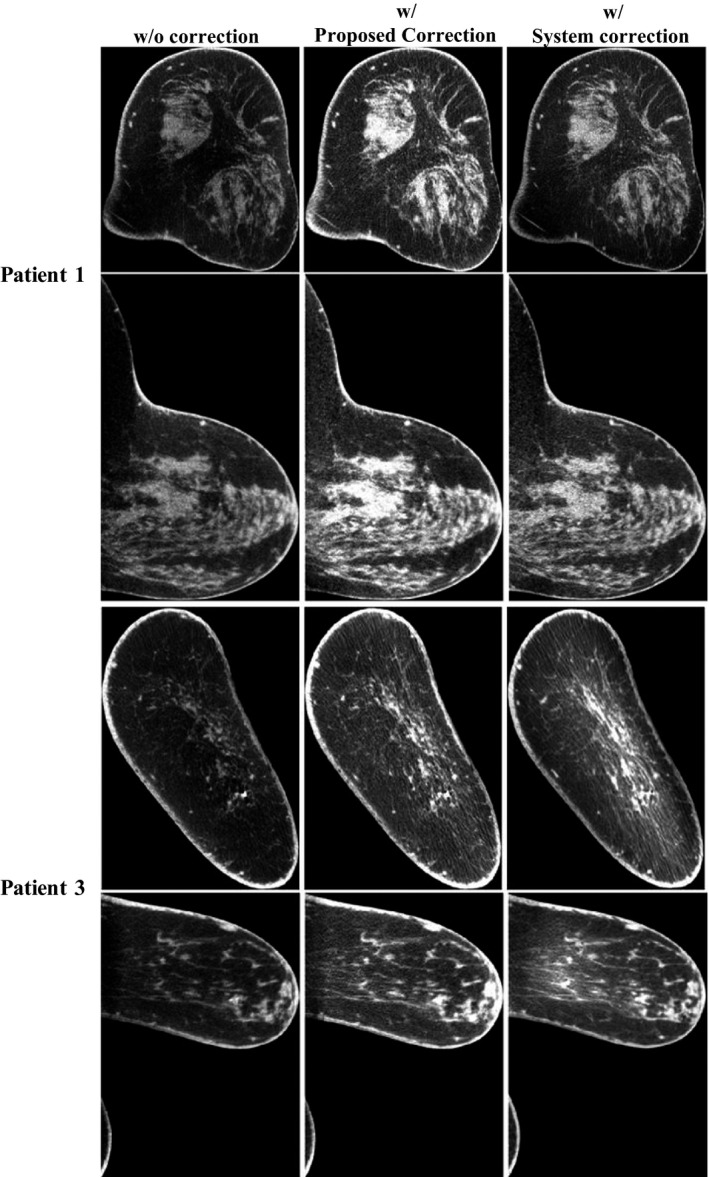
Comparison of the uncorrected image, the corrected image with the proposed scatter correction method and the corrected image with the system‐embedded software. The images are taken on Patient 1 and 3, but at slices different from those shown in Fig. 2. Display window: [0.2 0.3] cm−1.
Table 2.
Comparison of SNU and CDR increase ratios using the proposed and the system scatter correction methods. Results are listed for both coronal and sagittal views
| Patient # | Coronal view | Sagittal view | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SNU(%) | CDR Increase ratio | SNU(%) | CDR Increase ratio | |||||||
| w/o | Proposed | System | Proposed | System | w/o | Proposed | System | Proposed | System | |
| 1 | 8.31 | 2.25 | 7.64 | 1.52 | 1.13 | 12 | 4.52 | 9.75 | 1.87 | 1.2 |
| 3 | 2.12 | 1.91 | 7.33 | 1.26 | 0.66 | 5.46 | 2.35 | 3.86 | 1.16 | 1.03 |
4. Conclusion and discussion
In this work, we propose a highly practical and efficient scatter correction algorithm for CBBCT via a forward‐projection model. Scatter‐free primary projections are first simulated by forward projecting the binary‐object image segmented from the uncorrected CBBCT, and a first‐pass scatter estimate is then generated by subtracting the simulated primary projection from the raw measured projection. Only sparse samples of the first‐pass scatter estimate are used in the correction process to prevent tissue alteration caused by inaccurate segmentation. A Fourier‐Transform based algorithm, local filtration, is applied to efficiently obtain a global scatter distribution. We evaluate the method performance on six patients with different breast sizes and shapes representing the general population. The results show that the proposed method effectively reduces the image SNU from 8.27 to 1.91% for coronal views and from 6.50 to 3.00% for sagittal views. The CDR is improved by an average factor of 1.41. Comparisons on the image details reveal that the proposed scatter correction successfully preserves fine structures of fibroglandular tissues that are lost in the segmentation process.
Using subtraction‐based signal processing, our method cannot remove scatter noise and therefore has limited improvement on CNR due to the increased CT image noise after scatter correction.32 It is worth noting that, for practical implementations on clinical images, the term of CDR we use to quantitate the image quality is different from CNR. In the CDR calculation, the image contrast is computed as the mean signal difference between adipose and glandular tissue. To obtain a background “noise” level, we first segment adipose tissue from the entire image and calculate the signal standard deviation as “noise”. The calculated “noise” therefore includes statistical image noise as well as two additional terms: image non‐uniformity due to image artifacts and small background structures. In our studies, we find that the standard deviation of adipose signals may decrease after scatter correction mainly due to the removal of the cupping artifacts, leading to a larger increase ratio on CDR than that on CNR.
During the paper preparation, we notice a similar scatter correction approach in a recent publication by Zhao et al.33 Although both methods use a framework of segmentation, forward projection and scatter smoothing, two major differences should be noted. First, Zhao et al. use more sophisticated forward projection and image segmentation to guarantee the method performance for general CBCT imaging, while we aim to develop a scatter correction method for a dedicated CBBCT system only. Due to the relative simplicity of the breast geometry and material composition, we find that a simplified monochromatic projector and segmentation with a fixed threshold are sufficient for a satisfactory performance of scatter correction. Our method therefore has reduced computation compared to the Zhao method. Second, to suppress errors on a first‐pass estimate of scatter, Zhao et al. propose an iterative scheme which is computationally intensive. We design an analytical approach, i.e., the local filtration technique, to estimate a whole‐field scatter distribution from only sparse scatter samples. The method is able to selectively discard scatter samples with high estimated errors. Therefore, even if the simplified forward projection and segmentation result in large errors of scatter estimation, as seen in section 3.B, the proposed method still works well due to sparse sampling and the local filtration technique. Furthermore, the local filtration technique has a high computational efficiency since it consists of a few linear filtering steps and is implemented using FFT.
The proposed scatter correction using a forward‐projection model is attractive in clinical CBBCT imaging for the following three features. First, the method is readily implementable on a clinical system as a software plug‐in without modifications in current imaging protocols or system hardware. Second, the proposed algorithm does not make assumptions or approximations on the breast CT images, and therefore, the method performance is expected to be more stable than those of other existing algorithms using simplified scatter models. Third, the proposed approach has a high computational efficiency as it uses linear filtering on sparse scatter samples (i.e., the local filtration technique). Last, since a mono‐energetic x‐ray spectrum is used in the forward projection, the simulated primary signals do not contain beam‐hardening errors and therefore the proposed algorithm potentially removes low‐frequency beam‐hardening errors as well.
The algorithm is currently implemented in MATLAB with hardware acceleration of one single GPU. To shorten the computation down to a clinical acceptable time, we will convert the MATLAB codes into more efficient languages (i.e., C, C++) and use parallel computing on a multi‐GPU workstation. In addition, our future study will involve more patients to perform statistical analyses on the algorithm accuracy and stability. Human observer studies will be planned for investigations on the improvements in breast cancer detection enabled by the proposed method. We recently developed another scatter correction algorithm for CBBCT using a library‐based approach.21 Although not quantitatively demonstrated in this paper, a preliminary comparison shows that the forward projection‐based method appears to better preserve the high spatial resolution details than the library‐based method. A detailed comparative study of these two methods will be included in our investigations on a large cohort of patients.
Acknowledgment
Research reported in this publication was partially supported by the National Institute of Biomedical Imaging and Bioengineering, and the National Cancer Institute, of the National Institutes of Health under Award Numbers R21EB019597, R21EB021545, R21 CA134128 and R01 CA195512. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The project was also partially supported by the Ministry of Science and Technology of China Key Research and Development Project (Grant No. 2016YFC0101400) and by the National Natural Science Foundation of China (Grant No. 81671681).
Conflict of interest
The authors have no relevant conflicts of interest to disclose.
References
- 1. Chen B, Ning R. Cone‐beam volume CT breast imaging: Feasibility study. Med Phys. 2002;29:755–770. [DOI] [PubMed] [Google Scholar]
- 2. Boone JM, Nelson TR, Lindfors KK, Seibert JA. Dedicated breast CT: Radiation dose and image quality evaluation. Radiology. 2001;221:657–667. [DOI] [PubMed] [Google Scholar]
- 3. Vedantham S, O'Connell AM, Shi L, Karellas A, Huston AJ, Skinner KA. Dedicated breast CT: Feasibility for monitoring neoadjuvant chemotherapy treatment. J Clin Imaging Sci. 2014;4:64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. O'Connell AM, Karellas A, Vedantham S. The potential role of dedicated 3D breast CT as a diagnostic tool: Review and early clinical examples. Breast J. 2014;20:592–605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Lindfors KK, Boone JM, Nelson TR, Yang K, Kwan AL, Miller DF. Dedicated breast CT: Initial clinical experience. Radiology. 2008;246:725–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Prionas ND, Lindfors KK, Ray S, et al. Contrast‐enhanced dedicated breast CT: Initial clinical experience. Radiology. 2010;256:714–723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Kwan AL, Boone JM, Shah N. Evaluation of x‐ray scatter properties in a dedicated cone‐beam breast CT scanner. Med Phys. 2005;32:2967–2975. [DOI] [PubMed] [Google Scholar]
- 8. Chen Y, Liu B, O'Connor JM, Didier CS, Glick SJ. Characterization of scatter in cone‐beam CT breast imaging: Comparison of experimental measurements and Monte Carlo simulation. Med Phys. 2009;36:857–869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Altunbas MC, Shaw CC, Chen L, et al. A post‐reconstruction method to correct cupping artifacts in cone beam breast computed tomography. Med Phys. 2007;34:3109–3118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Yang K, Burkett G, Boone JM. A breast‐specific, negligible‐dose scatter correction technique for dedicated cone‐beam breast CT: A physics‐based approach to improve Hounsfield Unit accuracy. Phys Med Biol. 2014;59:6487–6505. [DOI] [PubMed] [Google Scholar]
- 11. Yang X, Wu S, Sechopoulos I, Fei B. Cupping artifact correction and automated classification for high‐resolution dedicated breast CT images. Med Phys. 2012;39:6397–6406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Niu TY, Zhu L. Overview of X‐ray scatter in cone‐beam computed tomography and its correction methods. Curr Med Imaging Rev. 2010;6:82–89. [Google Scholar]
- 13. Ruhrnschopf EP, Klingenbeck K. A general framework and review of scatter correction methods in x‐ray cone‐beam computerized tomography. Part 1: Scatter compensation approaches. Med Phys. 2011;38:4296–4311. [DOI] [PubMed] [Google Scholar]
- 14. Zhu L, Bennett NR, Fahrig R. Scatter correction method for X‐ray CT using primary modulation: Theory and preliminary results. Ieee T Med Imaging. 2006;25:1573–1587. [DOI] [PubMed] [Google Scholar]
- 15. Niu T, Sun M, Star‐Lack J, Gao H, Fan Q, Zhu L. Shading correction for on‐board cone‐beam CT in radiation therapy using planning MDCT images. Med Phys. 2010;37:5395–5406. [DOI] [PubMed] [Google Scholar]
- 16. Cai W, Ning R, Conover D. Scatter correction for clinical cone beam CT breast imaging based on breast phantom studies. J Xray Sci Technol. 2011;19:91–109. [DOI] [PubMed] [Google Scholar]
- 17. Boone JM, Seibert JA. An analytical model of the scattered radiation distribution in diagnostic radiology. Med Phys. 1988;15:721–725. [DOI] [PubMed] [Google Scholar]
- 18. Seibert JA, Boone JM. X‐Ray scatter removal by deconvolution. Med Phys. 1988;15:567–575. [DOI] [PubMed] [Google Scholar]
- 19. Li H, Mohan R, Zhu XR. Scatter kernel estimation with an edge‐spread function method for cone‐beam computed tomography imaging. Phys Med Biol. 2008;53:6729–6748. [DOI] [PubMed] [Google Scholar]
- 20. Sun M, Star‐Lack JM. Improved scatter correction using adaptive scatter kernel superposition. Phys Med Biol. 2010;55:6695–6720. [DOI] [PubMed] [Google Scholar]
- 21. Shi L, Vedantham S, Karellas A, Zhu L. Library based x‐ray scatter correction for dedicated cone beam breast CT. Med Phys. 2016;43:4529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Shi L, Vedantham S, Karellas A, Zhu L. Library‐based scatter correction for dedicated cone beam breast CT: A feasibility study. In: Proc. SPIE 9783, Medical Imaging 2016: Physics of Medical Imaging, 978330; 2016. [Google Scholar]
- 23. Colijn AP, Beekman FJ. Accelerated simulation of cone beam X‐ray scatter projections. IEEE Trans Med Imaging. 2004;23:584–590. [DOI] [PubMed] [Google Scholar]
- 24. Zbijewski W, Beekman FJ. Efficient Monte Carlo based scatter artifact reduction in cone‐beam micro‐CT. IEEE Trans Med Imaging. 2006;25:817–827. [DOI] [PubMed] [Google Scholar]
- 25. Bootsma GJ, Verhaegen F, Jaffray DA. Efficient scatter distribution estimation and correction in CBCT using concurrent Monte Carlo fitting. Med Phys. 2015;42:54–68. [DOI] [PubMed] [Google Scholar]
- 26. Baer M, Kachelriess M. Hybrid scatter correction for CT imaging. Phys Med Biol. 2012;57:6849–6867. [DOI] [PubMed] [Google Scholar]
- 27. De Wit TC, Xiao J, Nijsen JF, et al. Hybrid scatter correction applied to quantitative holmium‐166 SPECT. Phys Med Biol. 2006;51:4773–4787. [DOI] [PubMed] [Google Scholar]
- 28. Niu TY, Al‐Basheer A, Zhu L. Quantitative cone‐beam CT imaging in radiation therapy using planning CT as a prior: First patient studies. Med Phys. 2012;39:1991–2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Vedantham S, Shi L, Karellas A, O'Connell AM. Dedicated breast CT: Fibroglandular volume measurements in a diagnostic population. Med Phys. 2012;39:7317–7328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Siddon RL. Fast calculation of the exact radiological path for a three‐dimensional CT array. Med Phys. 1985;12:252–255. [DOI] [PubMed] [Google Scholar]
- 31. Vedantham S, Shi L, Karellas A, Noo F. Dedicated breast CT: Radiation dose for circle‐plus‐line trajectory. Med Phys. 2012;39:1530–1541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Zhu L, Wang J, Xing L. Noise suppression in scatter correction for cone‐beam CT. Med Phys. 2009;36:741–752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Zhao W, Vernekohl D, Zhu J, Wang L, Xing L. A model‐based scatter artifacts correction for cone beam CT. Med Phys. 2016;43:1736. [DOI] [PMC free article] [PubMed] [Google Scholar]


