An interactive framework for whole-brain maps at cellular resolution

Abstract

To deconstruct the architecture and function of brain circuits, it is necessary to generate maps of the neuronal connectivity and activity on a whole brain scale. New methods now enable large-scale mapping of the mouse brain at cellular and subcellular resolution. We developed a framework to automatically annotate, analyze, visualize, and easily share whole-brain data at cellular resolution, based on a scale-invariant and interactive mouse brain atlas. This framework enables connectivity and mapping projects in individual laboratories, across imaging platforms, as well as multiplexed quantitative information on the molecular identity of single neurons. As a proof of concept, we generated a comparative connectivity map of five major neuron types in the corticostriatal circuit, as well as an activity-based map to identify hubs mediating the behavioral effects of cocaine. Thus, this computational framework provides the necessary tools to generate brain maps that integrate data from connectivity, neuron identity and function.

The structural and functional mapping of the brain and neural circuits is currently a major endeavor in neuroscience^1,2. Large projects have been initiated to map the mouse brain in terms of cell types and their activity, long-range connectivity patterns and microcircuit connectivity³. Examples of projects to map connectivity and cell types include the Mouse Brain Architecture project⁴, the Allen mouse brain connectivity atlas⁵, and the Mouse connectome project⁶. A challenge central to all such large-scale efforts is the need to develop and implement standardized systems to collect, analyze, visualize and share whole-brain data⁷. Advances in experimental methods for the dissection of connectivity and function through for example genetic labeling of connections and neuronal activity at a whole-brain scale now enable the detailed mapping of circuits^8,9. As a consequence, in addition to the large-scale collaborative projects, an increasing number of individual laboratories have initiated ambitious brain-mapping projects^10–15. However, the lack of standardized and accessible computational tools often limits the power and feasibility of large-scale whole-brain mapping efforts.

Here we provide an open source software solution to support whole-brain mapping efforts to generate, organize and share whole-brain mapping projects derived from light microscopy. We have developed WholeBrain (http://wholebrainsoftware.org/), to allow investigators to quantify and spatially map multidimensional data from whole-brain experiments, and compare results across experiments, in a single standardized anatomical reference atlas. We further developed Openbrainmap (http://openbrainmap.org), to support visualization and sharing of data within and between laboratories, in an interactive web-based framework. The whole computational framework is designed to be robust and flexible, allowing its application to a wide variety of imaging systems (e.g. widefield, confocal, light-sheet), and labeling approaches (e.g. fluorescent proteins, immunohistochemistry and in situ hybridization). Together, this computational framework offers a wide range of tools: powerful image processing pipelines for mapping labeled neurons in a standardized brain atlas, Bayesian statistical packages handling nested hierarchical data, and a framework to produce interactive representations of neuroanatomical data. The framework is available as an open-source R package¹⁶, and we have produced intuitive and concrete guidance through step-by-step video tutorials, allowing for rapid implementation of the system in a standard laboratory environment. Here we demonstrate how WholeBrain and Openbrainmap can be employed to discover brain structure-function relationships, by integrating multidimensional anatomical, molecular, and functional datasets.

RESULTS

Vector and raster representation in neuroanatomy

All maps are the result of efforts to visually represent the physical world (Fig. 1a). A comprehensive neuroanatomical framework must be able to handle any type of data that can be described as spatially located within the volume of the brain, just as a geographical information system is used to analyze and represent different types of data mapped onto the earth’s surface.

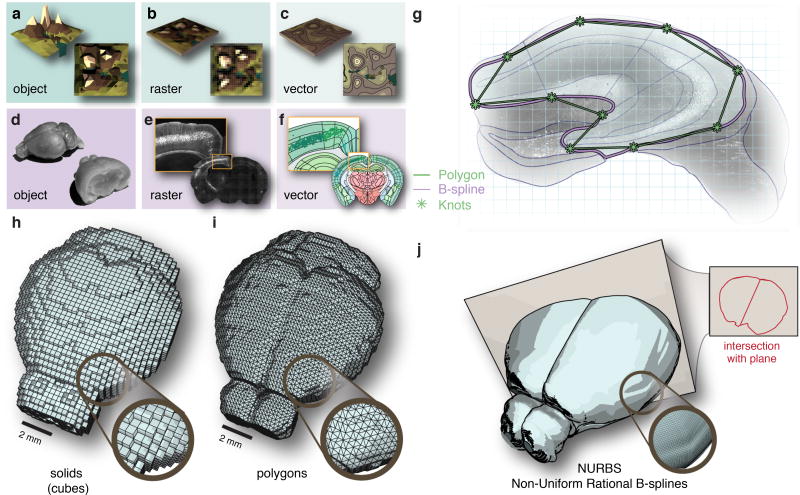
Figure 1. A reference atlas based on vector graphics.

In cartography an object (a) is usually represented either in raster format (b) or vector format (c). Similarly, brain tissue (d) can be represented as raster images (e) or composed of geometric points and curves in a vector format (f). (g) Brain regions defined by polygons (green) are non-scalable compared to regions obtained from Non-Uniform Rational B-splines, NURBS, (purple). In 3D reference atlases can be defined based on different geometrical primitives; (h) voxels can be reduced to primitive solids such as cubes, (i), polygon surfaces provide a more compact representation of the surface only, and (j) NURBS provide a representation of the surface based on smooth B-splines where intersections in the form of curves can be computed to an arbitrary cutting plane.

In general, maps can be constructed using either raster or vector graphics (Fig. 1b–c). Raster graphics represent data in a grid-cell structure (pixels or voxels) parceled into a row and column matrix (Fig. 1b). This raster-based analysis is the norm in neuroscience today, exemplified by approaches to processing whole-brain calcium imaging¹⁷ statistical parametric mapping in functional magnetic resonance imaging (fMRI)²⁹ , differential gene expression as in the Allen Gene Expression Atlas (AGEA)¹⁸, and analysis of whole-brain c-fos expression in behavioral conditions¹⁵ (additional comparisons of recent approaches to mouse brain mapping can be found in Supplementary Table 1). We have aimed to construct a comprehensive framework to represent data at cellular resolution, based on vector graphics to allow mapping of features through the use of points and curves (Fig. 1d–f). The advantage of this approach is that data can be represented simultaneously in multiple coordinate reference systems: image pixels, stereotactic coordinates, and the actual tissue dimensions, instead of only transforming data into a single spatial reference frame.

Scale-invariant reference atlas

Mapping of the tissue coordinates of individual features (e.g. neurons) into a standardized reference atlas is normally performed using raster or polygon graphics¹⁹. We have instead generated a reference atlas of the adult mouse brain based on smooth curves, which can enhance the possibilities to efficiently represent, share and edit anatomical definitions in a standardized reference atlas.

We therefore decided to represent brain regions as smooth surfaces using Non-Uniform Rational B-Splines (NURBS) (Fig. 1g). To generate a 3D anatomical reference atlas, we lofted points between adjacent coronal sections. Compared to existing reference atlases based on solids (Fig. 1h) or polygons (Fig. 1i), this approach offers a number of advantages. First, the atlas becomes scale-invariant and can be easily applied on images of any pixel resolution. This feature enables comparison of image data across microscope systems. Second, atlas intersections with an arbitrary angle can be computed (Fig. 1j). This feature supports projects where visualization of regions and pathways is better achieved at angles others that the canonical (e.g. coronal, sagittal). Third, the topological representation of brain regions becomes data efficient and project results can be efficiently shared in a small format. Fourth, the NURBS format enables editing of the brain atlas to accommodate customization and atlas improvements.

The reference atlas is based on the neuroanatomical definitions found in the Allen Institute mouse reference atlas, thereby integrating the available neuroanatomical and molecular data^5,19. As an example, this feature enables queries of gene expression from the Allen in situ hybridization atlas for any given stereotactic coordinate. In addition, the reference atlas can easily interfaced with other applications, for example by standardization of tissue sectioning using custom 3D printed brain blocks (Supplementary Fig. 1a–d), or through generation of polygon-shaped areas for automated laser capture microdissection (LCM) of defined brain nuclei (Supplementary Fig. 1e–j).

Interactive web interface

We further developed an interactive web interface to allow investigators to rapidly and in a standardized format visualize mapping results and also share data with collaborators. The aim was to develop an interface where data visualization could be performed directly in a standard Internet browser and without setting up a server. In this interface, detected features such as cell bodies and the fit of the reference atlas to the tissue can be visualized as an overlaid layer of vector graphics on the original raster image (Fig 2a–c), http://openbrainmap.org/example_section/, queried directly as tabulated summary statistics (Fig 2d–e), or rendered in stereotactic coordinates within the reference atlas (Fig 2f).

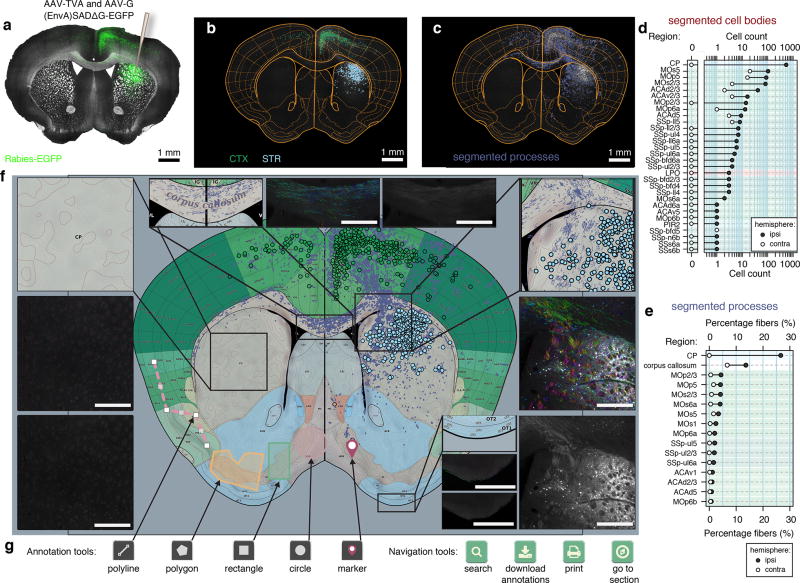
Figure 2. A framework for standardizing and sharing neuroanatomical data.

(a) Coronal section from D1-Cre mouse with rabies tracing targeted to the dorsal striatum, right hemisphere, green: rabies-EGFP, gray: bright-field. (b) Registration of atlas regions as well as segmentation of 1108 individual cell bodies, color coded according to region, light blue: striatum (STR), green: cortex (CTX). (c) Segmented rabies-EGFP labeled processes. (d) Quantification of segmented cell bodies. (e) Quantification of segmented processes. (f) Web-based vector representation of results registered to reference atlas. Scale bars: 500 µm (g) Interactive web-based annotation and navigation tools.

To enable rapid visualization and data sharing, output is provided as a browser-based HyperText Markup Language (HTML) file with associated image tiles. As an example, raster data from a single raw image of a coronal brain section (16 bit, 300–400 Mb) is represented as a set of JPEG tiles of different resolutions (approximately 20 Mb in total). For the purpose of transmission of segmentation and registration results over asynchronous browser/server communication, we constructed an open standard format for spatial features, along with their non-spatial attributes, based on JavaScript Object Notation (JSON), (see method section for further details). The web-interface is designed with mobile-first principles, supporting use in mobile devices, and offers users the ability to further draw, edit or define regions of interest (Fig. 2g).

Segmentation by multiresolution decomposition

Segmentation is the process of assigning labels to distinct parts of an image, in order to mark features of interest such as labeled cell bodies and fiber tracts. In large mapping projects, it is essential to implement automated approaches to feature segmentation, which can be applied to all images with minimal manual intervention.

We used multiresolution decomposition²⁰, as an approach to automatically segment fluorescently labeled cell bodies and fiber tracts. In this segmentation approach, features of different size (e.g. cell body, cell process) can be detected by their mapping on a distinct spatial scale. As an example, an apical dendrite (~1–2 µm thickness) is defined on a smaller spatial scale than a cell body (~10–20 µm diameter). Genetic labeling of dendrites and cell bodies can therefore be decomposed by designating segmentation of these features on separate scales.

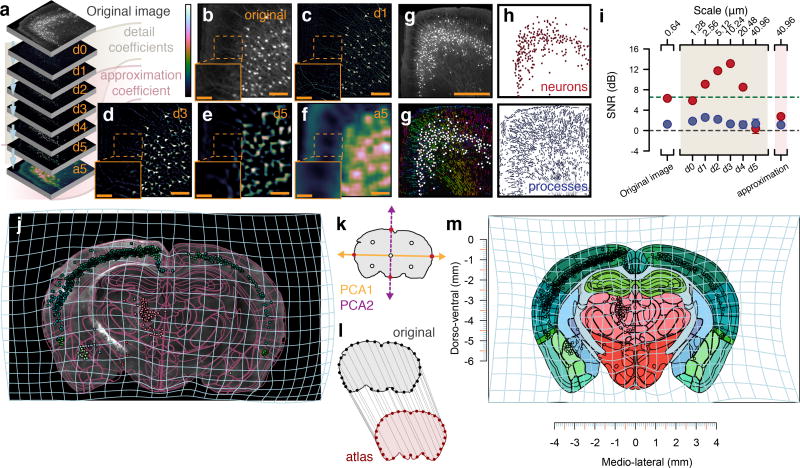
To decompose the image into different spatial scales (Fig. 3a–b) the image data is sent through a stationary wavelet filter bank composed of a set of high-pass and low-pass filters (Supplementary Fig. 2a–b). At each iteration, the output of the high-pass branch is stored as a set of coefficients, which are called detail coefficients (Fig. 3c–e). Detail coefficients contain information on the correlation between a wave-like function (wavelet) at a specific scale and the fluorescent signal at a specific location in the image. More decompositions at lower resolution levels are obtained by iterating the procedure on the output of the low-pass branch. The output of the low-pass branch at each iteration are called approximation coefficients because at each level the approximation to the image at that resolution level becomes coarser and the detail coefficients indicate what detail in the image is lost (Fig. 3a–f). We extracted individual features by thresholding the fluorescence intensity for the detail coefficients of interest (i.e. d3 for cell bodies in Fig. 3c–e) . We then extracted each feature by applying a standard connected components algorithm²¹, which groups connected pixels by their border (Fig. 3g–h).

Figure 3. Method for segmentation and registration.

(a) Wavelet multiresolution decomposition. (b) Original image tile. (c) Detail coefficients d1 at a scale period of 1.28 µm. (d) Coefficients at d3 with scale period 10.24 µm. (e) Coefficients at d5 with scale period 40.96 µm. (f) Approximation coefficients. (g) Top: original 16-bit image tile. Bottom: segmented processes with their direction color-coded by hue as well as cell bodies as white circles. Scale bar: 500 µm (h) Top: segmentation result separated into cell bodies. Bottom: segmented process. (i) Comparison of binary segmentation on different detail coefficients to a human annotator (n = 273 cell bodies), red: cell bodies, blue: processes, gray horizontal line: SNR of 1:1, green dashed line: Rose criteria SNR 5:1 [33]. Error bars: 95% confidence intervals around the mean. (j) Image section of rabies-EGFP targeted to dorsal striatum in D2-Cre mouse, purple lines: transformed reference atlas, light blue grid: backward warp transform from atlas to original image. (k) Segmentation of brains section based on autofluorescence (vertical purple line). Pink shaded area indicates range of fluorescent intensity where cell bodies can be found. (l) Correspondence generation by principal components, red dots: intersection with contour, white dots: midpoints. (m) 32 correspondence points between original contour, gray, and reference atlas, red. (n) Forward warp transform, light blue, of segmentation output into stereotactic space.

To address the sensitivity of the approach, we evaluated the signal-to-noise ratio (SNR) in manually defined regions of interest (neurons versus processes) after applying multiresolution decomposition, compared to binary thresholding of the fluorescent signal in the original image (Fig. 3g). We found that the SNR for segmentation of neurons reached a peak at a theoretical sampling scale period of 10.24 µm, similar to the size of a cell body (Fig. 3i). Similarly, we found that the SNR for processes reached a peak at sampling period of 2.56 µm (i.e. the approximate diameter of an apical dendrite). In summary, detail coefficients at separate spatial scales can be used to identify genetically marked cell bodies and processes.

In addition, multiresolution decomposition is particularly valuable for comparison and integration of imaging results obtained from different microscope systems. In essence, features segmented from low and high-resolution images can be directly compared by analyzing detail coefficients at scales with similar scale periods (Supplementary Fig. 2c–i). Multiresolution decomposition therefore supports data gathering and comparison of segmentation results across imaging platforms, projects and laboratories.

Registration to standardized atlas

Image registration is the process by which sets of images (e.g. coronal mouse brain sections) are transformed into another coordinate system (e.g. stereotactic coordinate system or a reference atlas). Traditional registration algorithms in neuroimaging follow a voxel-based analysis^15,18,22. Registration using voxel-based atlases such as Allen mouse brain Reference Atlas 2011¹⁹ or Waxholm space²³ are limited to 21.5 to 25 µm, and even newer isotropic renditions such as next generation common coordinate framework (CCF v3,²⁴) are still limited to a voxel resolution of approximately 10 µm. In order to decrease computational time, these registration approaches most often require matching of image resolutions by upsampling the lower-resolution atlas and downsampling the imaged brain sections. In contrast, we decided to perform image registration by segmenting out the contour of the brain section utilizing the inherent autofluorescence of the brain section itself (Fig. 3j–k). In this way, image registration does not introduce artifacts derived from pixel interpolation associated with upsampling of the reference atlas. In addition, it is not necessary to dedicate one imaging channel for the registration process, which reduces image acquisition time and facilitates fluorescent multi-channel experiments (multiplexing).

To generate landmarks between the brain tissue and the reference atlas, the segmented contour of the imaged brain section is reduced into a set of points²⁵. To achieve this, the two initial principal components are first extracted from the position of the pixels defining the tissue section contour (Fig. 3l). Next, intersection points between the principal components and the tissue contour are extracted and stored as the initial first level of reference points (Fig. 3m). By default, four iterations (n = 4) are executed resulting in 32 = 2ⁿ⁺¹ reference points along the contour of the brain section (Supplementary Fig. 3). The two sets of reference points (atlas and tissue section reference points) constitute a set of correspondence points, which align the atlas and the tissue section (Fig. 3m). These correspondence points are then pruned²⁶ in order to minimize effects of tissue damage or distortions on the registration result. These correspondence points are used as input to solve analytically the minimization of the bending energy of a thin-plate splines (TPS) deformation field²⁷. The deformation field can then be used to generate a mapping between every coordinate in the brain tissue section (Fig. 3j) to that of the reference brain atlas (Fig. 3n). Using this approach, a collection of individual brain sections can be reconstructed into a 3D representation of the imaged data a (Supplementary Video 1).

In cases where the automated registration has resulted in incorrect placement of region boundaries, it is possible to change or remove correspondence points manually and rerun the TPS algorithm (Supplementary Fig. 4). To estimate how the measurement accuracy depended on the angle of tissue sectioning and the registration plane, we compared detection of labeled neurons obtained in a number of regions from brains sectioned in the coronal or in the sagittal plane (Supplementary Fig. 5). As a measurement of registration accuracy, we defined the difference in the percentage of labeled cells found in each anatomical subregion in sagittal compared to coronal reconstructions. The average error across all anatomical regions was found to be 0.29% (SD = 0.96%, n = 239 brain regions) as defined by the Root Mean Squared Error (RMSE, see Supplementary Fig. 6–7). Importantly, reconstructed 3D brains can be resliced at arbitrary angles, although the sampling strategy will still impose limitations on the spatial resolution that can be obtained (Supplementary Fig. 8).

Fiber tract tracing

To construct mesoscale connectomes it is necessary to perform fiber tract tracing⁵. Fiber tracts are geometrical features extended in space (spatially coherent) with a set of orientations at different locations. We used the properties of coherency and orientation to further increase the SNR for segmentation of fiber tracts and cell processes by computing the structure tensor on the detail coefficients of interest followed by segmentation of topological skeletons (details in supplementary methods). The segmented topological skeletons together with the associated orientation of each pixel (Fig. 4e–g), can be used as input to tertiary tractography approaches²⁸.

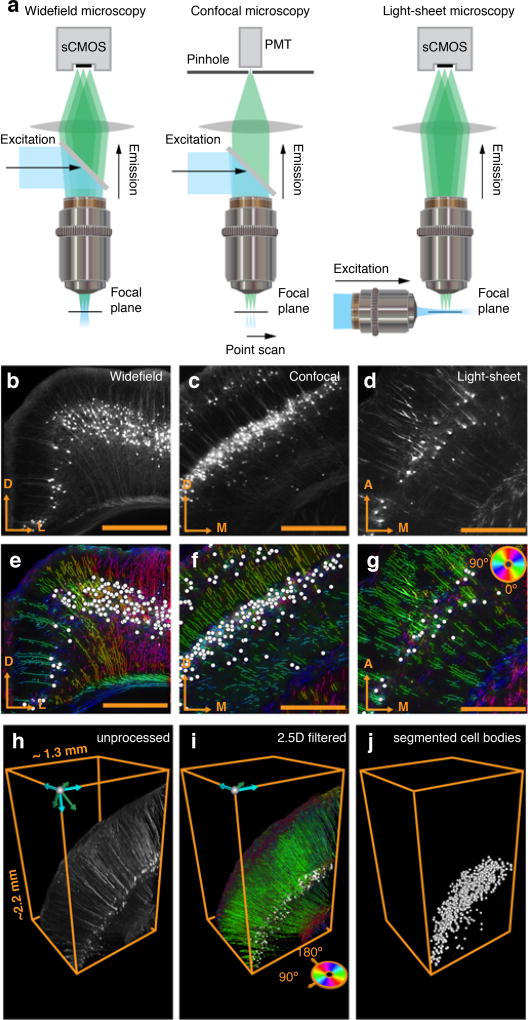
Figure 4. Compatibility of the framework with different imaging systems.

(a) Compatibility of the framework with different imaging systems, including widefield, confocal, and light-sheet fluorescent microscopy. Raw fluorescent images of rabies EGFP for (b) widefield (c) confocal, and (d) light-sheet microscopes. Segmentation result of both cell bodies (white circles) and processes (color coded according to angle) for (e) widefield (f) confocal, and (g) light-sheet images in (b–c). (h) Cortical neurons from a volume imaged with light-sheet microscopy in a Thy1-eYFP mouse. (i) Segmentation algorithm applied across z-stacks (2.5D filter). (j) Cell bodies individually segmented from fluorescent signal attributed to processes and fiber tracts.

Resolving identity of fiber tracts across sectioned tissue is challenging. It is therefore desirable to perform fiber tracing in 3D, for example in intact clarified brain tissue imaged using confocal or light-sheet microscopy (Fig. 4a–j). For processing of three dimensional image stacks (Fig. 4h) we developed a set of 2.5D algorithms that segments out processes and cell bodies along the z-stack plane (Fig. 4i). This approach is comparable in speed to the 2D image processing, but assures the accuracy of running 3D wavelet filters by running an additional connected components algorithm across the z-stack after combined wavelet and structure tensor on each z-plane.

Mapping of single cell co-expression

We further applied our approach to determine at the single neuron level the expression of markers after imaging of fluorescent proteins (e.g. EGFP) and immunohistochemistry (IHC).

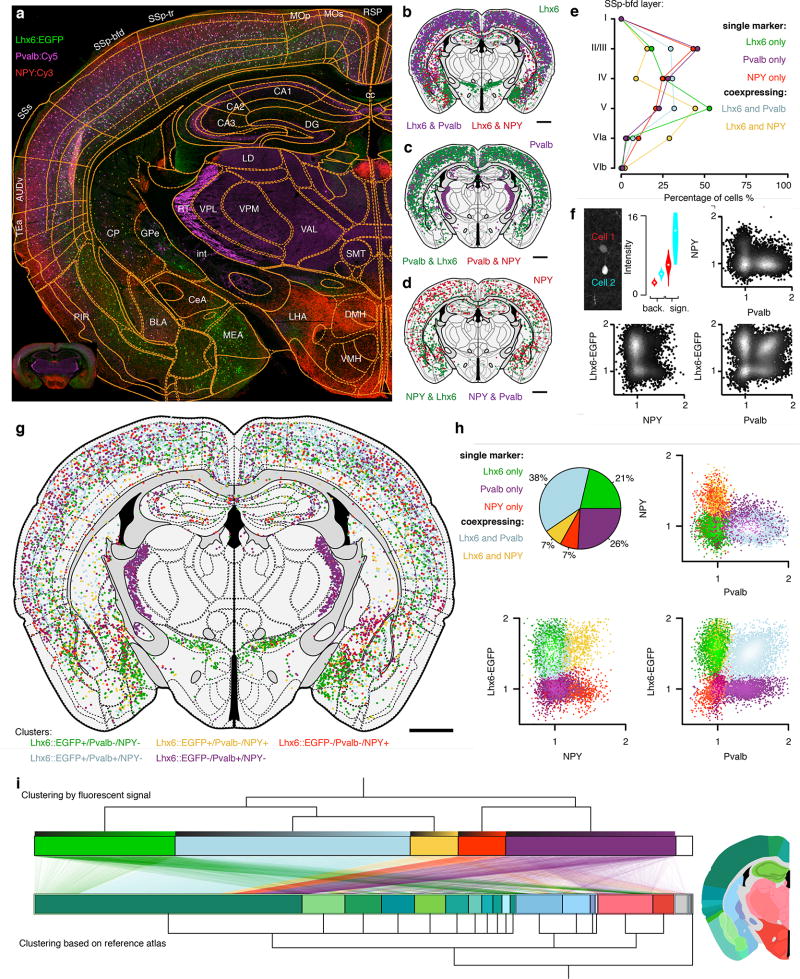
In order to map the anatomical distribution of neuron types, we chose to determine the spatial distribution of interneurons using transgenic labeling in combination with immunohistochemistry. We used a transgenic mouse line (Lhx6::EGFP) in combination with detection of parvalbumin-expressing (PVALB) and neuropeptide Y-expressing (NPY) interneurons. Automated image analysis resulted in the segmentation of 9021 labeled cells in a single coronal mouse brain section (Fig. 5): Lhx6::EGFP: 66% (n = 5958), PVALB::Cy5: 63% (n = 5701), NPY::Cy3: 15% (n = 1342). The processing time for segmentation and registration to the atlas was approximately 30 seconds, indicating the scalability of whole-brain mapping projects based on our framework. Further demonstrating the advantages of an automated framework, we could with high resolution assign the position of each of these 9021 labeled cell bodies to 116 unique regions (Fig. 5a–d). This type of comprehensive mapping of single neurons generates detailed anatomical definitions that can for example describe the relative distribution of neuron types across cortical layers and in different anatomical subregions (Fig. 5e). We confirmed the non-overlapping distribution of PVALB and NPY (n = 0) in Lhx6-expressing cells (Fig. 5g–h) (37% of cortical NPY co-express Lhx6::EGFP, n = 238, and 73% of cortical Pvalb co-express Lhx6::EGFP, n = 2752). In contrast to cortex, in the striatum 84% of NPY positive cells were also Lhx6::EGFP positive (n = 101).

Figure 5. Mapping of molecular identity and neuron types.

(a) Section of a Lhx6::EGFP transgenic mouse (green) stained for parvalbumin (magenta, PVALB::Cy5) and neuropeptide Y (NPY::Cy3). (b) Segmented Lhx6::EGFP positive cells and their co-expression with either PVALB (magenta) or NPY (red), green denotes Lhx6::EGFP neurons negative for both NPY and PVALB. (c) PVALB::Cy5 positive cells and their co-expression with either Lhx6::EGFP (green) or NPY (red), no co-expression between PVALB and NPY. (d) NPY::Cy3 positive cells (red) and co-expression with Lhx6::EGFP (green). (e) Laminar distribution of cell types in primary somatosensory cortex barrel field (SSp-bfd). (f) Definition of molecular signal at the single cell level (background, "back.", n = 400 pixels, signal, "sign.", n = 16 pixels). (g) 9021 segmented cell bodies registered to 116 unique regions in the reference atlas and clustered into five discrete classes based on fluorescent intensity alone. (h) Clustering of cells based on fluorescent intensity alone into five discrete populations (green: Lhx6-EGFP+ only, magenta: PVALB+ only, red: NPY+ only, yellow: NPY+/Lhx6-EGFP+ co-expressing, light blue: PVALB+/Lhx6-EGFP+ co-expressing). Pie chart illustrates percentage overlap. (i) Clustering based on marker identity (top) compared to clustering based on neuroanatomical location for each cell (bottom). Lines represent single neurons mapping between the two types of clustering (molecular identity versus anatomical). Neurons are sorted in ascending order according to their relative fluorescent intensity in each cluster (top gradient on each cluster). Anatomical color-coding is shown in the representative section, −1.5 mm from bregma (scale bar: 1 mm).

We further investigated the laminar distribution of the five different neuron clusters and found that PVALB+ (PVALB only) as well as NPY+ (NPY only) were primarily localized to layer II/III of primary somatosensory cortex barrel field (SSp-bfd), whereas Lhx6+ (Lhx6 only) and Lhx6+/NPY+ (Lhx6 and NPY co-expressing) were enriched in layer V (Fig. 5e).

Importantly, our framework further enables quantification of the average fluorescence intensity of each single cell for all labeling channels, resulting in a quantitative description of expression levels at the single cell level, and therefore also population clustering in a manner similar to gating in flow cytometry (Fig. 5f). Using the quantitative information for each fluorescent channel, we could cluster neurons into five distinct populations based on expected maximization with Gaussian mixture models (Fig. 5h,i). These clusters could then be superimposed on the reference atlas to align molecular and anatomical definitions of the map (Fig. 5h). For example, we found that the majority of PVALB-positive and Lhx6::EGFP-negative neurons (PVALB+/Lhx6−) can be found in the thalamic reticular nuclei (RT) (Fig. 5 g,i), and that Lhx6+ (Lhx6::EGFP+/PVALB-/NPY−) cells were for example found preferentially in zona incerta (ZI) and in medial amygdalar nucleus (MEA).

This approach can similarly quantify gene expression on the subcellular level through detection of single mRNA molecules with fluorescent in situ hybridization (Supplementary Figure 9)

Tracing connectivity using modified rabies virus and transgenic mice

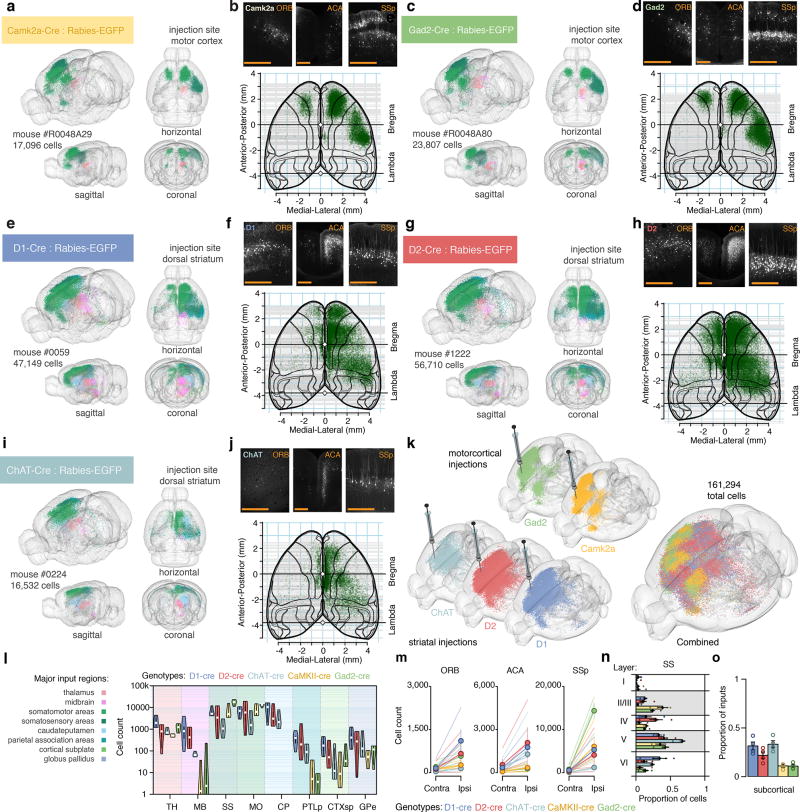
Whole-brain mapping of monosynaptic connectivity using modified rabies viruses can generate large datasets of cell-type-specific connectomes at the mesoscale level^29–31. We applied rabies virus tracing to identify the presynaptic partners of defined neuronal subtypes in the corticostriatal pathway (Supplementary Video 2). We used a Cre-mediated genetic targeting approach to limit the uptake of rabies virus to defined neuron types in Cre-expressing mouse lines. We first mapped the whole-brain inputs to excitatory versus inhibitory neurons in the motor cortex (MOp), through Camk2a-Cre and Gad2-Cre mice respectively (Fig. 6a–d). To target the main neuron types in striatum (CPu), we used D1-Cre, D2-Cre and Chat-Cre mice to target either medium spiny neurons (MSNs) of the direct versus indirect pathway, or cholinergic interneurons, respectively (Fig. 6e–j). We mapped the precise neuroanatomical distribution of the labeled presynaptic neurons at a whole-brain scale, which produced a rich dataset that included whole-brain tracing data from 15 mice and 349959 annotated neurons (Fig. 6k–l).

Figure 6. Retrograde monosynaptic tracing of corticostriatal networks.

(a) Reconstruction of inputs to Camk2a neurons in motor cortex by targeted injection of glycoprotein-deleted EGFP expressing EnvA pseudotyped rabies virus, SADΔG-EGFP(EnvA). EGFP labeled neurons are color-coded based on anatomical location, see (l). (b) Cortical input to Camk2a neurons in motor cortex in orbital cortex (ORB), anterior cingulate area (ACA) and primary somatosensory area, SSp. Bottom: cortical overview of inputs from cortical cells roughly above −2.25 mm dorsoventral from the midline cortical surface.(c,d) Same as (a,b) but for Gad2 neurons in motor cortex. (e, f) D1+ medium spiny neurons in dorsal striatum. (g, h) D2+ medium spiny neurons in dorsal striatum. (i, j) Cholinergic interneurons in dorsal striatum.(k) llustration of rabies-EGFP labeling in individual brains (from five different transgenic Cre-lines) used for cell-type specific input comparisons. The brain in the very front is a composite where all neurons are combined (n = 161,294 neurons across five mice). (l) Violin plot of monosynaptic inputs from major input regions (n = 4 mice for each genotype). (m) Laterality of cortical inputs in specific regions (ORB, ACA, SSp). (n) Layer-specificity of monosynaptic inputs from SSp. Colors as in (l). (o) Proportion of inputs from subcortical regions. Circles show individual mice. Colors as in (l). Error bars: +/− one standard error of measurement. Scale bars: 500 µm.

The quantitative comparison across a large number of animals and experiments allowed us to search for cortical regions that showed connectivity patterns similar to the thalamus (i.e. innervating both MOp and CPu), which can be anatomically and functionally described as contextual units^32,33, instead of input units to motor cortex. We therefore analyzed the whole-brain tracing dataset to specifically identify cortical subregions that exhibited dense targeting of both MOp and CPu. We identified three candidate regions that satisfied the criteria of serving as contextual units: primary somatosensory cortex (SSp), anterior cingulate area (ACA), and orbital cortex (ORB). We further analyzed the cell type-specific organization of SSp, ACA, and ORB inputs to striatum, and found that the ipsilateral inputs in ORB (ORBvl and ORBl) displayed a preferential targeting towards D1+ striatal cells (Fig. 6m). ORB cortex therefore displays a unique connectivity pattern among the corticostriatal network, preferentially targeting striatal D1+ neurons.

To investigate the laminar distribution of the corticostriatal organization further, we explored our dataset to identify proposed cell type-specific connectivity patterns. Unlike previous studies that have relied on a small number of cortical neurons^34,35, we quantified a large number of presynaptic neurons in the corticostriatal pathway (320055 neurons) after monosynaptic rabies tracing from distinct striatal subtypes. We analyzed the laminar distribution of the cell type-specific corticostriatal inputs in SSp and we found the major inputs to D1+ and D2+ striatal neurons were found in layer V, although we also found layer II/III and IV inputs (Fig. 6f,h,n). Inputs to Chat+ striatal neurons were primarily located in layer V and VI in SSp (Fig. 6j,n). In comparison, we found that inputs to Camk2a+ and Gad2+ in MOp primarily originated from layer II-III of SSp, but could be also found in layer V (Fig. 6n).

Comparing inputs to the striatal neuron subtypes on the whole-brain scale, we found that D2+ striatal neurons display preferential input from neurons in cortical regions compared to subcortical structures, whereas D1+ and Chat+ striatal cells receive a more balanced cortical-subcortical input (Fig. 6o). This evidence supports a discrete cell type-specific pattern of connectivity both in the corticostriatal pathway as well as in the input balance from cortical versus subcortical regions.

Decoding motor behavior from whole-brain intermediate early gene activity

In order to investigate the behavioral relevance of the corticostriatal organization identified by monosynaptic rabies tracing, we performed a whole-brain functional assay. Labeling of neurons based on expression of immediate early genes (e.g. c-fos) as a proxy measure of neural activity has been a valuable for the identification of regions and neuron types that are recruited during behavior³⁶.

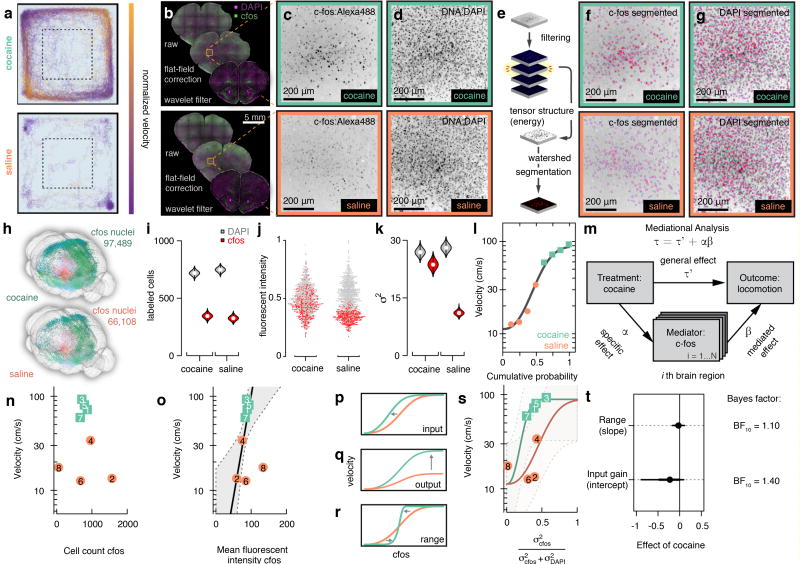
Studies have mapped the cocaine induced c-fos expression in cortical and basal ganglia circuits^37,38, and more recently similar approaches have mapped c-fos at a whole-brain scale^13,14. We selected acute cocaine administration as an assay to map how motor function recruits distinct corticostriatal circuits. We exposed mice to cocaine or saline and then imaged c-fos expression, to identify neurons and regions that displayed activation that correlated with increased motor activity. Motor response was monitored during 20 minutes in an open field (Fig. 7a) for mice injected with 20 mg/kg cocaine or saline (n = 4 mice, per group), and brains were sectioned (M = 93.6 sections per brain, SD = 11.2 sections per brain) and stained for c-fos as well as DAPI (Fig. 7b–d).

Figure 7. Decoding motor behavior by immediate early gene activity.

(a) Behavioural track tracing from open-field test in two mice injected with either cocaine or saline. (b) Coronal sections from the same mice showing the major steps of preprocessing before segmentation. (c) Close up on orbital cortex (ORB) and c-fos:Alexa488 staining. (d) Same field of view but DAPI. (e) Postfiltering segmentation steps include computing tensor structure and performing watershed-based segmentation. (f) Segmentation result, red, overlaid on images of c-fos, and (g) DAPI. (h) Whole-brain 3D reconstruction of same mice as in a–j. (i) Violin plot of cell count estimates obtained from ORB as shown in f–g, white circle marks median. (j) Normalized fluorescent intensity for 2135 individual nuclei in ORB. (k) Violin plot of variance σ² estimates of fluorescent intensity in ORB, white circle marks median. (l) Cumulative distribution of locomotor velocity in open field across eight mice, gray line best fit four-parametric Weibull. (m) Meditational regression analysis for c-fos whole-brain data. (n) Velocity in open-field test as a function of cell count of c-fos positive nuclei of the orbital cortex in saline (coral) and cocaine (turquoise) treated mice, numbers indicate animal identification number. (o) Velocity as function of mean fluorescent c-fos intensity, thick gray line indicates regression line when autofluorescence is added as a covariate, gray area; 80% CI. (p) Gain control by input gain. (q) Output gain, or (r) Range compression. (s) Velocity as a function of DAPI standardized c-fos variance. (t) Posterior estimates of the effect of cocaine on slope and intercept, error bars 70% (thick) and 80% (thin) CI. n = 4 mice per group (cocaine, saline).

In order to segment cell nuclei and determine the c-fos fluorescence intensity we computed the tensor energy on detail coefficients for subsequent watershed segmentation (Fig. 7e–g and Supplementary Fig. 9). The segmentation algorithm is based on spatial frequency analysis, allowing segmentation of nuclei independently of their signal intensity, which resulted in detection of c-fos signal over a wide dynamic range (Fig. 7c–f). We mapped the position of c-fos expressing neurons at the whole-brain scale (Fig. 7h).

We focused our analysis on activity mapping to ORB based on the corticostriatal connectivity pattern. We found that cocaine did not significantly change the number of c-fos positive nuclei in ORB (344 versus 325 c-fos positive nuclei, χ₁² = 1, P = 0.32, Fig. 7i). We instead found that cocaine significantly increased the c-fos intensity levels (t₄₉₂ = 15.21, P < .001 Fig. 7j), as well as the c-fos signal variance (Bartlett’s K² = 174.21, df = 2, P < .001, Fig. 7k).

To further map the brain regions that are functionally linked to the increased locomotion after cocaine administration we used linear mediational analysis on the whole-brain c-fos data. We first characterized the marginal distribution of the behavior across animals by a monotonic four-parametric cumulative Weibull distribution (Fig. 7l). As a measurement of the relative contribution of a specific brain region to the mediated effect we estimated the proportion of the total effect of cocaine on locomotion that is mediated by c-fos expression (i.e. relative mediated effect) (Fig. 7m). This analysis revealed that orbital cortex (ORB) is a key region mediating the behavioral effect and accounted for approximately 7% of the relative mediated effect (P_αβ = .071, 95% C.I. [0.00 – .898]). We found that the c-fos fluorescence intensity correlated to velocity better than absolute c-fos+ cell counts (Fig. 7n,o), and that variance in cell counts increased with average number of c-fos+ neurons (Supplementary Fig 11). We therefore normalized the variance in c-fos fluorescent intensity to DAPI in subsequent analysis. We asked whether we could classify the observed relation in ORB between c-fos induction and locomotion into a distinct form of gain control: either input gain, output gain or range compression. (Fig. 7p–r). We kept the saturation level fixed at a velocity of 90 cm/s and estimated the fixed-effect of cocaine on the other two cumulative Weibull parameters (slope and intercept) (Fig. 7s). Using the marginal cumulative density function as prior, we sampled from the posterior density distributions of the fixed-effect of cocaine. We compared the posterior fixed-effect of cocaine on either intercept or slope to that of our prior N(0, 0.1) based the Savage-Dickey density ratio test. We found that the cocaine-induced locomotion most likely depends on modulation of the input gain in orbital cortex ORB (BF₁₀ = 1.4) rather than range compression (BF₁₀ = 1.1) (Fig. 7t). Taken in combination with our tracing dataset (where ORB was identified as a contextual layer targeting preferentially D1+ striatal neurons) these data support ORB as a major corticostriatal hub mediating locomotor effects of cocaine.

DISCUSSION

For invertebrate model organisms, there has been considerable progress in developing methods to map and visualize the complete nervous system connectome based on electron microscopy reconstructions^39–41. Although detailed reconstruction of the mouse nervous system at a similar scale would be valuable, there are considerable challenges in acquiring and analyzing data at that scale⁴². To define the organization of circuits in the mouse brain, it is now becoming possible to generate a complete map of the cell type-specific connectivity using combinations of advanced transgenic, labeling and imaging methods at the cellular scale. In spite of great progress in labeling methods, methods to register and map neurons have to a large extent still relied on manual inspection or registration, and have not been scalable for the analysis of large datasets or for integration of multiple projects into one database. To address these needs, we have developed a computational framework to facilitate comprehensive investigations of mouse brain circuits at the cellular level.

We have developed a computational framework that enables the automated segmentation of labeled neurons at a whole-brain scale that is independent of imaging method. Based on this computational framework, data can be analyzed and presented in a scale-invariant whole-brain mouse atlas that allows for the rapid comparison and sharing of data between projects and laboratories. A key advantage of our framework is the ability to rapidly visualize and share whole-brain data using commonly available infrastructure. To facilitate integration of this platform, we provide video tutorials for common applications (http://wholebrainsoftware.org/tutorials).

We present the application of the computational framework to the whole-brain mapping of rabies tracing data derived from different neuron subtypes in the corticostriatal pathway, and in combination with whole-brain definition of cocaine-induced neuronal activity using c-fos mapping. Using whole-brain rabies tracing, we identified that orbital cortex (ORB) displays characteristics of a contextual layer in the corticostriatal pathway, possibly shaping interactions between primary motor cortex and the striatum, and furthermore preferentially targets the direct pathway D1-expressing striatal neurons. We could further integrate this connectivity pattern with cocaine-induced activity changes, using whole-brain segmentation of c-fos levels in single neurons after cocaine administration, which identified the ORB as a major mediator of cocaine induced locomotion.

We anticipate that the versatility and accessibility of this framework will promote integration of new technologies and user-based modifications. For example, neuroanatomical methods that leverage the power of next-generation sequencing will be of importance for the development of computational neuroanatomy, including: lineage tracing by barcoded DNA⁴³, connectivity tracing of individual neurons by expressing RNA barcodes⁴⁴, in situ sequencing^45,46, and spatial transcriptomics⁴⁷.

We expect that an increasing focus on whole-brain characterization of neurons, circuits and activity will benefit from a unified and intuitive approach to data analysis. Importantly, our framework can integrate future advances in imaging, incorporate new molecular data to improve neuroanatomical definitions, and support data sharing in mapping projects.

Methods

Virus construction and production

A protocol modified from⁴⁸ was used to produce rabies virus. To make EnvA pseudotyped rabies virus, unpseudotyped rabies viral particles were transferred onto BHKEnvA2 cell lines on day 1. To decrease the contamination of glycoprotein coated rabies virus, cells were then trypsinized, washed and replated in a new cell culture flask. This procedure was repeated for two days. Collected supernatants were then filtered by 0.45 µm filter and ultracentrifuged at 60,000 g for at least two hours on day 4. TVA, mCherry and RG were amplified from pCMMPTVA800²⁹ (Addgene plasmid 15778), pAAV--EF1adouble floxed-hChR2(H134R)-mCherry-WPRE-HGHpA (Addgene plasmid 20297), and pHCMV-Rabies G⁴⁹ (Addgene plasmid 15785) by Phusion High-Fidelity DNA polymerase (Finnzymes, Finland), respectively. One round of overlapping Polymerase Chain Reaction (PCR) was then performed to fuse TVA and mCherry together, using TVA Forward (NheI) and mCherry Reverse (AscI) as primers. A similar approach was used to create a TVA-t2A-RG PCR product. Inserts were digested by NheI and AscI (New England Biolabs, UK) and cloned into the pAAV-EF1a-DIO plasmid backbone. Transformation was done in NEB-10b E. coli (New England Biolabs, UK) and bacteria were plated on 50 mg/mL ampicillin LB agar plates. Plasmid DNA was extracted from cultured colonies and confirmed by NheI and AscI digestion. Positive clones were sent for sequencing (Eurofins MWG Operon, Germany), and the results were analyzed with National Center for Biotechnology Information (NCBI) BLAST. Confirmed plasmids were sent to Gene Therapy Center Vector Core at the University of North Carolina (North Carolina, NC) for virus production.

Viral injections

Animal experiments were carried out following guidelines of the Stockholm municipal committee, the Scripps Research Institutional Animal Care and Use Committee and the Stanford University Institutional review panel approval. All viral injections into the striatum (Drd1a-cre (EY262)⁵⁰ n = 4, Drd2-cre (ER44)⁵⁰ n = 3, Adora2a-cre [GENSAT: KG139] n = 1, Chat-IRES-cre [Jax: 006410] n = 4) were done at the following coordinates from bregma AP: +0.6 mm, ML: +2.2 mm, DV: −3.5 to −3.2 mm (500 nl). Injections into the motor cortex (Camk2a-cre [Jax: 005359] n = 4, Gad2-cre [Jax: 010802] n = 4) were done at AP: 1.5 mm, ML: 1.5 mm, DV: −0.4 mm (500 nl). Injections were performed in 2–6 months old mice under isoflurane anesthesia and injected with buprenorphine post surgery. In all mice the second injection was performed after 2–4 weeks with (EnvA)SADΔG-EGFP or (EnvA)SADΔG-ChR2(H134R)-mCherry (Adora2a-cre n = 1, D1-cre n = 2, Chat-cre n = 3) at the same location, for the striatal injections we either used AAV5-TVA-t2a-RG as or a dualvector helper virus system (AAV5-EF1a-DIO-TVA-mCherry and AAV5-EF1a-DIO-RG, 1:1 ratio). In experiments with Camk2a-cre and Gad2-cre animals we used AAV9-CAGFLEXRG [Addgene plasmid 48333] and AAV9-CAG-FLEX-TVA-mCherry [Addgene plasmid 48332] in 1:1 ratio.

Immunohistochemistry

All immunohistochemsitry was performed in either wild type C57BL/6J mice (n = 4 cocaine treated, n = 4 saline treated) for c-fos, or as in the example provided in quantitative single cell co-expression analysis provided a single Lhx6-EGFP [Jax: 3839374]. All animals were male and between 8–13 weeks old. Brain sections were cut at 40 µm thick on a vibratome (Leica VT1000, Leica Microsystems GmbH) and were placed in sodium citrate (10 mM Sodium Citrate, 0.05% Tween 20, pH 6) for 1–2 min for antigen retrieval followed by wash in TBST (0.3% Triton). After antigen retrieval blocking was performed with 5% donkey serum in TBST for one hour at room temperature (RT). Sections were then incubated with primary antibody (c-fos 1:1000 (Santa Cruz, anti-goat, sc-52, Lot G2612), parvalbumin 1:1000 (antiguinea pig, Swant, Lot GP72), neuropeptide Y 1:500 (anti-rabbit, Peninsula, Lot T-4070), or Forkhead box protein P2 1:500 (anti-rabbit, Abcam, Lot GR91556-1, for FoxP2 n = 3 C57BL/6J mice were used), on a shaker at RT overnight. The following day sections were washed at RT with TBST for 10 min followed by incubation for 5 hours with secondary antibody (1:500 Alexa Fluor 488-conjugated antibody (Jackson Immuno, 711-545-152, Lot: 100709), Cy5-conjugated (Jackson Immuno, 706-175-148, Lot: 110663), Cy3-conjugated (Jackson Immuno, 711-165-152, Lot: 114518)) at RT on a shaker. Washing was performed at RT in TBST for 10 min followed by TBS (10 min), and then with 1×PBS (10 min). For c-fos staining DAPI (1:50000, Biotium, 40011, Lot: 11D1017) was added to PBS and incubated for 4 min at RT. Sections were mounted with SlowFade Gold antifade reagent (Life Technologies, 10 ml, S36936) and then imaged.

In situ hybridization

RNA in situ hybridization was performed using the RNAscope fluorescent multiplex assay (Advanced Cell Diagnostics, ACD, Hayward, CA) according to the manufacturer’s instructions. In brief, C57BL/6J mouse brains were perfused with 4% paraformaldehyde and le for post-fixation in 4%PFA overnight. The brains were subsequently cryoprotected by being immersed in a 15% sucrose solution (in PBS) overnight at 4 °C, the process was repeated with a 30% sucrose solution. e brains were then frozen in OCT on dry ice and stored at −80 °C. Cryosections (14 µm) were made using CryoStar NX70 cryostat (ThermoScientific) and stored at −80 °C until further processing. Immediately before RNA in situ hybridization, cryosections were washed once in PBS (1×). Subsequently, the sections were boiled in pretreatment reagent 2 for 5 minutes, washed in ddH2O and immersed in 100% ethanol. Sections were dried at room temperature and a hydrophobic barrier was drawn around the individual sections using an ImmEdge Hydrophobic Barrier Pen (Vector Labs, Inc.). All following incubation steps were performed in a HybEZTM Hybridization System oven (ACD). Next, the sections were incubated with protease 4 solution (ACD) for 30 minutes at 40°C. Then sections were washed twice in fresh ddH2O and subsequently hybridized with multiplexed probes: MmSlc32a1-Ch1 (Alexa488), Mm-Slc17a6-Ch3 (Atto647) and Mm-Pdyn-Ch2 (Atto550) for two hours at 40 °C. After hybridization, the sections were washed twice in RNAscope wash buffer (ACD) and four consecutive amplification steps were performed using the RNAscope Fluorescent Multiplex Detection reagents 1–4 (amplifier 4 variant A was used for fluorescent labeling). After the last amplification step, the sections were immersed in DAPI for 30 seconds and immediately covered with a coverslip, using a protective fluorescent mounting medium. smFISH experiments were imaged on confocal microscope with 40× optical magnification and fifteen optical z-planes.

smFISH quantification

Segmentation of individual transcripts was done on each channel separately. Before binary segmentation of transcripts the raw confocal image was processed with a grey morphology top hat filter to decrease background noise. To assign individual transcripts to single cell nuclei the cell nuclei (DAPI) were segmented by first preprocessing the DAPI image by extracting the tensor structure energy followed by binary segmentation and watersheding. The perinuclear zone was then obtained by iterative dilatations on the binary segmented cell nuclei. Cell nuclei were then assigned to perinuclear zones by a point in polygon algorithm. The transcript gene identity, position within perinuclear zone as well as position within a given cell nuclei was used as input to the affinity propagation clustering algorithm⁴² using a negative squared distances similarity measure and initial number of clusters set to number of detected cell nuclei using the apclusterK() function in the apcluster R package⁵¹.

Widefield imaging

Imaging was done at 10×/0.40 NA (15506285 HCX PL APO 10×/0.40 CS, Leica Microsystems GmbH) on a fluorescent microscope (Leica DM6000B, Leica Microsystems GmbH) with motorized stage automatically controlled through µManager⁵². Images were acquired by a Hamamatsu OrcaFLASH 4.0 digital camera (C11440-22CUORCA-Flash4.0 V2 Digital CMOS camera, Hamamatsu Photonics K.K.) at 16 bit depth resolution with 2048 × 2048 pixels. All widefield imaging except for rabies injections done in Camk2a-cre and Gad2-cre animals were done on the Leica DM6000B. For Camk2a-cre and Gad2-cre mice we used an IN Cell Analyzer 6000 with the 10×/0.45 NA objective (GE Healthcare Life Sciences, Chicago, US).

Confocal imaging

Confocal imaging was done on a Zeiss LSM 510 or a LSM 800 confocal microscope (Zeiss GmbH). For co-localization with immunohistochemistry (Figure 5) a 15 step z-stack covering the 40 µm section was imaged using LSM 800 with 20x/0.8 NA objective. For in situ hybridization imaging was done using LSM 800 with 40x/1.3 NA oil immersion objective. All images had a 16 bit depth. Supplementary figure 2 used Zeiss LSM 510 for confocal images. Objectives for the Zeiss LSM 510 are specified in the supplementary figure.

Light-sheet CLARITY imaging

Brains were perfused and incubated with CLARITY monomer solution containing 1% acrylamide, 0.0125% bis-acrylamide, and 4% PFA and then polymerized at 37 °C for 6–7 hours. Brains were passively cleared in SDS Borate Buffer (pH 8.5) at 37 °C for 4–5 weeks, equilibrated in Focusclear for imaging and imaged using COLM methods⁵³. Analysis of light-sheet data differ from sectioned tissue in that the distance between adjacent optical planes is normally much smaller that the distance between adjacent sectioned planes. Therefore an additional post-processing step is needed for segmentation to assure that segmented connected components that accord across z-planes are not counted several times. This postprocessing step included a connected component algorithm running across the z-stacks on the binarized image.

Cocaine induced locomotion

To measure locomotion only open field test was performed as a behavioral test on wild type mice. Cocaine hydrochloride (C5776, Sigma-Aldrich) was dissolved in 9 mg/ml sodium chloride and administered at a single dose of 20 mg/kg by intraperitoneal injection. Mice were returned to the home cage for 5 minutes for the drug to begin to take hold and then placed inside the open-field arena. The control group (saline) were injected intraperitoneal with the vehicle (NaCl 9 mg/ml) . Mice (n = 4, per group, all male) were monitored in open field using the TSE Multi Conditioning System (TSE Systems GmbH). Mice were randomly assigned and counterbalanced by treatment (cocaine vs. saline), time of testing (done at four time points in the middle of the day) and conditioning system (box A vs. box B). After each 20 min session the mouse was brought back to its home cage and 90 minutes after the injection brains were harvested by transcardial perfusion with 1×PBS followed by 4% PFA under sodium pentobarbital (0.15 mg/kg) anesthesia. To aid immunohistochemistry perfusion was done with 4% PFA in 1 × PBS (pH 7.4) (with picric acid and glutaraldehyde) fresh on the day of perfusion. Brains were further fixated in 4% PFA at 4◦C overnight. All animals were housed in groups of 3–5 mice. All mice were housed on a 12:12h non-reversed light:dark cycle.

NURBS atlas

We started from the scalable vector graphics (SVG) files of the original 2008 Allen reference atlas. We manually redefined and adjusted each plate. After that we simplified points along the outer contours of each brain region using the same set of PCA generating correspondence points, starting with the brain section outline. Adjacent sections were then merged in a sequential manner by the lofting technique. The NURBS atlas was adjusted manually using the trial version of Maya (Autodesk, Inc) when needed.

Computing intersection of a plane with NURBS surfaces

We use a general strategy to obtain a curve from intersection of two surfaces where the steps involved are: (i) determining parametric curves, (i) transforming curve segments and surface patches to Bézier form, (iii) convex hull intersection test to determine whether the curve can be approximated by a line, (iv) obtain intersection points in Euclidean space from intersecting lines and quadrilaterals (v) connecting intersection points to curves by a marching scheme. Through this processes a set of tests are performed at each stage and in case a proper curve cannot be approximated the algorithm halts and throws an exception for that intersection.

JavaScript Object Notation (JSON) data format for serialization

Segmentation and registration results can either be transferred to collaborators as a tabulated tidy data frame or for serialization on the web through a collection of name/value pairs based on JavaScript Object Notation (JSON). The open format describes the neuroanatomical spatial features of an image, along with non-spatial attributes. The format is called RosettaBrainJSON (http://openbrainmap.org/rosettabrainjson/) and is licensed under Creative Commons (CC BY 4.0).

R package and dependencies

Higher level analysis and plotting functions were written in base R with image processing done through calls to C++ code via the Rcpp package^54,55. For plotting in R of raster images png package was used⁵⁶. For vector processing and import into R the packages grImport⁵⁷, XML⁵⁸ were used. For 3D rendering the packages rgl and misc3d were used^59,60. For general data handling and preprocessing dplyr was used⁶¹. All of these packages are dependencies of the Wholebrain R package.

The following C/C++ libraries were used: OpenCV 3.3 ⁶² (for image processing), FFTW3 3.3⁶³ (for computations of the discrete Fourier transform), Eigen 3.3⁶⁴ (for linear algebra, numerical solvers etc.). For providing open source C++ classes that we built upon we thank Rafat Hussain (wavelets), Matthias Schmieder (thin-plate splines), and Pete Gadomski (coherent point drift). C/C++ code was compiled using Apple LLVM version 8.1.0 (clang-802.0.42) on macOS, gcc 4.9 on Linux and Rtools 3.4 together with mingw-w64 v3 on Windows 7.

Multiresolution decomposition

A filter bank F transforms an input x into an output y = F(x). Let G_j be the low pass filter at the jth level and H_j the high pass filter at the jth level. As stated in the main text the Haar low pass filter G_j simply averages adjacent entries of its input, in matrix form:

$$G_j=\frac{1}{2}\left[\begin{array}{ccccccc}\hfill 1\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill \end{array}\right],$$

The Haar high pass filter H_j computes half the difference between successive input samples, in matrix form:

$$H_j=\frac{1}{2}\left[\begin{array}{ccccccc}\hfill 1\hfill & \hfill -1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill 1\hfill & \hfill -1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -1\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill \end{array}\right],$$

Where the size of the filters n × n matches the size of the image initially. Normally one would then downsample the signal to avoid antialiasing when reconstructing the signal. But in our case it is more important to create a shift-invariant output of the filter bank and this can be achieved by upsampling the filter by starting with the identity matrix and insert empty rows in it and multiply with the filter thereby creating holes of zeros in it, hence the original French name algorithm à trous (with holes), or more commonly the stationary wavelet transform (SWT) due to its shift-invariant properties⁶⁵. Upsampling is represented in matrix form as an array of size 2n × n:

$$U_j=\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill \end{array}\right],$$

The combined operation of low pass filtering and then upsampling is represented as the low pass branch L_j:

$$L_j=U_j{G}_j=\frac{1}{2}\left[\begin{array}{ccccccc}\hfill 1\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill \end{array}\right],$$

Similarly the high pass branch B_j is given by:

$$B_j=U_j{H}_j$$

The low pass branch is sent forward and at each stage the output from the high pass branch is stored as the set of detail coefficients d_j (Supplementary Figure 2b). The output can hence be seen as rewriting the input x in terms of another basis to produce the output y = F(x), so the output from a filter bank with three levels, J = 3, is:

$$y=\left[\begin{array}{c}\hfill L_3{L}_2{L}_1\hfill \\ \hfill B_3{L}_2{L}_1\hfill \\ \hfill B_2{L}_1\hfill \\ \hfill B_1\hfill \end{array}\right]x=\left[\begin{array}{c}\hfill a_3\hfill \\ \hfill d_3\hfill \\ \hfill d_2\hfill \\ \hfill d1\hfill \end{array}\right],$$

Where a_J is the set of approximation coefficients and d_j are the detail coefficients. When applying the filter bank to a two-dimensional signal one obtains additional detail coefficients row-wise, column-wise and diagonal.

Filter bank is merely one specific form of implementation of hierarchical decomposition. More generally put hierarchical decomposition via filter banks writes a signal in terms of new basis to find this basis one can use the dilation function, also known as at the scaling function:

$$\varphi (2^{j-1}t)=2\sum _{k}g(k)\varphi (2^{j}t-k),$$

as well as the wavelet function:

$$w(2^{j-1}t)=2\sum _{k}h(k)\varphi (2^{j}t-k),$$

For the Haar wavelet substituting the low pass filter into Equation 1 gives us the case definition:

$$\varphi (t)=\varphi 2t+\varphi (2t-1)=\{\begin{array}{cc}\hfill 1\hfill & \hfill \text{if }t\in [0,1)\hfill \\ \hfill 0\hfill & \hfill \text{otherwise}\hfill \end{array}$$

Equation 4 gives us the Haar scaling function. Likewise the high pass filter can be substituted into Equation 2, giving us the Haar wavelet function:

$$\varphi (t)=\varphi 2t-\varphi (2t-1)=\{\begin{array}{cc}\hfill 1\hfill & \hfill \text{if }t\in [0,0.5)\hfill \\ \hfill -1\hfill & \hfill \text{if }t\in [0.5,1)\hfill \\ \hfill 0\hfill & \hfill \text{otherwise}\hfill \end{array}$$

The Haar wavelet function is the simplest wavelet but WholeBrain comes packaged with a total of 44 different wavelets. It is still an open question, which wavelet is best suited for neuroanatomical segmentation but we are quite satisfied with the output from Debauchies wavelet 2 (db2). In addition to the filter bank implementation WholeBrain comes with the possibility to construct biorthogonal wavelets using the lifting scheme. The lifting scheme does not require any computation using the Fourier transform and it is also possible to construct an integer wavelet transform, that is, a wavelet transform that maps integers to integers which most of the time is more suitable for microscope images that are most of the time encoded with uint16 bit depth.

Segmentation of features by thresholding wavelet coefficients

Instead of running an inverse transform at each scale, hence increasing the computational time, we simply added the detail coefficients for a given scale together by a weighted average and this weighted average was subsequently used for binary segmentation by thresholds defined by the user. Individual features such as cell bodies are segmented from the thresholded weighted detail coefficients by a standard connected components algorithm²¹. In cases such as immunohistochemistry of cell nuclei (e.g. c-fos) additional steps with the computation of tensor structure on the detail coefficients and subsequent extraction of the tensor structure trace or energy, tr(T), (see Segmentation of processes using tensor structure) is done followed by thresholding and watersheding (see Supplementary Figure 10c,d). In the case of c-fos experiments we used the Shannon entropy based binary thresholding⁶⁶ for DAPI and c-fos cell nuclei segmentation.

Segmentation of processes using tensor structure

Anatomically a cell body can more or less be perceived as a point feature; the most important parameter is its location. This is not true for a fiber tract or a cell process outgrowth where it is better conceived as a geometrical feature extended in space (spatially coherent) with a set of orientations at different locations. We here leverage these additional properties of coherency and orientation to increase the SNR for segmentation of fiber tracts and processes. We extracted the orientation as well as coherency of fluorescent signals at the set of detail coefficients where the SNR for processes peaked (d1) by first computing the gradient magnitude from Scharr operator gradient⁶⁷ and then computing its associated structure tensor⁶⁸ defined for each location as the 2 × 2 symmetric positive matrix T:

$$T=\left[\begin{array}{cc}\hfill {\langle f_x,f_x\rangle }_w\hfill & \hfill {\langle f_x,f_y\rangle }_w\hfill \\ \hfill {\langle f_x,f_y\rangle }_w\hfill & \hfill {\langle f_y,f_y\rangle }_w\hfill \end{array}\right]$$

Where f_x and f_y are the Scharr derivatives of the detail coefficients d1(x, y), along the columns, x, and rows, y, respectively. Furthermore, the weighted inner product between two arbitrary images g and h is defined as:

$${\langle g,h\rangle }_w={\iint }_{{\mathrm{ℝ}}^2}w(x,y)g(x,y)h(x,y)\mathit{\text{dxdy}}$$

Where w is the Gaussian weighting function who’s standard deviation, or Kernel size, determines the area of interest, which is set and determined by the user’s imaging resolution relative to the size of the labeled cell outgrowth processes. Once the structure tensor, T, is computed it is trivial to obtain following three properties for each location in d1: orientation, coherency, and trace matrix.

Orientation, θ:

$$\theta =\frac{1}{2}\text{arctan}\left(2\frac{{\langle f_x,f_y\rangle }_w}{{\langle f_y,f_y\rangle }_w-{\langle f_x,f_x\rangle }_w}\right),$$

Coherency, C:

$$C=\frac{{\lambda }_{\text{max}}-{\lambda }_{\text{min}}}{{\lambda }_{\text{max}}+{\lambda }_{\text{min}}},$$

Where where λ_max and λ_min are the largest and the smallest eigenvalue of the tensor, respectively.

Trace, tr(T), is defined as:

$$\text{tr}(T)={\langle f_x,f_x\rangle }_w+{\langle f_y,f_y\rangle }_w,$$

The trace of the tensor structure is not primarily used for segmentation of processes, but mentioned in Segmentation of features by thresholding wavelet coefficients quite useful for segmentation of cell nuclei with differential fluorescent intensity (e.g. immunohistochemical fluorescent labeling of immediate early genes. Fig. 6, and Supplementary Fig. 10). The coherency on a set of small-period detail coefficients, e.g. d1, is used for binary segmentation of labeled processes.

For processes such as dendrites and axons, in order to obtain a thin shape that is equidistant to the boundaries of the labeled processes (i.e. a topological skeleton) we applied the Zhang-Suen thinning algorithm⁶⁹ on the binary segmented image. The skeleton is then pruned similar to⁷⁰ into end-points (less than two neighboring segmented pixels), junctions (more than two neighboring segmented pixels), and slabs (exactly two neighboring segmented pixels). The endpoints and junctions together with the segmented cell-bodies can then be seen as nodes which delineates the slabs as belonging to a subset of pixels defining vertices, all of which in the end are used for visualization of labeled processes online (Fig. 2c).

Since several pruning and tractograhy algorithms are already available^28,71–73, and the user might want to create their own, the output is also provided for each single pixel that form the segmented topological skeletons together with the pixel's associated orientation (seen represented as hue in Fig. 4e–g).

Registration with non-rigid free-form deformation (FFD) using thin-plate splines (TPS)

To map the coordinates of a target image to that of a reference image we here used the method of thin-plate splines (TPS). We start out by segmenting the overall contour of both the target brain section and the reference brain section from the standardized atlas. Using the contours of the overall brain section as well as any detected hollow regions within the boundaries of the brain section such as ventricles the algorithm then extracts the principal axes using principal component analysis. Based on the intersection of the principal axes with the contour we iteratively generated a set of homologous correspondence points between the two sections by the following algorithm²⁵:

1. Set level l = 1

2. While l ≤ L

3. Generate a midpoint q_i between p_i and p_i+1 such that q = (p_i + p_i+1)/2. Where the points are indexed based on their clockwise alignment on the contour perimeter.

4. Find a point x_i on the contour between p_i and p_i+1 such that x_i lies on the shortest distance from a line intersecting the contour and midpoint q_i perpendicularly to the line between p_i and p_i+1

5. Iterate steps 3–5 until the whole contour has been traced in a clockwise order, i.e. p_i = p_n] and p_i+1 = p₁.

6. Make a new vector p′ where all new x_i and qi are interleaved together with p_i.

7. Increment the level l = l + 1. Set p′ = p + q + x as the new vector p = p′.

The output of the above steps can be seen in Supplementary figure 2, it is up to the user to define how many levels L that is needed for getting a good correspondence. The more levels added the more correspondence points generated and the computational complexity of thin-plating itself is 0(n³) where n is the number of correspondence points.

The TPS interpolation δ(x, y) minimizes the bending energy:

$$I_{\delta }={\iint }_{{\mathrm{ℝ}}^2}({\delta }_{\mathit{\text{xx}}}^2+2{\delta }_{\mathit{\text{xy}}}^2+{\delta }_{\mathit{\text{yy}}}^2)\mathit{\text{dxdy}}$$

With the form:

$$\delta (x,y)=a_1+a_{x}x+a_{y}y+\sum _{i=1}^n{w}_{i}U(\Vert (x_i,y_i)-(x,y)\Vert ),$$

Where, a₁, a_x, a_y and U(r) = r²log r are the affine parameters and w_i are the thin-plate splines parameters. The TPS interpolation should have square integrable derivatives if the following two conditions hold:

$$\sum _{i=1}^n{w}_i=0\text{ and}\sum _{i=1}^n{w}_i{x}_i=\sum _{i=1}^n{w}_i{y}_i=0$$

A linear system is obtained for the TPS coefficients and a regularization parameter, λ = 0.001, is added to control amount of smoothing to avoid ripples in the obtained transform. If λ = 0 exact interpolation is performed2^27,25.

Statistical analysis

For all statistical inferences made we examined distribution assumptions with Kolmogorov–Smirnov test of equality as well as Bartlett’s test of equal variances, these tests are only reported when significant deviation from assumptions were observed. For non-parametric count data between two groups we used Pearson’s chi-squared test of independence. Student’s t-test was used when assumptions were met with adjusted degrees of freedom in cases where equal variances cannot be assumed. Only two-sided tests were performed. For clustering of single-cell coexpression analysis we used the R package Mclust with expected maximization and gaussian mixture models. For linear regression analysis of locomotion regressed on c-fos intensity background autofluorescent was added as a covariate rather than excluding data points with high autofluorescent due to staining variability. All statistical analysis were done in R⁵⁵. For Bayesian analysis as well as meditational analysis see section Estimating mediating effects of c-fos expression to cocaine induced locomotor activity and section Psychophysical scaling by gradient-based Markov chain Monte Carlo (MCMC). For signal-to-noise ratio evaluation in Figure 3 the Rose criteria⁷⁴ was used.

No statistical methods were used to pre-determine sample sizes but our sample sizes are similar to those reported in previous publications^30,31. Injections considered outside of the stereotactic coordinates were excluded and not further imaged or processed. We did not perform any replication experiments. Pseudo-randomization was performed for the cocaine administration study. In cocaine administration experiment we counter balanced the assignment of mice to each group (cocaine vs. saline) × (boxA vs. boxB) × (time of testing).

A Life Sciences Reporting Summary is available.

Estimating mediating effects of c-fos expression to cocaine induced locomotor activity

Mediational analysis was done in R using the MBESS package following⁷⁵.

Psychophysical scaling by gradient-based Markov chain Monte Carlo (MCMC)

We assume that motor behavior observed in Figure 7l can be described with the four parametric Weibull density distribution, f(x):

$$f(x;k;\lambda )=\{\begin{array}{cc}\hfill \frac{k}{\lambda }{\left(\frac{x}{\lambda }\right)}^{k-1}{e}^{-{(x/\lambda )}^k,}& \hfill x\ge 0\hfill \\ \hfill 0,& \hfill x<0\hfill \end{array}$$

Which give the cumulative density distribution:

$$F(x;k;\lambda )=\{\begin{array}{cc}\hfill 1+e^{-{(x/\lambda )}^k,}& \hfill x\ge 0\hfill \\ \hfill 0,& \hfill x<0\hfill \end{array}$$

Which we directly translate into the psychophysical scaling between average velocity for the ith mouse, ${\overline{v}}_i$, and relative variance in c-fos activation, x_i:

$${\overline{v}}_i=0.9(1-\text{exp}{\left(\frac{-x_i}{\lambda }\right)}^k)+1$$

Where x is defined as:

$$x=\frac{{\sigma }_{c-\text{fos}}^2}{{\sigma }_{c-\text{fos}}^2+{\sigma }_{\text{DAPI}}^2}$$

Where k is the shape, or slope, parameter and λ is the location, or intercept, parameter. 0.9 and 1 are estimated from the marginal distribution of the locomotor behavior itself and sets the output range. Likewise we set λ = 0.55 and k = 2.5 based on initial fit to the marginal distribution then we estimated the effect of cocaine with prior Gaussian(0, 0.1). Bayesian statistics was done in R using the rstan⁷⁶ package.

Code access and supplementary software instructions

Source code can be accessed at http://www.github.com/tractatus/.

Data availability statement

The datasets generated during and/or analyzed during the current study if not already available on www.wholebrainsoftware.org, www.github.com/tractatus or www.openbrainmap.org are available from the corresponding authors on reasonable request. Source code is licensed with GPLv3 license.