Coarse-grained simulations of actomyosin rings point to a nodeless model involving both unipolar and bipolar myosins

Abstract

Cytokinesis in many eukaryotic cells is orchestrated by a contractile actomyosin ring. While many of the proteins involved are known, the mechanism of constriction remains unclear. Informed by the existing literature and new three-dimensional (3D) molecular details from electron cryotomography, here we develop 3D coarse-grained models of actin filaments, unipolar and bipolar myosins, actin cross-linkers, and membranes and simulate their interactions. Assuming that local force on the membrane results in inward growth of the cell wall, we explored a matrix of possible actomyosin configurations and found that node-based architectures like those presently described for ring assembly result in membrane puckers not seen in electron microscope images of real cells. Instead, the model that best matches data from fluorescence microscopy, electron cryotomography, and biochemical experiments is one in which actin filaments transmit force to the membrane through evenly distributed, membrane-attached, unipolar myosins, with bipolar myosins in the ring driving contraction. While at this point this model is only favored (not proven), the work highlights the power of coarse-grained biophysical simulations to compare complex mechanistic hypotheses.

INTRODUCTION

It is well known that an actomyosin ring (AMR) drives cell division in most eukaryotic cells, but how it contracts and how force is transmitted to the membrane remain unclear (Balasubramanian et al., 2004; Pollard, 2010). Two components involved in contraction are actin filaments (F-actin) and the motor protein nonmuscle myosin II, which exerts tensile force on F-actin through a processive ATP-dependent power stroke mechanism (Geeves and Holmes, 2005). Both proteins are essential for cytokinesis and localize to an equatorial contractile ring during mitosis (Marks and Hyams, 1985; Kanbe et al., 1989; Bezanilla et al., 1997; Kitayama et al., 1997; May et al., 1997; Arai et al., 1998; Balasubramanian et al., 1998; Motegi et al., 2000; Wu et al., 2003). Fluorescence studies of ring assembly in Schizosaccharomyces pombe, a rod-shaped unicellular fission yeast that shares most of its cytokinesis genes with metazoans (Balasubramanian et al., 2004), showed that the ring components first form a broad band of nodes (Bähler et al., 1998; Wu et al., 2006) that coalesces into a ring at the division plane (Vavylonis et al., 2008). Recent electron cryotomography (ECT) of dividing fission yeast showed, however, that F-actin termini are apparently randomly distributed around the ring (Swulius et al., 2018), calling into question whether nodes continue to exist during constriction. F-actin in the contractile ring is contributed by both existing actin cables (Huang et al., 2012) and de novo nucleation, primarily by the formin Cdc12p (Evangelista et al., 1997), a barbed-end actin-capping dimeric protein that is essential for ring assembly in fission yeast (Chang et al., 1997). While it has been proposed that ring tension is transmitted to the membrane via a connection between the actin barbed end and Cdc12p, which either exists individually (Pollard, 2010) or at nodes (Laporte et al., 2011), this mechanism has not been proven.

There are two myosin type-II heavy chains (Myo2p and Myp2p) in the contractile ring. Myo2p, the essential type II myosin (Kitayama et al., 1997; May et al., 1997), plays the leading role in ring assembly, while the second, nonessential, unconventional type II myosin, Myp2p, is the major driver for ring constriction (Laplante et al., 2015), consistent with its arrival at the division site immediately prior to ring constriction (Wu et al., 2003). Recent evidence indicates that during constriction, Myo2p and Myp2p are distributed in two distinct concentric rings (Laplante et al., 2015), but the causes and functional implications of this segregation are unknown. While previous simulation studies have described myosin as bipolar (Jung and Mascagni, 2014; Stachowiak et al., 2014), and this assumption is supported by some in vitro evidence (Niederman and Pollard, 1975; Pollard, 1982), myosin has also been proposed to exist in a unipolar form with its C-terminal tail tethered to the membrane and its N-terminal motor domain in the cytoplasm, in a “bouquet-like” arrangement (Laporte et al., 2011; Laplante et al., 2016). Further study is needed to elucidate how myosin is organized within the ring and how it generates tension during constriction.

In addition to F-actin and myosin, the actin cross-linkers α-actinin and fimbrin have been reported to be important for assembly of the ring (Skau et al., 2011; Laporte et al., 2012). While α-actinin is present in the ring during constriction, it is not clear whether fimbrin is present as well (Wu et al., 2001). In vitro, however, addition of actin cross-linkers stalls ring contraction (Mishra et al., 2013). Thus, it is currently unclear how these actin cross-linkers affect ring contraction. Cofilin has also been reported to help maintain the structure of the ring, but its seemingly counterintuitive function as an F-actin severing protein (Nakano and Mabuchi, 2006; Chen and Pollard, 2011) leaves its role during ring constriction unclear.

Simulations have been used previously to explore constriction of the actomyosin ring (Pollard, 2014). In an early continuum model, discrete molecules were not described. Instead, the ring was represented by density values and the roles of myosin and cross-linkers were implicitly represented using coefficients of tension contribution (Zumdieck et al., 2007). Simulations based on this model suggested that actin depolymerization in the presence of end-tracking cross-linkers could drive constriction, but whether such a cross-linker exists is unknown. Later simulations further explored this same idea, modeling individual filaments as lines with defined polarity (Mendes Pinto et al., 2012). In more recent work, the ring was modeled as a two-dimensional (2D) band in which actin filaments were modeled as chains of beads and clusters of myosins were represented as single beads that exerted force on actin filaments in close proximity (Stachowiak et al., 2014). Parameters were found in which this 2D model produced tension similar to that measured in fission yeast protoplasts. Simulations have also explored the condensation of the ring before constriction (Bidone et al., 2014).

Prompted by ECT data revealing for the first time the native three-dimensional (3D) organization of the actin filaments and the membrane in dividing yeast cells (Swulius et al., 2018), here we developed more detailed and 3D coarse-grained simulations to explore different hypotheses about how actin and myosin might constrict the membrane. F-actin, unipolar and bipolar myosins, and actin cross-linkers were all modeled using a bead–spring representation. A flexible cylindrical membrane was also modeled. To make actomyosin interactions as realistic as possible, the ATPase cycle of myosin was implemented in step-by-step detail. Random forces were further added to mimic thermal fluctuation.

First, we introduced the basic components of the ring one by one to define a minimal set of components and rules necessary for constriction. In doing so, we found that actin cross-linkers are needed to propagate tension through the ring, and that introducing cofilin to sever bent F-actin helps reproduce the filament straightness observed by ECT. We then explored 16 candidate actomyosin architectures and ring-to-membrane attachments. Combined with ECT data, our results suggest that actomyosin does not exist in nodes during constriction. Judging by all currently available experimental data, our simulations favor a model in which the ring tension is generated primarily through interactions between bipolar myosins and actin filaments, and is transmitted to the membrane via unipolar myosins, which are individually attached to the membrane. Due to the 3D and dynamic nature of our data, which is much better presented in movies than in static figures, we encourage readers to begin by watching Supplemental Movie S1, which presents 1) the elements and properties of our 3D coarse-grained model of the contractile ring, 2) building the initial model, 3) exploration of different actomyosin configurations, and 4) a final model that best agreed with experimental data.

RESULTS

Basic components of the ring

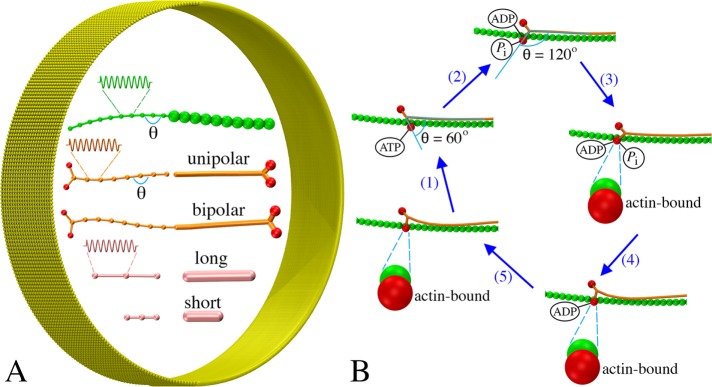
To build a coarse-grained model of the contractile ring, three main components of the ring, F-actin, myosin, and cross-linkers, were represented using a bead–spring model (Figure 1A). Each filament was modeled as a chain of beads connected by springs, each myosin was modeled as either unipolar or bipolar, and each cross-linker was modeled as having two actin-binding domains at the two ends. The membrane was modeled as a sheet of beads, originally having a cylindrical shape (Figure 1A). The actin–myosin interaction was modeled as occurring in a power-stroke manner in which the myosin ATPase cycle had five steps (Figure 1B). The power stroke was generated by changing the angle of the myosin head as it transitioned between its ATPase phases (see Materials and Methods for details).

FIGURE 1:

Coarse-graining the actomyosin system: (A) Models of F-actin (green), myosins (tail in orange, heads in red), actin cross-linkers (pink), and membrane (yellow) (see the text for details). Note the same visualizations and colors are used for all following figures unless otherwise stated. (B) The ATPase cycle of myosin was modeled in five steps: myosin (1) binds ATP and releases actin, (2) hydrolyzes ATP, (3) binds actin, (4) releases phosphate, and (5) releases ADP.

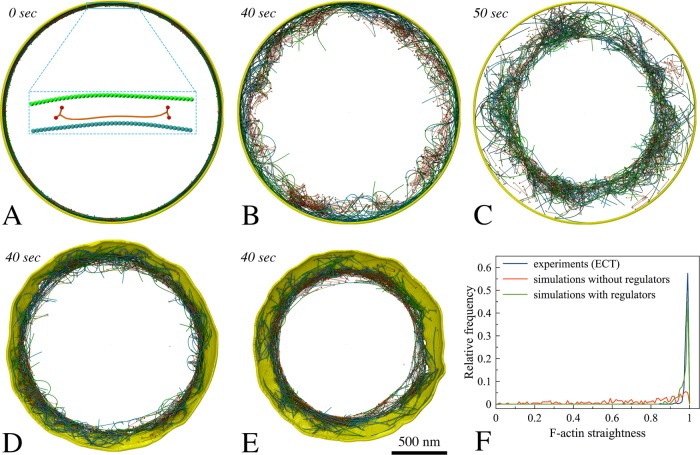
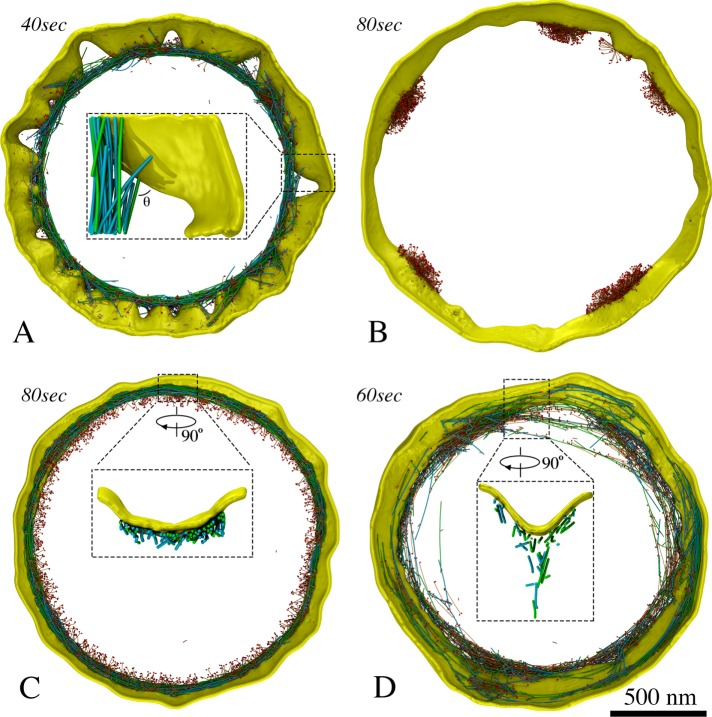
Many proteins are present at the midcell during constriction, but it is unclear which are essential for the contractility of the ring. We therefore started with a very simple model, testing interactions between bipolar myosin and F-actin of mixed polarities, originally arranged into a ring (Materials and Methods/Initial ring configuration). In this test, a membrane was added to confine the actomyosin system, but membrane constriction was not expected, since the membrane was not linked to the ring (Figure 2A). As myosin moved along F-actin toward its barbed ends in an ATPase-dependent power-stroke manner (Figure 1B), the filaments slid, bent, and oriented randomly, but the ring did not constrict because of the lack of long-range propagation of tension around the ring (Figure 2B; Supplemental Movie S1, at 2:10). On the assumption that cross-linking F-actin would help propagate tension, actin cross-linkers were added, and the ring began to contract, despite losing the original ringlike arrangement of F-actin (Figure 2C; Supplemental Movie S1, at 2:35). Linking the ring to the membrane (Materials and Methods/Membrane tethering) resulted in membrane constriction, showing that a ring composed of F-actin, myosin, and actin cross-linkers is capable of generating tension and constricting the membrane (Figure 2D; Supplemental Movie S1, at 3:01). As the membrane was pulled inward, cell wall material was added behind, preventing the membrane from relaxing back (Materials and Methods/Cell wall and turgor pressure). The ringlike arrangement of F-actin was now maintained, suggesting that membrane attachment contributes to maintenance of the ring structure. Note that in later simulations of Model 1, tethering the actin barbed end and unipolar myosin tail to membrane-bound nodes produced tension temporarily in the absence of cross-linkers. As the nodes were able to slide on the membrane to aggregate into separated large clusters, however, the ring was quickly broken (Supplemental Figure S2A), pointing again to the need for cross-linkers for ring constriction.

FIGURE 2:

Setting up basic components of the simulated constriction system: F-actin (opposing polarities in green and cyan), bipolar myosin, cross-linkers, and membrane. Italic font indicates simulated times. (A) The initial ring was composed of F-actin, bipolar myosin, and membrane. (B) The actomyosin ring did not contract in the absence of cross-linkers. (C) In the presence of cross-linkers, the ring did contract. (D) Adding tethers between F-actin and the membrane caused the ring to constrict the membrane. (E) Adding regulatory factors (tension-dependent interaction between actin and myosin, filament orientation-dependent cross-linking, cofilin function, and actin turnover) reduced F-actin bending. (F) Histogram of straightness factors for filaments visualized by ECT (Swulius et al., 2018) (blue), in simulations without regulatory factors (red), and in simulations with regulatory factors (green).

F-actin straightness regulatory factors

At this stage, the simulated F-actin did not mimic the consistently straight filaments observed experimentally (Swulius et al., 2018), but was highly bent (Figure 2, D and F; Supplemental Figure S1). To study how the myosin processivity would influence bending, we reduced the myosin duty ratio (see Materials and Methods/Myosin ATPase cycle for the definition). As the first step of the ATPase cycle was slowed 5 and 10 times, the duty ratio (originally ~0.72) was reduced to 0.35 and 0.21, slowing ring constriction and delaying filament bending, but this did not eliminate bending. Inspecting the simulation results, we identified at least two factors that contributed to filament bending. First, if an F-actin was cross-linked close to its pointed end while myosin was walking toward its free barbed end, the barbed end was pulled toward the pointed end, bending the filament (Supplemental Movie S1, at 3:42). As one proposed ability of F-actin is tension sensing (Galkin et al., 2012), and myosin is known to bind preferentially to F-actin under tension (Uyeda et al., 2011), we added a rule that myosin could bind to actin only if the filament was cross-linked upstream (closer to the barbed end). Note that even if we had tracked them in the simulation, other binding events would not have contributed tension, since loose filaments simply move when pulled. Later, in models where actin barbed ends were connected to the membrane either individually or at nodes, this rule was not applied, since the barbed end was always constrained.

Second, if an actin filament had each of its ends cross-linked to two different filaments sliding toward one another, the filament would bend (Supplemental Movie S1, at 4:03). We reasoned that bending was not seen in vivo because either 1) cross-links were released on the bent filament or 2) the filament was broken. Hypothesizing that torque facilitates cross-link release, we added a rule that the probability of cross-link release increases with the angle between two filaments at their cross-linked location (see Materials and Methods/Torque-facilitated cross-linker release for details). Next, considering that the actin-depolymerizing factor cofilin preferentially severs F-actin that is not under tension (Hayakawa et al., 2011), we introduced its function into the simulation by stipulating that the probability of filament breaking increases with bending angle (see Materials and Methods/Cofilin function for details).

Another factor that might affect F-actin bending is actin depolymerization, which has been shown to occur rapidly during constriction (Pelham and Chang, 2002). Actin turnover was therefore added. Further, turnover of myosin and cross-linkers was also implemented (see Materials and Methods/Protein turnover for details), since this occurs in fission yeast (Pelham and Chang, 2002; Clifford et al., 2008; Laporte et al., 2012). In the presence of these regulatory rules, F-actin bending was prevented in silico (Supplemental Movie S1, at 5:04; Figure 2, E and F), thus recapitulating the filament straightness observed experimentally (Swulius et al., 2018).

Exploration of actomyosin architecture models

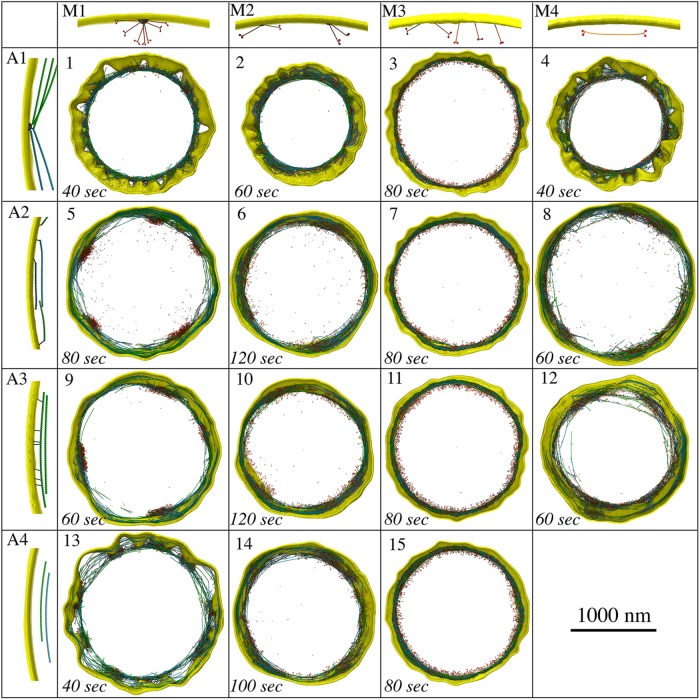
Having established a working core model, we explored 15 plausible configurations and arrangements of F-actin and myosin to study how they would constrict the membrane (Figure 3). We reasoned that the membrane must be tethered to either actin or myosin, or both, to enable membrane constriction. The four configurations of actin are illustrated in Figure 3 (panels A1–A4). In A1, F-actin barbed ends were tethered to 64 membrane-bound nodes, as shown for ring assembly (Laporte et al., 2011; Pollard and Wu, 2010). In A2, the barbed end of each F-actin was tethered to a random membrane bead. In A3, tethering could occur on any actin bead along the filament, and in A4, F-actin was not tethered to the membrane. The four configurations of myosin are illustrated in Figure 3 (panels M1–M4). In M1, unipolar myosins were tethered by their tails to 64 membrane-bound nodes, again, as shown for ring assembly (Pollard and Wu, 2010; Laporte et al., 2011). In M2, unipolar myosins were tethered to the membrane in pairs. In M3, each unipolar myosin was tethered to a random membrane bead and in M4, myosins were modeled as bipolar molecules, randomly distributed throughout the ring, unattached to the membrane. The basic principles of constriction that were discovered are presented below.

FIGURE 3:

Exploration of different actomyosin models resulting from combining four actin configurations (A1–A4) with four myosin configurations (M1–M4). Snapshots of the 15 plausible resultant models are presented. Note that the combination of A4 and M4 is not plausible, since there are no tethers between the contractile ring and the membrane.

Ring tension

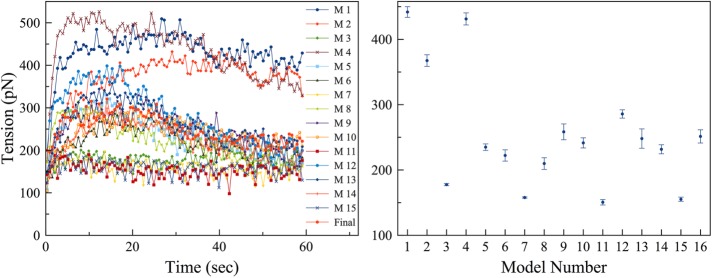
First, we calculated the ring tension of all the models (Figure 4). In models where actin and myosins were anchored to pull on one another in a tug-of-war manner (e.g., Models 1–4, where actin was connected in nodes, Model 3 being an exception), the ring produced a high tension. Meanwhile, the ring produced a low tension if myosins were unipolar and individually attached to the fluidic membrane (Models 3, 7, 11, 15). All models, however, produced tensions of order similar to that of the ring tension Stachowiak et al. (2014) observed experimentally on fission yeast spheroplasts. It is unclear, though, whether our simulated ring tensions or the experimental value reported by Stachowiak et al. are actually similar to the ring tension in intact cells, since our electron cryotomograms (Swulius et al., 2018) showed that the architecture of the cryopreserved actin ring is very different from that of the ring in spheroplasts as reported by Kamasaki et al. (2007). Thus, all the models exhibited ring tensions within reasonable bounds, at least as far as they are known at this time.

FIGURE 4:

The ring tension was calculated. Left, representative time courses of ring tensions in individual simulations of the 16 models; right, averages over five simulations for each model, with number 16 representing the final model. Error bars represent standard deviations.

Individually, homogeneously distributed unipolar myosins maintain membrane smoothness

Several scenarios led to loss of membrane smoothness and circularity. One obvious cause was focusing the constriction force on only a small number of membrane sites. The most severe distortion occurred when the ring was connected to the membrane via only 64 nodes, as in Models 1, 4, and 13, which resulted in membrane puckering during constriction (Figure 3; Supplemental Figures S2 and S3; Supplemental Movie S1, at 7:08). As new cell wall material filled the gap between the membrane and the cell wall, puckering also occurred on the leading edge of the septum (Supplemental Figure S2B, right panel), supporting the membrane puckers against turgor pressure. We found that our fluidic membrane model allowed nodes to slide (Supplemental Figure S4) with speeds comparable to those during ring assembly reported experimentally and via simulations (Vavylonis et al., 2008; Bidone et al., 2014). As a result of node sliding, in several cases, puckers coalesced, making large membrane deformations (Supplemental Figure S2C; Supplemental Movie S1, at 7:50). Neither halving the concentrations of actin, myosin, and cross-linkers (Supplemental Figure S2C) nor doubling them (Supplemental Figure S2D) mitigated puckering. The defects persisted even as the number of nodes increased from 64 to 140 (Supplemental Figure S2E); the latter was recently reported by Laplante et al. (2016). We then studied how puckering depended on the mechanosensitivity of cell wall growth by varying F_m, the minimal centripetal force on a membrane bead that induces cell wall growth (defined in Materials and Methods/Cell wall and turgor pressure). Increasing F_m 100 times suppressed cell wall growth when unipolar myosins were individually connected to the membrane, but this low mechanosensitivity did not prevent nodes-induced puckering (Supplemental Figure S5). We also ran simulations of Model 13 (myosins were at nodes, and actin was not connected to the membrane) without the myosin tension-sensing rule (myosin could bind to actin only if the filament was cross-linked upstream). Puckers still occurred in these simulations (Supplemental Figure S6), ruling out the possibility that this myosin tension-sensing rule might give a bias to higher ring tension and cause pucker formation.

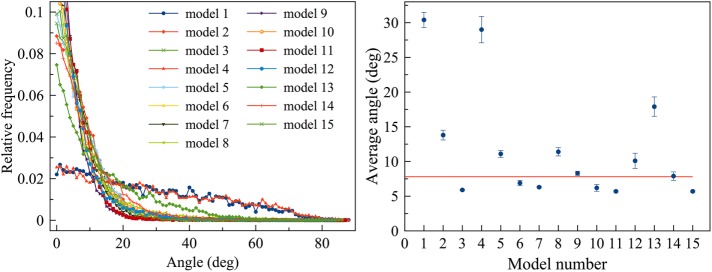
Because the membrane in every cryotomogram appeared smooth (Swulius et al., 2018), we know that small puckers do not form in vivo. However, puckers larger than the 200-nm-thick cryosections cannot be ruled out. In our simulations, the presence of membrane puckers often caused actin filaments to lie at large angles with respect to the membrane (Figure 5A; Supplemental Figures S2B and S3, B and C). In contrast, in other models that did not produce membrane puckers, filaments remained parallel to the membrane (Figure 6), which is consistent with experimental observation (Swulius et al., 2018). Smaller membrane puckers were observed in Model 2, where unipolar myosins were attached to the membrane in pairs (Figure 3; Supplemental Figure S3A; Supplemental Movie S1, at 8:11). On the other hand, in Models 3, 7, 11, and 15, where unipolar myosin was individually attached to the membrane, providing an abundance of attachments, the membrane constricted without losing smoothness and actin filaments stayed parallel to the membrane (Figures 3 and 6; Supplemental Figure S7; Supplemental Movie S1, at 11:27). Therefore, if unipolar myosins exist during constriction, they are likely attached to the membrane individually.

FIGURE 5:

Representative features produced by the first 15 models. (A) Membrane puckering, as in Model 1, and large angles between filaments and membrane. (B) Tethering membrane-bound unipolar myosins in nodes or pairs, as in columns 1 and 2 of Figure 3, resulted in aggregation. (C) Individual unipolar myosins, as in Model 11, pulled filaments close to the membrane. (D) Bipolar myosins, as in Model 12, pulled filaments away from the membrane.

FIGURE 6:

Angles between actin filaments and the membrane calculated after 60 s of simulated time. Left, representative histograms of angles in individual simulations; right, averages over five simulations for each model with error bars representing standard deviation and the red horizontal line indicating the average angle (7.8°) measured from electron tomograms for a reference. The presence of puckers, as in Models 1, 4, and 13, causes filaments to form angles larger than those observed experimentally.

Because a previous study observed that during ring assembly, actin and myosins in a broad band of nodes could coalesce into different structures when the cross-linker concentration varied (Bidone et al., 2014), we explored whether changing the cross-linker concentration influenced the ring architecture in our simulations. Doubling or halving the cross-linker concentration did not change the ring architecture or the basic outcome of any of our constriction models.

Attaching unipolar myosin individually to the membrane prevents aggregation

Among models with abundant membrane attachments, in 5, 6, 9, 10, and 14, membrane deformation still occurred due to myosin aggregation. In contrast to fluorescence microscopy observations (Laplante et al., 2015; Thiyagarajan et al., 2015; Zhou et al., 2015), myosins in these models gradually clumped together into a few large aggregates along the ring (Figure 5B). Aggregation of unipolar myosins occurred through entanglement as either membrane nodes (Models 5 and 9; Figure 3; Supplemental Figure S8; Supplemental Movie S1, at 8:31) or pairs of myosins (Models 6, 10, and 14; Figure 3; Supplemental Figure S9; Supplemental Movie S1, at 9:12) became caught on each other due to steric hindrance while sliding along the membrane. Entangled myosin clusters were in turn larger, increasing the chance for further entanglement and creating a positive feedback that exaggerated the defect as constriction proceeded. As aggregation eventually concentrated the constrictive force, membrane circularity was lost. Varying the myosin turnover rate in myosin-node Models 5 and 9 and myosin-pair Models 6, 10, and 14, we found that myosin nodes always aggregated, while aggregation of myosin pairs was mitigated (Supplemental Figure S10) when the myosin turnover rate was increased to 15 times or more higher than the rate we observed experimentally (Supplemental Figure S11; Supplemental Table S1). In Model 8, where actin barbed ends were tethered to the membrane and bipolar myosin was not, clustering of barbed-end tethers also led to myosin aggregation at these locations (Figure 3; Supplemental Figure S12; Supplemental Movie S1, at 10:23). In contrast, in Models 3, 7, 11, and 15, the uniform distribution of myosin provided a persistent, homogeneous distribution of constrictive force that preserved membrane smoothness and circularity (Figure 3; Supplemental Figure S7; Supplemental Movie S1, at 11:27), further supporting the notion that unipolar myosins are individually tethered to the membrane.

Bipolar myosins pull actin filaments away from the membrane

Next, we focused on the five models where the membrane remained smooth (Models 3, 7, 11, 12, and 15) and measured the distance between F-actin and the membrane (Supplemental Figure S13). The four models containing individually tethered unipolar myosins (Models 3, 7, 11, and 15) restricted filaments to ∼21 nm from the membrane (Figure 5C; Supplemental Figures S7, S13), while ECT showed an average distance of ∼60 nm (Swulius et al., 2018). Owing to membrane-tethering and pulling forces from the unipolar myosins, less than 0.2% of the actin beads in these four models were at a distance larger than 60 nm. In Model 12, untethered bipolar myosins tended to pull actin away from the membrane, producing a larger average distance of 32 nm, with nearly 10% of the actin beads at a distance larger than 60 nm (Figure 5D; Supplemental Figure S13). This suggested the presence of bipolar myosin within the ring in real cells. In some cases, actomyosin bundles consisting of unattached F-actin and bipolar myosins peeled off from the ring and depolymerized (Figure 5D; Supplemental Movie S1, at 10:51). This is consistent with previous observations by fluorescence microscopy (Laplante et al., 2015), further supporting the presence of bipolar myosins and suggesting that actin filaments are not attached to the membrane.

Final model: dual myosin configurations

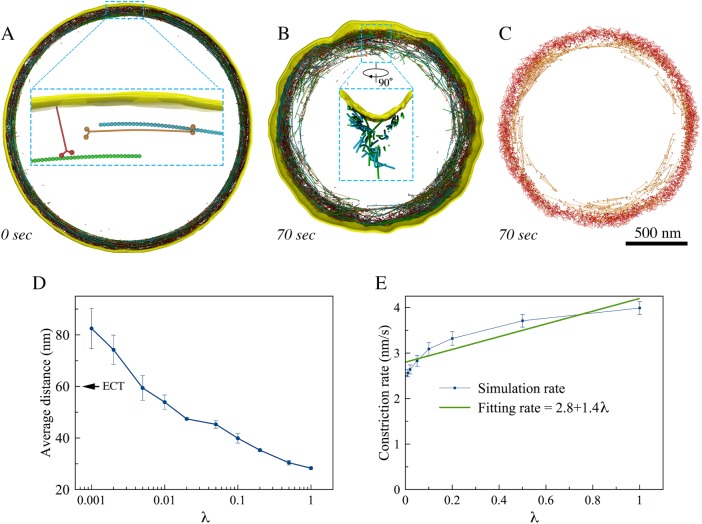
We therefore built a final model consisting of untethered F-actin, individual unipolar myosins, and bipolar myosins (Figure 7A). Simulating the final model resulted in normal constriction without visible defects of the membrane or ring (Figure 7B; Supplemental Movie S1, at 13:27). In this model, unipolar myosins remained at the outer edge of the ring due to their membrane attachment, while the bipolar form drifted inward, pulled toward the center by interaction with F-actin (Figure 7C; Supplemental Movie S2, at 13:54), matching the fluorescence microscopy result of the two myosin isoforms Myo2p and Myp2p (Laplante et al., 2015). In our simulations, interactions with bipolar myosins pulled actin filaments away from the membrane (Figure 7B, zoomed-in view; Figure 7D), approximately recapitulating the distances observed by ECT (Swulius et al., 2018), and occasionally caused actin/bipolar myosin bundles to peel off, as reported previously for actin/Myp2p bundles (Laplante et al., 2015). Reducing the ATPase rate of the unipolar myosin in the simulation caused actin/bipolar myosin bundles to peel off more frequently, again in agreement with fluorescence microscopy results, in which the loss of actin/Myp2p bundles occurred at greater frequency when the biochemical activity of Myo2p was reduced (Laplante et al., 2015).

FIGURE 7:

The final model. (A) A zoomed-in view shows initial configuration of the ring, including untethered F-actin (green and cyan), membrane-attached unipolar myosins (red), and bipolar myosins (orange). During constriction, (B) membrane smoothness and circularity were preserved and distances between F-actin and the membrane as observed in tomograms were recapitulated (as shown in a zoomed-in view), and (C) the membrane-attached unipolar myosins (red) occupied the outer edge of the ring while the unattached bipolar myosins (orange) occupied the inner edge. (D) Average distance between the simulated F-actin and the membrane (arrow indicates the average distance measured in tomograms) and (E) constriction rate as a function of the unipolar myosin’s ATPase rate scaling factor, λ. Error bars represent standard deviations (n = 5).

Reasoning that the balance of force between unipolar myosins pulling F-actin close to the membrane and bipolar myosins pulling it away would dictate its average distance to the membrane, we investigated how the average distance between F-actin and the membrane depended on the ATPase rate of the unipolar myosin by scaling it with a factor λ. As expected, the average distance between F-actin and the membrane increased as the ATPase rate of the unipolar myosin decreased, reaching the experimentally measured value of 60 nm at λ ∼ 0.005 (Figure 7D).

To further dissect the roles of the two forms of myosin, the simulated constriction rate, v = Δr/Δt, was defined as the ratio of average inward radial growth of the cell wall Δr to constriction time Δt, and we studied v as a function of the unipolar myosin’s ATPase rate (scaled with the factor λ) (Figure 7E). For simplicity, v was considered a linear combination of contributions from the bipolar myosin v_b and the unipolar myosin v_u. Fitting v = v_b + v_uλ to the simulated data yielded v_b = 2.8 nm/s and v_u = 1.4 nm/s. Because there were 2000 bipolar and 3200 unipolar myosin heads, on the average, each bipolar head contributed an amount of ∼1.4 pm/s to the constriction rate while each unipolar head contributed ∼0.4 pm/s. The efficiency of the bipolar myosins in our simulations was therefore several times that of the unipolar myosins, likely due to the fact that unipolar myosins were attached to the fluidic membrane. This is in agreement with the experiments that showed Myp2p contributes more to the constriction rate of real cells than Myo2p (Laplante et al., 2015).

DISCUSSION

From a methodological standpoint, we have demonstrated how 3D coarse-grained simulations can be used to explore complex models and hypotheses. The ring components were modeled in individual molecular detail, exerting force on a flexible membrane. Individual steps of myosin II’s ATPase cycle were also modeled to produce power stroke–driven movement of myosin along actin filaments. A major limitation of the work was that due to a lack of information, we only included ∼4 of the more than 100 proteins involved. Our model lacked all details about how and where formin polymerizes actin, for example, which, when discovered, will allow key improvements. Our results did nevertheless suggest several interesting principles.

The role of cross-linkers

Previous experimental studies have shown that cross-linkers such as α-actinin and fimbrin are essential for assembly of the fission yeast’s AMR ring, but their role during constriction has not been clear (Wu et al., 2001; Skau et al., 2011; Laporte et al., 2012). Earlier simulations showed that end-tracking cross-linkers and actin filament depolymerization could together drive contraction (Mendes Pinto et al., 2012), but α-actinin and fimbrin are not end-tracking, and it remains unclear whether end-tracking cross-linkers are present in the ring. It was also previously suggested that contractility could arise in the presence of thick myosin filaments if they functioned as cross-linkers by remaining bound to the barbed end of F-actin (Kruse and Jülicher, 2000). Although this might promote connectivity for long-range propagation of tension, it was unclear how such binding would be maintained, and thick myosin filaments were not seen in the cryotomograms (Swulius et al., 2018). Our simulations suggest that cross-linkers such as α-actinin and fimbrin allow long-range propagation of tension around the ring. This is consistent with findings on the contractility of in vitro ring-like systems (Ennomani et al., 2016) and disordered networks of actin (Bendix et al., 2008).

F-actin straightness

ECT revealed that F-actin filaments in dividing cells are remarkably straight (Swulius et al., 2018). While, in our first simulations involving only F-actin and myosin, the actin filaments became highly bent, here we identified two factors that likely reduce this bending in vivo. First, it has been shown in vitro that myosin binds preferentially to F-actins under tension (Uyeda et al., 2011). Biasing myosins to preferentially bind stretched F-actin filaments in our simulations reduced bending, and also helped maintain ring tension. It has also been shown in vitro that cofilin preferentially severs F-actins not under tension (Hayakawa et al., 2011). Biasing cofilin’s activity to bent filaments here promoted filament straightness. Our simulations therefore suggest one rationale for the otherwise puzzling presence in the ring of an actin-severing factor (Nakano and Mabuchi, 2006; Chen and Pollard, 2011).

Comparison with previous simulations/treatments of actomyosin systems

Dasanayake et al. (2011) studied 2D disordered networks of actin, myosin, and cross-linkers and found that they were by nature contractile, in agreement with our findings for the interplay of these three basic elements. Lenz also explored the behavior of disordered 2D networks and found analytically that “contractile forces result mostly from motors plucking the filaments transversely” (Lenz, 2014). The architecture of the AMR is very different, however, since the actins are parallel and bundled into a ring. As a result, contractile forces in our simulations arose from motors sliding parallel filaments past each other. Stachowiak et al. simulated a 2D actomyosin band where nodes containing 40 bipolar myosins each were modeled as single beads (Stachowiak et al., 2014). The authors observed clustering of myosin beads when protein turnover was stopped, but the cause of aggregation was very different from that seen here, because in their model, volume exclusion was not applied to all elements (e.g., objects could pass though actin filaments). In contrast, by modeling all the basic elements (including the membrane) in 3D and applying volume exclusion to all objects, we found that aggregation occurred when actin filaments and unipolar myosins were connected to the membrane in nodes or pairs, throughout a range of physiologically relevant turnover rates. Further, our simulations allowed the characteristics and consequences of different actomyosin configurations to be assessed in 3D and be compared directly with those observed in cryotomograms (Swulius et al., 2018). While Stachowiak et al.’s model already produced ring tension similar to that measured in fission yeast protoplasts, our results showed that many other actomyosin configurations can also produce ring tensions of similar order. Finally, the most closely related previous work was that of Bidone et al. (2014), who simulated how actin nodes placed on a 3D cylindrical surface can be drawn together into a tight ring by myosin filaments. The major difference with our work is that while Bidone et al. explored assembly of the ring, ours explored contraction, including changes in the shape of the cell wall boundary.

Do nodes exist during constriction?

Actin filaments and myosins have been shown to form nodes during the assembly of the ring (Bähler et al., 1998; Motegi et al., 2000; Wu et al., 2003, 2006; Vavylonis et al., 2008; Padmanabhan et al., 2011), and Laplante et al. (2016) recently suggested that nodes persist during constriction. In contrast, however, McDonald et al. recently reported an even distribution of the head domain of Myo2p along preconstriction rings (McDonald et al., 2017), and Wollrab et al. (2016) showed that myosin remains evenly distributed around division rings in fission yeast (though, interestingly, there did appear to be some separation into puncta in mammalian division rings). Our results point to a nodeless model because regardless of turnover rates or any other variation tested, nodes always bumped into one another and formed larger and larger aggregates, unlike anything seen in any fluorescence studies. Furthermore, in our simulations, whenever constrictive force was concentrated on nodes or aggregates, membrane puckers formed, unlike anything seen in cryotomograms (Swulius et al., 2018).

We note, however, that this finding (that concentrating force on the membrane leads to puckers) depended on the key assumption used throughout this study that where the ring pulls the membrane inward, cell wall growth follows. We assumed this because we imagine that the enzymes responsible for cell wall growth are regulated by very small changes in the spaces and pressures they experience. We note that two other recent simulation studies of the yeast division ring were based on the same key cause/effect assumption. Zhou et al. (2015), for instance, hypothesized that the cell wall would grow inward faster where the membrane had high local concave curvature (bulging out from the center of the cell). The authors speculated that tension in the ring would produce higher inward forces on the membrane in those locations, inducing cell wall growth and making the septum leading edge more circular. Likewise, in the “tension-sensitive” cell wall growth model by Thiyagarajan et al. (2015), the authors assumed the ring had uniform tension and followed the shape of the septum leading edge closely (which incidentally would require finely distributed connections rather than punctate nodes). Consequently, the ring pulled the membrane inward with centripetal forces at locations of negative curvature (where the cell wall bulged outward) and pushed the membrane outward with centrifugal forces at locations of positive curvature (where the cell wall ingressed toward the cell center). These authors then also assumed that these forces would cause cell wall growth at bulges and suppress it at ingressions, again making the septum leading edge more circular.

Thus, while we and others have assumed that inward force on the membrane results in local cell wall growth, we acknowledge that this is not the only possibility. Perhaps inward force on the membrane causes release of some messenger molecule that diffuses all around the ring, activating cell wall synthesis everywhere. Maybe force on the membrane in one location launches some kind of cell wall–synthetic machine that then moves around and around the leading edge of the septum, adding cell wall uniformly, and even pushing the membrane inward itself wherever necessary. We conclude that either nodes are not present during constriction or we do not understand yet what other cellular forces maintain smooth membranes when constrictive force is concentrated at nodes. Perhaps future experiments will provide new insight into how membrane puckers are prevented.

Actomyosin architecture

Instead of being directly attached to the membrane in nodes, our simulations suggest that actin filaments are not attached to the membrane. This rationalizes how bundles of actomyosin were able to separate from the membrane in fluorescence microscopy experiments (Laplante et al., 2015). Our simulations also favored models where unipolar myosins link the ring and the membrane. While no clear evidence of such connections was seen in cryotomograms (Swulius et al., 2018), the coiled-coil tail of a unipolar myosin is too thin and flexible to be resolved by ECT. Considering that Myo2p is the only myosin essential for viability (Kitayama et al., 1997; May et al., 1997), it is a reasonable candidate for this role. Unipolar Myo2p molecules have already been proposed to attach to the membrane at nodes during ring assembly (Laporte et al., 2011), but our results suggest they are more likely attached to the membrane individually to prevent aggregation and preserve membrane smoothness and circularity during ring constriction. Further, our results suggest that the myosin isoform Myp2p may exist in a bipolar configuration within the ring. This would explain fluorescence light microscopy experiments that showed that Myp2p primarily drives constriction, occupies the inner subdomain of the ring, and causes actomyosin bundles to peel away from the ring (Laplante et al., 2015).

MATERIALS AND METHODS

For convenience, the key parameters of our simulations are listed in Supplemental Table S2.

Actin filament

We modeled the actin filament (F-actin) as a chain of beads connected by springs (Figure 1). Considering the double-helical nature of the filament, for convenience, each model bead represented two globular actin monomers (G-actin). Because 13 G-actins, corresponding to 6.5 model beads, cover a length of 35.9 nm (Dominguez and Holmes, 2011), the relaxed length of the connecting spring isl_a= 5.5 nm. The tensile modulus of F-actin has been measured as E = 1.8 nN/nm² (Kojima et al., 1994). Estimating the cross-section of F-actin to be A ∼ 30 nm², we derived the force constant of our model springs as k_a = EA/l_a ∼10 nN/nm, reflecting the fact that F-actin is not easily stretched. To reduce the computational cost of simulating such stiff springs, however, we used a force constant of 1 nN/nm, considering that the stretching of the F-actin was still negligible with this constant. To reflect actin’s semiflexibility, bending at a bead with an angle θ was penalized with an energy of 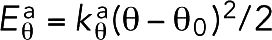, where θ₀ = 180° was the relaxed angle, and the bending stiffness constant 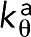was derived using the measured persistence length,L_p ∼ 10 μm (Isambert et al., 1995), to be 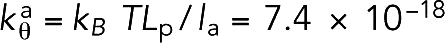J, where k_B is the Boltzmann constant and T = 295 K is the room temperature. Note that in initial simulations (see F-actin straightness regulatory factors), filaments became highly bent with the original bending stiffness 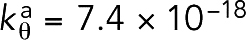J, but bending was prevented in the presence of straightness regulatory factors (Supplemental Figure S1). Bending was also prevented even after 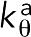was reduced three times to 2.4 × 10^–18 J, confirming that this reduction did not change the outcome of our simulations. Again, to reduce the computational cost, we then used 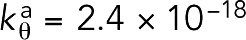J for the rest of our simulations.

Myosin configuration

Myosin was modeled as either unipolar or bipolar, and the same parameters were used for both configurations. Unipolar myosin was modeled as an eight-bead tail (representing the elongated C-terminal coiled-coil tail domain of two myosin heavy chains) connected to two head beads representing the N-terminal motor domains of the two heavy chains (Figure 1). Bipolar myosin was composed of two unipolar molecules connected at the tails. Like the actin filament, the beads were connected by springs of force constantk_m= 1 nN/nm and relaxed length l_m = 10 nm, which was chosen to reproduce a length of ∼80 nm reported for the fission yeast conventional myosin II (Bezanilla and Pollard, 2000). To recapitulate the experimentally reported pulling force of 3–4 pN from a single myosin head (Finer et al., 1994), simulations were done where a unipolar myosin interacted with an actin filament, from which the bending stiffness constant was determined to be 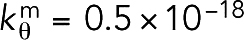J (Supplemental Figure S14). The relaxed angle was 180° on the tail, but at the head-to-tail junction it varied depending on the ATPase status of the head bead (see below for details).

Myosin ATPase cycle

To model interaction with actin, each myosin head was allowed to exist in five phases: bound to 1) ATP, 2) ADP and the hydrolyzed P_i, 3) ADP, P_i and actin, 4) ADP and actin (P_i was released), and 5) actin (ADP was released). The relaxed angle at the head–tail junction was 120° if the myosin head was in phase 2 or 3 and 60° if in phases 1, 4, or 5. Because ATPase rates for the individual phases of myosin II in fission yeast are not known, the probabilities of each phase transition were calculated based on studies of different species (De La Cruz and Ostap, 2009; Heissler et al., 2013). Specifically, ATP hydrolysis (phase 1 to 2 transition) occurred with probability p₁ = 25/s. If a myosin head in phase 2 was within an interaction distance D = 15 nm of an unbound actin bead, actomyosin binding (phase 2 to 3 transition) occurred with probability p₂ = 50/s. If there were more than one actin bead within D, the probability of being chosen for actin bead i was calculated as

(1)

where 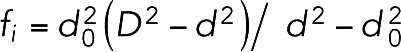was a function of the distance d between the myosin head and actin bead i and d₀ = 5 nm was the relaxed distance between them once they were bound to each other. Myosin II is known to walk on F-actin directionally from the pointed end to the barbed end. To model this property, for simplicity, binding between myosin and actin was allowed only if the angle θ formed by the head-to-tail myosin vector and the barbed-to-pointed-end actin vector was smaller than 90° (Supplemental Figure S15A). Release of P_i (phase 3 to 4 transition) occurred with probability p₃ = 25/s, generating a pulling force in a power stroke manner as the head–tail angle relaxed from 120° to 60° ADP release (phase 4 to 5 transition) occurred with probability p₄ = 25/s. Finally, ATP binding and actin release (phase 5 to 1 transition) occurred with a probability of p₅ = 150/s. Our implemented rates of the myosin ATPase cycle resulted in an average myosin duty ratio of 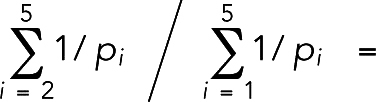0.72. While these rates set the upper limit of the load-free velocity of a myosin molecule as 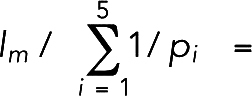70 nm/s, a previous experimental study reported a myosin load-free velocity of 500 nm/s (Lord and Pollard, 2004), reflecting a discrepancy in the literature.

Actin cross-linkers

Cross-linkers were modeled as two actin-binding domain (ABD) beads connected to a central bead by two springs of a force constant k_c and relaxed length l_c (Figure 1). To account for the existence of different potential cross-linkers in real cells, namely α-actinin and fimbrin (Wu et al., 2001), two types of cross-linkers were modeled. The one representing α-actinin had a length of 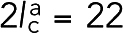nm, the combined length of two ABDs (5 nm each) and two spectrin repeats (6 nm each) estimated from PDB (Protein Data Bank) structure 4D1E (while human α-actinin has four, α-actinin of fission yeast has only two spectrin repeats; Murphy and Young, 2015), and 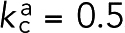nN/nm. The other, representing fimbrin, had 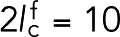nm (estimated from PDB structure 1RT8) and 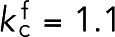nN/nm, which was chosen so that the two cross-linkers had the same Young’s modulus, meaning that 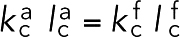. To promote stiffness, bending with an angle θ was penalized with an energy of 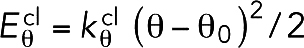, where θ₀ = 180° was the relaxed angle and the bending stiffness constant was J. Note that the spring constant for cross-linkers in our model was four orders of magnitude larger than that used in previous simulation work by Stachowiak et al. (2014), where the authors sourced experimental work by Claessens et al. (2006). In our opinion, Stachowiak et al. misinterpreted k_|| = 0.025 pN/nm (which was defined by Claessens et al. as the cross-linker’s effective shear stiffness at very small deformations) as the cross-linker’s extensional stiffness. Thermal forces would stretch cross-linkers of this unrealistically small spring constant tens of nanometers.

The binding of cross-linkers to actin was modeled as stochastic. The binding of a cross-linker ABD bead to an actin bead within the interaction distance D = 15 nm occurred with a probability of 100/s. Similarly to myosin–actin binding, if there were more than one actin bead within D, the probability of being chosen for actin bead i was calculated using Equation (1). Actin release from α-actinin and fimbrin occurred with probabilities of 3/s (Xu et al., 1998; Li et al., 2016) and 0.05/s, respectively (Skau et al., 2011).

Membrane

The membrane was modeled as a single layer of beads initially forming a cylinder (Figure 1). To preserve membrane integrity, attractive forces were introduced between neighboring beads. To do this, a mesh of nonoverlapping triangles with vertices on the beads was calculated, from which nonredundant pairs of neighbor beads were determined. If a pair of beads were separated at a distance d larger than d_pair= 20 nm, they were pulled together with a force of F_pull = k_pair (d – d_pair)², where k_pair = 20 pN/nm² was a force constant. To prevent the beads from being too close to each other, they were pushed apart with a force of F_push = k_pair (d_mb – d)² if d was smaller than a distanced_mb = 10 nm. Because a permanent pairwise interaction would have prevented membrane beads from moving away from one another, blocking fluidity, the nonoverlapping triangle mesh and therefore the nonredundant pair list were recalculated every 10⁴ steps. This allowed new pairs of beads to form based on their updated positions and made the membrane fluid. As we calculated the membrane tension during simulations, ∑Fd/A_m, which was the sum over all pairs where F and d were the force and distance between beads and A_m was the area of the membrane, the measurement varied between 0.05 and 1.0 pN/nm.

To generate membrane bending stiffness, a mesh of tetragons with vertices on the beads was calculated. If the four beads on each tetragon were not on the same plane so that the two diagonals were separated by a distance d, a springlike force, F_mb = k_mbd, was exerted on the beads to pull the two diagonals toward each other (Supplemental Figure S15B). Based on the reported membrane bending stiffness (Bo and Waugh, 1989), the force constant was calculated to be k_mb = 2 pN/nm. To prevent boundary artifacts, we applied a periodic boundary condition by translating the images of the beads of one edge to the other.

Torque-facilitated cross-linker release

If two filaments were cross-linked at an angle α that was larger than 60° (Supplemental Figure S15C), then once every 10⁴ time steps the cross-link was released with a probability P_ux= 0.5 – cos (α).

Cofilin function

If, at an actin bead, the angle α between the tangent and the position vector from the barbed end (Supplemental Figure S15D) was larger than 60°, once every 10⁵ time steps (the number was arbitrarily chosen, since the rate in real cells is not known), the filament was broken into two segments with a probability P_br = 1.0 – cos (α).

Protein turnover

To model the turnover of ring components, actin depolymerization, addition of new F-actin, myosin removal and addition, and cross-linker removal and addition were included. At the beginning, the G-actin pool was set empty for simplicity. Actin depolymerization was modeled to be stochastic, which removed an actin bead at the pointed end to the G-actin pool with a probability of once every second, considering that F-actin turnover was reported to occur in ∼1 min (Pelham and Chang, 2002). A new filament of randomly selected length was added to a random location along the ring with a probability of once every 10⁵ time steps if the G-actin pool had more than 100 monomers. If membrane-bound nodes were present, the barbed end of the added F-actin was tethered to a random node.

A simple turnover mechanism was modeled for myosin. If all the heads of a myosin molecule were unbound, it was removed and a new one was added to a random location along the ring with a rate r_t = 1/τ, where τ was the resident time of unbound myosins. For each model, we varied τ and measured the resultant average resident time of all myosins (bound and unbound). We report the resultant average resident times (Supplemental Table S1), which were close to 14 s, our experimentally measured resident time (Supplemental Figure S11), which is half of the previously reported value (Pelham and Chang, 2002; Clifford et al., 2008). To explore the role of myosin turnover, multiple simulations of each model were run with different values of τ. The particular values used to produce each figure shown are listed in Supplemental Table S1.

Similarly, to model cross-linker turnover, if both the ABD beads of a cross-linker were unbound, it was removed and a new one was added to a random location along the ring with a probability of once every 20 s (Laporte et al., 2012).

Protein binding force

If an actin bead and its binding partner (either a myosin head or a cross-linker ABD bead) were “bound” to each other at a given time step (see rules above for when they were considered bound), they exerted a spring-like force F_b = k_b (d – d₀) on each other, where k_b= 0.1 nN/nm was the force constant and d₀ = 5 nm was the relaxed distance.

Volume exclusion

To prevent the beads from overlapping with each other, if the distance d between any two beads was smaller thanr_off = 5 nm, they were pushed apart with a force F_V = k_V (r_off – d)²/(d – r_on)² to prevent them from approaching each other more closely than r_on = 4 nm, where k_V = 0.1 nN.

Membrane tethering

How tethering the ring to the membrane was modeled depended on the actomyosin configuration. In the node models, in which either F-actin barbed ends or unipolar myosin tails (or both) were tethered to the membrane-bound nodes, each node was modeled as a bead connected to 10 nearest-neighbor membrane beads determined at the beginning. If the distance d between a node and a tethering counterpart, either an actin barbed end, a unipolar myosin tail end, or a neighboring membrane bead, was larger than d_n = 20 nm, the pair were pulled closer to each other with a force F_n = k_n (d – d_n), where k_n = 0.2 nN/nm was the force constant. In the paired-unipolar myosin configuration, for simplicity the two tail-end beads were tethered to a small node including four additional nearest-neighbor membrane beads. In the other models, direct tethering of one membrane bead to actin and/or unipolar myosin was modeled. If the distance d between an actin bead and its membrane tethering counterpart was larger than d_t = 30 nm, the beads were pulled closer to each other with a force F_t = k_t (d – d_t), where k_t = 0.18 nN/nm was the force constant. If the distance d between a unipolar myosin tail-end bead and its membrane tethering counterpart was larger than d_my = 5 nm, the beads were pulled closer to each other with a force F_my =k_my(d – d_my), where k_my = 0.2 nN/nm was the force constant.

Cell wall and turgor pressure

Cell wall growth is needed to support ingression of the membrane, since the tension from the AMR is not sufficient to counter the effect of large turgor pressure (Proctor et al., 2012). Experiments have shown, however, that septum assembly slows fourfold (Proctor et al., 2012; Zhou et al., 2015) and becomes misshapen in the absence of the contractile ring (Swulius et al., 2018), suggesting that ring constriction guides septum assembly under normal conditions. For simplicity, the membrane was treated as squeezable and the wall was modeled as a semirigid layer that expanded inward following the membrane (Supplemental Figure S16). The net force from turgor pressure and the cell wall on the membrane was modeled to follow Hooke’s law: a membrane bead at a distance d from the wall surface was pushed by a force F_w = –k_w(d – d₀), where k_w = 0.05 pN/nm was the force constant and d₀ = 20 nm was the relaxed distance between the membrane and the wall. Previously, Zhou et al. (2015) and Thiyagarajan et al. (2015) proposed a tension-sensitive cell wall–growth model in which local cell wall growth occurs where the ring exerts force on the membrane. Similarly, to model cell wall growth, once every 10³ time steps, if the difference between d and d₀ was more than 0.1 nm (corresponding to a centripetal force of F_m = 0.005 pN) at a location, the wall moved inward 0.01 nm at the same location.

Note that because it is not currently known what force is required to initiate cell wall growth, this minimal centripetal force required to initiate cell wall synthesis (0.005 pN) was simply chosen as a value 20× smaller than the typical force from the ring (∼0.1 pN). To explore the role of this mechanosensitivity parameter, simulations were also run with much higher F_m values. We found that at F_m = 0.5 pN (increased 100 times), there was essentially no cell wall growth in the model where unipolar myosins were individually connected to the membrane (distributing the ring constriction force homogeneously), but in the model where nodes were present, cell wall growth did occur, but puckers still formed (Supplemental Figure S5). Therefore, puckers were consistently the result of force concentration at nodes, not an artifact of high mechanosensitivity.

Diffusion

To model thermal motion of the system, we introduced random forces on the beads. Each Cartesian component was generated following a Gaussian distribution using the Box–Muller transformation (Box and Muller, 1958). Each transformation converted two random numbers from a uniform 0–1 distribution, u₁ and u₂, into two random numbers of a Gaussian distribution:

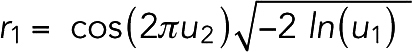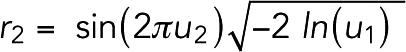For a system of N particles, 3N/2 transformations were used to generate 3N numbers. While a pseudorandom force can be generated by integrating a Gaussian random distribution with the time step, to reduce the computational cost, the random force was simply obtained by scaling the Gaussian random number with a force constant k_r. To determine k_r for actin, we ran simulations of free individual actin filaments in the presence of the random force and compared the simulated tangent correlation, cosθ, over distance L with the theoretical value 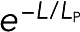, where L_P was the persistence length of the filament (Supplemental Figure S17). We found that the simulated tangent correlation matched the theory best at k_r = 20 pN. We then used the same k_r = 20 pN for the random force on myosins and cross-linkers, considering that they were also cytoplasmic proteins. In the absence of relevant experimental measurements, we arbitrarily chose k_r = 5 pN for the random force on the membrane.

Initial ring configuration

To determine a minimal list of basic components of the ring, our model started with an actomyosin ring 200 nm wide (dimension along the long axis of the cell) and 30 nm thick (dimension along the radial direction) inside a membrane 300 nm wide and 1000 nm in radius. The ring was composed of 400 F-actins of length chosen randomly in the range 270–810 nm (50–150 beads), resulting in ∼30–40 filaments per ring cross-section, well within the range of 14–60 filaments observed by ECT (Swulius et al., 2018). Eight hundred bipolar myosins were included. To study the role of cross-linkers, 600 α-actinins and 1000 fimbrins were added to the ring. Note that these protein concentrations were within the ranges reported experimentally (Wu and Pollard, 2005).

The same parameters for the membrane and cross-linkers were used for all 15 actomyosin configurations. The ring started 200 nm wide and 60 nm thick. Note that bundles of actomyosin peeled off the ring during constriction in Model 12, where actin filaments were directly tethered to the membrane (see Membrane tethering) and myosin was bipolar, and this was also observed in the ring that started 30 nm thick. Either 800 bipolar (Model 4, 8, or 12) or 1600 unipolar myosins (the other models) were present. The same ring configuration was used in simulations of the final working model, except that there were 1600 unipolar and 500 bipolar myosins coexisting in the system. In all modeled rings, F-actin existed in two opposing polarities.

Ring boundary

ECT showed that F-actins were strictly localized to the leading edge of the septum (Swulius et al., 2018). This might be the result of the ring tension or some physical barrier that was not distinguishable in the tomograms or both. The septin cytoskeletal proteins were thought to serve as such a barrier, as they form a pair of rings flanking the actomyosin ring during constriction (Dobbelaere and Barral, 2004). This proposal was challenged later, as the septin rings were reported to be dispensable for cytokinesis in budding yeast (Wloka et al., 2011). In addition, a barrier function of septins is unlikely in fission yeast, since the two rings do not contract during contraction of the actomyosin ring (Berlin et al., 2003; Tasto et al., 2003; Wu et al., 2003). Another barrier candidate, if required at all, could be the F-BAR protein Cdc15, as it was reported to form long filaments, likely wrapping around the division site several times (McDonald et al., 2015). This stable scaffold might restrict movement of partner proteins in the ring. To implement a diffusion barrier in our model, if a ring component bead moved a distance Δx outside the ring boundary, chosen to be 200 nm wide along the ring axis, it was simply pulled back with a force of k_brΔx, where k_br= 10 pN/nm was the force constant.

System dynamics

To track the evolution of the system, we used a simple molecular dynamics simulation. Specifically, the coordinate X(t) of each bead changed following the Langevin equation,

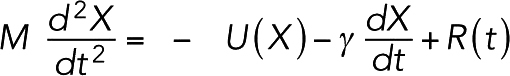where M is the mass of the bead, U the interaction potential, γ = 6 × 10^–6 Ns/m the damping constant, and R the random force on the bead (see Diffusion above). To select a large damping constant that made simulations computationally efficient, we ran simulations where a single myosin molecule walked on a fixed actin filament and characterized the myosin load-free velocity with respect to the damping constant (Supplemental Figure S18). A damping constant of γ = 6 × 10^–6 Ns/m was chosen to minimize computational cost without perturbing the myosin load-free velocity. Because we used the same damping constant for every bead in the system, the constant for a complex was proportional to the number of beads in the complex. Thus, a small node of ∼7 unipolar myosins (having ∼70 beads) experienced a damping constant of ∼420 pNs/mm, corresponding to a diffusion constant of ∼10 nm²/s, the experimental value reported by Vavylonis et al. (2008). Assuming the inertia of the bead was negligible, and thus M = 0, the displacement was simply a linear function of total force F:

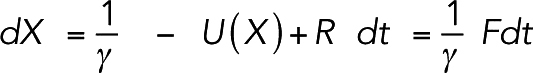To prevent a large force from moving a bead too far, we constrained the maximal displacement of any bead in any time step (corresponding to the maximal force F_max) to D_max= 0.01 nm. The displacement D of each bead was then calculated as

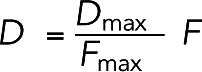Because the time step was not a constant in our simulations, the average time step was calculated at the end of each simulation, which fell in the range of 0.2 – 0.3 μs. Simulation codes were written in Fortran and the trajectories of each system were visualized using VMD (Visual Molecular Dynamics; Humphrey et al., 1996).

F-actin straightness

To compare actin filament straightness in the tomograms and the simulations, we defined “straightness” as the length of a straight line connecting the two ends L_{end–to–end} divided by the filament’s contour length, L_contour (Supplemental Figure S15E). Note that we did not compare persistence length, which is usually used to characterize free filaments not being pulled or acted upon by anything other than random thermal forces.

Actin–membrane distance

To compare the distances between the actin filaments and the membranes in the tomograms and the simulations, we defined the distance from an actin bead to the membrane as the smallest distance from the actin bead to any membrane bead.

Constriction rate

For simplicity, the constriction rate was calculated as the inward growth of the cell wall, Δr/Δt, averaged around its circumference, where Δr was the radial displacement of the cell wall leading edge and Δt was the duration of constriction.

Ring tension

To calculate the ring tension during constriction, first the ring radius R_r was calculated as the average distance from the actin beads to the cell axis. Then the ring tension was calculated as

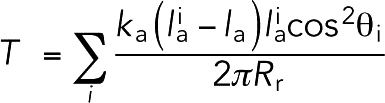where the sum was over all actin springs i that had length 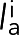greater than the relaxed length l_a, k_a was the actin spring constant, and θ_i was the angle by which spring i deviated from the circumferential direction. Note that including compressed springs (the ones with length 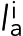smaller than the relaxed length l_a) in the equation resulted in an ∼30% reduction in ring tension.

Experimental procedures

Microscopy.

Mid–log phase cells were spotted on a 2% Agar pad supplemented with YES (yeast extract with supplements) media and observed under a custom-built spinning disk confocal microscope with an inverted Olympus IX-83,100×/1.4 plan-apo objective, a deep cooled Hamamatsu ORCA II –ER CCD camera, and a Yokogawa CSU:X1 spinning disk (Perkin–Elmer). A stack of 18–20 Z slices of Z step size 0.3 μm was collected every 2 min for an hour at 25°C using the Velocity software (Perkin–Elmer). Images were then rotated and cropped using the imageJ software to align cells, and 3D reconstruction was done using the Velocity software.

Fluorescence recovery after photobleaching.

Cells were mounted on a 2% agar pad supplemented with YES media and observed under a Leica TCS SP8 scanning confocal microscope with a 63× magnification, 1.4 numerical aperture oil-immersion objective. The experiments were performed at 25°C unless otherwise indicated. For excitation of GFP, we used a 488-nm argon laser. Images were collected with a scan speed of 400 Hz, 12× digital zoom, at 256 × 256 pixels. The laser intensity for photobleaching was adjusted to obtain ∼80% loss of fluorescence in the ∼0.2 × 0.2 μm circular bleached region of the cytokinetic ring. To allow rapid bleaching, we used a high laser intensity with 1–3 iterations of the bleaching scan. The filament’s contour length, L_contour, was collected before and after bleaching, using low laser intensities, and fluorescence recovery after photobleaching (FRAP) was monitored for 1.5–2 min. Data from the experiment were analyzed using ImageJ (National Institutes of Health, Bethesda, MD) with FRAP plug-in (www.embl.de/eamnet/frap/FRAP6.html) using the double normalization method (Phair et al., 2004). Normalized curves were fitted to single exponential functions to extract the mobile fraction and half-life.

Abbreviations used:

2D

two-dimensional

3D

three-dimensional

ABD

actin-binding domian

ADP

adenosine diphosphate

AMR

actomyosin ring

ATP

adenosine triphosphate

ECT

electron cryotomography

F-actin

filamentous actin

PDB

Protein Data Bank

YES

yeast extract with supplements