MS²PIP: a tool for MS/MS peak intensity prediction

Abstract

Motivation: Tandem mass spectrometry provides the means to match mass spectrometry signal observations with the chemical entities that generated them. The technology produces signal spectra that contain information about the chemical dissociation pattern of a peptide that was forced to fragment using methods like collision-induced dissociation. The ability to predict these MS² signals and to understand this fragmentation process is important for sensitive high-throughput proteomics research.

Results: We present a new tool called MS²PIP for predicting the intensity of the most important fragment ion signal peaks from a peptide sequence. MS²PIP pre-processes a large dataset with confident peptide-to-spectrum matches to facilitate data-driven model induction using a random forest regression learning algorithm. The intensity predictions of MS²PIP were evaluated on several independent evaluation sets and found to correlate significantly better with the observed fragment-ion intensities as compared with the current state-of-the-art PeptideART tool.

Availability: MS²PIP code is available for both training and predicting at http://compomics.com/.

Contact: sven.degroeve@UGent.be

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Mass spectrometry (MS) allows for high-throughput protein content measurements in samples by identifying and quantifying proteins in the form of digested peptide sequences. Tandem mass spectrometry (MS²) provides the means to match MS signal observations with the chemical entities that generated them. MS² produces signal spectra that contain information about the chemical dissociation pattern of a peptide that was forced to fragment using methods like ‘collision induced dissociation’ (CID). The signal peaks in an MS² spectrum indicate the presence of a peptide fragment ion with a specific mass. The intensity of a signal peak is dependent on a number of factors: the abundance of the peptide in the sample, the efficiency of the cleavage that generated the fragment, the proteotypicity of the fragment ion and other factors related to the peptide and the machine that generated the MS² spectrum (Barton and Whittaker, 2009).

Popular peptide identification tools such as Mascot (Perkins et al., 1999), OMSSA (Geer et al., 2004) and X!Tandem (Craig and Beavis, 2004) assume that MS² peaks for the most important fragment ions have a high intensity, and that fragment ions of different types have the same high intensity. Without an accurate model of the relationship between the amino acid composition of the peptide and the peak intensities in the corresponding MS² spectrum, these ad hoc approaches fail to match fragment ions for which low intensity peaks are expected to be observed. It has been shown that incorporating knowledge about this relationship between peak intensity and amino acid composition significantly improves peptide identification rates (Narasimhan et al., 2005; Sadygov et al., 2006; Tabb et al., 2007).

Despite the apparent need for accurate MS² signal peak intensity predictions from amino acid sequences, only few attempts have been published. A first approach, the MassAnalyzer tool (Zhang, 2004, 2005), was a deductive physicochemical model of peptide fragmentation. All parameters in the model were optimized on a dataset containing 8900 MS² spectra with confident peptide match (PSM). The authors showed that MassAnalyzer models MS² peak intensities more accurately as compared with ad hoc methods. At the same time, an inductive Bayesian decision tree approach was introduced (Elias et al., 2004). This research showed that a decision tree model representation is highly suitable for learning the diverse set of rules that govern peptide fragmentation. Their data-driven approach was able to visualize, from 27.000 PSMs, many of the known fragmentation rules and discovered several new ones. However, their approach does not model the peak intensities directly. Rather it models the probability of observing a certain fragment ion intensity. A similar study based on Bayesian neural networks was presented in Zhou et al. (2008) with a dataset of 13.900 PSMs.

Another inductive approach called PeptideART (Arnold et al., 2006) is based on feed-forward neural network representations. It implements an ensemble of neural networks that each models the most important fragment ion peak intensities in one multi-output feed-forward neural network. This method models the (normalized) peak intensities directly. The features used as input to the neural network are similar to ones suggested by Elias et al. The authors reported a systematic assessment of the accuracy of the current peptide MS/MS spectrum predictors for the most commonly used collision-induced dissociation instruments (Li et al., 2011). They found that PeptideART achieves generally higher accuracy on a wide range of proteomic datasets when trained on a dataset of 41.054 PSMs.

We show here that MS² signal peak intensity prediction can be significantly improved by exploiting the vast amount of PSM data that have been collected over the recent years. We constructed a dataset of 73.121 merged PSMs and present an inductive leaning approach for peak intensity regression that exploits all of the information contained in this large number of PSMs. Our approach still uses the non-linear decision tree representation for training the peak intensity prediction models. Both training and prediction procedures are implemented in a freely available tool called MS² Peak Intensity Prediction, or MS²PIP.

2 METHODS

2.1 Training dataset

A total of 3.965.456 OrbiTrap PSMs identified as true matches in 619 proteomics experiments (obtained by sampling human, mouse and rat as well as many plant and bacterial species) were queried from the ms-lims database (Helsens et al., 2010) of the proteome analysis and bioinformatics unit of Ghent University. All PSMs were scored as non-random matches by the Mascot search engine (versions ranging from 2.1.02 to 2.3.01) with allowed error rate estimates from 1 to 5%. We refer to this PSM data as the training dataset D. Signal peak intensities are normalized within each MS² spectrum such that we can compare these intensities between spectra. All peak intensities within a spectrum were divided by the sum of all peak intensities of that spectrum, i.e. normalization to total ion current (Degroeve et al., 2011). All intensities are log₂ transformed.

2.2 Evaluation datasets

Several publicly available MS² sample processing experiments, all performed on LTQ-OrbiTrap type instruments, were used for evaluating the intensity prediction models obtained from the training data. None of these data were generated by the Proteome Analysis and Bioinformatics Unit of Ghent University. The first set of processed samples was obtained from a study of the NCI funded Clinical Proteomic Technology Assessment for Cancer (CPTAC) Network (Paulovich et al., 2010). Herein, six digested yeast samples were analyzed by three different laboratories to generate the corresponding MS² spectra. For each laboratory, we make one evaluation dataset that contains all PSMs of the six proteomic experiments.

We will refer to these datasets as lab1, lab2 and lab3. The second set of processed samples originates from The Proteome Informatics Research Group (iPRG) of the Association of Biomolecular Resource Facilities and their 2009 study. This study used two different E. coli lysate samples, each processed as five technical replicates. We create two evaluation datasets, sample1 and sample2, each containing the respective PSMs for all five replicates.

All MS² spectra were searched with the Mascot peptide identification engine and post-processed by the Percolator PSM rescoring tool to produce PSMs with high confidence (FDR < 0.01). The number of PSMs in each evaluation dataset is shown in Table 1.

Table 1.

The number PSMs in the CPTAC and iPRG evaluation datasets

Dataset	Charge +2	Charge +3
Lab1	42 774	4435
Lab2	59 751	21 263
Lab3	42 174	15 808
Sample1	11 191	5114
Sample2	12 005	5428

2.3 Data processing

Our key idea is to partition the dataset D into disjoint subsets that represent regression learning tasks that are easier to solve by a machine learning method. This is possible by exploiting the vast amount of PSM training data available to us. As different PSM charge states c are known to fragment differently, dataset D is first partitioned based on the charge state of the PSM. In this research, we consider the most important charge states +2 and +3. We refer to these PSM datasets as D_c with c∈{+2,+3}. It is worth noting that the separate analysis of different peptide charge states has already been shown to be useful in identification results validation (Vaudel et al., 2011).

We take this one step further by partitioning each dataset D_c based on the peptide length l of the PSM. For this, we consider peptide lengths from 8 to 28 amino acids based on the typical lengths of identified peptides (Vandermarliere et al., 2013). As a result, we now have partitioned D into D_cl with c ∈ {+2,+3} and l ∈ [8,28]. As explained further, this will greatly simplify the representation of the PSMs by feature vectors, and therefore make it easier for a machine learning method to learn an accurate regression model.

To apply a machine learning method on the datasets D_cl, we need to compile each PSM into a feature vector and label that vector with a target for the regression. Table 2 lists the features we used to represent a PSM. These include previously described features (Elias et al., 2004) such as the mass-to-charge ratio of the peptide sequence and the two fragment ions as well as average values for different chemical properties of the amino acids in a peptide or fragment ion. Also, the amino acid composition is taken into account by counting the number of times each amino acid appears in the peptide (feature I_). The features (seq_<pos>_x) are new and can only be computed because we partitioned the training data based on the length l of the peptide. These features capture information from all positions in the amino acid sequence, not just from the positions in proximity to the cleavage site. For each position, we compute features that represent the presence of a specific, potentially modified amino acid. Similarly we compute features that contain the value of several chemical amino acid properties for each position in the peptide sequence.

Table 2.

Features used to represent the PSMs in datasets D_clf

Feature	Description
labeled	Set to 1 if the peptide has an n-terminal label, 0 otherwise
pep_mz	Computed mass value of the peptide sequence
ion_mz	Computed mass of the fragment ion f
ion_mz_other	Pep_mz minus ion_mz
avg_<chem>	Average of chemical property <chem> for all amino acids in the peptide
avg_<chem>_ion	Average of chemical property <chem> for all amino acids in the fragment ion f
I_	Number of occurrences of the amino acid <amino> in the peptide sequence
seq_<pos>_	Set to 1 if the amino acid at peptide sequence position <pos> is
seq_<pos>_<mod-a>	Set to 1 if the modified amino acid at peptide sequence position <pos> is
seq_<pos>_<chem>	The value of the chemical property <chem> of the amino acid at position <pos> in the peptide

Note: The different chemical properties <chem> are basicity, hydrophobicity, helicity and pI. The values are listed in Supplementary Table S1. The modified amino acids <mod-amino> in the training PSMs are C, K, M, N and R.

In this research, we build regression models for all the b_i, b++_i, b-H₂0_i, b-NH_3i, b++-H₂0_i, b++-NH_3i, y_i,y++_i, y-H₂0_i, y-NH_3i, y++-H₂0_i and y++-NH_3i fragment ions with i ranging from 1 to l-1 for a peptide of length l. We will refer to this set of fragment ions as frag(l). Each ion is searched for in the MS² spectra with a 0.8 Da error tolerance. If >1 signal peak is observed within the constructed error window, then the peak with the highest intensity is selected as the matching peak. For each fragment ion f ∈ frag(l), a training dataset D_clf is compiled that contains all PSMs with charge c and peptide length l and with the observed peak intensities for fragment ion f as targets for the regression. Just as for c and l, we here build separate models for each f ∈ frag(l).

Each dataset D_cl contains PSMs with the exact same peptide sequence and charge, but with different experimental MS² spectra. Instead of representing these PSMs as different feature vectors, we merged these spectra by computing the median intensity for each f ∈ frag(l) and computed only one feature vector from the merged PSMs. This reduces experiment induced intensity variance and limits the negative impact of outlying PSMs, i.e. PSMs not correctly identified by Mascot. This is similar to the spectrum averaging techniques used in spectral libraries (Lam et al., 2007).

To make spectrum merging meaningful, we removed all PSMs for which the peptide sequence is observed <10 times. This filter again reduces the impact of potentially incorrectly identified PSMs as such random matches are typically identified in only few experiments. Preferring to err on the side of caution, we assumed that many of these only occasionally observed identifications could be incorrect PSMs. The minimum threshold of 10 spectra identifying a peptide is selected as a balance between making the merging meaningful while still keeping enough PSM data for training the regression models. The number of non-redundant PSMs in each dataset D_cl is show in Table 3.

Table 3.

The number of (merged) PSMs used in each dataset D_cl

Peptide length	Charge +2	Charge +3
8	4972	40
9	6875	89
10	7627	155
11	7910	289
12	6855	355
13	5927	443
14	5131	615
15	4422	798
16	3633	951
17	2614	870
18	1900	895
19	1531	941
20	859	807
21	705	777
22	433	694
23	307	670
24	166	480
25	137	329
26	55	266
27	63	293
28	28	214
Total	62 150	10 971

Remark that our spectrum merging approach is a way of removing redundant PSMs from the datasets. In previous approaches, non-redundant sets of PSMs were obtained by selecting the match with the highest quality (typically implemented as selecting the PSM with the highest Mascot score). However, by merging the observed peak intensities for all observed PSMs, we try to exploit much more information from the 3.965.456 spectra in our PSM dataset.

2.4 Regression model induction

Signal peak intensity prediction models were induced from the compiled training datasets using the random forests (RF) regression method (Breiman, 2001). This algorithm computes an ensemble of ntree CART regression trees in which each tree is constructed from mtry randomly sampled features. A peak intensity prediction is then computed as the average of the outputs of the regression trees in the forest.

Let m be the number of features in a training dataset D_clf, then all combinations of ntree ∈ {10, 20, 40, 60, 100, 140, 200} and mtry ∈ {sqrt(m), m/4, m/3, m/2, m/1.5} are evaluated. The RF method uses an out-of-bag (oob) procedure that can be used to compute an unbiased estimate of the prediction performance. For each parameter combination, we induce a RF regression model and estimate the explained variance by computing the oob R² as the mean-squared error divided by the variance of the original observations and subtracted from one. We used the ‘randomForest’ R library version 4.6.7 from the Comprehensive R Archive Network (CRAN) as the RF implementation.

3 RESULTS

3.1 Training RF regression models

Table 3 shows the number of vectors for each dataset D_cl. There are many more experimental PSMs with charge +2 as compared with charge +3 PSMs. For charge +2 PSMs, the peptide length l = 11 is most likely to be observed, whereas for charge +3, this is l = 16. It is observed that training set sizes are different for the different regression tasks.

To investigate the regression target distribution in each dataset D_clf, we plotted the mean and standard deviation of this distribution for each dataset D_clf with f ∈ {b,y}. From this plot (Supplementary Fig. S1), we concluded that datasets D_clf with low mean intensity also have low variance. For these dataset, the signal peaks for fragment ion f are hardly ever observed, or they are in the noise. For these datasets, a baseline regression model that always predicts that no signal peak is observed will be hard to beat. So, for all datasets D_clf with a standard deviation of the regression target distribution smaller than 0.5, we do not induce an RF regression model but rather apply the baseline regression model.

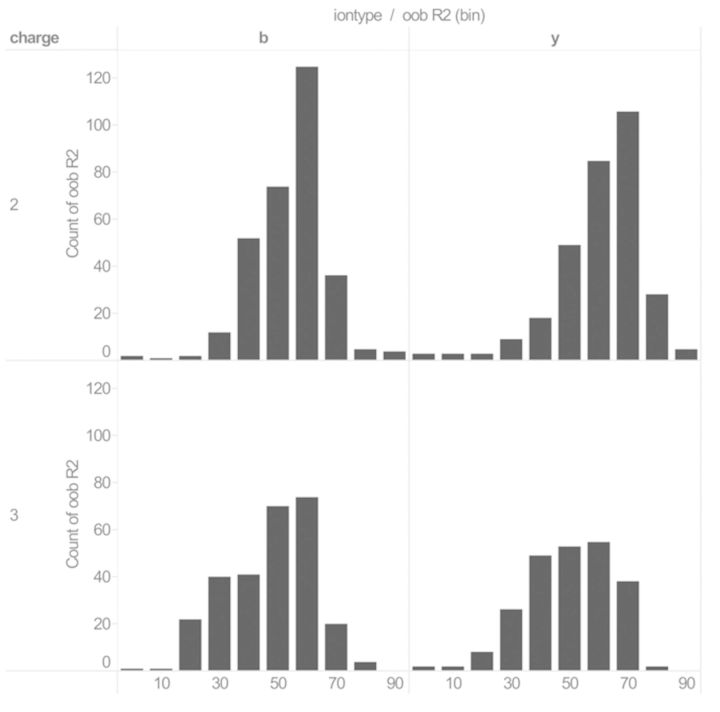
Figure 1 shows the distribution of the oob R² prediction performance results for b and y ion types. A more detailed visualization of the results can be found in Supplementary Figure S2. As known from previous research, learning charge +3 fragmentation rules is much harder than charge +2 rules. Because of this, the dataset D contains less charge +3 PSM examples, as it is harder for Mascot to assign the correct peptide in these cases. This is also reflected in the oob R² results, as RF regression, in general, performs less accurately on the +3 PSM datasets. Supplementary Figures S3a and S3b show detailed results for all the fragment ion types considered in this research. These plots show the accuracy of the prediction models differs significantly between the different ion types, charge states and peptide lengths. For less prominent ion types, such as b++-H20 and y++-NH3, the accuracy of the intensity predictions is low for all peptides. The prediction models computed for the b and y ions were most accurate. The ion types b++ and y++ could be modeled accurately only for the charge +3 peptides. We could also observe a clear difference in accuracy between the different peptide lengths for these ion types: models for peptides with length between 11 and 17 are significantly more accurate as those for length 8 or 9.

Fig. 1.

The distribution of the oob R² prediction performance results for the regression tasks D_clf, with f ∈{b,y}

3.2 Evaluating RF regression models

To estimate the true generalization performance of the trained RF regression models, they were applied to predict the fragment ion peak intensities in the PSMs of the evaluation datasets lab1, lab2, lab3, sample1 and sample2.

For each test, PSM with charge state c and peptide length l the corresponding models D_clf are applied to predict the signal peak intensities of the fragment ions. Next, the Pearson product-moment correlation coefficient (PCC) between the observed and the predicted signal intensities is computed. For this evaluation, we considered four sets of fragment ions as show in Table 4. For set1, we considered b and y ions only. For set2, set3 and set4 more fragment ions are added to the computation of the PPC values.

Table 4.

Different sets of fragment ions used for the evaluation of the performance of the peak intensity prediction models

Set	Fragment ions
Set1	bi, yi
Set2	bi, yi, b++i, y++i
Set3	bi, yi, b++i, y++i,, b-H2Oi, b-NH3i, y-H20i, y-NH3i
Set4	bi, yi, b++i, y++i,, b-H2Oi, b-NH3i, y-H20i, y-NH3i, b++-H2Oi, b++-NH3i, y++-H20i, y++-NH3i

The accuracy of the MS²PIP predictions is compared with those computed by PeptideART version 2.1. This implementation has no specific parameters to be set by the user. We did transform the predictions made by PeptideART to log₂-space.

Figure 2 shows the distribution of the PCC values computed from the b and y ion types (set1, Table 4) for the evaluation datasets lab1, lab2, lab3, sample1 and sample2. Results for the MS²PIP models are shown in dark gray, those for PeptideART in light gray. For the charge, +2 PSMs contributions are represented as the smaller bars. As concluded from the training datasets oob performance, prediction charge +2 PSMs models are more accurate than charge +3 models. Overall, the distributions clearly show that MS²PIP is significantly more accurate in predicting signal peak intensities for the PSMs considered in this research as compared with PeptideART.

Fig. 2.

The distribution of the PCC values computed from the b and y ion types (set1) for the evaluation datasets lab1, lab2, lab3, sample1 and sample2

Supplementary Figure S4 shows the results for all fragment ion sets from Table 4. The plot shows how MS²PIP consistently computes more accurate peak intensity predictions for these sets as compared with PeptideART. We also observe how the overall correlation between the observed and predicted fragmentation ion peaks for a spectrum decreases as more of the less prominent fragment ion types are included in the computation of the PPC.

In Supplementary Figure S5a–S5e, we plotted the PPC results for set1 as box-plots for each peptide length l and charge state c. Now the performance difference between PeptideART and MS²PIP becomes clearer. For both methods, predicting the peak intensities in the longer peptides (from ∼23 amino acids) is problematic for several evaluation sets. We observe this for both charge +2 and +3 peptides. However, for the shorter peptides (up to length 13), the MS²PIP models perform significantly better. This is somewhat surprising for the charge +3 models as these were trained relatively small datasets (Table 3). A final observation is that these conclusions are consistent for all evaluation sets.

4 CONCLUSIONS

MS²PIP is a tool that implements a number of new techniques for the induction of MS² signal peak intensity prediction models. First, following the conclusion made by (Elias et al., 2004) that decision tree representations are suitable for learning peptide fragmentation rules, MS²PIP applies a RF regression learning algorithm for constructing the prediction models. Second, the vast amount of available PSM data accumulated over the recent years allows MS²PIP to partition this PSM data to facilitate the construction of feature vectors from peptide sequences. Third, MS²PIP merges PSM data to reduce dataset sizes while still preserving the relevant intensity information contained in all PSMs.

The main conclusions we want to make from this research are the following. First, MS²PIP shows superior prediction performance for the fragment ion peak intensities considered in this research as compared with the neural network based PeptideART prediction tool. Second, MS²PIP and PeptideART both are significantly less accurate for the longer peptides, although MS²PIP is far more accurate than PeptideART for the smaller peptides. Third, the accuracy of the models differs significantly between the different fragment ion types. For less prominent ion types such as b++-H₂0 and y++-NH_3, the accuracy of the intensity predictions is low for both tools. The prediction models computed for the b and y ions were most accurate. The ion types b++ and y++ could be modeled accurately only for the charge +3 peptides.

Although additional research needs to be performed, we believe the main contribution of MS²PIP to the increased accuracy observed for MS² signal peak intensity prediction is the splitting of the PSM data based on charge state, peptide length and fragment ion type, making the learning task easier for the RF regression method. The observation that MS²PIP is far more accurate for the smaller peptides provides a strong indication for this statement.

In addition, our publicly available MS²PIP implementation allows for building peak intensity prediction models for all other types of fragment ions as well.

Funding: The seventh framework program of the European Union (Contract no. 262067- PRIME-XS) and by Ghent University (multidisciplinary research partnership ‘Bioinformatics: from nucleotides to networks’). IWT SBO grant ‘INSPECTOR’ (120025) (in part). Computations were performed on the Stevin Supercomputer Infrastructure at Ghent University, funded by Ghent University, the Hercules Foundation and the Flemish Government.

Conflicts of Interest: none declared.