Abstract
Motivation: The abundance of many transcripts changes significantly in response to a variety of molecular and environmental perturbations. A key question in this setting is as follows: what intermediate molecular perturbations gave rise to the observed transcriptional changes? Regulatory programs are not exclusively governed by transcriptional changes but also by protein abundance and post-translational modifications making direct causal inference from data difficult. However, biomedical research over the last decades has uncovered a plethora of causal signaling cascades that can be used to identify good candidates explaining a specific set of transcriptional changes.
Methods: We take a Bayesian approach to integrate gene expression profiling with a causal graph of molecular interactions constructed from prior biological knowledge. In addition, we define the biological context of a specific interaction by the corresponding Medical Subject Headings terms. The Bayesian network can be queried to suggest upstream regulators that can be causally linked to the altered expression profile.
Results: Our approach will treat candidate regulators in the right biological context preferentially, enables hierarchical exploration of resulting hypotheses and takes the complete network of causal relationships into account to arrive at the best set of upstream regulators. We demonstrate the power of our method on distinct biological datasets, namely response to dexamethasone treatment, stem cell differentiation and a neuropathic pain model. In all cases relevant biological insights could be validated.
Availability and implementation: Source code for the method is available upon request.
Contact: daniel.ziemek@pfizer.com
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
The abundance of many transcripts changes significantly in response to a variety of molecular and environmental perturbations. To understand the details of the transcriptional response, it is often useful to annotate the biological function of the changed transcripts using gene set enrichment methods. Ackermann and Strimmer (2009) give a comprehensive overview and Naeem et al. (2012) provide a recent performance assessment of many methods. However, a key question often remains: what intermediate molecular perturbations gave rise to the observed transcriptional changes? The situation is complicated by the fact that regulatory programs are not necessarily governed by transcriptional changes but also by protein abundance and post-translational modifications. As changes beyond the transcriptional level are rarely measured, direct inference of causal relationships is difficult and an active field of research. A number of statistical and network reconstruction methods have been used to identify potential gene regulatory networks directly from the gene expression profiles and large-scale datasets (Dhaeseleer et al., 2000; Schadt et al., 2005). Although these methods demonstrate great potential for deciphering mechanisms of regulation, they require a large number of expression profiles and genetic data. Moreover, determining the sign and direction of the causality can be challenging. Over the last decades, biomedical research has uncovered a plethora of causal signaling cascades. Such prior knowledge can be used to identify good candidates to explain a specific set of transcriptional changes and point to others that cannot be explained satisfactorily by current knowledge.
The use of prior network or pathway knowledge has received considerable attention in recent years. Emmert-Streib and Glazko (2011) provide a recent review. More closely related to our method, Pollard et al. (2005) developed an approach based on reasoning on structured collection of causal relationships to analyze the most likely regulators of expression changes derived from type 2 diabetes patients and recovered known key genes in diabetes and proposed new regulators. Chindelevitch et al. (2012) constructed a causal graph from a set of causal relationships extracted from the biomedical literature and introduced a scoring scheme to identify putative upstream regulators for any given input dataset based on the set of causal relationships encoded as the causal graph. Essentially, for each putative upstream regulator, the method makes predictions of the downstream transcriptional effects (upregulation or downregulation) using the causal relationships. The predictions are then compared with the observed data and based on the number of correct and incorrect predictions, a score is assigned to the upstream regulator. The statistical significance of the scores is measured using an analog of the Fisher’s exact test. Although this method is able to distinguish the upstream regulator whose associated transcripts have significantly different distribution form the background, it does not take the full topology of the network into consideration. More precisely, each regulator is considered in isolation and the joint distribution of the network is not taken into consideration. Moreover, the model makes no assumption on the applicability of the causal relations in the context under which the experiment is performed.
In this work, we construct a Bayesian network from the same knowledgebase as in Chindelevitch et al. (2012), consisting of a set of nearly 450 000 causal relations extracted from nearly 65 000 peer review PubMed full articles. The Bayesian network can be queried to suggest upstream regulators (hypotheses) that can be causally linked to the altered expression profile in a manner that takes the entire topology of the network as well as the context under which the experiment is performed into consideration. The noise in the observation is also taken into consideration directly.
Most methods integrating network data into the analysis process differ in at least one key point from our Bayesian approach, namely (i) the use of non-causal non-signed protein–protein interaction networks, (ii) the use of non-Bayesian approaches, (iii) a focus on identifying active subnetworks or enriched gene sets, but not the contextual prediction of upstream regulators active in a given experiment. A potential problem with our and related approaches is the availability of a suitable knowledgebase of causal relationships. Fortunately, public repositories are starting to appear. For our purposes, the OpenBEL portal (www.openbel.org) is the most relevant example. It provides an open-source framework to specify, parse and manipulate causal relationships and also offers a test corpus under a Creative Commons license of ∼70 000 causal statements manually extracted from 16 000 PubMed articles. The biological examples in this work rely on a licensed extended knowledgebase from commercial vendors, i.e. Ingenuity (www.ingenuity.com) and Selventa (www.selventa.com) that consists of about 450 000 statements. Selventa makes a subset of their knowledge base available at the OpenBEL site.
2 METHODS
2.1 Construction of the directed acyclic graph
In this section, we present the construction of a causal graph from causal relations extracted from the literature. We first need to introduce some notations and terminology used throughout the article. We use bold characters to denote vectors, upper case letters, such as X to denote a random variable and lower case letters such as x to denote an instantiation of the random variable.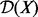 
denotes the domain of the random variable X. Subscripts are used to refer to individual random variables, whereas superscripts are used to distinguish specific values of a random variable. Pa(X) and Ch(X) denote the instantiated parents and the children of the node X, respectively. Finally, we use a negative subscript 
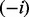to denote a vector whose i-th component is removed [e.g.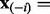 
].
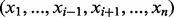We are concerned with biological entities and the causal relations between them; statements such as an increase in X lead to a decrease in Y. These statements are extracted from biomedical literature. Using these statements, we construct a signed causal graph where the set of nodes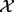 
consists of transcripts, proteins or compounds. An edge between nodes X and Y indicates the existence of causal relation between the source node X and the target node Y, whereas the sign of the edge specifies the direction of the regulation; 
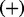if the regulation is positive, i.e. an increase in X leads to an increase in Y and 
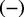if the regulation is negative, i.e an increase in X leads to a decrease in Y. Each edge in the causal network is annotated with a PubMed id and the corresponding medical subject headings (MeSH) terms. A regulator is a non-transcript node whose value is not known a priori. An evidence node is generally a transcript node whose value is determined from the gene expression data. However, other nodes in the network can also serve as evidence node if there is prior knowledge of their state.
The structure of the causal network reflects the dependencies and the direction of causality between the biological entities. In this work, we only consider the regulators that are directly connected to transcript nodes in the causal graph and leave longer paths as future work. As a consequence the graph is acyclic, but the remaining causal relationships in the network may still be applicable in a certain biological context only (e.g. organism, tissue, experimental conditions, etc.). Hence some of the edges of the network may not be applicable in the context of the experimental gene expression data. In the next section, we show how the gene expression data can be used to define the context of the experiment and determine the applicability of the remaining causal relations.
2.2 Defining the context
The causal relations (i.e edges) that are incident to nonzero transcript nodes of the network, as determined by the gene expression profile, provide a way to model the applicability of other edges of the network. We refer to these edges as the ‘nonzero’ network.
MeSH provide a comprehensive controlled database of terms that index the journal articles in PubMed. MeSH terms can serve to classify and model the context under which the causal relations are applicable. To define the context of the experiment, we performed an enrichment analysis to identify MeSH terms that the nonzero network is enriched with (see Supplementary Material for details). We used an False Discovery Rate (FDR) adjusted P-value of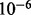 
as a cutoff threshold for determining the significant MeSH terms. To reduce the computation time, the significant MeSH terms were restricted to those with no more than 200 annotated edges in the network. An extra artificial MeSH term was also defined and every edge in the nonzero network was annotated to this MeSH term. As will be seen later, this is done to give the causal relations in the nonzero network a higher probability of being applicable. In the next section, we will show how these MeSH terms can be integrated into the network and used to infer the ‘applicability’ of individual causal relations.
2.3 Construction of the Bayesian network
2.3.1 Model
We construct a Bayesian network from the signed causal graph as follows. The nodes of the Bayesian network are discrete random variables. There are five classes of nodes in the network.
Transcript nodes
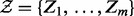: These are the transcripts whose values are observed from the gene expression data. These nodes have domain 
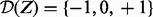where −1 represents downregulated, 0 represents not differentially expressed and 
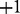represents upregulated.True state of the transcripts
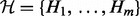: These nodes model the true state of the genes. The value of these nodes is not known a priori. These nodes are hidden and do not enter the computations explicitly. These nodes have domain 
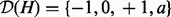where the additional state a stands for ‘ambiguous’. This state is necessary to model the conflict in the predictions for a node whose parents are in disagreement in the direction of regulation.Regulator nodes
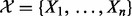: These are the proteins and the compounds in the network that potentially regulate the transcripts. Similar to transcript nodes, these nodes have domain 
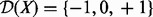, where −1 represents downregulated, 0 represents not regulated and 
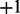represents upregulated.Applicability nodes
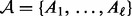: For each edge in the causal graph, an applicability node is added to the network. The nodes are connected to the corresponding true state nodes. The value of these nodes determines the applicability of the corresponding edge. These are binary nodes with domain 
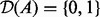with 0 representing ‘inapplicable’ and 1 representing ‘applicable’.Context nodes
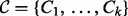: These correspond to the significant MeSH terms obtained from the enrichment analysis. The context nodes are connected to the applicability node of the edges that are annotated to the MeSH term. Similar to applicability nodes, these nodes are also binary with domain 
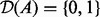with 0 representing ‘not in context’ and 1 representing ‘in context’.
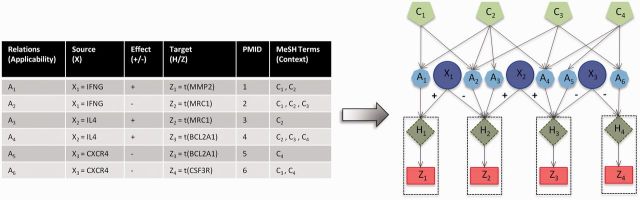
Figure 1 illustrates the Bayesian network. In Bauer et al. (2010), a somewhat similar model has been successfully applied to identify Gene Ontology terms.
Fig. 1.
Illustration of the Bayesian network: for each causal relation, an applicability node is constructed. The MeSH terms associated with the PubMed id of the article reporting the causal relation are used as context nodes that are then connected to the applicability node. To model the noise in observation, the causal relations are split into two steps: from the regulator to the true (hidden) state of the gene and from the hidden state of the gene to the observed value of the gene
2.3.2 Conditional probabilities
Let Ui denote either a regulator node Xi or an applicability node Ai. The Markov blanket of the node Ui is denoted by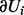 
and is defined to be the set of the parents of Ui together with its children and parents of its children. In a Bayesian network, the node Ui is independent of the rest of the random variables when conditioned on its Markov blanket, i.e. 
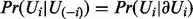. The Markov blanket of Ui can be partitioned as 
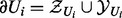, where 
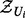represents the set of transcript (evidence) nodes along with their true state, and 
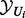the set of regulator, applicability or context nodes in 
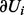. The transcript nodes and their corresponding true state nodes are collapsed into one node. Note that for each 
, 
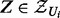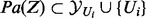. In particular, note that 
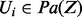. Let 
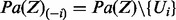. The probability distribution 
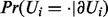is
 |
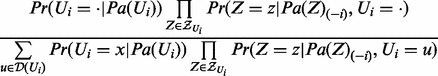(1) |
Note that in the aforementioned equation, all of the variables in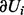 
are instantiated. We next define the conditional probabilities of the nodes that can be used to model the state propagation of the nodes using Equation (1).
Assume that Z is a transcript node with true state H and nZ number of parents. Assume that Pa(Z) is in the stat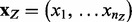e 
where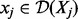 
. Let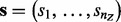 
be the signs of the corresponding edges. Then
 |
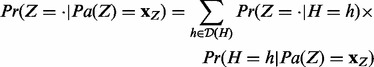(2) |
The conditional probabilities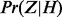 
are defined according to Table 1. These conditional probabilities are formulated to take the false-positive (α) and false-negative (β) rates of the gene expression data into consideration. In case where the true state of the gene is ambiguous, the conditional probabilities are assigned to be equally likely. The false-positive and false-negative rates of gene expression data are known estimated values. In our computations we used 
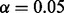and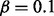 
. As later will be seen, the inference does not show sensitive dependence on α and β values.
Table. 1.
Conditional probability table of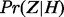 
|
|
|
|
|
|---|---|---|---|---|
|
|
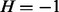
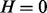
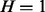
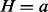
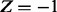
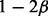
α | β | 1/3 |
|
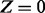
β |
|
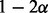
β | 1/3 |
|
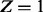
β | α |
|
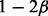
1/3 |
The Markov blanket of Z consists of a set of regulators and their corresponding applicability nodes. If an applicability node is assigned to 0, then the corresponding regulator is inapplicable and hence it should not have any influence on the value of Z (or H). Hence in defining the conditional probability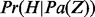 
, only the regulators whose corresponding applicability nodes are nonzero will be taken into consideration. Although this process will largely eliminate the ‘out of context’ edges, there is still a chance that the remaining edges are incorrect for reasons that are not being taken into consideration by the model. For this reason, each remaining edge is assigned a probability of being incorrect. This probability is assigned according to the value of Z, Pc if 
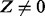and Pa if 
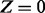. The dependence on Z is due to the fact that the applicable Markov blanket is largely determined by the context nodes, which in turn are obtained by enrichment analysis of the nonzero network. Hence an applicable causal relation that invokes a zero transcript is more likely to be incorrect for reasons not being considered by the model. The values of these parameters can be integrated in the inference algorithm (see Section 2.4) by introducing the corresponding parameter nodes in the network and discretizing the parameter values. However, this will substantially increase the computation time. Therefore, we choose reasonable values of 
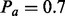and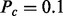 
and confirmed on our trial datasets that results were not sensitive to the exact choice.
The predicted H value is the vector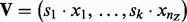 
. Let n1 and n2 be the number of 1 and −1 elements in the vector V and let 
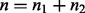be the total number of parents in nonzero sates. Define
 |
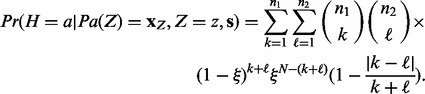(3) |
where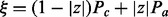 
. Here, we are combinatorially selecting k applicable edges for the parents predicting a positive value for H and 
applicable edges for the parents predicting a negative value for H. These edges each have probability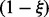 
of being correct. The last term of the sum is a measure of the disagreement in the value of H among the applicable parent nodes. Define
 |
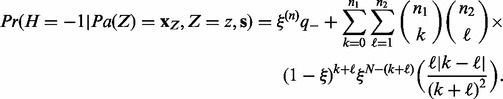(4) |
Similarly, define
 |
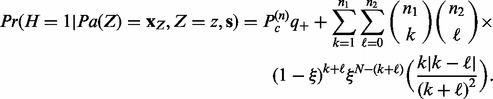(5) |
Here,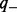 
and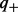 
are prior (background) probabilities of genes being upregulated or downregulated, which can be estimated using the gene expression data. Precisely, 
, 
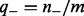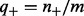where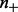 
and 
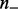represent the number of upregulated and downregulated genes in the expression data and m represents the total number of available genes in the network. The last two conditional probabilities in Equations (4) and (5) are obtained by scaling the probability of not being ambiguous (i.e. 
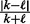) with the proportions of −1’s [i.e. 
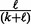] and 1’s [i.e. 
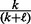], respectively. It is straightforward to show that the
 |
(6) |
Here,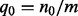 
is the prior probability of genes being not regulated, where 
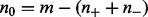. Intuitively, this means that the only way that the nonzero applicable parents can predict a zero state for H is when all the edges are incorrect, in which case the probability of a 0 true state is assigned according to the background model, i.e. q0.
If Xi is a regulator node, the prior probability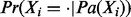 
is the same as the prior probability of the regulator and is defined by 
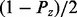, Pz and 
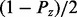for states −1, 0, and 1, respectively. Here, Pz denotes the prior probability of state 0 for the regulator. In our calculations, we used the 
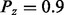. Intuitively, setting the prior probability of the state 0 for regulators to be high will impact the posterior probabilities in the same direction unless there exists substantial evidence to support the hypothesis that the regulator is active. If Xi is an applicability node with context parents say, 
in state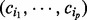 
, define
 |
(7) |
where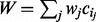 
. Here, wj is a set of weights assigned to the corresponding context node. In our calculations, we set the 
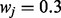. This is a desirable way for defining the conditional probability for two reasons. First, the probability of being in context increases as the number of nonzero parents increases. Second, this conditional probability has a transitional property: if the number of nonzero parents of an applicability node exceeds a certain limit, then the node value will be 1 with high probability.
Finally, for context nodes C, the conditional probability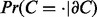 
is given by
 |
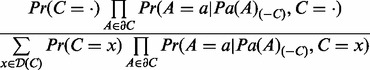(8) |
where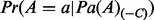 
, is defined by Equation (7) and the prior probability 
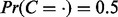. The state of artificially added context node is set to 1.
In the next section, we address the problem of inference from the Bayesian network.
2.4 Inference
Since exact inference in Bayesian networks are often impractical due to prohibitive time and memory demands, sampling techniques are commonly used for approximate inference. We wish to generate samples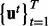 
from the joint probability distribution 
. Here,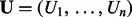 
represents the regulator (Xi), applicability (Ai) or context (Ci) nodes and 
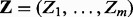represents the evidence (e.g. transcript) nodes. Note that the evidence node generally comprises the instantiated transcript nodes obtained from the gene expression data. However, the evidence node is not limited to transcripts only. For instance, if there is evidence that a certain regulator is active, or if a causal relation is inapplicable, the corresponding nodes can be treated as evidence nodes with fixed prespecified values. Using the generated samples, we can then approximate the posterior marginal 
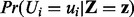of a given non-evidence node Ui by
 |
(9) |
where T denotes the total number of samples generated and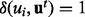 
if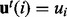 
and 0 otherwise. In our computations, we used Gibbs sampling, a Markov chain Monte Carlo method that is particularly well suited to sample the posterior distribution from a Bayesian network. All non-evidence nodes are first randomly initialized. The values of the nodes are then updated iteratively using Equations (1), (7) or (8) depending on the node type. When generating the tth sample for the random variable Ui, we use 
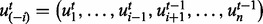to instantiate 
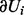, where the random variables U1 to 
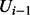are instantiated with their tth sample, and the random variables from 
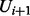to Un are instantiated with their previous sample, i.e. 
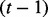th sample. Algorithm 1 summarizes the inference procedure.
It can be shown that the sequence of samples comprises a Markov chain whose stationary distribution is sought after distribution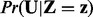 
. We generated samples from the joint distribution by running multiple chains of the Gibbs sampler in parallel. Moreover, to investigate the existence of alternative regulators, we can run the simulations in an iterative manner as follows. In the first iteration, the inference is performed and top regulators are selected. Next, the simulations are performed again while setting some or all of the previously selected regulators to 0. This iterative process can be continued for either a specific number of times or until no further regulators are produced.
Input : The Bayesian network over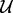 
and the evidence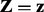 
Output : A set of samples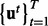 
Initialization : Assign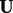 
to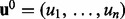 
where ui selected uniformly at random from the state space of the random variables.
for
to
T
do
for
tondo
generate a sample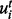 
from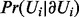 
;
set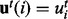 
;
end
end
Algorithm 1: Gibbs sampler
3 RESULTS
3.1 Simulated data
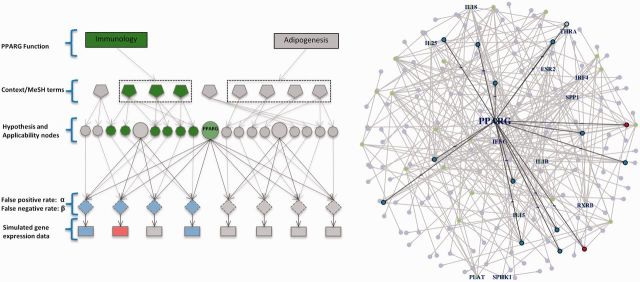
To test the performance of our method, we simulated data by perturbing a single regulator in a specific context. In our test, we used PPARG as an example of a protein with two distinct biological functions, i.e. (i) its role in immune system regulation and (ii) its function as a key enzyme of lipid metabolism and adipogenesis (Tontonoz and Spiegelman, 2008; Zieleniak et al., 2008). In each context, we selected related MeSH terms and the corresponding causal relations and then simulated the gene expression data at the false-positive rate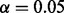 
and false-negative rate 
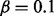, assuming upregulation of PPARG. Figure 2 illustrates the simulation. For each simulated input set, our method correctly predicted PPARG as the only upstream cause of the observed variation with high probability. Moreover, the MeSH enrichment analysis and the subsequent inference correctly recover the majority of the MeSH terms. In contrast, there were no significant regulators reported when generating random expression profiles of the same size. We also assessed the sensitivity of the predictions to parameters α and β by simulating gene expression data using different values of these parameters. We selected a grid 
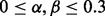with step size 0.02, simulating a total of 256 datasets. The case 
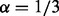and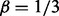 
corresponds to random data generation (see Table 1). In prediction step, the fixed values 
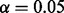and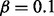 
were used. The simulation was performed in adipogenesis context where more genes (171) are downstream of PPARG. In 253 cases of 256 simulation runs, PPARG was selected as the top ranking regulator with high probability and in 201 of these cases PPARG was the only predicted regulator. Other cases included 1 (50 cases), 2 (3 cases) or 3 (2 cases) extra predicted regulators, mostly with low probabilities. See Supplementary Material for a heat map of false positives.
Fig. 2.
Figure on the left: simulation of gene expression by perturbing PPARG. A context is first selected and the associated MeSH terms are turned on. The corresponding applicability nodes and the associated causal relations are selected and the gene expression data is simulated at the false-positive rate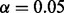 
and false-negative rate 
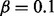. Figure on the right: part of the actual network of PPARG. Proteins and chemicals are colored in green. Simulated gene values are colored in blue for downregulated genes, red for upregulated genes and light blue for not regulated genes
3.2 Dexamethasone: recovering a known mode-of-action
To characterize the performance of our method on biological data, we analyzed an experiment of Stojadinovic et al. (2007) in which primary human keratinocytes were treated with dexamethasone. The objective of the original study was to investigate the detailed mechanisms of glucocorticoid receptor signaling in skin cells. The authors particularly highlight suppression of interferon gamma (IFNG) and suppression of transforming growth factor beta (TGFB) among the prominent pathways affected. A significant indication of the performance of our method is the concordance of the top regulators with the conclusions from the original study (Table 2). The primary experimental perturbation, dexamethasone, ranked highest followed by decreased lipopolysaccharide, a molecule commonly used experimentally to induce inflammation perhaps a surrogate for the known glucocorticoid effect of decreased inflammation. Note that decreased IFNG and decreased TGFB1 hypotheses follow closely among the top ranking regulators. Interestingly, glucocorticoid receptor itself (NR3C1) did not appear as a significant high ranking regulator in the first iteration. However, after accepting the dexamethasone as correct but wishing to find the molecule through which it asserts its function, we removed dexamethasone from consideration and ran a subsequent iteration. The activation of NR3C1, the primary target of dexamethasone, was correctly identified as the top regulator in this iteration. This exemplifies the possibility of using our methods in iterations to uncover the layers of signaling.
Table. 2.
Top regulators selected by BayesCRE in primary human keratinocytes treated with dexamethasone
| Regulator | Regulation | Probability | Iteration |
|---|---|---|---|
| Dexamethasone | Up | 0.955 | 1 |
| Lipopolysaccharide | Down | 0.948 | 1 |
| TGFB1 | Down | 0.912 | 1 |
| TNF | Down | 0.886 | 1 |
| IFNG | Down | 0.815 | 1 |
| CD 437 | Up | 0.659 | 1 |
| TP53 | Down | 0.656 | 1 |
| Retinoic acid | Down | 0.654 | 1 |
| RHOA | Up | 0.602 | 1 |
| NR3C1 | Up | 0.568 | 2 |
| Decitabine | Down | 0.563 | 1 |
| Hydrocortisone | Up | 0.538 | 1 |
| IL6 | Down | 0.538 | 1 |
| TP63 | Down | 0.518 | 1 |
| MYC | Up | 0.503 | 1 |
| Camptothecin | Down | 0.488 | 2 |
Note: Top regulators selected by BayesCRE as the upstream cause of the observed variation in the gene expression data from primary human keratinocytes untreated and treated with dexamethasone.
The inferred enriched MeSH terms are also in agreement with the biological context of the regulators including terms such as dexamethsone and glucocorticoid. Instances where MeSH terms could provide additional context information include the MeSH terms for TGFB1 where the most enriched term is ‘Dermis/drug effects’ consistent with the skin cell model used in the experiment.
3.3 In vivo model of pain
To further evaluate the ability of our method to identify transcriptional regulators of biological processes, we used a more complex dataset with no single perturbation. Costigan et al. (2009) undertook gene expression studies of dorsal horn tissue from the spinal cord of rats subjected to a surgical procedure designed to induce neuropathic pain. From this the authors hypothesized and subsequently experimentally confirmed that IFNG is required for the development of neuropathic pain. The raw data from this study were Robust Multichip Average normalized and limma was used to identify differentially expressed genes. Genes were considered significant if their FDR corrected P-value was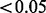 
(204 genes upregulated and 3 genes downregulated). Our method determined IFNG+ to have the greatest probability (0.958) and to correctly explain 48 of the gene expression changes—clearly confirming one validated molecular key aspect of the experiment.
3.4 Drivers of stem cell differentiation
Finally, we assessed our method by analyzing an in vitro differentiation model of pancreatic beta cell development (D’Amour et al., 2006; Gutteridge et al., 2013). At the time points analyzed (day 8 and day 11) the cells transition from NEUROG3+ pancreatic progenitor cells to NKX2-2+ endocrine cells capable of further differentiation into fully functional insulin producing cells upon implantation into mice (Kroon et al., 2008). The top causal regulators for this transition are shown in Table 3. The gene identified as the top ranked regulator, NEUROG3, is a bHLH family transcription factor that is known to be intimately involved in the development of the pancreatic endocrine cell lineage (Gradwohl et al., 2000; Rukstalis and Habener, 2009) and is itself strongly expressed at these time points. The MesH terms associated with NEUROG3 include ‘Pancreatic Ducts/embryology’ confirming the link to pancreatic development. Alongside NEUROG3, our method also highlights Beta-estradiol signaling as the second highest ranked regulator. Beta-estradiol is a hormone that is known to have an important role in both pancreatic function (Tiano and Mauvais-Jarvis, 2012) and the survival of insulin producing beta cells in particular (Nadal et al., 2009). In ranking these two regulators at the top, our method clearly shows that it is able to identify several of the key regulators of this complex and clinically important developmental process.
Table 3.
Top regulators selected by BayesCRE in Viacyte hESC directed differentiation cell model
| Regulator | Regulation | Probability | Iteration |
|---|---|---|---|
| NEUROG3 | Up | 0.968 | 1 |
| Beta estradiol | Up | 0.954 | 1 |
| CDKN1A | Down | 0.902 | 1 |
| THAP1 | Down | 0.794 | 1 |
| Retinoic acid | Down | 0.781 | 1 |
| IFNG | Up | 0.772 | 1 |
| TP53 | Down | 0.762 | 1 |
| TNF | Up | 0.707 | 1 |
| Calcitriol | Down | 0.625 | 1 |
| 1-alpha, 25-dihydroxy vitamin D3 | Down | 0.618 | 1 |
| NEUROD6 | Down | 0.617 | 1 |
| IL6 | Up | 0.616 | 1 |
| PDGF Complex family Hs | Up | 0.598 | 1 |
Note: Top regulators selected by BayesCRE as the upstream cause of the observed variation in the gene expression data from Viacyte hESC directed differentiation cell model.
As well as entities with well-established links to pancreatic development, the results also point toward perhaps surprising roles for several inflammatory cytokines including IFNG, TNF and IL6, upregulation of which are all proposed as causal drivers during this stage of development. IFNG has long been known to have a role, particularly in the context of type 1 diabetes, in modulating beta cell function (Nielsen et al., 2001), and the role of IL6 in pancreas function is supported by an emerging body of literature (da Silva Krause et al., 2012). The MeSH terms associated with IL6 include several relating to trypsin/chymotrypsin inhibition, which is a function of the pancreas. Recent experiments made directly on the model used here have shown a role for IL6 in the in vitro development of pancreatic endocrine cells (Gutteridge et al., 2013) confirming the BayesCRE prediction.
Interestingly IFNG is selected as a top regulator in all three experiments (upregulated in the model of pain and stem cell differentiation and downregulated in dexamethasone). In each case, the inferred MeSH term provides information on the context of the experiment. In the case of the dexamethasone, ‘Dexamethasone/antagonists & inhibitors’ is one of the top inferred MeSH terms, clearly distinguishing the experiment. In the case of stem cell differentiation, MeSH terms include ‘diabetes mellitus’ as well as ‘insulin like growth factor’ and ‘adrenomedullin’, indicating the association with beta cell differentiation and pancreas. These terms do not appear in other experiments. In the case of the model of pain, the inferred IFNG associated MeSH term is mostly related to IFNG function as an immune mediator. This is expected, given that the model of pain is a more generic whole animal system with no single obvious point of intervention.
4 DISCUSSION
In this article, we present a Bayesian methodology capable of identifying specific, plausible and testable biological hypothesis consistent with the observed gene expression data. We do this by reasoning over a massive knowledge base of prior biological knowledge extracted from the literature. Our method is an extension of the approach developed by Chindelevitch et al. (2012). There, the statistical significance of upstream regulators is tested in isolation, i.e. the existence of alternative regulators is not taken into consideration when assessing the significance. Our method generalizes this by constructing a Bayesian network from the knowledge base and considering the joint probability distribution of the possible molecular drivers of the observed expression profile (see Supplementary Material for benchmark results). Additionally, our new method models the context of the experiment by introducing the enriched MeSH terms of the network of differentially expressed genes as nodes in the Bayesian network. This will significantly remove the noise and redundancy in the network.
In conclusion, we find that our new method is well able to identify the key regulators in simulated and actual biological data. The nature of the output is well suited for the direct proposal of novel testable hypotheses, such as a role for IL6 of endocrine pancreas development or the causal aspect of IFNG in a system as noisy as a surgical in vivo model of pain. We are currently pursuing an extension of our method that will integrate higher-level causal drivers in the network. Finally, our method provides a natural framework for integrating omic-scale dataset with prior biological knowledge to identify concise, coherent and testable biological hypothesis.
Supplementary Material
ACKNOWLEDGEMENTS
The authors wish to thank Dr. Krzysztof Grzeda for helpful discussions and Ami Khandeshi for supporting the conversion of BEL networks from the OpenBEL.org website.
Funding: All authors were funded (as employees or contractors) by Pfizer, Inc.
Conflict of Interest: none declared.
REFERENCES
- Ackermann M, Strimmer K. A general modular framework for gene set enrichment analysis. BMC Bioinformatics. 2009;10:47. doi: 10.1186/1471-2105-10-47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer S, et al. Going Bayesian: model-based gene set analysis of genome-scale data. Nucleic Acids Res. 2010;38:3523–3532. doi: 10.1093/nar/gkq045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chindelevitch L, et al. Causal reasoning on biological networks: interpreting transcriptional changes. Bioinformatics. 2012;28:1114–1121. doi: 10.1093/bioinformatics/bts090. [DOI] [PubMed] [Google Scholar]
- Costigan M, et al. T-cell infiltration and signaling in the adult dorsal spinal cord is a major contributor to neuropathic pain-like hypersensitivity. J. Neurosci. 2009;29:14415–14422. doi: 10.1523/JNEUROSCI.4569-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- da Silva Krause M, et al. Physiological concentrations of interleukin-6 directly promote insulin secretion, signal transduction, nitric oxide release, and redox status in a clonal pancreatic beta-cell line and mouse islets. J. Endocrinol. 2012;214:301–311. doi: 10.1530/JOE-12-0223. [DOI] [PubMed] [Google Scholar]
- D’Amour KA, et al. Production of pancreatic hormone-expressing endocrine cells from human embryonic stem cells. Nat. Biotechnol. 2006;24:1392–1401. doi: 10.1038/nbt1259. [DOI] [PubMed] [Google Scholar]
- Dhaeseleer P, et al. Genetic network inference: from co-expression clustering to reverse engineering. Bioinformatics. 2000;16:707–726. doi: 10.1093/bioinformatics/16.8.707. [DOI] [PubMed] [Google Scholar]
- Emmert-Streib F, Glazko GV. Pathway analysis of expression data: deciphering functional building blocks of complex diseases. PLoS Comput. Biol. 2011;7:e1002053. doi: 10.1371/journal.pcbi.1002053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gradwohl G, et al. Neurogenin3 is required for the development of the four endocrine cell lineages of the pancreas. Proc. Natl Acad. Sci. USA. 2000;97:1607–1611. doi: 10.1073/pnas.97.4.1607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutteridge A, et al. Novel pancreatic endocrine maturation pathways identified by genomic profiling and causal reasoning. PLoS One. 2013;8:e56024. doi: 10.1371/journal.pone.0056024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kroon E, et al. Pancreatic endoderm derived from human embryonic stem cells generates glucose-responsive insulin-secreting cells in vivo. Nat. Biotechnol. 2008;26:443–452. doi: 10.1038/nbt1393. [DOI] [PubMed] [Google Scholar]
- Nadal A, et al. The role of oestrogens in the adaptation of islets to insulin resistance. J. Physiol. 2009;587(Pt 21):5031–5037. doi: 10.1113/jphysiol.2009.177188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naeem H, et al. Rigorous assessment of gene set enrichment tests. Bioinformatics. 2012;28:1480–1486. doi: 10.1093/bioinformatics/bts164. [DOI] [PubMed] [Google Scholar]
- Nielsen JH, et al. Regulation of beta-cell mass by hormones and growth factors. Diabetes. 2001;50(Suppl 1):S25–S29. doi: 10.2337/diabetes.50.2007.s25. [DOI] [PubMed] [Google Scholar]
- Pollard J, et al. A computational model to define the molecular causes of type 2 diabetes mellitus. Diabetes Technol. Ther. 2005;7:323–336. doi: 10.1089/dia.2005.7.323. [DOI] [PubMed] [Google Scholar]
- Rukstalis JM, Habener JF. Neurogenin3: a master regulator of pancreatic islet differentiation and regeneration. Islets. 2009;1:177–184. doi: 10.4161/isl.1.3.9877. [DOI] [PubMed] [Google Scholar]
- Schadt EE, et al. An integrative genomics approach to infer causal associations between gene expression and disease. Nat. Genet. 2005;37:710–717. doi: 10.1038/ng1589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stojadinovic O, et al. Novel genomic effects of glucocorticoids in epidermal keratinocytes: inhibition of apoptosis, interferon-gamma pathway, and wound healing along with promotion of terminal differentiation. J. Biol. Chem. 2007;282:4021–4034. doi: 10.1074/jbc.M606262200. [DOI] [PubMed] [Google Scholar]
- Tiano JP, Mauvais-Jarvis F. Importance of oestrogen receptors to preserve functional beta-cell mass in diabetes. Nat. Rev. Endocrinol. 2012;8:342–351. doi: 10.1038/nrendo.2011.242. [DOI] [PubMed] [Google Scholar]
- Tontonoz P, Spiegelman BM. Fat and beyond: the diverse biology of PPARgamma. Annu. Rev. Biochem. 2008;77:289–312. doi: 10.1146/annurev.biochem.77.061307.091829. [DOI] [PubMed] [Google Scholar]
- Zieleniak A, et al. Structure and physiological functions of the human peroxisome proliferator-activated receptor gamma. Arch. Immunol. Ther. Exp. (Warsz) 2008;56:331–345. doi: 10.1007/s00005-008-0037-y. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.