Optical coherence elastography for evaluating customized riboflavin/UV-A corneal collagen crosslinking

Abstract.

UV-induced collagen cross-linking is a promising treatment for keratoconus that stiffens corneal tissue and prevents further degeneration. Since keratoconus is generally localized, the efficacy of collagen cross-linking (CXL) treatments could be improved by stiffening only the weakened parts of the cornea. Here, we demonstrate that optical coherence elastography (OCE) can spatially resolve transverse variations in corneal stiffness. A short duration ($\le 1\mathrm{ms}$) focused air-pulse induced low amplitude ($\le 10\mu \mathrm{m}$) deformations in the samples that were detected using a phase-stabilized optical coherence tomography system. A two-dimensional map of material stiffness was generated by measuring the damped natural frequency (DNF) of the air-pulse induced response at various transverse locations of a heterogeneous phantom mimicking a customized CXL treatment. After validation on the phantoms, similar OCE measurements were made on spatially selective CXL-treated in situ rabbit corneas. The results showed that this technique was able to clearly distinguish the untreated and CXL-treated regions of the cornea, where CXL increased the DNF of the cornea by $\sim 51\%$. Due to the noncontact nature and minimal excitation force, this technique may be valuable for in vivo assessments of corneal biomechanical properties.

1. Introduction

The cornea is a critical component of vision because it provides $\sim 2/3$ of the total refracting power of the eye. Due to its shape and function, the biomechanical properties of the cornea are inherently tied to ocular health and visual performance.¹ Keratoconus can alter the biomechanical properties of cornea and cause conical deformation of the eye, reducing visual acuity or even causing blindness.² Riboflavin/UV-A corneal collagen cross-linking (CXL) is a clinical treatment for keratoconus that increases corneal stiffness and thereby defers further degeneration.^3,4 The current clinical CXL treatment protocol is uniform across the central cornea, despite diseased tissue localization.⁵ This is partly due to the inherent difficulty in quantifying corneal tissue properties and the inability of existing techniques to quantify spatial variations in corneal mechanical properties. Moreover, there is uncertainty about what factors contribute to variations in individual treatment responses. For example, disease dependent variations in tissue thickness or biochemical composition of tissues may be important determinants of treatment outcomes. An optimal treatment would consider individual pre-existing biomechanical properties and would incorporate the effects of the CXL treatment itself to produce more consistent, predictable, and desirable outcomes.⁵ Preliminary results from customized CXL treatments have shown promise and further demonstrate the need for a technique to accurately and noninvasively measure spatial variations in corneal biomechanical properties.⁶

Several devices and techniques have been proposed to assess the biomechanical properties of the cornea. The ocular response analyzer (Reichert Inc.)⁷ and CorVis ST (OCULUS Optikgeräte GmbH)⁸ are commercially available clinical devices that can measure differences in the biomechanical properties between healthy and keratoconic corneas.⁹ However, there is conflicting evidence on whether they can detect stiffness changes in the cornea after the CXL treatment,^10–13 and the large displacement amplitudes limit the ability of these techniques to resolve minute variations in spatial stiffness. Brillouin microscopy is a noninvasive confocal imaging technique capable of providing depth-resolved maps of the Brillouin frequency shift in the cornea.^14,15 While ocular applications of Brillouin microscopy are promising, it is still a challenge to quantitatively relate the observed Brillouin scattering phenomena to conventional material parameters, such as Young’s modulus. Elastography is a technique for obtaining the biomechanical properties of tissue by imaging externally induced displacements. Magnetic resonance elastography¹⁶ and ultrasound elastography¹⁷ are clinically useful tools for detecting various pathologies, but are not generally used for small and thin samples (e.g., cornea) because of their contact-based excitation, limited spatial resolution, and relatively large displacement amplitudes required for obtaining a detectable signal.

Optical coherence tomography (OCT) is a well-established imaging modality that can provide depth-resolved micrometer-scale structural images of tissues and has become a staple in ophthalmological applications due to its high resolution, rapid acquisition, and noninvasive imaging.^18,19 Naturally, functional extensions of OCT have been developed, and polarization-sensitive OCT (PS-OCT), in particular, provides robust structural information about the collagen organization in the cornea, which in turn could serve as a basis for detecting corneal diseases and evaluating CXL treatment outcomes.^20,21 However, PS-OCT cannot provide direct measurements of corneal biomechanical properties.

OCT-based elastography, termed optical coherence elastography (OCE), is a rapidly emerging technique for obtaining the biomechanical properties of tissues noninvasively.^22,23 Because OCE utilizes OCT for detecting displacements, OCE can obtain the biomechanical properties of tissues with micrometer-scale spatial resolution. Moreover, analyzing the phase of the complex OCT signal has enabled nanometer-scale displacement sensitivity.²⁴ Combining OCT with noncontact excitation, such as photothermal stimulation,²⁵ audio frequency excitation,²⁶ and mechanical loading with an air puff,²⁷ has enabled noncontact characterization of corneal biomechanical properties. To overcome the limitations of existing techniques (e.g., millimeter scale tissue displacements) and to spatially resolve material properties in vivo, we have developed a micro air-pulse stimulation technique that is capable of delivering a localized short duration ($\le 1\mathrm{ms}$) air-pulse to induce small amplitude (micrometer-scale) displacements in tissue.²⁸

While the local mechanical anisotropy^29–32 and microstructure³³ of the cornea have been studied previously, there have been limited investigations that have quantified the spatial elasticity heterogeneity of the cornea,^34,35 particularly after CXL treatments.^36–39 Most other techniques are either destructive or contact-based, limiting their use for in vivo investigations. A noncontact technique that can obtain the local biomechanical properties of the cornea would overcome these limitations and provide a deeper understanding of the changes in local corneal biomechanical properties due to diseases and/or therapeutic interventions, which in turn could provide a basis for customized CXL treatments.

Our previous work has utilized the propagation of an elastic wave to quantify tissue mechanical properties.^32,39–41 However, the spatial resolution is limited due to the relatively long wavelength of the elastic wave (order of mm). Therefore, we propose the use of a cofocused OCE technique^42,43 to measure local corneal biomechanical properties. In this work, we have utilized micro air-pulse induced deformations to spatially characterize the biomechanical properties of partially CXL-treated corneas. The low-amplitude (micrometer-scale) displacements were detected with a home-built phase-stabilized swept source optical coherence tomography (PhS-SSOCT) system, and the relaxation process of the local deformations was fitted to a simple kinematic model to quantify the damped natural frequency (DNF). The DNF is well correlated with Young’s modulus,^44,45 and thus, was mapped to reveal the localized stiffness of the corneas. The primary aim of this work is to evaluate the efficacy of air-pulse OCE at measuring spatial variations in stiffness as a technique for planning and evaluating spatially selective (i.e., customized) CXL treatments. We demonstrate that air-pulse OCE can noninvasively characterize spatial variations in soft-tissue stiffness to evaluate the effects of custom CXL treatments on local corneal biomechanical properties, and we describe a kinematic model linking the dynamic tissue response observed during OCE imaging, as quantified by the DNF, to the elastic modulus.

2. Methods

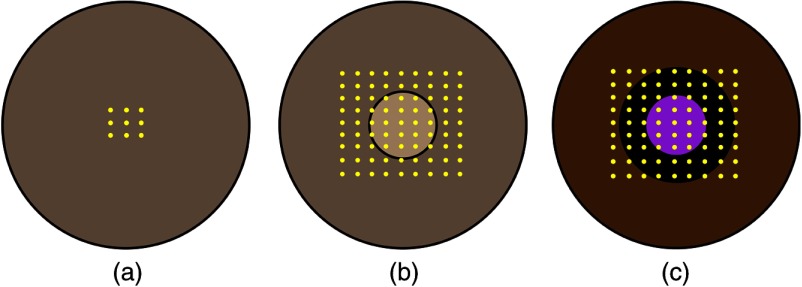
Preliminary experiments were conducted on tissue-mimicking agar phantoms to determine the feasibility of utilizing air-pulse OCE to spatially map the biomechanical properties of the cornea. Homogeneous agar (Becton, Dickinson and Company, New Jersey) phantoms of various concentrations (1%, 1.5%, and 2% w/w) were made by standard methods and cast in regular culture dishes with a diameter of 50 mm and height of 11 mm.⁴⁶ OCE measurements ($n=21$ for each position) were made every 1.5 mm over a $3\mathrm{mm}\times 3\mathrm{mm}$ central region on the homogeneous phantoms as shown in Fig. 1(a). Here, a single OCE measurement is defined as an air-pulse excitation and subsequent OCE measurement, which was an M-mode image. Twenty-one measurements were made at each position to ensure a reasonable average measurement of the regional stiffness. For each OCE measurement position, the air-pulse and OCT probe beam were cofocused and the sample was translated.^42,43 To demonstrate the spatial resolving ability of air-pulse OCE, heterogeneous phantoms were constructed with 1% agar surrounded by 2% agar to mimic the spatially selective stiffening of the partial CXL procedure as illustrated in Fig. 1(b). Here, a two-dimensional (2-D) grid of OCE measurements ($n=21$ at each position) was taken every 1.125 mm over a $9\mathrm{mm}\times 9\mathrm{mm}$ region. To relate the DNF of the relaxation process in the phantoms to elasticity, uniaxial mechanical compression testing (Model 5943, Instron Corp., Massachusetts) was performed on homogenous phantoms of each concentration ($n=4$ for each concentration).⁴⁶

Fig. 1.

OCE measurements for the phantoms and corneas where the yellow dots represent measurement positions. 2-D grid of OCE measurements on the: (a) homogeneous phantoms, (b) heterogeneous phantoms where the lighter central region represents the 1% agar and the darker outer region represents the 2% agar, and (c) corneas where the purple region represents the masked area during the partial CXL treatment. Figures are not to scale.

CXL was induced on all but a central 2 mm diameter circle of fresh mature rabbit corneas ($n=4$, Pel-Freez Biologicals, Arkansas) to induce a spatial variation of stiffness as depicted in Fig. 1(c). Additional OCE measurements were made on a separate sample before and after traditional CXL treatment. Apart from the UV mask in the partially CXL-treated samples, the CXL procedure mimicked the standard clinical CXL protocol.³ The epithelium from a $\sim 9\mathrm{mm}$ diameter central region was removed with a blunt surgical instrument. A 0.1% riboflavin solution (1 mg of riboflavin-5-phosphate in 1 mL of a 20% T-500 Dextran solution) was applied every 5 min for 30 min followed by 30 min of UV irradiation (365 nm, $3\mathrm{mW}/{\mathrm{cm}}^2$, 7 mm spot diameter). During irradiation, the riboflavin solution was instilled every 5 min as well. The intraocular pressure (IOP) was artificially controlled at 15 mmHg using a previously published closed-loop IOP control system⁴⁷ because the IOP can have a profound influence on the measured elasticity of the cornea.⁴⁸

The micrometer-scale displacements were induced by a home-built micro air-pulse delivery system.²⁸ The system employed an air gate and a control unit to provide the short-duration focused air-pulse ($\le 1\mathrm{ms}$). A channel for signal input allowed the air-pulse to be synchronized with the OCT system. The air source pressure was obtained from a standard pressure gauge, and the focused air-pulse was expelled out of a cannula port with a flat edge and inner diameter of $\sim 150\mu \mathrm{m}$. The localized air-pulse excitation was precisely positioned with a three-dimensional (3-D) micrometer stage.

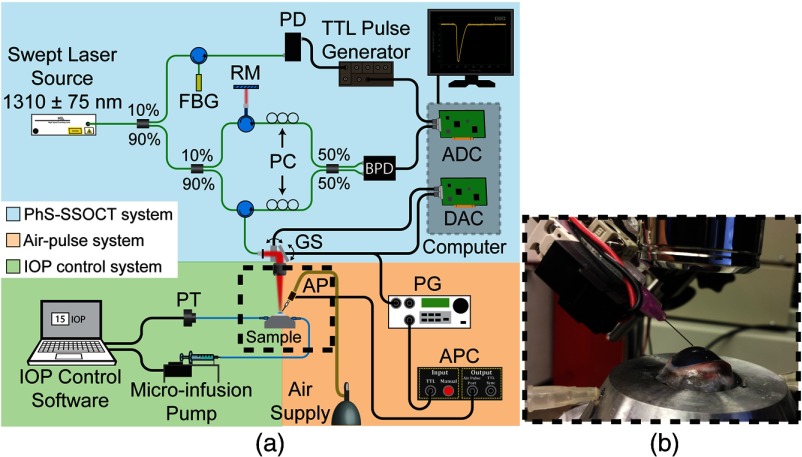
The air-pulse induced displacements in the in situ rabbit corneas in the whole eye-globe configuration were detected by a home-built phase-stabilize swept source OCT (PhS-SSOCT) system.⁴⁹ A schematic of the experimental setup is shown in Fig. 2. The PhS-SSOCT system was comprised of a broadband swept laser source (HSL2000, Santec Inc.) with a central wavelength of 1310 nm, bandwidth of 130 nm, and scan rate of 30 kHz. The full imaging depth in air was 9 mm. A fiber Bragg grating was used for A-scan acquisition triggering and phase-stabilization. The axial resolution of the system was $\sim 11\mu \mathrm{m}$ in air and the phase stability of the system, as defined as one standard deviation of the displacement during an M-mode scan with no excitation, was experimentally measured as $\sim 40\mathrm{nm}$ in the cornea.

Fig. 2.

(a) Schematic of the OCE setup during the cornea measurements with the different subsystems. ADC, analog-to-digital converter; AP, air-pulse port; APC, air-pulse controller; BPD, balanced photodetector; DAC, digital-to-analog converter; FBG, fiber Bragg grating; GS, galvanometer mounted mirror scanners; PC, polarization controller; PG, pulse generator; PT, pressure transducer; RM, reference mirror. (b) Inset of the air-pulse port, OCT scan lens, and in situ eye-globe shown as the dashed box in (a).

The air-pulse and the OCT probe beam were cofocused during all measurements,^42,43 and the distance between the air-pulse port tip and the cornea surface was kept at $\sim 400\mu \mathrm{m}$ during all experiments. The output air pressure of the system remains relatively stable when the distance between the air-port tip and sample surface is less than 10 mm.²⁸ Multiple M-mode images ($n=21$) were acquired every 0.5 mm for the partially CXL-treated corneas and every 1 mm for the traditionally CXL-treated corneas over a $4\mathrm{mm}\times 4\mathrm{mm}$ grid centered at the corneal apex as shown in Fig. 1(c). The output air-pulse pressure applied to the cornea surface was $\sim 2\mathrm{Pa}$.

The raw fringes, as obtained from M-mode imaging, were converted to the M-mode OCT signal, including both the intensity data and phase information, by a fast Fourier transform after resampling the raw fringes to linear k-space.^24,50 The unwrapped temporal phase profiles from the corneal surface, $\phi (t)$, were converted to displacement, $y(t)$ by⁴⁹

$$y(t)=\phi (t)\times \frac{{\lambda }_0}{4\pi n_{\mathrm{air}}},$$ (1)

where ${\lambda }_0$ was the central wavelength of the OCT system and $n_{\text{air}}$ was 1.

While we have shown that the rate of the relaxation process when fitted to a simple exponential equation is related to the stiffness of the material, no biomechanical properties were quantified.⁴² To overcome this limitation, a simple kinematic differential equation was used to model the air-pulse induced displacement recovery process^8,45

$$m\frac{{\mathrm{d}}^{2}y(t)}{\mathrm{d}{t}^2}+c\frac{\mathrm{d}y(t)}{\mathrm{d}t}+ky(t)=0,$$ (2)

where $m$ was the equivalent mass, $c$ was the viscosity coefficient, and $k$ was the spring constant. Two parameters were introduced to simplify the solution and subsequent analysis: $\zeta =c/(2\sqrt{mk})$ was the damping ratio and $\omega =\sqrt{k/m}$ with $\omega =2\pi f$, where $f$ was the DNF of the system. Substituting these two parameters into Eq. (2) yields:

$$\frac{{\mathrm{d}}^{2}y(t)}{\mathrm{d}{t}^2}+2\zeta \omega \frac{\mathrm{d}y(t)}{\mathrm{d}t}+{\omega }^{2}y(t)=0.$$ (3)

The analytical solution of Eq. (3) depends on the value of $\zeta$:

• 1.$y(t)=(A+Bt){\mathrm{e}}^{-\omega t}$ when $\zeta =1$;
• 2.$y(t)={\mathrm{e}}^{-\zeta \omega t}[A\cos (\omega t\sqrt{1-{\zeta }^2})+B\sin (\omega t\sqrt{1-{\zeta }^2})]$ when $0<\zeta <1$;
• 3.$y(t)={\mathrm{e}}^{-\omega t}(A{\mathrm{e}}^{\omega t\sqrt{{\zeta }^2-1}}+B{\mathrm{e}}^{-\omega t\sqrt{{\zeta }^2-1}})$ when $\zeta >1$.

Here, $A$ and $B$ were determined by the initial conditions of the displacement profiles. From the exponent forms of the solutions to Eq. (3), $f$ can also be described as the relaxation rate of the displacement and was obtained by least-squares variance-weighted (robust) fitting to the appropriate solution to Eq. (3) with the curve-fitting toolbox in MATLAB^® (Mathworks, Massachusetts). Any profile with a goodness of fit (i.e., $R^2$) of less than 0.98 was discarded from further analysis. The DNF values were then averaged for each OCE measurement position. The average DNF values were then plotted, where the data was interpolated and smoothed $100\times$ solely for plotting in OriginPro (OriginLab, Massachusetts). The kinematic model was chosen due to its link between the OCE measurements and a quantitative material parameters of stiffness (i.e., Young’s modulus),⁴⁴ which is not present for the exponential decay analysis in our previous work.⁴²

3. Results

3.1. Tissue-Mimicking Agar Phantoms

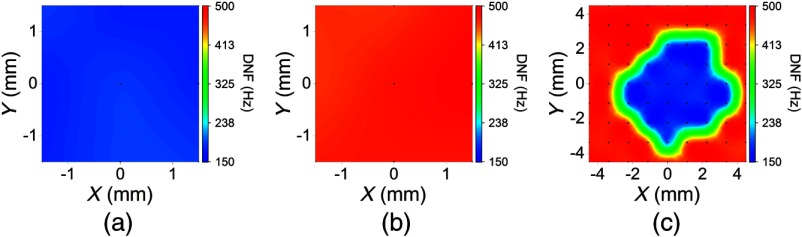
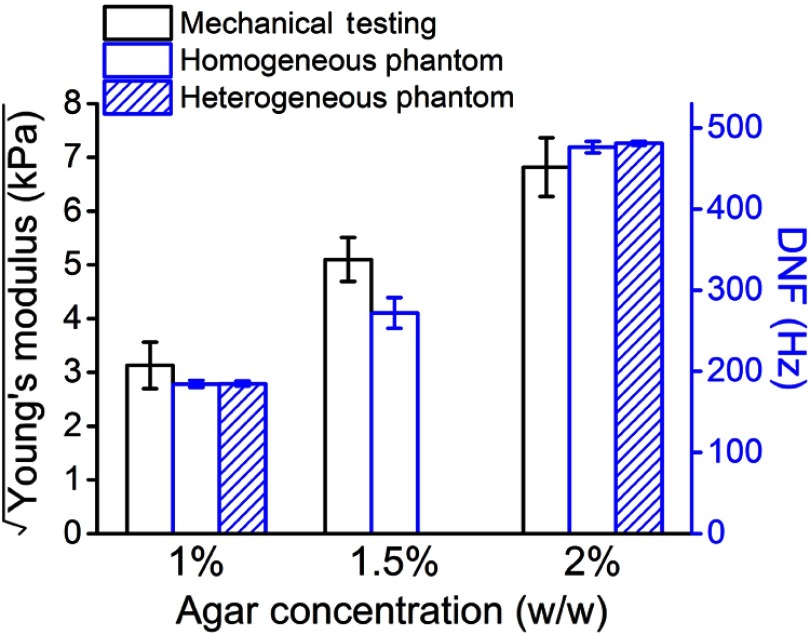
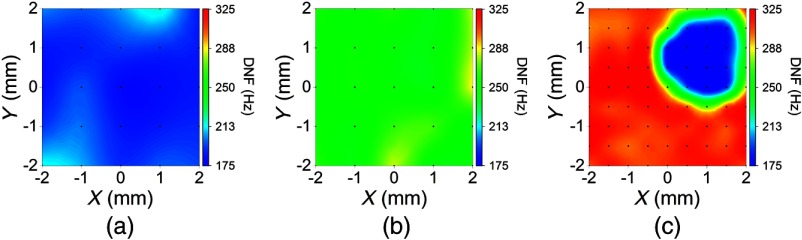
In the agar phantom samples, the damping ratio, $\zeta$, was found to be less than 1 during fitting. Therefore, the relaxation process of the air-pulse induced displacement was fitted to the second solution of Eq. (3), $y(t)={\mathrm{e}}^{-\zeta \omega t}[A\cos (\omega t\sqrt{1-{\zeta }^2})+B\sin (\omega t\sqrt{1-{\zeta }^2})]$ with $\omega =2\pi f$ to obtain $f$, which is also the DNF. Figure 3 is the DNF maps of the (a) homogeneous 1%, (b) homogeneous 2%, and (c) heterogeneous phantom simulating the spatially selective CXL procedure. The 95% confidence intervals (CI) of the mean DNFs for the homogeneous 1%, 1.5%, and 2% phantoms were [179, 190] Hz, [263, 281] Hz, and [468, 484] Hz, respectively, with $n=9$ OCE measurement positions for each concentration. In the heterogeneous phantom, the CIs for mean DNFs of the 1% and 2% regions were [182, 188] Hz and [479, 484] Hz with $n=24$ and 57 OCE measurement positions, respectively. The CIs for the mean Young’s moduli of the homogeneous 1%, 1.5%, and 2% phantoms ($n=4$ samples for each concentration) were [6.2, 13.2] kPa, [24.5, 27.5] kPa, and [42.1, 50.7] kPa as measured by mechanical testing. Figure 4 plots the square root of Young’s moduli as obtained by uniaxial mechanical compression testing and the DNFs of the agar concentrations in each type of phantom. The correlation between the square root of Young’s modulus as measured by mechanical testing and the DNF as measured by OCE of the homogeneous phantoms was $R^2=0.990$.

Fig. 3.

Damped natural frequency (DNF) maps in the agar phantoms where the black dots represent the OCE measurement positions, and the DNF scale is the same for direct comparison. DNF maps of the: (a) homogeneous 1%, (b) homogeneous 2%, and (c) heterogeneous phantoms.

Fig. 4.

Comparison of the square root of Young’s modulus as measured by uniaxial mechanical testing ($n=4$ samples for each concentration) to the DNF of the same homogeneous phantoms ($n=9$ OCE measurement positions for each concentration) and the corresponding heterogeneous phantom components ($n=24$ and 57 for 1% and 2% components, respectively). Error bars are the 95% confidence intervals of the means.

3.2. Corneal Samples

During fitting of the air-pulse induced displacement profiles from the corneal samples, $\zeta$ was found to be very close to 1 ($0.99\le \zeta \le 1$). Therefore, $\zeta$ was set to 1 and the first solution to Eq. (3), $y(t)=(A+Bt){\mathrm{e}}^{-\omega t}$ with $\omega =2\pi f$, was utilized to obtain, $f$, the DNF. Figure 5 shows DNF maps for a cornea (a) before and (b) after traditional CXL. An additional DNF map of a typical partially CXL-treated cornea is plotted in Fig. 5(c). The DNF scales are the same for all three corneal DNF maps to provide easy direct comparison. The CI of the average DNF of the untreated sample was [189, 197] Hz before CXL, which increased by $\sim 32\%$ to [251, 262] Hz after traditional CXL, indicating an increase in corneal tissue stiffness. In the partially treated sample shown in Fig. 3(c), the surrounding CXL-treated region was noticeably stiffer ($\sim 73\%$) than the central untreated region with CIs for the DNFs of [303, 311] Hz and [174, 183] Hz, respectively.

Fig. 5.

DNF maps of a cornea: (a) before and (b) after traditional CXL treatment. (c) DNF map of a typical partially CXL-treated rabbit cornea. The black dots are OCE measurement positions and the DNF scales are the same for easy direct comparison.

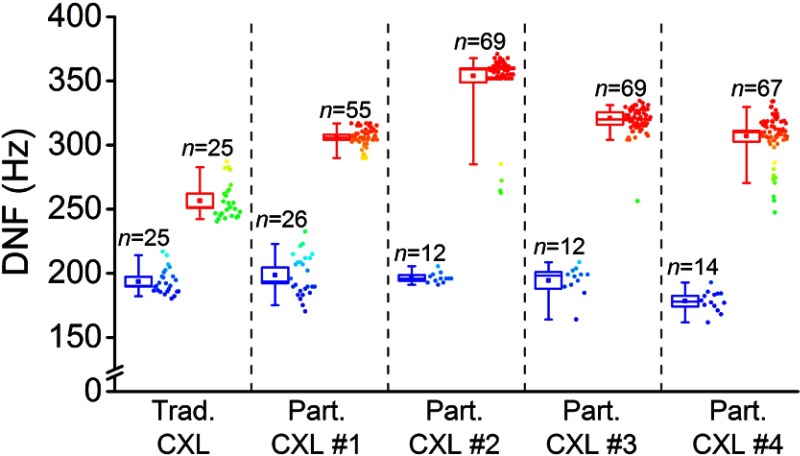
Figure 6 provides an overview of the DNFs of the corneas. The data is presented as a box and whisker plot where the outer box shows the 95% confidence interval of the mean, the whiskers are the 5th and 95th percentiles, the central line is the median, and the small inscribed box is the mean. In the case of the traditionally CXL-treated sample, the blue boxes correspond to DNFs from OCE measurements before the CXL treatment while the red boxes correspond to DNFs after CXL treatment. For the partially CXL-treated samples, the blue and red boxes correspond to data from the untreated and CXL-treated regions of the respective samples. The raw data is plotted alongside and is color-mapped according to the scales in Fig. 5 and the number of samples in each subset of data is labeled. The CI for the untreated tissue from all five samples was [204, 218] Hz, which increased by $\sim 51\%$ to [313, 321] Hz after CXL. The CI for the mean increase in the DNF after CXL in all five samples was [38%, 84%].

Fig. 6.

Box and whisker distribution plots of the DNF of air-pulse induced displacement as measured by OCE from in situ rabbit corneas. Blue and red boxes correspond to OCE measurements from untreated and CXL-treated corneal tissue, respectively. The outer box represents the 95% confidence interval and the whiskers are the 5th and 95th percentiles. The raw data distributions are shown beside the box plots with color maps corresponding to Fig. 5 and $n$ is the number of points measured for each subset.

4. Discussion

In this work, we have demonstrated the capability of air-pulse OCE to resolve transverse elasticity differences for evaluating custom CXL treatments. A simple kinematic model was utilized to characterize the air-pulse induced displacement relaxation process and obtain the DNF, which correlates strongly with the square root of Young’s modulus.^44,45 After demonstrating the feasibility of this method on spatially heterogeneous agar phantoms, this model was then applied to the cornea in situ in the whole eye-globe configuration. The results showed that CXL dramatically increased the DNF of all samples with an average increase in the DNF of $\sim 51\%$.

One of the primary challenges in quantifying material parameters from elastographic measurements is the influence and consideration of boundary conditions, which is critical for corneal elastography. We have previously shown that the boundary conditions and geometry of the cornea influence the measured elasticity with OCE and finite element modeling.⁵¹ However, this assessment relied on the velocity of a transversely propagating elastic wave, which is heavily influenced by boundary conditions due to its relatively long wavelength (mm scale). In contrast, the low amplitude displacement ($\le 10\mu \mathrm{m}$) and small spot size of the excitation (a few hundred $\mu \mathrm{m}$ diameter) in this work can provide accurate measurements of localized elasticity because the excitation and measurements are reasonably far from the boundaries (the corneal-scleral junction and posterior surface of the cornea).⁵² Thus, the proposed kinematic model can provide a quantitative measurement of corneal stiffness due to its simple link to Young’s modulus, rapid analysis, and low-amplitude displacement to minimize the effects of boundary conditions on measured stiffness.

We have utilized air-pulse OCE measurements in the presented fashion to map the viscoelasticity of pig skin to locate dermal filler injections and quantify their efficacy at increasing skin firmness.⁴³ However, the model utilized for quantifying the viscoelasticity of the skin assumed that the sample was of infinite thickness, which may be reasonably valid in skin because the amplitude of the air-pulse induced displacement is at least a few orders of magnitude less than the skin thickness. On the other hand, the technique for quantifying viscoelasticity of the skin from air-pulse induced displacement measurements would not be valid for the cornea because of the fluid structure interface at the corneal posterior surface and the relatively small thickness of the cornea. Moreover, it is well understood that the biomechanical properties of the cornea and the stiffening effects of CXL are not homogeneous depth-wise,^39,53–55 but the kinematic model used in this work cannot provide the depth-resolved biomechanical properties of the cornea. This will require a more rigorous mechanical model,⁵⁶ which we are currently adapting for air-pulse based OCE measurements on the cornea by incorporating the finite thickness of the cornea and the presence of the aqueous humor as we have done for elastic waves in the cornea.^57–59 Ultimately, a robust mechanical model that can link the air-pulse induced displacement profile measured by OCE in the cornea with quantitative biomechanical parameters would provide a stronger basis for planning and evaluating customized CXL procedures.^5,6

During the OCE measurements, the sample was manually translated to the various grid positions in a “snake” pattern to reduce the acquisition time as compared to raster scanning. Currently, the total acquisition time of tens of minutes is unfeasible for live measurements. Integration of a 3-D computer-controlled motorized linear stage with the OCE acquisition software would enable automated OCE measurements that would dramatically reduce the acquisition time, minimize the risk of errors, and increase the spatial accuracy and repeatability. Moreover, the OCT image can provide robust and accurate feedback for 3-D positioning to ensure that the measurements are safe and repeatable. We have developed such a system, are currently testing the feasibility of such a system, and optimizing it for live experiments. Additionally, a goniometric articulation system would further reduce the measurement time by removing the need to coalign the OCT probe beam and air-pulse excitation due to the corneal geometry, which would also ensure that the air-pulse incidence angle is maintained for all measurements. This would be particularly beneficial for measuring the biomechanical properties of the peripheral cornea, which has also been implicated in keratoconus progression. Previous work has shown histopathological and ultrastructural changes in the peripheral cornea due to keratoconus,^60,61 although the ectatic region is generally within the central area except in severe cases of keratoconus.⁶² Integrating such a system is the next development step for our automated air-pulse OCE system. On the other hand, the high-resolution 3-D image provided by OCT can also provide geometrical parameters for pinpointing regions of interest to hone the measurement area,^5,6,60–62 which is not feasible with techniques such as Brillouin microscopy without integration of an imaging modality.

Measurements from the ORA or CorVis ST can provide the viscoelasticity of the cornea after numerical simulations.⁶³ However, spatially resolving heterogeneous biomechanical properties of the cornea with these instruments may be limited due to their relatively large deformation amplitude (mm scale) and large deformation area (also mm scale). Our results show that our air-pulse OCE transverse spatial resolution is, at worst, several hundred micrometers, as evidenced by the transition regions between the untreated and CXL-treated tissue as seen by the green regions in Fig. 5(c). While this may be due to the transition in biomechanical properties between the untreated and CXL-treated regions (i.e., the spatial resolution of the partial CXL treatment), there is still a clear transition region in the phantom samples as evidenced by the green boundary in Fig. 3(c). Our future work is focused on determining the applicability of this technique on keratoconic samples and the absolute spatial resolution of air-pulse OCE. Contact-based OCE techniques have shown promise for obtaining spatially resolved corneal biomechanical properties.^35,37 However, there has not yet been a report of a quantitative measurement of material parameters with these contact-based OCE methods. Ultrasound elastography has been utilized to evaluate the transverse heterogeneity of CXL in vivo but required general anesthesia and application of an acoustic impedance matching medium,⁶⁴ which may not be comfortable for human applications.

The range of the Young’s modulus of the rabbit cornea in the literature spans a few orders of magnitude, from $\sim 1\mathrm{kPa}$ using atomic force microscopy,⁶⁵ to $\sim 11\mathrm{MPa}$ using mechanical extensiometry.⁶⁶ Generally, elastographic measurements by other modalities, such as those previously mentioned, provide much higher elasticity values than as measured by OCE. For example, numerical simulations from air-puff measurements showed Young’s modulus of the cornea to be several hundred kPa, while our wave-based OCE measurements generally show Young’s modulus of the cornea to be $\sim 100\mathrm{kPa}$.^39,57,59 Similarly, if we directly estimate the corneal elasticity from the agar phantom DNFs, we obtain a maximum stiffness of $\sim 30\mathrm{kPa}$, which is even less than our own wave-based quantification of corneal Young’s modulus. Likewise, changes in corneal biomechanical properties after CXL treatments have shown a wide variance in the literature, ranging from $\sim 100\%$ as assessed by Brillouin microscopy⁵⁴ to greater than $\sim 300\%$ as quantified by mechanical testing⁶⁷ and atomic force microscopy.⁵³ These discrepancies are primarily due to the fact that because the measurement technique, testing conditions (e.g., in situ, ex vivo, or in vivo), and IOP all have a profound influence on the measured stiffness, which is exacerbated by the nonlinearity of the corneal stress–strain curve.⁶⁸ In order to eliminate the effects of IOP on corneal stiffness measurements, the IOP was artificially controlled at 15 mmHg during all OCE measurements, but no mechanical testing was conducted on the corneal samples as with the phantoms because it is still a challenge to properly replicate in vivo or in situ conditions during corneal mechanical testing.⁶⁸ Similarly, our previous work has shown a difference of a few orders of magnitude in the elasticity of the cornea as assessed by OCE and mechanical testing.⁴⁷

On the other hand, the DNFs from the untreated tissue were relatively similar between samples. However, the DNFs from the CXL-treated corneal tissue varied much more between samples, as seen Fig. 6. The ocular samples were from mature rabbits ($>6\text{\hspace{0.17em}\hspace{0.17em}months}$) but not of a known age. Mechanical testing⁶⁹ and the presented air-pulse OCE⁴² technique have shown that the cornea stiffens with age. There may be an age dependency in corneal stiffening by CXL and investigating the age-related effects of CXL is an avenue of our future work. Moreover, previous CXL investigations have shown a large degree of intersample variance in the changes in stiffness of the cornea after CXL, indicating that changes in the biomechanical properties of the cornea after CXL may be case-specific.^64,67,70 This work shows similar results, with a relatively large intersample stiffening variability, with a 95% CI of 5 samples of [38%, 84%]. Nguyen et al.⁶⁴ postulated that the relatively large variability may be due to postmortem conditions, primarily collagen degeneration which could also explain why stiffening by CXL has large intersample variance in this work and the literature. Nevertheless, air-pulse OCE was able to spatially localize stiffened corneal tissue after the partial CXL treatment, showing promise for measuring spatial variations in corneal stiffness before and after customized CXL treatments.

5. Conclusion

In summary, we have shown that air-pulse OCE is capable of spatially resolving heterogeneous biomechanical properties of the in situ rabbit cornea in the whole eye-globe configuration after spatially selective CXL by analyzing the relaxation process of a micro air-pulse induced displacement. By quantifying the DNF of the relaxation process, the transversely spatially varying stiffness of the cornea was revealed. Due to the noncontact nature and minimal excitation force, this technique may be useful for determining spatial variations in corneal biomechanical properties in vivo for planning and evaluating custom CXL treatments.

Biographies

Manmohan Singh received his BSc degree in biomedical engineering from the University of Houston in 2014. Currently, he is pursuing his PhD in the Department of Biomedical Engineering at the University of Houston. Since the fall of 2010, he has been with Dr. Kirill Larin’s Biomedical Optics Laboratory. His research interests include utilizing biomedical imaging for the detection of diseases and utilizing and developing new elastographic methods for investigating the biomechanical properties of tissues.

Jiasong Li received his BSc degree in biomedical engineering from Northeastern University, Shenyang, Liaoning, China, in 2007. He became a graduate student at Huazhong University of Science and Technology, Wuhan, Hubei, China, in 2008. He received his PhD in biomedical engineering from the University of Houston in 2016. His current research is focused on development and applications of optical coherence tomography (elastography) systems.

Srilatha Vantipalli received her BS degree in optometry from the Birla Institute of Technology, Pilani, India, in 2010. Since 2012, she has been working with Dr. Michael Twa and received her PhD in physiological optics and vision science from the University of Houston College of Optometry in 2016. Her research is focused on evaluating the corneal biomechanical properties utilizing elastography methods, the effects of corneal crosslinking, and corneal ectatic disease, e.g., keratoconus.

Zhaolong Han received his BSc and PhD degrees in engineering from Shanghai Jiao Tong University, Minhang, Shanghai, China, in 2005 and 2013, respectively. Since 2014, he has been a postdoctoral fellow with the Department of Biomedical Engineering at the University of Houston. His research interests include computational mechanics, ocular biomechanics, fluid-structure interaction, and optical coherence elastography.

Kirill V. Larin is a professor of biomedical engineering at the University of Houston. He received his MSc degree in laser physics and mathematics from Saratov State University in 1995 and his PhD in biomedical engineering from the University of Texas Medical Branch in Galveston in 2002. He has published more than 100 papers in the field of biomedical optics and biophotonics. He is a fellow of SPIE in 2015 and OSA in 2016.

Michael D. Twa is a professor and the associate dean for research and graduate studies at the University of Alabama at Birmingham School of Optometry. He received his clinical doctorate in optometry in 1990 from UC Berkeley and his PhD in vision science from Ohio State University in 2006. He has more than 80 peer-reviewed publications related to ocular biomechanics, glaucoma, biomedical imaging, and image processing. His current research relates to the development and application of optical coherence elastography imaging for the eye.

Disclosures

No conflicts of interest, financial or otherwise, are declared by the authors.