Building a Surface Atlas of Hippocampal Subfields From High Resolution T2-weighted MRI Scans Using Landmark-free Surface Registration

Abstract

The hippocampus is widely studied in neuroimaging field as it plays important roles in memory and learning. However, the critical subfield information is often not explored in most hippocampal studies. We previously proposed a method for hippocampal subfield morphometry by integrating FreeSurfer, FSL, and SPHARM tools. But this method had some limitations, including the analysis of T1-weighted MRI scans without detailed subfield information and hippocampal registration without using important subfield information. To bridge these gaps, in this work, we propose a new framework for building a surface atlas of hippocampal subfields from high resolution T2-weighted MRI scans by integrating state-of-the-art methods for automated segmentation of hippocampal subfields and landmark-free, subfield-aware registration of hippocampal surfaces. Our experimental results have shown the promise of the new framework.

I. INTRODUCTION

The hippocampus is widely studied in neuroimaging field as it plays important roles in memory and learning. However, the complexity and heterogeneity folding anatomy of hippocampus usually present analytical challenges. To address these challenges, there has been notably increased interest in the recent literature in examining the subfields of the hippocampal formation using magnetic resonance imaging (MRI) [1]–[8].

Some existing subfield studies employed manual segmentation [1] [2] or semi-automated segmentation [3] [4]. They often require heavy labor work by professionals with long processing time, and thus are not applicable to large-scale datasets. To bridge this gap, we previously proposed an automatic framework [5] [6] for surface-based hippocamapl subfield morphometry by integrating FreeSurfer [9], FSL [10], and SPHARM [11] tools. However, there exist limitations in these prior studies [5] [6]. First, these studies analyze only regular T1-weighted MRI scans without detailed subfield information available. Second, the FreeSurfer version used in our prior studies for subfield segmentation was recently shown not optimal [8]. Third, there is a lack of subfield-guided hippocampal registration method in these studies.

To bridge these gaps, in this work, we present a new framework for building a surface atlas of hippocampal sub-fields from high resolution T2-weighted MRI scans by integrating state-of-the-art methods for automated segmentation of hippocampal subfields and landmark-free, subfield-guided registration of hippocampal surfaces. The strengths of our work are threefold, as described below.

First, our proposed framework is designed for hippocampal subfield morphometry using high resolution T2-weighted MRI scans. While the anatomical details of hippocampal subfields are difficult to be observed on regular T1-weighted MRI scans with resolution on the order of 1 × 1 × 1 mm³, recent studies [2] [7] [8] have shown promising results on analyzing hippocampal subfields by exploiting T2-weighted MRI scans with higher resolution of 0.4 × 0.4 × 2 mm³.

Second, to extract hippocampal subfields from these high resolution T2-weighted scans, we employ a well recognized segmentation tool named Automatic Segmentation of Hippocampal Subfields (ASHS) [7]. It jointly analyzes high resolution T2-weighted and regular T1-weighted MRI scans to achieve a dramatic improvement in accurate segmentation of hippocampal subfields. In the newly released FreeSurfer 6.0 (beta version), major updates have also been made to handle these high resolution T2-weighted scans [8]; and thus the new FreeSurfer software can serve as an alternative tool for hippocampal subfield segmentation in future studies.

Third, in our previous studies, we developed a pipeline to build a surface atlas of hippocampal subfields, in which SPHARM-based first order ellipsoid (FOE) method [11] was employed for 3D hippocampal surface registration. However, the important hippocampal subfield information was not used to align different hippocampal surfaces together. A possible approach to solve this problem is to identify landmarks on subfield boundaries, and use these landmarks to direct surface registration using landmark-guided approach presented in [12]. However, because of the complex formation of the hippocampus, it is challenging to identify corresponding landmarks between surfaces. Following [13], we previously demonstrated in [5] [6] that spherical parameterization, a continuous and uniform mapping from the object surface to the surface of a unit sphere, can be created. Thus, mapping subfield labels on the spherical parameterization can form a spherical image. The subfield-aware surface registration problem can then be resolved using spherical image registration method (e.g., Spherical Demons (SD) [14]) to align subfield label information across surfaces.

II. MATERIALS AND METHODS

We first describe our MRI data. Then we discuss how to segment the hippocampal subfields from MRI scans and how to create initial surface correspondence among hippocampi using spherical parameterization and SPHARM modeling. Next, we present how to use the Spherical Demons method to register two spherical label images together. Finally, we develop a procedure that iteratively identifies a surface label atlas as the mean of all the aligned individual label images.

A. Data

The sample includes 12 healthy control (HC) participants recruited at Indiana Alzheimer’s Disease Center (IADC). MRI scans were acquired on a Siemens MAGNETOM Prisma 3T MRI scanner. The scanning protocols include a T1-weighted (MPRAGE) whole-brain scan and a T2-weighted (TSE) partial-brain scan and an oblique coronal slice orientation (positioned orthogonally to the main axis of the hippocampus). Same protocols were adapted in [7] [15].

B. Subfield Segmentation and SPHARM parametrization

Hippocampal subfield segmentation was completed by using the Automatic Segmentation of Hippocampal Subfields (ASHS) software [7]. Topology fix was performed on segmentation results to ensure a spherical topology for each hippocampus. The hippocampal surface was constructed from a voxel-based binary volume, and subfields were assigned to surface locations as “Cornu Ammonis (CA, including CA1-3)”, “Dentate Gyrus (DG)”, or “Subiculum + Miscellaneous (SUB+MISC)”, using the strategy shown in [7]. Following [6], spherical parametrization was performed to establish a bijective mapping between each surface location v = (x, y, z)^T and a pair of spherical coordinates (θ, ϕ) while minimizing area distortion. This mapping can be represented as: v(θ, ϕ) = (x(θ, ϕ), y(θ, ϕ), z(θ, ϕ))^T. After that, the surface was expanded into a spherical harmonic (SPHARM) representation, and an initial alignment using the first order ellipsoid (FOE) approach was performed for each subject as detailed in [5]. Figure 1(a–c) shows two example results of spherical parameterization with initial alignment.

Fig. 1.

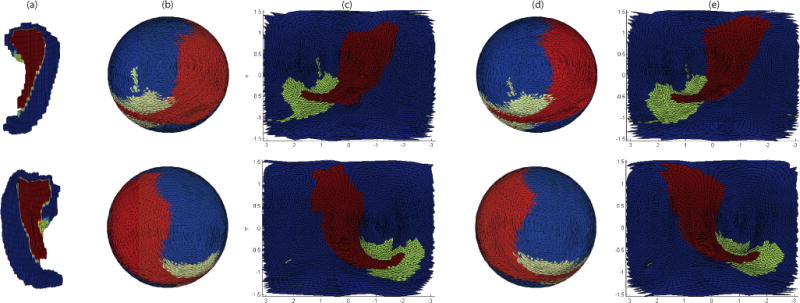
Example results of spherical parameterization (b–c) and SD registration (d–e): (a) Original object in Euclidean space, (b) original spherical mapping, (c) original spherical mapping unfolded to 2D plane, (d) registered spherical mapping using SD method, (e) registered spherical mapping unfolded to 2D plane. Red, blue and green colors correspond to SUB+MISC, CA, and DG respectively.

C. SD Registration and Atlas Construction

Placing subfield-aware landmarks on hippocampal surface is a challenging problem due to the complex anatomy of the hippocampus. Instead, we propose to apply the Spherical Demons (SD) registration [14], a landmark-free method, to directly perform subfield-aware hippocampal surface alignment.

For each subject, ASHS segmentation returns probabilistic maps indicating parcellation chances for each hippocampal subfield. By exploiting these probabilistic maps, labels are well defined on surfaces by selecting highest probabilities, as shown in Figure 1. We use spherical images containing label values to guide the following registration procedure by the SD method proposed in [14]. Let F be the spherical image template, and M be the individual spherical image to be aligned to the template, Γ be the desired transformation to register M to F, and γ be intermediate hidden transformation. We form our objective function as follows:

$$(\gamma \ast ,\mathrm{\Gamma }\ast )=\underset{\gamma ,\mathrm{\Gamma }}{\text{argmin}}{\Vert {\sum }^{-1}(F-M\circ \mathrm{\Gamma })\Vert }^2+\frac{1}{{\sigma }_x^2}\mathit{dist}(\gamma ,\mathrm{\Gamma })+\frac{1}{{\sigma }_T^2}\mathit{Reg}(\gamma )$$ (1)

while:

$$\mathit{dist}(\gamma ,\mathrm{\Gamma })={\Vert \gamma -\mathrm{\Gamma }\Vert }^2$$ (2)

$$\mathit{Reg}(\gamma )={\Vert \mathrm{\nabla }(\gamma -Id)\Vert }^2$$ (3)

where σ_x and σ_T control a trade-off between the image similarity measure and regularization of the objective function, and Σ is a diagonal matrix that models the variability of a feature at a particular vertex on the surface. Equation 2 indicates the geodesic distance from hidden transformation to optimization transformation. Equation 3 indicates regularization penalization on gradient magnitude of the displacement field γ−Id of γ. Algorithm 1 shows the SD algorithm, where $\overrightarrow{v}$ is a stationary velocity field that indicates transformation velocity. Detailed parameter explanations can be found in [14].

Algorithm 1.

Spherical Demons Registration Algorithm

1:	Input: n roughly registered subjects, each subject has a surface map indicating subfield distribution, which is marked as M.
2:	Output: Diffeomorphism Γ so that min dist(F − M ◦ Γ) achieved, where F is created by averaging all 12 registered subjects.
3:	while iter <= 4 do
4:	Template Surface Atlas $F=\frac{\sum M}{n}$
5:	for each subject with label map M do
6:	4-level multi-precision registration:
7:	for each level do
8:	repeat
9:	Step 1: Given γ(t)
10:	for each vertex k do
11:	Compute:
	$${\overrightarrow{v}}_k^{(t)}=\frac{F(x_k)-M\circ {\gamma }^{(t)}(x_k)}{{\sigma }_k^2}{E}_k{[E_k^T(\frac{{\overrightarrow{m}}_k{\overrightarrow{m}}_k^T}{{\sigma }_k^2}+\frac{S_k{(G_k^2)}^T{G}_k^2{S}_n^T}{{\sigma }_x^2})E_n+\epsilon I_{2\times 2}]}^{-1}{E}_k^T{\overrightarrow{m}}_k$$ (4)
12:	${\mathrm{\Gamma }}^{(t)}={\gamma }^{(t)}\circ \text{exp}({\overrightarrow{v}}^{(t)})$
13:	Step 2: Given Γ(t)
14:	for each vertex k do
15:	Update γ:
	$${\overrightarrow{\gamma }}^{(t+1)}=\underset{\overrightarrow{\gamma }}{\text{argmin}}\frac{1}{{\sigma }_x^2}{\displaystyle \sum _{k=1}^K{\Vert \overrightarrow{{\gamma }_n}-{\overrightarrow{{\gamma }_n}}^{(t)}\Vert }^2+\frac{2}{{\sigma }_T^2}{\Vert \overrightarrow{\gamma }\Vert }_V}$$ (5)
16:	until Convergence
17:	iter = iter + 1

By exploiting spherical vector spline interpolation theory [16], SD algorithm performs optimization procedures in two steps: (1) The first step is to resolve the first two terms in Equation 1 as a nonlinear least-square problem by Gauss-Newton optimization. (2) The second step is to resolve the last two terms in Equation 1 by a single convolution of the displacement field Γ with a smoothing kernel [17]. In addition, a multi-resolution strategy at different levels is employed in the SD algorithm. For each level, linear interpolation is performed to interpolate both template and subject to a predefined subdivided icosahedral mesh (radius = 100 in our experiments) with certain precisions: the first level contains 2,562 vertices, the second level contains 10,242 vertices, the third level contains 40,962 vertices, and the fourth level contains 163,842 vertices.

III. EXPERIMENTAL RESULTS

Root mean square distance (RMSD) is computed to evaluate the results of the SD registration:

$$\text{RMSD}(F,M)=\sqrt{\frac{1}{k}{\displaystyle \sum _{i=1}^k{\Vert F(x_i)-M(x_i)\Vert }^2}}$$ (6)

where k is the total vertex number for each interpolated surface, and F (x_i) and M(x_i) are the corresponding label values at vertex x_i of template and individual respectively.

Figure 2 shows the mean spherical images at each iteration of the SD registration. These images are visualized using the interpolated results at Level 3 (i.e., containing 40,962 vertices). Figure 2(a) shows that subfields are roughly aligned at the beginning so that boundaries among them are blurred. Figure 2(b–e) show that boundaries on the mean spherical images are sharpened in each iteration since subfields are warped and better aligned by implementing SD algorithm as we presented in Algorithm 1. Figure 2(f) shows a 2D unfolded version of spherical images in Figure 2(e). The mean spherical images shown in Figure 2(e–f) are the converging results of SD method and chosen to be our hippocampal subfield atlas.

Fig. 2.

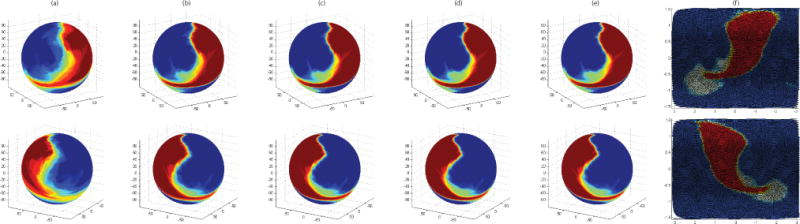
The top and bottom rows correspond to the left and right sides respectively. (a) Mean spherical images after spherical parameterization and FOE alignment. (b–e) Mean spherical images after 1st–4th iterations in SD registration. (f) Spherical images in (e) unfolded to 2D space. Red, blue and green colors correspond to SUB+MISC, CA, and DG respectively. The mean spherical images shown in (e–f) are the converging results of SD method and are chosen to be our resulting hippocampal subfield atlases.

Figure 3 shows the RMSD at each iteration for each subject. The mean RMSDs of 12 subjects are 0.49 and 0.52 respectively for left and right hippocampi at the initial stage. They reduce to 0.32 and 0.34 after 1st iteration, then keep reducing until reaching 0.18 and 0.20 at the convengence.

Fig. 3.

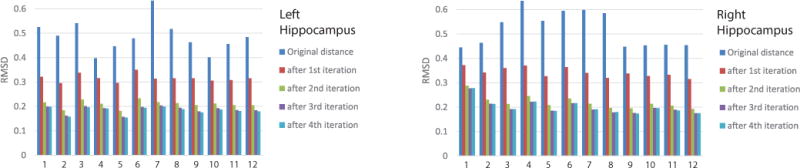
RMSD at each iteration for each subject (labeled from 1 to 12).

IV. CONCLUSIONS AND DISCUSSIONS

A novel computational framework has been presented to build a surface atlas of hippocampal subfields from high resolution T2-weighted MRI scans. Compared with previous studies, the major contributions of this work are threefold: (1) it demonstrates detailed and accurate hippocampal subfield partitions by using high resolution T2-weighted data; (2) it maps complex surface anatomical topology onto a sphere to establish surface correspondence across individuals; and (3) it provides a pathway for fast and accurate landmark free registration that embraces, rather than ignores, the very valuable subfield information. We have demonstrated its effectiveness by applying it to the IADC data. Instead of identifying landmarks on subfield boundaries, the landmark free registration makes use of surface label information to guide registration. One future direction is to include more data for large scale analyses, and compare group differences among HC, Mild Cognitive Impairment (MCI) and Alzheimer’s Disease (AD).