Magnetic resonance measurements of tissue quantity and quality using T₂* relaxometry predict temporal changes in the biomechanical properties of the healing ACL

Abstract

The purpose of this study was to develop a magnetic resonance T₂* relaxometry-based multiple linear regression model to predict the structural properties of the healing anterior cruciate ligament (ACL) over a 24-week healing period following ACL repair in Yucatan minipigs. Two hypotheses were tested: (1) that a regression model based on ACL sub-volumes containing short and long T₂* relaxation times would outperform a competing model based on sub-volumes of short T₂* relaxation times only; and (2) that an optimized regression model would be capable of predicting ACL structural properties between 6 and 24 weeks post-repair. ACLs were imaged in 24 minipigs (8/group) at either 6, 12, or 24 weeks after ACL repair. The structural properties of the ACLs were determined from tensile failure tests. Four multiple linear regression models of increasing complexity were fitted to the data. Akaike Information Criterion values and Bland-Altman tests were used to compare model performance and to test the hypotheses. The structural properties predicted from the multiple linear regression model that was based on the change in ACL sub-volumes of both the short and long T₂* relaxation times over the healing period were in closest agreement to the measured values, suggesting that the amounts of both organized and disorganized collagen, and the change in these quantities over time, are required to predict the structural properties of healing ACLs accurately. Clinical Significance: Our time-specific, T₂*-based regression model may allow us to estimate the structural properties of ACL repairs in vivo longitudinally.

Introduction

Anterior cruciate ligament (ACL) tear is one of the most common sports injuries requiring surgical treatment.^1,2 Whereas in vitro studies have provided insight into the strength of various surgical repair or reconstruction techniques at time zero,^3–7 and cross-sectional animal studies into the strength of healing via post-mortem testing,^8–15 the in vivo biomechanical properties of the healing ACL or graft remains largely unknown. Because of its non-invasive nature, magnetic resonance (MR) imaging is an attractive method to probe the relationship between MR signal properties and the structural properties of the native ACL or ACL graft in vivo.^16–18 Quantitative information related to in vivo ACL function would give researchers a means to monitor the integrity of the graft or ACL repair over time, and might give surgeons a quantitative metric with which to develop and gauge return to sport criteria.

We have previously developed a multiple linear regression model that predicts the structural properties of both the ACL graft and ACL repair in Yucatan minipigs.¹⁶ The minipig was selected because of its anatomic,¹⁹ biomechanical,²⁰ and biological²¹ similarities to human knees.²² We subsequently refined the regression model to use MR T₂* relaxation times¹⁷ to circumvent the pitfalls of using signal intensity, which can be both sequence and magnet-dependent.²³ Because T₂* relaxation time is related to collagen fibril organization, water content, and local magnetic field inhomogeneities,²⁴ and shorter T₂* relaxation times have been shown to reflect more highly organized meniscus²⁵ and ligament²⁶ structure, T₂* relaxation time provides an indication of tissue “quality”. Using this MR relaxometry approach, we determined that a combination of four ACL sub-volumes that spanned a range of T₂* relaxation times from 0–50ms predicted the structural properties (failure load, yield load and linear stiffness) of the ACL one year after ACL repair.¹⁷ Of the four ACL sub-volumes included in the model, the sub-volume containing the shortest T₂* relaxation times contributed most to the prediction outcomes. Although these regression models explained more than 75%, and up to 93%, of the variance in ACL structural properties as indicated by the coefficients of determination (R²), it remained unknown whether these same models could be extended to the earlier phases of healing after ACL repair, or whether separate models would be required for the acute, sub-acute, and chronic stages of ligament healing. The ideal regression model should be time-invariant, meaning that the relationship between the dependent variable and the predictor terms would be linear, and that the slope of this relationship would be the same irrespective of the stage of wound healing. If the model meets this criterion, then a single model could be used to predict structural properties over a range of post-operative healing periods within the time frame used to construct the model.

Although we have shown that the amount of collagen and the degree of organization are important determinants of the healing ACL structural properties,^16,17 the relative contribution of these two qualities are likely specific to each phase of wound healing.^9,27,28 At later stages of healing, collagen becomes more organized and thus the ACL sub-volume containing shorter T₂* relaxation times would be expected to dominate the performance of the model; however larger proportions of amorphous tissue, which are associated with scar formation, may be present at earlier stages of wound healing.²⁹ Therefore the amount of disorganized collagen – reflected by longer T₂* relaxation times – may be an important determinant of the ACL structural properties at earlier healing stages, and regression models that incorporate the transition from disorganized to organized collagen may perform better in predicting the structural properties over time.

In our previous regression models,^16,17 we utilized the R² value to evaluate the variability associated with our predicted structural properties. However, R² values do not necessarily provide the optimal means to compare model performance because they also increase as the number of predictor variables increases.³⁰ In contrast, the Akaike Information Criterion (AIC) provides an estimate of the information lost for a given regression model and it incorporates a penalty function for the number of model parameters. In this way, the AIC provides an objective measure of the trade-off between goodness of fit of the regression model versus its complexity, where lower AIC values indicate superior performance.³⁰

The study objective was to optimize a regression model to predict the structural properties of the healing ACL in ACL-repaired minipigs using MR T₂* relaxometry data acquired at 6, 12 and 24 weeks. We hypothesized that the AIC value of a linear regression model that included the ACL sub-volumes based on both short and long MR T₂* relaxation times and time-specific effects of healing would be lower than the AIC value of a more simplified model that focused on the sub-volume of the shortest MR T₂* relaxation times only. We further hypothesized that the structural properties predicted from the linear regression models that incorporated the multiple ACL sub-volumes and time-specific effects of healing would be in closer agreement to the actual values.

Methods

Animals and surgical procedure

Twenty-four (12 castrated males, 12 females; Sinclair Bio Resources, MO) 15 ± 1 month old Yucatan minipigs were randomized to receive primary ACL suture repair with (n=12; 6 female) or without (n=12; 6 female) a scaffold to enhance healing.³¹ The two procedures were used in an effort to increase the variability in the structural properties from which the regression model would be optimized. The sample size of n=24 was calculated to maintain >95% power to detect a significant increase in R² from 0.74 (based on our previous ACL MR signal analyses¹⁶) at alpha = 0.05. All animals were deemed healthy by veterinary staff prior to the start of the study, and all procedures were approved by the Institutional Animal Care and Use Committee. Animals were housed individually in pens (minimum pen size 22.4 ft²), which were located adjacent to one another, on a 12/12 hour light/dark cycle, fed twice daily with a lab-based died, had free access to drinking water, and were monitored daily by veterinary staff. Environments were enriched with toys on a regular basis. At the time of surgery, animals were sedated using telozol with xylazine, then intubated and maintained under general anaesthesia using isofluorane. The ACL was transected at the junction of the proximal and middle thirds of the ligament. Immediately following transection, animals received primary suture repair either with, or without, the scaffold.⁹ The enhanced repair procedure has been described in detail previously.³¹ Other than the scaffold, the two surgical procedures were equivalent. Animals were allowed unrestricted weight bearing following the surgery.

In vivo MR imaging

Animals were randomized in equal numbers to one of three imaging groups where the surgical knees were imaged in vivo just prior to euthanasia after 6, 12 or 24 weeks (w) of healing (n=8 per group; equal male/females within groups; equal number of ACL repairs with the scaffold versus without within each group). The baseline mean weights of the 6-, 12- and 24-week imaging group animals were 54.2 ± 4.9 kg, 53.1 ± 2.8 kg and 52.5 ± 4.2 kg, respectively. Throughout MR imaging, animals were sedated and maintained under general anesthesia using the same drug regimen described for the surgical procedures. The knees were imaged with a 3T magnet (Prisma; Siemens, Erlangen, Germany) using a six-channel flexcoil (Siemens), and a 3D gradient multi-echo sequence. The sequence for seven of the eight 6w pigs was run using the following parameters: FOV=160×160mm; ST/gap=0.8mm/0mm; TR=29ms; FA=12°. A 384×384 acquisition matrix (voxel size of 0.42×0.42×0.8mm) with 6 echoes at TE=2.48, 6.86, 11.24, 15.62, 20.00 and 24.38ms (scan time = 19:25). For all other animals, MR images were obtained from using a 512×512 matrix (voxel size of 0.31×0.31×0.8mm) and 4 echoes at TE=2.8, 7.88, 12.96 and 18.04ms (scan time = 25:50). The range of echo times was selected based on our previous work that has shown that these TEs capture MR signal intensities relevant to ACL healing specifically.^17,26 The matrix resolution was increased to enhance visualization of the ACL border. The differences in T₂* fit of these in vivo data as a result of differing echo number and resolution were minimal.³² Animals were euthanized immediately after imaging with an injection of Beuthanasia-D, and the hind limbs were harvested and frozen.

ACL T₂* estimation

ACLs were segmented manually (Mimics v16, Belgium) from the T₂* image stack by a single observer. T₂* relaxation times were determined by fitting an monoexponential decay function^33,34 to the segmented voxels across echo times (mean R² of the least-squares function fit was 0.87±0.04). ACL voxels were then binned into four sub-volumes based on increasing ranges of voxel T₂* relaxation times as previously reported:¹⁷ Vol₁=0–12.5ms; Vol₂=12.6–25ms; Vol₃=25.1–37.5ms; Vol₄=37.6–50ms. Vol₁ is the sub-volume (in mm³) of the ACL voxels containing the most organized collagen, whereas Vol₄ is the sub-volume containing the least organized collagen. All calculations were performed using custom-written software with Matlab (v2015b, Natick, MA).

ACL structural properties

Limbs were thawed to room temperature, and dissected leaving only the femur-ligament-tibia complex and the associated peri-ligamentous scar tissue surrounding the healing ACL.⁸ The proximal end of the femur and distal end of the tibia were potted in PVC pipe and urethane resin. The potted ends of the specimen were then rigidly mounted in a custom frame such that the long axis of the ACL was aligned with the direction of the applied tensile load. A servohydraulic material testing system (MTS 810; Prairie Eden, MN) applied the tensile loads to failure at a rate of 20mm/min.^8,35 Maximum load, yield load, and linear stiffness of the ACL were calculated from the load-displacement data.

Statistical methods

All regression modeling was carried out using proc glimmix in SAS version 9.4 (The SAS Institute, Cary, CN). All data were log-transformed to account for the skewed distribution. For each structural property, generalized linear modeling was used to build and compare four competing multiple linear regression models:

1. A 2-parameter model = Vol₁ only with no effect of healing time

2. A 4-parameter model = Vol₁ and Vol₄ with no effect of healing time

3. A 6-parameter model = Vol₁ at 6w, 12w, 24w and (Vol₁ × healing time) interaction

4. A 12-parameter model = the same six parameters as (3), with the addition of Vol₄ at 6w, 12w, 24w; (Vol_{1 ×} Vol₄) interaction; and three-way (Vol₁ × Vol₄ × healing time) interaction

The effect of healing time was modeled by considering 24w as the “baseline” for the Vol₁, Vol₄ and the interaction terms, and subsequently modeling the difference in values from baseline to 6 and 12w. Classical sandwich estimation was used to adjust for model misspecification. These models were fit by maximizing residual likelihood rather than minimizing variance. The resultant Akaike Information Criterion (AIC) was used to compare model performance. For each structural property, model predictions were then compared to the measured values in a separate optimized lognormal model, mimicking the application of the model formula in future testing datasets. Using the optimized models, the slopes of the predicted structural properties and the actual properties at each time point were compared to determine whether the optimized model was time-invariant. Modified Bland-Altman plots were constructed to visualize the agreement between model-predicted and actual values with the model’s predicted values on the x-axis (log-spaced) and the ratio of the actual value to the predicted value on the y-axis. In this way, a ratio equal to 1 on the y-axis indicates perfect agreement, with values greater than 1 indicating that the actual property was higher than the model-predicted, and below 1 indicating that the actual property was lower. These modifications to the traditional Bland-Altman plot were made because the distribution of the data was lognormal.

Results

At the time of MR imaging, we noted that only a small volume of tissue with hyperintense signal spanned the anatomical ACL location in one of the 6w enhanced repair surgeries. Failure of the ACL repair surgery in this one subject was confirmed at dissection, and the animal was excluded from the analyses. Data from 23 animals were included in the final analyses: 7 animals in the 6w imaging group, and 8 animals in each of the 12 and 24w imaging groups.

ACL sub-volumes

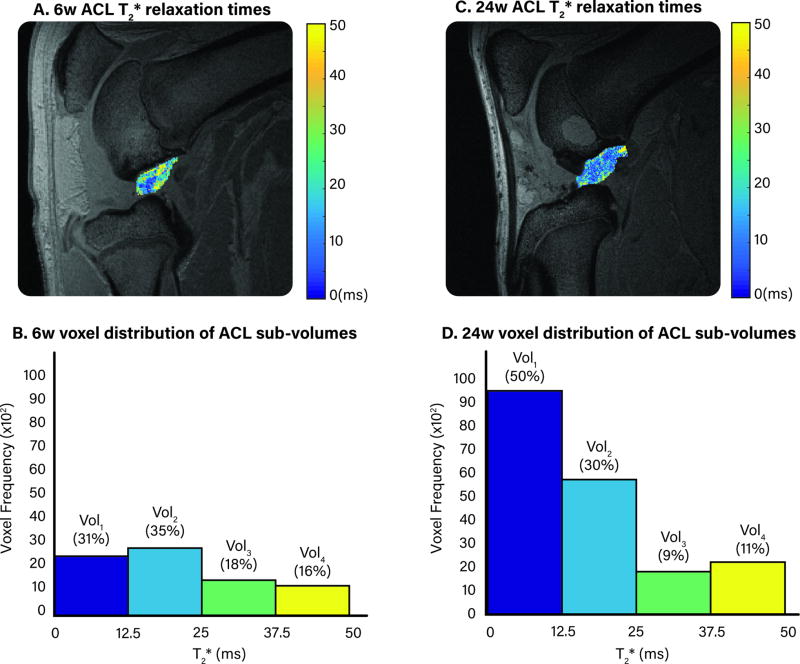
Vol₁ represented between 20% (6w) and 65% (24w) of the ACL total volume post-repair, and Vol₄ represented between 3% (24w) and 29% (6w). The T₂* relaxation times and corresponding distribution of ACL sub-volumes for representative subjects at 6 and 24w post-ACL repair is shown in Figure 1.

Figure 1.

A. & C. Maps of ACL T₂* relaxation times of a single MR slice for representative animals at either 6w (A) or 24w (B) after ACL surgery. B. & D. The distribution of voxel frequency that corresponds to the 6w (B) or 24w (D) ACL T₂* relaxation times. The percentages above each bar indicate the percent of total volume for each ACL sub-volume.

Model performance

The Akaike Information Criterion value for the failure load, yield load and linear stiffness models was lower for the models that included the time-specific effects of healing (Table 1).

Table 1.

Model AIC values (unitless).

	Failure Load	Yield Load	Stiffness
1. Vol1	38.89	40.22	32.68
2. Vol1 & Vol4	43.00	43.84	33.92
3. Vol1 with time	29.28	25.51	29.58
4. Vol1 & Vol4 with time	29.92	27.03	27.28

Optimized models

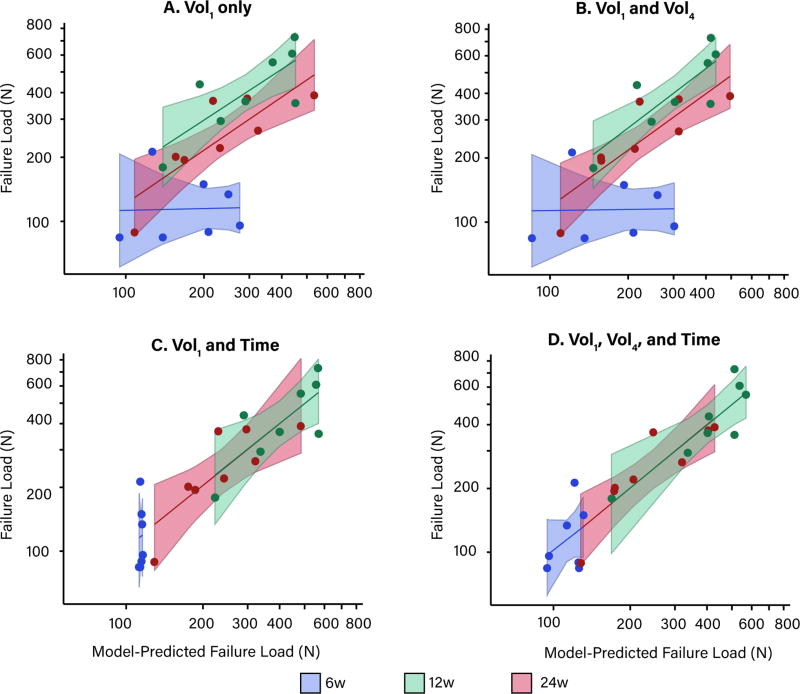
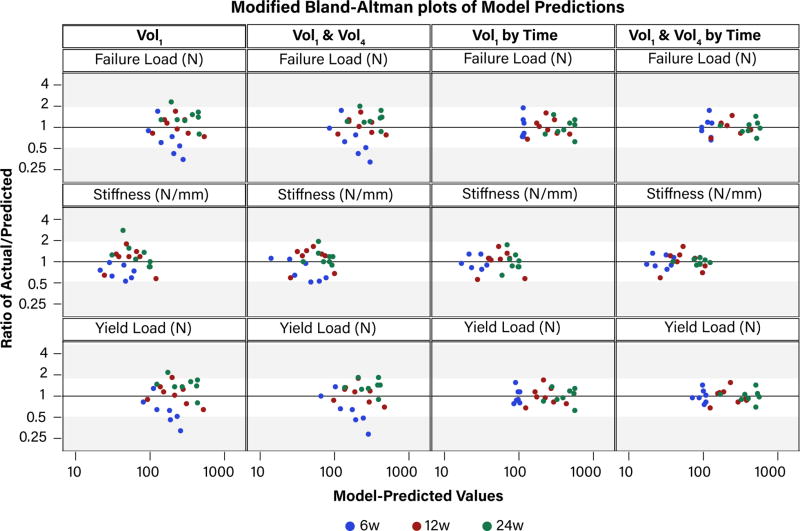
Without accounting for time, the slopes of the actual versus predicted structural properties at 6w were vastly different from the slopes at 12 and 24w (Figure 2, A, B). Incorporating the effect of healing time in the regression model parameters resulted in the slopes being equal at all post-operative time points (Figure 2, C). Including the Vol₄ sub-volume, in addition to the effect of healing time, further improved the model predictions at 6w in particular (Figure 2, D). Model predictions for failure load are shown in Figure 2, but yield load and stiffness model predictions followed the same pattern and are available in the online supplement. Modified Bland-Altman plots confirmed that as the model complexity increased, the ratio of actual to predicted structural properties were closer in agreement (i.e., closer to 1) (Figure 3).

Figure 2.

The model-predicted versus actual failure load for the (A) 2-parameter model; (B) 4-parameter model; (C) 6-parameter model; and (D) 12-paramter model. Shaded regions indicate ± 95% confidence interval of the model estimates.

Figure 3.

Modified Bland-Altman plots of the ratio of actual to predicted structural properties (y-axis) versus model-predicted values (x-axis). A value of ‘1’indicates that the model-predicted and actual values are in perfect agreement; larger y-values indicate the fold-change by which the model underestimates the structural properties; smaller y-values indicate the fold-change by which the model over-estimates the structural properties. The shaded regions are provided to enhance visualization across panels.

Optimized model coefficients

The coefficients of the optimized 12-parameter failure load, yield load and stiffness models used to predict the structural properties are shown in Table 2. The full 12-parameter models can be simplified to an applied format in order to predict the structural properties of the healing ACL at 6, 12 or 24w time intervals specifically. The coefficients (B) for these applied models are shown in the right-hand columns of Table 2 under “Applied Format”.

Table 2.

12-Parameter model coefficients. Healing time effects are denoted by “Δ”. SE = Standard error.

Dependent Variable	Independent Variable	Coefficient (B)		SE	P-value	Applied Format:		B
						Time	Parameter
Failure Load (N)
	24w Intercept	B0	35.08	12.15	0.01	6w	Intercept	27.59
	6w Δ Intercept	B1	−7.49	39.86	0.85		per Vol1	−3.88
	12w Δ Intercept	B2	−56.11	33.16	0.12		per Vol4	−4.68
	24w Vol1	B3	−4.29	1.96	0.05		per (Vol1 × Vol4)	0.80
	6w Δ Vol1	B4	0.41	6.20	0.95	12w	Intercept	−21.03
	12w Δ Vol1	B5	8.85	5.30	0.12		per Vol1	4.56
	24w Δ Vol4	B6	−8.52	2.83	0.01		per Vol4	3.99
	6w Δ Vol4	B7	3.84	6.37	0.56		per (Vol1 × Vol4)	−0.70
	12w Δ Vol4	B8	12.51	6.70	0.09	24w	Intercept	35.08
	24w (Vol1 × Vol4)	B9	1.28	0.46	0.02		per Vol1	−4.29
	6w Δ (Vol1 × Vol4)	B10	−0.48	0.98	0.64		per Vol4	−8.52
	12w Δ (Vol1 × Vol4)	B11	−1.97	1.07	0.09		per (Vol1 × Vol4)	1.28
Yield Load (N)
	24w Intercept	B0	22.21	11.16	0.07	6w	Intercept	29.66
	6w Δ Intercept	B1	7.44	27.22	0.79		per Vol1	−4.18
	12w Δ Intercept	B2	−37.86	34.15	0.29		per Vol4	−5.14
	24w Vol1	B3	−2.30	1.82	0.23		per (Vol1 × Vol4)	0.86
	6w Δ Vol1	B4	−1.88	4.26	0.67	12w	Intercept	−15.64
	12w Δ Vol1	B5	6.00	5.46	0.30		per Vol1	3.69
	24w Δ Vol4	B6	−5.64	2.63	0.06		per Vol4	2.97
	6w Δ Vol4	B7	0.50	4.56	0.91		per (Vol1 × Vol4)	−0.54
	12w Δ Vol4	B8	8.61	6.88	0.24	24w	Intercept	22.21
	24w (Vol1 × Vol4)	B9	0.83	0.43	0.08		per Vol1	−2.30
	6w Δ (Vol1 × Vol4)	B10	0.03	0.71	0.97		per Vol4	−5.64
	12w Δ (Vol1 × Vol4)	B11	−1.37	1.10	0.24		per (Vol1 × Vol4)	0.83
Stiffness (N/mm)
	24w Intercept	B0	68.05	4.47	<0.0001	6w	Intercept	−8.58
	6w Δ Intercept	B1	−76.63	18.29	0.002		per Vol1	1.91
	12w Δ Intercept	B2	−127.78	42.93	0.013		per Vol4	0.70
	24w Vol1	B3	−9.62	0.73	<0.0001		per (Vol1 × Vol4)	−0.10
	6w Δ Vol1	B4	11.53	2.84	0.002	12w	Intercept	−59.73
	12w Δ Vol1	B5	20.21	6.91	0.01		per Vol1	10.59
	24w Δ Vol4	B6	−15.74	0.99	<0.0001		per Vol4	11.41
	6w Δ Vol4	B7	16.43	2.89	0.0001		per (Vol1 × Vol4)	−1.90
	12w Δ Vol4	B8	27.14	8.56	0.009	24w	Intercept	68.05
	24w (Vol1 × Vol4)	B9	2.38	0.16	<0.0001		per Vol1	−9.62
	6w Δ (Vol1 × Vol4)	B10	−2.48	0.46	0.0002		per Vol4	−15.74
	12w Δ (Vol1 × Vol4)	B11	−4.28	1.38	0.01		per (Vol1 × Vol4)	2.38

Discussion

The AIC values of the linear regression models that incorporated the effects of healing time were lower than the AIC values of the more simplified models, indicating that these 6- and 12-parameter models performed better than the 2- and 4-parameter models for predicting ACL failure load, yield load, and stiffness (Table 1). Accordingly, the slopes across all healing times were co-linear only in the time-specific models (Figure 2, and Figures S1 and S2 in the online supplement), and modified Bland-Altman plots of the ratio of the actual to model-predicted values (Figure 3) showed that the 12-parameter model predictions were in closest agreement. These results supported our hypotheses that the AIC values would be lowest in models that incorporated the time-specific effects of healing and multiple ACL sub-volumes, and that the predicted structural properties predicted from this most complex model would be in closest agreement to the actual values.

The 2- and 6-parameter models focused on Vol₁ because this ACL sub-volume explained the greatest proportion of variance in our previous multiple linear regression models.¹⁷ We expanded these models to include both Vol₁ and Vol₄ sub-volumes and their interaction terms with time, resulting in a 12-parameter multiple linear regression model. Contrary to previous prediction models that were based primarily on the remodeling phase of healing at 52 weeks,¹⁷ the results presented here suggested that a prediction term that captures some elements associated with early healing is required in order to predict ACL structural properties at time points between 6 and 12w. Because Vol₄ encompasses voxels with much longer T₂* relaxation times compared to Vol₁ (35.6–50ms vs. 0–12.5ms, respectively), we believe that this sub-volume may capture these other constituents and biological processes associated with earlier stages of ACL healing.

Investigations in rabbit models of medial collateral ligament (MCL) wound healing have shown that the amount of disorganized scar tissue bridging the gap between ligament ends is a critical element in early extra-articular ligament healing.²⁹ Using the ligament maturity index (LMI), we found that the cellular subscores, in addition to the collagen organization scores, were predictive of the structural and material properties of the healing ACL in Yucatan minipigs.²⁸ In light of these studies, it seems reasonable to speculate that tissue quantity, even if it is disorganized and contains other tissue elements such as cells and vessels that are not directly reflected by short T₂* relaxation times, is an important factor during early phases of ligament healing. In addition to providing unique information related to biological processes that may precede collagen remodeling, Vol₄ encompasses voxels that are at the opposite end of the spectrum to the information represented by Vol₁ voxels. For this reason, it is the sub-volume that is the least correlated with Vol₁, and therefore most likely to enhance the regression model performance.

Despite models yielding similar AIC values, adding Vol₄ and its interaction terms had the effect of spreading out the predicted ACL failure load, yield load and stiffness values at 6w (compare x-axis values of Figure 2. C & D). This increased dispersion in the predicted structural properties resulted in closer agreement between the model-predicted and actual structural properties in the modified Bland-Altman plots (Figure 3). We can conclude from these results that, unlike the 6-parameter model, the 12-parameter model is likely to yield reasonable estimates of healing ACL structural properties at 6w. Because the addition of the Vol₄ sub-volume influenced the model performance predominantly at the 6w time point, it points to the fact that this sub-volume is especially important at early time points and reflects compositional elements related to the sub-acute healing process that may then modulate collagen organization at later phases of healing. Despite the complexity that the added terms of the 12-parameter regression model produces compared to the 6-parameter model, the similar AIC values of the two models suggests that the complexity is worth the tradeoff for superior model fit, and most importantly, the ability to predict structural properties throughout the transition from acute (6w) to chronic (24w) healing phases.

The signal to noise quotient (SNQ) is another non-invasive MR-based technique used to gauge ACL graft maturity that has been used by others.^18,36–39 The calculation involves sampling the MR signal intensity within a region of interest, and then normalizing the signal intensity to the background noise of the image slice. Like our linear prediction models, the SNQ of the ACL graft has shown some agreement with its underlying histological ultrastructure,^18,36–38 suggesting that normalized signal intensity yields relevant information regarding graft remodeling. In a way, inclusion of Vol₁ and Vol₄ voxels in our prediction models could be considered akin to the signal to noise quotient (SNQ) insofar as Vol₁ and Vol₄ sub-volumes represent the two extremes of MR T₂* properties much like the SNQ is based on two complementary sources of MR signal intensity information. However, it is important to point out the differences between the T₂* sub-volume approach and the SNQ metric: (1) whereas SNQ is dependent on discrete samples taken from a single image slice where the ACL is visible, the sub-volumes described here are based on the entire ACL; (2) signal intensity in the SNQ technique depends on the MR parameters used to acquire the images as well the hardware employed,²³ whereas T₂* is theoretically a more direct measure of tissue organization and composition given its dependence on the local magnetic field inhomogeneities arising from the spin-spin interactions of the protons bound to collagen, and the collagen fibril organization within the tissue;²⁴ and (3) T₂* relaxation times do not require normalization. Therefore, the T₂* approach offers many advantages over the alternative SNQ technique, and is a more direct proxy of in vivo ligament maturity and biomechanical function. Nevertheless, one limitation of the current sub-volume approach is that it does not account for ligament cross-sectional area. If, for example, there is a relative abundance of organized ACL tissue near the ligament origins (i.e., large Vol₁), but there is a region of the ACL with a smaller cross-sectional area, the ACL is likely to fail in this region despite a large overall volume of organized tissue. Defining the Vol₁ and Vol₄ composition within the region of smallest cross-sectional area could further enhance our approach.

Our study is not without limitations. Our sample size was small for a relatively complex multiple linear regression model. Inclusion of both the ACL repair with and without the scaffold in the same dataset served to increase the variation in the structural properties such that the data were nearly continuous over the three healing time intervals assessed. Removing the one failed 6w enhanced repair from the dataset did not affect this distribution, and therefore was not a concern given the study objective. Nevertheless, while the small sample size was sufficient to detect non-random relationships that we expected to observe based on prior experience,^16,17 the fit parameters drawn from this group of animals are likely to vary to some degree. Ideally, we would have preferred to conduct a second study to test the parameters that were optimized from the current dataset on a second, larger, independent group of minipigs. As an alternative to the ideal scenario, applying the parameter models to the same dataset from which the parameters were optimized allowed us to visualize the model slopes over time, and to construct modified Bland-Altman plots to assess the level of agreement between model-predicted and actual values. Although this approach may not be ideal, we were able to use these graphical representations to create context with which to interpret the unit difference in AIC values. Unlike the more widely-used coefficient of determination (R² statistic), unit differences in maximum residual likelihood fit statistics, such as the AIC statistic, are not readily interpretable beyond “less is better”, and is a limitation of the approach. Nevertheless, by interpreting the AIC values alongside both Figures 2 and 3, it became clear that a difference in AIC values of two units or less (Table 1, row 3 vs row 4) is inconsequential in terms of penalization for added parameters, and that the addition of the time-specific effects of Vol₄ does improve model predictions between the 6 and 24w intervals. Lastly, we do not know whether these regression models could be extended to ACL graft healing, to human studies, or whether time points other than 6, 12, and 24w post-surgery can be substituted. It is likely that ACL healing and graft ligamentization undergo similar biological processes such as cellular infiltration, neovascularization and collagen remodeling.^27,40 To this end, we did not find any differences in the tensile properties between ACL grafts and enhanced repair ACLs at 3, 6 or 12 months in Yucatan minipigs.^11,28 However, we have shown that combinations of histological characteristics (i.e., cellularity, collagen, vascularity) that predicted the tensile properties of the grafts or healing ACLs were different,²⁸ suggesting that the direct application of the optimized regression model parameters presented here to predict the structural properties of other ACL constructs should be done with caution. Moreover, our regression models are based on specific 6, 12 and 24w healing time points. A longitudinal study that includes measures of ACL T₂* relaxation times at two-week intervals within the 6–24w time frame is currently underway to investigate the feasibility of predicting healing ACL structural properties at 24 weeks using Vol₁ and Vol₄ measured at either single or multiple time intervals. This follow-up study will also allow us to investigate the change in ACL T₂* relaxation times, and to define how T₂* relaxations times, and the estimated structural properties, change over time within the same subject.

Using non-invasive MR T₂* relaxometry to quantify collagen organization at acute (6w), sub-acute (12w) and chronic (24w) stages of wound healing, we developed a 12-parameter multiple linear regression model to predict the in vivo structural properties of the ACL between 6 and 24 weeks in a preclinical model of ACL repair. In addition to the ACL sub-volume containing the most organized collagen, the sub-volume containing the least organized collagen and time-specific parameters were critical elements of the new regression models that will allow us to evaluate the functional status of the ACL repair in vivo, and with further development, may give surgeons a quantitative metric with which to develop and gauge return to sport criteria.