Synthetic Antiferromagnetic Spintronics

Abstract

Spintronic and nanomagnetic devices often derive their functionality from layers of different materials and the interfaces between them. This is especially true for synthetic antiferromagnets — two or more ferromagnetic layers that are separated by metallic spacers or tunnel barriers and which have antiparallel magnetizations. Here, we discuss the new opportunities that arise from synthetic antiferromagnets, as compared to crystal antiferromagnets or ferromagnets.

Introduction

Advances in nanofabrication techniques for magnetic materials — such as Fe, Ni, Co, Cr and their alloys — have, since the late 1980’s, enabled researchers to engineer stacks of thin (nanometers) layers of magnetic and nonmagnetic material. The study of such magnetic multilayers and superlattices – i.e., periodic multilayers – has led to many discoveries and potential applications. The first among these is the existence of a coupling between two magnetic layers adjacent to the same non-magnetic spacer.^1–3 This interlayer exchange coupling is essentially a Ruderman-Kittel-Kasuya-Yosida (RKKY) coupling that is rooted in spin - dependent Friedel-like spatial oscillations in the spin density of the non-magnetic spacer that are caused by the adjacent ferromagnets. The oscillating spin density in turn leads to an interlayer exchange coupling that oscillates with the distance between the ferromagnetic layers.^4–7 By changing the thickness of non-magnetic material between two magnetic layers one can therefore tune the interaction from ferromagnetic — preferring parallel alignment — to antiferromagnetic, preferring antiparallel alignment, whereas for thick spacers the interlayer exchange coupling is suppressed. Trilayers, multilayers or superlattices, in which the interaction between magnetic layers is antiferromagnetic are now commonly referred to as synthetic antiferromagnets (see Fig. 1). The antiferromagnetic coupling was crucial for the discovery that the resistance of metallic magnetic multilayers depends on the relative orientation of the magnetization in adjacent layers.^8,9 This finding — called giant magnetoresistance (GMR) or, in the case of a tunneling barrier, tunneling magnetoresistance (TMR) — kickstarted the field of nanomagnetism and spintronics.

Figure 1.

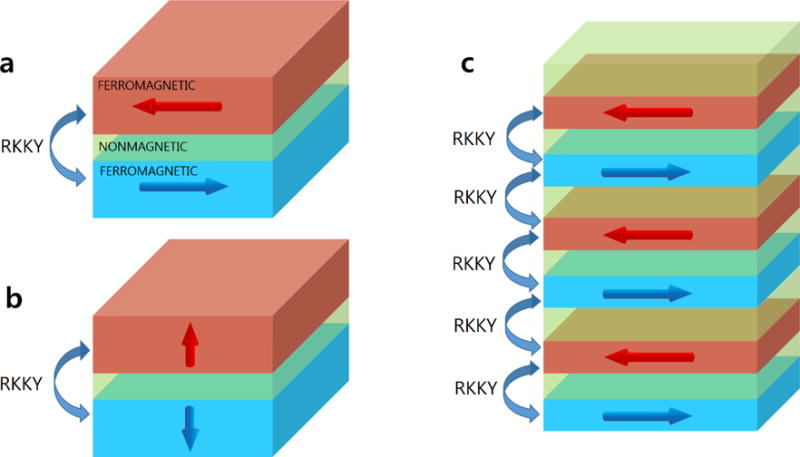
Schematic of synthetic antiferromagnets. a, bilayers with in-plane magnetization. b, bilayers with out-of-plane magnetizations. c, multilayers. The arrows within each ferromagnetic layer indicate the direction of magnetization. Depending on the magnetic configurations the RKKY coupling and dipolar fields add (a) or subtract (b) leading in part to the large degree of tunability of multilayers.

Let us first compare synthetic with crystal antiferromagnets, i.e., the antiferromagnets found in nature as bulk single crystals. An important difference is that the interlayer exchange coupling in synthetic antiferromagnets is much weaker than the direct exchange or superexchange coupling in crystal antiferromagnets. This difference allows for manipulation of the antiferromagnetic order more easily in synthetic antiferromagnets than in crystal antiferromagnets. Moreover, the magnetic state or texture in synthetic antiferromagnets is easily detectable by the magneto-optical Kerr effect or the anomalous Hall effect (when making thicknesses of two ferromagnetic layers slightly different). As a result, antiferromagnetic magnetization dynamics in synthetic antiferromagnets can be studied using conventional techniques employed for ferromagnets as e.g. shown in Ref. 10, an approach that is challenging for crystal antiferromagnets.

Another difference is that the repeat distance of the antiferromagnetic order in synthetic antiferromagnets is larger than in crystal antiferromagnets. While in the latter, the magnetic order alternates on atomic length scales, the layer thickness in magnetic multilayers is typically several nanometers. For most situations, electron transport within one magnetic layer is therefore appropriately described by a spin-dependent semi-classical model.¹¹ GMR, for instance, is typically modelled by taking into account electron diffusion within the magnetic layers supplemented with spin-dependent resistances of the various layers and interfaces between them, as well as spin relaxation. For crystal antiferromagnets this picture breaks down as the electrons are in that case phase coherent over a region that is larger than the length scale of the antiferromagnetic order.

Because of the above-mentioned energy and spatial scales, synthetic antiferromagnets are largely tunable via layer thickness and material composition. In the remainder of this commentary we review some features of synthetic antiferromagnets and discuss possible new directions that derive from this tunability.

Statics and dynamics

The tunability of synthetic antiferromagnets, and magnetic multilayers in general, allows for optimization of properties that are desirable for applications including magnetic-field sensing and magnetic random access memory (MRAM).^12–17 In these examples, the important physics is the tuning of stray fields to manipulate stability and sensitivity, and the extra degrees of freedom provided by the layers and coupling between them. The latter leads to additional – with respect to a single magnetic layer – dynamical modes that alter the dynamics and may decrease the switching time of the memory cells. These are also relevant for the development of spin-torque oscillators based on synthetic antiferromagnets¹⁸ with increased tunable frequency range and reduced linewidth, which is an active and ongoing research topic. The dynamics of synthetic antiferromagnets is also relevant for switching by spin-orbit torques that has recently been demonstrated in devices containing synthetic antiferromagnetic layers.^19,20.

An attractive research direction that brings the tunability to the next level is to alter the magnetic properties of the synthetic antiferromagnets in-situ by electric fields, rather than by engineering different systems with different properties. For example, it was theoretically proposed in Ref.²¹ that the interlayer exchange coupling can be switched from ferromagnetic to antiferromagnetic either by an electric field – as demonstrated experimentally very recently²² - or by making use of a ferroelectric layer.

While the magnetic layers in synthetic antiferromagnets are presently almost always metallic, an interesting possibility is to consider insulators. Structures based on insulators have, for example, been predicted to exhibit thermal spin torques leading, e.g., to dynamical instabilities such as switching and auto-oscillations²³. Moreover, the tunability and rich dynamics of magnetic multilayers could be put to use to enhance and manipulate effects, such as the spin Seebeck and the spin Peltier effects²⁴, that have been recently discovered in insulator spintronics. One of the most interesting prospects of this field is that of room-temperature spin superfluidity²⁵. Here, the partial cancellation of dipolar fields in a synthetic antiferromagnetic insulator would lead to the desired reduction of the critical current below which the spin superflow is prohibited. The workhorse of insulator spintronics is the magnetic insulator Yttrium Iron Garnet (YIG) of which it is very hard to make arbitrary heterostructures. Nonetheless, some progress has been made, for example in experiments on heterostructures of YIG and the antiferromagnetic insulator NiO that demonstrate spin transport through the NiO²⁶. More developments in this direction are expected in the near future.

Domain walls and solitons

The motion of domain walls and solitons in synthetic antiferromagnets has been studied both theoretically and experimentally.^27–31 Most of the ongoing research on current-driven domain wall motion focuses on multilayers that involve heavy elements with strong spin-orbit coupling, such as Pt or Ta, as the nonmagnetic layers. This spin-orbit coupling has several new physical consequences. First of all, the boundary between heavy nonmagnetic and magnetic metal leads to interface-induced Dzyaloshinskii-Moriya (DM) interactions^{32, 33} (see box). These interactions lead to chiral domain walls — domain walls in which the spins have a preferred sense of rotation. In particular, the interfacial DM interactions stabilize Ńeel domain walls that are efficiently driven by spin-orbit torques. These spin-orbit torques are also induced by the spin-orbit coupling in the heavy metallic layer. As shown in Ref. 10, the interlayer exchange coupling in synthetic antiferromagnets stabilizes the Ńeel structure of the walls such that they can be driven more efficiently by spin-orbit torques. On top of this, the interlayer exchange coupling leads to additional torques that efficiently drive the domain walls in both ferromagnetic layers in the same direction. It was experimentally shown in Ref. 10 that large domain wall velocities (of up to 750 m/s) are obtained for domain walls in synthetic antiferromagnets of Co/Ni magnetic layers, separated by thin layers of Ru. This large velocity is basically due to the interlayer-exchange-enhanced dynamics that we discussed previously in the context of magnetic memories and spin-torque oscillators.

BOX. DZYALOSHINSKII-MORIYA (DM) EXCHANGE INTERACTIONS.

Apart from the well-known Heisenberg-type exchange interactions between spins in ferromagnetic materials, there can exist so-called Dzyaloshinskii-Moriya (DM) interactions in magnetic systems that lack a center of inversion and exhibit spin-orbit coupling. In the situation of two magnetic atoms (spin S₁ and S₂) in presence of a third non-magnetic atoms with spin-orbit coupling (see figure) this interaction has the form ~D·S₁×S₂, with D the Dzyaloshinskii vector and R₁ and R₂ the respective positions of the magnetic atoms with respect to the non-magnetic one.

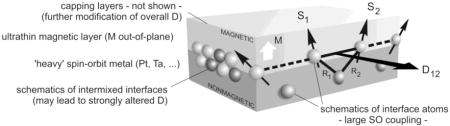
This interaction clearly favors a certain misaligned and turning sense (chirality) of the magnetic moments. Most important for magnetic multilayers are the DM interactions induced by interfaces between magnetic metals and metals with strong spin-orbit coupling. Figure adapted from Nature Nanotech. 8, 152 (2013).

Control of the motion of a completely different type of domain walls was demonstrated by Lavrijsen et al.³¹. The domain walls considered in this work are kink defects in the antiferromagnetic order of the synthetic antiferromagnet such that two adjacent magnetic layers have magnetizations that are parallel, rather than antiparallel. In a superlattice designed with different interlayer exchange coupling and different magnetic layer thicknesses, these authors were able to demonstrate injection and propagation of kinks by external field pulses. This latter work is an attractive example of how the large tunability of synthetic antiferromagnets, and magnetic multilayers in general, can be put to use to enable new functionalities.

Textures and spin waves

Most experimental research in magnetic multilayers has so far focused on magnetic states where the magnetization within one layer is approximately homogeneous. As the examples of spin superfluidity and domain walls show, it is interesting to move away from this paradigm and to consider inhomogeneity and/or propagation in the lateral direction. It has been known that the interplay between inter and intralayer exchange and magnetostatic effects may lead to interesting textured ground states. (See for example Ref. 34.) The interest in such textures has been revived in the context of magnetic skyrmions that are stabilized by DM interactions. In these developments, magnetic multilayers are playing an important role. The dynamics of skyrmions in synthetic antiferromagnets is particularly interesting. While there has not been much work yet in this direction, Ref. 35 pointed out that the Magnus force that acts on a skyrmion — or more generally on two-dimensional magnetic structures that have a nonzero winding number — and pushes them sideways is counteracted and cancelled by the interlayer exchange coupling in synthetic antiferromagnets. This is beneficial for applications in which skyrmions are driven along narrow wires, as the sideways motion may cause the skyrmions to interact with the edges of the wire and disappear.

Another active direction of current research is magnonics, which aims to exploit spin waves in building beyond-Moore devices. While this field has seen substantial experimental progress recently³⁶, it is mostly restricted to YIG because of its low spin-wave damping. Connecting to our earlier remarks about insulators, it would be interesting to put synthetic antiferromagnets to use for manipulating spin waves. Tuning their magnetic properties or spin textures would directly translate to tuning the properties, such as velocity and gap, of the spin waves. An example towards this direction is that in the presence of Dzyaloshinskii-Moriya interaction, a magnetic domain wall in a synthetic antiferromagnet serves as spin wave polarizer and retarder.³⁷ In general, spin waves have elliptical precession but with a well-defined rotational sense. In ferromagnets, they have only one sense, typically right-handed, but in antiferromagnets, they have both, allowing antiferromagnetic magnonics to mimic various functionalities of optics. Another example is that of Ref. 37 which shows that the spin-wave non-reciprocity can be tuned by the interlayer exchange coupling.

So far we have discussed synthetic antiferromagnets with a layered structure, so that the superlattice is one dimensional. A very different example is that of artificial spin ice³⁹. This is a synthetic antiferromagnet with a two-dimensional frustrated superlattice. While most of the interest in such systems is motivated by simulating and understanding equilibrium properties of frustrated magnets, artificial spin ice has recently also been exploited for manipulating spin waves.⁴⁰ More generally, going from one to two dimensions and using the superlattice geometry adds an interesting new degree of tunability that seems little explored in the context of spintronic functionalities, such as the interplay between magnetic order and spin and charge transport.

In conclusion, the examples we have discussed ultimately show that synthetic antiferromagnets should be thought of as materials with properties in between those of ferromagnets and antiferromagnets. Some of their properties derive from the ferromagnetic layers that constitute them, whereas other properties derive from the coupling between these layers. Engineering and exploiting their tunability will surely lead to new physics and applications for the years to come.