Network-Based Coverage of Mutational Profiles Reveals Cancer Genes

SUMMARY

A central goal in cancer genomics is to identify the somatic alterations that underpin tumor initiation and progression. While commonly mutated cancer genes are readily identifiable, those that are rarely mutated across samples are difficult to distinguish from the large numbers of other infrequently mutated genes. We introduce a method, nCOP, that considers per-individual mutational profiles within the context of protein-protein interaction networks in order to identify small connected subnetworks of genes that, while not individually frequently mutated, comprise pathways that are altered across (i.e., “cover”) a large fraction of individuals. By analyzing 6,038 samples across 24 different cancer types, we demonstrate that nCOP is highly effective in identifying cancer genes, including those with low mutation frequencies. Overall, our work demonstrates that combining per-individual mutational information with interaction networks is a powerful approach for tackling the mutational heterogeneity observed across cancers.

In Brief

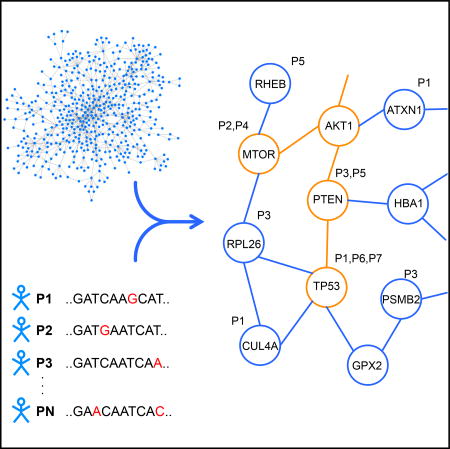
Cancer-relevant genes, including those rarely mutated across samples, can be effectively identified by considering perindividual mutational profiles in the context of interaction networks and uncovering small connected subnetworks of genes, presumably participating in shared processes, that together are altered across (i.e., “cover”) a large fraction of individuals.

INTRODUCTION

Cancer genomics initiatives have sequenced the protein-coding regions of thousands of tumor samples across tens of different cancer types (TCGA Research Network). Initial analyses of these data have revealed that while there may be numerous somatic mutations in a tumor that result in altered protein sequences, very few are likely to play a role in cancer development (Bozic et al., 2010; Vogelstein et al., 2013; Garraway and Lander, 2013). Therefore, a major challenge in cancer genomics is to develop methods that can distinguish the so-called “driver” mutations important for cancer initiation and progression from the numerous other “passenger” mutations.

Statistical approaches identify cancer-driving genes by highlighting those that are mutated more frequently in a cohort of patients than expected according to some background model (Youn and Simon, 2011; Dees et al., 2012; Lawrence et al., 2013). However, the genetic underpinnings of cancer are highly heterogeneous: even when considering a single cancer type, very few genes are found to be somatically mutated across large numbers of individuals (Hudson et al., 2010). Furthermore, genes altered only in a few individuals may also be important for tumorigenesis and cancer progression (Stratton et al., 2009). Clearly, these rarely mutated but cancer-relevant genes cannot be detected by purely frequency-based approaches.

A promising alternative viewpoint is to consider somatic mutations in the context of pathways instead of genes. It has been proposed that alterations within any of several genes comprising the same pathway can have similar consequences with respect to cancer development, and that this contributes to the mutational heterogeneity evident across cancers. Consistent with this, numerous analyses have shown that certain known pathways are frequently altered across tumor samples of a particular cancer via mutations in different genes (The Cancer Genome Atlas Network, 2012; McLendon et al., 2008). Early studies have leveraged this observation by analyzing known pathways for enrichment of somatic mutations (Jones et al., 2008; Cerami et al., 2010) and pinpointing those that are significantly mutated across patients (Wendl et al., 2011; Vaske et al., 2010). However, our knowledge of pathways is incomplete and thus unknown but altered pathways cannot be identified by these approaches.

De novo discovery of cancer-relevant pathways using large-scale protein interaction networks has thus been the focus of several newer methods (Vandin et al., 2011; Cerami et al., 2010; Ciriello et al., 2012; Paull et al., 2013; Shrestha et al., 2014; Bertrand et al., 2015; Cho et al., 2016), as proteins taking part in the same pathways and processes tend to be proximal in networks (Spirin and Mirny, 2003). One prominent class of techniques leverages this network structure by propagating mutational information through protein interaction networks and deriving pathways from the induced subnetworks (Vandin et al., 2011; Leiserson et al., 2015; Jia and Zhao, 2014; Babaei et al., 2013). However, such diffusion approaches can be highly influenced by frequently mutated genes (Leiserson et al., 2015) and, further, these methods do not consider whether most patients have mutations in any of the identified pathways.

Here we present a novel network-based approach to tackle cancer mutational heterogeneity by utilizing per-individual mutational profiles. Our method is based on the expectation that if a pathway is relevant for cancer, then (1) many individuals will have a somatic mutation within one of the genes comprising the pathway and (2) the genes comprising the pathway will interact with each other and together form a small connected subcomponent within the larger network. Therefore, given a biological network as well as patient sample data consisting of somatic point mutations, the goal of our approach is to find a set of candidate genes that both “cover” the majority of patients (i.e., individuals have mutations in one or more of these genes) and are connected in the network (i.e., these genes are likely to participate in the same cellular pathway or process). In contrast to network diffusion approaches, our framework focuses on per-individual mutational profiles, and as a result the “influence” of frequently mutated genes is not spread through the network. We note that network-based coverage approaches have been previously introduced to identify pathways that are dysregulated (Ulitsky et al., 2010; Chowdhury and Koyuturk, 2010; Kim et al., 2011) or mutated (Dand et al., 2013; Kim et al., 2015) across samples. However, either patients were required to be covered by these approaches (Ulitsky et al., 2010; Chowdhury and Koyuturk, 2010; Kim et al., 2011, 2015), in some cases multiple times (which is especially relevant for dysregulated genes, since there are many of them), or these approaches were designed for datasets with significantly fewer mutations (Dand et al., 2013); both cases lead to very different optimizations and algorithms that are not effective for the task at hand. Alternatively, other approaches have attempted to find sets of mutated genes that cover not patients but instead genes dysregulated in cancers, with coverage defined by short paths in interaction networks (Bashashati et al., 2012; Shrestha et al., 2014; Bertrand et al., 2015).

We devise a simple yet intuitive objective function that balances identifying a small subset of genes with covering a large fraction of individuals. Our objective has just a single parameter that is automatically set using a series of cross-validation tests, thus eliminating the need of many previous approaches to manually select values for various thresholds and parameters. We develop an integer linear programming formulation to solve this problem and also give a fast heuristic algorithm. We apply our method—network-based coverage of patients (nCOP)—to 24 cancer types from The Cancer Genome Atlas (TCGA) (TCGA Research Network) and uncover both well-known and newly predicted cancer genes, including those that are rarely mutated. We demonstrate that nCOP is superior to previous methods that do not use network information, including a state-of-the-art frequency-based method (Lawrence et al., 2013) and a “set cover” version of our approach that attempts to find a set of genes that covers cancer samples without considering network connectivity. Finally, we compare nCOP with recent network-based methods that aggregate mutational information and show that our per-patient approach readily outperforms them.

RESULTS

Algorithm Overview

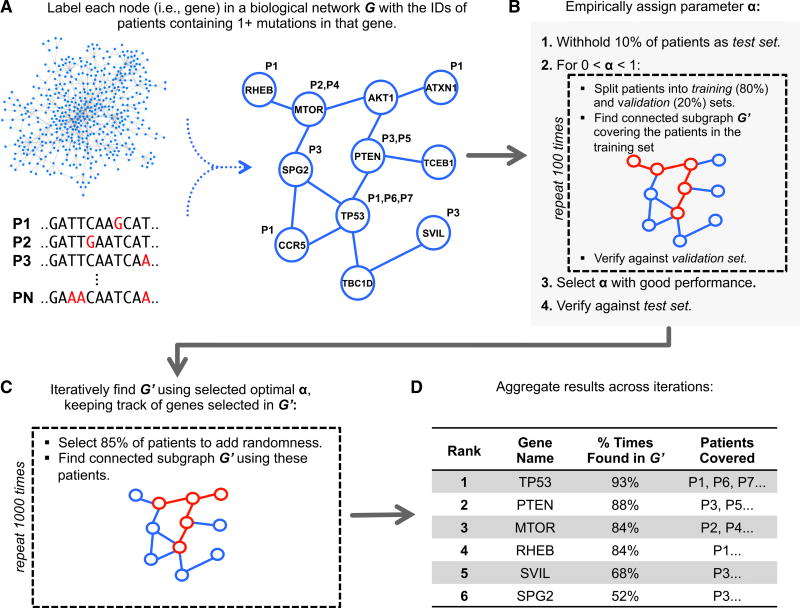
We begin by giving a brief summary of our method (Figure 1). The biological network is modeled as an undirected graph where each vertex represents a gene, and there is an edge between two vertices if an interaction has been found between the corresponding proteins. Each node is annotated with the IDs of the individuals having one or more mutations in the corresponding gene (Figure 1A). We aim to find a relatively small connected component such that most individuals have mutations in one of the genes within it. A small subgraph is more likely to consist of functionally related genes and is less likely to be the result of overfitting to the set of individuals whose diseases we are analyzing. However, we would also like our model to have the greatest possible explanatory power—that is, to account for, or cover, as many individuals as possible by including genes that are mutated within their cancers. We formulate our problem to balance these two competing objectives with a parameter α that controls the trade-off between keeping the subgraph small and covering more patients.

Figure 1. Overview of Our Approach.

(A) Somatic mutations are mapped onto a protein-protein interaction network. Each node is associated with the set of individuals whose cancers have mutations in the corresponding gene. The overall goal is to select a small connected subnetwork such that most individuals in the cohort have mutations in at least one of the corresponding genes (i.e., are “covered”).

(B) nCOP automatically selects a value for the parameter α by performing a series of cross-validation tests. First, 10% of the individuals are withheld as a test set. Next, the remaining individuals are repeatedly and randomly split into two groups, a training set (80%) and a validation set (20%). For each split, the nCOP search heuristic is run for 0 < α < 1 using the individuals comprising the training set. An α is selected to obtain high coverage of the individuals in the validation sets while maintaining similar coverage on the training sets (i.e., not overfitting to the training sets). Coverage of individuals in the initially withheld test set is also calculated and confirmed to be similar to the validation sets.

(C) Once α is selected, to avoid overfitting on the entire dataset, nCOP is run 1,000 times using random subsets of 85% of the individuals.

(D) Finally, the subnetworks output across the runs are aggregated and candidate genes are ranked by the number of the times they appear across these subnetworks.

For a fixed value of α, we have developed two approaches to solve the underlying optimization problem. One is based on integer linear programming and the other is a fast greedy heuristic (see STAR Methods). We use the greedy heuristic in the context of a carefully designed cross-validation procedure to select a value for α that results in good coverage of patients but avoids overfitting to them (Figure 1B). Once α is selected, this value is used within our objective function and we next analyze the entire patient cohort. In particular, multiple independent trials using α are run on randomly chosen subsets of the patient data (Figure 1C), as we have found that introducing a small amount of randomness helps increase performance in comparison with a single run on the full dataset. Each trial outputs a subgraph, and our final aggregated output is an ordered list of candidate genes ranked by how frequently each has been selected over the trials (Figure 1D).

We run nCOP, using the greedy heuristic algorithm, on somatic point mutation data from 24 different TCGA cancer types. Results in the main paper use the HPRD network (Prasad et al., 2009) for all analysis and highlight kidney renal clear cell carcinoma (KIRC) with 416 samples as an exemplar.

Automatic Parameter Selection Reveals Generalizability of Uncovered Subnetworks

Our optimization function for uncovering a subnetwork of mutated genes that covers many patients has one parameter, α. Large values of α result in a larger number of selected genes that cover more patients, yet may contain more irrelevant genes; this may especially be a factor if there are many samples where missense mutations are not the driving event. To choose an appropriate value for α on a dataset, we split our cancer samples into training, validation, and test sets, run our greedy heuristic using samples in the training set, then choose an α where patient coverage deviates between the training and validation sets (see STAR Methods). This framework differs from a traditional machine learning cross-validation setting in that there is no training using a set of trusted examples; instead, our intuition is that cancer-relevant genes that are uncovered using the training samples should also cover samples outside of this set.

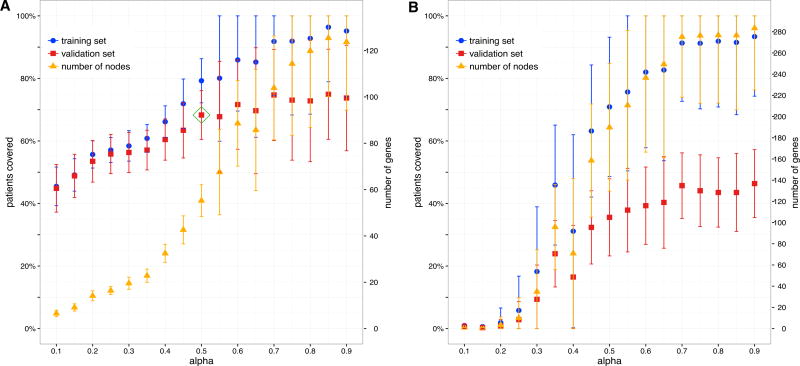
We demonstrate that, across the 24 cancer types, our cross-validation framework is a highly effective approach for choosing an α that balances patient coverage with subnetwork size. For all cancers, as α increases, the total number of genes in the chosen subnetwork G′ increases (as expected), as does the fraction of patients in the training set that are covered by these genes (Figures 2A and S1). For smaller values of α, coverage on the validation sets closely matches that obtained on the training sets; that is, the sets of genes chosen using patients in the training sets are also effective in covering patients in the corresponding validation sets. For KIRC, when α = 0.5, genes chosen using the training sets cover on average nearly 70% of patients in the corresponding validation sets, with coverage on the completely withheld test set within 5% of this. The fact that a small subnetwork can be found that covers a large fraction of previously unseen patients is consistent with the hypothesis that a shared pathway or process plays a role in most (but not all) of these patients’ cancers.

Figure 2. Automatic Parameter Selection.

For each random split of individuals, we run our algorithmon the training set for different values of α, and next plot the fraction of covered individuals in the training (blue) and validation (red) sets. We also give the number of proteins in the uncovered subgraphs (orange). For each plotted value, the mean and SD over 100 random splits are shown. The approach is illustrated using the KIRC dataset and the HPRD network.

(A) When using somatic missense mutations, at higher values of α, overfitting occurs as the coverage on the validation set levels while coverage on the training set continues to increase. An automated heuristic procedure selects α (green rhombus) so that coverage on the validation set is good while overfitting on the training set is not extreme.

(B) When using somatic synonymous mutations, there is poor coverage on the validation set regardless of coverage on the training set. Furthermore, compared with using missense mutation data, significantly more genes are required to cover the same fraction of individuals.

For larger values of α (>0.6 for KIRC), however, coverage on the validation sets lags behind that observed on the training sets. For even larger values of α (>0.85 for KIRC), the algorithm selects many genes, and eventually increases the coverage for most cancers on the training sets to nearly 100%. However, larger values of α do not substantially increase coverage of the withheld patients. This difference between the training and validation curves captures the overfitting of the model and also illustrates the trade-off between covering more patients and keeping the solution parsimonious. We note that the eventual plateau of the validation curve is consistent across cancer types (Figure S1). For each cancer type, values of α are selected by an automated procedure (see STAR Methods); this value is α = 0.5 for the KIRC dataset shown in Figure 2A.

As a control, we repeat the same procedure using only synonymous mutations (Figure 2B). Although coverage of course increases as more nodes are added, it never exceeds 50% on the validation sets even when α is increased to 1 or when we have nearly perfect coverage on the training set, despite adding many more nodes. This poor coverage is consistent with the expectation that synonymous mutations do not result in altered protein sequences and do not disturb cellular pathways. Hence, given the differences observed between using missense versus silent mutation data and when comparing training and validation sets, our formulation appears to be well suited for investigating mutational profiles in the context of interaction networks.

nCOP Effectively Uses Network Information to Uncover Known Cancer Genes

Having shown in the previous section how to select a value for the only parameter in the model, we next evaluate nCOP’s performance in uncovering known cancer genes (CGCs) (Futreal et al., 2004).

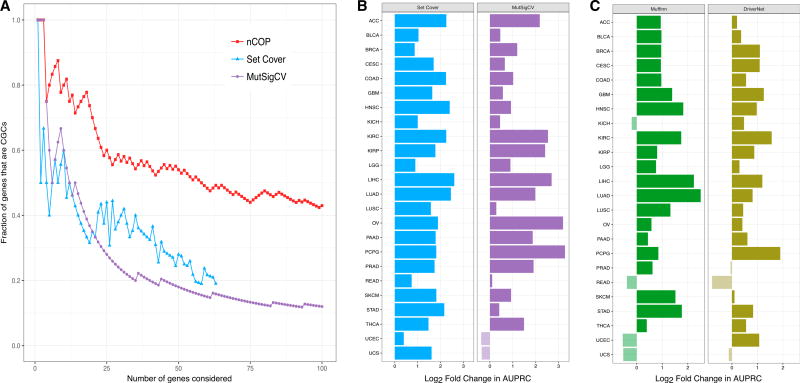
We first consider the KIRC dataset, and find that our top predictions include a high fraction of CGC genes (Figure 3A). To illustrate the power of our network-based method, we compare its performance with those of two approaches that do not consider any network information: a “set cover” version of our approach that simply tries to cover patients and the commonly used frequency-based method, MutSigCV (Lawrence et al., 2013). For the same number of predicted genes, nCOP consistently has a larger fraction of CGCs than either approach, demonstrating the advantage of using network information.

Figure 3. nCOP Is More Successful than Other Methods in Identifying Known Cancer Genes.

(A) Our network-based algorithm nCOP, a set cover version of our algorithm that ignores network information, and MutSigCV, a frequency-based approach, are compared on the KIRC dataset. nCOP ranks genes based on how frequently they are output, and MutSigCV ranks genes by q values. The set cover approach is run for increasing values of k until all patients are covered. For each method, as an increasing number of genes are considered, we compute the fraction that correspond to CGCs. Over a range of thresholds, our algorithm nCOP outputs a larger fraction of CGC genes than the other two approaches.

(B) Comparison of nCOP to two network-agnostic methods across 24 cancer types. For each cancer type, we compute AUPRCs for nCOP, the set cover approach, and MutSigCV, using their top 100 predictions. We give the log₂ ratios of nCOP’s AUPRCs to the other methods’ AUPRCs. Our approach nCOP outperforms the set cover approach on all 24 cancers, and MutSigCV on 22 of the 24 cancer types.

(C) Comparison of nCOP with two network-based methods, Muffinn and DriverNet, across 24 cancer types. Our approach nCOP outperforms Muffinn and DriverNet on 20 and 21, respectively, of the 24 cancer types.

We next compare nCOP with these two non-network approaches using the area under the precision-recall curve (AUPRC) across all 24 cancer types, and find that it outperforms MutSigCV in 22 of the 24 cancers and the set cover approach in all cancers, thus demonstrating the clear advantage of using network information. The performance improvement of nCOP over the set cover approach is particularly notable, as the main difference between these approaches is the additional use of network information by nCOP. In several cancers, the performance improvements of nCOP are substantial. For example, nCOP shows a 4-fold improvement over MutSigCV in uncovering cancer genes for liver hepatocellular carcinoma and an 8-fold improvement over MutSigCV on pheochromocytoma and paraganglioma (PCPG). The overall results are consistent across different lists of known cancer genes (Figures S2A and S2B), numbers of predictions considered (Figure S2C), and networks (Figure S2D).

Having shown that nCOP better identifies cancer-relevant genes than two approaches that do not use network information, we next consider whether the specific way in which nCOP uses network information is beneficial. First, to confirm the importance of network structure to nCOP, we run it on randomized networks and find that (as expected) overall performance deteriorates across the cancer types (Figure S2E). Second, we verify that genes are not more likely to be picked by nCOP simply because they have higher degree: among all newly predicted genes found across all cancer types, we find that most have degree less than 15, and there are only a couple with high degree (≥50). Finally, we compare the effectiveness of nCOP in uncovering cancer genes with that of Muffinn (Cho et al., 2016), a method that considers mutations found in interacting genes, and DriverNet (Bashashati et al., 2012), a method that finds driver genes by uncovering sets of somatically mutated genes that are linked to dysregulated genes. We find that nCOP outperforms Muffinn on 20 and DriverNet on 21 of the 24 cancer types (Figure 3C). We also compare nCOP with Hotnet2 (Leiserson et al., 2015), a cutting-edge network diffusion method. As Hotnet2 does not output a ranked list of genes, we do not compute an AUPRC. Instead, examining the complete list of genes highlighted by both methods, we observe that nCOP exhibits significantly better precision while trailing slightly in recall (Figure S3).

nCOP Newly Predicts Rarely Mutated Cancer Genes

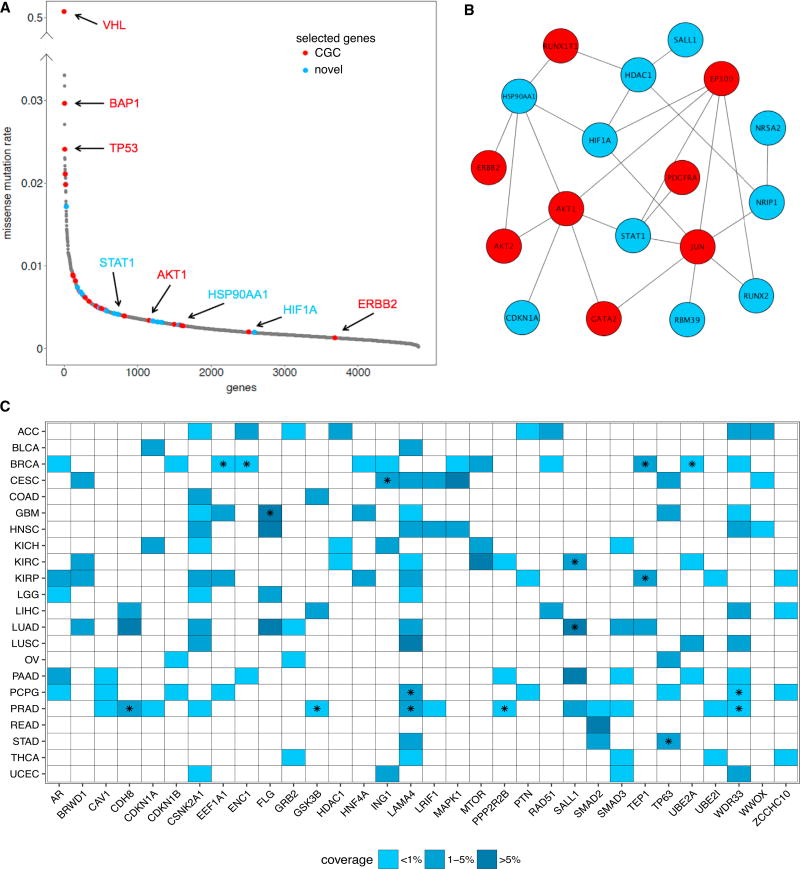
We next demonstrate that nCOP highlights genes with a range of mutation rates. When considering genes that are output by nCOP in at least 50% of the trials on the KIRC samples, we see many well-known cancer players: some are highly mutated, such as VHL, BAP1, and TP53, while others, such as ERBB2 and RUNX1T1, are each mutated only in a handful (<1%) of samples. While the former set of genes can be uncovered by any frequency-based technique, the latter have missense mutation rates that are similar to those of genes not relevant for cancer (Figure 4A) and are thus difficult to uncover by frequency-based methods. Indeed, of the 4,818 genes that have any missense mutation across the KIRC samples, nCOP identifies 47 as cancer relevant, with 24 of those in the bottom 90% of mutated genes with respect to their missense mutation rates. Among these 24 genes, 12 are CGCs (p < 10⁻⁸, hypergeometric test). The statistically significant enrichment of CGC genes in the rarely mutated genes found by nCOP is true across all cancers except for uterine carcinosarcoma, where nCOP predicts only six genes. Thus, nCOP provides a means for pulling out cancer genes from the “long tail” (Garraway and Lander, 2013) of infrequently mutated genes.

Figure 4. nCOP Identifies Rarely Mutated Genes.

(A) The missense mutation rates, computed for each gene as the total number of missense mutations observed within it divided by the product of the number the samples and the length of the gene in nucleotides per 10³ bases, are sorted from high to low and are shown for all mutated genes in the KIRC dataset. Genes that are output by nCOP in at least half the trials are shown in red for known cancer genes and in blue for new predictions. All other genes are shown in gray. Well-known cancer genes output by nCOP, such as VHL and TP53, are at the peak of the distribution. nCOP is also able to uncover known cancer genes with very low mutational rates lying at the tail of the distribution.

(B) Several of the infrequently mutated genes selected by nCOP form a module with five genes that belong to the prominent cancer PI3K-AKT signaling pathway. Red nodes denote CGC genes and blue nodes denote novel predictions.

(C) Shown are all newly predicted, non-CGC genes that are uncovered by nCOP in more than three cancer types. The majority of these predictions are mutated in less than 5% of the samples in the corresponding cancers in which they are implicated. A star indicates that the gene covers an individual of a particular cancer type who does not have any protein coding affecting variant in any CGC gene.

In addition to ranking known cancer genes highly, nCOP also gives high ranks to several non-CGC genes that may or may not be implicated in cancer, as our knowledge of cancer-related genes is incomplete. Among these novel predictions for KIRC are HIF1A, NR5A2, and SALL1, which have all recently been suggested to play a role in cancers (Schwab et al., 2012; Wolf et al., 2014; Lin et al., 2014) and are each mutated in less than 3% of the samples. SALL1 is a zinc-finger transcription factor that plays a role in kidney development (Chai et al., 2006), and mutations within it have been linked to Townes-Brocks syndrome, a rare genetic disease associated with kidney abnormalities and malformation (Kohlhase et al., 1998). Among the individuals in the KIRC dataset covered by the SALL1 gene, one has no mutations affecting protein coding in any known cancer gene. Thus, while this particular individual’s tumor is not driven by mutations in known cancer genes, nCOP pinpoints a role for SALL1.

Several of the genes uncovered by nCOP with low missense mutation rates in KIRC are part of the PI3K-AKT signaling pathway, a prominent cancer pathway that promotes cell survival and growth. When considering the 28 genes output by nCOP with missense mutation rates lower than that of AKT2, a key component of this pathway, we find that 18 of them form a small connected component (Figure 4B) and together are mutated in ~14% of the samples. Three of our novel predictions, STAT1, CDKN1A, and HSP90AA1, interact with AKT1. Existing literature (Pensa et al., 2013; Koromilas and Sexl, 2013; Cazier et al., 2014; Chu et al., 2013) supports a possible role of these genes in tumor progression. Notably, STAT1, a gene that modulates diverse cellular processes, such as proliferation, differentiation, and cell death, also covers an individual with no variants in any known cancer gene. When we consider the full ranked list of genes output for KIRC and perform a rank-based gene set enrichment analysis using the GSEA tool (Subramanian et al., 2005), four pathways from the KEGG database, all cancer relevant, are enriched at p < 0.05 (microRNAs in cancer, pathways in cancer, jak stat signaling pathway, and choline metabolism in cancer).

When run individually on all 24 cancer types, nCOP newly implicates 32 genes as relevant in at least three cancer types (Figure 4C). These genes typically are infrequently mutated, with 93% of them mutated in fewer than 5% of the samples in each of the cancers in which they are predicted to play a functional role. Several of the novel genes unveiled by nCOP are found in individuals whose cancers do not harbor somatic mutations in any known cancer gene; thus, somatic mutations within these novel genes are promising as candidate driver events within these cancers. Across all cancer types, there are 285 patients who do not have mutations affecting protein coding in any known cancer gene, and nCOP covers 114 of them (40%) by selecting 100 genes. The selection of these novel genes is not driven by samples with large numbers of mutations (Figure S4A), and 13 appear in more than 3 cancers (Figure 4C). While some newly uncovered genes may be false positives, others (such as SALL1 and STAT1) are strong candidate genes for further investigation. This analysis illustrates the power of nCOP to zoom in on rarely mutated genes and to help uncover the genetic underpinnings of the studied tumor samples.

DISCUSSION

We have shown that nCOP, a method that incorporates individual mutational profiles with interaction networks, is a powerful approach for uncovering cancer genes. Our method is based on an intuitive mathematical formulation, is more effective than other recent methods in identifying known cancer genes, and is particularly well suited to highlight infrequently mutated genes that are nevertheless relevant for cancer. Our approach therefore complements existing frequency-based methods that generally rely on comparisons with background mutational models and lack the statistical power to detect genes mutated in fewer individuals.

In the future, nCOP can be extended in a number of natural ways. First, while nCOP currently analyzes only mutations within genes, other alterations are also commonly observed in cancers. For example, copy-number variations (CNVs) are found frequently in cancers and can play critical functional roles (Zack et al., 2013). Indeed, as the numbers of CNVs and point mutations found within each cancer genome appear to be inversely related (Ciriello et al., 2013), considering both types of alterations will increase the power of our approach. Second, nCOP may also benefit from incorporating gene weights that reflect likelihood to play a role in cancer. While we currently consider weights based on gene length, alternative gene weights may be derived from existing approaches to detect significantly mutated genes or to assess the functional impact of mutations. Finally, while nCOP can output groups of genes that are not part of a single connected component due to our randomized aggregation procedure, extending nCOP’s core algorithms to explicitly consider multiple subnetworks corresponding to distinct pathways may be a particularly promising avenue for future work.

We have applied nCOP across 24 different cancer types and have shown that it is broadly effective in identifying cancer genes in each of them. However, cancers affecting the same tissue can often be grouped into distinct subtypes based on molecular features (e.g., see Perou et al., 2000). In future applications, nCOP could be used to study how different known subtypes of a given type of cancer yield overlapping or differing perturbed pathways. Even more interesting, and with immediate clinical relevance, would be to extend nCOP to stratify patients into different cancer subtypes (e.g., see the network method of Hofree et al. [2013]) based upon the differently perturbed modules uncovered by nCOP.

We conclude by noting that researchers can use our framework to rapidly and easily prioritize cancer genes, as nCOP requires only straightforward inputs and runs on a desktop machine. Indeed, nCOP’s efficiency, robustness, and ease of use make it an excellent choice to investigate cancer as well as possibly other complex diseases. As sequencing costs plummet and cancer and other disease sequencing mutational data become more abundant, the predictive power of our method should only increase (Figure S4B). In sum, we expect that our method nCOP will be of broad utility and will represent a valuable resource for the cancer community.

STAR*METHODS

Detailed methods are provided in the online version of this paper and include the following:

• KEY RESOURCES TABLE

• CONTACT FOR REAGENT AND RESOURCE SHARING

• METHOD DETAILS

  • General Formulation

  • Integer Linear Programming Formulation

  • Greedy Heuristic

  • Parameter Selection and Solution Aggregation

  • Data Sources and Pre-processing

• QUANTIFICATION AND STATISTICAL ANALYSIS

  • Performance Evaluation

• DATA AND SOFTWARE AVAILABILITY

STAR*METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Mona Singh (mona@cs.princeton.edu).

METHOD DETAILS

General Formulation

We model the biological network, as usual, as an undirected graph G = (V,E) where each vertex represents a gene, and there is an edge between two vertices if an interaction has been found between the corresponding protein products. Each vertex v_j is associated with a set C_j containing the IDs of the individuals who have somatic mutations in the corresponding gene. We formulate our problem as that of finding a connected subgraph G’ of G so as to minimize

$$\alpha X+(1-\alpha )\mathit{\text{ Size}}(G\prime ),$$

where X is the fraction of patients that do not have an alteration in a gene included in G’ (i.e., they are uncovered), Size(G’) is the size of the subgraph, and 0 ≤ α ≤ 1 is a fixed parameter controlling the trade-off between keeping the subgraph G’ small and covering more patients. A patient with ID i is covered if $i\in \underset{v_j\in G\prime }{\cup }{C}_j$, and uncovered otherwise. We note that our problem is similar, though not identical, to the Minimum Connected Set Cover Problem (Shuai and Hu, 2006), a NP-hard problem.

A simple and natural measure for the size of a subnetwork is its number of nodes (i.e., Size(G′)=|G′|). However, longer genes may tend to acquire more mutations simply by chance. We correct for that by associating with each node v_j a weight w_j that is equal to the ratio of the length of the gene to the total number of mutations it has. The size of the subcomponent is then defined as $\mathit{\text{Size}}(G\prime )=\sum _{v_j\in G\prime }{w}_j$. This way, genes having longer length will be weighted more, correcting for a possible bias towards selecting longer genes. We note that since our objective function balances the fraction of uncovered patients with the size of the graph, we would like the size of the graph to be between 0 and 1; thus, we normalize each node weight by dividing by the unnormalized size of what we call a fully covering subgraph G^f—a connected subgraph of G that covers all patients. (In practice, we compute G^f using the greedy heuristic described below, with α = 1).

Integer Linear Programming Formulation

The problem of finding a minimum connected subgraph that covers as many patients as possible can be solved using constraint optimization. Let n be the number of patients in our sample. For each patient i, we define a binary variable p_i that is set to 1 if patient i is covered by the chosen subgraph G’, and 0 otherwise. For each vertex (or gene) v_j, we define a binary variable x_j that is set to 1 if the vertex is included in the chosen subgraph G’, and 0 otherwise. It is straightforward to set up constraints to ensure that a patient is considered uncovered if none of its mutated genes are part of G’, and covered if at least one of its mutated genes is selected as part of G’ (see Equations 1 and 2 below).

The challenging part of the ILP is setting up constraints to ensure that the chosen nodes form a connected subgraph G’. For this task, we employ a flow of commodity technique (Even and Tarjan, 1975), which we now briefly describe. We inject |G′| units of flow into G’ (i.e., we inject ΣX_i units of “flow” into a vertex that is included in the chosen subnetwork). Flow can move from one vertex to any of its neighbors in the network, and each vertex removes exactly one unit of flow as the flow passes through it. All flow must be removed from the subnetwork, and we set the constraints so that this is possible only if the subnetwork G’ is connected. For the source of the flow we use an artificial external node v_extr. The main issue is that we do not know which node v_extr should be connected to, as we do not know the nodes of G’ in advance. To resolve this, we decide that v_extr connects to the node that covers the largest number of patients v_max; this is equivalent to determining in advance that v_max^∈ G’, though as an alternate approach we could also decide to choose this node probabilistically and run the ILP several times. Finally, to handle the flow constraints, for each edge (i,j)∈ E, we introduce integer variables y_i,j and y_j,i to represent the amount of flow from node i to node j and from node j to node i, respectively. The full integer linear program is:

• Minimize

  $$\alpha (n-\sum _i{p}_i)/n+(1-\alpha )\sum _j{x}_j{w}_j$$
• Subject to

  $$p_i\ge x_j\forall i,j\mathrm{s}.\mathrm{t}.i\in C_j$$ (Equation 1)

  $$p_i\le \sum _{j:i\in C_j}{x}_j\text{ for each patient }i$$ (Equation 2)

  $${\sum }_{i:(i,j)\in E}{y}_{i,j}=x_j+{\sum }_{i:(i,j)\in E}{y}_{j,i}\text{ for each vertex }{v}_j$$ (Equation 3)

  $$\sum _{j:(i,j)\in E}{y}_{i,j}\le \left|V\right|x_i\text{ for each vertex }{v}_i$$ (Equation 4)

  $$\sum _i{x}_i=y_{\mathit{\text{extr}},\mathit{\text{max}}}$$ (Equation 5)

  $$p_i,x_i,y_{i,j}\in \{0,1\}\text{ for all such variables}$$ (Equation 6)

Equation 1 ensures that a patient is considered covered if one of his or her somatically mutated genes is included in G’. Equation 2 ensures that a patient is not considered covered if none of his or her somatically mutated genes is chosen to be part of the subgraph. Equations 3, 4, and 5 enforce the connectivity requirement. Equation 3 requires that the flow going out of each vertex in the chosen subnetwork is 1 less than the flow coming in. Equation 4 requires that if a vertex is not part of the chosen subgraph, the flow going through it is 0. Equation 5 sets the amount of flow injected into the subgraph to be equal to the number of chosen nodes.

Greedy Heuristic

Solving the ILP yields an exact solution but is computationally difficult. Thus, we have also developed an efficient greedy heuristic. Our heuristic procedure initializes G’ by randomly choosing the first gene from among the five most mutated genes, with probability proportional to the number of patients it is found mutated in. It then expands the subgraph G’ iteratively as follows. At each iteration, all vertices that are at most distance 2 from a vertex in G’ are examined and the one that improves the objective function the most is chosen; any ties are broken uniformly at random. If this vertex is not directly adjacent to the nodes in the subnetwork, the intermediary node is also added. The heuristic terminates when no improvement to the objective is possible. We repeat this heuristic multiple times, as it is probabilistic.

In practice, the greedy heuristic finds a solution that is on average ~90% of the best value for the objective function as determined by the ILP formulation using CPLEX (ILO, 2016). For example, on the glioblastoma dataset of 277 individuals, the ILP finds 61 genes covering 90% of the patients when using α=0.5. In comparison, for this value of α, the greedy heuristic finds on average 66 genes covering 88% of the patients with 39 genes in common. In the rest of the paper, we use the greedy optimization as it has comparable performance to the ILP, while being much faster.

Parameter Selection and Solution Aggregation

We split our samples into training, validation and test sets. A test set of 10% of the patients is completely withheld. While varying α in small increments in the interval (0;1), the remaining data is repeatedly split (100 times for each value of α) into training (80%) and validation (20%) sets. For each split, the greedy heuristic algorithm is run on the training set to find G’. The fractions of patients covered (by the selected G’) in the training and validation sets are compared. The parameter α is selected where performance on the validation sets deviates as compared to the training sets. While this can be done visually, for all results reported here we do this automatically using a simple two-rule procedure that selects the smallest α for which the difference in average coverage between the training and validation set exceeds 5% and for which average performance on the validation set is within 10% from the maximum observed one for any α. Finally, the coverage of patients on the (completely withheld) test set is computed to ensure it is similar to the one on the validation set.

Once α is chosen for a set of cancer samples, we repeatedly (1000 times) run the algorithm on this set, each time withholding a fraction (15%) of the patients in order to introduce some randomness in the process. Genes are then ranked by the number of times they appear in G’. In practice, we have found that this improves performance as compared to running the algorithm once on the full data set.

Data Sources and Pre-processing

We downloaded all level 3 cancer somatic mutation data from The Cancer Genome Atlas (TCGA Research Network) that was available as of October 1, 2014, and processed it as in Przytycki and Singh (2017). This data consists of a total of 19,460 genes with somatic point mutations across 24 cancer types. For each cancer, samples that are obvious outliers with respect to their total number of mutated genes are excluded. See Table S1 for a list of the cancer types, the cancer-specific thresholds to determine outlier samples, the number of patient samples considered for each cancer type, and other statistics about the TCGA somatic mutation dataset.

We use two different biological networks in our analysis: HPRD (Prasad et al., 2009) (Release 9_041310) and BioGrid (Stark et al., 2006) (Release 3.2.99, physical interactions only). Biological networks can exhibit several nodes with very high connectivity, often due to study bias. As such high connectivity destroys the usefulness of network information, we remove all nodes whose degrees are clear outliers with unusually high degree (degree > 900 and more than 10 standard deviations away from the mean). For BioGrid, this removes UBC, APP, ELAVL1, SUMO2, CUL3. For HPRD, we remove no nodes. For both networks, we exclude the nine longest genes (TTN, MUC16, SYNE1, NEB, MUC19, CCDC168, FSIP2, OBSCN, GPR98) as they tend to acquire numerous mutations by chance while covering many patients.

To further handle the connectivity arising within the networks due to high-degree nodes, we filter edges using the diffusion state distance (DSD) metric introduced in Cao et al. (2013); the DSD metric captures the intuition that edges between nodes that also share interactions with low degree nodes are more likely to be functionally meaningful than edges that do not (and thus are assigned closer distances). For each edge, the DSD scores (as computed by the software of Cao et al. (2013)) between the corresponding nodes are Z-score normalized, and edges with Z-scores >0.3 are removed. We note that the overall performance of our approach improves when performing this filtering (data not shown), supporting the claim of Cao et al. (2013) that preprocessing a biological network in this manner is an important step. The final number of nodes and edges, respectively, for the filtered networks are 9,379 and 36,638 for HPRD, and 14,326 and 102,552 for BioGrid.

QUANTIFICATION AND STATISTICAL ANALYSIS

Performance Evaluation

To evaluate the gene rankings of all the tested methods, we use the curated list of 517 cancer census genes (CGCs) available from COSMIC (Futreal et al., 2004). All genes in this list are considered as positives, and all other genes are considered as negatives. Though we expect that there are genes other than those already in the CGC list that play a role in cancer, this is a standard approach to judge performance (e.g., see Jia and Zhao (2014)) and gives us an idea of how methods are performing as cancer genes should be highly ranked by methods that perform well. To avoid potential biases due to using a single list of positives, we additionally tested using two different sets of cancer genes (Figure S2). Since only the top predictions by any method are relevant for cancer gene discovery, we judge performance by computing the area under the precision-recall curve (AUPRC) using the top 100 genes predicted by each method (without thresholding the output of any method by score or level of significance). If a method returns less than 100 genes total, we extend the precision-recall curve to 100 genes assuming that it performs as a random classifier. We note that reasonable changes to the number of predictions considered does not change our overall conclusions (Figure S2).

Other Approaches

To ascertain the contribution of network information, we compare nCOP to two approaches that do not use network information: (1) MutSigCV (Lawrence et al., 2013), a method that identifies genes that are mutated more frequently than expected according to a background model, and (2) a set cover approach that tries to find mutated genes that simply cover as many patients as possible. We formulate the set cover approach as an ILP that tries to find a good cover consisting of k vertices. Using the same notation as for nCOP, the set cover objective is to $\mathit{\text{maximize }}\sum _i{p}_i$, subject to Equations 1 and 2 of nCOP, and with the additional constraints that $\sum _j{x}_j\le k\text{ and }\sum _j{x}_j\ge k$. We also compare nCOP to HOTNET2 (Leiserson et al., 2015), Muffinn (Cho et al., 2016), and DriverNet (Bashashati et al., 2012), three recent network-based approaches. To ensure fair comparisons, all methods are run on exactly the same cancer mutation data. Similarly, Hotnet2, Muffinn and nCOP are run on the same network. DriverNet instead uses an influence (i.e., functional interaction) graph and transcriptomic data; we use their default influence graph and provide as input TCGA normalized expression data. MutSigCV, Hotnet2, Muffinn, and DriverNet are run with default parameters (for Hotnet2, this is 100 permuted networks, and β = 0.2 for the restart probability for the insulated heat diffusion process).

DATA AND SOFTWARE AVAILABILITY

Description: https://github.com/Singh-Lab/nCOP.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
DriverNet	Bashashati et al., (2012)	https://www.bioconductor.org/packages/release/bioc/html/DriverNet.html
DSD	Cao et al. (2013)	http://dsd.cs.tufts.edu/server/
GSEA	Subramanian et al. (2005)	http://www.ilog.com/products/cplex/
ILOG CPLEX	ILO (2016)	http://www.ilog.com/products/cplex/
Hotnet2	Leiserson et al. (2015)	https://github.com/raphael-group/hotnet2
Muffinn	Cho et al. (2016)	http://www.inetbio.org/muffinn/
MutSigCV	Lawrence et al. (2013)	http://archive.broadinstitute.org/cancer/cga/mutsig
nCOP	this paper	https://github.com/Singh-Lab/nCOP
Other
Biogrid	Stark et al. (2006)	https://thebiogrid.org/
HPRD	Prasad et al. (2009)	http://www.hprd.org/
TCGA	TCGA Research Network	https://cancergenome.nih.gov/

Highlights.

• Network method for discovering cancer genes using perpatient mutational profiles

• Finds small subnetworks where many patients have a mutation in ≥1 component gene

• Comprehensive analysis across 24 cancer types demonstrates the method’s power

• Pinpoints cancer-relevant genes, even those that are rarely mutated across samples