Optimized Lennard-Jones Parameters for Drug-Like Small Molecules

Abstract

Meaningful efforts in computer-aided drug design (CADD) need accurate molecular mechanical force fields to quantitatively characterize protein-ligand interactions, ligand hydration free energies and other ligand physical properties. Atomic models of new compounds are commonly generated by analogy from the pre-defined tabulated parameters of a given force field. Two widely used approaches following this strategy are the General Amber Force Field, GAFF, and the CHARMM General Force Field (CGenFF). An important limitation of using pre-tabulated parameter values is that they may be inadequate in the context of a specific molecule. To resolve this issue, we previously introduced the General Automated Atomic Model Parameterization (GAAMP) for automatically generating the parameters of atomic models of small molecules using the results from ab initio quantum mechanical (QM) calculations as target data. The GAAMP protocol uses QM data to optimize the bond, valence angle, and dihedral angle internal parameters, and atomic partial charges. However, because the treatment of van der Waals interactions based on QM is challenging and may often be unreliable, the Lennard-Jones 6-12 parameters are kept unchanged from the initial atom types assignments (GAFF or CGenFF), which limits the accuracy that can be achieved by these models. To address this issue, a new set of van der Waals Lennard-Jones 6-12 parameters was systematically optimized to reproduce experimental neat liquid densities and enthalpies of vaporization for a large set of 430 compounds covering a wide range of chemical functionalities. Calculations of the hydration free energy indicate that optimal accuracy for these models is achieved when the molecule-water van der Waals dispersion is rescaled by a factor of 1.115. The final optimized model yields an average unsigned error in the hydration free energies of 0.79 kcal/mol.

Graphical abstract

Introduction

Molecular dynamics (MD) simulations based on classical molecular mechanical (MM) force fields are increasingly used to provide atomic-level insights in studies of biological phenomena.¹ Force fields aim to represent the quantum-mechanical (QM) Born-Oppenheimer (BO) potential energy surface of molecular systems in terms of physically meaningful components that are modeled via a combination of simple analytic functions with multiple parameters. While force fields that explicitly treat induced polarization are progressing rapidly,^2-3 non-polarizable additive potential functions that represent polarization in an average manner with effective fixed partial charges achieve a reasonably accurate representation of the condensed phase. To date, the most widely used additive force fields for MD simulations of biomolecular systems are CHARMM,^4-8 AMBER,⁹ OPLS,¹⁰ and GROMOS.¹¹ These force fields were empirically optimized to reproduce a number of calculated QM and experimental properties for basic biological constituents, including proteins, nucleic acids, carbohydrates and lipids.¹² As a result, they cover only a fairly restricted set of chemical functionalities and models of additional compounds are typically generated by chemical similarity. One of the challenges encountered in computer-aided drug design (CADD) occurs when compounds that have no close analogs within the existing biomolecular force fields are needed. Meaningful efforts in computer-aided drug design (CADD) required accurate molecular mechanical force fields to quantitatively characterize protein-ligand interactions.^13-17 The best way to address this issue is to have an objective algorithmic procedure to automatically parameterize an arbitrary molecule from pre-defined tabulated values in a manner that is consistent with a given force field.^{13, 18-20}

Currently two of the most widely used are the general Amber force field (GAFF);^{13, 21} and the CHARMM general force field (CGenFF).^{14, 20} The program Antechamber²² in AmberTools automatically parameterizes small compounds in accord with GAFF;^{13, 21} atom types and internal parameters (bonds, angles, dihedrals and improper dihedrals) of a given compound are assigned automatically from tabulated values according to an AMBER-consistent classification while atomic charges are fitted to match the results of quantum mechanical (QM) or semi-empirical calculations.²³ CGenFF generates CHARMM-consistent force field parameters for small compounds and drug-like molecules according to knowledge-based rules.^{14, 20, 24} These computational tools represent important advances that greatly broaden the range of chemical systems that can be studied with simulations by enabling an objective and automatic parametrization of novel molecules. More importantly, such procedures avoid the subjective manual adjustments of force field parameters, which ultimately undermine the predictive value of computations based on atomic models. As an extension of these methods aimed at achieving an automatic parametrization for small molecules, we introduced the General Automated Atomic Model Parameterization (GAAMP),²⁵ which was designed to determine force field parameters using ab initio QM calculations as the primary target data. The method has been implemented in a web server (GAAMP, http://gaamp.lcrc.anl.gov/) and can also be setup locally as a script (https://github.com/gaamp). The overall algorithm comprises four main steps. First, GAAMP generates starting atomic models consistent with the atom-type assignments from either GAFF,^{13, 21} or from CGenFF.^{14, 20} Second, GAAMP optimizes the geometry using QM and then refines the internal structural parameters (bonds and angles). Third, GAAMP optimizes the atomic partial charges by simultaneously seeking to match the QM electrostatic potential (ESP) as well as compound-water interactions determined from QM calculations. Fourth, GAAMP automatically identifies the “soft” dihedrals (i.e., those with low energy barriers that are most likely to undergo conformational change), and then iteratively refines the associated dihedral parameters on the basis of QM data.²⁵

The resulting GAAMP models retain the internal topology and the van der Waals (i.e. Lennard-Jones (LJ)) parameters from the initial force field (GAFF or CGenFF), but with bond, angle, dihedral, and atomic partial charge parameters re-optimized on the basis of QM data. The bond, angle and dihedral parameters are optimized from QM data with high confidence, and avoid the context-dependent limitations that necessarily arise from tabulated standard values. Similarly, the electrostatic charges of the model can be determined with high confidence by combing ESP^{9, 26} and water interactions,⁴ which yields more accurate models.²⁵ The GAAMP protocol makes the best use of QM data to determine all the needed parameters, free from the constraint of tabulated parameters that may be inadequate in the context of a specific molecule. It is important to note, however, that the LJ parameters are directly transferred from the initial atom type assignments of GAFF or CGenFF. By choice, the LJ parameters are not modified by the GAAMP algorithm because an automated treatment of van der Waals interactions based on QM is challenging and may often be unreliable. Although GAFF and CGenFF were certainly developed with great care, this remains one aspect of the final GAAMP model that may be a concern because the properties of solvated systems can be highly sensitive to very small changes in the LJ parameters. The situation severely limits the accuracy that can be achieved by automated parametrization procedures to model arbitrary small drug-like molecules.

The goal of the present work is to derive a set of optimal LJ parameters, which dominate the thermodynamics properties of pure liquids,²⁷ adjusted to reproduce experimental neat liquid densities and enthalpies of vaporization²⁷ and hydration free energies for a large set of more than 400 compounds covering a wide range of chemical functionalities. To date, empirical optimization of LJ parameters targeting experimental data has yielded models that accurately reproduce the targeted set of data though may be limited in their ability to satisfactorily reproduce a wider range of experimental data. There have been a number of attempts to improve the ability of force fields to describe experimental observables, especially in the context of biomolecules. Head-Gordon and coworkers optimized solvent-water van der Waals interactions to reproduce experimental hydration free energies for a set of 47 small molecules that incorporated all of the chemical functionalities of standard protein side chains and backbone groups.²⁸ In the present effort we extend that approach by starting with the known GAFF or CGenFF LJ parameters, which act as a high quality initial guess, and optimize the parameters in a redundant fashion (i.e. multiple molecules contain the same LJ atom type) targeting an extended set of experimental data. This effort involved MD simulations of neat liquids conducted to calculate densities and enthalpies of vaporization for more than 400 compounds with known experimental values. Subsequently, free energy perturbation simulations were carried out to calculate the hydration free energies for a set of 426 compounds.

Method

The functional form of the potential function used in the parametrization is,²⁹

$$U=\sum _{\text{bonds}}{K}_b{(b-b_0)}^2+\sum _{\text{angles}}{K}_{\theta }{(\theta -{\theta }_0)}^2+\sum _{\text{dihedrals}}{K}_{\phi }(1+\mathit{\text{cos}}(n\phi -{\phi }_0))+{\sum }_{\text{non}-\text{bonded pairs}}\frac{q_i{q}_j}{4\pi {\in }_0{r}_{ij}}+4E_{min}^{(i,j)}[{\left(\frac{R_{min}^{(i,j)}}{r_{ij}}\right)}^{12}-2{\left(\frac{R_{min}^{(i,j)}}{r_{ij}}\right)}^6],$$ (1)

With some small variances regarding the internal energy terms, this functional form is essentially the same as that used in the non-polarizable AMBER³⁰ and CHARMM⁴ force fields, e.g., CHARMM includes Urey-Bradley that are absent from AMBER. The most important difference concerns the 1-4 non-bonded charge-charge interactions, which are scaled by a factor of 0.833 in the AMBER force field and scaled by a factor of 1.0 in the CHARMM force field. The choice of 1-4 non-bonded scaling factor affects potential energies about dihedral angles, such that the associated dihedral parameters must be optimized in a fashion that is consistent with this choice. Unless specified otherwise, the LJ parameters for pairs of atoms i and j are constructed using the Lorentz-Berthelot combination rule,³¹ $E_{min}^{(i,j)}={\left(E_{min}^{(i,i)}{E}_{min}^{(j,j)}\right)}^{1/2}$ and $R_{min}^{(i,j)}=\left(R_{min}^{(i,i)}{R}_{min}^{(j,j)}\right)/2$.

The GAAMP algorithm²⁵ was used to generate initial molecular mechanics models based on the Generalized Amber Force field GAFF^{13, 21} for all the small compounds. Starting from a structure file in protein data bank (pdb) or mol2 formats comprising all atoms, GAAMP parametrization proceeded in three mains steps: (1) verification and adjustment of equilibrium bond length and angle parameters, (2) charge fitting using QM target data including ESP and specific interaction with water molecules, and (3) dihedral parameter fitting using QM target data. Previous results suggest that including compound-water interactions as target data can substantially improve the quality of partial charges derived from RESP when a compound has hydrogen-bond donors/acceptors.²⁵ All the ab initio calculations required by GAAMP were performed with the program Gaussian 09,³² though other QM codes could be utilized. AM1 was used for the pre-optimization for the initial structure before calling Antechamber²¹ to generate an initial force field based on GAFF^{13, 21} with AM1-BCC charges.²³ In the following, this initial model is referred as “GAFF/AM1-BCC”. For GAAMP models, calculations at the HF/6-31G* level were used for geometry optimization as well as ESP calculation. The interactions between water and the target molecule to parametrize were calculated at the HF/6-31G* level without BSSE, following the recommended prescription as developed in the context of the CHARMM additive force field.^{5, 14, 20, 24} This involves scaling the target HF/6-31G* interaction energies by 1.16 in the case of neutral species while no scaling (scale factor = 1.0) is used for charged species. Calculation at the HF/6-31G* or MP2/6-31G* level were used to perform adiabatic 1D dihedral potential energy scans (PES), in which a single dihedral angles was constrained with geometry optimization of the remaining degrees of freedom at each step in the PES. The gradient-based optimizer L-BFGS^33-34 was used for charge and dihedral parameter optimization. Augmented Lagrangian algorithm^35-36 conjugated with L-BFGS^33-34 was used for the geometry optimization with constraints on selected soft dihedrals for GAAMP.

To optimize the complete set of LJ well-depth and radii parameters (p₁, p₂, …, p_n) associated with all the atom types, we construct an objective function,

$$F(p_1,p_2,\dots ,p_n)={\sum }_m{W}_V{(\frac{V_m^{\text{calc}}}{V_m^{exp}}-1)}^2+W_{\mathrm{\Delta }H}{(\frac{\mathrm{\Delta }{H}_m^{\text{calc}}}{\mathrm{\Delta }{H}_m^{exp}}-1)}^2,$$ (2)

where the sum runs over all the molecules m in the training set, $V_m^{\text{calc}}$ and $V_m^{exp}$ are the calculated and experimental pure solvent molecular (specific) volume for molecule m, respectively, $\mathrm{\Delta }{H}_m^{\text{calc}}$ and $\mathrm{\Delta }{H}_m^{exp}$ are the calculated and experimental enthalpy of vaporization for molecule m, respectively, and W_V and W_ΔH are the statistical weight ascribed to these two properties in the objective function. Equal weights were used in the present optimization. The molecular volume is calculated from MD simulations as the average total volume of the liquid box divided by the number of molecules in the system, V = 〈V_box〉/N, and the enthalpy of vaporization is calculated as,

$$\mathrm{\Delta }{H}_m^{\text{calc}}=k_{\mathrm{B}}T+\langle u_{\text{gas}}\rangle -\langle u_{\text{liquid}}\rangle ,$$ (3)

where 〈u_gas〉 is the average potential energy of one isolated molecule in the gas phase and 〈u_liquid〉 is the average potential energy per molecule in the liquid box. The derivative of the objective function with respect to an arbitrary LJ parameter, p_i can be expressed as,

$$\frac{\partial F}{\partial p_i}=2{\sum }_m{W}_V(\frac{V_m^{\text{calc}}}{V_m^{exp}}-1)\frac{1}{V_m^{exp}}\frac{\partial V_m^{\text{calc}}}{\partial p_i}+W_{\mathrm{\Delta }{H}_{\text{vap}}}(\frac{\mathrm{\Delta }{H}_m^{\text{calc}}}{\mathrm{\Delta }{H}_m^{exp}}-1)\frac{1}{\mathrm{\Delta }{H}_m^{exp}}\frac{\partial \mathrm{\Delta }{H}_m^{\text{calc}}}{\partial p_i},$$ (4)

where the derivative of a property Q (molecular volume or the potential energy) with respect to the parameter p_i can be expressed as,

$$\frac{\partial \langle Q\rangle }{\partial p_i}=\langle \frac{\partial Q}{\partial p_i}\rangle -\frac{1}{k_{B}T}(\langle Q\frac{\partial U}{\partial p_i}\rangle -\langle Q\rangle \langle \frac{dU}{\partial p_i}\rangle ).$$ (5)

It should be noted that the first term 〈∂Q/∂p_i〉 is non-zero only if Q depends explicitly on the parameter p_i (i.e., this term is absent for the molecular volume for not for the enthalpy of evaporation).

The optimization of the LJ parameters aims at better reproducing the experimental densities and enthalpies for a large training set of 430 neutral model compounds. The gradient-based optimizer L-BFGS^33-34 was used for charge and dihedral parameter optimization while in-house programs to drive the LJ optimization were written in C++, bash shell script and Python. Analytical gradients were used for the L-BFGS optimizer. To determine the average properties of the neat liquid of each compound, a box of comprising roughly 200-300 molecules (volume is roughly 35 × 35 × 35 ų) was constructed and simulated for 2 ns with MD under periodic boundary condition (PBC). The simulation length was progressively increased to 5 ns in the final stages of optimization to reduce the statistical uncertainty. At every cycle of optimization, the MD simulations were started from the previously equilibrated systems with new LJ parameters. The systems were simulated at constant pressure and temperature using Langevin thermostat and Langevin piston.³⁷ Long-range electrostatic interactions were computed using particle mesh Ewald (PME) summation^38-39 with a Ewald splitting parameter 0.34 Å^-1, a grid spacing of ∼0.6 Å, and a sixth-order interpolation of the charge to the grid. Non-bonded van der Waals interactions were smoothly switched to zero between 10 and 12 Å and a long-range correction for missing van der Waals dispersion interactions was applied.⁴⁰ The RATTLE algorithm⁴² was used to fix the length of those bonds connecting heavy atoms and hydrogen atoms in the compound. All MD simulations were carried out using the program NAMD.⁴³

The initial LJ parameters for all the compounds in the training set were based on GAFF^{13, 21} while the atomic charges and dihedral parameters were determined using GAAMP²⁵. These initial LJ parameters were then optimized in two distinct stages. In the first stage, the liquid properties for all the compounds of the training set were recalculated at each optimization step using the new set of LJ parameters while the charges and dihedral parameters determined from the initial GAAMP parametrization were kept unchanged. In the second stage, the parameters were further optimized according to the same procedure but the charges and dihedral parameters were periodically re-generated using GAAMP to insure full consistency of the models. A total of 3 full cycle of optimization was carried out on all the atom types in this second stage.

The LJ parameters of almost all the GAFF atom types were optimized, including H, C, N, O, S, F, Cl, and Br;I was not included due to lack of experimental data. A small number of new atom types were added for C, Cl, H, and O when deemed necessary. The parameters of hydrogen atoms were normally optimized together with the heavy atoms to which they are bonded, with the exception of the polar hydroxyl H, which was assigned a zero LJ well depth and radius by convention. A progressive strategy was adopted in which seven main groups of compounds with different chemical functionalities were considered. Group 1 comprises H and C atoms (9 atom types) from nonpolar alkanes (24 compounds), group 2 comprises H and C atoms (2 atom types) in aromatic rings (14 compounds), group 3 comprises additional H and C atoms (6 atom types) in other compounds with only CH elements (32 compounds), group 4 comprises carbon, oxygen and associated polar H atoms (9 atom types) in other compounds with only CHO elements including alcohols, phenols, ketones, aldehydes, and carboxylic acids (148 compounds), group 5 and 6 comprises N and associated polar H atoms (4 atom types) in compounds with only CHN elements (71 compounds), and finally, group 7 comprises S, F, Cl, Br and associated H atoms (4 atom types) in sulfurs and halogen containing compounds (93 compounds). A total of 382 compounds were considered for stage 1 of the optimization. In stage 1, about 10 to 20 iterations of LJ optimization were carried out for each group. No noticeable improvement of the objective function could be achieved with additional iterations beyond 10-20 iterations because the gradients are noisy. An additional subset of about 78 compounds that were not included in the training set was also considered periodically to check the overall consistency and the correctness of the experimental data. Creation of new atom types from the initial GAFF set was deemed necessary when large disparities were observed. The LJ parameters were further optimized according to the same progressive strategy in the second stage, carrying out about 5-10 steps before regenerating the charges and dihedrals via GAAMP. The complete optimization resulted in new LJ parameters for a total of 41 atom types (See file in Supp. Information).

To provide an additional test of set of optimized LJ parameters, we calculated the hydration free energy of 426 compounds using the new GAAMP models with optimized LJ. The absolute solvation free energy of the compounds was calculated and decomposed into three components (repulsive, dispersive and charge term) following an alchemical free energy perturbation (FEP) replica-exchange molecular dynamics (REMD) simulation protocol developed in our group.^44-46 The systems were simulated with PBC under conditions of constant pressure and constant temperature with PME summation.^38-39 A replica-exchange method^{45, 47} was used to enhance the sampling to achieve better convergence. The implementation of the alchemical FEP/REMD⁴⁵ into NAMD⁴⁸ was utilized for these calculations. The compounds were solvated in a cubic water box of TIP3P water molecules⁴⁹ with an edge of 20 Å. The CHARMM version of the TIP3P water model was used, in which small LJ potentials are ascribed to the two hydrogens.⁴ For each value of the thermodynamic coupling parameter, λ, equilibrium properties were averaged over a 500 ps MD simulation after an initial equilibration of 300 ps. Exchanges of neighboring replica were attempted every 200 fs. Weighted histogram analysis method (WHAM)⁵⁰ was used in data processing. A long-range correction for missing dispersion interactions⁴⁰ was added to the calculated solvation free energy. The hydration free energies calculated using the standard GAFF/AM1-BCC parameters^{13, 21, 23} are also included for comparison, relying principally on the values previously reported by Mobley and co-workers^51-52. Those hydration free energies calculated using the standard GAFF/AM1-BCC also include a long-range correction for missing dispersion⁴⁰. All the information about the model compounds and the set of optimized LJ parameters is provided in the Supplementary Information.

Although the current set of LJ parameters shows high accuracy and transferability in reproducing experimental properties of 430 diverse compounds, it is important to consider the performance of the model for compounds independent from the training set. Intuitively, the overall performance of the model ought to be better, on average, for compounds that are similar to the members of the training set. Inaccuracies and uncertainty should increase for compounds that differ markedly from the training set. Atom types that appear frequently in the training are more globally constrained by experimental data than atom types that appear only infrequently. Accordingly, we define a simple empirical similarity fitness score of a compound as,

$$S=\frac{1}{N}\sum _{i=1}^{N}W({\alpha }_i)$$ (6)

where N is the number of atoms in the compound,α_i is the atom type ascribed to the atom i, and W(α) is the normalized statistical frequency the atom type α in the entire training set of 430 compounds. The set of statistical weights W(α) extracted from the training set is shown in Supplementary Figure S1 and also given in Supplementary Information (training_atom_types_weights.xls). The atom types occurring with the highest frequency are hydrogen atom attached to carbon with 3 (HC33) or 2 (HC32) hydrogens, sp2 aromatic carbon (CA), hydrogen on aromatic carbon (HA), sp3 carbon atoms with 2 (C32) or 3 (C33) hydrogens, hydrogen atom attached to carbon in a closed ring (HC3), sp3 carbon in a closed ring (C3R), carbonyl oxygen (O) and carbon (C), ether and ester oxygen (OS), chloride not on aromatic cycle (CL). As expected, the model yields more accurate results when the empirical similarity fitness score S is larger (Supplementary Figure S2). Typically, the error on the molecular volume is generally less than 2-3% for the majority of compounds, but errors larger than 5% are more frequent when the empirical similarity fitness score is S smaller 0.11. The error on the enthalpy of evaporation is generally less than 5% for the majority of compounds when S is larger than 0.11, but errors larger than 10% are considerably more frequent when S is smaller than 0.11. On the basis of this analysis, we now consider the performance of the model for compounds from a validation set independent from the training set. To better illustrate the performance of the model, we deliberately selected 12 compounds with a high value of S and 12 compounds with a low value of S (Supplementary Tables S1-S3). The validation set enables us to compare 10 computed neat liquid densities, 9 computed neat liquid enthalpies of vaporization, and 10 computed hydration free energies with experimental data. Again, the results from this validation set show that the model is reliably more accurate for compounds that display a high degree of similarity to the set of atom types found in the training set. The average error on the molecular volume is 3% for the 5 compounds with S>0.092 but 8% for the 5 compounds with S<0.057 (Supplementary Table S1). The average error on the enthalpy of evaporation is 5% for the 5 compounds with S>0.1 but 11% for the 4 compounds with S<0.062 (Supplementary Table S2). However, the average unsigned error on the hydration free energy is 0.74 kcal/mol for the 5 compounds with S>0.1 and 0.68 kcal/mol for the 5 compounds with S<0.035 (Supplementary Table S3), which suggests that the model is apparently more robust with respect to this property. This is encouraging since the free energy is critical to determine the binding affinity of drugs.

Results and Discussion

The GAAMP²⁵ algorithm was used to generate initial models based on GAFF.^{13, 21} The dihedral parameters, which are indirectly affected by the 1-4 non-bonded interactions, were kept constant during most of the optimization and re-calculated at each cycle toward the end of the global optimization. However, as these parameters are affected by the 1-4 LJ interactions, they should be re-optimized to match the QM torsion PES every time the LJ parameters are changed. In practice, the impact of the dihedral re-parametrization on the liquid properties is minor. To ensure complete consistency, the dihedral parameters were re-generated in the last iteration of the optimization. A gradient-based optimizer (L-BFGS) was used to systematically optimize the LJ parameters, starting from the GAFF parameters for 41 atom types. The optimization aims at better reproducing the experimental densities and enthalpies for a large training set of 430 model compounds by seeking to minimize the objective function F(p₁, p₂, …, p_n), as expressed in Eq. (2). The target experimental data for the training set of model compounds is given in Supp. Info. As shown in Figure 1, the set of compounds in the training set covers the chemical functionalities and atom types present in drug molecules found in DrugBank.

Figure 1.

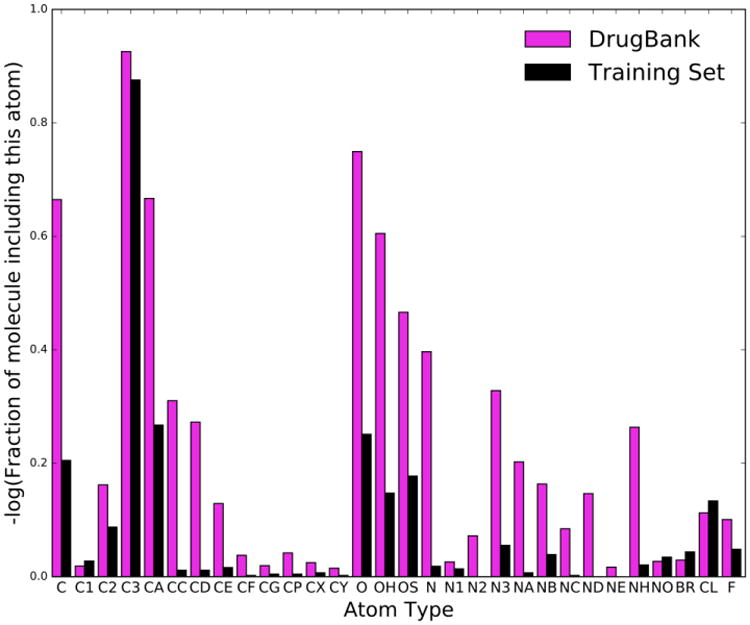
Mapping the atom types from 6,207 molecules taken from DrugBank compared with the set of 430 compounds used to optimize the LJ parameters.

Global optimization of the LJ parameters was carried out in stages, progressively increasing the chemical complexity of the compounds. For the different groups of compounds described above, about 10-20 iterations were performed, yielding a total of ∼40 iterations. During the optimization, the total error associated with the different atom types was monitored, and new atom types were introduced to better represent specific chemical contexts. In the following we refer to the resulting molecular mechanical force field model as GAAMP/GAFF-LJ*. Moreover, 4 atom types for carbon, hydrogen, oxygen, and chloride from the initial GAFF model were expanded into 11 new atom types, yielding a total of 52 atom types in the final model. One notable example is the carbon atoms C3 of GAFF, which was expanded to 5 different carbon types: C30 (sp3 carbon atoms with 0 bonded hydrogen atom), C31 (sp3 carbon atoms with 1 bonded hydrogen atom), C32 (sp3 carbon atoms with 2 bonded hydrogen atom), C33 (sp3 carbon atoms with 3 bonded hydrogen atom), and C3R (sp3 carbon in cyclic aliphatic molecules such as cyclohexane). The original C3 atom is removed from the final force field. In addition, the GAFF hydrogen atom type HC has been expanded to HC31 (hydrogen atom attached to carbon with 1 hydrogen), HC32 (hydrogen atom attached to carbon with 2 hydrogens), HC33 (hydrogen atom attached to carbon with 3 hydrogens), and HC3R (hydrogen atom attached to carbon in a cyclic aliphatic system); the GAFF atom type OH has been expanded to OH for general hydroxyl, and OHP for hydroxyl on aromatic ring (e.g., phenol); and the GAFF atom type Cl has been expanded to CL as a general chloride, and CLA for chloride on an aromatic ring.

The fitted liquid properties for the 430 compounds are compared with experiment in Figure 2. The average unsigned relative errors for the molecular volume are 2.8% and 1.8% using the parameters from the standard GAFF/AM1-BCC and GAAMP/GAFF-LJ*, respectively. Least-square linear regression for the experimental/simulation molecular volume displays a slope close to unity for GAFF/AM1-BCC (0.9828x+3.532) and GAAMP/GAFF-LJ* (0.9937x+ 0.5142), indicating that both models provide a reasonable picture of packing, though the slightly larger intercept at the origin is indicative of a small systematic mismatch with GAFF/AM1-BCC (about 3.5 ų). The average unsigned relative error on the enthalpy of vaporization is 17.9% and is 5.9% using the parameters from GAFF/AM1-BCC and GAAMP/GAFF-LJ*, respectively. The experimental-simulation Pearson correlation coefficient is improved from 0.86 with GAFF/AM1-BCC to 0.96 with GAAMP/GAFF-LJ*. Least-square linear regression for the experimental/simulation enthalpy of vaporization is 1.290x–1.968 for GAFF/AM1-BCC, and 1.032x–0.26281 for GAAMP/GAFF-LJ*. GAFF/AM-BCC displays a slope that is considerably larger than unity (1.290) and a large intercept at the origin (1.968), indicative of a systematic bias in the model. In this regard, it is important to note that the GAFF/AM1-BCC neat liquid models were simulated without a long-range correction to account for the missing dispersion interactions. If such a long-range correction were included, the enthalpy of vaporization in Figure 2 would shift up, yielding an even worse agreement with experimental values. In contrast, there is a significant improvement with the GAAMP/GAFF-LJ* model, both with respect to the slope close to unity and the small intercept at the origin. The evolution of the LJ parameters from their initial GAFF values to their final optimized values is displayed in Figure 3. Overall, the LJ parameters resulting from the global optimization remained fairly close to their initial values, with maximum changes on the order of 0.1 kcal/mol and 0.1 Å in E_min and R_min, respectively. Thus, it was possible to improve the accuracy of the initial model with relatively small changes to the LJ parameters, which highlights the great sensitivity of the results to the non-bonded interactions. Of importance, it can be observed that the specific atom types that were introduced diverged in opposite direction from their initial GAFF value to produce the final LJ parameters (e.g., OH and OHP, CL and CLA).

Figure 2.

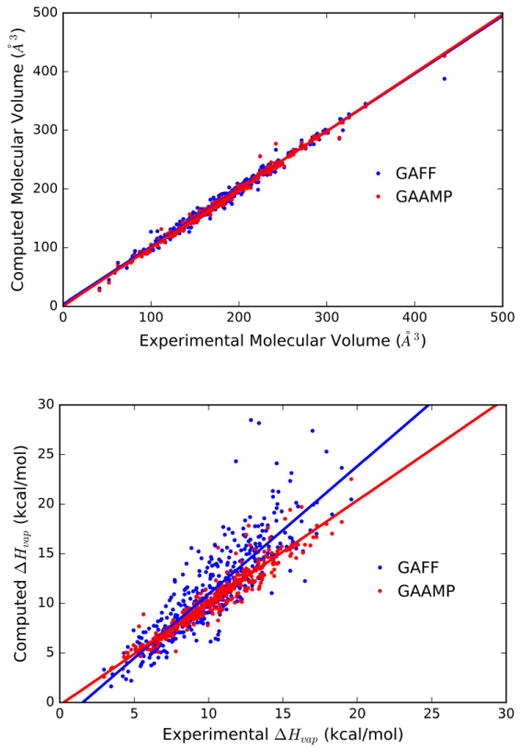
Liquid properties calculated for 430 small molecules. (a) Correlation plot for molecular volume of the neat liquid from 430 small molecules modeled from GAFF (blue) and from GAAMP with optimized LJ parameters (red). (b) Correlation plot for the enthalpy of the neat liquid for 430 small molecules modeled from GAFF (blue) and from GAAMP with optimized LJ parameters (red).

Figure 3.

Evolution of the LJ parameters during the optimization process from the starting point of the original GAFF parameters.

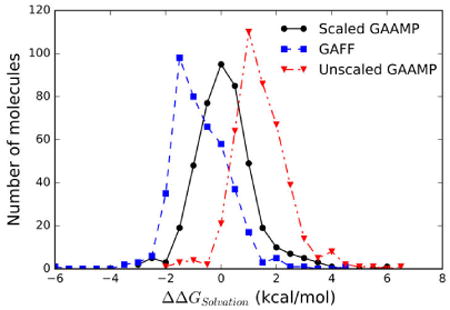
To provide an additional test of the optimized set of LJ parameters, free energy perturbation simulations were carried out to calculate the hydration free energies for 426 compounds. There have been a number of studies aimed at examining the accuracy of MM force fields by computing the solvation free energy for a large set of compounds ^{46, 52-55}. What distinguishes the present effort with these previous studies is that the calculated solvation free energy here are based on the GAAMP charges and dihedral potentials combined with a set of LJ parameters specifically optimized to fit the properties of the neat liquids. The Pearson correlation coefficients between the calculated hydration free energies and experiments is 0.94 for both GAFF/AM1-BCC and GAMMP/GAFF-LJ* models. The average unsigned error is 1.04 and is 1.47 kcal/mol using the parameters from GAFF/AM1-BCC and GAAMP/GAFF-LJ*, respectively. Least-square linear regression yields 0.8972x-0.9273 for GAFF/AM1-BCC, and 0.9016x+1.158 for GAAMP/GAFF-LJ*. The distribution of deviations of the calculated hydration free energy relative to the experimental values is shown in Figure 4. The GAAMP/GAFF-LJ* calculated hydration free energies are systematically overestimated by about +1.8 kcal/mol relative to the experimental target values. In comparison, the hydration free energies from the GAFF/AM1-BCC model are underestimated by about -1.5 kcal/mol compared to experiment, although the deviations are broader. Thus, while significant improvement with GAAMP/GAFF-LJ* occurs with the neat liquids, there is a small degradation relative to the GAFF/AM1-BCC for the hydration free energies.

Figure 4.

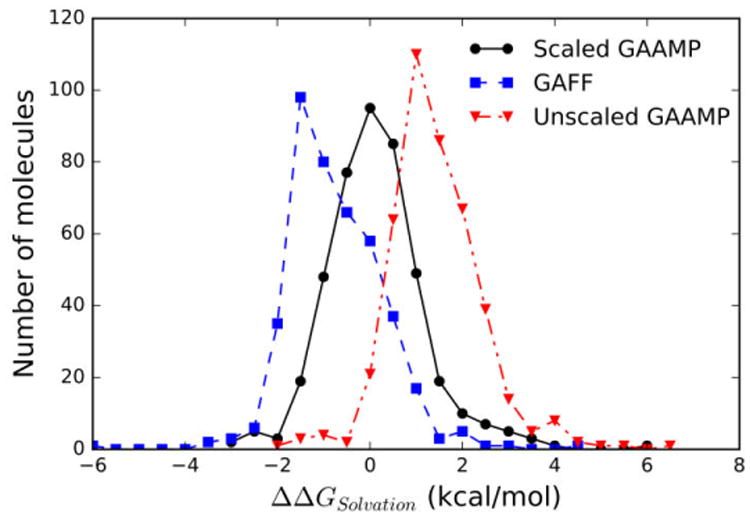
Distribution of the deviation relative to the experimental value for the hydration free energy of 426 small molecules modeled from GAFF/AM1-BCC (blue),⁵² and GAAMP with optimized LJ parameters (red), and with a pair-specific scaling of the solute-water van der Waals dispersion by γ=1.115(black).

Given the substantial improvement of the neat liquid properties with the optimized LJ parameters, this result is somewhat disconcerting. After all, as observed in Figure 3, the agreement of the average properties of the neat liquids with experiment is significantly better with the GAAMP/GAFF-LJ* model compared to the original GAFF/AM1-BCC model. One consideration is that the GAAMP/GAFF-LJ* models are treated with a long-range correction for missing van der Waals dispersion. However, the long-range dispersion correction should make the calculated hydration free energies systematically more favorable, whereas the GAAMP/GAFF-LJ* are not sufficiently favorable. Consistent with this is a recent study that examined the hydration free energy of more than 500 compounds modeled from GAFF/AM1-BCC. That study, which employed a long-range dispersion correction, reported an average error of 0.31 kcal/mol, unsigned error of 1.12 kcal/mol, and a Pearson R value of 0.933. The smaller average error in that study, as compared to the value of 1.5 kcal/mol determined in this work, is consistent with the inclusion of the long-range dispersion correction. However, including a long-range LJ correction would significantly increase the deviation of the enthalpies of evaporation calculated from the GAFF/AM1-BCC model with respect with experiment, as the values are already too favorable (see Figure 2). These results indicate the challenge of obtaining a nonbond model that accurately treats both the neat liquid and aqueous solvation thermodynamic properties, though it is critical to employ a force field model that matches both the properties of neat liquids and solvation free energies. This is particular important because the binding of drug molecules correspond to a transfer from an aqueous environment to the interior of a protein that is more akin to an organic solvent.

Further considerations suggested that the systematic overestimation of the hydration free energies might be due to the underestimation of van der Waals dispersive interactions arising from the water model used in the simulation.^56-58 In a study of unfolded and disordered states of proteins, Best et al⁵⁹ concluded that protein conformations were too collapsed because the nonspecific protein-water dispersion interactions in the context of the TIP3P model were not sufficiently strong. Simply rescaling the Lennard-Jones well depth resulting from the Lorentz-Berthelot combination rule, $E_{min}^{(i,j)}=\gamma {\left(E_{min}^{(i,i)}{E}_{min}^{(i,j)}\right)}^{1/2}$ by a factor of γ=1.10 was found to produce more realistic dimensions of unfolded and intrinsically disordered proteins. Such a mild perturbation is not expected to affect the overall behavior of folded proteins in MD simulations. Similarly, Piana et al⁵⁷ re-designed the dispersion interactions of the TIP4P water model to producing disordered protein states that more closely agree with experimental measurements and a correction to the CHARMM TIP3P water model on the context of the additive CHARMM36 force field has been presented.⁵⁸ Following up with these ideas, we determined the optimal rescaling of the van der Waals dispersion interactions between the compounds and water to shift the calculated hydration free energies toward the experimental values. The change in free energy produced by the scaling could be evaluated using free energy perturbation theory based on the unperturbed simulations. As observed in Figure 4, a modest strengthening of the small molecule-water interactions van der Waals interactions by a scaling factor of γ=1.115 is sufficient to remove the systematic deviation between the calculated and measured hydration free energy. Let us denote this model as GAAMP/GAFF-LJ*-γ. Using the latter, the mean error on the solvation free energy of 426 compounds is 0.12 kcal/mol, the average unsigned error is 0.79 kcal/mol, the least-square linear regression is 0.876x-0.202, and the Pearson correlation coefficient with the experimental values is 0.93. Using a similar scaling factor with GAFF/AM1-BCC, the mean error on the solvation free energy of 426 compounds is -0.73 kcal/mol, and the average unsigned error is 1.04 kcal/mol. The smaller impact of the scaling factor on GAFF/AM1-BCC is due to the truncation of the LJ interactions. With the scaled GAAMP/GAFF-LJ*-γmodel, the absolute error on the solvation free energy is less than 1 kcal/mol for 75% of the compounds in the training set. In contrast, only 49% of the compounds satisfy this criterion for the original GAFF model. Interestingly, the errors on the solvation free energy from GAFF/AM1-BCC and GAAMP/GAFF-LJ*-γrelative to the experimental values are fairly uncorrelated (Pearson correlation coefficient of 0.28). This suggests there is no systematic source of inaccuracy common to both model.

The value of the solute-solvent scaling factor of γ=1.115 is remarkably similar to the scaling factor of 1.10 previously proposed by Best et al⁵⁹ in the context of unfolded proteins. It is noteworthy that both studies represented the solvent water with the TIP3P model⁴⁹ in its CHARMM version, with small LJ potentials ascribed to the two hydrogens.⁴ The main rational for rescaling the solute-water dispersion is that this avoids perturbing the properties of the neat liquid. In the present study water oxygen atom LJ well depth was scaled to shift the hydration free energy. It should be noted, however, that this procedure also affects its effective radius based on the LJ repulsive contribution. Consequently, while the scaling makes the overall dispersive energy of a solute-solvent more favorable, it also reduces the hydrogen bonding energy with water very slightly. For example, the hydrogen bonding interaction between a hydroxyl group donor and a water molecule acceptor decreases by 0.15 kcal/mol and the donor-acceptor distance increases by 0.02 Å in the case of a water molecule (acceptor) and a hydroxyl group (donor). Alternatively, one might rebalance the dispersive interaction of a solute with water by scaling up the LJ well depth of the TIP3P hydrogen HT as the radii of the hydrogen is small (R_min/2 = 0.2245 Å) such that alteration of the well depth is less expected to significantly impact hydrogen bonding.⁵⁸ For the sake of simplicity, only a scaling of the LJ well depth of the TIP3P oxygen OT was considered here. In practice, scaling of the LJ well depth is easily implemented within the CHARMM parameter file by changing the LJ well depth of the TIP3P oxygen OT from its normal value of -0.1521 to the value of -0.18909, which will affect all interactions of the solutes with water, and then restoring the correct water-water LJ interactions (OT-OT, OT-HT, and HT-HT) via the pair-specific NBFIX option to make them consistent with the CHARMM version of theTIP3P water model. While the solute-solvent scaling factor would yield a more accurate solvation free energy for small compounds, the mild perturbation would not affect the overall behavior of folded proteins in MD simulations.

The present results reflect the inherent limitations of additive non-polarizable force fields with respect to the treatment of nonbond interactions. While optimization of the density and enthalpy of vaporization of neat liquids as well as the hydration free energies could be performed simultaneously, the present results with both GAAMP and GAFF indicate that the quality of the fit to the individual properties (neat vs. aqueous condensed phases) would be significantly sacrificed. This limitation is, in part, due to the additive nature of the force field such that the nonbond model, which includes overestimation of the charges to treat to omission of explicit polarization in the model, cannot satisfy both the neat and aqueous environments. From the present study, the GAAMP optimization of the electrostatic parameters combined with the subsequent LJ optimization yields excellent enthalpies of vaporization for the neat liquids from a large collection of compounds. Assuming that the interior of a protein is akin to an organic liquid, the set of optimized LJ parameters shall yield a more accurate representation of ligand-protein interactions. However, despite the improvement with the neat liquid properties, it was observed that the calculated hydration free energies were not favorable enough. This issue was addressed here by scaling the solute-water dispersion interactions by a factor γ=1.115, though an alternative would be to further overestimate the partial atomic charges (i.e. make the solutes intrinsically more polarized) thereby making the interactions with water more favorable leading to better agreement with the hydration free energies. However, a strategy based on charge rescaling would be challenging because it would require a global optimization of the neat liquid properties together with the hydration free energies. Furthermore, it is unclear if charge rescaling could improve the hydration free energy of nonpolar compounds. Ultimately, extension of force fields to explicitly include electronic polarization may help to overcome this limitation, though efforts in our laboratories with the polarizable Drude force field indicate that limitations in treating the full range of condensed phase environments at a high level of accuracy is still challenging.^{3, 60}

Conclusion

Molecular mechanical force fields are constructed from a combination of simple analytic functions with multiple parameters for the purpose of accurately representing the potential energy surface of the system. Relying on pre-tabulated parameters optimized for a large training set of molecules,^{14, 20, 24} or determining those parameters from ab initio QM calculations^61-63 correspond to two extreme approaches for producing a final molecular mechanical model. Both have advantages and disadvantages. Force fields relying on empirical parameters trained on a very large set of representative compounds display internal robustness, while force fields with parameters determined from ab initio calculations provide the most relevant representation of the specific properties of a given molecule.^64-65 In practice, however, both the empirical and the ab initio approaches have their limitations. For instance, transferability can be an issue with a data-driven approaches relying on pre-tabulated parameters when the training set does not fully cover all the relevant chemical space, causing a failure of the force field to accurately represent the Born-Oppenheimer potential energy surface in the context of specific chemical functionalities. On the other hand, the accuracy of QM approaches can vary widely depending on the ab initio level especially in the context of dispersive interactions, which is typically limited by the necessity to remain computationally affordable.

The force field designed here by combining the GAAMP algorithm with optimized LJ parameters represents a compromise between these two extremes. Whenever accurate parameters can be determined consistently and with high confidence from moderate-level QM calculations, then this advantage ought to be exploited as much as possible. For example, the electrostatic charges of the model are determined by combining ESP^{9, 26} and water interactions.⁴ A previous investigation indicate that this procedure yields reliably accurate models.²⁵ Similarly, internal energy terms such as the bond, angle and dihedral parameters can be optimized from QM data. Determination of the dihedral parameters from QM is particularly important because it avoids the context-dependent limitations that necessarily arise from tabulated standard dihedral values. In this regards, it is important to understand that the effective torsion potential for a given molecule is affected by both the dihedral parameters ascribed to this torsion but also by the 1-4 van der Waals and electrostatic interactions. Consistency between 1-4 nonbonded interactions and torsion potential may be achieved if all the parameters of a force field model are determined from pre-tabulated values, as in CGenFF. However, internal inconsistencies may arise when the charges are determined via QM but dihedral parameters rely on pre-tabulated values, as in GAFF.^{13, 21} Generally, it is difficult to achieve sufficient coverage of the chemical space with a training set and pre-tabulated values ultimately become limited. The LJ parameters stand as an exception to this rule. An accurate treatment of van der Waals interactions from ab initio QM calculations, while feasible, requires high-level approaches to be consistently reliable. However, a treatment of van der Waals interactions based on moderate-level QM calculations can be extremely unreliable. While freeing the LJ parameters from the constraint of pre-tabulated values would be useful, this does not seem to be practical at this point. For this reason, it seems more advantageous to use a set of empirically LJ parameters assigned from the chemical context and optimized for a large series of compounds. The atom types assignments could be obtained either from GAFF^{13, 21} or CGenFF.^{14, 20} In the present effort, the initial atom types from GAFF were used. To achieve better accuracy, the set of 41 atom types of the GAFF model was expanded to a total of 52 atom types. This remains a relative small number of empirical LJ parameters. Hydration free energy of a large set of compounds did not markedly improve the performance of the GAFF/AM1-BCC model, but a modest strengthening of the solute-water interactions van der Waals interactions by a factor of 1.115 considerably improved the results, with an average unsigned error of 0.79 kcal/mol. This improved GAAMP/GAFF-LJ* force field, which can be fully general and automatized, will enable us to carry out free energy computations of chemical accuracy in a wide range of applications. While the accuracy of the hydration free energy from the final set of optimized LJ parameters (with the solute-solvent re-scaling) is good but imperfect, it is also important to keep in mind that the accuracy of the liquid properties was improved considerably compared to the GAFF/AM1-BCC. As the binding free energy of a compound depend on its free energy in the protein site relative to its free energy in bulk water, the improved liquid properties of a wide range of liquids should hopefully yield a better representation of the interactions of small molecules in a protein environment as well. A similar strategy is currently being used to optimize the LJ parameters for the Drude polarizable force field.