Automatic intraoperative stitching of nonoverlapping cone‐beam CT acquisitions

Abstract

Purpose

Cone‐beam computed tomography (CBCT) is one of the primary imaging modalities in radiation therapy, dentistry, and orthopedic interventions. While CBCT provides crucial intraoperative information, it is bounded by a limited imaging volume, resulting in reduced effectiveness. This paper introduces an approach allowing real‐time intraoperative stitching of overlapping and nonoverlapping CBCT volumes to enable 3D measurements on large anatomical structures.

Methods

A CBCT‐capable mobile C‐arm is augmented with a red‐green‐blue‐depth (RGBD) camera. An offline cocalibration of the two imaging modalities results in coregistered video, infrared, and x‐ray views of the surgical scene. Then, automatic stitching of multiple small, nonoverlapping CBCT volumes is possible by recovering the relative motion of the C‐arm with respect to the patient based on the camera observations. We propose three methods to recover the relative pose: RGB‐based tracking of visual markers that are placed near the surgical site, RGBD‐based simultaneous localization and mapping (SLAM) of the surgical scene which incorporates both color and depth information for pose estimation, and surface tracking of the patient using only depth data provided by the RGBD sensor.

Results

On an animal cadaver, we show stitching errors as low as 0.33, 0.91, and 1.72 mm when the visual marker, RGBD SLAM, and surface data are used for tracking, respectively.

Conclusions

The proposed method overcomes one of the major limitations of CBCT C‐arm systems by integrating vision‐based tracking and expanding the imaging volume without any intraoperative use of calibration grids or external tracking systems. We believe this solution to be most appropriate for 3D intraoperative verification of several orthopedic procedures.

1. Introduction

Intraoperative 3D x‐ray cone‐beam computed tomography (CBCT) during orthopedic and trauma surgeries has the potential to reduce the need of revision surgeries¹ and improve patient safety. Several works have emphasized the advantages that C‐arm CBCT offers for guidance in orthopedic procedures for head and neck surgery,^{2, 3} spine surgery,⁴ and Kirschner wire (K‐wire) placement in pelvic fractures.^{5, 6} Other medical specialties, such as angiography,⁷ dentistry,⁸ or radiation therapy,⁹ have reported similar benefits when using CBCT. However, commonly used CBCT devices exhibit a limited field of view of the projection images, and are constrained in their scanning motion. The limited view results in reduced effectiveness of the imaging modality in orthopedic interventions due to the small volume reconstructed.

For orthopedic traumatologists, restoring the correct length, alignment, and rotation of the affected extremity is the goal of any fracture management strategy regardless of the fixation technique. This can be difficult with the use of conventional fluoroscopy with limited field of view and lack of 3D cues. For instance, it is estimated that malalignment (>5° in the coronal or sagittal plane) is seen in approximately 10%, and malrotation (>15°) in up to approximately 30% of femoral nailing cases.^{10, 11}

Intraoperative stitching of 2D fluoroscopic images has been investigated to address these issues.¹² Radiopaque markers attached to surgical tools were used to perform the stitching. Trajectory visualization and total length measurement were the most frequent features used by the surgeons in the stitched view. The outcome of 2D stitching was overall reported promising for future development. Similarly, x‐ray translucent references were employed and positioned under the bone for 2D x‐ray mosaicing.^{13, 14} An alternative approach used optical features acquired from an adjacent camera to recover the stitching transformation.¹⁵ The aforementioned methods only addressed stitching in 2D, and their generalization to 3D stitching has remained a challenge.

Orthopedic sports‐related and adult reconstruction procedures could benefit from stitched 3D intraoperative CBCT. For example, high tibial and distal femoral osteotomies are utilized to shift contact forces in the knee in patients with unilateral knee osteoarthritis. These osteotomies rely on precise correction of the mechanical axis to achieve positive clinical results. Computer‐aided navigation systems and optical tackers have shown to help achieve the desired correction in similar procedures;^{16, 17, 18} however, they impose changes to the workflow, for example, by requiring registration and skeletal fixed reference bases. Moreover, navigation systems are complex to setup, and rely on preoperative patient data that is outdated. Intraoperative CBCT has the potential to provide a navigation system for osteotomies about the knee while integrating well with the conventional surgical workflow.

Another promising use for intraoperative CBCT in orthopedics is for comminuted fractures of the mid femur. Intraoperative 3D CBCT has the potential to verify length, alignment, and rotation, and to reduce the need for revision surgery due to malreduction.¹ In Fig. 1, the difficulty in addressing rotational alignment in mid‐shaft comminuted femur fractures and the clinical impact of misalignment is demonstrated. Fig. 2 demonstrates the anatomical landmarks used to estimate the 3D position of the bone. Traditionally, to ensure proper femoral rotation, the contralateral leg is used as a reference: First, an AP radiograph of the contralateral hip is acquired, and particular attention is paid to anatomical landmarks such as how much of the lesser trochanter is visible along the medial side of the femur. Second, the C‐arm is translated distally to the knee and then rotated ∼90° to obtain a lateral radiograph of the healthy knee with the posterior condyles overlapping. These two images, the AP of the hip and lateral of the knee, determine the rotational alignment of the healthy side. To ensure correct rotational alignment of the injured side, an AP of the hip (on the injured side) is obtained, attempting to reproduce the AP radiograph acquired of the contralateral side (a similar amount of lesser trochanter visible along the medial side of the femur). This ensures that the position of both hips is similar. The C‐arm is then moved distally to the knee of the injured femur and rotated ∼90° to a lateral view. This lateral image should match that of the healthy side. If they do not match, rotational correction of the femur can be performed, attempting to obtain a lateral radiograph of the knee on the injured side similar to that of the contralateral side. This procedure motivates the need for intraoperative 3D imaging with large field of view, where leg length discrepancy and malrotation can be quantified intraoperatively and compared with the geometric measurements from the preoperative CT scan of the contralateral side. CBCT can also be used in robot‐assisted intervention and provide navigation for continuum robots used for minimally invasive treatment of pelvic osteolysis¹⁹ and osteonecrosis of the femoral head.²⁰

Figure 1.

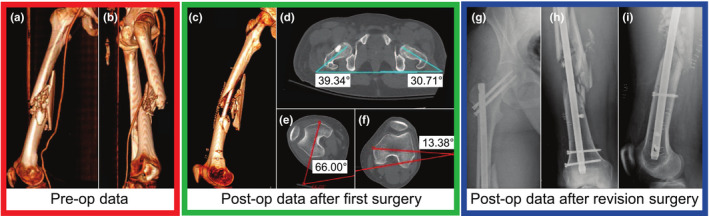
Difficulties arise in addressing rotational alignment in long bone fractures—the 3D preoperative CT scan of the right femur of a patient with a ballistic fracture of the femoral shaft is shown in (a, b). As seen in these images, due to the significant comminution, there are few anatomical cues as to the correct rotational alignment of the bone. (c) shows the postoperative CT of the same femur after reduction and placement of a cephallomedullary nail. The varus/valgus alignment appears to be restored (see Fig. 2); however, significant rotational malalignment is present with excessive external rotation of the distal aspect of the femur. Axial cuts from the postoperative CT scan are shown in (d–f). As shown in (d), the hips are in relatively similar position (right hip ∼10° externally rotated vs. the left). However, in (e), the operative right knee is over 40° more externally rotated than the healthy contralateral side in (f). Figures (g–i) show the anteroposterior (AP) view of the right hip, AP view of the right femur, and the lateral postoperative radiographs after revision cephalomedullary nailing with correction of the rotational deformity. The revision surgery includes removal and correct replacement of the intramedullary nail. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 2.

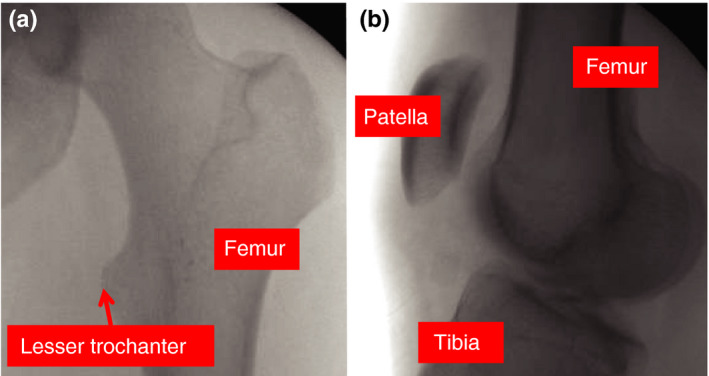
Contralateral images for guidance in rotational alignment—(a) and (b) are intraoperative fluoroscopic images from the revision surgery; AP view of the contralateral hip and lateral view of the contralateral knee. These images were utilized to guide rotational alignment of the fractured femur. By visualizing landmarks on these radiographs and understanding the change in angulation of the C‐arm, the surgeon can estimate the rotational alignment of the healthy femur and attempt to recreate this alignment on the operative side. [Color figure can be viewed at wileyonlinelibrary.com]

To produce larger volumes, panoramic CBCT is proposed in Ref. [9] by stitching overlapping x‐ray images acquired from the anatomy. Reconstruction quality is ensured by requiring sufficient overlap of the projection images, which in return increases the x‐ray dose. Moreover, the reconstructed volume is vulnerable to artifacts introduced by image stitching. An automatic 3D image stitching technique is proposed in Ref. [21]. Under the assumption that the orientational misalignment is negligible, and subvolumes are only translated, the stitching is performed using phase correlation as a global similarity measure, and normalized cross‐correlation (NCC) as the local cost. Since NCC depends only on information in the overlapping area of the 3D volumes, sufficient overlap between 3D volumes is imperative. To reduce the x‐ray exposure, Lamecker et al.²² incorporated prior knowledge from statistical shape models to perform 3D reconstruction.

To optimally support the surgical intervention, our focus is on CBCT alignment techniques that do not require the change of workflow or additional devices in the operating theater. To avoid excessive radiation, we assume that no overlap between CBCT volumes exists.²³ These constraints motivate our work and led to the development of three novel methods presented in this paper. We also discuss and compare the results of this work to the technique proposed in Ref. [24] as the first self‐contained system for CBCT stitching. To avoid the introduction of additional devices, such as computer or camera carts, we coregister the x‐ray source to a color and depth camera, and track the C‐arm relative to the patient based on the red‐green‐blue‐depth (RGBD) observations.^{25, 26, 27, 28} This allows the mobile C‐arm to remain self‐contained, and independent of additional devices or the operating theater. Additionally, the image quality of each individual CBCT volume remains intact, and the radiation dose is linearly proportional to the size and number of individual CBCT volumes.

2. Experimental setup and data acquisition

2.A. Experimental setup

Our system is composed of a mobile C‐arm, ARCADIS Orbic 3D, from Siemens Healthineers and an Intel Realsense SR300 RGBD camera. The SR300 is relatively small (X = 110.0 ± 0.2 mm, Y = 12.6 ± 0.1 mm, Z = 3.8−4.1 mm), and integrates a full‐HD RGB camera, and an infrared projector and infrared camera, which enable the computation of depth maps. The SR300 is designed for short ranges from 0.2 to 1.2 m for indoor use. Access to raw RGB and infrared data is possible using the Intel RealSense SDK. The C‐arm is connected via Ethernet to the computer for CBCT data transfer, and the RGBD camera is connected via powered USB 3.0 for real‐time frame capturing.

2.B. CBCT volume and video acquisition

To acquire a CBCT volume, the patient is positioned under guidance of the lasers. Then, the motorized C‐arm orbits 190° around the center visualized by the laser lines, and automatically acquires a total of 100 2D x‐ray images. Reconstruction is performed using a maximum‐likelihood expectation‐maximization iterative reconstruction method,²⁹ resulting in a cubic volume with 512 voxels along each axis and an isotropic voxel size of 0.2475 mm. For the purpose of reconstruction, we use the following geometrical parameters provided by the manufacturer: source‐to‐detector distance: 980.00 mm, source‐isocenter distance: 600.00 mm, angle range: 190°, detector size: 230.00 × 230.00 mm.

3. Geometric calibration and reconstruction with the RGBD augmented C‐arm

To stitch nonoverlapping CBCT volumes, the transformation between individual volumes needs to be recovered. In this work, we assume that only the relative relationship between CBCT volumes is of interest, and that the patient does not move during the CBCT scan. In contrast to previous external tracking systems, our approach relies on a 3D color camera providing depth (D) information for each red, green, and blue (RGB) pixel. To keep the workflow disruption and limitation of free workspace minimal, the RGBD camera is mounted on the C‐arm gantry close to the detector as shown in Fig. 5.

Figure 5.

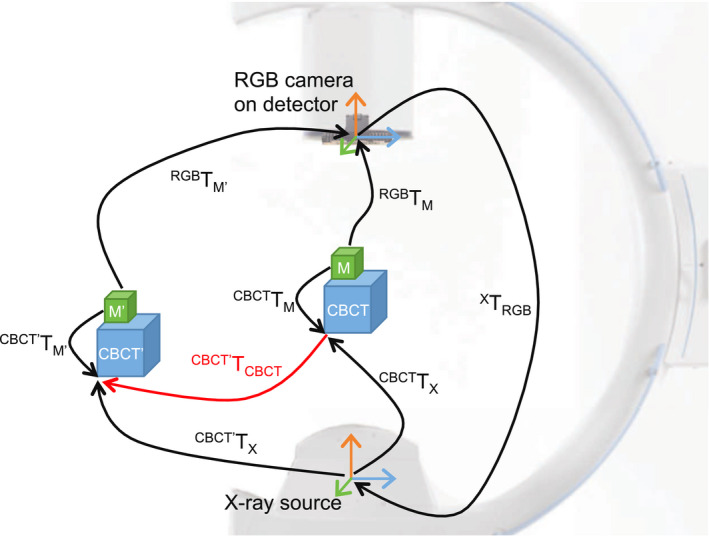
The relative displacement of CBCT volumes (${}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{\mathtt{CBCT}}$) is estimated from the tracking data computed using the camera mounted on the C‐arm. This requires the calibration of the camera and x‐ray source ( ^X T _RGB ), and the known relationship of the x‐ray source and CBCT volume ( ^CBCT T _X ). The pose of the marker is observed by the camera ( ^RGB T _M ), while the transformation from marker pose to CBCT volume ( ^CBCT T _M ) is computed once and assumed to remain constant. [Color figure can be viewed at wileyonlinelibrary.com]

After a one‐time calibration of the RGBD camera to the x‐ray source, CBCT reconstruction is performed. Next, we use the calibration information and the 3D patient data to perform vision‐based CBCT stitching.

3.A. RGB camera, depth sensor, and x‐ray source calibration

To simultaneously calibrate and estimate relationships among RGB, depth, and x‐ray camera, we designed a radiopaque checkerboard that can also be detected by the color camera and in the infrared image of the depth sensor. This hybrid checkerboard, shown in Fig. 3, allows for offline calibration of the imaging sources which takes place when the patient is not present. Due to the rigid construction of the RGBD camera on the C‐arm gantry, the relative extrinsic calibration will remain valid as long as the RGBD camera is not moved on the C‐arm. To calibrate the RGB camera and depth sensor, we deploy a combination of automatic checkerboard detection and pose estimation³⁰ and nonlinear optimization,³¹ resulting in camera projection matrices P _RGB and P _D . In this camera calibration approach, the checkerboard is assumed to be at Z = 0 at each pose. This assumption reduces the calibration problem from x _i = P _i X _i to ${\mathbf{x}}_i={\mathbf{H}}_i{\tilde{\mathbf{X}}}_i$, where x _i is the image points in homogeneous coordinates for the ith pose, P _i is the camera calibration matrix, X _i = [X _i , Y _i , Z _i , 1] ^⊤ is the checkerboard corners in 3D homogeneous coordinates, H _i is a 3 × 3 homography, and ${\tilde{\mathbf{X}}}_i=[X_i,Y_i,1]$ ^⊤ . H _i is solved for each pose of the checkerboard, and then used to estimate the intrinsic and extrinsic parameters of the cameras. The output of this closed‐form solution is then used as initialization for a nonlinear optimization approach³² that minimizes a geometric cost based on maximum‐likelihood estimation. The radial distortion is modeled inside the geometric cost using a degree 4 polynomial. The general projection matrices can be solved for all i = {1,···, N} valid checkerboard poses CB _i , with N ≥ 3. For each of the checkerboard poses, we obtain the transformations from camera origin to checkerboard origin ${}^{{\mathtt{CB}}_i}{\mathbf{T}}_{\mathtt{RGB}}$, and from depth sensor origin to checkerboard origin ${}^{{\mathtt{CB}}_i}{\mathbf{T}}_{\mathtt{D}}$.

Figure 3.

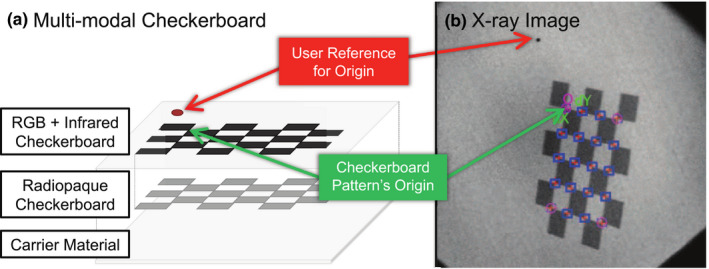
Checkerboard is designed to be fully visible in RGB, depth, and x‐ray images. [Color figure can be viewed at wileyonlinelibrary.com]

Thin metal sheets behind black checkerboard squares make the pattern visible in x‐ray as they cause a low contrast between different checkerboard fields and the surrounding image intensities. After labeling the outer corners of the checkerboard, the corner points within this rectangle are detected automatically. The user reference point shown in Fig. 3 is used to ensure consistent labeling of checkerboard corners with respect to the origin. The checkerboard poses ${}^{{\mathtt{CB}}_i}{\mathbf{T}}_{\mathtt{x}}$ and camera projection matrix P _X can then be estimated similarly to an optical camera. In contrast to a standard camera, the x‐ray imaging device provides flipped images to give the medical staff the impression that they are looking from the detector toward the source. Therefore, the images are treated as if they were in a left‐hand coordinate frame. An additional preprocessing step needs to be deployed to convert the images to their original form. This preprocessing step includes a 90° counterclockwise rotation, followed by a horizontal flip of the x‐ray images.

Finally, for each checkerboard pose CB _i the RGB camera, depth sensor, and x‐ray source poses are known, allowing for a simultaneous optimization of the three transformations: RGB camera to x‐ray source ^X T _RGB , depth sensor to x‐ray source ^X T _D , and RGB camera to depth sensor ^D T _RGB .³³ This process concludes the one‐time calibration step required at the time of system setup.

3.B. CBCT reconstruction

We hypothesize that the relationship between each x‐ray projection image and the CBCT volume ( ^CBCT T _X ) is known by means of reconstruction. To obtain the accurate and precise projection matrices, we performed a CBCT volume reconstruction and verified the x‐ray source extrinsics using 2D/3D registration. This registration was initialized by the projection matrices provided by the C‐arm factory calibration. Next, an updated estimate of the projection geometry was computed, and the final projection matrices were constructed based on the known x‐ray source geometry (intrinsics) and the orbital motion (extrinsics).

If the orbital C‐arm motion deviates from the assumed path, it leads to erroneous projection matrices. Utilizing 2D/3D registration based on digitally reconstructed radiographs, NCC similarity cost,³⁴ and bound constrained by quadratic approximation optimization,³⁵ we verified the x‐ray source extrinsics for each projection image. It is important to note that CBCT‐capable C‐arms are regularly recalibrated when used in the clinical environment. In cases where the internal calibration of the C‐arm differs slightly from the true scan trajectory, the volumetric reconstruction will exhibit artifact. In the presence of small artifacts, it is still possible to measure geometric information such as length and angles. However, in case of significant deviation, the prior hypothesis of a known relationship between x‐ray source origin and CBCT is no longer valid and requires recalibration of the C‐arm.

4. Vision‐based stitching techniques for nonoverlapping CBCT volumes

After calibration of the cameras and x‐ray source, the intrinsics and extrinsics of each imaging device are known. The calibration allows to track the patient using the RGB camera or depth sensor and apply this transformation to the CBCT volumes. In Sections 4.A., 4.B., 4.C., we introduce stitching using visual markers, 3D color features, and surface depth information.

To measure the leg length and the anatomical angles of a femur bone, two CBCT scans from the two ends of the bone are sufficient. Therefore, in the following sections, we only discuss the stitching of two nonoverlapping CBCT volumes. However, all the proposed solutions can also be deployed to stitch larger numbers of overlapping or nonoverlapping CBCT volumes.

4.A. Vision‐based marker tracking techniques

This tracking technique relies on flat markers with a high contrast pattern that are easily detected in an image. The pose can be retrieved as the true marker size is known.³⁶ In the following, we investigate two approaches: first, a cubical marker is placed near the patient and the detector is above the bed. Second, an array of markers is attached under the bed and the detector is below the bed while the C‐arm is repositioned. These two marker strategies are shown in Fig. 4. The underlying tracking method is similar among these two methods, but each of the two approaches has its advantages and limitations which are discussed in Section 5.B..

Figure 4.

Tracking using visual marker is performed by (a) placing a cubical visual marker near the patient, or (b) attaching an array of markers below the surgical bed. [Color figure can be viewed at wileyonlinelibrary.com]

4.A.1. Visual marker tracking of patient

To enable visual marker tracking, we deploy a multimarker strategy and arrange markers on all sides of a cube, resulting in an increased robustness and pose‐estimation accuracy. The marker cube is then rigidly attached to the anatomy of interest and tracked using the RGB stream of the camera.

After performing the orbital rotation and acquiring the projection images for the reconstruction of the first CBCT volume, the C‐arm is rotated to a pose for which ${}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{X}}$ is known (see Section 1). Ideally, this pose is chosen to provide an optimal view of relative displacement of the marker cube, as the markers are tracked based on the color camera view. The center of the first CBCT volume is defined to be the world origin, and the marker cube M is represented in this coordinate frame based on camera to x‐ray source calibration:

$${}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{M}}={}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{X}}·{}^{\mathtt{X}}{\mathbf{T}}_{\mathtt{RGB}}·{}^{\mathtt{RGB}}{\mathbf{T}}_{\mathtt{M}}.$$ (1)

The transformations are depicted in Fig. 5. The surgical table or the C‐arm is repositioned to acquire the second CBCT volume. During this movement, the scene and the marker cube are observed using the color camera, allowing for the computation of the new pose of the marker cube ${}^{\mathtt{RGB}}{\mathbf{T}}_{{\mathtt{M}}^{\prime }}$. Under the assumption that the relationship between CBCT volume and marker [Eq. (1)] did not change as the marker remained fixed to the patient for the duration between two CBCT scans, the relative displacement of the CBCT volumes is expressed as:

$$\begin{array}{cc}\hfill {}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{\mathtt{X}}=& {}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{M}}·{}^{\mathtt{RGB}}{\mathbf{T}}_{{\mathtt{M}}^{\prime }}^{-1}·{}^{\mathtt{X}}{\mathbf{T}}_{\mathtt{RGB}}^{-1},\hfill \\ \hfill {}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{\mathtt{CBCT}}& ={}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{\mathtt{X}}·{}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{X}}^{-1}\hfill \end{array}$$ (2)

4.A.2. Visual marker tracking of surgical table

In many orthopedic interventions, the C‐arm is used to validate the reduction of complex fractures. This is mostly done by moving the C‐arm rather than the injured patient. Consequently, we hypothesize that the patient remains on the surgical table and only the relationship between table and C‐arm is of interest, which has also been assumed in previous work.¹⁵

A predefined array of markers is mounted on the bottom of the surgical table, which allows the estimation of the pose of the C‐arm relative to the table. While rearranging the C‐arm to acquire multiple CBCT scans, the C‐arm detector is positioned under the bed where the RGBD camera observes the array of markers. Again, this allows for the estimation of ${}^{\mathtt{RGB}}{\mathbf{T}}_{{\mathtt{M}}^{\prime }}$ and, thus, stitching.

4.B. RGBD simultaneous localization and mapping for tracking

RGBD devices allow for fusion of color and depth information and enable scale recovery of visual features. We aim at using RGB and depth channels concurrently to track the displacement of patient relative to a C‐arm during multiple CBCT acquisitions.

Simultaneous localization and mapping (SLAM) has been used in the past few decades to recover the pose of a sensor in an unknown environment. The underlying method in SLAM is the simultaneous estimation of the pose of perceived landmarks, and updating the position of a sensing device.³⁷ An RGBD SLAM was introduced in Ref. [38] where the visual features are extracted from 2D frames, and later the depth associated with those features are computed from the depth sensor in the RGBD camera. These 3D features are then used to initialize a RANdom SAmple Consensus (RANSAC) method to estimate the relative poses of the sensor by fitting a 6‐DOF rigid transformation.³⁹

RGBD SLAM enables the recovery of the camera trajectory in an arbitrary environment without prior models; rather, SLAM incrementally creates a global 3D map of the scene in real‐time. We assume that the global 3D map is rigidly connected to the CBCT volume, which allows for the computation of the relative volume displacement using Eq. (3), where f _RGB and f _{RGB ′} are sets of features in RGB and RGB′ frames, π is the projection operator, d is the dense depth map, and x is the set of 2D feature points.

$$\begin{array}{cc}\hfill {}^{{\mathtt{RGB}}^{\prime }}{\widehat{\mathbf{T}}}_{\mathtt{RGB}}=& \underset{{}^{{\mathtt{RGB}}^{\prime }}{\mathbf{T}}_{\mathtt{RGB}}\in \mathbb{S}E(3)}{\text{arg min}}\left|{\mathbf{f}}_{\mathtt{RGB}}(\mathbf{x})-{\mathbf{f}}_{{\mathtt{RGB}}^{\prime }}({\pi }^{{\mathtt{RGB}}^{\prime }}{\mathbf{T}}_{\mathtt{RGB}}(\mathbf{dx}))\right|,\hfill \\ \hfill {}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{\mathtt{CBCT}}& ={}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{{\mathtt{RGB}}^{\prime }}·{}^{{\mathtt{RGB}}^{\prime }}{\widehat{\mathbf{T}}}_{\mathtt{RGB}}·{}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{RGB}}^{-1}.\hfill \end{array}$$ (3)

4.C. Surface reconstruction and tracking using depth information

Surface information obtained from the depth sensor in an RGBD camera can be used to reconstruct the patient's surface, which simultaneously enables the estimation of the sensor trajectory. KinectFusion provides a dense surface reconstruction of a complex environment and estimates the pose of the sensor in real‐time.⁴⁰ Our goal is to use the depth camera view and observe the displacement, track the scene, and consequently, compute the relative movement between the acquisition of CBCT volumes. This tracking method involves no markers, and the surgical site is used as a reference (real‐surgery condition).

KinectFusion relies on a multiscale Iterative Closest Point (ICP) with a point‐to‐plane distance function and registers the current measurement of the depth sensor to a globally fused model. The ICP incorporates points from both the foreground as well as the background and estimates rigid transformations between frames. Therefore, a moving object with a static background causes unreliable tracking. Thus, multiple nonoverlapping CBCT volumes are only acquired by repositioning the C‐arm instead of the surgical table.

Similar transformations shown in Fig. 5 are used to compute the relative CBCT displacement ${}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{\mathtt{CBCT}}$, where D defines the depth coordinate frame, ${}^{{\mathtt{D}}^{\prime }}{\widehat{\mathbf{T}}}_{\mathtt{D}}$ is the relative camera pose computed using KinectFusion, V _D and V _{D ′} are vertex maps at frames D and D′, and N _D is the normal map at frame D:

$$\begin{array}{cc}\hfill {}^{{\mathtt{D}}^{\prime }}{\widehat{\mathbf{T}}}_{\mathtt{D}}& =\underset{{}^{{\mathtt{D}}^{\prime }}{\mathbf{T}}_{\mathtt{D}}\in \mathbb{S}E(3)}{\text{arg min}}{∥{\left({}^{{\mathtt{D}}^{\prime }}{\mathbf{T}}_{\mathtt{D}}^{-1}{\mathbf{V}}_{{\mathtt{D}}^{\prime }}-{\mathbf{V}}_{\mathtt{D}}\right)}^{\top }{\mathbf{N}}_{\mathtt{D}}∥}_2,\hfill \\ \hfill {}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{\mathtt{CBCT}}& ={}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{{\mathtt{D}}^{\prime }}·{}^{{\mathtt{D}}^{\prime }}{\widehat{\mathbf{T}}}_{\mathtt{D}}·{}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{D}}^{-1}.\hfill \end{array}$$ (4)

5. Related workS as reference techniques

To provide a reasonable reference to our vision‐based tracking techniques, we briefly introduce an infrared tracking system to perform CBCT volume stitching (Section 5.A). This chapter concludes with a brief overview of our previously published vision‐based stitching technique²⁴ (Section 5.B) put in context of our chain of transformations.

5.A. Infrared tracking system

In the following, we first discuss the calibration of the C‐arm to the CBCT coordinate frame, and subsequently, the C‐arm to patient tracking using this calibration.

5.A.1. Calibration

This step includes attaching passive markers to the C‐arm and calibrating them to the CBCT coordinate frame. This calibration later allows us to close the patient, CBCT, and C‐arm transformation loop and estimate relative displacements. The spatial relation of the markers on the C‐arm with respect to the CBCT coordinate frame is illustrated in Fig. 6 and is defined as:

$${}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{Carm}}={}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{IR}}·{}^{\mathtt{Carm}}{\mathbf{T}}_{\mathtt{IR}}^{-1}.$$ (5)

Figure 6.

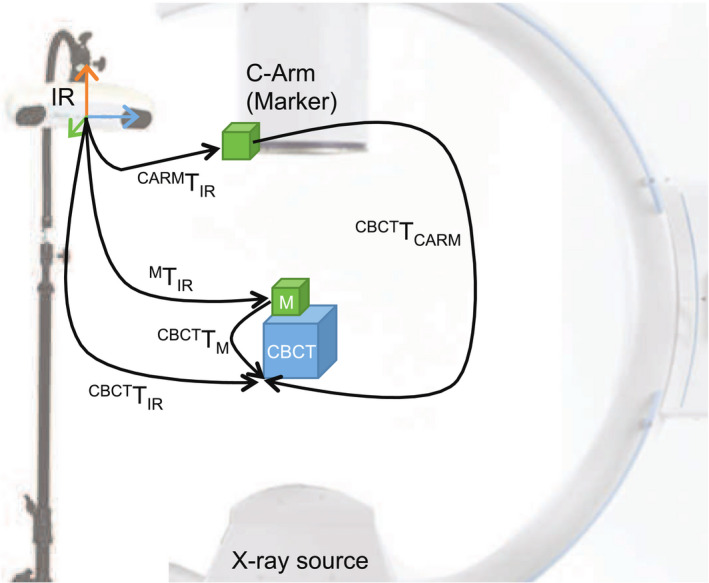
An infrared tracking system is used for alignment and stitching of CBCT volumes. This method serves as a reference standard for the evaluation of vision‐based techniques. [Color figure can be viewed at wileyonlinelibrary.com]

The first step in solving Eq. (5) is to compute ${}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{IR}}$. This estimation requires at least three marker positions in both CBCT and IR coordinate frames. Thus, a CBCT scan of another set of markers (M in Fig. 6) is acquired and the spherical markers are located in the CBCT volume. Here, we attempt to directly localize the spherical markers in the CBCT image instead of x‐ray projections.⁴¹ To this end, a bilateral filter is applied to the CBCT image to remove noise while preserving edges. Next, weak edges are removed by thresholding the gradient of the CBCT, while strong edges corresponding to the surface points on the spheres are preserved. The resulting points are clustered into three partitions (one cluster per sphere), and the centroid of each cluster is computed. Then, an exhaustive search is performed in the neighborhood around the centroid with the radius of ±(r + δ), where r is the sphere radius (6.00 mm) and δ is the uncertainty range (2.00 mm). The sphere center is localized by a least‐square minimization using its parametric model. Since the sphere size is provided by the manufacturer, we avoid using classic RANSAC or Hough‐like methods as they also optimize over the sphere radius. We then use the noniterative least squares method suggested in Ref. [42] and solve for ${}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{IR}}$ based on singular value decomposition. Consequently, we can close the calibration loop and solve Eq. (5) using ${}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{IR}}$ and ${}^{\mathtt{Carm}}{\mathbf{T}}_{\mathtt{IR}}$ which is directly measured from the IR tracker.

5.A.2. Tracking

The tracking stream provided for each marker configuration allows for computing the motion of the patient. After the first CBCT volume is acquired, the relative patient displacement is estimated before the next CBCT scan is performed.

Considering the case where the C‐arm is repositioned (from Carm to Carm′ coordinate frame) to acquire CBCT volumes (CBCT and CBCT′ coordinate frames), and the patient is fixed on the surgical table, the relative transformation from IR tracker to CBCT volumes are defined as follows:

$$\begin{array}{cc}\hfill {}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{IR}}& ={}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{Carm}}·{}^{\mathtt{Carm}}{\mathbf{T}}_{\mathtt{IR}},\hfill \\ \hfill {}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{\mathtt{IR}}& ={}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{{\mathtt{Carm}}^{\prime }}·{}^{{\mathtt{Carm}}^{\prime }}{\mathbf{T}}_{\mathtt{IR}}.\hfill \end{array}$$ (6)

The relation between the C‐arm and the CBCT is fixed, hence ${}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{Carm}}\stackrel{\mathrm{def}}{=}{}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{{\mathtt{Carm}}^{\prime }}$. We can then define the relative transformation from CBCT to CBCT′ as:

$${}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{\mathtt{CBCT}}={}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{\mathtt{IR}}·{}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{IR}}^{-1}$$ (7)

To consider patient movement, markers (coordinate frame M in Fig. 6) may also be attached to the patient (e.g., screwed into the bone), and tracked in the IR tracker coordinate frame. ${}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{M}}$ is then defined as:

$${}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{M}}={}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{Carm}}·{}^{\mathtt{Carm}}{\mathbf{T}}_{\mathtt{IR}}·{}^{\mathtt{M}}{\mathbf{T}}_{\mathtt{IR}}^{-1}$$ (8)

Assuming that the transformation between CBCT and marker is fixed during the intervention $({}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{{\mathtt{M}}^{\prime }}\stackrel{\mathrm{def}}{=}{}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{M}})$ and combining Eqs. (6) and (8), volume poses in the tracker coordinate frame are defined as:

$$\begin{array}{cc}\hfill {}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{IR}}& ={}^{\mathtt{CBCT}}{\mathbf{T}}_{\mathtt{M}}·{}^{\mathtt{M}}{\mathbf{T}}_{\mathtt{IR}},\hfill \\ \hfill {}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{\mathtt{IR}}& ={}^{{\mathtt{CBCT}}^{\prime }}{\mathbf{T}}_{{\mathtt{M}}^{\prime }}·{}^{{\mathtt{M}}^{\prime }}{\mathbf{T}}_{\mathtt{IR}}.\hfill \end{array}$$ (9)

solving Eq. (9) leads to recovery of CBCT displacement using Eq. (7).

5.B. Two‐dimensional feature tracking

In this approach, the positioning laser in the base of the C‐arm is used to recover the 3D depth scales of feature points observed in RGB frames, and consequently stitch the subvolumes. The details for estimating the frame‐by‐frame transformation are discussed in Ref. [24].

6. Experiments and results

In this section, we report the results of our vision‐based methods to stitch multiple CBCT volumes as presented in Section 2.B.. The same experiments are preformed using the methods outlined in Section 4.A.1., namely using a commercially available infrared tracking system, and our previously published technique.²⁴ Finally, we compare the results of the aforementioned approaches to image‐based stitching of overlapping CBCT volumes.

6.A. Calibration results

The calibration of the RGBD/x‐ray system is achieved using a multimodal checkerboard (see Fig. 3), which is observed at multiple poses using the RGB camera, depth sensor, and the x‐ray system. We use a 5 × 6 checkerboard where each square has a dimension of 12.655 mm. The radiopaque metal checkerboard pattern is attached to the black‐and‐white pattern that is printed on a paper. Therefore, the distance between these two checkerboards is equal to the thickness of a sheet of paper which is considered negligible. For the purpose of stereo calibration, we can then assume all three cameras (RGB, infrared, and x‐ray cameras) observe the same pattern. In total, 72 image triplets (RGB, infrared, and x‐ray images) were recorded for the stereo calibration. Images with high reprojection errors or significant motion blurring artifacts were discarded from this list for a more accurate stereo calibration.

The stereo calibration between the x‐ray source and the RGB camera was eventually performed using 42 image pairs with the overall mean error of 0.86 pixels. The RGB and infrared cameras were calibrated using 59 image pairs, and an overall reprojection error of 0.17 pixels was achieved. The mean stereo reprojection error ${\overline{\mathrm{d}}}_{\mathit{repro}}$ is defined as:

$${\overline{\mathrm{d}}}_{\mathit{repro}}=\frac{1}{2\times N\times M}{\left[{∥\mathrm{x}-\widehat{\mathrm{x}}∥}_2^2+{∥{\mathrm{x}}^{\prime }-\widehat{{\mathrm{x}}^{\prime }}∥}_2^2\right]}^{\frac{1}{2}}$$ (10)

where N is the total number of image pairs, M is the number of checkerboard corners in each frame, {x ↔ x′} are the vectors of detected checkerboard corners among the image pairs, and $\widehat{\mathbf{x}}$ and ${\widehat{\mathbf{x}}}^{\prime }$ are vectors containing the projection of the 3D checkerboard corners in each of the images.

The stereo calibration was repeated twice while performing the stitching experiments. The mean translational and rotational change in the stereo extrinsic parameters were 1.42 mm and 1.05°, respectively.

6.B. Stitching results

Our vision‐based tracking methods are all tested and evaluated on an animal cadaver (pig femur). For these experiments, we performed the stitching of CBCT volumes with each method individually under realistic surgery conditions. The C‐arm was translated for the acquisition of multiple CBCT volumes when the detector was located at AP orientation. The geometric relation of the AP view to the C‐arm was estimated using an intensity‐based 2D/3D registration with a target registration error of 0.29 mm. Subsequently, we measured the absolute distance between the implanted landmarks inside the animal cadaver and compared the results to a ground truth acquired from a CT scan. The CT scan had an isotropic voxel size of 0.5 mm. The outcome of these experiments was compared to an infrared‐based tracking approach (baseline method), as well as image‐based stitching approach. Stitching errors for all proposed methods are reported in Table 1. This stitching error is defined as the difference in the distance of the landmarks on the opposite sides of the bone (femoral head and knee sides). For each pair of landmarks, the error distance BB landmarks is computed as $\left|{∥B{B}_{(F)}^{(S)}-B{B}_{(K)}^{(S)}∥}_2-{∥B{B}_{(F)}^{(G)}-B{B}_{(K)}^{(G)}∥}_2\right|$ where superscripts (S) and (G) refer to measurements from stitching and the ground‐truth data, respectively. The subscripts (F) and (K) refer to landmarks on the femoral head and the knee side of the femur bone, respectively. Standard deviation is also reported based on the variations in these stitching errors for all pairs of BB landmarks. In Fig. 7, the nonoverlapping stitching of the CBCT volumes of the pig femur are shown.

Table 1.

Errors are computed by measuring the average of the absolute distances between eight radiolucent landmarks implanted in the femur head, greater trochanter, patella, and the condyle. The residual distances are measured between the opposite sides of the femur (hip to knee). Errors in angular measurements for tibiofemoral (TF) and lateral‐distal femoral (LDF) are reported in the last two columns. Each method is tested twice on the animal cadaver. The C‐arm translation was nearly 210 mm to acquire each nonoverlapping CBCT volume. The first four rows present the results using vision‐based methods suggested in this paper. We then present the errors of registration using external trackers as well as image‐based stitching of overlapping CBCT volumes with NCC similarity measure. Note that in this table the results of stitching using 2D features (Section 5.B) are not presented as measurements on a similar animal specimen were not reported in Ref. [24]. All errors are measured by comparing the stitching measurements with the measurements from a complete CT of the porcine specimen as ground truth

Tracking method error	Stitching error (mm)	Absolute distance error (%)	TF error	LDF error
	Mean ± SD	Mean	Mean ± SD	Mean ± SD
Marker tracking of patient (Section 4.A.1)	0.33 ± 0.30	0.14	0.6° ± 0.2°	0.5 ± 0.3°
Marker tracking of surgical bed (Section 4.A.2)	0.62 ± 0.21	0.26	0.7 ± 0.3°	2.2 ± 0.4°
RGBD‐SLAM tracking (Section 4.B)	0.91 ± 0.59	0.42	0.5 ± 0.2°	0.6 ± 0.4°
Surface data tracking (Section 4.C)	1.72 ± 0.72	0.79	1.0 ± 0.7°	3.1 ± 1.9°
Infrared tracking (Section 5.A)	1.64 ± 0.87	0.73	0.3 ± 0.1°	2.4 ± 0.8°
Image‐based registration	9.27 ± 2.11	6.52	1.2 ± 0.5°	2.7 ± 1.5°

Figure 7.

Parallel projection through two CBCT volumes acquired from an animal cadaver to create a DRR‐like visualization. [Color figure can be viewed at wileyonlinelibrary.com]

The lowest tracking error of 0.33 ± 0.30 mm is achieved by tracking the cubical visual marker attached to the patient. Marker‐less stitching using RGBD‐SLAM exhibits submillimeter error (0.91 mm), while tracking only using depth cues results in a higher error of 1.72 mm. The alignment of CBCT volumes using an infrared tracker also has errors larger than a millimeter. The stitching of overlapping CBCT volumes yielded a substantially higher error (9.27 mm) compared to every other method in Sections 2.B. and 4.A.1.. Fig 8 shows the convergence of the NCC registration cost when stitching using image information. The NCC similarity cost between the (k)th and (k + 1)th CBCT is defined as:

$$\text{NCC}=\sum ^{|{\mathrm{\Omega }}_{k,k+1}|}\frac{CBC{T}_{(k)}·CBC{T}_{(k+1)}^{(\mathbf{R},\mathbf{t})}}{{\sigma }_k{\sigma }_{k+1}}$$ (11)

where Ω _k,k+1 is the common spatial domain of the mean normalized volumes CBCT _(k) and CBCT _(k+1), (R , t) are rotation and translation parameters, and σ _k and σ _{k + 1} are the standard deviations of the CBCT intensities. In this experiment, seven CBCT scans were acquired to image the entire phantom. Every two consecutive CBCT scans were acquired with 50.0–60.0 mm in‐plane translation of the C‐arm in between to ensure nearly half volume overlap (CBCT volume size along each dimension is 127 mm). The optimization never reached the maximum number of iteration threshold that was set to 500. Image‐based registration was performed on the original volumes, with no filtering or down‐sampling of the images.

Figure 8.

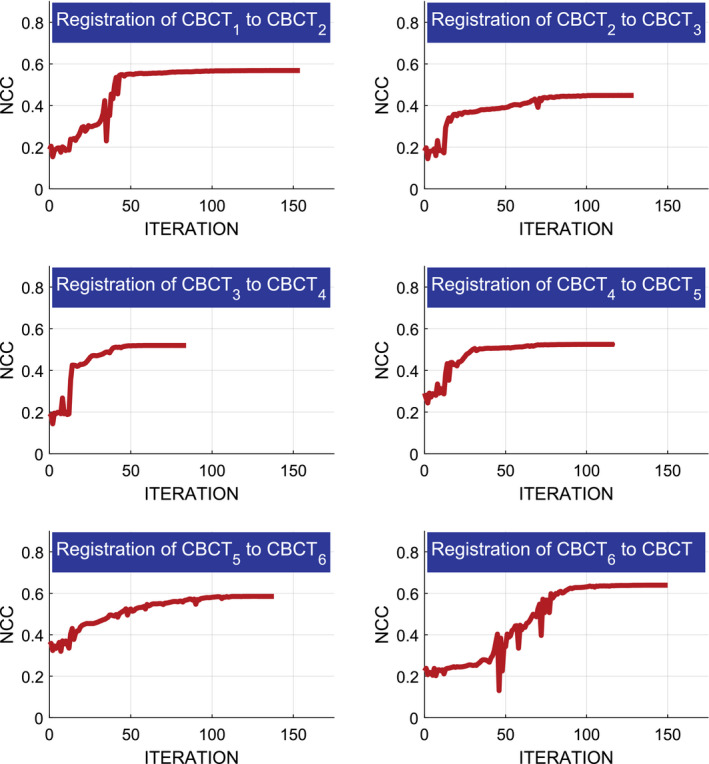
Optimization of the NCC similarity cost for registering multiple overlapping CBCT volumes acquired from a femur phantom. [Color figure can be viewed at wileyonlinelibrary.com]

In Table 1, we also report the angles between the mechanical and the anatomical axes of the femur (tibiofemoral angle), as well as the angle between the mechanical axis and the knee joint line (lateral‐distal femoral angle) using the vision‐based stitching methods. The results indicate minute variations among different methods.

These methods are also evaluated on a long radiopaque femur phantom. The stitched volumes are shown in Fig. 9, and the stitching errors for each method are reported in Table 2.

Figure 9.

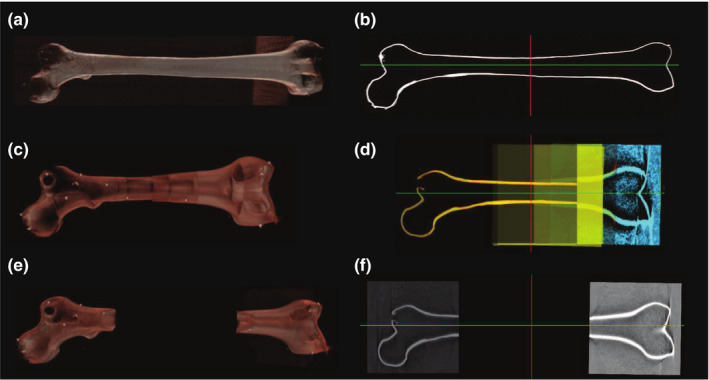
(a, b) are the volume rendering and a single slice from a CT scan of a femur phantom. (c, d) are the corresponding views of the volume using image‐based registration. The image‐based registration uses seven overlapping CBCT volumes and results in significantly shorter total length of the bone (results in Table II). This incorrect alignment is due to insufficient amount of information in the overlapping region, especially for volumes acquired from the shaft of the bone. The shaft of the bone is a homogeneous region where the registration optimizer converges to local optima. (e, f) are the similar views of a nonoverlapping stitched volume using RGBD‐SLAM. [Color figure can be viewed at wileyonlinelibrary.com]

Table 2.

The errors on a long femur phantom are reported similar to the measurements in Table 1. The length from the femur neck to the intercondylar fossa of the dry phantom is approximately 369 mm. To measure the distance errors, a total of 12 landmarks are attached to the femur (6 metal beads on each end). Stitching with each method is repeated three times, and all errors are computed by comparing the measurements to the ground‐truth measurements in a CT scan of the phantom

Tracking method error	Stitching error (mm)	Absolute distance error (%)	TF error	LDF error
	Mean ± SD	Mean	Mean ± SD	Mean ± SD
Marker tracking of patient (Section 4.A.1)	0.59 ± 0.37	0.20	0.8 ± 0.3°	2.9 ± 0.5°
Marker tracking of surgical bed (Section 4.A.2)	0.66 ± 0.18	0.23	0.7 ± 0.4°	2.3 ± 0.8°
RGBD‐SLAM tracking (Section 4.B)	1.01 ± 0.41	0.38	0.8 ± 0.6°	0.9 ± 0.6°
Surface data tracking (Section 4.C)	2.53 ± 1.11	0.87	1.9 ± 0.9°	4.1 ± 2.2°
Infrared tracking (Section 5.A)	1.76 ± 0.99	0.61	1.1 ± 0.3°	2.7 ± 0.6°
2D feature tracking (Section 5.B)24	1.18 ± 0.28	0.62	–	–
Image‐based registration	68.6 ± 22.5	23.4	3.9 ± 2.0°	5.2 ± 1.7°

7. Discussion and conclusion

In this work, we presented three vision‐based techniques to stitch nonoverlapping CBCT volumes intraoperatively. Our system design allowed for tracking of the patient or C‐arm movement with minimal increase of workflow complexity and without introduction of external tracking systems. We attached an RGB and depth camera to a mobile C‐arm, and deployed computer vision techniques to track changes in C‐arm pose and, consequently, stitch the subvolumes. The proposed methods employ visual marker tracking, RGBD‐based SLAM, and surface tracking by fusing depth data to a single global surface model. These approaches estimate the relative CBCT volume displacement based on only RGB, a combination of RGB and depth, or only depth information. As a result, stitching is performed with lower dose, linearly proportional to the size of nonoverlapping subvolumes. We anticipate our methods to be particularly appropriate for intraoperative planning and validation for long bone fractures or joint replacement interventions, where multiaxis alignment and absolute distances are difficult to visualize and measure from the 2D x‐ray views.

The RGBD camera is mounted on the C‐arm using a rigid construction to ensure that it remains fixed with respect to the image intensifier. Previous studies showed the validity of the one‐time calibration of an optical camera on the C‐arm.²⁵ However, due to mechanical sagging of the C‐arm, the stereo extrinsic parameters between the RGBD device and the x‐ray source are subject to small changes when the C‐arm rotates to different angles.⁴³

During the rearrangement of the C‐arm and the patient for the next CBCT acquisition, the vision‐based tracking results are recorded. For this rearrangement, we consider the clinically realistic scenario of a moving C‐arm and a static patient. However, as extensively discussed in Section 2.B., for marker‐based methods, the relative movement of the patient to C‐arm is recorded; hence, there are no limitations on allowed motions.

We performed the validation experiments on an animal cadaver, and compared the nonoverlapping stitching outcome to an infrared tracking system and image‐based registration using overlapping CBCT volumes. In these experiments, we used a CT scan of the animal cadaver as the ground‐truth data. The visual marker‐based tracking achieved the lowest tracking error (0.33 mm) among all methods. The high accuracy is due to utilizing a multimarker strategy which avoids tracking in shallow angles. The RGBD camera has a larger field of view compared to the x‐ray imaging device. Therefore, the marker can be placed in the overlapping camera views. For example, in the case of imaging, the femoral head and the condyle, the visual marker can be placed near the femoral shaft. The marker only needs to remain fixed with respect to the patient for the duration which the C‐arm is repositioned and need not be present for the CBCT acquisitions. Therefore, certain clinical limitations, such as changes to the scene, draping, patient movement, or the presence of surgical tools in the scene are not limiting factors.

Visual marker tracking of patient (Section 4.A.1) requires an additional marker to be introduced directly into the surgical scene. Doing so is beneficial, as C‐arm displacements are tracked with respect to the patient, suggesting that patient movements on the surgical bed will be accurately reflected in the stitching outcome. Yet, this approach increases setup complexity, as sterility and appropriate placement of the marker must be ensured. On the other hand, tracking of the surgical table with an array of visual markers under the bed (Section 4.A.1) does not account for patient movement on the bed. However, it has the benefit of not requiring any additional markers attached to the patient. Furthermore, since the array of markers is larger in dimensions compared to the cube marker, the tracking accuracy will not decrease significantly for larger displacements of the C‐arm. This consistent tracking quality using the array of markers is seen when comparing the stitching errors in Tables 1 and 2 where the error only increases from 0.62 to 0.66 mm. The standard deviation for this tracking method is also the lowest compared to every other tracking approach shown in the tables.

Stitching based on the tracking with RGB and depth information together has 0.91 mm error, and tracking solely based on depth information has 1.72 mm error. In a clinically realistic scenario, the surgical site comprises drapes, blood, exposed anatomy, and surgical tools which allows the extraction of large number of useful color features in a color image. The authors believe that a marker‐less RGBD‐SLAM stitching system can use the aforementioned color information, as well as the depth information from the cocalibrated depth camera, and provide reliable CBCT image stitching for orthopedic interventions.

The angular errors in Tables 1 and 2 indicate a larger ranking in error for LDF angles compared to TF. TF angular error is most affected by the translational component along the shaft of the bone. Lower TF errors therefore indicate lower errors in leg length. On the other hand, LDF angular errors correlate with in‐plane malalignment.

The use of external infrared tracking systems to observe the displacement of patients are widely accepted in clinical practice, and are usually not deployed to automatically align and stitch multiple CBCT volumes. A major disadvantage of external tracking systems is the introduction of additional hardware to the operating room, and the accumulation of tracking errors when tracking both the patient and C‐arm.

Prior method for stitching of CBCT volumes uses an RGB camera attached near the x‐ray source.²⁴ In this method, all image features are approximated to be in the same depth scale from the camera base. Hence, very limited number of features close to the laser line are used for tracking. This will contribute to poor tracking when the C‐arm is rotated as well as translated.

The stitching errors of the vision‐based methods are also compared to image‐based stitching of overlapping CBCT volumes in Tables 1 and 2. Image‐based approach yielded high errors for both the animal cadaver (9.27 mm) as well as the dry bone phantom (68.6 mm) because of insufficient and homogeneous information in the overlapping region. The errors are reported lower when registering the porcine specimen due to shorter length of the bone and the presence of soft tissue in the overlapping region.

In Fig. 8, we demonstrated the cost for registering multiple overlapping CBCT volumes. The NCC similarity measure reached higher values (0.6 ± 0.04) when registering CBCT volumes acquired from the two ends of the bone which had more dominant structures, and yielded lower similarity scores at the shaft of the phantom. Results of image‐based registration in Tables 1 and 2, and Fig. 9 show high stitching error using only image‐based solution, as the registration converged to local optima at the shaft of the bone.

We also avoided stitching of projection images due to the potential parallax effect which causes incorrect stitching and the length and angles between the anatomical landmarks will not be preserved in the stitched volume.

The benefits of using cameras with a C‐arm for radiation and patients’ safety, scene observation, and augmented reality have been emphasized in the past. This work presents a 3D/3D intraoperative image stitching technique using a similar opto‐x‐ray system. Our approach does not limit the working space, and only requires minimal additional hardware which is the RGBD camera near the C‐arm detector. The C‐arm remains mobile, self‐contained, and independent of the operating room. Further studies are underway to evaluate the effectiveness of CBCT stitching for interlocking and hip arthroplasty procedures on cadaver specimens. Finally, we plan to integrate the RGBD sensor into the gantry of the C‐arm to avoid accidental misalignments.²⁵

7.A. Considerations for clinical deployment

The success of translation for each of the proposed vision‐based stitching solutions depends on the requirements of the surgery. While our visual marker‐based approach yielded very low stitching errors, it increased the setup complexity by requiring external markers to be fixed to the patient during C‐arm rearrangement. Conversely, RGBD‐SLAM tracking allowed for increased flexibility as no external markers are required. However, this flexibility came at the cost of slightly higher stitching errors. Yet, in angular measurements, RGBD‐SLAM outperformed the marker‐based tracking and yielded smaller errors. The stitching errors for both marker‐based and marker‐less methods were well below 1.00 cm, which is considered “well tolerated” for leg length discrepancy in the orthopedic literature.⁴⁴ An angular error greater than 5° in any plane is considered as malrotation in orthopedics literature.¹⁰ All methods proposed in this manuscript exhibited angular errors below this threshold.

Conflict of interest

The authors have no conflicts to disclose.