The coevolution of cooperation and cognition in humans

Abstract

Cooperative behaviours in archaic hunter–gatherers could have been maintained partly due to the gains from cooperation being shared with kin. However, the question arises as to how cooperation was maintained after early humans transitioned to larger groups of unrelated individuals. We hypothesize that after cooperation had evolved via benefits to kin, the consecutive evolution of cognition increased the returns from cooperating, to the point where benefits to self were sufficient for cooperation to remain stable when group size increased and relatedness decreased. We investigate the theoretical plausibility of this hypothesis, with both analytical modelling and simulations. We examine situations where cognition either (i) increases the benefits of cooperation, (ii) leads to synergistic benefits between cognitively enhanced cooperators, (iii) allows the exploitation of less intelligent partners, and (iv) the combination of these effects. We find that cooperation and cognition can coevolve—cooperation initially evolves, favouring enhanced cognition, which favours enhanced cooperation, and stabilizes cooperation against a drop in relatedness. These results suggest that enhanced cognition could have transformed the nature of cooperative dilemmas faced by early humans, thereby explaining the maintenance of cooperation between unrelated partners.

1. Introduction

Hunting and gathering was the main subsistence strategy of archaic humans over the last 2 million years, until the advent of agriculture 10 000 years ago [1,2]. Modern hunter–gatherer societies live in small bands mainly composed of unrelated individuals [3,4]. However, the first hunter–gatherers of the genus Homo, more than 1.5 million years ago, lived in smaller groups where partners were probably more related than in modern hunter–gatherers [5–9]. The higher relatedness in archaic hunter–gatherers could explain, at least partially, a range of cooperative behaviours, such as group hunting and meat sharing, because the benefits of cooperation were likely to be shared with relatives (kin selection; [10]). The problem is to explain how a similarly high level of cooperation can be preserved during the transition to larger groups of unrelated individuals.

Our hypothesis is that after cooperation had evolved in small groups, via kin selection, coevolution with another trait increased the returns from cooperation, allowing it to be maintained when group size increased and relatedness decreased. In particular, we suggest that once cooperation had evolved, natural selection favoured additional traits, such as enhanced cognition, which increased the efficiency of cooperative behaviours, or even enabled synergistic effects between individuals involved in cooperative actions, such that cognitively enhanced cooperators were able to produce larger benefits than without cognition. Examples of such potential traits range from increased relative brain size, changes in brain connectivity and functionality, to genes involved in language [11–15]. These innovations are believed to have augmented the social and technical intelligence of early humans, and might have been the basis for stone tool technologies, hunting, as well as the ability to imagine future outcomes, and take the mental perspective of others [7,16–26]. These enhanced cognitive capacities could have transformed the nature of some cooperative dilemmas faced by early humans, such that cooperation could still be stable, with low or negligible relatedness.

However, it is not clear whether cognition can coevolve with cooperation in the way that would be required by our hypothesis. While sociality is at the centre of most explanations for the evolution of cognition (the ‘social brain hypothesis’), the role of relatedness between social partners has often been argued to be of minor importance, at least in the later stages of human evolution [7,23,27,28]. Theoretical studies have, therefore, focused on situations where conflict, either within- or between-groups was the underlying factor promoting higher cognition [16,29–31]. Furthermore, higher cognitive abilities could enable individuals to generate larger benefits for their group and, at the same time, take advantage of their social partners through deception [16,26]. Hence, it is still unknown what the relationships are between relatedness and the benefits from both cooperation and cognition, and under what conditions both traits can coevolve and remain stable.

We test the theoretical plausibility of our hypothesis, by examining when cognition can coevolve with cooperation in groups of related individuals, and whether this coevolution can stabilize cooperation, even if subsequently relatedness between social partners decreases. In an analytical model, we consider different scenarios where cognition allows individuals to (i) gain greater benefits from cooperation by enabling them to either generate larger gains for the same cost (e.g. by predicting a prey's reactions), (ii) generate synergistic benefits as the number of cognitively enhanced individuals increases (e.g. through better coordination and/or communication with each other [22,32–34]) and (iii) exploit less intelligent partners through manipulation or deception [16,26]. Second, we ask whether some level of cooperation can be maintained once a cognitive trait has evolved, even though group size increases and relatedness decreases. We confirmed the robustness of our analytical results with individual-based simulations. Although we focus on human cognition, we stress that our theory applies more generally to other intelligent species, such as primates and cetaceans, where cognition is likely to have evolved in groups of related individuals [32,35–37].

2. Model

(a). Model description

We consider an infinitely large population, which is subdivided into an infinite number of patches of size n [38]. Individuals are haploid, and interact socially within patches. We assume that social interactions affect an individual's fecundity. After the social interactions, adults on patches produce a very large number of juveniles, and die. Juveniles all disperse to some new patch. Competition between juveniles reduces patch size to n individuals. We assume that individuals on each patch can be related, although we do not yet specify how relatedness comes about (e.g. juveniles might not disperse independently). Generations are non-overlapping and competition is global. We later expand our model to include limited dispersal and overlapping generations, and let relatedness vary in terms of the parameters of the life cycle.

Individuals carry two social traits: (i) a cooperative trait x, determining the probability of contributing, at personal fecundity cost c > 0, a baseline public good b > 0 that is shared equally among all group members and (ii) a cognitive trait y, determining the probability of investing into better cognition capabilities early in development, at personal cost d > 0. We assume that both traits can be expressed independently, e.g. y can be expressed even though x is not, and we also assume no genetic correlation between the two traits, such that a change in the value of one trait does not influence that of the other trait.

We assume that cognition can enhance the contribution of a focal individual in two different ways. First, the contribution of individuals expressing y might merely generate better returns compared to the baseline contribution b. In this case, the benefit generated is increased by an amount b_C ≥ 0. Second, individuals expressing the y trait might interact together in order to produce increasingly large public goods, i.e. synergy could occur between cognitively enhanced individuals, with a parameter α ≥ 0 controlling synergistic effects. Specifically, synergy occurs when α > 0. Importantly, all individuals in the group enjoy an equal share of the total contributions of both normal and cognitively enhanced individuals.

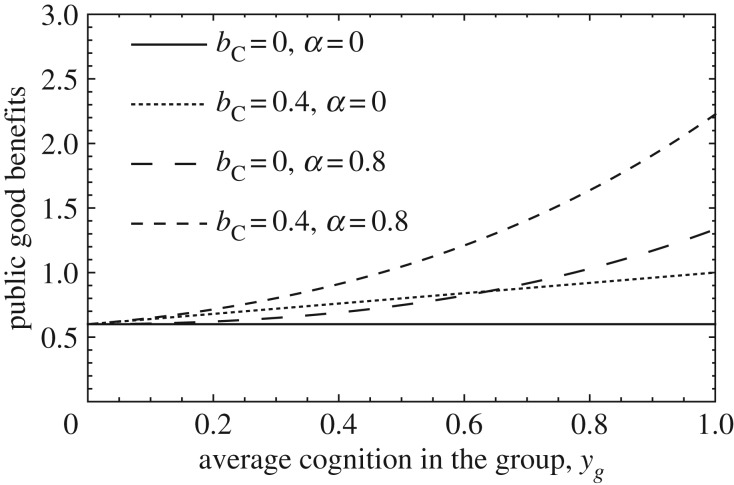
Following from our assumptions, the amount of public good received by a focal individual takes the form B(x_g, y_g) = x_g(1 − y_g)b + x_gy_g(b + b_C)e^αy_g, where x_g and y_g are the group average cooperation and cognition traits, respectively, in the focal individual's group (including itself). Depending on the parameters b_C and α, this production function covers scenarios in which cognition may allow for (i) larger contributions, (ii) synergism between cognitively enhanced contributors or (iii) both (figure 1).

Figure 1.

Public good production functions. Varying both b_C and α allows us to capture different potential effects that cognition might have on the per capita benefit from a public good that is rivalrous B(x_g, y_g). In case of a non-rivalrous public good, the per capita benefit received by a focal individual is nB(x_g, y_g). Parameters: x_g = 1 and b = 0.6.

These assumptions reflect a type of public good that is rivalrous because the per capita share depends on the number of consumers in the group (i.e. patch size n). However, our model can also reflect a non-rivalrous public good (e.g. cultural knowledge, such as the ability to create a tool) by multiplying the per capita benefit B(x_g, y_g) by n, so that individuals receive a public good which only depends on the number of contributors in the group. As a consequence, the conditions for cooperation and cognition to be stable can be recovered from table 1; electronic supplementary material, tables S1 and S2, except that the benefits from the public good need to be multiplied by n.

Table 1.

Conditions for full cooperation and full cognition to be favoured (i.e. H(1, 1) > 0 and K(1, 1) > 0) for different scenarios. Parameters: R_o, relatedness; c, cooperation cost; d, cognition cost; b, cooperation benefit; b_C, cognition benefit; α, synergy factor; n, group size.

bC	α	H > 0	K > 0
=0	=0		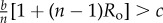0 > d
>0	=0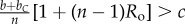
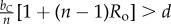=0	>0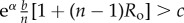
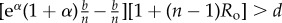>0	>0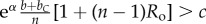

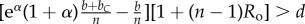With our assumptions, the fitness w of a focal individual is given by w = F/F. Here, F = 1 − x₀c − y₀d + B(x_g, y_g) is the fecundity of the focal individual, where x₀ and y₀ are the focal's cooperation and cognition traits, respectively, and F = 1 − xc − yd + B(x, y) is the average fecundity in the population.

We follow the approach on the joint evolution of multiple social traits of Brown & Taylor [39]. Specifically, we consider the successive invasion of mutants in one trait in a resident population that is monomorphic for both traits, and where a mutant for one of the two traits (holding the other constant) differs only slightly from that of the resident population. We assume that a mutant will be rare globally, but potentially common in the local group, due to relatedness.

We determine Hamilton's selection gradient for both traits to investigate when an increase in either trait is favoured by selection [40,41]. We denote R the relatedness of the focal individual to a random group member, including itself (i.e. ‘whole-group’ relatedness). For simplicity, we assume that relatedness is the same at both loci. Hence, the marginal inclusive fitness effects for cooperation and cognition are given by H(x, y) = ∂w/∂x₀ + R∂w/∂x_g and K(x, y) = ∂w/∂y₀ + R∂w/∂y_g, respectively, where all derivatives are evaluated at x₀ = x_g = x and y₀ = y_g = y.

We use the inclusive fitness effects above to determine when selection favours the evolution of cooperation and cognition by looking at when H > 0 and K > 0, respectively. We are mainly interested in the cases where a population playing full cooperation and full cognition (i.e. x*, y* = 1) is stable. Hence, the conditions for the extreme point x, y = 1 to be stable are if both H(1, 1) > 0 and K(1, 1) > 0. We later confirm these stability conditions, using individual-based simulations (electronic supplementary material, figures S6–S8).

Our expression for Hamilton's selection gradient is in terms of ‘whole-group’ relatedness which includes relatedness to self. However, this measure of relatedness can also be expressed in terms of group size and ‘others-only’ relatedness R_o [42], which measures the relatedness of a focal individual to a random member in the group (excluding the focal). By substituting R = (1 + (n − 1)R_o)/n into H(x, y) and K(x, y), we can determine when full cooperation and full cognition remain stable when varying both group size n and R_o.

3. Results

By substituting the benefit and fitness functions into H(x, y) and K(x, y), we find that, assuming the population average fecundity is always positive, the selection gradients for cooperation H(x, y) and cognition K(x, y) are positive if

3.1a

and

3.1b

respectively. Both selection gradients comprise the marginal returns from cooperation and cognition (last term on the left-hand side in inequality (3.1)), weighted by relatedness of the individual to itself (i.e. 1) and to the other n − 1 group members. Table 1 provides a summary of the conditions for full cooperation and full cognition (x, y = 1) to be favoured. Electronic supplementary material, table S1 gives the same conditions in the absence of relatedness (R_o = 0).

In the electronic supplementary material (§1), we consider a more explicit life cycle, where relatedness within patches emerges as a consequence of demographic processes, such as the probability of adult survival s and juvenile dispersal m [43,44]. We find that the conditions for cooperation and cognition to be favoured remain the same as in inequality (3.1) and table 1, except that R_o is replaced by κ = {2(1 − m)s}/{n[2 − m(1 − s)] + 2(1 − m)s}, where κ is the scaled relatedness coefficient which is demographically scaled so as to capture the effect of both increased genetic assortment and increased local competition between kin [45]. Our value of κ recovers that presented in [45] for this life cycle.

(a). The evolution of cooperation

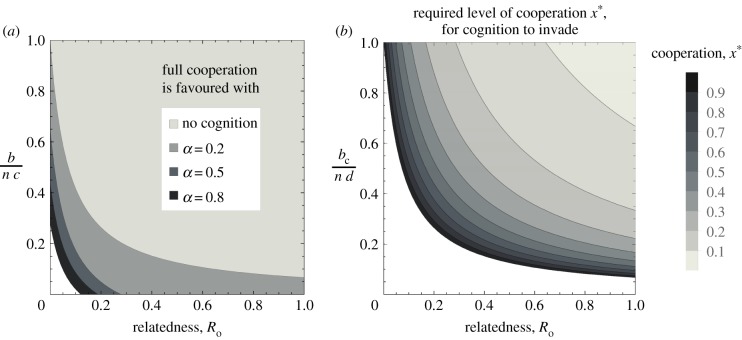
We first consider the evolution of cooperation, assuming no cognition in the population (y → 0). In this case, cooperation will be favoured if, and only if (n − 1)R_ob/n > c − b/n (figure 2a; electronic supplementary material, figure S1). That is, if the benefits received from the proportion of relatives among the n − 1 group members are greater than the net cost of contributing (i.e. cost of contribution minus own share). In other words, the indirect fitness benefits need to outweigh the direct fitness cost. This condition is Hamilton's Rule for the linear public goods game [46,47]. Selection for cooperation is frequency-independent, and so the population will always converge towards full cooperation if Hamilton's Rule is satisfied. However, assuming b/n < c, cooperation can never be favoured in the absence of relatedness, in which case the population will converge towards full defection.

Figure 2.

Invasion and stability conditions for cooperation and cognition. (a) Parameter space where full cooperation is stable (and can invade), with and without cognition, as a function of relatedness and the per capita benefit to cost ratio from cooperation (scaled by group size n). Increasing the synergy factor α increases the stability of full cooperation, even without relatedness (R_o = 0). (b) Level of cooperation required for cognition to invade, in function of relatedness and the per capita share to cost ratio from cognition (scaled by group size n). Parameters in (a) b_C = 2.5; in both panels n = 15, c = 0.1, and d = 0.05.

(b). The evolution of cognition

If there is a sufficient level of cooperation in the population, then cognition can be favoured. Specifically, if x* ≥ d/{[1 + (n − 1)R_o]b_C/n} (figure 2b). Here, both larger d and n increase the required amount of cooperation for cognition to be favoured, while larger b_C and R_o decrease it. Assuming that cooperation has fully invaded the population (x = 1), then cognition will invade if [1 + (n − 1)R_o]b_C/n] > d. The initial invasion of cognition does not depend on synergy, because cognition can only provide synergistic returns if there is already some cognition in the population (i.e. y > 0). Consequently, if cognition only allows synergy, but no larger additive returns, then cognition can never increase from rarity (i.e. K(x, 0) < 0 if d > 0 and b_C = 0). However, this follows from our assumption of weak selection with continuous phenotypes, and would not necessarily occur with discrete phenotypes and strong selection.

(c). The coevolution of cooperation and cognition

If cognition is favoured and increases in the population, it will in turn increase the selection pressure on cooperation and vice versa. This is because, as the level of cognition (cooperation) increases in the population, the cognitively enhanced cooperators benefit increasingly from both their own contribution and that of their relatives. This can be seen from inequality (3.1), where H and K are increasing in y and x, respectively. The population will then converge towards full cooperation and full cognition (i.e. x, y = 1).

To summarize, cooperation can only evolve if there is sufficient relatedness R_o and benefits b (for a given c), whereas cognition can only evolve if there is sufficient cooperation (x*), relatedness and benefits from cognition b_C (for a given d). In all cases, increasing group size n hinders the evolution of both traits. Therefore, it follows that the population can only end up in one of three different states: (i) full defection and no cognition, (ii) full cooperation and no cognition and, (iii) full cooperation and cognition.

The analytical conditions for full cooperation and cognition to be stable are summarized in table 1. Full cooperation with full cognition is favoured by increasing the additional gains allowed by cognition (b_C), synergy (α) and relatedness (R_o) but disfavoured by increasing group size n and the cost of either cooperation c or cognition d (figure 2a). In the absence of synergy, only the stability of cooperation, but not that of cognition, increases with increasing baseline benefit b. By contrast, with synergy only, increasing b increases the stability of both traits.

(d). The transition from high to low relatedness

Assuming that a population has converged towards full cooperation and cognition, how stable would this population be in case of a subsequent decrease in relatedness? We can answer this by substituting R_o = 0 into the conditions shown in table 1 which gives the results in electronic supplementary material, table S1.

The results depend upon the type of benefits provided by cognition. If cognition only allows for larger benefits from cooperation, then cooperation is stable if the share from the public good (b + b_C)/n exceeds the cost of contributing c, whereas cognition is stable if the share from the benefit of cognition (b_C/n) exceeds the cost of cognition d.

By contrast, if cognition only allows for synergy (b_C = 0 and α > 0) then cooperation and cognition can be stable under less stringent conditions, and increasing synergy increases their stability. Finally, if cognition allows for both larger gains and synergy between cognitively enhanced individuals (b_C > 0 and α > 0), then full cooperation and full cognition are stable over an even wider range of parameter space (figure 2a; electronic supplementary material, figure S2–S5). As before, increasing patch size n disfavours cooperation and cognition, such that there is a threshold patch size above which they will not be stable (electronic supplementary material, figure S2–S5). In our more explicit life cycle, selection for cooperation and cognition decreases if the scaled relatedness coefficient κ decreases. This occurs if migration m and patch size n increase, or if survival s decreases (electronic supplementary material information, §1).

(e). Computer simulations

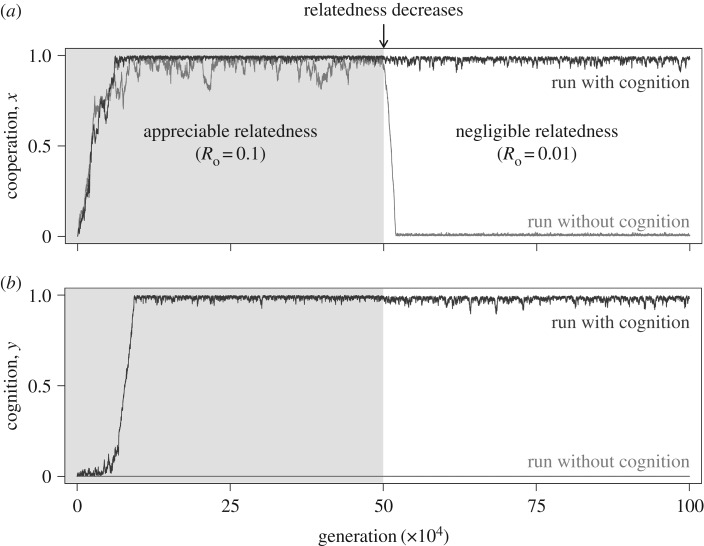
We used individual-based simulations to confirm whether a population at the equilibrium can remain stable even as relatedness decreases. We give a detailed description of the simulation model in electronic supplementary material, §2. We started our simulations with different levels of relatedness, and halfway through, we reduced relatedness to a value of R_o = 1/100. We then checked the long-term average of both cooperation and cognition in the population. All simulations were run for 10⁶ generations.

As predicted by our analytical model, full cooperation and full cognition remained locked even after a drop in relatedness, provided sufficient synergy and additive gains from cognition (figure 3; electronic supplementary material, figures S7 and S8). In the absence of cognition and whenever the direct benefits from cooperation and cognition were too low, populations which initially evolved cooperation were invaded by defectors as soon as relatedness decreased to negligible values. We confirmed these results for a large range of parameter values (electronic supplementary material, figures S6–S8).

Figure 3.

Joint evolution of cooperation and cognition in individual-based simulations. We compare the stability of cooperation (a) and cognition (b), with and without cognition. In both panels, the blue (grey) line represents the same simulation run with (without) cognition. In the run with cognition, the synergy factor α = 0.4. Relatedness was decreased halfway through each run (i.e. k = 10 and k = 100 in the first and second half, respectively, with R_o = 1/k). Parameters: n = 15, c = 1, b = 7, d = 0.5, b_C = 3.5, μ_h = μ_c = 0.01 and σ = 0.01.

(f). Machiavellian cognition

So far, we have assumed that cognition was beneficial for all group members, because the presence of cognitively enhanced individuals increased the share received by each of their patch members. However, it has been argued that cognition could be used for selfish profits through manipulation and deception of social partners (the ‘Machiavellian Intelligence hypothesis’ [16,26]). In this section, we explore how this negative aspect of cognition affects its coevolution with cooperation.

We expand our baseline model by assuming that relatively more intelligent individuals can exploit their partners by taking more than their fair share of the public good, e.g. through manipulation. Specifically, the benefit received by a focal individual with cognition y₀ is now B(x_g, y_g)(1 + gy₀)/(1 + gy_g). The parameter g controls the magnitude of exploitation in the following way: if g → 0 or if y₀ = y_g, a focal individual will receive the same public good share as everyone else. If y₀ ≠ y_g and g → ∞, the focal individual will receive a proportion y₀/y_g of the per capita benefit from the public good. Here, the cognition trait is analogous to the exploitation trait investigated in [39], except that cognition can increase and, at the same time, decrease the public good benefit to others if α, b_C > 0 and g > 0, respectively.

The selection pressure on cooperation does not change in this scenario (electronic supplementary material, §3). This comes from the fact that cognition still has the same effect on the public good created as in the baseline model. However, if there is cooperation in the population, the selection pressure for cognition is considerably larger than in our baseline model (electronic supplementary material, table S2, figure S9). This is because larger b and g also increase the marginal benefit from cognition. So, cognition can invade from rarity even in the absence of relatedness, if there is a sufficient level of cooperation in the population (i.e. x* ≥ dn/[b_C + bg(n − 1)]). As a consequence, full cognition is also stable under a larger area of parameter space (electronic supplementary material, table S2). Full cognition can even be stable in the absence of both larger benefits and synergism (b_C, a = 0). This is not surprising, because in a population with full cooperation and full cognition, a focal mutant with a lower level of cognition will be exploited by its partners.

We also find that increasing relatedness can sometimes have a negative effect on the evolution of Machiavellian cognition (electronic supplementary material, §3). The reason is that exploiting partners leads to indirect fitness costs if too many partners are relatives. In the extreme case where cognitively enhanced individuals produce neither larger nor synergistic benefits (b_C, α = 0), higher relatedness always hinders the evolution of cognition (electronic supplementary material, §3).

4. Discussion

We found that coevolution between cooperation and cognition can lead to a transition in the nature of the cooperative dilemma—from a state where cooperation can only evolve and be maintained with sufficient relatedness, to a state where it is stable even without relatedness. In small groups of related individuals, cooperation can evolve (figure 2b). If cognition enables individuals to either generate larger gains from cooperation and/or exploit less intelligent partners, then cognition can invade into cooperative societies (figure 2b). When cooperation and cognition are both favoured, an increase in either trait will increase selection pressure for the other trait, leading to an evolutionary feedback loop until the population has converged towards full cooperation and cognition. At this point, if relatedness drops via an increase in either group size or dispersal, such that cooperation on its own would not have been favoured, the combination of cooperation and cognition can still be stable. Cognition can, therefore, lead to a population being ‘locked’ in a stable cooperative state (figures 2 and 3).

(a). Cooperation and cognition

Cognition can only evolve in our model if there is a sufficient level of cooperation in the population (figure 2b). We focused on relatedness as the underlying factor promoting the emergence of cooperation. That relatedness can often play a key role in the evolution of cooperation, in scenarios where it is then less important for its maintenance, as has also been argued with reciprocity, punishment and group augmentation [48–52]. However, we believe that our conclusion on how cognition could have transformed the type of dilemmas faced by early humans does not rely on relatedness. In fact, processes where an additional trait can transform the pay-off matrix into a game where cooperation maximizes selfish profits have been argued to be common in nature [53]. Cooperation could have been promoted if individuals within groups depended on each other's cooperation to survive against predators, environmental catastrophes or other groups (the ‘interdependence hypothesis’ [28,31,49,54–56]). In turn, cooperation is likely to have introduced selection pressures on individuals to benefit from cooperation even more, or at a reduced cost [53]. For example, Gavrilets [31] showed that cooperation and cognition could evolve without relatedness when groups compete with each other. Gavrilets investigated a different productivity function for the baseline public good, and cognition did not have any synergistic effects on cooperation. Therefore, cognition in his model did not change the nature of the cooperative dilemma in the same way as in our model, and so cooperation might not remain stable if inter-group conflict becomes less frequent.

We also found that, if cognition does not allow for exploitation of others, it could evolve only if cognitively enhanced individuals are able to generate a larger amount of public good (figure 2b). The kin benefits from cognition need to outweigh the cost of developing cognition, which implies sufficiently high relatedness between partners and gains from cognition. However, our assumption that cognition provides benefits only through group cooperation is restrictive. In nature, cognition might have provided benefits in various additional contexts, such as tool making or foraging, thereby favouring its evolution [57].

Furthermore, we found that synergy is not important for the invasion of cognition. This is because cognition cannot provide significant synergistic returns to rare mutants, unless there is already some level of cognition in the population. On the other hand, synergy is crucial for the stability of both traits in the absence of relatedness (figures 2a and 3). Biologically, synergy could occur if cognition allows high coordination between hunters, via the use of planning and sign language, or acting according to the other hunters’ movement [32]. The stabilizing effect of synergism on cooperation is well known [58–63]. However, most previous studies investigating nonlinear production functions focused on a single cooperative trait (although see Brown & Taylor [39]). By contrast, we separated synergistic cooperation into two different traits. This allowed us to determine how both cooperation and synergistic cognition alter the selection pressure on each other.

(b). Machiavellian cognition

We have also shown that cognition initially evolves and remains stable more readily if it allows the exploitation of less intelligent partners (Machiavellian Intelligence Hypothesis [16,26]). This is in line with previous studies which found that cooperation creates selection pressures for higher cognitive abilities leading to the deception and manipulation of others [29,30]. Our scenario is also very similar to that in [39], where cooperation coevolves with an exploitative trait that reduces the amount of public good for personal profit. Our model complements these studies as we have incorporated both the beneficial and harmful consequences of cognition. This revealed that both Machiavellian and beneficial cognition can evolve together, provided the beneficial effect of cognition on the public good is sufficiently large. This suggests that, in accordance with the ‘social intelligence hypothesis’, cognition could have evolved due to its various effects on social interactions [16,17,22,26,55]. On the other hand, we showed that in the absence of greater benefits from cognition (b_C, α = 0), Machiavellian cognition evolves more easily in groups with low, rather than high relatedness, as was previously suggested [29].

(c). Key predictions

Our model can be validated by either testing our assumptions or predictions. First, one of our assumptions was that cognition rapidly increases the benefits (or decreases the costs) of cooperation, i.e. there is synergy between cognitively enhanced individuals. Because it is difficult to determine cognition in real-world collective actions, a starting point would be to estimate it indirectly. One proxy for cognition would be the level of specialization (skills acquired through learning) required for hunting parties in modern hunter–gatherers. Hence, demonstrating synergy requires showing that, for example, the success rate of groups with 10 specialized hunters is more than twice that of groups with five specialized hunters. An important point here is to control for observability, because hunters in smaller groups might be more isolated from each other, thereby providing more opportunities for cheating. Specialized hunters might also simply be better at detecting cheats. Second, our prediction that cognition allows for the maintenance of cooperation in the absence of other promoting factors can be tested in laboratory experiments, by artificially manipulating cognition. A possible experiment would be to recreate a situation similar to that in our figure 3. For example, in a cooperative task where coordination (or learning) provides larger benefits, cooperation could be initially promoted (e.g. through global competition [64]). Then, the cooperation-promoting mechanism could be removed halfway through. We would then expect cooperation to remain stable in a treatment where coordination/learning is allowed, compared to when it is not allowed.

Third, another prediction from our model is that cognition allows stable cooperation levels without relatedness or any enforcement mechanism, such as reciprocity, partner choice or punishment [51]. Indeed, enforcement mechanisms usually require cognition and can also maintain cooperation without relatedness [51,53]. Hence, one way to validate our prediction would be to compare relatedness between social partners across different cooperative tasks within primate species. We would then expect lower relatedness between social partners and the absence of partner control in those cooperative tasks that are more cognitively demanding. Finally, a more general prediction is that we expect more cooperation in more intelligent species. This could be tested with comparative analyses on different primate species, by looking at the correlation between cooperation and relatedness, and including cognition as a covariate. This is already partially supported by the positive correlation between cooperation and deception observed in primates [30]. As before, an important point here will be to distinguish between cases of cooperation with and without partner control mechanisms.

Data accessibility

The simulation code and data are available from the OSF data repository (osf.io/7p6us).

Author's contributions

M.d.S and S.A.W. conceived the study and contributed to modelling. M.d.S. performed the simulations. M.d.S. and S.A.W. wrote the paper. All authors gave their final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

M.d.S. is funded by the Swiss National Science Foundation (grant no. P2LAP3-158669).