A Weighted SNP Correlation Network Method for Estimating Polygenic Risk Scores

Abstract

Polygenic scores are useful for examining the joint associations of genetic markers. However, because traditional methods involve summing weighted allele counts, they may fail to capture the complex nature of biology. Here we describe a network-based method, which we call weighted SNP correlation network analysis (WSCNA), and demonstrate how it could be used to generate meaningful polygenic scores. Using data on human height in a US population of non-Hispanic whites, we illustrate how this method can be used to identify SNP networks from GWAS data, create network-specific polygenic scores, examine network topology to identify hub SNPs, and gain biological insights into complex traits. In our example, we show that this method explains a larger proportion of the variance in human height than traditional polygenic score methods. We also identify hub genes and pathways that have previously been identified as influencing human height. In moving forward, this method may be useful for generating genetic susceptibility measures for other health related traits, examining genetic pleiotropy, identifying at-risk individuals, examining gene score by environmental effects, and gaining a deeper understanding of the underlying biology of complex traits.

1 Introduction

While genome-wide association studies (GWAS) have led to some ground-breaking discoveries [1], overall their success has been somewhat underwhelming. In general, GWAS have not been very effective in identifying the genetic contributions to complex traits that do not follow Mendelian laws of inheritance [2]. In general, many of the results coming out of GWAS fail to replicate, or for those markers that are independently validated, the majority only explain a very small proportion of the variance in a given trait [3, 4]. This is a valid concern as it impedes the ability to incorporate “personalized medicine” into disease prevention and treatment.

GWAS relies on linkage to examine the association between loci and a given trait. Due to recombination during meiosis, the markers in a GWAS—single-nucleotide polymorphisms, or SNPs—are used as proxies for detecting nearby variants, which are potentially causal [5]. In a typical GWAS, the association between the trait of interest and a large number m of SNPs (often in the millions) is assessed using m regression models where for each model, the trait is regressed on a single SNP. Such approaches fail to capture the complex nature of biology, and suffer from a number of statistical limitations that impede our ability to identify replicable molecular mechanisms. For instance, because GWAS require testing of millions of hypotheses, these studies tend to lack the power needed to detect the very small individual effects observed for most SNPs [2]. Further, there is significant evidence suggesting that many complex traits are highly polygenic [6], implying multiple causal variants contribute simultaneously to the genetic susceptibility of a trait. Thus, examination of genetic scores, rather than individual SNPs, may lead to better insights when studying the genetic contributions to complex traits.

Polygenic methods that move beyond the one marker approach have the ability to aid in genetic association studies by (1) increasing statistical power to detect true effects via dimension reduction; (2) providing biological insight regarding important pathways; and (3) improving our ability to examine gene by environment interactions. In 2007, Wray et al. proposed a method for examining the aggregate influence of multiple genetic markers [7]. The method involved generating a Polygenic Risks Score (PRS) based on results from a GWAS. After running a GWAS on a discovery sample, SNPs are selected for inclusion in the PRS on the basis of their association with the phenotype. Using a validation sample, the PRS can be calculated as a sum of the phenotype-associated alleles (often weighted by the SNP-specific coefficients from the GWAS). Using this score, the joint association of multiple SNPs with the given trait can be evaluated. Overall, PRS techniques have become increasingly popular, facilitating genetic discoveries for complex traits [6, 8–11]. However, given that they are based on linear combinations of markers, traditional PRS may fail to capture nonlinearity between SNPs.

While PRSs often account for a larger proportion of the variance in a trait than individual SNPs, much of the heritability remains unaccounted for—a phenomenon known as “missing heritability” [12]. One hypothesis is that the surprisingly low proportion of heritability being explained may be due to the exclusion of gene–gene interactions—or genetic network structure [13, 14]. However, very few methods exist that generate PRSs by incorporating gene network topology.

Weighted gene correlation network analysis (WGCNA) has been used repeatedly for the successful identification of epigenetic and transcriptomic networks, which relate to a number of physical, behavioral, and disease traits [15–19]. In WGCNA, network modules are identified using unsupervised machine learning methods—hierarchical clustering based on topological overlap similarity measure—and then represented using a single synthetic profile referred to as the “eigengene” or more generally eigen-node, which can be used to examine the association between a module (network) and the trait of interest [20, 21]. However, the underlying linkage-based structure of GWA data prevents the use of SNPs in traditional WGCNA methods.

Here we present a WGCNA-based method that can be applied to SNP data, which we call the weighted SNP correlation network analysis (WSCNA). Aside from accounting for the influence of LD, this method also incorporates a semisupervised machine learning approach that will facilitate the detection of modules that are trait specific. We demonstrate this method using human height as the phenotype. Human height has been extensively studied using GWAS, PRS, and heritability analyses. It is also predicted to be approximately 80% heritable and highly polygenic.

2 Materials

In order to conduct WSCNA one either needs access to genotype data or published GWAS results from multiple studies/cohorts. For our analytic example, we used genotype data from 10,466 persons of European ancestry who were participants in the Health and Retirement Study (HRS), a nationally representative longitudinal study of health and aging in the US. Genotyping was done using the Illumina Human Omni-2.5 Quad beadchip, with coverage of approximately 2.5 million single nucleotide polymorphisms (SNPs). Depending on both sample size and the number of genotyped markers, the ability to carry out WSCNA will also likely require access to a multi-core, 64 GB computer. For our example we used both [1] the University of Southern California’s high performance super computer (https://hpcc.usc.edu/), for GWA, clumping, PRS estimation; and [2] a 24-core desktop workstation with 64GB of memory, for WSCNA and validation.

3 Methods

3.1 Using Published GWAS Results

As mentioned previously, WSCNA can be run using published GWAS results or by generating new GWAS results. When using published results, many of the same criteria and concerns that go into constructing traditional PRS apply. Namely, one should be aware of strand ambiguous SNPs (A/T and C/G), linkage disequilibrium (LD), and overlap in availability of SNPs across datasets. While using results from imputed data will help with the latter concern, when it comes to strand-ambiguous SNPs, likely the safest option is to drop them. To account for LD, conventional practice is to prune data prior to conducting analysis—clump SNPs based on R² (typically between 0.1 and 0.5) and physical distance (typically around 500 kb), and then select the most significant SNP to represent the given block. One issue in pruning for WSCNA is that unlike PRS, the analysis requires multiple sets of GWAS results in order to look at SNP-SNP correlations. For that reason, identifying “the most significant SNP” in an LD block is ambiguous, but a natural solution is to select SNPs based on meta-analysis P values.

3.2 Running GWAS for WSCNA

When conducting original GWAS for WSCNA it is essential to use a training sample that is completely independent from the sample that will be used to assess the predictive ability of the score/s. In our example, we randomly divided our samples into a training set (70%) and a test set (30%). Before conducting the GWAS, quality control filters must be applied, which in our case resulted in 1,224,285 SNPs retained for the analysis. Additionally, principal components were generated in accordance with the methods described by Patterson et al. [22] to use as covariates to adjust for population structure.

As mentioned before, SNPs need to be pruned according to LD. To do so, a GWAS should be carried out in the training set, and results should be used to clump SNPs according to linkage disequilibrium (R² > 0.5) and physical distance (≤250 kb), such that only the most significant SNP is used to represent a given haplotype block. Once SNPs have been pruned and QC has been performed, one can now conduct the GWAS that will be used as input for WSCNA. Because the network structure in WSCNA is based on pairwise correlations of beta coefficients for individual SNPs, multiple GWAS have to be run using either different samples or different phenotypes. For our example, the training data was used to create 60 subsamples of 500 participants each (with replacement) and a GWAS for human height was run for each of the subsamples using only those SNPs selected from the clumping procedure, producing 60 GWAS results for each SNP.

3.3 Preparing Data for WSCNA

Once one has either (1) collected results from multiple published GWAS or (2) generated original results from multiple GWAS, inclusion criteria based on significance can be used to select SNPs for WSCNA. While it is possible to use all SNPs, this will likely be very computationally demanding. Therefore, as with traditional polygenic score estimation, we suggest significance criteria to select SNPs (e.g., consider all SNPs with P < 0.05) in the training data. For instance, in our example, we selected SNPs with P < 0.05 (n = 32,284). The P-values used for selecting SNPs can be the same as used for inclusion criteria when pruning. After SNPs of interest have been selected, the beta coefficients from each of the GWAS can be used to populate an n × m matrix, where n refers to the number of examined SNPs, and m refers to the number of GWAS from which results have been gathered. In the case of our example, we had a 32,284 × 60 matrix. Assuming all results files are placed in the current working directory, the following R code can be used to generate the appropriate matrices.

    Mat=matrix(NA,nrow=32284,ncol=60)
    for (i in 1:60){
     temp=read.csv(paste(“Height_sample”,i,“.assoc.
   linear”, sep=“”), sep=“”)
   Mat[,i]=temp$BETA
   }
    Data=as.data.frame(Mat)datSNP=as.data.frame(t (Data[,]))

3.4 Module/Network Detection Using WSCNA

WSCNA (using the WGCNA package in R) is run much like WGCNA; however, instead of using levels of expression or methylation as inputs, it uses the SNP associations with the trait/s of interest, with the goal of identifying trait-specific SNP networks, also known as modules. Weighted network construction requires a user-specified soft-thresholding power, β, to which SNP-SNP relationships are raised to calculate adjacency. Adjacency, as shown in Eq. (1), implies that the weighted adjacency a_ij between two SNPs is proportional to their similarity on a logarithmic scale,

$$a_{ij}=s_{ij}^{\beta },$$ (1)

As suggested by Zhang et al., the value for β could be selected so that the resulting network is approximately scale-free. The WGCNA package provides the functions pickSoftThreshold for evaluating scale-free topology as a function of β.

The next step in WSCNA is module detection. Modules represent clusters (or networks) of densely interconnected SNPs. Topological Overlap Matrix (TOM) is used to define a dissimilarity matrix that is then used as input to cluster SNPs into modules by applying hierarchical clustering. In order to define modules, one can select to implement either a constant- or variable-height tree cut—the latter is known as the Dynamic Tree Cut [23]. The constant-height tree cut allows the user to visually inspect the dendrogram and decide on a cut height that will be used to differentiate modules. However, in most cases, there is no single cut height that captures all prominent branches. For this reason, the Dynamic Tree Cut can be employed, in which branches below the cut height can be evaluated based on various branch shape measures and sufficiently “different” branches are called separate modules [23].

In addition to selecting the branch cutting methods and the β (thresholding power), as described above, a number of other network construction and module identification options can be specified, including the correlation function (Pearson correlation or the robust biweight midcorelation), signed vs. unsigned network, minimum module size and the sensitivity of Dynamic Tree Cut to branch splits (argument deepSplit). The deepSplit command specifies a value between 0 and 4 (lower values will produce larger, less finely split clusters). Signed vs. unsigned networks refer to whether negative SNP-SNP correlations are considered connected or not. In a signed correlation network, negative correlations are considered unconnected. Conversely, in unsigned correlation networks, network adjacency is based on the absolute value of correlation, such that strong negative correlations are treated as strong connections.

3.5 Network-Based Polygenic Scores

Using the network modules identified from WSCNA, we estimate the module eigen-nodes in our validation sample. Eigen-nodes are defined as the first singular vector of all SNP profiles in a given module and values can be interpreted as module-specific polygenic scores. The input data to calculate eigen-nodes for a validation subsample includes a matrix of m SNPs by n participants, where each cell represented a participant’s minor allele count for that given SNP. This is similar to the information that would be summed to generate a traditional polygenic score. The module eigen-nodes can then be used to validate the modules in respect to the phenotype of interest.

3.6 Gaining Biological Insight from SNP Correlation Networks

Biological insights can be gained from network modules by examining their topology and relationships to known pathways, biological processes, and molecular functions. For instance, for relevant networks, intramodular connectivity can be calculated for each gene in the network. The function intramodularConnectivity in the WGCNA R package computes the whole network connectivity (kTotal), the within module connectivity (kWithin), kOut = kTotal-kWithin, and kDiff = kIn-kOut = 2*kIN-kTotal.

    ADJ1=abs(cor(datSNP,use=“p”))^8
     Alldegrees1=intramodularConnectivity(ADJ1, moduleColors)

The measure of within module connectivity can be used to identify hub SNPs within the module. Similarly, module membership values can be estimated to identify hubs, by examining how strongly SNPs relate to module eigen-nodes.

    datKME=signedKME(daSNP, datME, outputColumnName=“MM.”)

Finally, SNPs within modules of interest can also be mapped to genes to be used as input in pathway enrichment and Gene Ontology (GO) analyses.

4 Results

4.1 Identification of SNP Networks Using WSCNA

Here we illustrate the use of WSCNA using height as a phenotype. For this example, we conducted original GWAS, rather than incorporating existing GWAS results. All GWAS were carried out on European populations and included adjustments for age, sex, and population stratification (using the first four principal components). SNPs with P < 0.05 were selected and pruned, resulting in 32,284 SNPs to perform WSCNA with. These SNPs were used to conduct 60 GWAS—one for each training subsample of 500 subjects—and the resulting beta coefficients were used to create a 32,284 × 60 matrix. Scale-free topology analysis of this network was used to select a soft-thresholding power of 8.

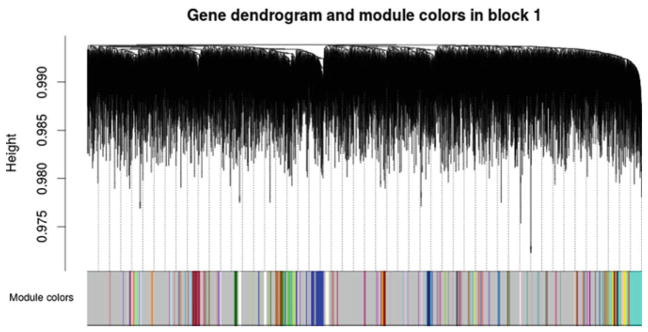
WSCNA was run using the following specifications to identify SNP modules: signed network, dynamic tree cut, a module detection cut-height of 0.998, soft-thresholding power of 8, minimum module size of 50, biweight midcorrelation, and a medium branch split sensitivity (deepSplit = 2). Fifty-five modules (excluding the grey module, which represents ungrouped SNPs) were identified (Fig. 1).

Fig. 1.

WSCNA SNP clustering tree and modules. SNP clustering tree (dendrograms) obtained from hierarchical clustering of SNPs based on their WSCNA dissimilarity. Module assignment for each SNP is indicated in the color row below the dendrograms. Each module is represented by a single color, grey represents unassigned SNPs

4.2 Validation for Associations between SNP Modules and Human Height

We used a single linear model to relate all module eigen-nodes, which represent network-specific polygenic models, to human height in the validation samples. Seven modules were found to be associated with height (Table 1). The most significant was the lightgreen module (P = 3.84E–6), which contains 193 SNPs. Next, we compared the amount of the variance in human height explained by WSCNA-based polygenic scores (module eigen-nodes) versus traditional polygenic scores. Three traditional polygenic scores were calculated using various significance based inclusion criteria after SNP pruning—SNPs with P < 0.05 in the original GWAS (n = 32,284; the same SNPs included in WSCNA), SNPs with P < 0.005 in the original GWAS (n = 4318), and SNPs with P < 0.0005 in the original GWAS (n = 570). Traditional polygenic scores were estimated in accordance with the methods outlined by Wray et al., such that the score was equal to the sum of the minor alleles, weighted by the beta coefficients from the GWAS. We examined correlations between the three polygenic scores and the seven module scores and found evidence that they were unique from one another (Fig. 2). Overall most correlations between the traditional polygenic scores and the WSCNA scores were less than r = 0.20.

Table 1.

Significant modules identified using WSCNA

Modules	SNPs	SNPs that mapped to genes	Beta coefficient (P-value)
Light green	193	100	0.305 (3.84E–6)
Salmon	235	90	−0.236 (0.003)
Ivory	109	48	0.187 (0.015)
Navajo white2	63	37	0.162 (0.021)
Violet	131	66	−0.150 (0.028)
Thistle2	85	38	0.145 (0.030)
Dark orange2	93	49	−0.137 (0.043)

Beta coefficients and P-values come from a single model with the residual of height (adjusting for age, sex and PC1–4) as the dependent variable and all 55 modules identified in WSCNA as the independent variables

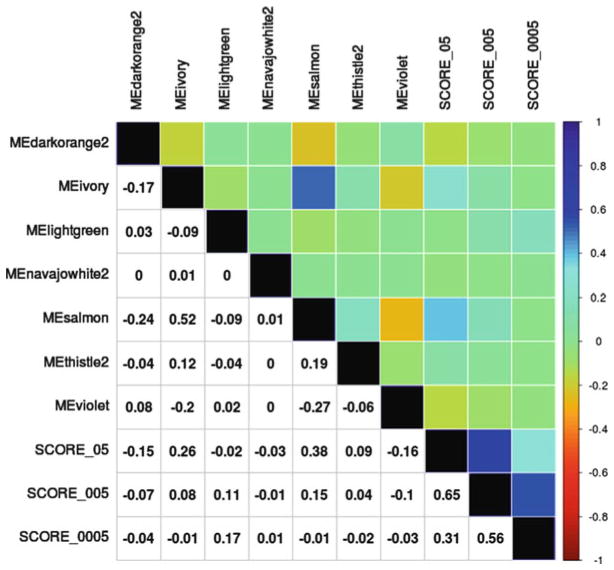
Fig. 2.

Correlations between WSCNA and traditional polygenic scores. Pearson’s correlations between the seven significant polygenic scores (eigen-nodes of WSCNA modules), labeled using module colors, and three traditional polygenic scores—SCORE_05 (included SNPs with P < 0.05), SCORE_005 (included SNPs with P < 0.005), SCORE_0005 (included SNPs with P < 0.0005), are displayed both numerically (bottom) and using a heatmap (top). In general, SNP scores were weakly correlated (R < 0.20). The strongest correlation between a WSCNA score and a traditional polygenic score is found between the score for the Salmon module and SCORE_05 (r = 0.38)

The results for the comparison of the WSCNA polygenic scores versus the traditional scores are shown in Table 2. Overall, the traditional polygenic scores for SNPs with P < 0.05, 0.005, and 0.0005 had adjusted R² of 0.0093, 0.0082, and 0.0079, respectively. Conversely, the model with the seven significant modules of interest had an adjusted R² of 0.0139, while a model with just the light green module had an adjusted R² of 0.0066. This is noteworthy, given the adjusted R² for the model containing the significant WSCNA scores was 50–70% higher than the R² for the models containing the first two traditional polygenic scores, even though it was based on information from only 909 SNPs, compared to 32,284 and 4318 SNPs, respectively.

Table 2.

Variance in human height explained by models containing different polygenic scores

Independent variable/s in each model	R2	Adjusted R2
PRS 0.05 (n = 32,284)	0.0096	0.0093
PRS 0.005 (n = 4318)	0.0084	0.0082
PRS 0.0005 (n = 507)	0.0083	0.0079
Light green module (n = 193)	0.007	0.0066
The seven significant WSCNA modules (n = 909)	0.0163	0.0139

n refers to the number of SNPs used to generate the polygenic score/s in each model

4.3 Hub Genes, Pathways, and Gene Ontology

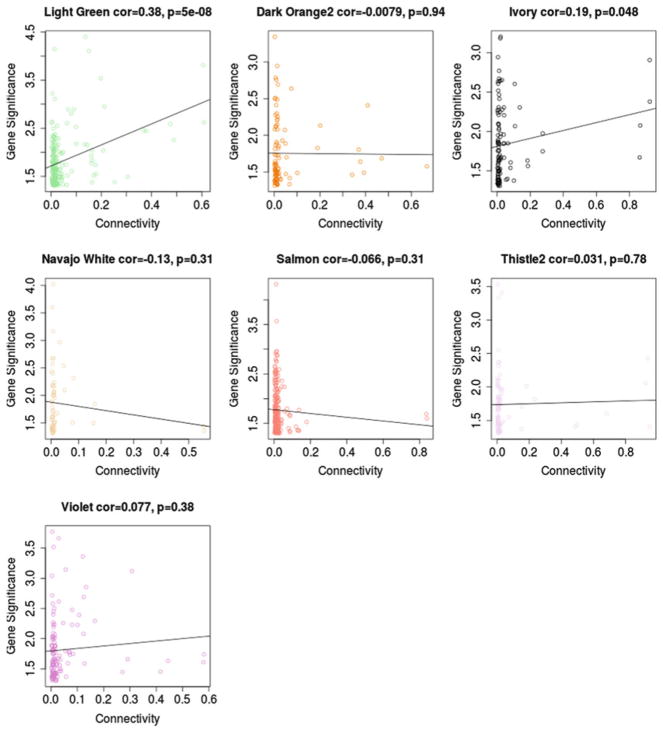
Intra-modular connectivity was calculated for each SNP in the seven significant modules. We then examined whether more connected SNPs, which can be thought of as hubs, had higher significance (−log10(P)) in the training sample (Fig. 3). Results showed a significant association between connectivity and significance for the light green module (r = −0.28, P = 8 × 10⁻⁵), suggesting that hub SNPs for this module tended to be SNPs that were highly significant in our original training GWAS. Next SNPs were mapped to genes. We find that genes mapped from the hub SNPs in the light green module included HHIP (kWithin = 0.213), as well as its neighboring gene ANAPC10 (kWithin = 0.605). HHIP has been implicated in both GWAS and microarray studies examining genes related to height [24] and has a well-established role in chondrogenesis [25].

Fig. 3.

Module connectivity and significance in the GWAS. Within module connectivity for each SNP in the seven significant modules is plotted against significance of that SNP in the original GWAS. Overall, we find a moderately strong correlation between connectivity and significance among SNPs in the light green module, suggesting that hub SNPs in this module tended to be those that had more significant relationships to height in our training sample

Finally, pathway enrichment, GO, and protein interaction network module analysis were performed using WebGestalt (http://bioinfo.vanderbilt.edu/webgestalt/). When examining all the genes from the seven networks (n = 428), we find enrichment for “Signaling events mediated by the Hedgehog Family” (enrichment = 4.99, Bonferroni adjusted P = 0.046), “Calcium signaling” (enrichment = 3.73, adjusted P = 0.001), and “G alpha (q) signaling events” (enrichment = 3.76, adjusted P = 0.046). “Signaling events mediated by the Hedgehog Family” also was found to be enriched when only examining genes in the light green module (enrichment = 14.20, adjusted P = 0.011). This pathway has been repeatedly shown to influence height in genetic association studies [26–28].

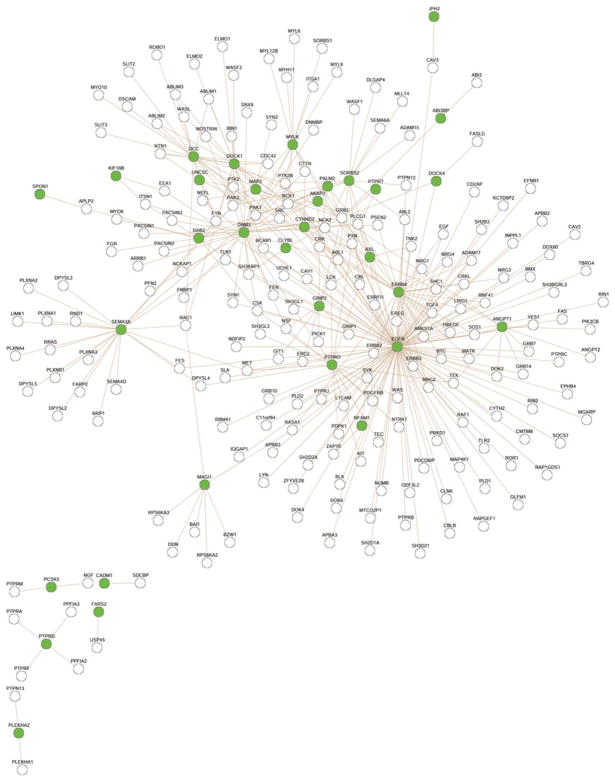
We also found significant enrichment for GO biological processes involved in “anatomical structure development” (enrichment = 1.32, adjusted P = 0.046). Lastly, we identified a significantly enriched protein-protein interaction network using WebGestalt (enrichment ratio of 2.22, adjusted P-value = 0.0006), shown in Fig. 4, which was highly associated with the molecular function, “non-membrane spanning protein tyrosine kinase activity.”

Fig. 4.

Protein-protein interaction network enriched in genes mapped to significant SNP modules. This PPI network was significantly enriched in genes that mapped to SNPs in the seven significant modules. Of the 619 genes in this protein interaction network, 32 are present on our gene list (enrichment ratio of 2.22, Bonferroni adjusted P-value = 0.0006). Genes present in our WSCNA modules are shown in green

5 Conclusion

We illustrate here the methodology for performing WSCNA using results from GWAS. We also show that the incorporation of network structures in the analysis of large-scale genetic association data can be used to estimate genetic scores for specific traits, identify hub SNPs/genes, and lead to biological insight into the pathways involved. Our example also demonstrated that the scores generated from WSCNA can more closely relate to the phenotype of interest in validation analysis than traditional polygenic risk scores. We were also able to identify hub genes and pathways that are known to relate to human height. This is consistent with what has been found for co-expression analysis, for which the use of topological overlap matrix, coupled with a signed correlation network gives rise to biologically meaningful modules [29]. The ability to identify hub genes/SNPs is a significant advantage of this methodology, as it has been demonstrated that intramodular hub genes are often biologically meaningful and represent the module [30, 31].

The presented methodology also has important limitations. First, since WSCNA relies on results of multiple GWAS, care must be taken to ensure the underlying GWAS results are reliable. Thus, it may be more reliable to use previously published results or including as many studies as possible. Along those same lines, the number of participants needed to carry out such analyses may be quite large. In our example we used GWAS results from only 7,326 participants; however, sample sizes will need to increase in order to improve efficacy of gene scores, particularly for traits whose heritability is not as high as that of human height. Second, WSCNA is relatively computationally expensive and may require the user to have access to a multi-core workstation or a supercomputing cluster. Third, users have to specify various parameters for network construction and module identification.

The WSCNA method presented here offers a new and innovative way to incorporate networks—a dominant feature in biology and physiology—into genetic association studies of complex traits. In moving forward, this type of methodology may be useful for generating genetic susceptibility measures for other health related traits, examining genetic pleiotropy, identifying at-risk individuals, examining gene score by environmental effects, and gaining a deeper understanding of the underlying biology of complex traits.