Abstract
A common statistical doctrine supported by many introductory courses and textbooks is that t-test type procedures based on normally distributed data points are anticipated to provide a standard in decision-making. In order to motivate scholars to examine this convention, we introduce a simple approach based on graphical tools of receiver operating characteristic (ROC) curve analysis, a well-established biostatistical methodology. In this context, we propose employing a p-values-based method, taking into account the stochastic nature of p-values. We focus on the modern statistical literature to address the expected p-value (EPV) as a measure of the performance of decision-making rules. During the course of our study, we extend the EPV concept to be considered in terms of the ROC curve technique. This provides expressive evaluations and visualizations of a wide spectrum of testing mechanisms' properties. We show that the conventional power characterization of tests is a partial aspect of the presented EPV/ROC technique. We desire that this explanation of the EPV/ROC approach convinces researchers of the usefulness of the EPV/ROC approach for depicting different characteristics of decision-making procedures, in light of the growing interest regarding correct p-values-based applications.
Keywords: : AUC, expected p-value, partial AUC, partial expected p-value, power, p-value, ROC curve, t-test, Wilcoxon test
1. Introduction
In this article, we introduce and extend a simple and objective statistical technique called the expected p-value (EPV) that allows us to compare characteristics associated with test statistics of interest. As an illustrative example, we reassess the performance of test statistics that are almost habitually used in everyday statistical decision-making (e.g., t-test and Wilcoxon test type procedures). To be concrete, we exemplify our points using a case–control study statement of problem.
The central idea of the case–control study is the comparison of a group having the outcome of interest to a control group with regard to one or more characteristics. In health-related experiments, the case group usually consists of individuals with a given disease, whereas the control group is disease free. Consider a biomarker example with myocardial infarction (MI). MI is commonly caused by blood clots blocking the blood flow of the heart, leading to heart muscle injury. Heart disease is a leading cause of death, affecting about 20% of the population, regardless of ethnicity, according to the Centers for Disease Control and Prevention (Schisterman et al., 2001, 2002). The use of biomarkers to assist medical decision-making, the diagnosis and prognosis of individuals with a given disease, is increasingly common in both clinical settings and epidemiological research. This has spurred an increase in exploration for and development of new biomarkers. The biomarker high-density lipoprotein (HDL)-cholesterol is often used as a discriminant factor between individuals with and without MI disease. The HDL-cholesterol levels can be examined from a 12-hour fasting blood specimen for biochemical analysis at baseline, providing values of measurements regarding HDL biomarker to be collected on cases who survived an MI and on controls who had no previous MI.
Note that oftentimes measurements related to biological processes follow a log-normal distribution (see for details Limpert et al., 2001; Vexler et al., 2016: pp. 13–14). Thus, one may be interested in how often a log-transformed HDL-cholesterol level of the case group, say X, outperforms a log-transformed HDL-cholesterol level of the case group, Y. Typically, this research statement is associated with the measure  that is assumed to be examined using n independent and normally distributed data points
that is assumed to be examined using n independent and normally distributed data points 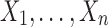 as well as m independent and normally distributed observations
as well as m independent and normally distributed observations  (e.g., Vexler et al., 2008). In this scenario, to test the hypothesis
(e.g., Vexler et al., 2008). In this scenario, to test the hypothesis 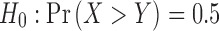 versus
versus  , the traditional statistical literature commonly suggests using t-test type procedures (e.g., Browne, 2010). Researchers are encouraged to apply t-test type decision-making mechanisms when the underlying data follow a normal distribution.
, the traditional statistical literature commonly suggests using t-test type procedures (e.g., Browne, 2010). Researchers are encouraged to apply t-test type decision-making mechanisms when the underlying data follow a normal distribution.
Student's t-test statistic and Welch's t-test statistic are mainstays in statistical practice and are introduced in most introductory statistical classes. Student's t-test statistic has the form
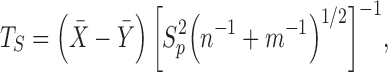 |
and Welch's t-test statistic is
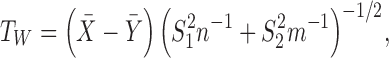 |
where 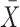 is the sample mean based on
is the sample mean based on 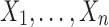 ,
, 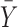 is the sample mean based on
is the sample mean based on  ,
, 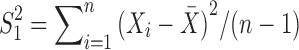 and
and 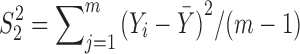 are the unbiased estimators of the variances
are the unbiased estimators of the variances  and
and 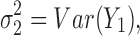 respectively, and
respectively, and 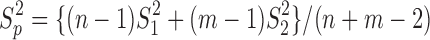 is the pooled sample variance.
is the pooled sample variance.
In the two-sample framework, if we observe normally distributed data points, the choice would be made between Student's t-test or Welch's t-test (e.g., Julious, 2005; Zimmerman and Zumbo, 2009), but it is anticipated that TS- and TW-based tests are somewhat better than the corresponding Wilcoxon rank-sum test (e.g., Ahmad, 1996). The Wilcoxon rank-sum test, which is a nonparametric test, is generally recommended when the data are assumed to be from a non-normal distribution. In this article, we target to propose a simple approach for examining this stereotypical view.
Conventional statistical power comparisons of various statistical procedures can hardly lead to a consistent decision that one method is preferred to other methods over a range of scenarios. The choice of a desired user-specified significance level  can largely affect the power properties of tests. Oftentimes, one method is more powerful than others with a certain
can largely affect the power properties of tests. Oftentimes, one method is more powerful than others with a certain  , but this conclusion would not be maintained with different values of
, but this conclusion would not be maintained with different values of  . Toward this end, an alternative idea can be used, that is, the concept based on p-values in the comparison of test procedures. For this purpose, we need to consider that the p-value as a function of the data is a random variable with the probability distribution. This fact may hamper the usage of the p-value to examine the performance of statistical test procedures (e.g., Wasserstein and Lazar, 2016).
. Toward this end, an alternative idea can be used, that is, the concept based on p-values in the comparison of test procedures. For this purpose, we need to consider that the p-value as a function of the data is a random variable with the probability distribution. This fact may hamper the usage of the p-value to examine the performance of statistical test procedures (e.g., Wasserstein and Lazar, 2016).
The distribution of the p-value is conditional on the null hypothesis being either true or not, which needs to be taken into account to interpret the magnitude of the relevant p-value. That is, under the null hypothesis, typically, p-values exactly (or asymptotically) have the Uniform(0,1) distribution. Under the alternative hypothesis, a non-Uniform(0,1) distribution will be assumed for the p-values where multiple factors including the difference between the null and true parameters and sample size affect the distribution.
Dempster and Schatzoff (1965) proposed the concept of the expected significance level addressing the stochastic aspect of the p-value. The term EPV was coined by Sackrowitz and Samuel-Cahn (1999) who further investigated the approach relative to the expected significance level. In their article, they touted the various potential usages of the EPV. Vexler et al. (2017) advanced the concept of the EPV, especially presenting the strong tie between the EPV concept and receiver operating characteristic (ROC) curve methodology, a popular biomarker discriminant analysis tool (e.g., Vexler et al., 2016). Such a relationship between the EPV and ROC curve comes in handy for assessing and observing the properties of various decision-making procedures in the p-value-based context, since advanced methodologies relative to ROC curve and area under the ROC curve (AUC) are readily adaptable for EPV methodologies. This approach was successfully applied to construct optimal multiple testing procedures (Vexler et al., 2017). In this article, we propose to use a partial expected p-value (pEPV) as a simple method for comparing statistical tests in an ROC curve framework especially with the partial AUC technique addressed extensively in the biostatistical literature. We demonstrate that the presented EPV/ROC technique encompasses the conventional power characterization of tests.
This article is organized as follows. Section 2 sets the notations related to the ROC curve methodology and the EPV definition. The key is that it is conceptually straightforward to associate the ROC curve tools with the EPV concept. The ROC–EPV connection implies new tools for examining statistical decision-making procedures. In Section 3, we exemplify how an application of the EPV/ROC approach can show a critical concern regarding the t-tests' optimality. An applicability of the proposed method is illustrated through a real-life example of MI disease in Section 4. In Section 5, we provide concluding remarks.
2. The ROC Curve, AUC, and EPV Terminologies
2.1. ROC curve and AUC
The ROC curve analysis is a popular tool to assess the discriminability of different biomarkers. Briefly speaking, the ROC curve is a method to summarize and depict distance between two distribution functions. Suppose that random variables X and Y are from the continuous distribution functions FX and FY. In a typical setting of a biomarker study (e.g., the MI disease study introduced in Section 1), often we impose the meaning on the variables that X and Y present biomarker values from diseased and nondiseased subjects, respectively. Now, the ROC curve has the form
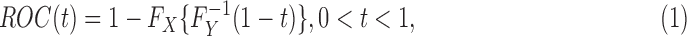 |
where 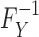 represents the inverse or quantile function of FY, such that
represents the inverse or quantile function of FY, such that  ,
, 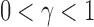 . Definition (1) clearly shows that the ROC curve is a special case of a probability–probability plot (P-P plot) (e.g., Vexler et al., 2016). In the plot of the points
. Definition (1) clearly shows that the ROC curve is a special case of a probability–probability plot (P-P plot) (e.g., Vexler et al., 2016). In the plot of the points  , the farther apart the two distributions FX and FY in terms of location gives rise to the more the ROC curve shift to the top left corner. With a biomarker that separates the diseased and nondiseased subjects well, the ROC curve will be coming close to the top left corner. If a biomarker has no discriminability, a diagonal line from the points (0,0) to (1,1) would be shown for the ROC curve.
, the farther apart the two distributions FX and FY in terms of location gives rise to the more the ROC curve shift to the top left corner. With a biomarker that separates the diseased and nondiseased subjects well, the ROC curve will be coming close to the top left corner. If a biomarker has no discriminability, a diagonal line from the points (0,0) to (1,1) would be shown for the ROC curve.
The ROC curve places biomarkers values on the same scale in the comparison of accurate discriminant ability. Such a feature allows us to assess different diagnostic biomarkers conveniently.
One summary index of the ROC curve is the AUC. The AUC expresses the overall performance of a biomarker, indicating that a larger value of the AUC implies a more accurate discriminating ability of a given marker. That is, values of the AUC vary from 0.5, in the case of no differentiation between the diseased and nondiseased patients, to 1, where the diseased and nondiseased patients are perfectly separated. The AUC can be expressed in the following succinct form (Bamber, 1975)
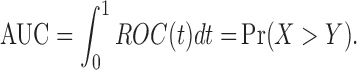 |
Now, let us consider the partial area under the ROC curve (pAUC), the area under a part of the ROC curve. Specifically, the pAUC with two fixed a priori values t0 and t1 is expressed as
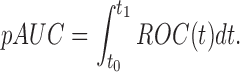 |
The partial AUC summarizes the area of interest only under a part of the ROC curve, rather than summarizing the entire ROC curve.
2.2. Expected p-value (EPV)
Let 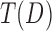 denote a test statistic, which is a random variable, depending on data D. We define its associated distribution Fi under the hypothesis
denote a test statistic, which is a random variable, depending on data D. We define its associated distribution Fi under the hypothesis 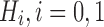 , where the subscript i indicates the null (i = 0) and alternative (i = 1) hypotheses, respectively. With continuous Fi, we denote
, where the subscript i indicates the null (i = 0) and alternative (i = 1) hypotheses, respectively. With continuous Fi, we denote 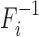 to be the quantile function of Fi, thus,
to be the quantile function of Fi, thus, 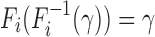 , i = 0,1. In this setting, without loss of generality, we consider tests of the form: the event
, i = 0,1. In this setting, without loss of generality, we consider tests of the form: the event 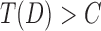 rejects H0, where C is a prefixed test threshold. The corresponding p-value is
rejects H0, where C is a prefixed test threshold. The corresponding p-value is  . We define independent random variables T0 and TA that have distributions F0 and F1, respectively. Noting that
. We define independent random variables T0 and TA that have distributions F0 and F1, respectively. Noting that
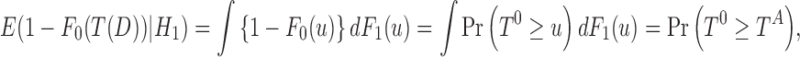 |
Sackrowitz and Samuel-Cahn (1999) proved that the EPV is
 |
Relationship (2) clearly indicates the strong connection between EPV and AUC. In the consideration of the fact that the ROC curve depicts a distance between the distribution functions F0 and F1, Relationship (2) leads us to rethink the EPV in the context of the AUC, obtaining that EPV is 1-AUC.
Furthermore, the value of 1-EPV has an interpretation of the uniform integration of the statistical power of a test over the range of significance level 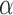 from 0 to 1 as presented in the following notation:
from 0 to 1 as presented in the following notation:
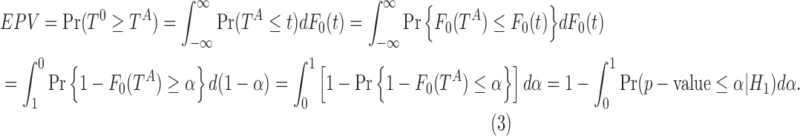 |
A possible caveat of Expression (3) is that the EPV summarizes the power over the entire range of the significance levels  , where most of the values of
, where most of the values of  are not of interest since they are not traditionally used in practice of statistical decision-making (e.g.,
are not of interest since they are not traditionally used in practice of statistical decision-making (e.g., 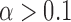 ). Instead, adapting the concept of the pAUC, the power can be integrated over significance levels of
). Instead, adapting the concept of the pAUC, the power can be integrated over significance levels of  in a specific interesting range. For some fixed upper level
in a specific interesting range. For some fixed upper level 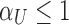 , we have
, we have
 |
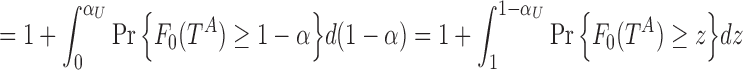 |
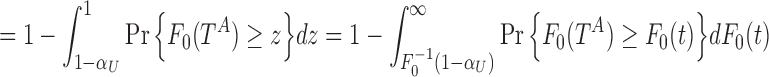 |
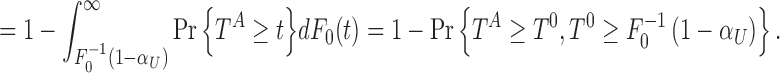 |
In general, one can define the function  . Consider
. Consider  that implies the power at a significance level of
that implies the power at a significance level of  .
.
An essential property of efficient statistical tests is unbiasedness. A statistical test is unbiased when the probability of committing a type I error is less than the significance level and a proper power is greater than the significance level, that is,  and
and  . In parallel with this definition, it is reasonable to consider the inequality
. In parallel with this definition, it is reasonable to consider the inequality
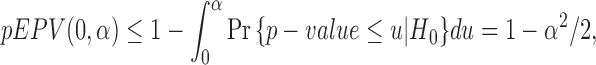 |
since  (i.e.,
(i.e., 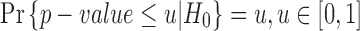 ) under H0 and we assume
) under H0 and we assume  . In this case,
. In this case,
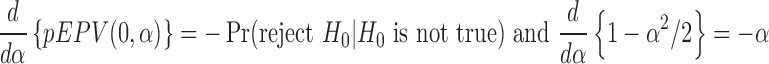 |
when 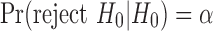 . However, it is clear that the requirement
. However, it is clear that the requirement 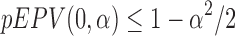 is weaker than that of
is weaker than that of  . Thus, the EPV-based concept extends the conventional power characterization of tests.
. Thus, the EPV-based concept extends the conventional power characterization of tests.
The EPV approach can provide an alternative approach to the Neyman–Pearson concept of testing statistical hypotheses (e.g., Vexler et al., 2016). The EPV corresponds to the integrated power of a test through all possible values of  evaluating the performance of the test procedure globally. Smaller values of EPV indicate superior qualities of tests in a universal manner. As opposed to this, the Neyman–Pearson lemma uses the concept that a viable statistical testing procedure maintains the type I error rate under a user-specified significance level,
evaluating the performance of the test procedure globally. Smaller values of EPV indicate superior qualities of tests in a universal manner. As opposed to this, the Neyman–Pearson lemma uses the concept that a viable statistical testing procedure maintains the type I error rate under a user-specified significance level,  , together with maximizing the power in a uniform manner. Consequently, superior test procedures may be different in general for different values of
, together with maximizing the power in a uniform manner. Consequently, superior test procedures may be different in general for different values of 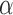 . In contrast, the EPV-based approach enables comparison between decision-making rules to be more objective. Also, the EPV, a single number tool for assessing performance of testing procedures, can rank-order the different procedures more easily.
. In contrast, the EPV-based approach enables comparison between decision-making rules to be more objective. Also, the EPV, a single number tool for assessing performance of testing procedures, can rank-order the different procedures more easily.
3. Comparison of the Test Statistics
In this section, we demonstrate the comparison of TS, TW, and the Wilcoxon rank-sum test statistic using the EPV/ROC approach. The results given in this section can be obtained analytically, since the distribution functions of the statistics TS, TW, and the Wilcoxon rank-sum test statistic under H0 and H1 have specified forms. Alternatively, we provide the following R Code (R Development Core Team, 2002) that can be easily modified to be applied to evaluate various decision-making procedures using the accurate Monte Carlo approximations to the EPV/ROC instruments. To exemplify the proposed approach for comparing the test statistics, the R Code given below provides simulation-based evaluations of the ROC curves based on values of the test statistics related to the null and alternative hypotheses, using the R built-in procedure pROC. In this scenario, we assume, for example, that  and
and  under H0, whereas
under H0, whereas 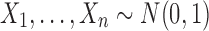 and
and  , under H1.
, under H1.
library(pROC)
N<-100000 #Number of the Monte Carlo data generations
W0<-array()
T0<-array()
W1<-array()
T1<-array()
n<-25 #The sample size n
m<-25 #The sample size m
for(i in 1:N){
x0<-rnorm(n,0,1) #Values of X from N(0,1) generated under hypothesis H0
y0<-rnorm(m,0,1) #Values of Y from N(0,1) generated under hypothesis H0
x1<-rnorm(n,0,1) #Values of X from N(0,1) generated under hypothesis H1
y1<-rnorm(m,-0.5,10) #Values of Y from N(−0.5,10) generated under hypothesis H1
W0[i]<-wilcox.test(x0,y0,alternative = c(‘‘greater’’))$stat[[1]]/(n*m)
#Values of the Wilcoxon test statistic under H0
W1[i]<-wilcox.test(x1,y1,alternative = c(‘‘greater’’))$stat[[1]]/(n*m)
#Values of the Wilcoxon test statistic under H1
EV<-FALSE #This parameter indicates the use of Welch's t-test statistic
#EV<-TRUE #This parameter indicates the use of Student's t-test statistic
T0[i]<-t.test(x0,y0,alternative = c(‘‘greater’’),var.equal = EV)$stat[[1]]
#Values of the t-test statistic under H0
T1[i]<-t.test(x1,y1,alternative = c(‘‘greater’’),var.equal = EV)$stat[[1]]
#Values of the t-test statistic under H1
}
#Plotting the ROC curves
Ind<-c(array(1,N),array(0,N))
W<-c(W0,W1)
T<-c(T0,T1)
plot.roc(Ind, W,type = l, legacy.axes = TRUE,xlab = ‘‘t’’,ylab = ‘‘ROC(t)’’)
lines.roc(Ind,T,col = red,lty = 2)
Figure 1 shows the obtained ROC curves 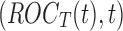 and
and 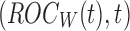 , where
, where
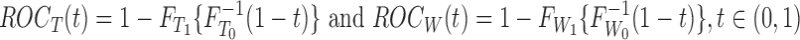 |
FIG. 1.
Values of the functions  (curve “- - - -”) and
(curve “- - - -”) and  (curve “-----”) plotted against
(curve “-----”) plotted against 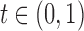 .
.
with the distribution functions  and
and 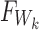 that correspond to the t-test statistic and the Wilcoxon rank-sum test statistic distributions under
that correspond to the t-test statistic and the Wilcoxon rank-sum test statistic distributions under 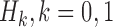 , respectively.
, respectively.
In the executed R Code, we focus on Welch's t-test statistic (the parameter EV<-FALSE), which is reasonable in the considered setting of data distributions' parameters. It is interesting to remark that when examining Student's t-test statistic (the parameter EV<-TRUE), the graphs show that there are no significant differences between the relative curves. Similar observations are in effect, regarding the considerations shown below.
Analyzing EPVs for the one-sided two-sample t-test and Wilcoxon test based on normally distributed data points (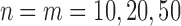 ), Sackrowitz and Samuel-Cahn (1999) concluded that “The t test is best both for the Normal distribution (not surprising!) and the Uniform distribution.” To compute EPVs corresponding to the considered example, we can execute the following code.
), Sackrowitz and Samuel-Cahn (1999) concluded that “The t test is best both for the Normal distribution (not surprising!) and the Uniform distribution.” To compute EPVs corresponding to the considered example, we can execute the following code.
Troc<-roc(Ind, T)
Wroc<-roc(Ind, W)
EPV_t<-1-auc(Troc) # EPV of the t-test
EPV_W<-1-auc(Wroc) # EPV of the Wilcoxon test
Indeed, the computed EPV of the t-test is 0.431 that is <0.439 of that related to the Wilcoxon test. However, Figure 1 shows that for 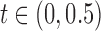 , the Wilcoxon test is somewhat better that the t-test. This motivates us to employ the pEPV for this analysis. Toward this end, we denote the function
, the Wilcoxon test is somewhat better that the t-test. This motivates us to employ the pEPV for this analysis. Toward this end, we denote the function
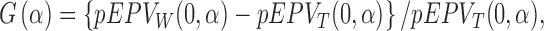 |
where 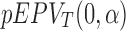 and
and 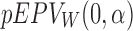 are the function
are the function 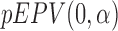 defined in Section 2.2 and computed with respect to the t-test and the Wilcoxon rank-sum test, respectively. To depict the result, we use the following code.
defined in Section 2.2 and computed with respect to the t-test and the Wilcoxon rank-sum test, respectively. To depict the result, we use the following code.
pEPV_t<-function(u) 1-auc(Troc, partial.auc = c(0,u))[[1]]
pEPV_W<-function(u) 1-auc(Wroc, partial.auc = c(0,u))[[1]]
G<-function(u) (pEPV_W(u)-pEPV_t(u))/(pEPV_t(u))
GV<-Vectorize(G)
plot(GV,0,1,xlab = ‘alpha’,ylab = ‘G(alpha)’)
Figure 2 shows the curve of 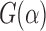 . In this case, it is clear that the Wilcoxon test outperforms the t-test, when the significance level
. In this case, it is clear that the Wilcoxon test outperforms the t-test, when the significance level 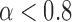 .
.
FIG. 2.
The relative comparison between the t-test and the Wilcoxon rank-sum test using their pEPVs through the function 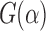 plotted against
plotted against  . pEPVs, partial expected p values.
. pEPVs, partial expected p values.
Let us fix  and calculate the corresponding powers of the tests using the following code.
and calculate the corresponding powers of the tests using the following code.
Wc<-quantile(W0,0.95) # the 95% critical value of the Wilcoxon test
Tc<-quantile(T0,0.95) # the 95% critical value of the t-test
PowW<-mean(1*(W1> = Wc)) #the power of the Wilcoxon test
PowT<-mean(1*(T1> = Tc)) #the power of the t-test
print(c(PowT,PowW))
We obtain that the power of the Wilcoxon test is 0.12, whereas the power of the t-test is 0.08.
Remark 1. In this study, we applied the simulation-based computations through 100,000 Monte Carlo repetitions of the underlying data points. Assume a probability type parameter p is evaluated using 100,000 Monte Carlo repetitions of data points. In this case, we can anticipate the Monte Carlo error in order of 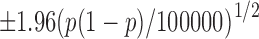 , taking into account the central limit theorem. We also used 1,000,000 Monte Carlo repetitions in the context of the analysis shown in this section. The obtained results were very close to those presented in this note.
, taking into account the central limit theorem. We also used 1,000,000 Monte Carlo repetitions in the context of the analysis shown in this section. The obtained results were very close to those presented in this note.
Remark 2. Assume we are interested in the measure  . A fast way to evaluate
. A fast way to evaluate 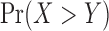 can be based on the R command
can be based on the R command
wilcox.test(X,Y,alternative = c(‘‘greater’’))$stat[[1]].
In the setting of the example mentioned in this section, one can use
nn<-5000000
x1<-rnorm(nn,0,1)
y1<-rnorm(nn,-0.5,10)
wilcox.test(x1,y1,alternative = c(‘‘greater’’))$stat[[1]]/(nn*nn)
In our simulation, the code above gives an approximated value of 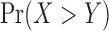 under H1 as 0.5192665 that corresponds to
under H1 as 0.5192665 that corresponds to  .
.
Remark 3. In various scenarios with 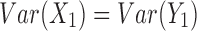 under H1, it was observed using the function
under H1, it was observed using the function  that the t-test procedures and the Wilcoxon rank-sum test provide approximately same properties.
that the t-test procedures and the Wilcoxon rank-sum test provide approximately same properties.
4. Data Example
In this section, a real-life data example introduced in Section 1 is presented to illustrate an applicability of the proposed method. The data set is based on a sample from a study that evaluates biomarkers related to the MI. The study was focused on the residents of Erie and Niagara counties, 35–79 years of age. The New York State department of Motor Vehicles drivers' license rolls were used as the sampling frame for adults between the age of 35 and 65 years, whereas the elderly sample (age 65–79 years) was randomly chosen from the Health Care Financing Administration database. We consider the biomarker HDL-cholesterol. A total of 61 measurements of HDL-cholesterol biomarker were evaluated in the study, where 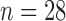 data points were collected on cases who survived on MI and the other
data points were collected on cases who survived on MI and the other 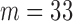 on controls who had no previous MI.
on controls who had no previous MI.
Figure 3 depicts the histograms based on values of the log-transformed HDL-cholesterol levels,  and
and  , respectively. The Shapiro–Wilk test for normality provides the p-values 0.5799 and 0.1581 corresponding to
, respectively. The Shapiro–Wilk test for normality provides the p-values 0.5799 and 0.1581 corresponding to  and
and  , respectively.
, respectively.
FIG. 3.
Histograms of the log-transformed biomarkers of interest corresponding to HDL-cholesterol cases (panel (a): the estimated mean and the estimated standard deviation of log(HDL-cholesterol) are 4.090 and 0.259, respectively) and HDL-cholesterol controls (panel (b): the estimated mean and the estimated standard deviation of log(HDL-cholesterol) are 3.938 and 0.236, respectively). HDL, high-density lipoprotein.
The R code presented in Section 3 can be easily modified to provide the EPV/ROC analysis based on the real data. To this end, the variables “x0” and “y0” can be simulated corresponding to H0 (e.g., as  and
and  ) and the variables “x1” and “y1” can be sampled from the observed
) and the variables “x1” and “y1” can be sampled from the observed 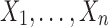 and
and  in a bootstrap manner at each loop iteration in “for(i in 1:N){…}.” Executing this procedure (with N<-50,000 simulations), we obtain the graphs shown in Figure 4 in parallel with Figures 2 and 3.
in a bootstrap manner at each loop iteration in “for(i in 1:N){…}.” Executing this procedure (with N<-50,000 simulations), we obtain the graphs shown in Figure 4 in parallel with Figures 2 and 3.
FIG. 4.
The HDL-cholesterol data-based graphs related to a) the functions  (curve “- - - -”) and
(curve “- - - -”) and  (curve “-----”) plotted against
(curve “-----”) plotted against 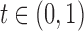 , and b) the relative comparison between the t-test and the Wilcoxon test via their pEPVs, the function
, and b) the relative comparison between the t-test and the Wilcoxon test via their pEPVs, the function 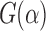 plotted against
plotted against  .
.
In conjunction with the explorations presented in Section 3, Figure 4 induces applying the Wilcoxon rank-sum test rather than the t-test in the context of the HDL-cholesterol case–control study. Note that, in this case, the Wilcoxon rank-sum test and Welch's t-test demonstrate the p-values of 0.045 and 0.0555, respectively.
5. Concluding Remarks
Our objective has been to show a simple technique that can provide intrinsic evaluations of statistical decision-making strategies. The proposed approach involves correct p-values-based mechanisms. We have exemplified scenarios when the EPV/ROC concept yields a critical concern regarding uses, without doubt, of t-test type procedures, when underlying data are normally distributed. It has been demonstrated that the nonparametric Wilcoxon rank-sum test may clearly outperform the t-tests. Our desire to incorporate preanalyses of test procedures before their use in practical applications provided the EPV/ROC method, presuming its place in the toolkit of the well-equipped statistician. We have seen that the EPV/ROC technique is a very useful and succinct measurement tool of the performance of decision-making mechanisms.
There are many possible avenues of research that can be done in the context of the EPV/ROC methodology. One in particular is that asymptotic theoretical results can be developed with respect to the EPV/ROC concept in parametric and nonparametric frameworks. We also anticipate that efficient data-driven Bayesian-type methods can be derived to assess test properties in terms of the EPV/ROC frame. These topics can warrant further strong empirical and methodological investigations.
Acknowledgment
Drs. Vexler and Yu's efforts were supported by the National Institutes of Health (NIH) (Grant No. 1G13LM012241-01).
Author Disclosure Statement
No competing financial interests exist.
References
- Ahmad I.A. 1996. A Class of Mann-Whitney-Willcoxon type statistics. Am. Stat. 50, 324–327 [Google Scholar]
- Bamber D. 1975. The area above the ordinal dominance graph and the area below the receiver operating characteristic graph. J. Math. Psychol. 12, 387–415 [Google Scholar]
- Browne R.H. 2010. The t-test p value and its relationship to the effect size and P(X>Y). Am. Stat. 64, 30–33 [Google Scholar]
- Dempster A.P., and Schatzoff M. 1965. Expected significance level as a sensitivity index for test statistics. J. Am. Stat. Assoc. 60, 420–436 [Google Scholar]
- Julious S.A. 2005. Why do we use pooled variance analysis of variance? Pharm. Stat. 4, 3–5 [Google Scholar]
- Limpert E., Stahel W.A., and Abbt M. 2001. Log-normal distributions across the sciences: Keys and clues on the charms of statistics, and how mechanical models resembling gambling machines offer a link to a handy way to characterize log-normal distributions, which can provide deeper insight into variability and probability—normal or log-normal: That is the question. BioScience. 51, 341–352 [Google Scholar]
- R Development Core Team. 2002. R: A language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria [Google Scholar]
- Sackrowitz H., and Samuel-Cahn E. 1999. P values as random variables-expected p-values. Am. Stat. 53, 326–331 [Google Scholar]
- Schisterman E.F., Faraggi D., Browne R., et al. 2001. TBARS and cardiovascular disease in a population-based sample. J. Cardiovasc. Risk. 8, 219–225 [DOI] [PubMed] [Google Scholar]
- Schisterman E.F., Faraggi D., Browne R., et al. 2002. Minimal and best linear combination of oxidative stress and antioxidant biomarkers to discriminate cardiovascular disease. Nutr. Metab. Cardiovasc. Dis. 12, 259–266 [PubMed] [Google Scholar]
- Vexler A., Hutson A.D., and Chen X. 2016. Statistical Testing Strategies in the Health Sciences. Chapman and Hall/CRC, New York [Google Scholar]
- Vexler A., Liu A., Eliseeva E., et al. 2008. Maximum likelihood ratio tests for comparing the discriminatory ability of biomarkers subject to limit of detection. Biometrics. 64, 895–903 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vexler A., Yu J, Zhao Y., et al. 2017. Expected p-values in light of an ROC curve analysis applied to optimal multiple testing procedures. Stat. Methods Med. Res. In press. DOI: 10.1177/0962280217704451 [DOI] [PMC free article] [PubMed]
- Wasserstein R.L., and Lazar N. 2016. The ASA's statement on p-values: Context, process, and purpose. Am. Stat. 70, 129–133 [Google Scholar]
- Zimmerman D.W., and Zumbo B.D. 2009. Hazards in choosing between pooled and separate-variance t tests. Psiologica. 30, 371–390 [Google Scholar]






