Abstract
Statistical mediation analysis is used to investigate intermediate variables in the relation between independent and dependent variables. Causal interpretation of mediation analyses is challenging because randomization of subjects to levels of the independent variable does not rule out the possibility of unmeasured confounders of the mediator to outcome relation. Furthermore, commonly used frequentist methods for mediation analysis compute the probability of the data given the null hypothesis, which is not the probability of a hypothesis given the data as in Bayesian analysis. Under certain assumptions, applying the potential outcomes framework to mediation analysis allows for the computation of causal effects, and statistical mediation in the Bayesian framework gives indirect effects probabilistic interpretations. This tutorial combines causal inference and Bayesian methods for mediation analysis so the indirect and direct effects have both causal and probabilistic interpretations. Steps in Bayesian causal mediation analysis are shown in the application to an empirical example.
Keywords: causal inference, potential outcomes, Bayesian methods, mediation analysis
Introduction
The central goal of many research areas is to study intermediate variables, known as mediators, through which an independent variable affects a dependent variable. This goal is accomplished using statistical mediation1 analysis (Baron & Kenny, 1986; Judd & Kenny, 1981; MacKinnon, 2008). The ubiquitous nature of mediating processes has made methods for mediation analysis the focus of numerous methodological developments (Krull & MacKinnon, 1999; MacKinnon, Lockwood, & Williams, 2004; MacKinnon, Lockwood, Brown, Wang, & Hoffman, 2007; Maxwell & Cole, 2007; Preacher, Zyphur, & Zhang, 2010; Shrout & Bolger, 2002). Two of the most important developments in mediation methods are the application of the potential outcomes model to estimate causal mediation effects (Coffman & Zhong, 2012; Imai, Keele & Tingley, 2010; Jo, Stuart, MacKinnon, & Vinokur, 2011; Valeri & VanderWeele, 2013) and the use of Bayesian methods to create more intuitive interpretations of mediation analysis results (Enders, Fairchild, & MacKinnon, 2013; Yuan & MacKinnon, 2009).
This paper demonstrates how the benefits of Bayesian estimation can be applied to the potential outcomes framework for causal mediation and provides researchers with computer code to carry out these analyses in four different software packages. The potential outcomes framework for causal inference provides formal assumptions for the causal interpretation of the indirect and direct effects independent of choice of statistical models for the mediator and outcome; and Bayesian analysis, through the use of Markov chain Monte Carlo (MCMC) estimation, is able to take into account the asymmetrical (non-normal) distribution of the indirect effect and the results have probabilistic interpretations.
The tutorial starts with an introduction of statistical mediation analysis and the potential outcomes framework. The next section describes Bayesian estimation in the single mediator model. Finally, we describe the steps to compute the Bayesian causal effects for the single mediator model and show the computation with four different software packages. In order to conserve space, details about Bayesian statistics and the potential outcomes framework for causal inference had to be excluded, thus we recommend consulting introductions to Bayesian statistics (Kruschke, 2014; van de Schoot & Depaoli, 2014; van de Schoot et al., 2014) and introductions to the potential outcomes framework for causal inference (Hernán & Robins, 2016; Imbens & Rubin, 2015; VanderWeele, 2015) for more on these topics.
Statistical Mediation Analysis
The goal of mediation analysis is to investigate the causal sequence from the independent variable (X) to the mediator (M) to the outcome (Y; Wright, 1934; Kendall & Lazarsfeld, 1950; Lazarsfeld, 1955; Judd & Kenny, 1981; Baron & Kenny, 1986; MacKinnon, 2008; Sobel, 1990; VanderWeele, 2015). Recent examples of mediation analyses include the examination of how parental characteristics affect offspring memory (Valentino et al., 2014), how chronic stress affects body mass index (Chao, Grilo, White, & Sinha, 2015), and how depression affects antiretroviral therapy adherence among HIV patients (Magidson, Blashill, Safren, & Wagner, 2014). Statistical mediation is also used to improve the efficiency of interventions in prevention research where treatment programs are designed to change mediating variables hypothesized to change important health outcomes (MacKinnon & Dwyer, 1993; MacKinnon et al., 1991).
The simplest form of mediation analysis is the single mediator model (see Figure 1) described using the following three regression equations (MacKinnon, 2008):
| (1) |
| (2) |
| (3) |
where c represents the total effect of the independent variable X on the dependent variable Y; a represents the relation between X and the mediator M; b represents the relation between M and Y adjusted for the effect of X; and c′ represents the effect of X on Y adjusted for the effect of M. Terms i1, i2, and i3 represent regression intercepts, and e1, e2, and e3 are the equation residuals.
Figure 1.
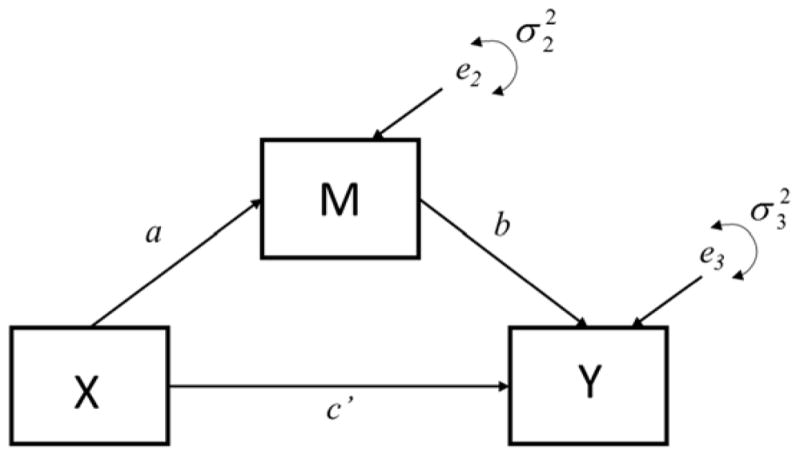
Single mediator model.
The estimate of the indirect effect in a model with linear effects and continuous M and Y can be computed either as the product of coefficients ab, or as a difference in coefficients c-c′; the two computations yield identical estimates of the indirect effect for most analyses (MacKinnon, Warsi, & Dwyer, 1995). In the frequentist framework, evidence for the presence of mediation is obtained by testing the statistical significance of the product of two regression coefficients, ab, but the non-normal distribution of the product of the two regression coefficients (and consequently the poor performance for testing the indirect effect with normal theory methods) has led to the development of methods that either take the asymmetric distribution of the product into account or make no distributional assumptions at all (Cheung 2007, 2009; MacKinnon, Fritz, Williams, & Lockwood 2007; MacKinnon, Lockwood, & Williams, 2004; MacKinnon, Lockwood, Hoffmann, West, & Sheets, 2002; MacKinnon, et al., 1995; Shrout & Bolger, 2002; Tofighi & MacKinnon, 2011; Valente, Gonzalez, Miočević, & MacKinnon, 2016). This tutorial makes use of Bayesian methods to make inferences about direct and indirect effects (Yuan & MacKinnon, 2009). Among the many strengths of Bayesian methods is the ability to represent the asymmetric distribution of the indirect effect and causal effects through the flexible Markov-Chain Monte Carlo estimation.
Potential Outcomes Framework for Mediation Analysis
The potential outcomes framework for mediation applies the potential outcome framework for a single experimental manipulation and a single outcome (Holland, 1986, 1988; Neyman, 1923; Rubin, 1974) to mediation models. The potential outcomes approach to mediation is more complex than the traditional mediation methods because it provides a general framework for handling non-linear models and effects.
For example, in some situations the relationship between the mediator (M) and the dependent variable (Y) is not the same for all levels of the independent variable (X), i.e., the independent variable moderates the relationship between the mediator and the dependent variable. In order to test if the moderation effect is statistically significant, an interaction term (XM) is added to the model predicting Y (as shown in Equation 3), thus yielding the equation:
| (4) |
If the h interaction coefficient in Equation 4 is statistically significant, this means that the indirect effect varies between levels of X more than expected by chance alone. Ignoring the existence of the XM interaction in the population can lead to a biased estimate of the indirect effect (Merrill, MacKinnon, & Mayer, 1994). Methods have been developed to estimate moderated mediated (indirect) effects for linear models (Edwards & Lambert, 2007; Fairchild & MacKinnon, 2009; MacKinnon, 2008; Muller, Judd, & Yzerbyt, 2005; Preacher, Rucker, & Hayes, 2007; Wang & Preacher, 2015) but drawbacks of these methods include a lack of formal assumptions for a causal interpretation of indirect effects and a reliance on the linear model for the interpretation of indirect effect estimates. The potential outcomes framework, however, provides a general definition of causal indirect effects and formal assumptions for the causal interpretation of indirect effects that handle the XM interaction and other non-linear effects. With some assumptions, the indirect effect in the potential outcomes framework will have a causal interpretation that does not depend on the statistical models used for the mediator and/or the outcome (i.e., non-parametric identification of effects; Imai et al., 2010; Pearl, 2001, 2014; VanderWeele & Vansteelandt, 2009; VanderWeele, 2015).
Including a mediator in the classic potential outcomes framework leads to the formulation of five average level causal effects that incorporate the XM interaction (using notation from Valeri & VanderWeele, 2013): the controlled direct effect (CDE), the pure natural direct effect (PNDE), the total natural direct effect (TNDE), the pure natural indirect effect (PNIE), and the total natural indirect effect (TNIE; Pearl, 2001; Robins & Greenland, 1992). E[Y (x, m)] denotes the average potential outcome for individuals under the manipulation level x and mediator level m. The treatment variable, X, can take the value x = 0, representing the control group, or x = 1, representing the treatment group. The mediator variable, M, can take any observed value of the mediator (m). Assuming M is a continuous variable with possible values ranging from 1 to 9, m can represent any one of the possible values from 1 – 9. Each effect is presented as both the mean difference between two potential outcomes and the function of corresponding regression coefficients from Equations 2 and 4 (MacKinnon, 2017; MacKinnon, Valente, & Wurpts, 2016).
The controlled direct effect of X on Y is the direct effect of treatment on the outcome had we intervened and fixed the mediator at value m in the population:
| (5) |
Thus the CDE is similar to the direct effect in traditional mediation analysis but evaluated at a fixed value of the mediator for all participants.
The natural direct effect of X on Y is different from the CDE in that instead of intervening and setting M to a fixed value for all participants, the mediator is set to the level M(x), which is the value of the mediator evaluated at level x of the treatment variable, X. This corresponds to intervening on M for each participant and setting the value of mediator to the value that we would have observed if the participants were at level x of X. For example, for a participant in the control group (x = 0), the value of the mediator would be denoted M(0) but we could conceive of this same participant as having a hypothetical value of the mediator had they been in the treatment group (x = 1) denoted M(1) even though this value was not observed. Therefore, there are two natural direct effects corresponding to (1) an effect that would have occurred had the entire population taken on the value of the mediator in the treatment group and (2) an effect that would have occurred had the entire population taken on the value of the mediator in the control group.
In the case of M(0), the pure natural direct effect, PNDE, is the direct effect of X on Y had we intervened at the population level and fixed the mediator value to the value it would have been in the control condition. Simply put, this is analogous to a direct effect in the control group.,
| (6) |
It is important to note the average potential outcome, E[Y(1, M(0))] is impossible to observe because it is the average value of Y for participants in the treatment group but at a mediator value that would have been observed had they been in the control group (Lok, 2016). It is impossible to observe this potential outcome because a participant cannot simultaneously be in the treatment group but take on the value they would have had on the mediator had they been in the control group. Although this average potential outcome is impossible to observe, its value can be predicted assuming some no unmeasured confounder assumptions which are discussed later in this paper.
The total natural direct effect, TNDE, is the direct effect of X on outcome Y had we intervened at the population level and fixed the mediator value to the value it would have been in the treatment condition. Simply put, this is analogous to a direct effect in the treatment group.
| (7) |
The pure natural indirect effect, PNIE, is the effect of X on Y through M had we intervened at the population level and fixed the relation between X and Y to the value it would have had in the control group. In other words, this is analogous to an indirect effect in the control group.
| (8) |
The average potential outcome, E[Y(0, M(1))], is impossible to observe because a participant cannot simultaneously be in the control group but take on the mediator value they would have, had they been in the treatment group.
The total natural indirect effect (TNIE) is the effect of X on Y through M had we intervened at the population level and fixed the relation between X and Y to the value it would have had in the treatment group. In other words, this is analogous to an indirect effect in the treatment group.
| (9) |
The total effect, c, from Equation 1, is equal to the sum of PNDE and the TNIE, which is also equal to the sum of PNIE and the TNDE (For an alternative decomposition of the total effect, see Coman, Thoemmes, & Fifield, 2017; VanderWeele, 2014). The PNDE differs from TNDE and the PNIE differs from TNIE by the quantity ah which can be estimated as a separate parameter (Coman et al., 2017). However, for the case of continuous M and Y, if the interaction between X and M in Equation 4 is zero, then the PNDE = TNDE = CDE = c′ and PNIE = TNIE = ab.
For the application to mediation, VanderWeele and Vansteelandt (2009) describe four no unmeasured confounding assumptions. The four no unmeasured confounder assumptions are:
No unmeasured confounders of the relation between X and Y.
No unmeasured confounders of the relation between M and Y.
No unmeasured confounders of the relation between X and M.
No measured or unmeasured confounders of M and Y that have been affected by treatment X.
Assumptions 1 and 3 are satisfied, in expectation, when X is a randomized experimental manipulation. However, the randomization of individuals to levels of X does not satisfy assumptions 2 or 4 because randomization of individuals to levels of X does not ensure that individuals have been randomized to levels of the mediator, M. For the purpose of this demonstration, we assume assumptions 1–4 hold, however, there is also a growing literature that provides some solutions to violations of assumption 2 (Coffman & Zhong, 2012; Cox, Kisbu-Sakarya, Miočević, & MacKinnon, 2014; MacKinnon & Pirlott, 2015; VanderWeele, 2010) and assumption 4 (Daniel, De Stavola, Cousens, & Vansteelandt, 2015; Imai & Yamamoto, 2013; VanderWeele & Vansteelandt, 2013; Vansteelandt, 2009) when X is a randomized experimental manipulation.
In addition to the four no unmeasured confounder assumptions, there is the Stable Unit Treatment Value Assumption (SUTVA; Imbens & Rubin, 2015; Rubin, 2005) and a set of non-parametric structural equation modeling assumptions (NPSEM; Pearl, 2009; 2014). SUTVA is a two part assumption. First, the treatment level assigned to one participant does not affect the outcome for other participants and second, for a specific treatment level, there are no different forms of treatment. The NPSEM assumes nonparametric functions for all relations (e.g., the effect of treatment on the mediator) and all error terms for said functions are mutually independent.
The causal effects based on the potential outcomes framework are traditionally computed using a frequentist framework and several Bayesian approaches for causal inference in more complex models have been developed (Daniels, Roy, Kim, Hogan, & Perri, 2012; Elliott, Raghunathan, & Li, 2010; Forastiere, Mealli, & VanderWeele, 2015; Park & Kaplan, 2015), however, a Bayesian approach for the single mediator causal model has yet to be described. Next, we introduce Bayesian methods and steps to obtain posterior distributions of the causal effects.
Bayesian Methods
There are philosophical differences in how frequentist and Bayesian statistics define probability, which influences the interpretation of analysis results. In frequentist statistics, probability is defined as the long run frequency of an event, and the interpretations of both p-values and confidence intervals rest on the assumption of repeated sampling. The p-value is correctly interpreted as the proportion of times one would obtain a data set as extreme or more extreme than the observed data set, assuming the null hypothesis is true (Jackman, 2009). The correct interpretation of the 95% confidence interval is that upon repeated sampling, 95% of confidence intervals will include the population parameter (Jackman, 2009). In Bayesian statistics, one can make probabilistic statements about the parameter because inferences are based on a posterior distribution which captures the relative probabilities of values of a parameter. Parameters are assigned a prior distribution to represent prior information that gets updated with observed data, thus yielding a posterior distribution of possible values for that parameter. The posterior distribution can be summarized using point and interval summaries, neither of which includes the assumption of repeated sampling in the interpretation (Jackman, 2009). In this section we describe the main components of Bayesian estimation, (1) prior distributions for parameters, (2) the Markov-chain Monte Carlo method to combine the prior information and the observed data (i.e., likelihood function), and (3) ways to summarize the posterior distribution.
Prior information
The first step in a Bayesian analysis is to express the current state of knowledge by specifying a prior distribution. When specifying a prior distribution, one needs to select a distributional form (e.g., normal, uniform, Cauchy) and numerical values of parameters of the prior distribution (hyperparameters) that govern the shape (and thus the information) of the prior distribution. If there is available prior information from a pilot study, a meta-analysis, a published article, and/or expert opinion, then this information can be used to construct an informative prior distribution. If there is no knowledge about a given parameter, then a diffuse (non-informative) prior distribution is assigned.
Markov chain Monte Carlo estimation
Once the prior distribution has been specified, it is updated with observed data using Markov Chain Monte Carlo (MCMC) estimation. MCMC methods approximate posterior distributions when an analytical solution for the posterior cannot be obtained (Levy & Choi, 2013). The target distribution of MCMC is set to be the posterior distribution, and multiple draws (forming one or more chains) are taken to approximate the posterior distribution. Once the chains converge to the target distribution, MCMC draws, in limit, may be taken as draws from the desired posterior distribution. These draws ultimately result in a joint posterior distribution of all model parameters (Gelman, Carlin, Stern, & Rubin, 2004). There are several possible MCMC samplers one could use to approximate a posterior distribution; this tutorial makes use of the Gibbs sampler (Casella & George, 1992).
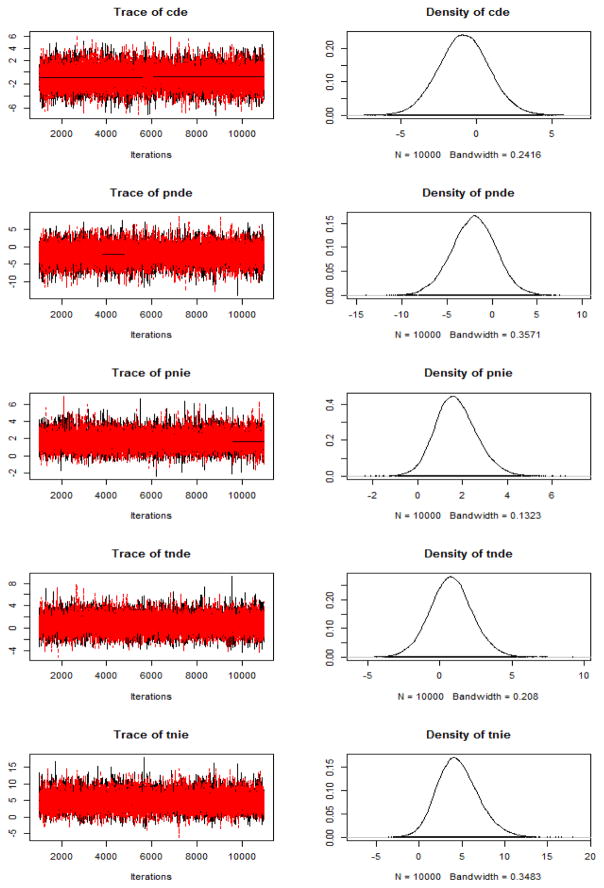
There is no way of knowing whether MCMC chains have converged to the target (here the posterior) distribution, however, there are tools for evaluating whether the chains are mixing well, which is predictive of convergence, and indices for diagnosing convergence (Cowles & Carlin, 1996). For the sake of brevity, we do not go into detail on convergence diagnostics, but refer the reader to articles by Cowles and Carlin (1996), Sinharay (2003, 2004), Yuan and MacKinnon (2009), and the chapter by Levy and Choi (2013). This tutorial uses trace plots to evaluate the mixing of the chains, and the PSR (Potential Scale Reduction) factor to diagnose convergence. Trace plots show draws plotted against the iteration number for each parameter (Brooks, 1998). Chains that are said to “mix well” (and therefore converge faster) are shown in Figure 2; in the interest of conserving space we do not discuss trace plots in depth, however, we refer readers to Sinharay (2003) for instructions on how to interpret them (note: the author calls these plots time-series plots). The PSR factor is computed as the square root of within and between chain variance divided by within chain variance (Gelman & Rubin, 1992; Brooks & Gelman, 1998). Values of PSR slightly above 1 and preferably below 1.1 (Gelman et al., 2004) are considered evidence of convergence.
Figure 2.
Trace plots and posterior distributions of the potential outcomes estimates from WinBUGS.
Summarizing Posteriors
The posterior distributions for all model parameters can be summarized using either point or interval summaries. Most commonly used point summaries are the mean and the median, and one could opt for either equal-tail or highest posterior density (HPD) intervals. HPD intervals are constructed so no value outside the interval has a higher probability than any value inside the interval, and are a better choice than equal-tail intervals for summarizing asymmetrical posterior distributions, such as the distribution of the indirect effect (Gelman, Carlin, Stern, & Rubin, 2004). The following sections will explain the theoretical framework for Bayesian computation of causal effects based on the potential outcomes framework, and then illustrate the procedures using an empirical example.
Bayesian Computation of Causal Effects in the Single Mediator Model
There are at least two ways to fit the single mediator model in the Bayesian framework (Enders et al., 2013; Yuan & MacKinnon, 2009). These two methods are referred to as the method of coefficients (Yuan & MacKinnon, 2009), and the method of covariances (Enders et al., 2013; Miočević & MacKinnon, 2014; Miočević, MacKinnon & Levy, 2017). In the method of coefficients, prior distributions are specified for the parameters in Equations 2 and 4, i.e., the regression coefficients and the residual variances. In the method of covariances, the entire covariance matrix of X, M, and Y is assigned a prior distribution, and the product of coefficients ab is computed using the elements from the covariance matrix of X, M, and Y (Enders et al., 2013). Given that the potential outcomes estimators can be expressed as functions of paths in the single mediator model (as shown in Equations 5–9), this tutorial uses the method of coefficients.
The parameters of the single mediator model are intercepts, regression coefficients, and residual variances. In this tutorial, model parameters are given conjugate priors, which are prior distributions that lead to posterior distributions from the same distributional family. The conjugate priors for intercepts and regression coefficients are normal priors, and the conjugate priors for residual variances are inverse-gamma distributions. Normal distributions have a mean parameter that governs the central tendency of the distribution, and a variance parameter that governs the spread of the distribution. In Bayesian statistics the spread of a normal distribution is often quantified using precision, which is the inverse of variance (both parameterizations can be found in software packages). Inverse-gamma distributions have a shape and a scale parameter, both of which must be positive. It is possible to assign a joint diffuse prior for all model parameters, but for the purpose of this tutorial only univariate diffuse prior distributions will be used, meaning that the joint prior distribution for the model will be the product of all of the univariate priors. In summary, the strengths of using a Bayesian framework in statistical mediation analyses is that (1) MCMC can accommodate the asymmetry of the empirical distribution of the indirect effect, (2) it provides a mechanism to incorporate existing prior information about model parameters, and (3) the indirect effect ab has a probabilistic interpretation (Enders, et al., 2013; Yuan & MacKinnon, 2009; Miočević, MacKinnon & Levy, 2017).
Current applications of Bayesian methods for causal inference exist for principal stratification (Elliott, Raghunathan, & Li, 2010), nonparametric Bayesian methods for models with a continuous mediator and a binary response (Daniels, Roy, Kim, Hogan, & Perri, 2012), encouragement designs (Forastiere, Mealli, & VanderWeele, 2015), and G-computation in multilevel models (Park & Kaplan, 2015). Computing causal effects for the single mediator model in the Bayesian framework requires fitting the model represented by Equations 2 and 4, and using the values of the coefficients at each MCMC draw to compute the causal effects in Equations 5–9. The meaning of the causal effects is similar as in the frequentist framework, e.g., the TNIE is still the indirect effect of X on Y through M had we intervened and set the relation between X and Y to the value it would have been had all participants been in the treatment group. Because the causal effects are functions of products of regression coefficients, their distributions will not be normal. The strength of Bayesian analysis is that the posterior distribution of each of the causal effects is approximated using MCMC, taking into account these asymmetrical distributions. The result of the analysis is not a single point but a whole (posterior) distribution for the causal effects with a probabilistic interpretation. The procedures for Bayesian causal mediation analysis are illustrated using four statistical software packages applied to a real data example, and point and interval summaries for the causal indirect and direct effects are interpreted in the next section.
Empirical Example
Data
Data for the empirical example come from a study of memory for words from a large university in the United States. In a classroom setting the experimenter randomly assigned 44 students to either a repetition condition where students were instructed to repeat the words they hear (X=0), or to an imagery condition where students were instructed to make images of the words (X=1) (MacKinnon, 2017; MacKinnon, Valente, & Wurpts, 2014). Students then heard a list of 20 words, and reported the extent to which they made images for the words (on a scale from 1-not at all to 9-absolutely), and wrote down as many words from the list as they remembered. The independent variable was memory strategy condition (X), the mediator was the extent to which students made images for words (M), and the dependent variable was the number of words recalled (Y). The interaction between X and M was included in the model predicting Y. For this example, the mediator was mean-centered and then the product of X and M was computed and included as another variable in the dataset.
Statistical Analysis
The code in four statistical programs used to calculate the Bayesian causal effects for the single mediator model is described next. Two of these examples use freeware WinBUGS and JAGS through R (Lunn, Thomas, Best, & Spiegelhalter, 2000; Plummer, 2003; R Core Team, 2014), and the other two examples use commercial software Mplus and SAS (Muthén & Muthén, 1998–2016; SAS Institute Inc., 2009). When specifying prior distributions, SAS, JAGS, and WinBUGS use the precision parameterization and Mplus uses the variance parameterization. Precision τ is defined as the inverse of the variance σ2, such as τ = 1/σ2. Thus, the normal priors in SAS, JAGS, and WinBUGS have τ denoting the informativeness, and for Mplus the informativeness is denoted by σ2. Information about installation and setup of the freeware (R, WinBUGS, and JAGS) for the analysis is available in an online appendix at https://psychology.clas.asu.edu/research/labs/research-prevention-laboratory-mackinnon.
For the empirical example we discuss model specification, basic plotting, extracting MCMC draws, and computation of HPD intervals and density plots in R with the coda package (Plummer, Best, Cowles, & Vines, 2006). The analytic strategy is to use Equations 2 and 4 to fit the model, and then use Equations 5–9 to create user-defined variables to represent the causal effects and approximate their posterior distribution using MCMC draws for necessary model parameters. In order to make inferences, the marginal posterior distributions of the controlled direct effect (CDE), the pure natural direct effect (PNDE), the total natural direct effect (TNDE), the pure natural indirect effect (PNIE), and the total natural indirect effect (TNIE) are summarized using point and interval summaries. We used the same prior distributions, number of retained draws (10,000), number of chains (2), and number of burn-in draws (1,000) for each of the four programs. Initial parameter values for the two chains were generated using program defaults. Priors for each of the parameters in the analysis are presented in Table 1 in both precision and variance parametrizations.
Table 1.
Priors for parameters in Equations 2 and 4 for the single mediator model.
| Precision Parametrization | Variance Parametrization | ||
|---|---|---|---|
| a ~ N(0,.001) | a ~ N(0,1000) | ||
| b ~ N(0,.001) | b ~ N(0,1000) | ||
| c′ ~ N(0,.001) | c′ ~ N(0,1000) | ||
| h ~ N(0,.001) | h ~ N(0,1000) | ||
| i2 ~ N(10,.04) | i2 ~ N(10,25) | ||
| i3 ~ N(10,.04) | i3 ~ N(10,25) | ||
|
|
|
||
|
|
|
Note: Symbols N, G, and IG stand for normal, gamma, and inverse-gamma prior distributions (respectively).
WinBUGS through the R Statistical Software
WinBUGS (WINdows Bayesian inference Using Gibbs Sampling) is a free, flexible program that uses the Gibbs sampler to perform Bayesian estimation. Although WinBUGS has a graphic-user interface, the analysis we present here is carried out with the R2WinBUGS package in the R statistical program (Sturtz, Ligges, & Gelman, 2005). Code for the analysis in WinBUGS is presented in Appendix A.
The first step of the analysis is to open the R console, and load both the dataset (Lines 1–2, Appendix A) and the R2WinBUGS package. The model is specified as an R string variable using WinBUGS syntax (Lines 3–31). Prior distributions for the intercepts, regression coefficients, and error precisions of M and Y are specified first (Lines 6–15). Next, the causal effects from Equations 5–9 are defined (Lines 17–21). Finally, the conditional means of M and Y are specified as functions of the variables in the statistical mediation model, and the conditional distribution for M and Y depend on their own conditional mean and the error precision (Lines 25–30). WinBUGS is then instructed to write out a text file for the model syntax in the working directory (Line 34).
After model specification, R2WinBUGS needs information about the dataset and details governing Bayesian estimation. R objects that specify the number of cases, the number of variables in the dataset, and each of the variables in the mediation model (X, M, Y, and XM) have to be created as numeric types, and saved into a list (Lines 37–44). The user then specifies a parameter object with the names of parameters for which draws need to be saved (Lines 46–48). For our illustrative example, we need to keep track of the regression coefficients, intercepts, error precisions, and the causal effects. Finally, the number of chains, number of draws to discard (burn-in), thinning parameter (setting this parameter to 1 means no thinning), and number of total iterations have to be specified (Lines 52–55). The number of total iterations is equal to the sum of (1) the number of draws the user specifies to be in the posterior distribution and (2) the number of draws used in the burn-in phase. By specifying all of the above information in the bugs()command and the path where the WinBUGS program is located, users can call WinBUGS from R to run the specified model and return an R bugs object with all of the post burn-in draws (Lines 58–71).
coda Package post-processing
Although users can get information about the posterior mean, standard deviation, distribution percentiles, and potential scale reduction (PSR) factor for chain convergence by calling on the R bugs object, the coda package in R gives users greater flexibility to plot MCMC draws and obtain additional information about convergence. Appendix B shows code for the post-processing of the individual parameter draws in coda. First, the bugs object in R is transformed into a type mcmc, which turns the R bugs object into a list with the size determined by the number of chains requested for the Bayesian analysis (Line 4). For each element in the list there is a matrix that contains the draws for the posterior distribution in the rows and the parameters in the columns. Users can get density and trace plots for a specific parameter by extracting a single column of the matrix in the list (Line 17). Furthermore, users can combine the elements in the mcmc list by using the do.call()command (Lines 20–21) in order to obtain summary statistics for the parameters (Line 24) and calculate the HPD confidence intervals for each of the parameters (Lines 27–28). Results from the analysis in the R2WinBUGS package are presented in Table 2.
Table 2.
Bayesian point and interval summaries of the potential outcomes for the effect of the number of words (X) and imagery (M) on the number of words recalled (Y).
| Parameter | Mean | SD | 2.50% | Median | 97.50% | 95% HPD lower | 95% HPD Upper |
|---|---|---|---|---|---|---|---|
| WinBUGS through R | |||||||
|
| |||||||
| PNDE | −2.055 | 2.499 | −7.160 | −2.016 | 2.765 | −7.181 | 2.721 |
| PNIE | 1.721 | 0.932 | 0.018 | 1.666 | 3.681 | −0.035 | 3.619 |
| TNDE | 0.787 | 1.456 | −2.052 | 0.765 | 3.724 | −2.171 | 3.598 |
| TNIE | 4.563 | 2.456 | 0.179 | 4.395 | 9.817 | 0.174 | 9.814 |
| CDE | −0.811 | 1.665 | −4.065 | −0.816 | 2.486 | −3.983 | 2.548 |
|
| |||||||
| JAGS through blavaan | |||||||
|
| |||||||
| PNDE | −1.942 | 2.569 | −7.074 | −1.908 | 3.038 | −7.203 | 2.859 |
| PNIE | 1.638 | 0.941 | −0.076 | 1.581 | 3.641 | −0.136 | 3.558 |
| TNDE | 1.119 | 1.454 | −1.685 | 1.102 | 4.082 | −1.846 | 3.889 |
| TNIE | 4.699 | 2.514 | 0.165 | 4.562 | 10.010 | 0.073 | 9.873 |
| CDE | −0.561 | 1.677 | −3.784 | −0.571 | 2.780 | −3.936 | 2.603 |
|
| |||||||
| PROC MCMC in SAS | |||||||
|
| |||||||
| PNDE | −1.953 | 2.554 | −7.031 | −1.888 | 2.892 | −7.031 | 2.891 |
| PNIE | 1.636 | 0.968 | −0.080 | 1.561 | 3.686 | −0.280 | 3.457 |
| TNDE | 1.136 | 1.462 | −1.684 | 1.097 | 4.061 | −1.784 | 3.887 |
| TNIE | 4.725 | 2.491 | 0.291 | 4.544 | 10.046 | 0.049 | 9.695 |
| CDE | −0.560 | 1.641 | −3.760 | −0.557 | 2.642 | −3.690 | 2.679 |
|
| |||||||
| Mplus | |||||||
|
| |||||||
| PNDE | −2.085 | 2.498 | −7.146 | −2.051 | 2.799 | −7.222 | 2.687 |
| PNIE | 1.718 | 0.944 | −0.001 | 1.665 | 3.725 | −0.072 | 3.642 |
| TNDE | 0.791 | 1.472 | −2.049 | 0.777 | 3.794 | −2.198 | 3.613 |
| TNIE | 4.595 | 2.448 | 0.210 | 4.448 | 9.863 | −0.044 | 9.526 |
| CDE | −0.826 | 1.670 | −4.091 | −0.828 | 2.427 | −4.095 | 2.420 |
JAGS through the blavaan Package in R
JAGS (Just Another Gibbs Sampler) also performs Bayesian estimation using MCMC with a Gibbs sampler. Prior information for parameters in JAGS is specified the same way as in WinBUGS. An advantage of JAGS over WinBUGS is that it can work on Mac computers without an emulator. JAGS can interface with R through a variety of packages, but we present the newly developed blavaan package (Merkle & Rosseel, 2015) that allows for specification of structural equation models in the lavaan syntax (Rosseel, 2012) and estimation of those models using JAGS. The code for the empirical example for blavaan is shown in Appendix C.
The first steps in carrying out this analysis are to load the dataset (Line 1, Appendix C) and the blavaan package (Line 3) in the R console. First, the model is specified as an R character string (Lines 9–30). Users familiar with lavaan (Rosseel, 2012) will notice that the model for the example is specified as if it were a model estimated in the frequentist framework, however the model uses the command bsem to call JAGS to estimate the model. Prior distributions are specified in blavaan through lavaan modifiers, which are variable labels written in the following format: prior(“dnorm(0,.001)”)*x (e.g., Line 10). This modifier indicates that variable x has a normal prior distribution with a mean of 0 and a precision of .001. The same distributions used in JAGS are available in blavaan. Furthermore, in order to use parameters to compute causal effects it is necessary to give parameters labels with modifiers. Due to lavaan’s limitation of only allowing one modifier per variable, all of the variables in the model have to be listed twice (once per lavaan modifier; e.g., Lines 14–15). The model specification ends with the user-defined variables for causal effects based on Equations 5–9 (Lines 25–29).
By using the bsem command, users call JAGS for Bayesian estimation of the model (Lines 32–34). Users can specify the model they want to fit, the dataset, the number of chains, number of burn-in iterations, and the number of draws to retain post burn-in. The output is obtained by asking for the summary of the object where the draws for parameters were saved (Line 34). The package blavaan provides the posterior mean and posterior standard deviation for each model parameter and user-defined parameter, their HPD credible interval, the PSR factor value, and the assigned prior distribution. Results are presented in Table 2. If the user wants to see the trace plots, they can use the trace command provided within blavaan, or they can post-process the MCMC draws by extracting the external$jags information from the summary R object (Lines 36–37), convert the draws to an mcmc object type, and examine the draws using the coda package as explained in the WinBUGS section and shown in Appendix B. The draws for each coefficient are saved in each column in the order given by the command coef() used on the R object that holds the results from bsem (Line 37). Draws for the user-defined parameters are not available through JAGS, but their posterior distribution can be obtained by using Equations 5–9 to compute their value at each draw.
PROC MCMC in SAS
The statistical program SAS 9.4 conducts Bayesian estimation in several procedures, and the procedure designed specifically for Bayesian estimation is PROC MCMC (SAS Institute Inc., 2009). PROC MCMC has been previously used to compute the indirect effect (Miočević & MacKinnon, 2014). A current limitation of PROC MCMC is that it is not able to run multiple parallel chains at the same time. Recent SAS macros have been developed to overcome this limitation, but we decided to run the model twice to achieve the same results as in the previous programs. Code for our illustrative example in SAS is presented in Appendix D.
The first line in the code calls PROC MCMC for Bayesian estimation and requires that the user provides the data (with the interaction term included in the dataset), a name for the dataset where the MCMC draws will be saved ( outpost), the number of iterations to be discarded in the burn-in phase ( nbi), and the number of draws to be retained after burn-in ( nmc; Lines 1–2 ). The user can also specify a thinning parameter and a seed value; the default in SAS PROC MCMC is set to no thinning, i.e., a thinning rate of 1. The plot commands indicate the types of plots to output and the parms command indicates the starting values for the chain for each parameter (Line 3). The prior command specifies the prior distributions for the parameters (Lines 5–7) that are defined in the equations for statistical mediation (Lines 8–9). Finally, the model command indicates that variables M and Y are normally distributed, with a mean parameter defined in the statistical mediation equation (Lines 10–11) and a residual precision defined in the prior command (Line 7).
After saving the draws from PROC MCMC, a data step is needed to calculate the residual variances (instead of residual precisions) for M and Y and the causal effects from the individual draws of the model parameters according to Equations 5–9 (Lines 14–24). Then the user can use PROC UNIVARIATE to get percentiles from the distribution of the potential outcomes estimators or PROC SGPLOT to get density plots for each of the potential outcomes estimators (Lines 30–40). Results from the analysis are presented in Table 2. Alternatively, the user can also export the draws from PROC MCMC (Lines 42–43) and bring them into R to process using the coda package, as demonstrated in the WinBUGS section (Appendix B).
Mplus
Mplus 7.31 performs Bayesian estimation for many structural equation models. A current limitation of Mplus is that it is not as flexible as WinBUGS and JAGS about the specification of priors for different parameter classes (Muthén & Muthén, 1998–2016, pg. 698). We make use of the MODEL CONSTRAINT command in Mplus to define the causal effects. Although current versions of Mplus compute the causal effects automatically through the MODEL INDIRECT command, this option is not available for Bayesian estimation as of Mplus 7.31. The Mplus code for the illustrative example is presented in Appendix E.
The Mplus syntax starts with the typical specification of the data and variables used in the analysis (Lines 1–3). Next, Bayesian estimation is requested by using ESTIMATOR=BAYES in the ANALYSIS command. We specify FBITERATIONS=20000 so that 10,000 draws form the posterior distribution (the first half are used in the burn-in phase), and CHAINS=2 to obtain two chains (Lines 5–6). The mediation model is specified using Equations 2 and 4 (Lines 8–16), and the user needs to assign labels to coefficients in order to subsequently specify prior distributions for the parameters in the MODEL PRIOR command (Lines 18–26) and calculate the causal effects in the MODEL CONSTRAINT command (Lines 28–34). Recall that Mplus uses the variance parametrization for prior distributions, and this explains the different numerical values of hyperparameters in Mplus code compared to other software packages in this tutorial. Under OUTPUT, the user needs to specify tech8 to obtain the PSR factor to examine if the chains converged (Line 35). Plots of posteriors can be requested within Mplus, or can be created in the coda package by saving the Mplus draws with the SAVEDATA option and indicating a file to save the BPARAMETERS (Lines 36–37). Mplus automatically saves the burn-in draws, so the user would have to drop those draws before plotting.
Interpretation and reporting of effects in Bayesian Causal Mediation Analysis
This section illustrates how to interpret results of a Bayesian causal mediation analysis (see Table 2). For the sake of brevity, only results from the analysis in WinBUGS will be interpreted and discussed, however, the interpretations are identical for the results from other software packages.
The result of a Bayesian analysis is a posterior distribution which is then plotted and summarized using point and interval summaries. This tutorial interprets the mean and HPD intervals from the posterior distributions of the CDE, PNDE, PNIE, TNDE, and TNIE. Figure 2 contains the plots of the posteriors of the CDE, PNDE, PNIE, TNDE, and TNIE; the x-axes of these plots represent the numerical values of the parameter, and the y-axes represent the density. All of the posteriors were unimodal, thus reporting one point summary and two limits per credibility interval is appropriate.
The results from WinBUGS show that the mean of the posterior for the CDE is equal to −0.811, and since the mediator was mean-centered for these analyses (i.e., the mean value of 6.16 was subtracted from each score so the mean of M became 0), this indicates that the direct effect of treatment on the outcome at the mean value of the mean-centered imagery score was equal to −0.811. The 95% HPD interval for the CDE indicates that participants who have an average level of making images for words have 95% probability of remembering between 4 fewer words and 2.5 more words. The mean of the posterior for the PNDE is −2.055, so the direct effect of the manipulation in the control (repetition) group led to recalling on average 2 fewer words. The 95% HPD interval for the PNDE ranges between −7.181 and 2.721, so group membership led to the recall between approximately 7.2 fewer and 2.7 more words in the control group with 95% probability. The mean of the posterior for the PNIE is 1.721, thus in the control group the effect of group membership through making images for words led to recalling on average 1.7 additional words. The 95% HPD intervals for the PNIE suggest that with 95% probability the indirect effect in the control group lies between −0.035 and 3.619, so the effect of group membership on the number of words recalled through making images for words could have led to recalling no additional words to recalling 3.6 additional words. The mean of the posterior of TNDE is 0.787, so that in the treatment (imagery) group the direct effect of group membership on number of words recalled was on average equal to 0.8, and there is a 95% probability that this effect lies between the values of −2.171 and 3.598. The mean of the posterior of TNIE is 4.563, indicating that in the treatment group the indirect effect of group membership on the number of words recalled by making images for words equals on average 4.6. This effect lies between 0.174 and 9.814 with 95% probability. The potential outcomes estimators were also computed in Mplus using frequentist maximum likelihood estimation, and the results are reported in Table 3.
Table 3.
Frequentist maximum likelihood estimates of the potential outcomes for the effect of the number of words (X) and imagery (M) on the number of words recalled (Y).
| Parameter | Estimate | S.E. | Est./S.E. | Two-Tailed p-value |
|---|---|---|---|---|
| PNDE | −2.194 | 2.369 | −0.926 | 0.354 |
| PNIE | 1.816 | 0.886 | 2.049 | 0.040 |
| TNDE | 0.701 | 1.322 | 0.530 | 0.596 |
| TNIE | 4.711 | 2.314 | 2.036 | 0.042 |
| CDE | −0.878 | 1.553 | −0.565 | 0.572 |
Note that even though these results are numerically similar to the results using Bayesian methods, the ML estimates do not have probabilistic interpretations. In other words, the Bayesian summary intervals provide a 95% probability of containing the true value, and the frequentist confidence interval interpretation is that given an infinite number of samples like the one in the study, 95% of them would contain the true value.
Discussion
This tutorial described steps and software for the computation of causal effects in the single mediator model in the Bayesian framework. The empirical example used diffuse prior distributions, thus in this case the main advantages of using a Bayesian approach are the probabilistic interpretation of the results and the potential of HPD intervals to accommodate the asymmetry of the distributions of causal effects. However, in situations where there is existing prior information about the parameters of the single mediator model, this information can be used to do a Bayesian analysis with informative prior distributions. The code presented in this tutorial can be modified to create informative prior distributions by changing the hyperparameters of the prior distributions. For example, if a previous study of the relation between X and M found that the value of the a path was 3.5 with a standard error of 0.87, this information could be converted into a normal prior distribution for the a path with a mean hyperparameter of 3.5 and a variance hyperparameter equal to 0.757, the square of 0.87 (or the precision hyperparameter equal to 1.321, the inverse of 0.757). Note that this approach creates a prior as informative as the sample size of the study providing the information, which may or may not be larger than the sample in the main analysis. If there is reason to suspect that the prior information comes from a different population and/or the prior data were collected using different methods, it is good practice to reduce the influence of the informative prior distribution by making the variance hyperparameter of the normal prior larger (i.e., the precision hyperparameter smaller). As of now, guidelines for how much to increase the variance hyperparameter have yet to be developed.
This tutorial focused on the single mediator model, however, potential outcomes estimators for two mediator models have begun to appear in the literature (Albert & Nelson, 2011; Avin, Shpitser, & Pearl, 2005; Daniel, De Stavola, Cousens, & Vansteelandt., 2015; Imai & Yamamoto, 2013; Lange, Rasmussen, & Thygesen, 2013; Nguyen, Webb-Vargas, Koning, & Stuart, 2016; Taguri, Featherstone, & Cheng, 2015; VanderWeele & Vansteelandt, 2013; Wang, Nelson, & Albert, 2013; Yu, Fan, & Wu, 2014; Zheng & Zhou, 2015) and analogous methods as those described in this paper could be applied to do Bayesian potential outcomes mediation analysis with more than one mediator. There is a growing literature examining potential outcomes estimation in the Bayesian framework for more complex models (Daniels, Roy, Kim, Hogan, & Perri, 2012; Elliott, Raghunathan, & Li, 2010; Forastiere, Mealli, & VanderWeele, 2015; Park & Kaplan, 2015). The goal of this paper was to provide a step-by-step introduction with code in several software packages that illustrates how to do causal Bayesian mediation analysis for the single mediator model. The motivation for this tutorial was to facilitate making both causal and probabilistic claims about mediation analysis results.
Supplementary Material
Acknowledgments
This research was supported in part by National Institute on Drug Abuse, Grant No. R01 DA09757 and National Science Foundation Graduate Research Fellowship under Grant No. DGE-1311230.
Footnotes
We use the term “statistical mediation” to describe intervening variable effects in the social science literature (MacKinnon, 2008). We reserve the terms “causal mediation” and “causal mediated effects” when assuming no-unmeasured confounding of the relations in the single mediator model (Muthén & Asparouhov, 2015). For a detailed discussion on the distinction between statistical modeling and causal effect estimation see Pearl, 1998, 1999, 2001, 2013, 2017.
References
- Albert JM, Nelson S. Generalized causal mediation analysis. Biometrics. 2011;67(3):1028–1038. doi: 10.1111/j.1541-0420.2010.01547.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avin C, Shpitser I, Pearl J. Identifiability of path-specific effects. Proceedings of the 19th Joint Conference on Artificial Intelligence; San Francisco, CA: Morgan Kaufmann Publishers Inc; 2005. pp. 357–363. [Google Scholar]
- Baron RM, Kenny DA. The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of personality and social psychology. 1986;51(6):1173–1182. doi: 10.1037//0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Brooks SP. Markov chain Monte Carlo method and its application. The Statistician. 1998;47:69–100. [Google Scholar]
- Brooks SP, Gelman A. Convergence assessment techniques for Markov chain Monte Carlo. Statistics and Computing. 1998;8:319–335. [Google Scholar]
- Casella G, George EI. Explaining the Gibbs sampler. The American Statistician. 1992;46:167–174. [Google Scholar]
- Chao A, Grilo CM, White MA, Sinha R. Food cravings mediate the relationship between chronic stress and body mass index. Journal of health psychology. 2015;20(6):721–729. doi: 10.1177/1359105315573448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung MW. Comparison of approaches to constructing confidence intervals for mediating effects using structural equation models. Structural Equation Modeling: A Multidisciplinary Journal. 2007;14(2):227–246. [Google Scholar]
- Cheung MW. Comparison of methods for constructing confidence intervals of standardized indirect effects. Behavior Research Methods. 2009;41(2):425–438. doi: 10.3758/BRM.41.2.425. [DOI] [PubMed] [Google Scholar]
- Coffman DL, Zhong W. Assessing mediation using marginal structural models in the presence of confounding and moderation. Psychological Methods. 2012;17(4):642–664. doi: 10.1037/a0029311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coman EN, Thoemmes F, Fifield J. Commentary: Causal effects in mediation modeling: An introduction with applications to latent variables. Frontiers in Psychology. 2017;8(151):1–3. [Google Scholar]
- Cowles MK, Carlin BP. Markov chain Monte Carlo convergence diagnostics: A comparative review. Journal of the American Statistical Association. 1996;91:883–904. [Google Scholar]
- Cox MG, Kisbu-Sakarya Y, Miočević M, MacKinnon DP. Sensitivity plots for confounder bias in the single mediator model. Evaluation Review. 2014;37(5):405–431. doi: 10.1177/0193841X14524576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daniel RM, De Stavola BL, Cousens SN, Vansteelandt S. Causal mediation analysis with multiple mediators. Biometrics. 2015;71(1):1–14. doi: 10.1111/biom.12248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daniels MJ, Roy JA, Kim C, Hogan JW, Perri MG. Bayesian inference for the causal effect of mediation. Biometrics. 2012;68(4):1028–1036. doi: 10.1111/j.1541-0420.2012.01781.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards JR, Lambert LS. Methods for integrating moderation and mediation: a general analytical framework using moderated path analysis. Psychological methods. 2007;12(1):1–22. doi: 10.1037/1082-989X.12.1.1. [DOI] [PubMed] [Google Scholar]
- Elliott MR, Raghunathan TE, Li Y. Bayesian inference for causal mediation effects using principal stratification with dichotomous mediators and outcomes. Biostatistics. 2010;11:353–372. doi: 10.1093/biostatistics/kxp060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enders CK, Fairchild AJ, MacKinnon DP. A Bayesian approach to estimating mediation effects with missing data. Multivariate Behavioral Research. 2013;48(3):340–369. doi: 10.1080/00273171.2013.784862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fairchild AJ, MacKinnon DP. A general model for testing mediation and moderation effects. Prevention Science. 2009;10(2):87–99. doi: 10.1007/s11121-008-0109-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forastiere L, Mealli F, VanderWeele TJ. Identification and Estimation of Causal Mechanisms in Clustered Encouragement Designs: Disentangling Bed Nets using Bayesian Principal Stratification. Journal of the American Statistical Association. 2015:1–44. doi: 10.1080/01621459.2015.1125788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian data analysis. CRC press; 2004. [Google Scholar]
- Gelman A, Rubin DB. Inference from iterative simulation using multiple sequences. Statistical Science. 1992;7:457–472. [Google Scholar]
- Hernán MA, Robins JM. Causal Inference. Boca Raton: Chapman & Hall/CRC; 2016. forthcoming. [Google Scholar]
- Holland PW. Statistics and causal inference. Journal of the American Statistical Association. 1986;81(396):945–960. [Google Scholar]
- Holland PW. Causal inference, path analysis, and recursive structural equations models. Sociological Methodology. 1988;18(1):449–484. [Google Scholar]
- Imai K, Keele L, Tingley D. A general approach to causal mediation analysis. Psychological methods. 2010;15(4):309–326. doi: 10.1037/a0020761. [DOI] [PubMed] [Google Scholar]
- Imai K, Yamamoto T. Identification and sensitivity analysis for multiple causal mechanisms: Revisiting evidence from framing experiments. Political Analysis. 2013;21(2):141–171. [Google Scholar]
- Imbens GW, Rubin DB. Causal inference in statistics, social, and biomedical sciences. Cambridge University Press; 2015. [Google Scholar]
- Jackman S. Bayesian analysis for the social sciences. John Wiley & Sons; 2009. [Google Scholar]
- Jo B, Stuart EA, MacKinnon DP, Vinokur AD. The use of propensity scores in mediation analysis. Multivariate Behavioral Research. 2011;46(3):425–452. doi: 10.1080/00273171.2011.576624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Judd CM, Kenny DA. Process analysis estimating mediation in treatment evaluations. Evaluation review. 1981;5(5):602–619. [Google Scholar]
- Kendall PL, Lazarsfeld PF. Problems of survey analysis. In: Merton RK, Lazarsfeld PF, editors. Continuities in social research; studies in the scope and method of “The American soldier”. Glencoe, IL: The Free Press; 1950. pp. 133–196. [Google Scholar]
- Krull JL, MacKinnon DP. Multilevel mediation modeling in group-based intervention studies. Evaluation Review. 1999;23(4):418–444. doi: 10.1177/0193841X9902300404. [DOI] [PubMed] [Google Scholar]
- Kruschke J. Doing Bayesian data analysis: A tutorial with R, JAGS, and Stan. Academic Press; 2014. [Google Scholar]
- Lange T, Rasmussen M, Thygesen LC. Assessing natural direct and indirect effects through multiple pathways. American Journal of Epidemiology. 2013;179(4):513–518. doi: 10.1093/aje/kwt270. [DOI] [PubMed] [Google Scholar]
- Lazarsfeld PF. Interpretation of statistical relations as a research operation. In: Lazarsfeld PF, Rosenberg M, editors. The language of social research: A reader in the methodology of social research. Glencoe, IL: Free Press; 1955. pp. 115–125. [Google Scholar]
- Levy R, Choi J. Structural Equation Modeling: A Second Course. 2. Information Age Publishing; 2013. Bayesian Structural Equation Modeling; pp. 563–623. [Google Scholar]
- Lok JJ. Defining and estimating causal direct and indirect effects when setting the mediator to specific values is not feasible. Statistics in Medicine. 2016;35(22):4008–4020. doi: 10.1002/sim.6990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lunn DJ, Thomas A, Best N, Spiegelhalter D. WinBUGS - a Bayesian modelling framework: concepts, structure, and extensibility. Statistics and Computing. 2000;10:325–337. [Google Scholar]
- MacKinnon DP. Introduction to statistical mediation analysis. 2. New York, NY: Erlbaum; 2008. 2017. [Google Scholar]
- MacKinnon DP, Dwyer JH. Estimating mediated effects in prevention studies. Evaluation review. 1993;17(2):144–158. [Google Scholar]
- MacKinnon DP, Fritz MS, Williams J, Lockwood CM. Distribution of the product confidence limits for the indirect effect: Program PRODCLIN. Behavior research methods. 2007;39(3):384–389. doi: 10.3758/bf03193007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Johnson CA, Pentz MA, Dwyer JH, Hansen WB, Flay BR, Wang EYI. Mediating mechanisms in a school-based drug prevention program: first-year effects of the Midwestern Prevention Project. Health Psychology. 1991;10(3):164–172. doi: 10.1037//0278-6133.10.3.164. [DOI] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Brown CH, Wang W, Hoffman JM. The intermediate endpoint effect in logistic and probit regression. Clinical Trials. 2007;4(5):499–513. doi: 10.1177/1740774507083434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychological methods. 2002;7(1):83–104. doi: 10.1037/1082-989x.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Williams J. Confidence limits for the indirect effect: Distribution of the product and resampling methods. Multivariate behavioral research. 2004;39(1):99–128. doi: 10.1207/s15327906mbr3901_4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Pirlott A. Statistical approaches to enhancing the causal interpretation of the M to Y relation in mediation analysis. Personality and Social Psychology Review. 2015;19(1):30–43. doi: 10.1177/1088868314542878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Valente MJ, Wurpts IC. Research in Prevention Laboratory Technical Report. 2014. Data from experimental studies of a rehearsal manipulation on imagery and word recall. [Google Scholar]
- MacKinnon DP, Valente MJ, Wurpts IC. Benchmark validation of statistical models: application to mediation analysis of imagery and memory. 2016 doi: 10.1037/met0000174. Manuscript submitted for publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Warsi G, Dwyer JH. A simulation study of mediated effect measures. Multivariate behavioral research. 1995;30(1):41–62. doi: 10.1207/s15327906mbr3001_3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magidson JF, Blashill AJ, Safren SA, Wagner GJ. Depressive symptoms, lifestyle structure, and ART adherence among HIV-infected individuals: A longitudinal mediation analysis. AIDS and Behavior. 2015;19(1):34–40. doi: 10.1007/s10461-014-0802-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maxwell SE, Cole DA. Bias in cross-sectional analyses of longitudinal mediation. Psychological methods. 2007;12(1):23–44. doi: 10.1037/1082-989X.12.1.23. [DOI] [PubMed] [Google Scholar]
- Merkle EC, Rosseel Y. blavaan: Bayesian structural equation models via parameter expansion. 2015 arXiv preprint arXiv:1511.05604. [Google Scholar]
- Merrill RM, MacKinnon DP, Mayer LS. Estimation of moderated mediation effects in experimental studies. 1994. Unpublished manuscript. [Google Scholar]
- Miočević M, MacKinnon DP. SAS® for Bayesian Mediation Analysis. Proceedings of the 39th annual meeting of SAS Users Group International; Cary, NC: SAS Institute, Inc; 2014. [Google Scholar]
- Miočević M, MacKinnon DP, Levy R. Power in Bayesian Mediation Analysis for Small Sample Research. Structural Equation Modeling: A Multidisciplinary Journal. 2017:1–18. doi: 10.1080/10705511.2017.1312407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller D, Judd CM, Yzerbyt VY. When moderation is mediated and mediation is moderated. Journal of personality and social psychology. 2005;89(6):852–863. doi: 10.1037/0022-3514.89.6.852. [DOI] [PubMed] [Google Scholar]
- Muthén B, Asparouhov T. Causal effects in mediation modeling: An introduction with applications to latent variables. Structural Equation Modeling: A Multidisciplinary Journal. 2015;22(1):12–23. [Google Scholar]
- Muthén LK, Muthén BO. Mplus User’s Guide. 6. Los Angeles, CA: Muthén & Muthén; 1998–2016. [Google Scholar]
- Neyman J. On the application of probability theory to agricultural experiments: Essay on principles (with discussion). Section 9. In: Dabrowska DM, Speed TP, translators. Statistical Science. Vol. 5. 1923. pp. 465–480. [Google Scholar]
- Nguyen TQ, Webb-Varga Y, Koning IM, Stuart EA. Causal mediation analysis with a binary outcome and multiple continuous or ordinal mediators: Simulations and application to an alcohol intervention. Structural Equation Modeling: A Multidisciplinary Journal. 2016;23:368–383. doi: 10.1080/10705511.2015.1062730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park S, Kaplan D. Bayesian Causal Mediation Analysis for Group Randomized Designs with Homogeneous and Heterogeneous Effects: Simulation and Case Study. Multivariate Behavioral Research. 2015;50(3):316–333. doi: 10.1080/00273171.2014.1003770. [DOI] [PubMed] [Google Scholar]
- Pearl J. Graphs, causality, and structural equation models. Sociological Methods & Research. 1998;27(2):226–284. [Google Scholar]
- Pearl J. Causal Models and Intelligent Data Management. Berlin, Heidelberg: Springer; 1999. Statistics, causality, and graphs; pp. 3–16. [Google Scholar]
- Pearl J. Direct and indirect effects. In: Breese J, Koller D, editors. Proceedings of the 17th Conference on Uncertainty in Artificial Intelligence. San Francisco, CA: Morgan Kaufmann; 2001. pp. 411–420. [Google Scholar]
- Pearl J. Causality. New York, NY: Cambridge university press; 2009. [Google Scholar]
- Pearl J. Statistics and causality: Separated to reunite—Commentary on Bryan Dowd’s “Separated at Birth”. Health Services Research. 2011;46(2):421–429. doi: 10.1111/j.1475-6773.2011.01243.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearl J. Linear models: A useful “microscope” for causal analysis. Journal of Causal Inference. 2013;1(1):155–170. [Google Scholar]
- Pearl J. Interpretation and identification of causal mediation. Psychological Methods. 2014;19(4):459–481. doi: 10.1037/a0036434. [DOI] [PubMed] [Google Scholar]
- Pearl J. A Linear “microscope” for interventions and counterfactuals. Journal of Causal Inference. 2017;5(1):1–15. [Google Scholar]
- Plummer M. JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. Proceedings of the 3rd international workshop on distributed statistical computing; 2003. [Google Scholar]
- Plummer M, Best N, Cowles K, Vines K. CODA: convergence diagnosis and output analysis for MCMC. R news. 2006;6(1):7–11. [Google Scholar]
- Preacher KJ, Rucker DD, Hayes AF. Addressing moderated mediation hypotheses: Theory, methods, and prescriptions. Multivariate behavioral research. 2007;42(1):185–227. doi: 10.1080/00273170701341316. [DOI] [PubMed] [Google Scholar]
- Preacher KJ, Zyphur MJ, Zhang Z. A general multilevel SEM framework for assessing multilevel mediation. Psychological methods. 2010;15(3):209–233. doi: 10.1037/a0020141. [DOI] [PubMed] [Google Scholar]
- R Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing; Vienna, Austria: 2014. URL http://www.R-project.org/ [Google Scholar]
- Robins JM, Greenland S. Identifiabilty and exchangeability for direct and indirect effects. Epidemiology. 1992;3(2):143–155. doi: 10.1097/00001648-199203000-00013. [DOI] [PubMed] [Google Scholar]
- Robins JM, Richardson TS. Alternative graphical causal models and the identification of direct effects. Causality and psychopathology: Finding the determinants of disorders and their cures. 2010:103–158. [Google Scholar]
- Rosseel Y. lavaan: An R Package for Structural Equation Modeling. Journal of Statistical Software. 2012;48(2):1–36. [Google Scholar]
- Rubin DB. Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology. 1974;66(5):688–701. doi: 10.1037/h0037350. [DOI] [Google Scholar]
- Rubin DB. Causal inference using potential outcomes. Journal of the American Statistical Association. 2005;100(469):322–221. [Google Scholar]
- SAS Institute Inc. SAS/STAT® 9.2 User’s Guide. 2. Cary, NC: SAS Institute Inc; 2009. [Google Scholar]
- Shrout PE, Bolger N. Mediation in experimental and nonexperimental studies: new procedures and recommendations. Psychological methods. 2002;7(4):422–445. [PubMed] [Google Scholar]
- Sobel ME. Effect analysis and causation in linear structural equation models. Psychometrika. 1990;55(3):495–515. [Google Scholar]
- Sturtz S, Ligges U, Gelman A. R2WinBUGS: a package for running WinBUGS from R. Journal of Statistical software. 2005;12(3):1–16. [Google Scholar]
- Taguri M, Featherstone J, Cheng J. Statistical Methods in Medical Research. 2015. Causal mediation analysis with multiple causally non-ordered mediators. Advance online publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen EJT, VanderWeele TJ. On identification of natural direct effects when a confounder of the mediator is directly affected by exposure. Epidemiology (Cambridge, Mass) 2014;25(2):282–291. doi: 10.1097/EDE.0000000000000054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tofighi D, MacKinnon DP. RMediation: An R package for mediation analysis confidence intervals. Behavior research methods. 2011;43(3):692–700. doi: 10.3758/s13428-011-0076-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van de Schoot R, Depaoli S. Bayesian analyses: Where to start and what to report. European Health Psychologist. 2014;16(2):75–84. [Google Scholar]
- van de Schoot R, Kaplan D, Denissen J, Asendorpf JB, Neyer FJ, Aken MA. A gentle introduction to Bayesian analysis: Applications to developmental research. Child development. 2014;85(3):842–860. doi: 10.1111/cdev.12169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shrout PE, Bolger N. Mediation in experimental and nonexperimental studies: new procedures and recommendations. Psychological methods. 2002;7(4):422–445. [PubMed] [Google Scholar]
- Sinharay S. Assessing convergence of the Markov chain Monte Carlo algorithms: A review. ETS Research Report Series. 2003;2003(1):i-52. [Google Scholar]
- Sinharay S. Experiences with Markov chain Monte Carlo convergence assessment in two psychometric examples. Journal of Educational and Behavioral Statistics. 2004;29(4):461–488. [Google Scholar]
- Sturtz S, Ligges U, Gelman A. R2WinBUGS: a package for running WinBUGS from R. Journal of Statistical software. 2005;12(3):1–16. [Google Scholar]
- Valente MJ, Gonzalez O, Miočević M, MacKinnon DP. A note on testing mediated effects in structural equation models: Reconciling past and current research on the performance of the test of joint significance. Educational and Psychological Measurement. 2015 doi: 10.1177/0013164415618992. Advance online publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valentino K, Nuttall AK, Comas M, McDonnell CG, Piper B, Thomas TE, Fanuele S. Mother–child reminiscing and autobiographical memory specificity among preschool-age children. Developmental psychology. 2014;50(4):1197–1208. doi: 10.1037/a0034912. [DOI] [PubMed] [Google Scholar]
- Valeri L, VanderWeele TJ. Mediation analysis allowing for exposure–mediator interactions and causal interpretation: Theoretical assumptions and implementation with SAS and SPSS macros. Psychological Methods. 2013;18(2):137–150. doi: 10.1037/a0031034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ. Bias formulas for sensitivity analysis for direct and indirect effects. Epidemiology. 2010;21(4):540–551. doi: 10.1097/EDE.0b013e3181df191c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ. A unification of mediation and interaction: A 4–way decomposition. Epidemiology. 2014;25(5):749–761. doi: 10.1097/EDE.0000000000000121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele T. Explanation in causal inference: methods for mediation and interaction. Oxford University Press; 2015. [Google Scholar]
- VanderWeele TJ, Vansteelandt S. Conceptual issues concerning mediation, interventions and composition. Statistics and Its Interface (Special Issue on Mental Health and Social Behavioral Science) 2009;2:457–468. [Google Scholar]
- VanderWeele TJ, Vansteelandt S. Mediation analysis with multiple mediators. Epidemiologic Methods. 2013;2(1):95–115. doi: 10.1515/em-2012-0010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vansteelandt S. Estimating direct effects in cohort and case-control studies. Epidemiology. 2009;20(6):851–860. doi: 10.1097/EDE.0b013e3181b6f4c9. [DOI] [PubMed] [Google Scholar]
- Wang W, Nelson S, Albert JM. Estimation of causal mediation effects for a dichotomous outcome in multiple-mediator models using the mediation formula. Statistics in Medicine. 2013;32(24):4211–4228. doi: 10.1002/sim.5830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Preacher KJ. Moderated mediation analysis using Bayesian methods. Structural Equation Modeling: A Multidisciplinary Journal. 2015;22(2):249–263. [Google Scholar]
- Wright S. The method of path coefficients. The annals of mathematical statistics. 1934;5(3):161–215. [Google Scholar]
- Yu Q, Fan Y, Wu X. General multiple mediation analysis with an application to explore racial disparities in breast cancer survival. Journal of Biometrics and Biostatistics. 2014;5(2):1–9. [Google Scholar]
- Yuan Y, MacKinnon DP. Bayesian mediation analysis. Psychological Methods. 2009;14(4):301–322. doi: 10.1037/a0016972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng C, Zhou XH. Causal mediation analysis in the multilevel intervention and multicomponent mediator case. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2015;77(3):581–615. doi: 10.1111/rssb.12082. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.