Playing ‘hide-and-seek’ with factor H: game-theoretical analysis of a single nucleotide polymorphism

Abstract

As a part of the complement system, factor H regulates phagocytosis and helps differentiate between a body's own and foreign cells. Owing to mimicry efforts, some pathogenic microorganisms such as Candida albicans are able to bind factor H on their cell surfaces and, thus, become similar to host cells. This implies that the decision between self and foreign is not clear-cut, which leads to a classification problem for the immune system. Here, two different alleles determining the binding affinity of factor H are relevant. Those alleles differ in the SNP Y402H; they are known to be associated with susceptibility to certain diseases. Interestingly, the fraction of both alleles differs in ethnic groups. The game-theoretical model proposed in this article explains the coexistence of both alleles by a battle of the sexes game and investigates the trade-off between pathogen detection and protection of host cells. Further, we discuss the ethnicity-dependent frequencies of the alleles. Moreover, the model elucidates the mimicry efforts by pathogenic microorganisms.

1. Introduction

Complement factor H (also known as CFH) plays an important role in the immune system, as it helps to distinguish between intact host cells and modified or damaged host cells and foreign cells or microbes. It belongs to the alternative pathway of the complement system of the innate immune response [1].

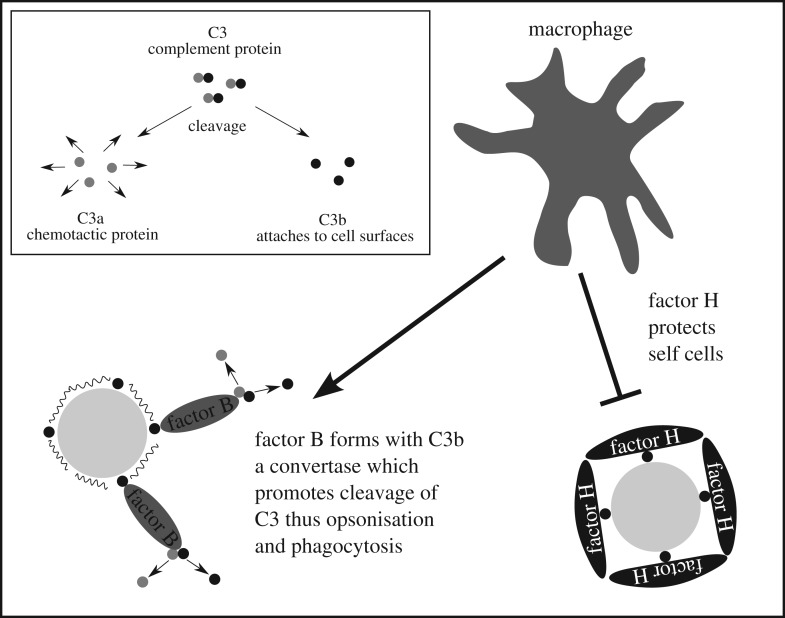
Factor H is structured as a chain of 20 units, called either short consensus repeat (SCR) or complement control protein module. Each of them consists of about 60 amino acids [2,3]. The alternative pathway is permanently activated by the cleavage of the complement protein C3 in C3a and C3b. C3a particles diffuse and act as chemotactic proteins, whereas C3b particles can attach to any cell surface and opsonize it to enhance the clearance by phagocytosis. This complement activation is controlled by multiple regulatory proteins. Depending on the cell surface, different regulators bind to C3b. On target cells, factor B binds to C3b and is cleaved into Ba and Bb, and forms the protease complex C3-convertase, which generates more C3b by cleaving C3. Thus opsonization is promoted. On self cells membrane-bound regulators inhibit complement activation. In addition, factor H binds to C3b where it accelerates the cleavage of the C3-convertase and thus limits the C3b production (figure 1). Therefore, the host cells are not opsonized and hence protected by factor H [1,3].

Figure 1.

Function of factor H. Spontaneous cleavage of complement protein C3 (inset) enhances opsonization of a cell surface by the fragment C3b. Complement regulators, e.g. factor H, discriminate between self and non-self surfaces.

Many pathogenic microorganisms express surface proteins that recruit factor H and therefore escape the immune system and increase their pathogenicity [1]. This is an example of molecular mimicry or camouflage, a widespread mechanism in biological systems. The general mechanism of mimicry originates in a similarity between two organisms that has evolved because the apparent resemblance is selectively advantageous for one species relating to a common signal receiver.

Mimicry was first described by the English naturalist Henry Walter Bates. He was immediately aware of the extensive consequences of his discovery for evolutionary biology. He wrote: ‘The process by which a mimetic analogy is brought about in nature is a problem which involves that of the origin of all species and all adaptations’ [4, p. 511]. Subsequently, besides Batesian mimicry, several other forms of mimicry were described (see also [5]).

Besides mimicry at the macroscopic level, also molecular mimicry has been studied [6] and related to autoimmune diseases [7–9]. Our work theoretically analyses an example of the latter category.

Poltermann et al. [10] discovered that the yeast Candida albicans binds factor H with its surface protein CaCRASP-1 via the two binding sites SCR 6 − 7 and SCR 19 − 20. Factor H remains active and provides a protection against the complement system. Similar strategies have been found for other fungi. For example, Aspergillus fumigatus and Aspergillus terreus strongly bind C4bp [11]. C4bp also has the ability to bind C3b and accelerate the decay of C3-convertase [12].

Related behaviour has also been found in different bacterial species, e.g. Bordetella pertussis [13] or Streptococcus pyogenes [14,15]. Here, binding of C4bp is mediated by SCRs 1 − 2. Escherichia coli binds the SCR 3 of C4bp, conferring serum resistance [16]. By contrast Campylobacter jejuni and Helicobacter pylori use lipopolysaccharides for mimicry on the level of the adaptive immune response [17].

Defects in the complement regulation system can lead to diseases caused by both undesirable damage of host cells and accumulation of immunological debris. Examples for the first case are the atypical haemolytic uraemic syndrome (aHUS) [18], dense-deposit disease (DDD) [19] and age-related macular degeneration (AMD) [20] occurring in different organs including the kidney and eyes. On the other hand, mimicking pathogens may escape phagocytosis and cells may exhibit unrestricted growth [1].

Factor H occurs in two different variants (alleles), which differ in only one single amino acid [21,22]. This single nucleotide polymorphism (SNP) is defined rs1061170 and affects the nucleotide position 43097, which can be either thymine or cytosine. As the result, the amino acid at position 402 of factor H (lying in SCR 7) becomes translated either into tyrosine (Y) or histidine (H). Therefore, this SNP is also called Y402H. These two variants are named CFH-402H and CFH-402Y. The SNP is located in the binding site for C-reactive protein (CRP), which activates the complement system. CFH binds CRP and inhibits the immune response [23]. The CFH-402H variant shows a significantly reduced binding to CRP [24]. This leads to a higher proinflammatory state, in general [25], and to an increased severity in autoimmune diseases. The CFH-402H variant is significantly associated with AMD [26–30]. Also, patients with DDD and aHUS are found to have a high prevalence of the CFH-402H variant of factor H [31].

The frequency of the H allele differs between human ethnic groups. It is about 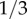for Caucasians, African-Americans and Somalis, about 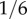for Hispanics and about 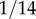for Japanese (cf. table 1). The frequency of this allele may even vary between Caucasian subpopulations [34]. Subsequently, the prevalence of diseases caused by defects in complement regulation differs in populations of miscellaneous descent, too. For example early AMD in Japanese populations is much less frequent than in Caucasians of European descent [38].

Table 1.

Distribution of factor H polymorphism in different cultural areas identified by Hunter & Whitten [32]. Cultural areas marked with (*) are subareas. The pay-off of the YY genotype was calculated according to formula (2.9).

cultural area	frequency H-allele	frequency Y-allele	YH pay-off (wYH)	references
South America (native)	0	1	1	[33]
North America (native)	0.03	0.97	1.03	[33]
South Asia	0.05–0.09	0.91–0.95	1.06–1.11	[32–35]
Mesoamerica (*)	0.15–0.17	0.73–0.85	1.21–1.59	[33,36]
Oceania	0.22	0.78	1.39	[33]
Middle East	0.27–0.3	0.7–0.73	1.59–1.75	[33]
Africa	0.31–0.35	0.65–0.7	1.75–2.17	[33–35]
Europe	0.3–0.36	0.64–0.7	1.75–2.29	[33–35]
Iceland (*)	0.39	0.61	2.77	[35]
Finland (*)	0.43	0.57	4.07	[37]

Mathematical models describing mimicry have been presented for higher organisms [39–41], e.g. for hoverflies imitating wasps [42]. By contrast, models describing molecular mimicry of pathogenic fungi or bacteria are rare and are desperately needed to understand infections and autoimmune diseases (e.g. AMD and aHUS). Our approach aims to fill this gap of understanding by extending the theoretical framework of molecular mimicry, especially for interactions between pathogenic microorganisms and the immune system.

Evolutionary game theory (EGT) is an established and profound method to describe biological interactions between species. It has been successfully applied to models of host–pathogen interactions [43–50]. Mimicry is a form of deception, which has been analysed by EGT earlier [51]. In this work, we present a game-theoretic model analysing whether and to what extent the human immune system can distinguish between self and foreign in spite of the mimicry of the pathogens. We consider the (stable) existence of both alleles as two alternative strategies and its ratio within an ethnic group as an evolutionarily stable equilibrium.

2. Methods and model

2.1. The basic game

In each individual, the two genes—maternal and paternal—of factor H (where the polymorphism is localized) are viewed as players and the concrete realizations of the SNP (Y or H) as the respective strategy. We are not interested in details in the underlying biological processes but rather in an abstract description of the phenomena. That is why we use the framework of evolutionary games. The pay-off is given by the (average) fitness for the concrete genotype (YY, YH or HH). Moreover, the two heterozygous cases (YH and HY) gain the same fitness. Consequently, the pay-off for both players (genes) is the same and the pay-off matrix becomes symmetric, so that the game has a high degree of symmetry. In game theory, situations where the pay-off matrix is symmetric are called partnership games [52,53].

	Y	H
Y	wYY	wYH
H	wYH	wHH

Let w_YY be the pay-off for the homozygous genotype resulting in YY, w_YH be the pay-off for the heterozygous and symmetric cases (i.e. YH and HY ) and w_HH be the pay-off for the homozygous genotype resulting in HH. We assume that w_YY, w_YH, w_HH are real values and pairwise different. Thus individuals with different specific allele combinations differ in their fitness. From a game-theoretical point of view these three genotypes can be considered as the result of two different strategies realized by the two genes in a concrete individual.

We assume that the given deviating allele frequencies within ethnic groups represent different evolutionarily stable solutions for the trade-off between the false positive and false negative cell detection. Let y*∈(0, 1) denote the evolutionarily stable frequency of the allele realization Y in the population. In particular, populations with homozygous individuals, either pure HH or pure YY, can be invaded by the contrary strategy, respectively (cf. table 1). Thus, there must be a pay-off advantage to a heterozygous individual to have both strategies. In population genetics this case is called overdominance [54]. Considering this, we can derive directly the inequalities

2.1

and

2.2

The evolutionarily stable frequency y*∈(0, 1) of the allele realization Y in the population can be calculated by using the Bishop–Cannings theorem [55] (see also [56], appendix A):

2.3

Although the value of y^* varies in different populations, its values are always higher than 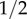[34]; cf. table 1. Together with equation (2.3) we derive the condition

2.4

meaning that comparing the two homozygous cases shows that YY gets a higher pay-off than HH. Combining the inequalities (2.1), (2.2) and (2.4), we get

2.5

A symmetric game with this pay-off relation is a battle of the sexes game. This is one subtype of the leader game, a classical two-player two-strategy game with mixed Nash equilibria. Here, the follower does not have a disadvantage in pay-off compared to the leader. Thus, it is on the boundary between the battle of the sexes game and another subtype of the leader game (cf. [56]). In the interpretation (cover story) of the battle of the sexes game, that parameter combination means that both partners enjoy the togetherness equally (pay-off w_YH), independent of the event they visit together [56].

The inequalities (2.5) simplify the pay-off matrix. As parameter values can be normalized without loss of generality [57], it can be assumed that

2.6

and

2.7

The value of y^* can then be reduced with equation (2.3) to

2.8

or, expressed for the value of w_YH:

2.9

For example, the frequency of the H allele (which equals 1 − y*) is about 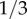for Caucasians, about 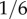for Hispanics and about 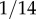for Japanese [34]. The value of w_YH then becomes 2, 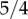and 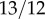, respectively. Therefore, for example, the pay-off matrix for Caucasians becomes

	Y	H
Y	1	2
H	2	0

We summarized several studies addressing the factor H polymorphism and calculated the expected pay-offs of the H allele (see equation (2.9)). The examined ethnic groups are organized in cultural areas. The cultural areas coincide with seven of the eight cultural areas identified by Hunter & Whitten [32] (North Asia is missing due to lack of data). For a more detailed view three subareas, i.e. Mesoamerica, Finland and Iceland are included.

2.2. Relating the pay-offs to false positives and false negatives

In the previous section, we analysed the observation of the two alleles, where H occurs less often than Y . The conclusion was that, for an individual, being heterozygous is most advantageous, whereas being homozygous HH is least advantageous. The next step is to find an appropriate explanation for this order of the pay-off values. For this, we have a closer look on the task of factor H and the difference of the two alleles.

A significant role of factor H is to distinguish between foreign cells (or cells to be cleared) and intact self cells (cells to be protected from complement attack and phagocytosis). Cells that are labelled with factor H are protected against the damage function of the innate immune system. Thus, these cells can be defined as labelled to be negative. Cells without factor H are indirectly labelled as positive, independently of whether the cell of interest is host or foreign. This represents a classical classification problem.

If factor H binds to host cells, the labelling is true negative (TN). A detection of foreign cells, by not binding to their surfaces, is a true positive labelling (TP). In the distinction between self and foreign two inevitable errors occur: (I), foreign cells erroneously recognized as self cells, i.e. false negatives (FN) and (II) self cells erroneously recognized as foreign, i.e. false positives (FP). See table 2 for an overview.

Table 2.

Possible outcomes of cell labelling: TP, FP, FN and TN.

	foreign cell	host cell
label a cell as foreign	TP	FP
label a cell as host	FN	TN

Let f₁ be the number of foreign cells that bind factor H in relation to all foreign cells and f₂ be the number of all host cells that do not bind factor H in relation to all host cells. Thus the probabilities for the two errors can be denoted by

2.10

and

2.11

How do the different alleles Y and H influence these errors? The value of f₂, the probability of clearing a host cell, is influenced by the CFH-402Y allele as it binds well to CRP on the cells [24]. This leads to a lower opsonization (and thus a lower rate of phagocytosis) and thus a lower value of f₂. On the other hand, CFH-402H is less able to bind [24], resulting in a higher value of f₂:

2.12

If equation (2.12) described the only effect by the SNP, then minimizing the error with genotype YY would provide the optimum, i.e. the highest pay-off. With equation (2.5) and table 1, this has to be rejected and we hypothesize that there is also an advantage of CFH-402H.

Recalling the ability of pathogens to bind factor H, the low binding affinity of CFH-402H [24] might prevent pathogens from reducing the opsonization too much. This means that f₁, the probability of not recognizing a foreign cell, is lower in the presence of CFH-402H than of CFH-402Y:

2.13

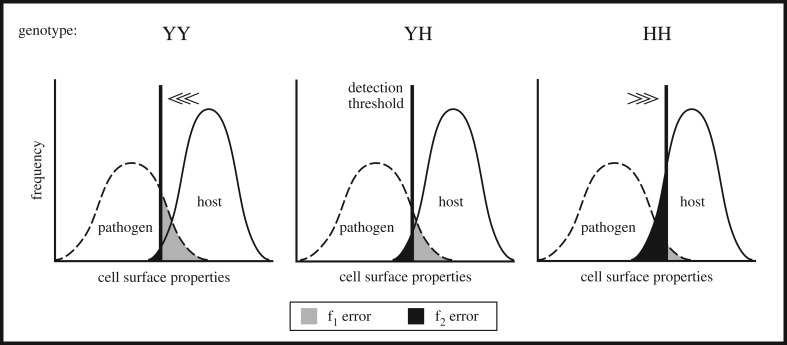
How is the classification problem of self and foreign cells (i.e. the labelling) triggered by the CFH polymorphism? And, how and to which extent does the heterozygous genotype influence the values of the f₁ and f₂ errors? Let all surface properties promoting factor H binding be summarized by a single hypothetical parameter collapsing down to one single dimension (figure 2). Low values of this parameter may reflect surface conditions where factor H readily binds to a cell surface. High values instead reflect surface properties with a decreased binding affinity of factor H. Further let the existence of self cells and pathogens satisfy two distinct (e.g. bell-shaped) distributions forming two probability density functions (PDF), for host and pathogenic cells, within this dimension. Note distributions are not necessarily bell-shaped.

Figure 2.

Sketch of the classification problem of self and foreign cell detection. Illustration of the two errors for each genotype: f₁, number of foreign cells erroneously labelled as host cells divided by all foreign cells; f₂, number of host cells erroneously labelled as foreign cells divided by all host cells; see equations (2.10) and (2.11). The detection threshold for genotype YH is between the detection thresholds of the homozygous genotypes and leads to a trade-off between the f₁ and f₂ errors. A similar figure showing two bell-shaped distributions was also proposed by Holen & Johnstone [42].

A major task of the immune system is to distinguish between those two PDFs. Whereas their relative positions are not of major relevance, their degree of overlap is. Thus a considerable overlap exacerbates the classification problem. The reliability of distinction of both surface types by the immune system decreases. We expect the specific detection threshold of a host to be determined by its genotypic state. The integrated area under the pathogen's PDF on the right of the threshold (light grey area) represents the pathogen's probability of not being detected by the host. It represents the error f₁ where molecular mimicry is valuable to the pathogen. Accordingly, the integrated area under the host's PDF on the left of the threshold (dark grey area) represents the probability of self cells not being protected and prone to clearance. This area reflects the error f₂.

Every possible detection threshold with f₁, f₂ > 0 is a Pareto-efficient state. This means that every decrease of f₁ increases f₂ and vice versa, which represents the trade-off between pathogenic detection and the tenuous control of self cells. Hence, both errors at once are not minimal at any genotype. There are three possible thresholds given by the three possible genotypes. For each genotype the threshold is fixed, whereas the PDFs of host and pathogen cells depend on environmental differences.

For the homozygous genotype YY , we expect the degree of opsonization (and phagocytosis) being generally lower for host cells and also for pathogens binding factor H. This results in a low f₂ error, on the one hand, as host cells are well protected, but also in a high f₁ error, on the other hand, as pathogens are less well detected (figure 2a). For the homozygous genotype HH, we expect a high degree of opsonization leading to a low f₁ error. Here the factor H binding abilities of pathogens are low, thus molecular mimicry is futile. Simultaneously the f₂ error is high, as the host cells are less well protected (figure 2c). Our model predicts an intermediate degree of opsonization for the heterozygous genotype, i.e. YH (figure 2b). This implies that the extent of errors (i.e. f^YH₁ and f^YH₂), occurring in the heterozygous genotype, also exhibits an intermediate state:

2.14

and

2.15

Consider a fitness function F depending on the position of the threshold t: F = F(t). Different environmental and internal conditions (e.g. pathogen load and ethnicity, respectively) lead to differently shaped distributions for host and pathogenic cells, resulting in different parameters λ of F = F_λ(t). Independently of λ, according to the normalization (2.6), (2.7) the (normalized) fitness function F should fulfil two equations for the thresholds of the two homozygous genotypes t_YY and t_HH:

2.16

and

2.17

As we showed in the previous section that the fitness (pay-off) for the genotype YH is higher than for the homozygous genotypes (inequality (2.5)), F must increase beyond t_YY, reach a maximum and decrease until t_HH. Of course, F_λ(t_YH) = w_YH, but it need not be the maximum value of F. In EGT, the expected pay-off is maximized, i.e. the evolutionarily stable Y-allele frequency y* is not the result of maximizing the fitness of the heterozygous genotype, but of maximizing the fitness of the whole population.

3. Discussion

In this manuscript, we investigated a SNP within the human complement factor H, i.e CFH-H402Y. This SNP was identified to represent a typical classification problem prompting two Pareto-efficient errors during the detection between ‘self’ and ‘foreign’ by the innate immune system. We emphasize the dilemma between an efficient defence against pathogenic agents and an attentive handling of self cells. Allele frequencies are found to deviate significantly between ethnic groups (cf. table 1). Here we interpret allele variants as alternative evolutionary strategies and current allele frequencies as evolutionarily stable within the above-mentioned ethnic groups. Sticking to classical EGT, the identified game type is a special case of the battle of the sexes game.

Molecular mimicry describes the ability of pathogens to adapt the structure of their proteins and carbohydrates to the structure of those of the host to evade the immune recognition and attack by the host. This strategy has been observed for bacteria, viruses, fungi, parasites and protozoa. These pathogenic agents achieve mimicry through molecular surfaces that mimic host protein surfaces, which have been obtained by convergent evolution [6]. It has also been theorized that these similar protein folds have been obtained by horizontal gene transfer [58]. This further supports the theory that microbial organisms have evolved a mechanism of concealment similar to that of higher organisms such as the African praying mantis or chameleon that camouflage themselves so that they can mimic their background so as not to be recognized by others [58].

Investigating the host's consequences of molecular mimicry contributes to a deeper understanding of the arms race between host and pathogen. While the pathogen's objective is to be as similar as possible to the cells of its host, the host aims to improve its sensitivity to detect pathogens while not promoting autoimmune reactions. Analogous trends have been shown for parasites, which adapt to the locally common genotypes of its host [43]. Within the overlapping range of cell surface properties (figure 2) the distinction of self cells and foreign surfaces are incompatible aspects. We showed that the two errors during cell detection cannot be minimized simultaneously. For this type of bi-criteria problem methods of Pareto optimization are helpful [59]. This is reminiscent of classical test statistics, where the sensitivity and specificity trade-off is imminent. Typical optimization problems including contradicting aspects are often part of biological questions, i.e. classification problems, inverse problems, sequence and structure alignment, protein structure prediction, system optimization and experimental design [60]. Furthermore, scenarios of optimization problems with multiple (also conflicting) aspects can be found in daily life. To tackle those problems, several multi-objective optimization tools are developed [61].

An alternative approach to solving the problem under study could be based on population genetics, an academic discipline originating in the pioneering work of Ronald Fisher, John B. S. Haldane and Sewall Wright [62]. In population genetics, equations have been derived that are practically equivalent to the Bishop–Cannings Theorem (equation (2.3)) for the case of partnership games [53,54,63]. Relative fitness is usually written as 1 − s_i, where s_i denotes the selection coefficient for allele i [54]. Some authors write the equation for the equilibrium frequency of alleles in a form that is very close to the Bishop-Cannings Theorem [53,54, ch. 4.6]. For the relation between game theory and population genetics, see also [52, ch. 22].

Here, we have adopted a game-theoretical approach. Finding the evolutionarily stable strategies is analogous to calculating equilibrium allele frequencies in the presence of selection. As we study frequency-dependent interactions, it is more convenient to use a game theory approach. Although it is, to some extent, a matter of taste, we consider this to be an intuitive and comprehensible way of understanding complex genetic phenomena.

Our model predicts a high susceptibility to infectious diseases for the YY-homozygous genotype due to low detection capabilities of foreign cells (see figure 2). Accordingly, the HH-homozygous genotype should tend to suffer autoimmune diseases, e.g. AMD, with an increased probability. Our model predicts the highest expected pay-off for the YH-heterogeneous genotypes (see equation (2.5)), as its detection threshold tends to minimize both errors. Self-evidently, the location of the detection thresholds underlies a tremendous selection pressure, on the one hand for pathogenic agents and on the other hand, for the potential host. Whereas the purpose of the pathogen is to be undetected by imitating self cell surface properties, i.e. by molecular mimicry, self cells have to fit a well tuned trade-off between pathogenic detection (and clearance) and the tenuous control of self cells.

Exploring the predictive potential of the here presented model admits an outlook on the opposite effect. Whereas a high H-allele frequency should promote a right-shifted detection threshold with high probabilities to distinct surfaces of pathogenic agents simultaneously the risk for erroneous self cell detection is increased (f₁ ≫ f₂), an essential part of the pathology promoting autoimmune diseases. This is in good accordance with the hypothesis of [34] that populations with a higher prevalence of AMD also have a higher prevalence for the H-allele. This fact has also been claimed by several other authors (see references cited in table 1). Further, so far unidentified genetic parameters that are important in the pathogenesis of AMD are suggested [34]. Factor H like protein (FHL-1) is an alternative product of the factor H gene. It mainly consists of the first seven (of the 20) SCRs, and therefore also contains the first binding site for CRP. The SNP effect is stronger, as the second binding site (SCR 20) is not present [24]. As the function is basically the same as for factor H [1], for this argumentation, it is not necessary to make a distinction between factor H and FHL-1. Thus, the here presented model can also be applied to this situation.

It is believed that specific T cells can cross-react with self-epitopes, thus leading to tissue pathology (autoimmunity) [64]. Nevertheless, Xu et al. [65] state that the Y402H variant in factor H is not associated with exudative AMD in a northern Chinese population, and Kim et al. [66] did not find a statistically significant proof for this relation in Koreans. It is likely that the lack of statistical significance is based on the fact that the Y402H variant is very rare in the South Asian cultural area. Thus, to gain statistical significance for rare events larger sample groups are necessary.

As the frequency y* of the Y-allele significantly varies between ethnic groups (table 1), we conclude that the fitness costs of detection errors, i.e. f₁ and f₂, may also vary between these groups. Thereby ordering of pay-offs is constant and equation (2.5) always holds true. Thus a low frequency y^* also implies a lower expected pay-off a and a left-shifted position of the detection threshold (f₁ ≫ f₂) with a suboptimal detection of pathogenic agents. Consequently the H-allele frequency could be interpreted as a proxy for severity of the local pathogen pressure on the corresponding ethnic group. Severity here represents the degree of local pathogens to mimic self cell surfaces. According to the allele frequencies given by Grassi et al. [34], Caucasians, Somalis (H-allele frequency 0.347 + −0.03) and African-Americans (0.357 + − 0.04) originate from environments with more aggressive pathogens. Africa in general has a greater disease prevalence than all other regions and a different spectrum of infectious pathogens [67], showing good accordance of the allele frequencies to the prevalence of pathogens. We conclude that the fitness consequences of the f₁ and f₂ trade-off may vary locally. Note that the pay-off of an individual is determined by its genotypic state and its environment.

The distribution of pathogens has been critical in shaping historical patterns of conquest and settlement, and the role of pathogens in shaping ethnic diversity cannot be overestimated [68]. With their emigration to America, Europeans have introduced many diseases, whereas no new severe diseases awaited Europeans in the New World [69]. By contrast, the Hispanics (0.177 + −0.03) mainly originate from Central and South America, regions with a great richness of pathogens but a very low prevalence [67]. The origin of the Japanese (0.077 + −0.02) has low pathogen richness and prevalence [67].

Focusing on just two alleles is an obvious simplification of the biological problem, as in the whole factor H gene region 30 SNPs have been detected [70]. Here the SNP 8 corresponds to Y402H and lies in the first of three haplotype blocks containing four haplotypes. De Córdoba & De Jorge [3] state that there are a dozen of SNPs in the promotor region or coding sequence of the factor H gene. An allocation of strategies to the haplotypes instead of alternative nucleotides, i.e. Y402H, would be also valid, and the expected results are identical. Several susceptible and also protective haplotypes have been identified ([26,71,72]). Nevertheless, Hageman et al. [26] found, among five haplotypes with a set of the eight most informative SNPs, that the haplotype bearing the major risk for AMD includes the Y402H SNP. Li et al. [72] investigated haplotypes on the basis of five SNPs and also found the Y402H SNP to be the most common risk haplotype. Also Francis et al. [71] found a haplotype with the Y402H SNP which is strongly associated with AMD.

The here presented model aims to contribute to understanding host–pathogen interactions, especially the host's perspective. The concept of molecular mimicry is a useful tool in understanding the aetiology, pathogenesis, treatment and prevention of autoimmune disorders. Mimicry can only be improved at some cost to the mimetic organism and on an evolutionary timescale [42,51]. Therein, evolutionary game theoretical models of mimicry were developed. Quality of mimicry, frequency of models and mimics, costs on the operator due to contact with mimics are considered to explain different mimicry scenarios. Molecular mimicry is, however, only one mechanism by which an autoimmune disease can occur in association with a pathogen [73]. Understanding the mechanism of molecular mimicry may allow future research to be directed towards uncovering the initiating infectious agent as well as recognizing the self-determinant. This way, future research may be able to design strategies for treatment and prevention of autoimmune disorders.

Data accessibility

The datasets supporting this article are included in the main paper.

Authors' contributions

S.H. and C.G. designed the study, set up the mathematical model and performed the analysis. S.H., S.G., P.F.Z., C.S. and S.S. interpreted the results, S.G. and S.S. coordinated the study, S.H., C.G. and C.H. wrote the manuscript, S.L. and C.H. aided in interpretation and S.L., S.G., P.F.Z., C.S. and S.S. contributed to writing the manuscript.

Competing interests

We have no competing interests.

Funding

The authors acknowledge support by the Deutsche Forschungsgemeinschaft (DFG) in the CRC/Transregio 124 FungiNet sub-projects B1 (S.S.), C4 (C.S.) and C6 (P.F.Z.) and in the Jena School for Microbial Communication (C.G. and S.L.).