Abstract
Controversy exists regarding the suitability of fully developed versus measured inlet velocity profiles for image-based computational fluid dynamics (CFD) studies of carotid bifurcation hemodynamics. Here, we attempt to resolve this by investigating the impact of the reconstructed common carotid artery (CCA) inlet length on computed metrics of “disturbed” flow. Twelve normal carotid bifurcation geometries were reconstructed from contrast-enhanced angiograms acquired as part of the Vascular Aging—The Link That Bridges Age to Atherosclerosis study (VALIDATE). The right carotid artery lumen geometry was reconstructed from its brachiocephalic origin to well above the bifurcation, and the CCA was truncated objectively at locations one, three, five, and seven diameters proximal to where it flares into the bifurcation. Relative to the simulations carried out using the full CCA, models truncated at one CCA diameter strongly overestimated the amount of disturbed flow. Substantial improvement was offered by using three CCA diameters, with only minor further improvement using five CCA diameters. With seven CCA diameters, the amounts of disturbed flow agreed unambiguously with those predicted by the corresponding full-length models. Based on these findings, we recommend that image-based CFD models of the carotid bifurcation should incorporate at least three diameters of CCA length if fully developed velocity profiles are to be imposed at the inlet. The need for imposing measured inlet velocity profiles would seem to be relevant only for those cases where the CCA is severely truncated.
1 Introduction
The hemodynamic environment at the carotid artery bifurcation has been widely studied due to its predilection for atherosclerosis. The increasing reliance on image-based CFD for such studies necessitates a close look at the various implicit and explicit assumptions [1]. For example, it is reasonable to question the choice of boundary conditions and assumptions used in the CFD simulation for the purposes of inferring an individual’s exposure to “disturbed” flow. (Hereafter, the quotations marks around this vague term are implied.) While realistic geometric boundary conditions can now be reconstructed adequately using in vivo imaging tools such as computed tomography (CT), ultrasound, angiography, and magnetic resonance imaging (MRI), acquiring the desired boundary conditions for the hemodynamic modeling is often challenging. In many cases, typical characteristic flow waveforms readily available in the literature or easily acquired from volunteers are commonly adopted as boundary conditions in the image-based CFD modeling. For simplicity, axisymmetric, fully developed velocity profiles are commonly assumed at the flow inlets based on the measured or assumed flow rates. However, recent reports of phase-contrast MRI measurements at the CCA have revealed that the majority of CCA velocity profiles are skewed, often exhibiting the crescent shape characteristic of strong Dean-type flow in a curved tube [2,3]. The common assumption of fully developed or axisymmetric flow in image-based CFD analysis may therefore introduce errors in the estimation of flow structure and wall shear rates at the bifurcation, as well as masking potentially important nonuniform wall shear variations at the CCA itself.
Earlier work by Moyle et al. [4] on the influence of inlet velocity profile skewing on carotid bifurcation hemodynamics pointed out that “given sufficient entrance length of realistic geometry […] simplification to fully developed axial flow may be made without penalty.” The authors found that the effects of secondary velocities in the inlet profile on the disturbed flow quantities broke down within a few diameters of the inlet in their bifurcation models with extended, helical entrance length. Moreover, the errors made in the assumptions of fully developed inlet profiles were found to be substantially less than those due to the uncertainties inherent in the model construction process. On the other hand, Wake et al. [5], in a recent study that compared the effects of MRI-measured versus fully developed velocity boundary conditions on disturbed flow at a carotid geometry, reported pronounced influence of inflow boundary conditions on the computed hemodynamics. They recommended the use of in vivo measured velocity distributions to model hemodynamics in anatomically realistic carotid bifurcation models. It is worth noting, however, that the bifurcation geometry used in that study had a relatively short CCA inlet length, possibly explaining the contradictory findings of the two studies.
No studies to date have offered adequate insights to answer the question of how much CCA length is sufficient in order to confidently model the carotid bifurcation hemodynamics using fully developed inlet boundary conditions. In this study, we aimed to quantitatively assess the impact of CCA length on image-based CFD simulations of normal carotid bifurcation flow dynamics by progressively truncating the CCA of actual bifurcation geometries reconstructed down to the thoracic origins of the carotid arteries.
2 Methods
2.1 Study Participants and Imaging Protocols
Data from this study are a subset of the ongoing Vascular Aging—The Link That Bridges Age to Atherosclerosis (VALIDATE) study, a carotid MRI investigation of vascular markers of aging in participants recruited from the Baltimore Longitudinal Study of Aging [6]. Twelve VALIDATE participants without known coronary, cerebral, or peripheral artery disease and without carotid artery stenosis were randomly selected for this study. The bifurcation geometries and inlet/outlet velocities of each participant were acquired from contrast-enhanced angiography (CEMRA) and phase contrast MRI (PCMRI) sequences, respectively, imaged on a 3 T MRI scanner (Philips Healthcare, Andover, MD) as part of the VALIDATE carotid MRI protocol. Written informed consent was obtained from all the participants, and approval for VALIDATE was given by the institutional review board. Approval for the use of participants’ anonymized images in the current study was given by the VALIDATE study center.
The CEMRA images were obtained using a 3D acquisition having the following scan parameters: 1.0 mm coronal slice thickness with 0.5 mm overlap, square 33 cm field-of-view, and 408 × 405 acquisition matrix zero padded to 512 × 512. Retrospectively gated cine PCMRI images of the through-plane velocity component were acquired transverse to the nominal long axis of the right CCA at a distance 1.5 cm proximal to the flow divider and a separate acquisition 0.5 cm distal to the flow divider through the internal and external carotid arteries (ICA and ECA, respectively). Scan parameters included 5 mm slice thickness, square 13 cm field-of-view, 256 × 128 acquisition matrix zero padded to 256 × 256, encoding velocity of 70 cm/s, and 32 uniformly spaced time points per cardiac cycle.
2.2 Lumen Geometry and Flow Rate Extraction
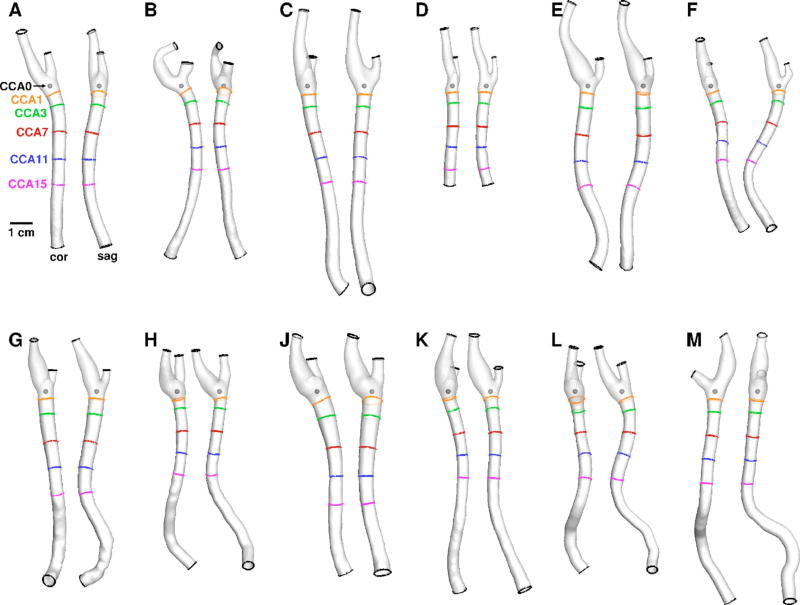
For each participant (age: 64 ± 9 years; range: 52–80 years), the right carotid artery lumen geometry was reconstructed from its brachiocephalic origin to well above the bifurcation using the opensource Vascular Modeling Toolkit (vmtk) [7]. Following automated identification of the CCA origin (i.e., CCA0) by vmtk [8], the CCA was truncated normal to the CCA axis at locations three (CCA3), seven (CCA7), 11 (CCA11), and 15 (CCA15) CCA radii proximal to this point, roughly corresponding to lengths one, three, five, and seven diameters proximal to the section where the CCA begins to flare (CCA1). Figure 1 shows all the models with their CCA0, CCA1, and cut plane locations indicated. Flow extensions of four inlet radii were added to all CFD models for transition from cut plane to circular cross section area.
Fig. 1.
Twelve carotid bifurcation models (cases A–M) reconstructed from CEMRA, shown in coronal and sagittal views. As labeled in panel A, shown also are the locations of the CCA0 origin, the CCA1 plane defining the beginning of the nonflared CCA, and the various cut planes used to truncate the CCA length.
For each of the 32 time points per PCMRI study, the lumen boundaries were determined from the magnitude image using a semi-automated, in-house software package employing a gradient-based segmentation method [9]. Flow rates at the CCA, ICA, and ECA were calculated by integrating the velocity profile within the respective lumen boundaries. Because of the effects of compliance, small branches, or errors and uncertainties in the PCMRI measurements, it is possible for the instantaneous inflow CCA and outflow ICA+ECA rates not to match exactly [10,11]. To ensure instantaneous mass conservation for the rigid CFD models, we first temporally aligned the CCA, ICA, and ECA waveforms and then reset the instantaneous ICA and ECA flow rates by scaling the instantaneous CCA flow rate by the instantaneous ICA:ECA flow division.
2.3 CFD Simulations and Scalar Metrics of Disturbed Flow
CFD simulations were carried out using a previously validated in-house solver [12,13]. Quadratic tetrahedral-element meshes were generated by icem-cfd (ANSYS Inc., Canonsburg, PA) with a node spacing of 0.1–0.2 mm, which was previously shown to successfully resolve wall shear stresses (WSSs) at normal carotid bifurcation geometries [4]. Fully developed, pulsatile velocity profile boundary conditions were imposed at the CCA inlet and ICA outlet based on the measured pulsatile flow rates from the PCMRI acquisitions. Traction-free boundary conditions were imposed at the ECA outlet. Rigid walls and constant blood viscosity of 0.035 cm2 /s were assumed for all models.
The CFD simulations were carried out using up to 4800 time steps per cardiac cycle, and at least three cycles were simulated to damp initial transients. For each model, the oscillatory shear index (OSI), cycle-averaged WSS magnitude, and relative residence time (RRT) surface distribution were computed, and the latter two variables were normalized by their nominal values at the CCA3 location.
Following Lee et al. [14], the degree of disturbed flow was quantified as the relative surface areas (SAs), bounded by CCA3, ICA5, and ECA2, exposed to WSS ≤ 0.481, RRT ≥ 2.944, or OSI ≥ 0.145. These thresholds corresponded to the upper (for WSS, lower) quintiles based on 50 cases. Each case was assigned a scalar value, hereafter denoted as SAWSS, SARRT, or SAOSI, representing the proportion of its surface exposed to disturbed flow.
3 Results
The cycle-averaged flow rates in the CCA and ICA were 6.59 ± 1.32 ml/min and 4.67 ± 1.30 ml/min, respectively, for the N=12 participants, consistent with previously reported data [10].
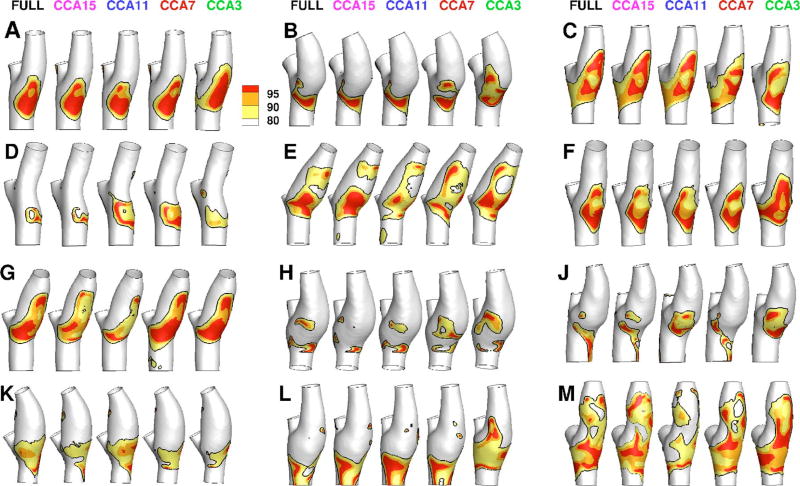
Figure 2 shows that the RRT distributions derived using the full-length models varied broadly among the 12 cases. Relative to the respective CFD simulations carried out using the full length of the CCA, simulations based on the CCA3 truncated models showed apparent qualitative differences in the extent and distribution of elevated RRT. These differences were subdued, but not entirely eliminated, by extending the CCA length. Qualitatively, the CCA15 models showed the closest agreement with the full-length model. Similar trends were also observed for WSS and OSI distributions (not shown).
Fig. 2.
Color-coded distributions of RRT for all 12 participants for the various CCA lengths indicated at the top row. Black contour lines on each surface identify the area exposed to RRT above its 80th percentile value, as described in Sec. 2. Grayscales (colors online) indicate the areas exposed above the 80th, 90th, and 95th percentile values. Geometries are clipped at the CCA3, ICA5, and ECA2 locations used to bind the surface for disturbed flow calculations.
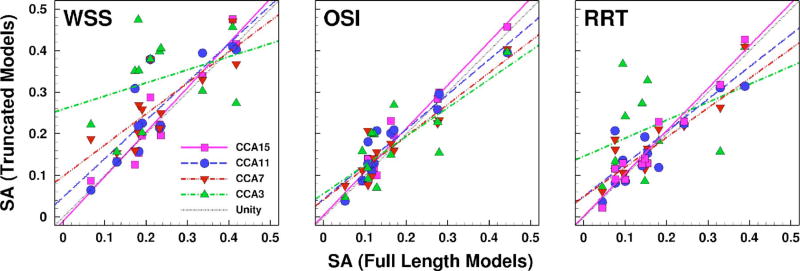
To quantify the effects of CCA length on the computed disturbed flow quantities, Fig. 3 shows the linear regressions of SAWSS, SAOSI, and SARRT derived from different truncated models. Table 1 reports the slopes and regression coefficients. The CCA3 models showed the weakest correlations, suggesting that the disturbed flow quantities were poorly predicted in this set of truncated models. Quantitative improvement was found after extending the CCA length in the CCA7 model but only slightly improved by extending the CCA length from CCA7 to CCA11. Better agreement with the full-length models was observed in CCA11 and CCA15 models. Compared with the full-length models, only the slope of SAWSS in CCA3 models was significantly different from unity (95% CI: −0.31 to 0.95), whereas slopes of other disturbed flow quantities in other truncated models were not significantly different from unity.
Fig. 3.
Scatter plots of SA exposed to various disturbed flow indicators (WSS, OSI, and RRT), derived from the truncated models and compared against the corresponding SA from the full-length models. Colored lines are linear regressions through the respective colored data points. The black dotted line represents the line of unity.
Table 1.
Comparison of R2 and slopes from linear regressions of different disturbed flow indicators based on truncated models versus participant-specific full-length models
| Slope | R2 | |||||
|---|---|---|---|---|---|---|
|
|
|
|||||
| Full length versus | WSS | OSI | RRT | WSS | OSI | RRT |
| CCA3 | 0.31 | 0.69 | 0.43 | 0.10 | 0.62 | 0.17 |
| CCA7 | 0.75 | 0.76 | 0.78 | 0.66 | 0.86 | 0.80 |
| CCA11 | 0.99 | 0.84 | 0.71 | 0.79 | 0.88 | 0.75 |
| CCA15 | 1.07 | 1.04 | 1.02 | 0.90 | 0.95 | 0.94 |
4 Discussion
4.1 Summary and Implications of Findings
Our findings are in agreement with the study of Moyle et al., namely, that the lumen surface exposure to disturbed flow in carotid bifurcations can be reasonably captured using simplified fully developed inflow profiles if “sufficient” CCA length is included in the computational model [4]. There appears no significant difference in the disturbed flow quantities and distribution between the full-length models and the truncated models of CCA7, suggesting that at least three CCA diameters (i.e., six radii between locations CCA1 and CCA7) proximal to the bifurcation flare are sufficient to model the bifurcation hemodynamics. (N.B. Cases A, B, and C of Moyle et al. were truncated at locations equivalent to CCA5, CCA7, and CCA6 locations, respectively, thus explaining their finding of relative insensitivity to the shape of the upstream helical inlet sections.) Extending the truncated CCA improves the correlation with the full-length model. CCA length of seven diameters from the bifurcation flare (i.e., CCA15) produces unambiguous disturbed flow quantities, as seen in the full-length models.
When blood flows through the CCA, the CCA curvature sets up the flow to increase the fluid inertia, leading to more coherent fluid structures along the flow direction. Such coherent, forward-directed flow structure exhibits its own dynamic consequences, for instance, helical, spiral, or swirl flow, and may reduce the likelihood of flow disturbances, as seen in healthy arteries [15–17]. For example, Houston et al. [18] found that carotid atheromatous disease is associated with a reduction in the prevalence of a systolic helical flow pattern in the aortic arch. This interaction of geometry and hemodynamics is consistent with the findings of Lee et al. [14], i.e., moderating influence of CCA-ICA tortuosity on disturbed flow. Increasing the tortuosity of truncated models in the current study also showed improved disturbed flow agreement with those of full-length models, suggesting the dependence of disturbed flow at the distal bifurcation on the proximal CCA geometry. In models with severely truncated CCA length, for example, CCA3 models, the lack of CCA curvature prior to the bifurcation flare prevented the flow to redevelop its “true” dynamics, thus giving rise to the disagreement with the full-length models.
Similar factors may have contributed to the dispute between the disturbed flow computed using MRI-measured versus fully developed inflow profile in the study by Wake et al. [5]. Their study adopted a bifurcation model with relatively short CCA length, comparable to the CCA3 models in the current study. Interestingly, the MRI-measured velocity flow profile shown by Wake et al. was skewed, which hints that the skewed velocity profile may have been induced by nonstraight CCA segment proximal to the MRI acquisition plane [5]. Therefore, in the situation where the length of the reconstructed CCA is relatively short, the commonly used fully developed velocity profile boundary condition may indeed not be ideal in deriving the bifurcation hemodynamics, and extra care is needed when comparing the hemodynamics of severely truncated versus full-length CCA models.
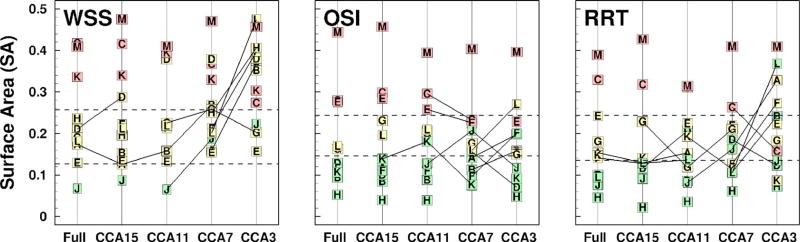
Interindividual differences in the qualitative appearance of disturbed flow regions between full-length, CCA15 and CCA11 models were well preserved irrespective of the assumed flow conditions and CCA inlet length. This has important implications for large-scale studies that are more interested in relative rather than absolute values of hemodynamic risk. To see this, in Fig. 4 we show all models ranked according to the various disturbed flow metrics and subdivided into categories of low, medium, and high risk of disturbed flow exposure using lower and upper tertiles derived from the data of Lee et al. [14]. Comparing the risk categories computed using the truncated models and the full-length models, we found multiple crossovers of risk categories, indicating that the category of risk changed when different CCA lengths were used to compute the disturbed flow exposure. The risk category in the current study was more evidently altered in going from CCA3 to CCA7 models and was well preserved when going from CCA11 to CCA15 to full-length models. Interestingly, the risk category is constantly downgraded when moving from CCA3 to full-length models, confirming that the truncated models have a tendency to overestimate the amount of disturbed flow, as discussed above, and thus may represent risk category in a more conservative way.
Fig. 4.
Rank plots of SA exposed to various disturbed flow indicators (WSS, OSI, and RRT) as a function of the CCA length. The dashed lines separate SA into lower, middle, and upper tertiles according to the distributions of exposure levels found by Lee et al. [14]. Symbols denote the case identifier, and green, yellow, and red are used to highlight the cases (i.e., full-length models) falling into the lower, middle, and upper tertiles, respectively. Connecting lines identify adjacent pairs for which the tertile is different.
This change in risk category is unlike our previous study [19], which examined the sensitivity of flow waveform shape on the risk orders, where the risk category remained unchanged regardless of flow rate waveforms. When comparing the regressions of the disturbed flow quantities from the flow waveform study and the current study, we note that the CCA entrance length effect introduces more variations in the computed disturbed flow quantities. In other words, the bifurcation and proximal CCA geometry, rather than the inflow waveform, primarily determine the associated risk of an individual’s exposure to disturbed flow. The inflow waveform only induces secondary effects in hemodynamics modeling.
This importance of including sufficient entrance length in a computational model is also valid for other vascular territories. Marzo et al. [20] compared the hemodynamics of three aneurysms using plug and Womersley velocity profiles as inlet conditions and showed that assumptions made on the inflow profile have little influence on the local hemodynamics in the aneurysm, provided that a sufficient extension of the afferent vasculature is considered. Work by Castro et al. [21] also confirmed similar findings. Myers et al. [22] found that both parabolic and blunt inlet velocity profiles quickly responded to the local arterial geometry in a cast right coronary artery cast model and did not substantially influence the WSS pattern beyond nine diameters from the origin. Together, these observations suggest the importance of entrance length over the choice of inflow velocity profile in hemodynamic modeling. Therefore, we reiterate the recommendation of Moyle et al. that, for image-based CFD studies of the carotid bifurcation hemodynamics, priority should be given to more accurate and detailed geometric reconstruction, as it is the primary influence on physiologically significant indicators [4]. While this may be straightforward for 3D coronal acquisitions as in the present case, it might prove challenging for 2D axial acquisitions since more slices, and hence more time, will be needed to image the additional CCA length.
Although the geometry dominates the behavior of the bifurcation hemodynamics, there remain other variables and assumptions that could influence the disturbed flow quantities and distributions, such as rigid wall, Newtonian fluid, and the exclusion of small branching vessels. The superior thyroid artery was found to have a significant effect on both the flow and wall shear stress in the common-external side branch but very little effect on the flow field and wall shear stress distribution in the common-internal side branch [23]. Lee et al. [24] compared the two different non- Newtonian models to a Newtonian fluid assumption in carotid bifurcations and found that sensitivity of disturbed flow quantities to the various rheological assumptions was nearly seven times less than that due to geometric uncertainty and on the same order as the effect of inflow boundary condition assumptions. Besides this, the instantaneous flow mismatch between the ICA+ECA and CCA suggests that wall compliance may not be overlooked in carotid bifurcation modeling. The assumption of a rigid wall model has been found to underestimate the temporal and spatial magnitude of the slow moving flow in carotid bifurcation [25]. Mean shear stress in the compliant model was reported 25–30% smaller in experimental studies [26] and computational studies [27]; however, the global characteristics of the disturbed flow and shear stress patterns were preserved. Furthermore, owing to the in vivo compliant CCA, there is likely to be phase shift and attenuation/dispersion of the flow waveform along the length of the whole CCA: The inflow pulsatility prescribed for the truncated models, reflecting conditions in the cervical CCA just proximal to the carotid bifurcation, may not reflect the pulsatility present at the thoracic CCA. Under such condition, the velocity profile prior to the bifurcation flare, and hence the disturbed flow exposure, in our rigid wall model may be different in a compliant model. The interplay between inflow boundary condition and vessel wall motion in carotid bifurcation modeling requires further investigation, particularly when a longer segment of CCA is included. Nevertheless, the errors associated with these assumptions are unlikely to be of a similar order to the effects of CCA inlet length found in the present study.
5 Conclusions
In summary, it would appear that image-based CFD models of the normal carotid bifurcation should include at least three diameters of CCA length prior to bifurcation flare to avoid non-negligible errors in the prediction of disturbed flow. The disturbed flow in bifurcations with CCA length of seven diameters from bifurcation flare agreed unambiguously with the full-length model, echoing the recommendation of Moyle et al. [4] and further strengthening the need for more extensive and accurate geometry reconstruction. The recommendation of using MRI-measured velocity profile in estimating the carotid hemodynamics by Wake et al. [5] would seem to be germane only for those cases where the CCA length is severely truncated.
Acknowledgments
This study was supported by Grant No. MOP-62934 from the Canadian Institutes of Health Research. The VALIDATE study is supported by Contract No. NO1-AG-3-1003 from the National Institute on Aging, NIH and, in part, by the Intramural Research Program of the National Institute on Aging, NIH. Y.H. and D.A.S. also acknowledge the support of a Heart and Stroke Foundation Research Fellowship Award and Career Investigator Award, respectively.
Contributor Information
Yiemeng Hoi, Biomedical Simulation Laboratory, Department of Mechanical and Industrial Engineering, University of Toronto, Toronto, ON, Canada M5S 3G8.
Bruce A. Wasserman, The Russell H. Morgan Department of Radiology and Radiological Sciences, Johns Hopkins University, Baltimore, MD 21205
Edward G. Lakatta, Laboratory of Cardiovascular Science, Intramural Research Program, National Institute on Aging, National Institutes of Health, Baltimore, MD 20892
David A. Steinman, Biomedical Simulation Laboratory, Department of Mechanical and Industrial Engineering, University of Toronto, Toronto, ON, Canada M5S 3G8
References
- 1.Taylor CA, Steinman DA. Image-Based Modeling of Blood Flow and Vessel Wall Dynamics: Applications, Methods and Future Directions. Ann. Biomed. Eng. 2008;38(3):1188–1203. doi: 10.1007/s10439-010-9901-0. [DOI] [PubMed] [Google Scholar]
- 2.Ford MD, Xie YJ, Wasserman BA, Steinman DA. Is Flow in the Common Carotid Artery Fully Developed? Physiol. Meas. 2008;29(11):1335–1349. doi: 10.1088/0967-3334/29/11/008. [DOI] [PubMed] [Google Scholar]
- 3.Sui B, Gao P, Lin Y, Qin H, Liu L, Liu G. Noninvasive Determination of Spatial Distribution and Temporal Gradient of Wall Shear Stress at Common Carotid Artery. J. Biomech. 2008;41(14):3024–3030. doi: 10.1016/j.jbiomech.2008.07.026. [DOI] [PubMed] [Google Scholar]
- 4.Moyle KR, Antiga L, Steinman DA. Inlet Conditions for Image-Based CFD Models of the Carotid Bifurcation: Is it Reasonable to Assume Fully Developed Flow? ASME J. Biomech. Eng. 2006;128(3):371–379. doi: 10.1115/1.2187035. [DOI] [PubMed] [Google Scholar]
- 5.Wake AK, Oshinski JN, Tannenbaum AR, Giddens DP. Choice of In Vivo Versus Idealized Velocity Boundary Conditions Influences Physiologically Relevant Flow Patterns in a Subject-Specific Simulation of Flow in the Human Carotid Bifurcation. ASME J. Biomech. Eng. 2009;131(2):021013. doi: 10.1115/1.3005157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ferrucci L. The Baltimore Longitudinal Study of Aging BLSA: A 50-Year-Long Journey and Plans for the Future. J. Gerontol., Ser. A. 2008;63(12):1416–1419. doi: 10.1093/gerona/63.12.1416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Antiga L, Piccinelli M, Botti L, Ene-Iordache B, Remuzzi A, Steinman DA. An Image-Based Modeling Framework for Patient-Specific Computational Hemodynamics. Med. Biol. Eng. Comput. 2008;46(11):1097–1112. doi: 10.1007/s11517-008-0420-1. [DOI] [PubMed] [Google Scholar]
- 8.Antiga L, Steinman DA. Robust and Objective Decomposition and Mapping of Bifurcating Vessels. IEEE Trans. Med. Imaging. 2004;23(6):704–713. doi: 10.1109/tmi.2004.826946. [DOI] [PubMed] [Google Scholar]
- 9.Ladak HM, Thomas JB, Mitchell JR, Rutt BK, Steinman DA. A Semi-Automatic Technique for Measurement of Arterial Wall From Black Blood MRI. Med. Phys. 2001;28(6):1098–1107. doi: 10.1118/1.1368125. [DOI] [PubMed] [Google Scholar]
- 10.Hoi Y, Wasserman BA, Xie YJ, Najjar SS, Ferruci L, Lakatta EG, Gerstenblith G, Steinman DA. Characterization of Volumetric Flow Rate Waveforms at the Carotid Bifurcations of Older Adults. Physiol. Meas. 2010;31(3):291–302. doi: 10.1088/0967-3334/31/3/002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Marshall I, Papathanasopoulou P, Wartolowska K. Carotid Flow Rates and Flow Division at the Bifurcation in Healthy Volunteers. Physiol. Meas. 2004;25(3):691–697. doi: 10.1088/0967-3334/25/3/009. [DOI] [PubMed] [Google Scholar]
- 12.Minev PD, Ethier CR. A Characteristic/Finite Element Algorithm for the 3-D Navier-Stokes Equations Using Unstructured Grids. Comput. Methods Appl. Mech. Eng. 1998;178(1–2):39–50. [Google Scholar]
- 13.Ethier CR, Prakash S, Steinman DA, Leask RL, Couch GG, Ojha M. Steady Flow Separation Patterns in a 45 Degree Junction. J. Fluid Mech. 2000;411:1–38. [Google Scholar]
- 14.Lee SW, Antiga L, Spence JD, Steinman DA. Geometry of the Carotid Bifurcation Predicts Its Exposure to Disturbed Flow. Stroke. 2008;39(8):2341–2347. doi: 10.1161/STROKEAHA.107.510644. [DOI] [PubMed] [Google Scholar]
- 15.Stonebridge PA, Hoskins PR, Allan PL, Belch JF. Spiral Laminar Flow In Vivo. Clin. Sci. 1996;91(1):17–21. doi: 10.1042/cs0910017. [DOI] [PubMed] [Google Scholar]
- 16.Morbiducci U, Ponzini R, Grigioni M, Redaelli A. Helical Flow as Fluid Dynamic Signature for Atherogenesis Risk in Aortocoronary Bypass. A Numeric Study. J. Biomech. 2007;40(3):519–534. doi: 10.1016/j.jbiomech.2006.02.017. [DOI] [PubMed] [Google Scholar]
- 17.Kilner PJ, Yang GZ, Mohiaddin RH, Firmin DN, Longmore DB. Helical and Retrograde Secondary Flow Patterns in the Aortic Arch Studied by Three-Directional Magnetic Resonance Velocity Mapping. Circulation. 1993;88(5):2235–2247. doi: 10.1161/01.cir.88.5.2235. [DOI] [PubMed] [Google Scholar]
- 18.Houston JG, Gandy SJ, Sheppard DG, Dick JB, Belch JJ, Stonebridge PA. Two-Dimensional Flow Quantitative MRI of Aortic Arch Blood Flow Patterns: Effect of Age, Sex, and Presence of Carotid Atheromatous Disease on Prevalence of Spiral Blood Flow. J. Magn. Reson Imaging. 2003;18(2):169–174. doi: 10.1002/jmri.10341. [DOI] [PubMed] [Google Scholar]
- 19.Hoi Y, Wasserman BA, Lakatta EG, Steinman DA. Carotid Bifurcation Hemodynamics in Older Adults: Effect of Measured Versus Assumed Flow Waveform. ASME J. Biomech. Eng. 2010;132(7):071006. doi: 10.1115/1.4001265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Marzo A, Singh P, Reymond P, Stergiopulos N, Patel U, Hose R. Influence of Inlet Boundary Conditions on the Local Haemodynamics of Intracranial Aneurysms. Comput. Methods Biomech. Biomed. Eng. 2009;12(4):431–444. doi: 10.1080/10255840802654335. [DOI] [PubMed] [Google Scholar]
- 21.Castro MA, Putman CM, Cebral JR. Computational Fluid Dynamics Modeling of Intracranial Aneurysms: Effects of Parent Artery Segmentation on Intra-Aneurysmal Hemodynamics. AJNR Am. J. Neuroradiol. 2006;27(8):1703–1709. [PMC free article] [PubMed] [Google Scholar]
- 22.Myers JG, Moore JA, Ojha M, Johnston KW, Ethier CR. Factors Influencing Blood Flow Patterns in the Human Right Coronary Artery. Ann. Biomed. Eng. 2001;29(2):109–120. doi: 10.1114/1.1349703. [DOI] [PubMed] [Google Scholar]
- 23.Zhao SZ, Xu XY, Collins MW, Stanton AV, Hughes AD, Thom SA. Flow in Carotid Bifurcations: Effect of the Superior Thyroid Artery. Med. Eng. Phys. 1999;21(4):207–214. doi: 10.1016/s1350-4533(99)00046-6. [DOI] [PubMed] [Google Scholar]
- 24.Lee SW, Steinman DA. On the Relative Importance of Rheology for Image-Based CFD Models of the Carotid Bifurcation. ASME J. Biomech. Eng. 2007;129(2):273–278. doi: 10.1115/1.2540836. [DOI] [PubMed] [Google Scholar]
- 25.Zhao SZ, Xu XY, Hughes AD, Thom SA, Stanton AV, Ariff B, Long Q. Blood Flow and Vessel Mechanics in a Physiologically Realistic Model of a Human Carotid Arterial Bifurcation. J. Biomech. 2000;33(8):975–984. doi: 10.1016/s0021-9290(00)00043-9. [DOI] [PubMed] [Google Scholar]
- 26.Anayiotos AS, Jones SA, Giddens DP, Glagov S, Zarins CK. Shear Stress at a Compliant Model of the Human Carotid Bifurcation. ASME J. Biomech. Eng. 1994;116(1):98–106. doi: 10.1115/1.2895710. [DOI] [PubMed] [Google Scholar]
- 27.Perktold K, Rappitsch G. Computer Simulation of Local Blood Flow and Vessel Mechanics in a Compliant Carotid Artery Bifurcation Model. J. Biomech. 1995;28(7):845–856. doi: 10.1016/0021-9290(95)95273-8. [DOI] [PubMed] [Google Scholar]