Cross multivariate correlation coefficients as screening tool for analysis of concurrent EEG‐fMRI recordings

Abstract

Over the past decade, the simultaneous recording of electroencephalogram (EEG) and functional magnetic resonance imaging (fMRI) data has garnered growing interest because it may provide an avenue towards combining the strengths of both imaging modalities. Given their pronounced differences in temporal and spatial statistics, the combination of EEG and fMRI data is however methodologically challenging. Here, we propose a novel screening approach that relies on a Cross Multivariate Correlation Coefficient (xMCC) framework. This approach accomplishes three tasks: (1) It provides a measure for testing multivariate correlation and multivariate uncorrelation of the two modalities; (2) it provides criterion for the selection of EEG features; (3) it performs a screening of relevant EEG information by grouping the EEG channels into clusters to improve efficiency and to reduce computational load when searching for the best predictors of the BOLD signal. The present report applies this approach to a data set with concurrent recordings of steady‐state‐visual evoked potentials (ssVEPs) and fMRI, recorded while observers viewed phase‐reversing Gabor patches. We test the hypothesis that fluctuations in visuo‐cortical mass potentials systematically covary with BOLD fluctuations not only in visual cortical, but also in anterior temporal and prefrontal areas. Results supported the hypothesis and showed that the xMCC‐based analysis provides straightforward identification of neurophysiological plausible brain regions with EEG‐fMRI covariance. Furthermore xMCC converged with other extant methods for EEG‐fMRI analysis.

1. INTRODUCTION

It is well established that the quantitative analysis of large‐scale spatiotemporal brain dynamics in humans is constrained by limitations of the available imaging techniques in terms of spatial and temporal resolution. A sizable literature has emphasized the obvious difference in the physiological processes reflected in fMRI and EEG: The blood oxygen dependent (BOLD) signal is thought to reflect magnetic field changes in response to a chain of events that begins with local neural activity, followed by influx of oxygenated hemoglobin molecules, which in turn alters the ratio between oxygenated and deoxygenated hemoglobin molecules in local blood vessels (Menon & Kim, 1999). On the other hand, Electroencephalography (EEG) reflects to a large extent the summation and massive spatial low‐pass filtering of postsynaptic events occurring simultaneously in large populations of cortical neurons with similar spatial orientation (Nunez & Srinivasan, 2006).

Although the biophysics of the neural‐to‐hemodynamic transfer function are not fully understood, several studies have demonstrated the benefit of combining electrocortical information with BOLD, for example to characterize potential cerebral sources of a given scalp EEG/ERP phenomenon, or to conduct EEG‐informed fMRI analyses that more selectively reflect a given neural process, compared to BOLD‐alone approaches (Huster, Debener, Eichele, & Herrmann, 2012). In translational and clinical studies, the concurrent analysis of EEG and fMRI has shown promise for improving localization accuracy and sensitivity/specificity, for example in the pre‐surgical evaluation of epilepsy (Gotman, Kobayashi, Bagshaw, Bénar, & Dubeau, 2006). The strengths and weaknesses of different approaches—useful for different research questions and in the context of different paradigms—are discussed in introductory reviews (Huster et al., 2012; Laufs, 2012).

Consistent with recent empirical studies into the nature of the BOLD signal (Logothetis, Pauls, Augath, Trinath, & Oeltermann, 2001; Logothetis, 2015), and with the biophysics of EEG (Nunez & Srinivasan, 2006), the present approach assumes that covariation between EEG and fMRI signals accounts only for fraction of the variance of each measure (Herrmann & Debener, 2008). Specific aspects of the correlation between EEG and fMRI signals may reflect responses to experimental events seen in both modalities, mixing trivial effects of joint reactivity of EEG and fMRI to salient external events with correlations of interest such as condition‐specific covariation, or covariation with various cognitive states (Liu, Huang, McGinnis‐Deweese, Keil, & Ding, 2012a). In addition, and of relevance in the absence of experimental stimulation, specific portions of the covariance between modalities may reflect neural‐hemodynamic dependencies in spontaneous, ongoing brain activity. To capture and separate these different types of covariation, we propose an exploratory framework to quantify the spatial‐temporal correlations between the time series of fMRI BOLD and EEG‐derived features, which is based on a novel linear dependency measure (Figure 1). The present approach primarily contributes to EEG‐informed fMRI analysis (Huster et al., 2012), and identifies EEG features and sensor (or source) locations with strong linear dependency relative to specific hemodynamic processes of interest. Thus, it may address questions regarding localization of specific EEG features and assist in screening for multivariate relations between measurement modalities. Importantly, although the present approach does require estimation of temporal lag between neural and hemodynamic events, it does not involve strong assumptions regarding a specific shape of the hemodynamic response function (HRF), which has been discussed as potential limitation in EEG‐fMRI fusion (Huster et al., 2012).

Figure 1.

Integration of EEG and fMRI with cross multivariate correlation coefficients. (1) EEG and fMRI are recorded simultaneously (2) Artifact handling and preprocessing for EEG and fMRI separately 3. Fusion of EEG and BOLD time series: a) EEG feature extraction b) EEG‐derived feature predictors are selected and grouped into regions with differential correlation between EEG and BOLD. c) Cross multiple correlation of the two modalities with xMCC. 4. Method check and statistical inference: a) Determining time lags between EEG and BOLD. b) Quantifying the contribution of EEG features as proportional reduction of error in BOLD prediction; c) Cross multivariate correlation maps are thresholded based on a permutation test. [Color figure can be viewed at http://wileyonlinelibrary.com]

Linear relation (correlation) is arguably one of the most fundamental concepts in statistics (Mari & Kotz, 2001), and variants of correlation analyses are at the core of most analytic techniques in neuroimaging and electrophysiology (Pourahmadi & Noorbaloochi, 2016), including recent trends towards spatial network analysis (Henriksson, Khaligh‐Razavi, Kay, & Kriegeskorte, 2015; Park & Friston, 2013). Many alternative methods for EEG‐BOLD fusion exist, and the present paper cannot address all of these methods. For example, information theoretic approaches (Ostwald, Porcaro, & Bagshaw, 2010; Ostwald, Porcaro, & Bagshaw, 2011) have been proposed, which apply information criteria such as mutual information to quantify the association of multimodal signals. Although mutual information is computed from the probability distribution of the signal, which encompasses correlations at any order and captures nonlinear dependencies as well, it is difficult to estimate with small samples and quite sensitive to free parameters (the number and size of bins, the upper and lower limit of the bins in each dimension, etc.), especially for high‐dimensional variables (Principe, Xu, & Fisher, 2000; Chen et al., 2013). In our study, we intended to capture the relationship between multiple EEG features and fMRI responses recorded simultaneously, which poses additional challenges for reliably estimating their joint distribution. The present framework at its core combines a segmentation and identification method for EEG features with a multivariate correlation approach, which is robust and capable of capturing event‐related as well as spontaneous covariation between electrophysiological and hemodynamic time series. Given its ability to address these issues with a mathematically straightforward approach, the present framework may represent a valuable first step towards identifying symmetrical BOLD‐EEG dependencies, which can be followed up by means of more complex fusion methods (see Abbott, 2016, for a review).

To introduce and validate this approach, we use data from an experiment in which EEG and fMRI were recorded simultaneously while participants viewed periodically (10 Hz) phase‐reversing Gabor patches (sine‐wave gratings), evoking steady‐state visual potentials (ssVEPs). The ssVEP is an oscillatory response of the visual cortex elicited by luminance or contrast‐modulated stimuli, which equals that of the driving stimulus (Regan, 1989; Spekreijse, Dagnelie, Maier, & Regan, 1985). Because ssVEPs are defined as activity in a single, known, bin of the EEG spectrum, they typically possess high signal‐to‐noise ratios and can be reliably quantified at the level of individual trials (Keil et al., 2008). The ssVEP technique thus represents a robust and reliable method for non‐invasively isolating population‐level neuronal responses at low levels of the traditional visual hierarchy, very well suited for cross‐validation of EEG‐fMRI analyses, in which it has been previously used (Sammer et al., 2005). In addition to introducing the xMCC framework, we use concurrent recordings of ssVEPs and BOLD signals to identify brain regions in which BOLD co‐fluctuates with the amplitude of the visuo‐cortical popultion activity indexed by ssVEPs. Previous work with ssVEPs has observed task‐driven (Muller et al., 2006; Wang, Clementz, & Keil, 2007) as well as spontaneous fluctuations (Keil et al., 2008; Moratti & Keil, 2009) in this signal, which covary with performance in cognitive tasks (Andersen, Hillyard, & Muller, 2008) and physiological arousal (Keil, Moratti, Sabatinelli, Bradley, & Lang, 2005). One hypothesis to account for these fluctuations in visuo‐cortical response amplitude is that reentrant modulatory signals act to amplify visuo‐cortical gain in situations that require selective attention or are associated with heightened arousal, or vigilance (Desimone & Duncan, 1995; Bradley et al., 2003). Fronto‐parietal as well as anterior temporal and midbrain structures have been proposed as potential sources of these modulatory signals (Hamker, 2005; Keil et al., 2009; Pessoa & Adolphs, 2010). Testing the reentrant hypothesis and identifying sources of modulatory signals has however been difficult with EEG‐alone or BOLD‐alone techniques. The present study examines the potential of combined EEG‐fMRI recordings for addressing this question while introducing the individual algorithms that make up the framework proposed. Using different features of the time‐varying ssVEP, we present algorithms for identifying EEG predictors and for quantifying correspondence between specific BOLD signals and the EEG predictor. We then compare the results of this EEG‐informed fMRI analysis with fMRI‐alone analysis and quantify the performance of the xMCC approach for complementing BOLD with rich dynamics inherent in concurrently recorded EEG. We also provide initial comparisons with alternative methods used for EEG‐fMRI analysis.

2. MATERIALS AND METHODS

2.1. Participants

Participants were 11 (5 female; age: mean = 21.5 SD = 3.2) undergraduate and graduate students who, after giving informed consent, participated on a volunteer basis or received course credit in the General Psychology course taught at the University of Florida. This sample size was used to parallel previous studies quantifying EEG‐BOLD covariation across time, without specific consideration of different experimental conditions (Ben‐Simon, Podlipsky, Arieli, Zhdanov, & Hendler, 2008). It was also chosen to facilitate reports of individual parameters obtained for each participant (see results). All participants were screened for metallic implants, claustrophobia, and history of seizure episodes. Female participants self‐administered a pregnancy test prior to participation.

2.2. Stimuli

Stimuli consisted of sinusoidal gratings multiplied with a Gaussian envelope (i.e., Gabor patches) oriented at either 15 ° or 345 ° relative to the vertical meridian, which reversed their phase every 100ms to evoke a ssVEP. Consistent with previous studies of phase‐reversal ssVEP (Keil, Miskovic, Gray, & Martinovic, 2013, see Norcia et al. [2015] for a review), we analyzed the second harmonic response (i.e., 10Hz). Gabor patches had a maximum Michelson contrast of 95% (maximum = 110 cd/m²; minimum = 2.1 cd/m²) and a spatial frequency of 0.45 cycles per degree. Gratings were presented at a horizontal visual angle of 15.5 ° respectively, on a MR‐compatible monitor placed outside the scanner bore, which participants viewed via a mirror placed on the MR head‐coil positioned 8.5 cm from eyes. All visual stimuli were presented on a black background (1.2 cd/m²).

The data include 40 total trials per participant, each trial was being presented for 5100 ms. An inter‐trial interval (ITI) consisted of an initial gray cross (37.5 cd/m²; 1 ° of visual angle) presented in the middle of the screen for a random duration between 0 – 8 s followed by a white cross (149.0 cd/m²) for a duration of 3 s, immediately preceding trial onset with Gabor patch presentation. Each participant was instructed to remain still while in the scanner and to maintain fixation on the center of the screen.

2.3. Apparatus and data collection

EEG data were recorded on a 32‐channel MR compatible system (Brain Products). This system consisted of 31 Ag/AgCl electrodes placed on the head according to the 10‐20 system and one electrode placed on the upper back to record heart rate, for addressing cardioballistic artifacts. The reference was positioned at FCz, the ground electrode was placed 1cm anterior to Oz. Impedances were reduced to below 20 kΩ for all scalp electrodes and below 50 kΩ for the cardio electrode, as suggested by the Brain Products manual. EEG data were recorded online at 5 kHz and digitized to 16‐bit while the digitized data is transferred via a fiber‐optic cable to the computer. The system was synchronized to the internal clock of the scanner and event markers were added for further signal processing.

MRI data were collected with a 3T Philips Achieva scanner, an Avotec Silent Scan headphone system was used to diminish gradient noise. Data were acquired during gradient‐echo echo‐planar imaging sequence (echo time [TE], 30 ms; repetition time [TR], 1.98 s; flip angle, 80°; slice number, 36; field of view, 224 mm; voxel size, 3.5 × 3.5 × 3.5mm³; matrix size 64 × 64). The first four functional scans were discarded to allow for scanner stabilization. Slices were acquired in ascending order, oriented parallel to the plane connecting the anterior and posterior commissure during an 1850 ms interval with 130 ms between each TR, during which no images were collected and allowed visual inspection of the EEG data during recording when the MR gradient artifact is absent. A T1‐weighted high‐resolution structural image was obtained after completion of all functional scans.

2.4. Artifacts handling and preprocessing

Raw EEG data were preprocessed using standard functions in Brain Vision Analyzer 2.0 (Brain Products) to remove gradient artifacts and pulse artifacts, band‐pass filtered to 0.5 to 30Hz, and subsequently downsampled to 250Hz. A semiautomatic ICA‐based procedure as implemented in EEGLAB (Bell & Sejnowski, 1995; Debener, Ullsperger, Siegel, & Engel, 2006) was used to remove non‐cerebral components (i.e., eye movements and residual BCG artifacts). These components were identified based on their topography and time course. A maximum of one component was removed for each type of artifact (residual cardioballistic artifacts, horizontal eye movements, blinks, vertical eye movements). Finally, the data were re‐referenced to the common average to remove global noise.

Preprocessing of BOLD fMRI data was completed using SPM12. We followed the standard preprocessing routines suggested by SPM: timing differences were compensated by slice timing correction. Head movements were estimated by realigning each scan to match one representative scan with rigid transformation. Images were normalized and registered to the Montreal Neurological Institute (MNI) space as a standard in SPM during which functional volume images were resampled to a spatial resolution of 3 × 3 × 3 mm³. Images were smoothed using a Gaussian kernel with a full‐width at half‐maximum of 6 mm. Low‐frequency temporal drifts were removed from the BOLD data using a 1/128 Hz high‐pass filter.

2.5. EEG‐BOLD fusion analysis

The present paper introduces a framework for EEG‐fMRI analysis, which relates EEG features (e.g., band power at given frequency, time‐varying coherency, etc.) selected by the user, in the context of the conceptual and methodological goals of the study, to concurrently recorded BOLD signals. After identifying such EEG‐based features (Panel 3a in Figure 1), the framework proposed here has two core procedures: cross multivariate correlation analysis based on the cross multivariate correlation coefficient (xMCC; Panel 3b in Figure 1) and a graph‐based electrode selection and grouping procedure for reducing the spatial dimensions of the EEG data (Panel 3c in Figure 1).

2.5.1. EEG features

In the present study, we selected three descriptors (features) of the scalp‐recorded ssVEP as candidate predictors of the BOLD signal. The ssVEP is an oscillatory EEG response, quantified in the frequency or time‐frequency domain, at a specific known frequency. Deviating from the widely used algorithms for EEG‐informed fMRI analysis (see Debener et al., 2006; Liu, Huang, McGinnis‐Deweese, Keil, & Ding, 2012b), in which EEG features are typically used at the trial level, the present framework estimates one value of the desired EEG feature per sensor (or sensor pair), for each TR of the BOLD signal (here: 1980ms, or 495 EEG sample points after downsampling). As depicted in Figure 2, three different indices of oscillatory brain activity were extracted: (1) the ssVEP amplitude (Mijovi'c et al., 2008), (2) the phase locking index (PLI; Tallon‐Baudry, Bertrand, Peronnet, & Pernier, 1998), and (3) the inter‐site phase locking index (iPLI; Lachaux, Rodriguez, Martinerie, & Varela, 1999; McTeague, Gruss, & Keil, 2015; Moratti, Keil, & Miller, 2006).

Figure 2.

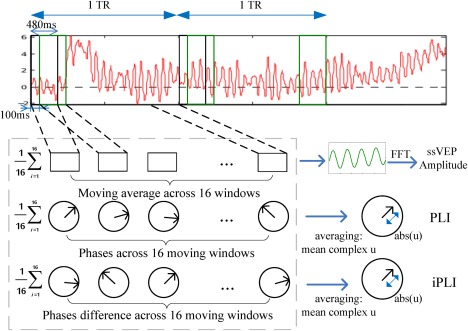
Illustration of the three different feature types extracted from ssVEPs in the present study: ssVEP amplitude, PLI and iPLI. For each method, a feature descriptor was extracted, representing that feature during the duration of one fMRI scan. The resulting feature vectors then possess the same temporal resolution as the BOLD time series. [Color figure can be viewed at http://wileyonlinelibrary.com]

2.5.2. Cross multiple correlation analysis

The xMCC is an extension of the multivariate correlation coefficient (MCC; Wang & Zheng, 2014), with additional steps similar in nature to the standard cross‐correlation analysis (xCA; Wei, 1989). It measures the correlation between EEG‐derived features and fMRI‐BOLD as a function of time lag in the BOLD signal, thus quantifying the spatial‐temporal relation between neuro‐electric activity (EEG) and subsequent metabolic (BOLD) events. Extending the traditional multiple correlation coefficient (Johnson et al., 1992), the xMCC and its counterpart, the cross multivariate uncorrelation coefficient (xMUC), are symmetrical measures, both of which allow quantification of the linear dependency (or independency) of all included variables. Both xMCC and xMUC are bounded within the range (0, 1), and their squared sum is equal to one. xMCC equals 1 (or equivalently, xMUC equals 0) if—and only if—these variables are linearly dependent, and equals 0 (xMUC equals 1) if—and only if—these variables are perpendicular to each other. Mathematical details are given in Appendix B. In the present framework, we use MUC for identifying and grouping the EEG predictors, xMUC for predictors selection, and xMCC for the quantification of BOLD‐EEG covariation. A short mathematical description is given here:

Suppose we select k feature vectors $\left\{{\mathbf{a}}_1,{\mathbf{a}}_2\dots {\mathbf{a}}_k\right\}$ from all EEG features (e.g., frequency bands, time segments, sensors) to approximate the $l^{th}$ fMRI response ${\mathbf{b}}_l$ with linear combination ${\stackrel{⁁}{\mathbf{b}}}_l={\mathrm{\beta }}_1{\mathbf{a}}_1+{\mathrm{\beta }}_2{\mathbf{a}}_2+\cdots +{\mathrm{\beta }}_k{\mathbf{a}}_k+{\mathrm{\beta }}_0\mathbf{1}$, where 1 is the vector whose entries are all ones, ${\mathrm{\beta }}_i$ are the coefficients of the linear combination. The predictability in this equation reflects the proportion of the variance in the BOLD signal that is linearly predicted from the EEG‐derived features. Let ${\mathrm{\omega }}_{{\mathbf{a}}_1{\mathbf{a}}_2\cdots {\mathbf{a}}_k{\mathbf{b}}_l}\left(\mathrm{\tau }\right)$ be the cross multivariate uncorrelation coefficients (xMUC) among multiple EEG feature vectors ${\mathbf{a}}_1,{\mathbf{a}}_2\cdots {\mathbf{a}}_k$ and the target ${\mathbf{b}}_l$, which $\mathrm{\tau }$ controls the temporal shift between the EEG‐derived features and the BOLD response, ${\mathrm{\omega }}_{{\mathbf{a}}_1{\mathbf{a}}_2\cdots {\mathbf{a}}_k}$ be the internal MUC of EEG feature vectors. The mean squared error (MSE) between ${\stackrel{⁁}{\mathbf{b}}}_l$ and ${\mathbf{b}}_l$ can then be computed by the compact equation:

$$MSE\left({\stackrel{⁁}{\mathbf{b}}}_l,{\mathbf{b}}_l\right)={\mathrm{\sigma }}_{{\mathbf{b}}_l}^2{\mathrm{\omega }}_{{\stackrel{⁁}{\mathbf{b}}}_l,{\mathbf{b}}_l}^2={\mathrm{\sigma }}_{{\mathbf{b}}_l}^2\frac{{\mathrm{\omega }}_{{\mathbf{a}}_1{\mathbf{a}}_2\cdots {\mathbf{a}}_k{\mathbf{b}}_l}^2\left(\mathrm{\tau }\right)}{{\mathrm{\omega }}_{{\mathbf{a}}_1{\mathbf{a}}_2\cdots {\mathbf{a}}_k}^2}$$ (3)

Thus minimizing the mean squared error (MSE) between ${\stackrel{⁁}{\mathbf{b}}}_l$ and ${\mathbf{b}}_l$ is equivalent to minimizing ${\mathrm{\omega }}_{{\stackrel{⁁}{\mathbf{b}}}_l,{\mathbf{b}}_l}$. The above equation (3) offers a direct guideline for selecting predictors of interest for EEG‐BOLD fusion: The selected vectors (here: predictive EEG features ${\mathbf{a}}_1,{\mathbf{a}}_2\cdots {\mathbf{a}}_k$) ideally possess small internal correlation (among each other) but together possess strong linear relation relative to the target variable (BOLD time series ${\mathbf{b}}_l$). In Appendix C, we show that the above criterion is equivalent to maximizing the multiple correlation coefficient (Johnson et al., 1992), the normalized xMCC is defined accordingly.

2.5.3. Identifying and grouping of EEG predictors

These considerations directly lead to a pre‐screening algorithm to reduce the searching space: Utilizing a graph‐based segmentation technique (Felzenszwalb & Huttenlocher, 2004; Zahn, 1971, described in 2.7, below) while adapting MUC to measure the intra‐cluster association, EEG channels are grouped into spatial clusters. Channels belonging to the same cluster are highly correlated, and channels in different spatial clusters are weakly correlated. Only one candidate channel in each spatial cluster is selected, which excludes sensor combinations that have strong internal correlation. Selecting single sensors minimizes spatial smearing and signal attenuation that are often associated with averaging across sensors (Thigpen, Kappenman, & Keil, 2017). A brief mathematical description follows.

Let G = (V, E) be an undirected graph. The vertices V are the set of EEG channels to be segmented, and the edges in E link a pair of neighboring vertices. Each edge has a corresponding weight $\mathrm{\omega }\left(v_i,v_j\right)$ that denoted the dissimilarity between EEG channels $v_i$ and $v_j$, which is measured by MUC between the extracted feature vectors. In the present study, the averaged MUCs from the three different types of EEG features (i.e., the ssVEP amplitude, PLI, and iPLI) were then used for predictor (EEG channel) identification. Other studies may consider frequency bands or time points as additional feature dimensions.

The edges in E are first sorted by non‐decreasing order and each vertex is an individual cluster. Iteratively for each edge $\left(v_i,v_j\right)\in E$, a separate versus merge decision is taken between two clusters containing vertices $v_i$ and $v_j$. The merge decision is taken when $\mathrm{\omega }\left(v_i,v_j\right)$ is small compared to the minimal internal difference, which is defined as:

$$MInt\left(C_i,C_j\right)=\min \left(Int\left(C_i\right)+\frac{s}{\left|C_i\right|},Int\left(C_j\right)+\frac{s}{\left|C_j\right|}\right)$$ (4)

|C| is the number of channels that fall in the cluster C, and s is a scale parameter, in that a larger s causes a preference for larger clusters. We use the MUC to measure the internal dissimilarity among the EEG feature vectors within that component.

$$Int\left(C\right)={\mathrm{\omega }}_{\left\{{\mathbf{a}}_k\right\}},a_k\in C,k=1,\cdots ,\left|C\right|$$ (5)

The scale parameter s was chosen to be 0.2 in this study, to balance spatial accuracy/specificity and computational load, leading to 32 channels being grouped into 12 clusters as shown in Figure 3. See below for a discussion of the impact of parameter selection.

Figure 3.

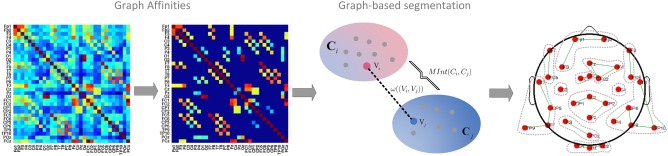
Spatial clustering of EEG sensors. Graph affinities between channels are measured using the average of three different EEG‐derived features across participants. The warmer the color, the bigger the similarity between channels. Non‐neighbors are excluded. The decision to merge sensor(s) into one cluster is made based on the comparison of inter‐cluster associations and intra‐cluster associations, measured by the MUC. Output clusters are separated by gray dashed lines and red dots indicate the location of electrodes. [Color figure can be viewed at http://wileyonlinelibrary.com]

Given the number of predictors and specific BOLD voxels from a target region of interest selected by the user, the xMCC framework then finds the best set of predictors (sensors) in an iterative process. The algorithm starts with the first of the previously identified sensor clusters, then loops through all channel combinations in the Cartesian product of all selected clusters and retains the best predictors that minimize the MSE, which is computed with equation (3). The critical challenge of this step is to avoid over fitting (by including too many predictors) while at the same time retaining the sensitivity of the method. To address this problem, the present method stops adding predictors when including additional predictors does not result in a reduction of prediction error greater than 5 percent (see results).

2.6. Control analyses and statistical inference

2.6.1. Manipulation check: evaluating effects of time lag

In the present framework, the user sets the time lag parameter τ, which controls the temporal shift between the EEG‐derived features and the BOLD response. The correlation between the selected EEG predictors and fMRI BOLD can be quantified by applying xMCC with a specific time lag τ. The selection of this parameter is therefore an important step. In the present report, we compared two approaches for selecting τ, which may be tailored to best address different research questions. (a) As a primary and generally applicable approach, we first examined the sensitivity and specificity of the xMCC method when using a canonical, fixed temporal lag of 4 seconds between EEG features and BOLD, based on widely accepted BOLD latency estimates vis‐à‐vis neural events. (b) Because our example analysis was based on ssVEP signals with known neural sources in visual cortex, we compared and cross‐validated this approach to results obtained with a ROI‐based approach. In this second approach, we use the BOLD time series obtained from specific regions of interest (consisting of 9 voxels at the occipital pole, center MNI: ‐24, ‐94, 5) in visual cortex (the known origin of the ssVEP signal) as a temporal reference. This optional approach enables the empirical selection of the time lag for which the BOLD time series in a given ROI is maximally related to the EEG features of interest. The time lag τ for this ROI‐based approach is then estimated for each individual participant. Note that this optional step strongly biases the results towards the ROI chosen by the user, and thus should be compared against a standard lag, or a lag determined for a control ROI.

2.6.2. Quantifying the unique contribution of EEG to BOLD variability

To quantify the proportion of additional variance explained by the EEG‐derived predictors, compared to fMRI alone, we used a proportional reduction of error (PRE) measure. Specifically, we compare the error made in predicting the BOLD without EEG features with the error made when making predictions that include information from EEG. The PRE metric used here was then calculated as defined below:

$$PRE=\left(E1-E2\right)/E1$$ (6)

E1 stands for MSE of the prediction based on the HRF model (HRF convolved with the event onsets), E2 is the MSE made when the prediction is based on the HRF model and additional information from the EEG features. E1 and E2 can be calculated with equation (3) directly without computing the linear coefficients.

2.6.3. Statistical inference: permutation testing

To assess the statistical significance of EEG‐fMRI correlations, we applied permutation tests, determining the threshold for rejecting the null hypothesis (i.e., no linear relation between EEG and BOLD) based on shuffled data.

In many implementations, fMRI analysis makes use of a canonical hemodynamic response function (HRF), which models the dynamic changes in both blood oxygenation and blood volume following the stimuli events (Buxton et al., 1998). For example, the canonical HRF used in SPM 12 comprises the sum of two gamma functions that exhibit a rising slope peaking around 4–6 sec, followed by an undershoot. To explicitly model the variations in BOLD that are time‐locked to the stimuli in our experiment, a typical convolution and correlation analysis was used: The HRF (taken from SPM 12) was resampled to the EEG sampling frequency (250 Hz) and convolved with the vector containing the event onsets. The output was downsampled to match the time resolution of the empirical fMRI data and appended across all 11 subjects to be correlated with the observed fMRI data at each voxel, using the xMCC measure, which in this case converges with the Pearson correlation coefficient. This control allows (1) comparison of the xMCC framework with a traditional BOLD‐alone analysis, and (2) also allows quantifying the amount of unique variance captured by the EEG‐derived feature time series, above and beyond what is explained by knowing the timing of events and assuming a standard HRF.

For BOLD‐alone analyses, the null hypothesis is that there is no association between the onset of events and the observed BOLD time series. Thus, we assigned random shifts ranging from ‐5 s and +5 s around the onset trigger, then convolved the randomly shifted pseudo‐onsets with the HRF and correlated the result with BOLD, resulting in values under the null‐hypothesis, suitable for a random permutation test. The equivalent approach (shuffling the BOLD data while retaining contiguous temporal segments) was applied to the BOLD‐EEG covariation analyses, in which the null hypothesis is that temporal variation in EEG features is not related to BOLD fluctuations. In all cases, 100,000 Monte‐Carlo simulations with randomly shuffled data were conducted and the 0.99 tail of the resulting distribution of correlation values was used as the 1 percent significance threshold. This approach is suitable to avoid potential biases for data with residual periodicity (i.e., time series with non‐flat autocorrelation functions; Nichols & Holmes, 2001). In addition, because multiple predictors have stronger linear representation ability and lead to higher correlation values in mean, we evaluated the critical thresholds for different combinations of predictors and target areas in separate permutations. Alternatively, appropriate controls for multiple comparisons are needed as discussed extensively elsewhere (Keselman, Burt, & Cribbie, 1987; Nichols & Holmes, 2002). Thresholds for different analyses are shown in Table 1. For all statistical inference analyses, EEG features (for matching electrode dimensions) and fMRI time series (for corresponding voxels) for all subjects were concatenated by appending them along the time dimension. This procedure helps to capture the temporal variance in brain response across subjects and the two modalities (Calhoun et al., 2009; Huster et al., 2012; Mijovi'c et al., 2012).

Table 1.

Significance thresholds of xMCC r values as determined by random permutation tests, at an alpha level of 0.01. N specifies the number of predictors

	N = 1	N = 2	N = 3	N = 4	N = 5	N = 6	N = 7
4S	0.0532	0.0628	0.07	0.0755	0.08	0.0845	0.0885
Occipital	0.053	0.0623	0.0697	0.0752	0.0803	0.0849	0.089

3. RESULTS

3.1. EEG data quality and topography

As expected and as reported previously (Petro et al., 2017), robust ssVEP signals were obtained in the fMRI scanner environment, with the present experimental design. An example time series average from a representative participant and the Grand Mean ssVEP, including their spectral and topographical properties, are shown in Figure 4.

Figure 4.

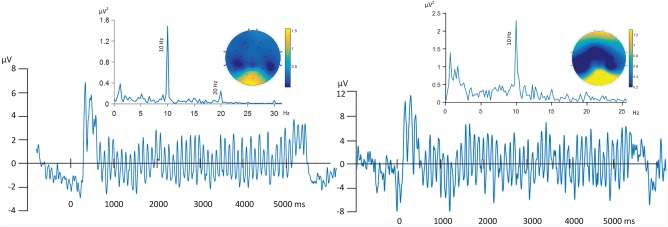
Left panel: Grand Mean ssVEP time series, frequency spectrum, and amplitude topography, averaged across all trials and 11 participants. Right panel: ssVEP time series, frequency spectrum, and amplitude topography shown for a representative single participant. [Color figure can be viewed at http://wileyonlinelibrary.com]

3.2. BOLD‐alone analysis

With a significance level of 0.01 given 100,000 Monte‐Carlo simulations, voxels with correlation coefficients above 0.0932 were considered significantly related to Gabor patch processing. As a result, and as expected, the fMRI‐HRF (BOLD‐alone) analysis identified a range of visual and extra‐visual cortical regions that selectively responded to the phase‐reversing gratings: As shown in Table 3, we identified clusters in extended visual cortical regions, including the bilateral calcarine fissure; inferior (right), middle, and superior occipital gyrus; cuneus; lingual and fusiform gyrus; as well as superior and middle temporal gyrus.

Table 3.

Results for fMRI‐alone analysis. The size of clusters with voxels exceeding a threshold of P < 0.01 is given. MNI Coordinates, normalized xMCC of correlation peaks are reported. R: Right; L: Left

Location	Cluster size (voxels)	xMCC (Max)	MNI Coordinates
L Calcarine	361	0.2801	−15 −94 −4
R Calcarine	379	0.289	15 −91 −4
L Lingual	221	0.2547	−15 −91 −1
R Lingual	297	0.2865	15 −88 −7
L Cuneus	213	0.2118	−6 −94 17
R Cuneus	223	0.2069	18 −73 26
L Superior occipital	46	0.2068	−15 −94 5
R Superior occipital	103	0.2304	21 −94 5
L Middle Temporal	77	0.1226	−60 −40 2
R Middle Temporal	81	0.1201	63 −34 −7
L Middle occipital	100	0.2795	−15 −91 −7
R Middle occipital	58	0.2055	24 −97 5
L Superior temporal	37	0.1147	−57 −25 14
R Superior temporal	86	0.1359	66 −7 8
L Fusiform	70	0.2124	−27 −76 −10
R Fusiform	74	0.1994	24 −82 −10
L Inferior Occipital	25	0.2834	−15 −94 −7
R Inferior Occipital	46	0.2487	21 −91 −4
L Cerebelum 4/5	21	0.1444	−15 −49 −10

3.3. EEG‐BOLD fusion analysis

3.3.1. Selection of predictors

We first used a standard time lag of 4 seconds, consistent with the HRF used in SPM software and in the extant literature (Serences, 2004; Sabatinelli, Lang, Bradley, Costa, & Keil, 2009). In this analysis, the best 1 to 7 predictors were: (POz), (POz,Fz), (POz, Fz, Oz), (POz, Fz, Oz, C4), (POz, Fz, Oz, C4, F8), (POz, Fz, Oz, C4, F8, CP2), (POz, Fz, Oz, C4, F8, CP1, P7), all using the PLI feature. Applying the selection process described above to the features and channels, with time lag defined on the basis of an ROI in occipital cortex, the PLI feature was again selected with the following channels identified as the best 1 to 7 predictors: (Oz), (Oz, POz), (Oz, POz, Fz), (Oz, POz, Fz,CP1), (Oz, POz, Fz, CP1, CP6), (Oz, POz, Fz, CP1, CP6, T7), (Oz, POz, Fz, CP1, CP6, T7, C3). Thus, for the 4‐second approach and for ROI‐based channel selection procedures, PLI time series collected from Oz and POz consistently emerged as major sources of systematic variability.

Table 2 shows the electrode selection results (the PLI feature at the listed electrodes was selected throughout), the maximum xMCC, the SNR for the ssVEP frequency, calculated by dividing the spectral peak at 10 Hz by the mean of neighboring bins in the spectral range between 0.5 and 30 Hz, and the mean ssVEP amplitude, for each participant, and for the group analysis. The table shows that electrode selection was remarkably consistent, and did not covary with SNR and amplitude differences between participants.

Table 2.

Selected EEG features with increasing number of predictors for BOLD in occipital and for each subject. Signal‐to‐noise ratio and power of ssVEP were calculated for each subject and for grand average across subjects. N specifies the number of predictors

	N=1	N = 2	N = 3	N = 4	N = 5	xMCC (N=5)	SNR	ssVEP AMP
S1	(Oz)	(Oz POz)	(Oz POz Pz)	(Oz POz Pz C4 )	(Oz POz Pz C4 TP10)	0.40	10.96	2.62
S2	(Oz)	(Oz POz)	(Oz POz Fz)	(Oz POz Pz C4)	(Oz POz C4 CP2 FC1)	0.31	3.52	0.53
S3	(Oz)	(Oz POz)	(Oz POz T7)	(Oz POz T7 CP2)	(Oz POz T7 CP2 C4)	0.25	17.10	2.27
S4	(Oz)	(Oz POz)	(Oz POz FC6)	(Oz POz FC6 F7)	(Oz POz F7 CP2 C4)	0.26	19.50	3.23
S5	(Oz)	(Oz POz)	(Oz POz Fz)	(Oz POz Fz FC6)	(Oz POz Fz FC6 P7)	0.26	15.12	3.18
S6	(Oz)	(Oz POz)	(Oz POz Fz)	(Oz POz Fz FC6)	(Oz POz Fz FC6 P7)	0.23	2.39	0.38
S7	(Oz)	(Oz POz)	(Oz POz Fz)	(Oz POz Fz FC6)	(Oz POz Fz CP6 F7)	0.22	14.77	2.79
S8	(Oz)	(Oz POz)	(Oz POz CP6)	(Oz POz CP6 F8)	(Oz POz F7 FC6 CP6)	0.21	14.83	2.08
S9	(Oz)	(Oz POz)	(Oz POz Fz)	(Oz POz Fz FC6)	(Oz POz Fz FC6 CP6)	0.15	3.40	0.63
S10	(Oz)	(Oz POz)	(Oz POz Fz)	(Oz POz Fz CP1)	(Oz POz Fz FC6 CP1)	0.14	6.14	1.30
S11	(Oz)	(Oz POz)	(Oz POz Fz)	(Oz POz Fz CP1)	(Oz POz Fz CP6 CP1)	0.14	4.85	0.59
All	(Oz)	(Oz POz)	(Oz POz Fz)	(Oz POz Fz CP1)	(Oz POz Fz CP6 CP1)	0.14	24.92	1.16

Figure 5 illustrates the selection process and its consequences for EEG‐BOLD covariation. Glass view brain volumes are shown with the thresholded xMCC coefficients (normalized) for each voxel and for increasing numbers of EEG features used in the prediction. Larger and more contiguous brain areas appear with increasing numbers of predictors in A1 and B1. The locations of selected EEG channels are marked on the scalp maps A2 and B2. In these figures, stronger coupling with BOLD and earlier selection of a given sensor is shown as increasing size of this sensor's symbol. As expected, the mean square error (MSE) of prediction decreases with the increase of the number of EEG predictors and the gradient of the MSE curve decreases. Similarly, little change was observed in A1 and B1 when the number of predictors was larger than 3 and 4, respectively. Therefore, 3 predictors (POz, Fz, Oz) for the 4s analysis and 4 predictors (Oz, POz, Fz, CP1) for the time lag based on an occipital ROI were selected for the analyses included in this report.¹

Figure 5.

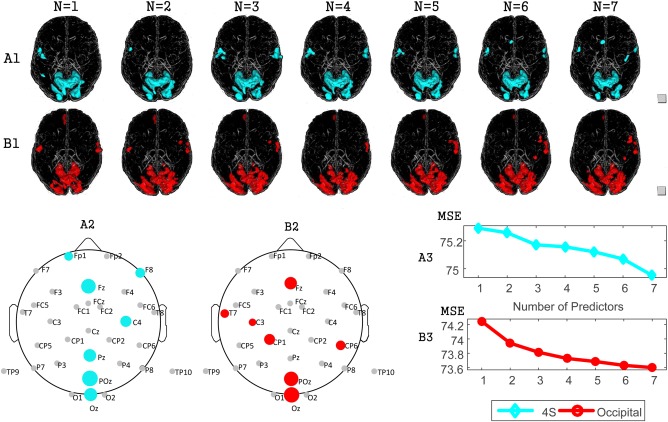
Correlation maps as a function of the number of EEG predictors. N indicates the number of predictors. (A) Analysis with a standard 4s lag, (B) analysis when determining the time lag parameter based on an ROI in occipital cortex. (A1, B1): Glass views from left to right show the co‐varying areas with 1‐7 predictors. (A2, B2): The locations of electrodes selected with standard (A2) and occipital ROI‐based lags (B2). The size of the electrodes reflects the order of selection. (A3, B3): Mean square error (MSE) of the EEG‐BOLD prediction with increasing numbers of predictors, determined for a standard lag (A3) and the ROI‐based lag (B3). [Color figure can be viewed at http://wileyonlinelibrary.com]

3.3.2. EEG‐BOLD results based on a standard time lag

Figure 6 and Table 4 compare the EEG‐BOLD covariation using a standard 4‐second delay with the BOLD‐alone results. Correlations above 0.07 and PRE above 0.49 were considered statistically significant in these analyses. As expected, the spatial extent of areas reflecting significant PRE‐values is smaller than the spatial extent of the areas showing BOLD changes because the PRE‐analysis specifies the unique contribution of EEG predictors above and beyond the timing information inherent in the stick function used for BOLD‐alone analysis. Overlapping areas between the two analyses included the calcarine, cuneus, occipital, and fusiform gyrus. Additional unique areas of EEG‐BOLD covariation were seen in the postcentral cortex, the rolandic operculum, superior temporal gyrus, para‐hippocampal gyrus, and lingual gyrus as well as the gyrus rectus. By contrast, the results for the areas unique to the fMRI‐alone indicated areas in the middle temporal gyrus.

Figure 6.

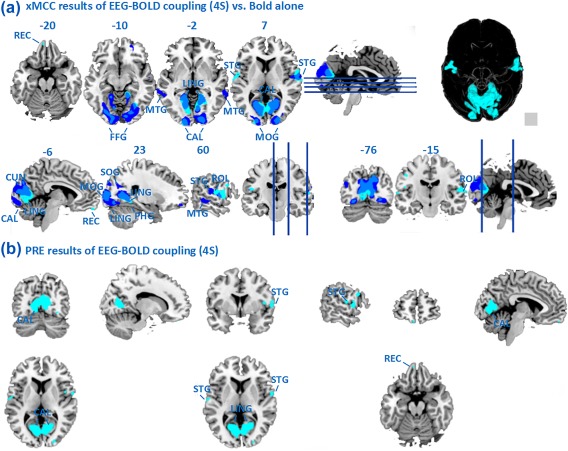
(A) Maps of EEG‐BOLD correlation (PLI in POz, Fz, Oz, cyan) using a standard 4‐second delay, in contrast to the fMRI‐alone analysis (blue); (B) Statistical maps showing PRE (unique improvement of BOLD prediction when using PLI in POz, Fz, Oz with 4 seconds delay in BOLD). Maps are thresholded at P < 0.01. [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 4.

Results for EEG‐BOLD coupling with a standard 4‐second time delay. Clusters exceeding a threshold of P < 0.01 are reported with their cluster sizes. MNI Coordinates, normalized xMCC and PRE of correlation peaks are given. R: Right; L: Left

Location	Cluster size(voxels)	xMCC (Max)	PRE (%)	MNI Coordinates
L Calcarine	263	0.1331	1.0952	‐18 ‐70 5
R Calcarine	271	0.1390	1.1940	12 ‐67 14
L Lingual	250	0.1453	1.4415	‐15 ‐70 2
R Lingual	248	0.1382	1.1734	24 ‐58 2
L Cuneus	65	0.1134	0.8378	0 ‐76 20
R Cuneus	112	0.1155	0.8562	3 ‐76 20
R Superior occipital	33	0.1035	0.6036	21 ‐94 8
L Middle occipital	52	0.1186	0.9054	‐15 ‐97 2
R Middle occipital	30	0.1076	0.559	24 ‐94 8
L Superior temporal	22	0.0902	0.6659	‐57 ‐7 8
R Superior temporal	66	0.0908	0.634	60 ‐1 2
R Fusiform	33	0.1037	0.7473	27 ‐58 ‐1
R ParaHippocampal	8	0.1005	0. 0.818	21 ‐43 ‐4
L Postcentral	43	0.0843	0.619	‐57 ‐7 44
L Rolandic Oper	21	0.0946	0.6871	‐54 ‐4 8
R Rolandic Oper	57	0.0835	0.579	60 ‐13 14
L Rectus	13	0.0755	0.595	‐6 56 ‐19

3.3.3. EEG‐BOLD results based on individually determined time lags

In Figure 7A, the xMCC maps obtained with the selected predictors (PLI in Fz, POz, Oz, CP1) and ROI‐based lags are superimposed with the patterns observed in the BOLD‐alone analysis. Figure 7B shows the PRE maps when using the same (optimal) predictors. Here, correlations above 0.0752 and PRE values above 0.56 were considered statistically significant (permutation controlled) at P < 0.01. Not surprisingly, visual cortical areas such as the calcarine sulcus and cuneus are visible in fMRI‐alone as well as in EEG‐BOLD analyses. High correlation values were seen in large portions of extended visual cortex, including inferior, middle, superior occipital gyrus, as well as fusiform gyrus. Unique areas identified by the EEG‐BOLD analysis include areas in the middle and inferior occipital gyrus, lingual gyrus, fusiform gyrus, gyrus rectus, and cerebellum. Further unique regions included observed in the cerebellum gyrus and rolandic operculum with multiple predictions, differing from the BOLD‐alone analysis.

Figure 7.

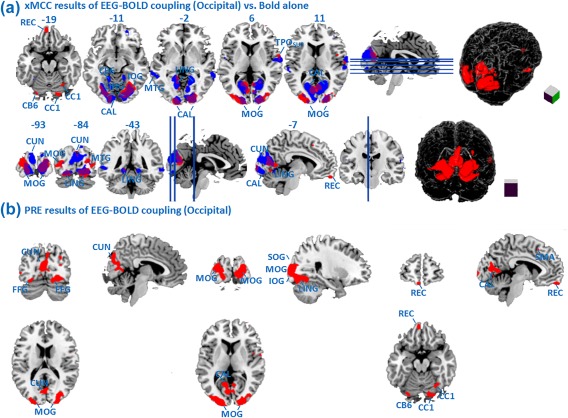
(A) Maps of EEG‐BOLD correlation (xMCC) with selected predictors (Oz, POz, Fz, CP1, red), with time lag determined for the occipital ROI, in contrast to fMRI‐alone analysis (blue); (B) Maps of the EEG‐BOLD PRE measure with the same predictors (Oz, POz, Fz, CP1, red), and lag determined for the occipital ROI. All maps are thresholded at P < 0.01. [Color figure can be viewed at http://wileyonlinelibrary.com]

3.4. Comparison of xMCC with alternative preprocessing methods

3.4.1. Comparison of xMCC with PCA

Although a complete benchmarking of xMCC against similar methods is outside the scope of the present report, we compared the graph‐based segmentation step for feature selection in the xMCC framework with principal component analysis (PCA).

PCA is an efficient approach for reducing the dimensionality and for capturing endogenous components in electrophysiological time series (Donchin, Ritter, & Mccallum, 1978; Spencer, Dien, & Donchin, 1999). Spatial PCA was conducted on the PLI time series extracted from the ssVEP signal, using the covariance between electrode sites across time to obtain a set of principal components. The first principal component was clearly related to the ssVEP stimulation, as supported by the focal occipital scalp distribution of the factor loadings, as shown in Figure 8B. We then related the time varying factors scores of this first component to the BOLD time series using the standard 4 seconds time delay (Figure 8A). Again, the same type permutation test was applied and regions above the threshold 0.0532 were identified as significant. Comparison of the sensitivity (number of significant voxels) as well as inspection of the locations displaying EEG‐BOLD correspondence showed large areas of overlap with the xMCC analysis. In addition, analysis of non‐overlap between them suggests that PCA is less sensitive to the neurophysiological plausible ventral, occipito‐temporal covariations highlighted by the xMCC analysis. Instead, covariation between this PCA component and BOLD was uniquely seen primarily in parietal areas.

Figure 8.

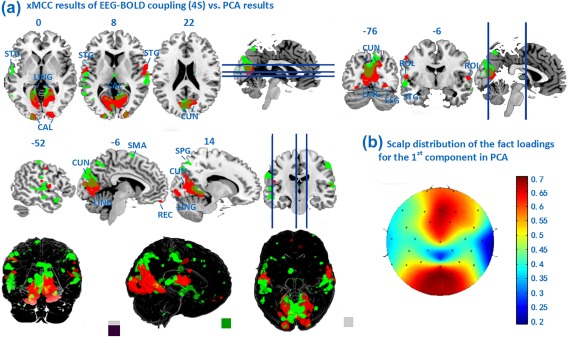
(A) Maps of xMCC EEG‐BOLD correlation (PLI in POz, Fz, Oz,red) with 4 seconds delay, in contrast to the PCA‐based preprocessing described above (green); Maps are thresholded at P < 0.01. (B) Scalp distribution of the factor loadings for the first component in the PCA analysis. [Color figure can be viewed at http://wileyonlinelibrary.com]

Given the broad distribution of the PCA component, and the orthogonality constraint, interpretation of these findings, while feasible, is less straightforward: Finally, the PCA preprocessing step, not being interactively optimized vis‐à‐vis BOLD prediction, appears to lead to a noisier correlation map, compared to the xMCC framework.

3.4.2. Comparison of xMCC clustering with the ssVEP peak set

As shown by the topographic map of the Grand Mean ssVEP in Figure 4, the peak of ssVEP power was located across a set of three channels (O1, Oz, O2), paralleling a large body of work with ssVEPs. We therefore calculated the mean across three occipital EEG channels Oz, O1, and O2 to quantify the ssVEP feature for EEG‐BOLD analysis. Using this spatially constrained (posterior) EEG information resulted in more focal areas showing EEG‐BOLD coupling, all constrained to posterior visual areas. The results (Figure 9) show that the xMCC clustering is more sensitive to topographical variability of the ssVEP signal and may help to identify areas of covariation that are located outside posterior visual cortex. Such areas are of interest, for example, in studies of higher‐order visual cognition and visuo‐motor behavior.

Figure 9.

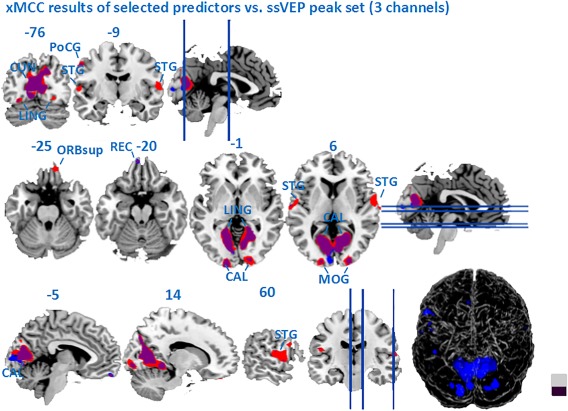
Map of xMCC‐based EEG‐BOLD coupling (computed with the standard 4‐second lag and the optimum predictors), in contrast to the correlation map based on an a‐priori ssVEP peak of three occipital sensors (Oz, O1, O2, blue). [Color figure can be viewed at http://wileyonlinelibrary.com]

4. DISCUSSION

The present study set out to implement and test a new screening framework for EEG‐fMRI fusion. We applied this framework to test the hypothesis that fluctuations in visuo‐cortical response amplitudes are correlated with BOLD in extended visual cortex, but also in anterior structures, thus identifying potential sources of reentrant modulatory signals that act to modulate visuo‐cortical gain during sustained stimulus viewing. The method shares properties with EEG‐informed fMRI analysis algorithms in that it identifies brain regions in which BOLD covaries with specific EEG variables. The current framework intends to maximally preserve information in each processing step, and its two main steps also benefit from the mathematical properties of the xMCC approach: (1) the selection of features and spatial clustering of EEG channels and (2) the quantification of partial error reduction when adding EEG predictors to the BOLD‐alone analysis.

In this initial illustration of the xMCC framework, we used a robust electrophysiological signal, the ssVEP, with known neural origins in lower‐tier visual cortex, to enable predictions regarding the location of brain areas showing covariation of BOLD and EEG‐derived features. Notably, BOLD alone analyses (implemented by using a canonical HRF and the stimulus timing information) in the present data showed strong covariation with the phase‐reversing stimulus in extended visual cortical areas. The ssVEP‐informed BOLD analysis largely pointed to the same regions, with very few lateral temporal cortical areas unique to BOLD‐alone results. In addition to these regions, the electrophysiological predictors reliably pointed to covariation of BOLD and ssVEP features in anterior areas, most notably, the superior temporal gyrus and orbitofrontal regions, including the gyrus rectus. These results largely converge when using a standard 2‐TR (4 second) latency for temporal alignment of BOLD and ssVEP features and when using a target region in visual cortex for defining the temporal lag between EEG and BOLD time series. BOLD‐based studies of large‐scale brain networks identified through inter‐area correlations have suggested that different parts of the visual cortex share reliable, but temporally varying relations with different extra‐visual structures (Mitra, Snyder, Hacker, & Raichle, 2014). In line with these findings, BOLD in a subset of extra‐visual regions (supplementary motor cortex, orbitofrontal cortex) was found to differentially covary with the ssVEP features, when the features were temporally aligned with BOLD in the occipital pole. Thus, while xMCC analysis with a standard lag appeared to be informative and robust, the present demonstration also highlights the advantage of a‐priori seed regions for establishing specific networks characterized by distinct temporal dynamics of BOLD (Sabatinelli et al., 2009). Future work may examine the role of BOLD dynamics vis‐à‐vis electrophysiological markers in greater detail.

In alternative approaches for integrating EEG and fMRI based on parametric task manipulation (Liu et al., 2012b; Debener et al., 2006), a suitable EEG predictor is identified and convolved with a canonical (standard) HRF for each trial. This convolved time series is then orthogonalized relative to event onsets, to avoid inflation of EEG‐fMRI correlation by shared responses to experimental events, and used as parametric modulator in the General Linear Model of BOLD (Eichele et al., 2008). The present approach adds to this widely used method in that it does not require a‐priori reduction of the EEG information into a trial‐wise predictor variable, but uses the empirical time series of both modalities to identify combinations of predictors with maximum joint dependency. This in turn enables quantification the unique contribution of continuous EEG predictors to explain BOLD fluctuations across the original time series, by means of a proportional reduction of error (PRE) measure. Similar to the alternative preprocessing methods discussed above, the current framework identifies EEG features based on certain criteria. As such, preprocessing steps such as ICA or PCA are needed for identifying the pertinent characteristics of the spatio‐temporal EEG matrix that are to be used for EEG‐BOLD fusion. The present xMCC framework uses multivariate correlation both at the stages of feature selection and channel grouping. This approach does not involve additional orthogonality or independency assumptions of the spatial components. It also avoids electrode averaging, known to diminish the internal consistency of EEG‐derived measures in many cases (Thigpen et al., 2017).

Finally, the PRE measure taken in the present framework quantifies the unique contribution of the individual EEG‐based predictors, because it reflects the reduction of prediction error when adding EEG features. In addition, the order in which sensors were selected provides information regarding their respective contribution: The channels or features are selected in a non‐incremental fashion, meaning that prediction based on k features may not include (all of) the features used in the prediction with k−1 features.

As expected, posterior electrode locations contributed most to the prediction of BOLD in this ssVEP paradigm. In addition, frontal sensors Fz and FCz consistently contributed substantial variability towards improving prediction. This consistent observation is in line with the finding that a number of extra‐visual, anterior, brain areas displayed strong linear relation with the ssVEP signal. Conceptually, these findings can be taken to support the hypothesis that fluctuations of neural mass activity during sustained stimulus viewing reflect bidirectional large‐scale communications between visual and anterior cortical areas. As outlined in the introduction, such signals are thought to include reentrant signals originating in orbitofrontal and temporoparietal cortices (Friston & Kiebel, 2009; Chaumon, Kveraga, Barrett, & Bar, 2013). Future work may apply the xMCC approach to data collected under experimental manipulations that lead to clear predictions for involvement of anterior structures in modulating activity in visual cortex.

Another potential concern related to using the ssVEP signal is the applicability of the xMCC framework to other electrophysiological signals. A comparison of individual participants suggests, however, that the graph‐based feature (electrode) selection will not be strongly affected by differences in SNR. Similarly, the xMCC showed no linear correspondence with SNR across participants. Several electrophysiological signals that are of interest to cognitive neuroscientists possess SNRs in the same range as the ssVEP, notably alpha oscillations and late positive ERP complexes. Future work may examine the sensitivity of the xMCC approach to these electrophysiological phenomena, in suitable experimental paradigms. The advantages of the xMCC approach may be particularly beneficial for studies with continuous, “resting” data sets, in which no trial structure is available, and computationally intense, data‐driven approaches are widely used (Ben‐Simon et al., 2008). Such analytical strategies include approaches based on regression‐based classifiers aiming to identify EEG states that predict activity in certain brain regions (Meir‐Hasson, Kinreich, Podlipsky, Hendler, & Intrator, 2014). These computationally demanding advanced approaches could be informed and simplified by first identifying regions of interest through xMCC.

In the present study, prediction of BOLD was consistently more accurate when based on the PLI feature compared to the amplitude or inter‐site phase‐locking features. This finding may reflect the fact that ssVEPs have been shown to be best captured and predicted by their phase consistency across trials (Moratti, Rubio, Campo, Keil, & Ortiz, 2008). Such an advantage of phase‐based measures is true especially for the 10 Hz band, in which the presence of large alpha oscillations may interfere with accurate measurement of concurrent ssVEP amplitude based on single segments (Keil et al., 2008). Future work may explore the sensitivity of EEG‐BOLD analyses to stimulation frequency.

In summary, the present framework combines a set of computationally straightforward methods with few prior assumptions and few free parameters. It is largely data driven and readily interpreted, providing multiple ways for evaluating the statistical contribution of EEG signals to explaining BOLD time series. It also highlights EEG features (sensor locations, frequencies, indices) with maximum predictive value relative to a given BOLD phenomenon, thus informing EEG interpretation and allowing for convergent validation across imaging modalities.

CONFLICT OF INTEREST STATEMENT

None of the authors has any conflicts of interest to disclose.

AUTHOR CONTRIBUTIONS

Conceptualization, Keil, A. and Ji, H.; Methodology, Ji, H., Wang, J.J., Yuan, Z.J. and Keil, A.; Investigation, Ji, H. and Petro, M.N.; Formal Analysis, Petro, M.N.; Writing Ji, H., Keil, A., Chen, B. D.; Supervision, Chen, B. D., Keil, A.; Funding Acquisition, Chen, B. D., Zheng, N. N. and Keil, A. All authors had full access to all the data in the study and take responsibility for the integrity of the data and the accuracy of the data analysis.

APPENDIX A.

For each index, a 480ms window (padded with 20ms of zeros for a total of 500ms) was shifted across each single scan period in steps of 100ms, and the following computations executed for a total of 16 moving windows:

• ssVEP amplitude: Estimates of oscillatory amplitude were obtained by averaging the EEG traces in the moving windows in the time domain. The resulting average was submitted to a Discrete Fourier Transform to get the 10Hz ssVEP amplitude. The robustness of this approach is described in (Keil et al., 2005), with excellent internal consistency of the short‐segment amplitude estimates (Cronbach0s α > 0.85) for trial counts in the range of 15.

• PLI: Different from intrinsic (spontaneous) brain oscillations, the ssVEP is phase‐locked to the periodically modulated stimulus (here: the phase‐reversing Gabor patch) and thus expected to possess stable phase in windows that are aligned to the external stimulus. The standard PLI algorithm (Lachaux et al., 1999) was applied here. Again, DFT was applied for each moving window separately, the complex Fourier coefficients were normalized to map on a unit circle, and then averaged across windows. The modulus of the averaged complex Fourier coefficients then indicates the amount of phase stability across the 16 sliding windows, with a PLI of 1 representing phase identity and 0 random phase.

• iPLI: The iPLI measures the consistency/stability of the phase difference between channels and is often used as an estimate of connectivity between recording sites. In the present ssVEP study, we did not compute all pairwise iPLI values but focused on the occipital midline electrode location (Oz) and its synchrony relative to all other sensors: For each sliding window, we again obtained the normalized complex phase dividing the Fourier coefficients at the ssVEP frequency by its power. The difference of these complex values between each sensor location and reference site Oz was then normalized and again averaged across segments in a scan, resulting in a measure of inter‐site phase synchrony between the occipital pole and the remainder of the recording array. The value of this descriptor is also bounded between 0 and 1.

APPENDIX B.

For EEG feature vectors ${\left\{{\mathbf{a}}_i\right\}}_{i=1,\dots ,m},{\mathbf{a}}_i\in {\Re }^n$ where ${\mathbf{a}}_i$ denotes the feature vector for the ith EEG channel, with m equal to the number of EEG channels, and the sequences of BOLD response ${\left\{{\mathbf{b}}_l\right\}}_{l=1,\dots ,L},{\mathbf{b}}_l\in {\Re }^n$, where ${\mathbf{b}}_l$ denotes the response sequence from the lth voxel, with L the number of voxels, and n equal to the number of fMRI scans. Let $r_{{\mathbf{a}}_i\hspace{0.17em}{\mathbf{a}}_j}$ be the Pearson's correlation coefficient between ${\mathbf{a}}_i$ and ${\mathbf{a}}_j$, $i,j\in \left\{1,2,\cdots ,m\right\}$, and $r_{{\mathbf{a}}_i\hspace{0.17em}{\mathbf{a}}_j}\left(\mathrm{\tau }\right)$ be the correlation coefficient between ${\mathbf{a}}_i$ and $a_j$, $1\le t\le n$, where ${\mathbf{b}}_l\left(t-\mathrm{\tau }\right)$ denotes ${\mathbf{b}}_l$ with time lag τ. We define the following cross correlation matrix ${\mathbf{R}}_{\mathrm{\tau }l}$:

$${\mathbf{R}}_{\mathrm{\tau }l}=\left[\begin{array}{ccccc}1& r_{{\mathbf{a}}_1\hspace{0.17em}{\mathbf{a}}_2}& \cdots & r_{{\mathbf{a}}_1\hspace{0.17em}{\mathbf{a}}_m}& r_{{\mathbf{a}}_1\hspace{0.17em}{\mathbf{b}}_l}\left(\mathrm{\tau }\right)\\ r_{{\mathbf{a}}_2\hspace{0.17em}{\mathbf{a}}_1}& 1& \cdots & r_{{\mathbf{a}}_2\hspace{0.17em}{\mathbf{a}}_m}& r_{{\mathbf{a}}_2\hspace{0.17em}{\mathbf{b}}_l}\left(\mathrm{\tau }\right)\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ r_{{\mathbf{a}}_m\hspace{0.17em}{\mathbf{a}}_1}& r_{{\mathbf{a}}_m\hspace{0.17em}{\mathbf{a}}_1}& \cdots & 1& r_{{\mathbf{a}}_m\hspace{0.17em}{\mathbf{b}}_l}\left(\mathrm{\tau }\right)\\ r_{{\mathbf{b}}_l\hspace{0.17em}{\mathbf{a}}_1}\left(\mathrm{\tau }\right)& r_{{\mathbf{b}}_l\hspace{0.17em}{\mathbf{a}}_2}\left(\mathrm{\tau }\right)& \cdots & r_{{\mathbf{b}}_l\hspace{0.17em}{\mathbf{a}}_{\mathrm{m}}}\left(\mathrm{\tau }\right)& 1\end{array}\right]$$

The cross multivariate correlation coefficient (xMCC) r, and the cross multivariate uncorrelation coefficients (xMUC) $\mathrm{\omega }$ among multiple EEG feature vectors ${\mathbf{a}}_1,{\mathbf{a}}_2\cdots {\mathbf{a}}_m$ and the l^th fMRI response ${\mathbf{b}}_l$ are then defined as

$$\begin{array}{l}{r}_{{\mathbf{a}}_1\hspace{0.17em}{\mathbf{a}}_2\cdots {\mathbf{a}}_m{\mathbf{b}}_l}\left(\mathrm{\tau }\right)=\sqrt{1-\det \left({\mathbf{R}}_{\mathrm{\tau }l}\right)}\\ {\mathrm{\omega }}_{{\mathbf{a}}_1\hspace{0.17em}{\mathbf{a}}_2\cdots {\mathbf{a}}_m{\mathbf{b}}_l}\left(\mathrm{\tau }\right)=\sqrt{\det \left({\mathbf{R}}_{\mathrm{\tau }l}\right)}\end{array}$$ (B1)

respectively, where $\det \left({\mathbf{R}}_{\mathrm{\tau }l}\right)$ is the determinant of ${\mathbf{R}}_{\mathrm{\tau }l}$.

APPENDIX C.

The square of the coefficient of multiple correlation can be computed using the vector $\mathbf{c}={\left(r_{{\mathbf{a}}_1\mathbf{b}}\left(\mathrm{\tau }\right),r_{{\mathbf{a}}_2\mathbf{b}}\left(\mathrm{\tau }\right),\cdots r_{{\mathbf{a}}_k\mathbf{b}}\left(\mathrm{\tau }\right)\right)}^T$ of correlations $r_{{\mathbf{a}}_i\hspace{0.17em}\mathbf{b}}\left(\mathrm{\tau }\right)$ between the predictor variables ${\mathbf{a}}_i$, i = 1,2,•••, k (independent variable) and the target variable $\mathbf{b}$ (dependent variable), and the correlation matrix ${\mathbf{R}}_{xx}$ of inter correlations between predictor variables. It is given by:

$${\mathbf{R}}^2={\mathbf{c}}^T{\mathbf{R}}_{xx}^{-1}\mathbf{c}$$ (C1)

where ${\mathbf{c}}^T$ is the transpose of $\mathbf{c}$, and ${\mathbf{R}}_{xx}^{-1}$ is the inverse of the matrix.

$${\mathbf{R}}_{xx}=\left[\begin{array}{cccc}1& r_{{\mathbf{a}}_1\hspace{0.17em}{\mathbf{a}}_2}& \cdots & r_{{\mathbf{a}}_1\hspace{0.17em}{\mathbf{a}}_k}\\ r_{{\mathbf{a}}_2\hspace{0.17em}{\mathbf{a}}_1}& 1& \cdots & r_{{\mathbf{a}}_2\hspace{0.17em}{\mathbf{a}}_k}\\ ⋮& ⋮& \ddots & ⋮\\ r_{{\mathbf{a}}_k\hspace{0.17em}{\mathbf{a}}_1}& r_{{\mathbf{a}}_k\hspace{0.17em}{\mathbf{a}}_2}& \cdots & 1\end{array}\right]$$ (C3)

We then form a block matrix

$${\displaystyle \sum =\left[\begin{array}{cc}{\mathbf{R}}_{xx}& \mathbf{c}\\ {\mathbf{c}}^T& 1\end{array}\right]}$$ (C3)

According to the rule of determinant of block matrix (Golub and Van Loan, 1986), the criteria in the right side of equation (3) can be written as

$$\begin{array}{l}{\mathrm{\omega }}_{\stackrel{⁁}{\mathbf{b}}\mathbf{b}}=\frac{{\mathrm{\omega }}_{{\mathbf{a}}_1\hspace{0.17em}{\mathbf{a}}_2\cdots {\mathbf{a}}_k\mathbf{b}}}{{\mathrm{\omega }}_{{\mathbf{a}}_1\hspace{0.17em}{\mathbf{a}}_2\cdots {\mathbf{a}}_k}}=\sqrt{\frac{|{\displaystyle {\sum }_{\mathrm{\tau }}}|}{\left|{\mathbf{R}}_{xx}\right|}}=\sqrt{\frac{\left|{\mathbf{R}}_{xx}\right|\left|1-{\mathbf{c}}^T{\mathbf{R}}_{xx}^{-1}\mathbf{c}\right|}{\left|{\mathbf{R}}_{xx}\right|}}\\ =\sqrt{\left|1-{\mathbf{c}}^T{\mathbf{R}}_{xx}^{-1}\mathbf{c}\right|}=\sqrt{1-{\mathbf{c}}^T{\mathbf{R}}_{xx}^{-1}\mathbf{c}}\end{array}$$ (C4)

For $1-{\mathbf{c}}^T{\mathbf{R}}_{xx}^{-1}\mathbf{c}$ is a scalar.

$$r_{\stackrel{⁁}{\mathbf{b}},\mathbf{b}}^2=1-{\mathrm{\omega }}_{\stackrel{⁁}{\mathbf{b}},\mathbf{b}}^2={\mathbf{c}}^T{\mathbf{R}}_{xx}^{-1}\mathbf{c}$$ (C5)

Therefore, minimizing ${\mathrm{\omega }}_{\stackrel{⁁}{\mathbf{b}},\mathbf{b}}$ is equivalent to maximizing the multiple correlation $\mathbf{R}$. Furthermore, xMCC of $\left\{{\mathbf{a}}_1,{\mathbf{a}}_2,\cdots {\mathbf{a}}_k,\mathbf{b}\right\}$ is between the MCC of $\left\{{\mathbf{a}}_1,{\mathbf{a}}_2,\cdots {\mathbf{a}}_k\right\}$ and 1 (Wang and Zheng, 2014), the normalized xMCC can be defined by implementing a unity‐based normalization.

$$r_{{\mathbf{a}}_1,{\mathbf{a}}_2\cdots {\mathbf{a}}_k\mathbf{b}}^{\prime }\left(\mathrm{\tau }\right)=\sqrt{1-\frac{\left|{\displaystyle {\sum }_{\mathrm{\tau }}}\right|}{\left|{\mathbf{R}}_{xx}\right|}}$$ (C6)

Ji H, Petro NM, Chen B, et al. Cross multivariate correlation coefficients as screening tool for analysis of concurrent EEG‐fMRI recordings. J Neuro Res. 2018;96:1159–1175. https://doi.org/10.1002/jnr.24217