Skip to main content
PMC home page
Royal Society of Chemistry logoLink to Royal Society of Chemistry
. 2018 May 29;10(23):11021–11027. doi: 10.1039/c8nr02279h

Bulk-terminated or reconstructed Fe3O4(001) surface: water makes a difference†

Hongsheng Liu a, Cristiana Di Valentin a,✉
PMCID: PMC6001776  PMID: 29868664

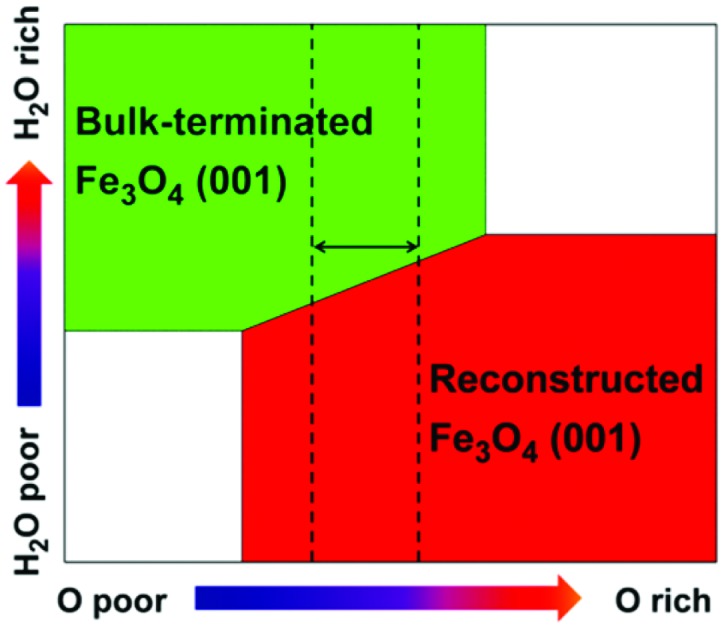
graphic file with name c8nr02279h-ga.jpgThe presence of water may invert the relative stability of the bulk-terminated and reconstructed Fe3O4(001) surface.

Abstract

Surfaces and their interaction with water play an important role in most of materials’ applications. Magnetite has attracted continued interest in the fields of catalysis, spintronic devices, magnetic resonance imaging (MRI) and drug delivery. In this work, water adsorption and its effect on the stability diagram and on the electronic structure of the Fe3O4(001) surface are investigated by hybrid density functional theory calculations combined with an ab initio atomistic thermodynamic approach. We span a wide range of gaseous O2 and vapor H2O partial pressures. At low water pressure, a reconstructed SCV surface model is confirmed to be the most stable model at common working O2 partial pressures. However, at high water coverage, an unexpected stability inversion is observed that makes the hydrated bulk-terminated DBT surface the most favored. These results open up new horizons in Fe3O4 surface chemistry when working in an aqueous environment and are of key importance to develop rational strategies to surface engineering for high performance Fe3O4 nanomaterials.

Introduction

The ubiquity of water in the ambient environment ensures that its interaction with solid surfaces plays a crucial role in most applications. Besides the influence on physical and chemical properties, an overlayer of water was recently proved to change the reconstruction of the technologically relevant TiO2 rutile (011) surface.1 Therefore, the adsorption mechanism of water on metal oxide surfaces is a key aspect to be investigated in order to control and improve processes that take place at the solid/liquid interface.

Magnetite (Fe3O4) is a relevant material in catalysis,2–4 magnetic resonance imaging (MRI), drug delivery5 and spintronic devices.6 At room temperature, magnetite crystallizes in an inverse spinel structure with oxygen anions arranged in a slightly distorted face centered cubic lattice and iron atoms occupying tetrahedral and octahedral interstitial sites. Below 858 K, magnetite is a ferrimagnet, with the cations at octahedral sites coupling antiferromagnetically with the cations at tetrahedral sites.7 At a temperature of about 120 K, bulk Fe3O4 shows an interesting phase transition, called the Verwey transition.8–10 However, whether this is a semiconductor–semiconductor or a semiconductor–metal transition is still under debate.11–30 Very recently, a hybrid functional study showed that, upon symmetry breaking, a clear band gap arises in bulk magnetite above the Verwey temperature.30

The structure and termination of the Fe3O4(001) surface, which is one of the most important low-index facets,31 have also been discussed at length. The stacking sequence in the [001] direction consists of A layers that contain tetrahedral iron (FeTet) and B layers that contain oxygen and octahedral iron (FeOct). Based on the (√2 × √2)R45° reconstruction that appears in experiments,32–37 different atomic structure models33–39 have been proposed for the (001) surface of Fe3O4. An A layer termination, where half of the tetrahedral iron is missing,33–35 and a B layer, with oxygen vacancies or hydroxyl groups,36,37 were proposed in the early stage. Later, based on DFT calculations, R. Pentcheva and co-workers proposed a distorted bulk truncation (DBT) model,38 thermodynamically more stable than the other configurations mentioned above.38,40 However, the Pendry reliability factor (RP) for the low-energy electron diffraction (LEED) investigation was somewhat poor (RP = 0.34)41 and the DBT model could not explain the site preference of Au adatoms deposited on the Fe3O4(001) surface.39,42 In 2014, Bliem et al. proposed a new reconstructed surface model (SCV): a B layer terminated Fe3O4(001) surface with an extra interstitial FeTet atom in the second layer, replacing two FeOct atoms that are removed from the third layer, per the (√2 × √2)R45° unit cell.39 The SCV model agrees well with the surface X-ray diffraction43 and shows a much better agreement with experimental LEED IV (RP = 0.125)39 compared with the DBT model (RP = 0.34).41 In addition, the SCV model shows, at the DFT+U level of theory, a higher thermodynamic stability than DBT over the entire range of oxygen chemical potentials accessible under experimental conditions and can well explain the site preference of Au adatoms when deposited on the Fe3O4(001) surface.39

Regarding water adsorption, several studies have been carried out.44–51 Temperature programmed desorption experiments44 on epitaxially grown Fe3O4(001) thin films on MgO(001) substrates detected three desorption peaks at 320 K, 280 K, and 225 K, which were attributed to different chemisorbed states. Using scanning tunneling microscopy (STM), Parkinson and co-workers observed the dissociative chemisorption of water on the Fe3O4(001) surface at room temperature.45 Combining X-ray photoemission (XPS) and density functional theory (DFT) calculations, Kendelewicz and co-workers proposed that at low water vapor pressure (≤10–4–10–5 Torr) and room temperature, water would not adsorb dissociatively on the Fe3O4(001) surface, except on defect sites.46,47 In contrast, progressive dissociation into surface hydroxyl species was observed at water vapor partial pressures between 10–4 and 10–2 Torr.46,47 At high water coverage, a mixed adsorption mode (dissociated/undissociated water molecules) was suggested by LEED,48 XPS47 and high-resolution electron energy loss spectroscopy (HREELS).49 On the theoretical side, a classical molecular dynamics study, based on empirical potentials, showed that water adsorbs dissociatively on the Fe3O4(001) surface, when modeled by an A layer termination configuration.50 DFT+U calculations on the DBT model indicate that isolated water molecules tend to dissociate at both defect sites and the regular terrace of Fe3O4(001) surfaces and that, at high water coverage, water favors a mixed adsorption mode, where every second molecule is dissociated.48,51 In contrast, the interaction of water on the SCV model39 of the Fe3O4(001) surface, which was experimentally proved to be the most stable reconstruction,39 has not been investigated yet.

In this work, we present a systematic comparative study of water adsorption on both reconstructed (SCV) and bulk-terminated (DBT) surface models, based on accurate hybrid functional calculations and combining them with an ab initio thermodynamic approach. We span a wide range of gaseous O2 and vapor H2O partial pressures to investigate the relative stability of the different surface models. Hybrid density functional theory calculations confirm that at low water pressure, a reconstructed SCV surface model is the most stable model at common working O2 partial pressures, as observed in previous DFT+U studies.39 However, at high water coverage, an unexpected stability inversion is observed that makes the hydrated bulk-terminated DBT surface the most favored. These results open up new horizons in the Fe3O4 surface chemistry when working in an aqueous environment and are of key importance to develop rational strategies to surface engineering for high performance Fe3O4 nanomaterials.

Computational methods

The spin polarized DFT+U calculations were performed using the plane-wave-based Quantum ESPRESSO package.52 The projector augmented wave (PAW) potentials were adopted to describe the electron–ion interactions with Fe (3s, 3p, 3d, 4s) and O (2s, 2p) treated as valence electrons. The exchange and correlation interaction was described by the Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA). To properly deal with the strong correlation effects among Fe 3d electrons, an on-site Coulomb correction with an effective U–J value of 3.5 eV was adopted according to our previous work on bulk magnetite.30 Energy cutoffs of 64 Ryd and 782 Ryd (for kinetic energy and charge density expansion, respectively) were adopted for all calculations. The convergence criterion of 0.026 eV Å–1 for force was used during geometry optimization and the convergence criterion for total energy was set to 10–6 Ryd.

Hybrid functional calculations (HSE0653) were carried out using the CRYSTAL14 package54,55 based on DFT where the Kohn–Sham orbitals are expanded in Gaussian-type orbitals (the all-electron basis sets are H|5-11G*, O|8-411G* and Fe|8-6-411G*, according to the scheme previously used for Fe3O4 (ref. 30)). The convergence criterion of 0.023 eV Å–1 for force was used during geometry optimization and the convergence criterion for total energy was set to 10–6 Hartree for all the calculations.

For the Fe3O4(001) surface, two structural models were considered, DBT and SCV, as shown in Fig. 1. An inversion symmetric slab with 9 B layers and 8 A layers was adopted for both DBT and SCV structures as reported previously.39 A (√2 × √2)R45° supercell for the (001) surface was used for the DBT and SCV models containing 124 (Fe52O72) and 122 (Fe50O72) atoms, respectively. In the z direction a vacuum of more than 12 Å was introduced to avoid the spurious interaction between periodic images. For water adsorption, molecules were put on both sides of the slabs. Three B and two A layers in the middle are kept fixed to the bulk position (see Fig. 1) and the other layers are fully relaxed during geometry optimization. To evaluate the stability of water adsorption on the Fe3O4(001) surface, the adsorption energy (Ead) was calculated as follows:

Ead = (Etotal – Eslab – NH2O × EH2O)/NH2O, 1

where Etotal is the total energy of the whole system (surface slab and adsorbed water), Eslab is the energy of the Fe3O4 surface slab, NH2O is the number of water molecules adsorbed and EH2O is the energy of one isolated water molecule.

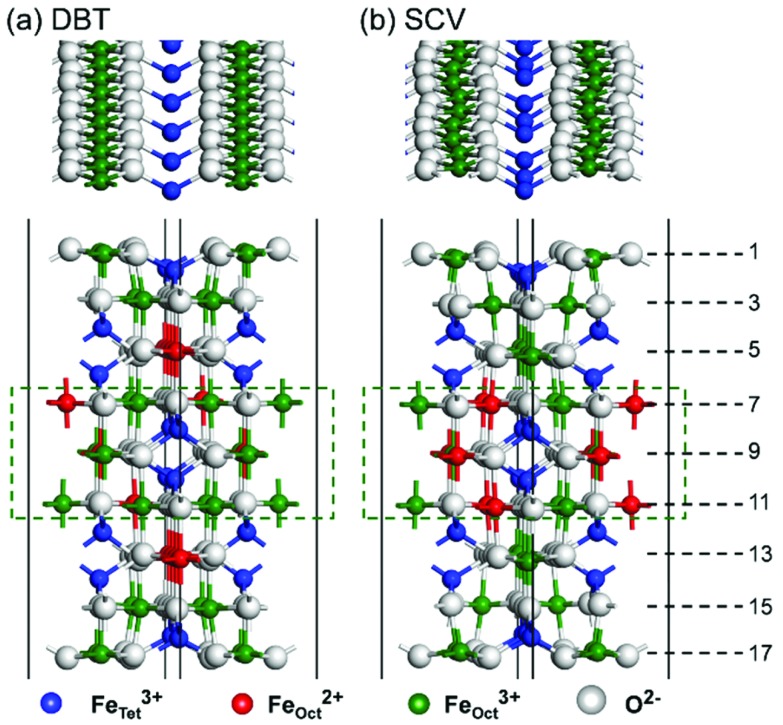
Fig. 1. Top and side views of HSE optimized atomic structures of the (a) DBT and (b) SCV Fe3O4(001) surface models. Layers are numbered on the right. Atomic layers in the dashed rectangles are kept fixed in the bulk positions during atomic relaxation.

Fig. 1

Open in a new tab

To compare the relative stability of different surface models before and after water adsorption, the surface energy γ was calculated as a function of chemical potential of oxygen and water:56

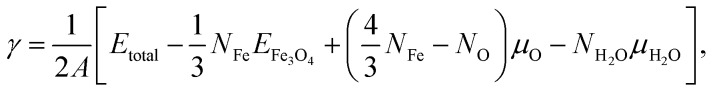graphic file with name c8nr02279h-t1.jpg 2

where A is the surface area of the (√2 × √2)R45° supercell, Etotal is the total energy of the whole system (surface slab and adsorbed water) and EFe3O4 is the total energy of bulk Fe3O4 per formula unit. μO and μH2O are the chemical potential of oxygen and water, respectively. NFe, NO and NH2O are the numbers of Fe atoms, oxygen atoms and H2O molecules, respectively (for clean surface, NH2O = zero).

According to a previous report,29 inclusion of the van der Waals correction (DFT+D2)57 only slightly changes the adsorption energy of water on the Fe3O4(110) surface. We further checked that the water monolayer structure in this work is not affected by the introduction of the D2 correction. Since the variations are within 0.1 Å, no dispersion correction will be presented in the following. Also, we did not consider the spin–orbit coupling in our calculations, since spin–orbit splitting of the 3d band was found to be two orders of magnitude smaller than the crystal field splitting in previous calculations for cubic Fe3O4.58

Results and discussion

Structural and electronic properties of the Fe3O4(001) surface

We first present a comparative analysis of HSE06 vs. PBE+U calculations of the structural and electronic properties of the bare Fe3O4(001) surface using both the bulk-truncated DBT and reconstructed SCV fully relaxed models. These two functionals provide similar geometries, as shown in Fig. 1. For the DBT surface, in contrast with a previous DFT+U report, where, however, only 13 atomic layers were used,38 no undulation along the FeOct rows on the surface (i.e. layers 1 and 17 in Fig. 1) is observed. The undulations in the SCV surface model are very pronounced (see the top view in Fig. 1), in agreement with previous DFT+U calculations.39 For both DBT and SCV surfaces, the distance between the first two layers is largely compressed with respect to the bulk value (0.724 and 0.681 Å vs. 1.048 Å, respectively), while the distance between the second and the third layers is almost unchanged (by about 0.1 Å).

As indicated in Fig. 1a, in the outermost two layers of the DBT model all FeOct are Fe3+, as a consequence of the low Fe : O stoichiometry in these layers. In contrast, all FeOct in layers 5 and 13 (hereafter referred to as “deep surface layers”) are Fe2+. In the layers that are kept fixed during atomic relaxation (from 7 to 11), Fe2+ and Fe3+ ions alternate, as clearly observed in the bulk phase.30 The Fe2+/Fe3+ ion distribution is slightly different in the SCV model, as shown in Fig. 1b. Herein, the Fe : O ratio in the surface layers is even lower due to the Fe vacancies present in the third layer. Consequently, all FeOct in the fully relaxed layers are Fe3+. An equal number of Fe3+ and Fe2+ exists in the fixed layers, exactly as in the bulk phase. Iron cations at tetrahedral sites are always Fe3+, whether in the surface layers or in the pseudo-bulk layers. This charge distribution in the SCV model is in accordance with XPS measurements.39

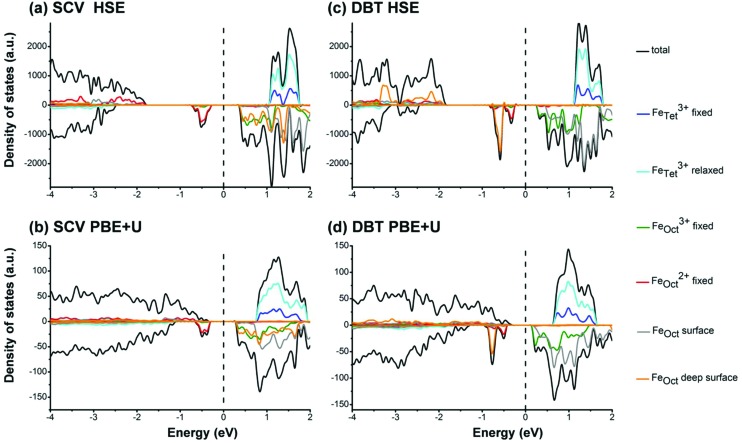
To investigate the electronic properties of the Fe3O4(001) surface, we computed the total density of states and their projection (PDOS) on different Fe d states for SCV and DBT models, as shown in Fig. 2. In the case of SCV, both HSE (Fig. 2a) and PBE+U (Fig. 2b) give a clear band gap (0.69 and 0.61 eV, respectively), which is in net contrast with what was presented in a previous PBE+U study, where low DOS exists at the Fermi level.39 As we observed for the bulk before,30 the band gap is between the t2g states from FeOct2+ and from FeOct3+ in the inner bulk-like layers. The band gap (see gray lines in Fig. 2a and b) decreases from the surface to the bulk and is expected to finally converge to the bulk value (about 0.2 eV (ref. 30)) for an infinite number of atomic layers in the slab model. The charge density plot for the valence band maximum and conduction band minimum states is presented in Fig. S1 in the ESI.†

Fig. 2. Projected density of states (PDOS) on the d states of different Fe ions in the SCV and DBT slab models. (a) and (c) are calculated using HSE; (b) and (d) are calculated using PBE+U. The legend of colors is on the right. The black lines represent the total DOS. The blue and cyan lines represent PDOS on the d states of FeTet3+ in the fixed layers and relaxed layers, respectively. The green and red lines represent PDOS on the d states of FeOct3+ and FeOct2+ in the fixed layers. The gray lines represent PDOS on the d states of FeOct in the surface layers (layer1 + layer3 + layer15 + layer17). The orange lines represent PDOS on the d states of FeOct in the deep surface layers (layer5 + layer13). The Fermi level is scaled to zero as indicated by the dashed black lines.

Fig. 2

Open in a new tab

The DBT structure also shows a semiconductor character, in agreement with previous DFT+U calculations,40,48,59 with a calculated band gap of 0.56 eV (HSE) or 0.60 eV (PBE+U). Similar to the SCV structure, the band gap is between the t2g states from FeOct2+ and FeOct3+ in the inner bulk-like layers (Fig. 2c and d).

The DOS from PBE+U and HSE calculations is slightly different, as far as the position of the valance band is concerned. In the DOS from PBE+U (Fig. 2b), below the Fermi level, the spin-up states show a clear increase starting from –0.5 eV and below. However, in the DOS from HSE06 (Fig. 2a), the spin-up states arise only at about –1.8 eV. Based on experimental photoemission spectroscopic measurements, it was reported that spin-up states arise at around –0.5 eV and show a sharp increase at about –1 eV,14,16 in closer agreement with PBE+U DOS. On the other hand, both PBE+U and HSE present a similar prominent and crucial feature in the DOS, i.e. the presence of a peak in the spin-down states centered at –0.5 eV, which has also been observed in many experimental studies.14–18,21 Moreover, both HSE and PBE+U give a small band gap around the Fermi level.30 Therefore, even in the specific case of Fe3O4, HSE06 is a good alternative to PBE+U,30 as it is generally recognized for other strongly correlated systems.60–63 The differences between PBE+U and HSE calculations are due to the different approaches used to correct the self-interaction error (SIE). In PBE+U a U term (an additional orbital-dependent interaction) is included in the GGA calculation, whereas in the hybrid functional HSE06 a 25% of exact exchange is introduced in the exchange functional. This portion being free from any SIE reduces the overall SIE in the calculation.

Water adsorption on the Fe3O4(001) surface

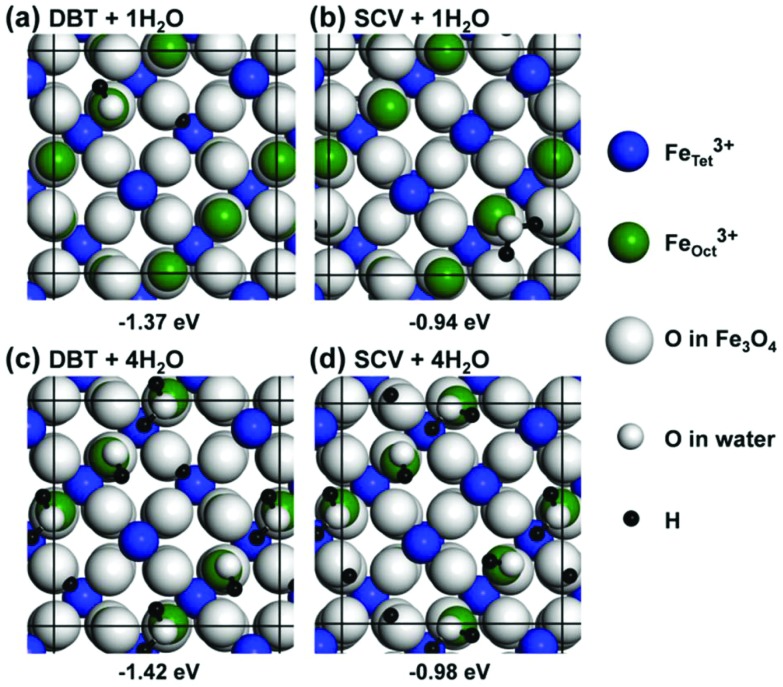
Water adsorption on the Fe3O4(001) surface at different coverages, from one water molecule up to four water molecules on a (√2 × √2)R45° unit cell, has been investigated using the HSE functional. An isolated water molecule prefers to adsorb molecularly on the top of one FeOct of the reconstructed SCV surface (Fig. 3b). The dissociated adsorption mode is unfavored by +0.26 eV (Fig. S2d in the ESI†). This agrees well with the experimental observation that at very low H2O vapor pressure, water would not adsorb dissociatively on the Fe3O4(001) surface, except on defect sites.46,47 In sharp contrast, the dissociation of one isolated water molecule is preferred on the bulk-truncated DBT surface (Fig. 3a), resulting in a hydroxyl bonded to a surface FeOct ion and H transferred to a surface O (those not bonded to an FeTet ion in the second layer are preferred). The molecular adsorption mode of an isolated water is less stable by +0.27 eV (Fig. S2a in the ESI†).

Fig. 3. Top views of the most stable configurations for water adsorption on DBT and SCV surfaces with different coverages: (a) a single partially dissociated water molecule on the DBT surface, (b) a single undissociated water molecule on the SCV surface and (c, d) four alternating dissociated/undissociated water on DBT and SCV surfaces, respectively. Big blue, green and white balls represent FeTet3+, FeOct3+ and O in Fe3O4, respectively. Small white and black balls represent O and H from water. The black squares represent the (√2 × √2)R45° unit cell used in the calculations. The adsorption energies Ead per water molecule are listed under the corresponding structures.

Fig. 3

Open in a new tab

The full water coverage was investigated by putting one molecule on each of the four FeOct surface sites in a (√2 × √2)R45° unit cell. Under these conditions, a mixed adsorption mode, where every second molecule is dissociated (Fig. 3c and d), is preferred on both SCV and DBT surfaces. One undissociated molecule and one hydroxyl group form a pair through a H-bond with a distance of 1.51 Å. Between each water–hydroxyl dimer, the H–O distance is over 3 Å. A mixed adsorption mode is fully consistent with previous LEED,48 XPS47 and HREELS49 experimental data. The totally undissociated and totally dissociated adsorption modes at full coverage are higher in energy by 0.37 eV and 0.38 eV for the DBT surface (0.04 eV and 0.36 eV for the SCV surface) (Fig. S2 in the ESI†).

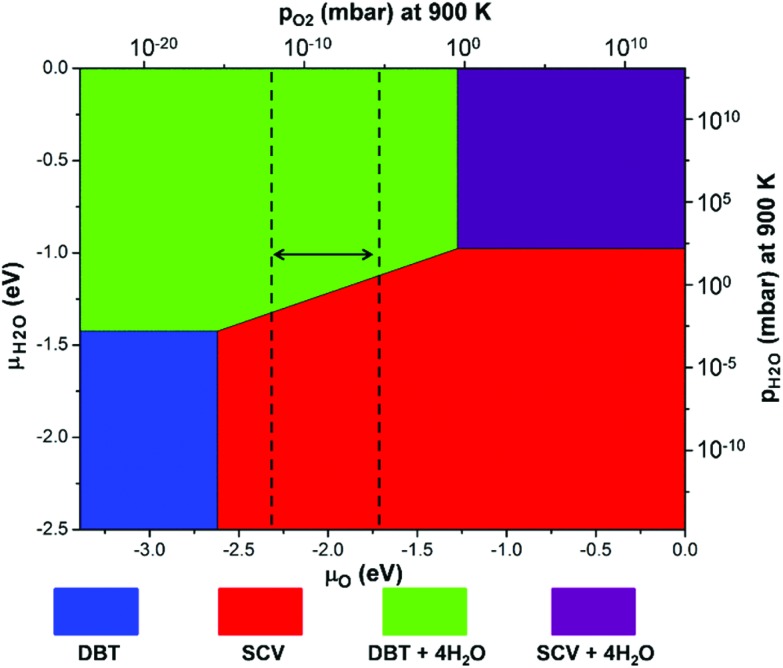
The relative stability of Fe3O4(001) surfaces was compared by calculating the surface energies according to eqn (2) in the Computational methods. A surface phase diagram of Fe3O4(001) is displayed in Fig. 4, which shows the most stable configurations as a function of chemical potential of oxygen and water (μO and μH2O). Under water-poor conditions, the reconstructed SCV surface is more stable than the bulk-truncated DBT surface in a large range of μO, in agreement with a previous report.39 However, under water-rich conditions, the DBT surface, fully covered by water, becomes the most stable phase in a reasonable range of oxygen chemical potentials (vertical dashed lines in Fig. 4). Therefore, water adsorption stabilizes the bulk-truncated DBT surface and even reverses the stability of DBT with respect to the SCV surface. This result is extremely relevant for most of the applicative conditions: the surface structure of Fe3O4 nanoparticles prepared in aqueous solution differs from that in UHV or low water vapor pressure.

Fig. 4. A surface phase diagram of Fe3O4(001) showing the most stable configurations as a function of μO and μH2O. μO and μH2O have been converted into pressures at 900 K. The energy references for μO and μH2O are set to be half the total energy of an isolated O2 molecule and the total energy of an isolated H2O molecule, respectively. The blue and red areas represent the clean DBT and SCV surfaces as shown in Fig. 1a and b. The green and purple areas represent the DBT and SCV surfaces with full water coverage in the mixed adsorption mode, as shown in Fig. 3c and d. Vertical dashed lines indicate a reasonable range of oxygen chemical potentials or O2 partial pressure in experiments.39.

Fig. 4

Open in a new tab

On the other hand, water adsorption has little influence on the electronic structure of the Fe3O4(001) surface according to the PDOS (Fig. S3 in the ESI†). As a consequence, the STM of the surface with water adsorption shows the similar character as that without water but with a stronger contrast as shown in Fig. 5.

Fig. 5. Simulated STM of Fe3O4(001) surfaces with different configurations: (a) a clean DBT surface, (b) a DBT surface with full coverage of water in the mixed adsorption mode as shown in Fig. 3c, (c) a clean SCV surface, and (d) a SCV surface with full coverage of water in the mixed adsorption mode as shown in Fig. 3d.

Fig. 5

Open in a new tab

Finally, we would like to comment on the fact that some experimental studies reported water adsorption at defects sites,45–47 such as oxygen vacancies. We have made an attempt to compute surface energies for model slabs of DBT and SCV containing this type of defect. However, our calculations lead to very high energy costs, as evidenced from the comparative plots in Fig. S4 in the ESI,† suggesting a low density of these defects on the Fe3O4 (100) surface.

Conclusions

In summary, both clean and water covered Fe3O4(001) surfaces were carefully investigated by hybrid functional calculations. The clean surface shows an Fe3+ rich character and a small band gap of about 0.6 eV. Isolated water would not dissociate on the SCV surface, which is the most stable phase under water-poor conditions, which is in perfect agreement with experimental observations.46,47 A mixed adsorption mode is favored on both DBT and SCV Fe3O4(001) surfaces at a high coverage, indicating that the cooperative effects between adjacent water molecules are important in the dissociation reaction. Interestingly, the less stable bulk-truncated DBT surface, under water-poor conditions, is stabilized by water adsorption and becomes the most stable phase in a water-rich environment. Our results provide a clear understanding of water adsorption on the Fe3O4(001) surface and its effect on the relative stability of the bulk-truncated vs. reconstructed surface, which are crucial for most applicative preparation conditions of Fe3O4 nanomaterials.

Conflicts of interest

The authors declare no competing financial interest.

Supplementary Material

Click here for additional data file. (984.9KB, pdf)

Acknowledgments

The authors are grateful to Lorenzo Ferraro for his technical help. This project has received funding from the European Research Council (ERC) under the European Union's HORIZON2020 research and innovation programme (ERC Grant Agreement No [647020]).

Footnotes

†Electronic supplementary information (ESI) available: The charge density plot for the valence band maximum and conduction band minimum of different Fe3O4(001) surfaces; top views of selective configurations of water adsorption on different Fe3O4(001) surfaces with different coverages; projected density of states of Fe3O4(001) surfaces with full coverage of water adsorption; and simulated STM of Fe3O4(001) surfaces with different configurations. See DOI: 10.1039/c8nr02279h

References

  1. Balajka J., Aschauer U., Mertens S. F. L., Selloni A., Schmid M., Diebold U. J. Phys. Chem. C. 2017;121:26424–26431. doi: 10.1021/acs.jpcc.7b09674. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Ohe K., Tagai Y., Nakamura S., Oshima T., Baba Y. J. Chem. Eng. Jpn. 2005;38:671–676. [Google Scholar]
  3. Katsumata H., Kaneco S., Inomata K., Itoh K., Funasaka K., Masuyama K., Suzuki T., Ohta K. J. Environ. Manage. 2003;69:187–191. doi: 10.1016/s0301-4797(03)00145-2. [DOI] [PubMed] [Google Scholar]
  4. Martos C., Dufour J., Ruiz A. Int. J. Hydrogen Energy. 2009;34:4475–4481. [Google Scholar]
  5. Sun C., Lee J. S., Zhang M. Adv. Drug Delivery Rev. 2008;60:1252–1265. doi: 10.1016/j.addr.2008.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Eerenstein W., Palstra T. T. M., Saxena S. S., Hibma T. Phys. Rev. Lett. 2002;88:247204. doi: 10.1103/PhysRevLett.88.247204. [DOI] [PubMed] [Google Scholar]
  7. Keffer F., Handbuch Der Physik, Springer, New York, 1966, vol. 18. [Google Scholar]
  8. Verwey E. J. W. Nature. 1939;144:327. [Google Scholar]
  9. Iizumi M., Koetzle T. F., Shirane G., Chikazumi S., Matsui M., Todo S. Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem. 1982;38:2121–2133. [Google Scholar]
  10. Senn M. S., Wright J. P., Attfield J. P. Nature. 2012;481:173–176. doi: 10.1038/nature10704. [DOI] [PubMed] [Google Scholar]
  11. Siratori K., Suga S., Taniguchi M., Soda K., Kimura S., Yanase A. J. Phys. Soc. Jpn. 1986;55:690–698. [Google Scholar]
  12. Lad R. J., Henrich V. E. Phys. Rev. B: Condens. Matter Mater. Phys. 1989;39:13478–13485. doi: 10.1103/physrevb.39.13478. [DOI] [PubMed] [Google Scholar]
  13. Chainani A., Yokoya T., Morimoto T., Takahashi T., Todo S. Phys. Rev. B: Condens. Matter Mater. Phys. 1995;51:17976–17979. doi: 10.1103/physrevb.51.17976. [DOI] [PubMed] [Google Scholar]
  14. Morton S. A., Waddill G. D., Kim S., Schuller I. K., Chambers S. A., Tobin J. G. Surf. Sci. 2002;513:L451–L457. [Google Scholar]
  15. Schrupp D., Sing M., Tsunekawa M., Fujiwara H., Kasai S., Sekiyama A., Suga S., Muro T., Brabers V. A. M., Claessen R. Europhys. Lett. 2005;70:789–795. [Google Scholar]
  16. Tobin J. G., Morton S. A., Yu S. W., Waddill G. D., Schuller I. K., Chambers S. A. J. Phys.: Condens. Matter. 2007;19:315218. doi: 10.1088/0953-8984/19/31/315218. [DOI] [PubMed] [Google Scholar]
  17. Kimura M., Fujiwara H., Sekiyama A., Yamaguchi J., Kishimoto K., Sugiyama H., Funabashi G., Imada S., Iguchi S., Tokura Y. J. Phys. Soc. Jpn. 2010;79:064710. [Google Scholar]
  18. Wang W., Mariot J. M., Richter M. C., Heckmann O., Ndiaye W., De Padova P., Taleb-Ibrahimi A., Le Fèvre P., Bertran F., Bondino F. Phys. Rev. B: Condens. Matter Mater. Phys. 2013;87:085118. [Google Scholar]
  19. Taguchi M., Chainani A., Ueda S., Matsunami M., Ishida Y., Eguchi R., Tsuda S., Takata Y., Yabashi M., Tamasaku K. Phys. Rev. Lett. 2015;115:256405. doi: 10.1103/PhysRevLett.115.256405. [DOI] [PubMed] [Google Scholar]
  20. Yu Q., Mottaghizadeh A., Wang H., Ulysse C., Zimmers A., Rebuttini V., Pinna N., Aubin H. Phys. Rev. B: Condens. Matter Mater. Phys. 2014;90:075122. [Google Scholar]
  21. Park J. H., Tjeng L. H., Allen J. W., Metcalf P., Chen C. T. Phys. Rev. B: Condens. Matter Mater. Phys. 1997;55:12813–12817. [Google Scholar]
  22. Jordan K., Cazacu A., Manai G., Ceballos S. F., Murphy S., Shvets I. V. Phys. Rev. B: Condens. Matter Mater. Phys. 2006;74:085416. [Google Scholar]
  23. Hevroni A., Bapna M., Piotrowski S., Majetich S. A., Markovich G. J. Phys. Chem. Lett. 2016;7:1661–1666. doi: 10.1021/acs.jpclett.6b00644. [DOI] [PubMed] [Google Scholar]
  24. Akira Yanase K. S. J. Phys. Soc. Jpn. 1984;53:312–317. [Google Scholar]
  25. Zhang Z., Satpathy S. Phys. Rev. B: Condens. Matter Mater. Phys. 1991;44:13319–13331. doi: 10.1103/physrevb.44.13319. [DOI] [PubMed] [Google Scholar]
  26. Yanase Hamada N. A. J. Phys. Soc. Jpn. 1999;68:1607–1613. [Google Scholar]
  27. Noh J., Osman O. I., Aziz S. G., Winget P., Bredas J. L. Sci. Technol. Adv. Mater. 2014;15:044202. doi: 10.1088/1468-6996/15/4/044202. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Noh J., Osman O. I., Aziz S. G., Winget P., Brédas J.-L. Chem. Mater. 2015;27:5856–5867. [Google Scholar]
  29. Aschauer U., Selloni A. J. Chem. Phys. 2015;143:044705. doi: 10.1063/1.4927327. [DOI] [PubMed] [Google Scholar]
  30. Liu H., Di Valentin C. J. Phys. Chem. C. 2017;121:25736–25742. doi: 10.1021/acs.jpcc.7b09387. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Parkinson G. S. Surf. Sci. Rep. 2016;71:272–365. [Google Scholar]
  32. Gaines J. M., Bloemen P. J. H., Kohlhepp J. T., Bulle-Lieuwma C. W. T., Wolf R. M., Reinders A., Jungblut R. M., van der Heijden P. A. A., van Eemeren J. T. W. M., aan de Stegge J. Surf. Sci. 1997;373:85–94. [Google Scholar]
  33. Tarrach G., Bürgler D., Schaub T., Wiesendanger R., Güntherodt H. J. Surf. Sci. 1993;285:1–14. doi: 10.1103/physrevb.47.9963. [DOI] [PubMed] [Google Scholar]
  34. Chambers S. A., Thevuthasan S., Joyce S. A. Surf. Sci. 2000;450:L273–L279. [Google Scholar]
  35. Mijiritskii A. V., Boerma D. O. Surf. Sci. 2001;486:73–81. [Google Scholar]
  36. Stanka B., Hebenstreit W., Diebold U., Chambers S. A. Surf. Sci. 2000;448:49–63. [Google Scholar]
  37. Voogt F. C., Fujii T., Smulders P. J. M., Niesen L., James M. A., Hibma T. Phys. Rev. B: Condens. Matter Mater. Phys. 1999;60:11193–11206. [Google Scholar]
  38. Pentcheva R., Wendler F., Meyerheim H. L., Moritz W., Jedrecy N., Scheffler M. Phys. Rev. Lett. 2005;94:126101. doi: 10.1103/PhysRevLett.94.126101. [DOI] [PubMed] [Google Scholar]
  39. Bliem R., McDermott E., Ferstl P., Setvin M., Gamba O., Pavelec J., Schneider M. A., Schmid M., Diebold U., Blaha P. Science. 2014;346:1215–1218. doi: 10.1126/science.1260556. [DOI] [PubMed] [Google Scholar]
  40. Łodziana Z. Phys. Rev. Lett. 2007;99:206402. doi: 10.1103/PhysRevLett.99.206402. [DOI] [PubMed] [Google Scholar]
  41. Pentcheva R., Moritz W., Rundgren J., Frank S., Schrupp D., Scheffler M. Surf. Sci. 2008;602:1299–1305. [Google Scholar]
  42. Novotný Z., Argentero G., Wang Z., Schmid M., Diebold U., Parkinson G. S. Phys. Rev. Lett. 2012;108:216103. doi: 10.1103/PhysRevLett.108.216103. [DOI] [PubMed] [Google Scholar]
  43. Arndt B., Bliem R., Gamba O., van der Hoeven J. E. S., Noei H., Diebold U., Parkinson G. S., Stierle A. Surf. Sci. 2016;653:76–81. [Google Scholar]
  44. Peden C. H. F., Herman G. S. Z., Ismagilov I., Kay B. D., Henderson M. A., Kim Y.-J., A S. Catal. Today. 1999;51:513–519. [Google Scholar]
  45. Parkinson G. S., Novotný Z., Jacobson P., Schmid M., Diebold U. J. Am. Chem. Soc. 2011;133:12650–12655. doi: 10.1021/ja203432e. [DOI] [PubMed] [Google Scholar]
  46. Kendelewicz T., Liu P., Doyle C. S., Brown G. E., Nelson E. J., Chambers S. A. Surf. Sci. 2000;453:32–46. [Google Scholar]
  47. Kendelewicz T., Kaya S., Newberg J. T., Bluhm H., Mulakaluri N., Moritz W., Scheffler M., Nilsson A., Pentcheva R., Brown G. E. J. Phys. Chem. C. 2013;117:2719–2733. [Google Scholar]
  48. Mulakaluri N., Pentcheva R., Wieland M., Moritz W., Scheffler M. Phys. Rev. Lett. 2009;103:176102. doi: 10.1103/PhysRevLett.103.176102. [DOI] [PubMed] [Google Scholar]
  49. Liu S., Wang S., Li W., Guo J., Guo Q. J. Phys. Chem. C. 2013;117:14070–14074. [Google Scholar]
  50. Rustad J. R., Felmy A. R., Bylaska E. J. Geochim. Cosmochim. Acta. 2003;67:1001–1016. [Google Scholar]
  51. Mulakaluri N., Pentcheva R., Scheffler M. J. Phys. Chem. C. 2010;114:11148–11156. [Google Scholar]
  52. Giannozzi P., Baroni S., Bonini N., Calandra M., Car R., Cavazzoni C., Ceresoli D., Chiarotti G. L., Cococcioni M., Dabo I. J. Phys.: Condens. Matter. 2009;21:395502. doi: 10.1088/0953-8984/21/39/395502. [DOI] [PubMed] [Google Scholar]
  53. Krukau A. V., Vydrov O. A., Izmaylov A. F., Scuseria G. E. J. Chem. Phys. 2006;125:224106. doi: 10.1063/1.2404663. [DOI] [PubMed] [Google Scholar]
  54. Dovesi R., Orlando R., Erba A., Zicovich-Wilson C. M., Civalleri B., Casassa S., Maschio L., Ferrabone M., De La Pierre M., D'Arco P. Int. J. Quantum Chem. 2014;114:1287–1317. [Google Scholar]
  55. Dovesi R., Saunders V. R., Roetti C., Orlando R., Zicovich-Wilson C. M., Pascale F., Civalleri B., Doll K., Harrison N. M. and Bush I. J., et al., Crystal14 User's Manual, University of Torino, Torino, Italy, 2014. [Google Scholar]
  56. Reuter K., Scheffler M. Phys. Rev. B: Condens. Matter Mater. Phys. 2001;65:035406. [Google Scholar]
  57. Grimme S. J. Comput. Chem. 2006;27:1787–1799. doi: 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
  58. Antonov V. N., Harmon B. N., Antropov V. P., Perlov A. Y., Yaresko A. N. Phys. Rev. B: Condens. Matter Mater. Phys. 2001;64:134410. [Google Scholar]
  59. Novotny Z., Mulakaluri N., Edes Z., Schmid M., Pentcheva R., Diebold U., Parkinson G. S. Phys. Rev. B: Condens. Matter Mater. Phys. 2013;87:195410. [Google Scholar]
  60. Tran F., Blaha P., Schwarz K. Phys. Rev. B: Condens. Matter Mater. Phys. 2006;74:155108. [Google Scholar]
  61. Jollet F., Jomard G., Amadon B. Phys. Rev. B: Condens. Matter Mater. Phys. 2009;80:235109. [Google Scholar]
  62. Finazzi E., Di Valentin C., Pacchioni G., Selloni A. J. Chem. Phys. 2008;129:154113. doi: 10.1063/1.2996362. [DOI] [PubMed] [Google Scholar]
  63. Da Silva J. L. F., Ganduglia-Pirovano M. V., Sauer J., Bayer V., Kresse G. Phys. Rev. B: Condens. Matter Mater. Phys. 2007;75:045121. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (984.9KB, pdf)

Articles from Nanoscale are provided here courtesy of Royal Society of Chemistry

RESOURCES