Abstract
Background
Small populations that have been isolated by conflict make vaccination and surveillance difficult, threatening polio eradication. Silent circulation is caused by asymptomatic infections. It is currently not clear whether the dynamics of waning immunity also influence the risk of silent circulation in the absence of vaccination. Such circulation can, nevertheless, be present following a declaration of elimination as a result of inadequate acute flaccid paralysis surveillance (AFPS) or environmental surveillance (ES).
Methods
We have constructed a stochastic model to understand how stochastic effects alter the ability of small populations to sustain virus circulation in the absence of vaccination. We analyzed how the stochastic process determinants of the duration of silent circulation that could have been detected by ES were affected by , waning dynamics, population size, and AFPS sensitivity in a discrete individual stochastic model with homogeneous contagiousness and random mixing. We measured the duration of silent circulation both by the interval between detected acute flaccid paralysis (AFP) cases and the duration of circulation until elimination.
Results
As increased and population size increased, the interval between detected AFP cases and the duration of circulation until elimination increased. As AFPS detection rates decreased, the interval between detected AFP cases increased. There was up to a 22 chance of silent circulation lasting for more than 3 years with 100 AFP detection. The duration of silent circulation was not affected by the waning immunity dynamics.
Conclusion
We demonstrated that small populations have the potential to sustain prolonged silent circulation. Surveillance in these areas should be intensified before declaring elimination. To further validate these conclusions, it is necessary to realistically relax the simplifying assumptions about mixing and waning.
Keywords: Poliovirus, Silent circulation, Acute flaccid paralysis surveillance, Microsimulation model, Gillespie algorithm
Abbreviations
- AFP
acute flaccid paralysis
- AFPS
acute flaccid paralysis surveillance
- ES
environmental surveillance
1. Introduction
After polio was on the precipice of elimination in Nigeria based upon the WHO criteria of three years without a paralytic case (Henderson, 1989), there were several new paralytic cases of poliovirus type 1 in an area of small villages in Borno State (Nnadi et al., 2017). After an attempt at exhaustive vaccination coverage, there was unanticipated emergence. A possible cause is that communities were not reachable by the intervention program. This could either be due to political impediments such as Boko Haram terrorism or due to noncompliance (MM & Ayivor, 2012). Furthermore, Fulani communities are migratory populations that are present in this and in neighboring states in Northern Nigeria (Callaway, 2013, Molineauz and Gramiccia, 1980). Their nomadic lifestyle makes them difficult to reach with comprehensive vaccination coverage, which represents a second potential source of an unanticipated paralytic case following the three years with no such observed case.
The paralytic cases are a result of a silent circulation of the virus in the population. In this paper, we focus on small and somewhat isolated populations that have endemic circulation of poliovirus. The question we aim to answer is: how long, and under what conditions, can a silent circulation persist in small populations in the absence of vaccinations? A silent circulation either ends when there are no longer infected individuals in the population or a paralytic case of polio is detected. We investigate this situation using a microsimulation model of polio transmission in village sizes between and . We assume transmission takes place in the absence of intervention against polio. This allows for the understanding of polio transmission in a natural setting, and, in particular, to ascertain the distribution of times until the infected population reaches zero as well as the distribution of times between consecutive appearances of paralytic cases. It also raises the question as to whether AFPS is a sufficient monitoring strategy to declare areas of small populations free of poliovirus.
There are two surveillance systems used to detect poliovirus in a population: AFPS and ES. AFPS uses reported cases of polio-induced AFP to detect circulating poliovirus. This surveillance system can only be used to identify an individual's first contact with the virus since these are the only individuals with the potential to be symptomatic (Koopman et al., 2017, Thompson et al., 2013). ES can be used to detect silently circulating poliovirus in a population. Poliovirus is excreted when an individual has an active infection regardless if they are symptomatic or asymptomatic (Fine and Carneiro, 1999, Grassly et al., 2012, Mayer et al., 2013, Tebbens et al., 2013, Thompson et al., 2013). ES involves testing sewage for evidence of the virus. In the case where there are no symptomatic individuals, poliovirus found in the sewage can demonstrate that the virus is silently circulating in the population (Fine & Carneiro, 1999). ES may not be feasible either due to monetary limitations or to the lack of a sewage system or at least a common drainage area for defecations. For these reasons, AFPS is, currently, the most used method of poliovirus detection. AFPS is not without its limitations. This method of detection requires that individuals report the symptoms of paralysis to a healthcare worker. Instances of under-reporting can cause cases of polio to go undetected. This may lead to countries being declared polio-free prematurely. Under-reporting of polio-induced paralysis cases can be the result of political instability or geographical isolation.
The waning of immunity and subsequent reinfections can cause silent circulation or asymptomatic transmission. Neither infection from poliovirus nor infection from vaccination provide life-long immunity from the virus (Famulare et al., 2016, Grassly et al., 2012). Once immunity to poliovirus has waned, there is a possibility of reinfection. To capture the waning immunity dynamics, Koopman et al. (2017) explored three different waning scenarios. The first is that the immunity wanes quickly after recovery from the infection, but the individual retains a significant amount of immunity. This is defined as fast-shallow waning. The second is that the individual preserves a high level of immunity for a long period of time, but then loses a large portion of their immunity to the virus. This is defined as slow-deep waning. The third is an intermediate between fast and slow in both speed and depth. In this paper, we focus on these three waning scenarios.
The small population sizes that are emphasized in this paper are, indeed, realistic village sizes in Nigeria. There is a cluster of villages in Pampaida, Nigeria that are associated with the Millennium Villages Project (Millennium Villages Project: Pampaida, Nigeria, 2006). These villages are comprised of both the Hausa and the Fulani, two of the main tribal groups found in Nigeria. There are a total of four villages with approximately individuals. This implies that the average village size contains individuals. The Garki project provided a population census for the Garki District in northern Nigeria from 1969 to 1976 (Molineauz & Gramiccia, 1980). In February of 1972, the 8 villages that were considered for the project had a total of individuals. If we assume a constant growth rate of 0.0088 individuals per year (birth rate minus death rate) (Molineauz & Gramiccia, 1980) then, over the last 44 years, the population of these villages has increased to individuals. On a per village basis, the population sizes are all within the range considered in our simulations.
2. Methods
2.1. The microsimulation model
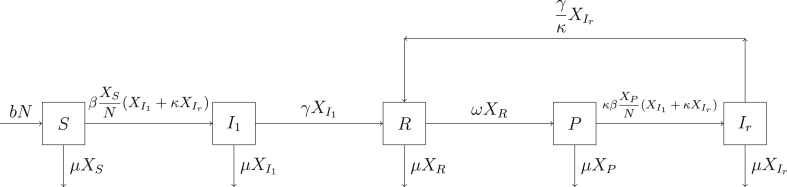
We introduce a counting process on 5 states, labeled S (susceptible), (first infection), R (full immunity from infection), P (partial susceptibility), and (reinfection). The vector of counts for has entries defined by , where is the number of individuals in state i at time t, for i any of the five states. Movement of individuals among the states is constrained by the directed graph in Fig. 1.
Fig. 1.
The schematic diagram of the simplified model (Koopman et al., 2017).
Associated with the states are set of events , defined by the entries in the first column of Table 1. Each event is associated with a rate of occurrence, , , specified by the entries in column 3 of Table 1. It is important to note that the rates depend on the population counts in .
Table 1.
These are the transitions with transition rates for the microsimulation model.
| Transition | Movement | Rate of Transition |
|---|---|---|
| birth | ||
| death in S | ||
| death in | ||
| death in R | ||
| death in P | ||
| death in | ||
| first infection | , | |
| first infected recovery | , | |
| wane | , | |
| reinfection | , | |
| reinfected recovery | , |
The parameters used for simulation, as given in Table 2, are the same as those defined in (Koopman et al., 2017) with the exception of population size (N) and the upper bound on β. Koopman et al. (2017) cites the parameter values found in (Tebbens et al., 2013). We give some insight into the derivation and value of each parameter. The transmission rate (β) is the product of the number of contacts per individual per year and the transmission probability given a contact (Koopman et al., 2017). The transmission probability given a contact is fixed at 0.5 (Koopman et al., 2017). Thus, modifying β implies modifying the number of contacts per individual per year. In this paper, the β values were chosen to represent a range of average ages at first infection seen in the prevaccine era in endemic regions with poor sanitation. The formula for the average age at first infection can be derived to be either in the case in which there is a constant death rate across all ages (the formula used in this paper) (Dietz, 1975) or in the case in which all individuals die at age L, where L is the average lifespan of the individual and is the basic reproduction number. The equation follows from the equation for the force of infection , where . The equation can be obtained by noting that S can be approximated by both and . Using the next generation matrix method (Diekmann, Heesterbeek, & Roberts, 2010), refer to the equations in the Appendix to get . We use the following values: (average age of first infection of 5.6 years, ), (average age of first infection of 3.6 years, ), and (average age of first infection of 2.6 years, ) (Fine and Carneiro, 1999, Ofosu-Amaah et al., 1977, Paul and Horstmann, 1955, Paul et al., 1952). The rate of recovery from a first infection with poliovirus (γ) is a determined quantity based upon “expert assessment” (Tebbens et al., 2013). The birth (b) and the death rate (μ) are assumed to be equal to keep the population size constant (Koopman et al., 2017, Tebbens et al., 2013). The waning of the immunity is comprised of two processes: the depth to which the immunity wanes () and the speed at which the immunity wanes (ω). The depth is controlled by three factors, all of which are set equal to each other for simplification purposes. The three components are the relative susceptibility of partially susceptible individuals to fully susceptible individuals, the relative contagiousness of reinfected individuals to first infected individuals, and the relative duration of infection of reinfected individuals with respect to first infected individuals (Koopman et al., 2017). In (Koopman et al., 2017), the waning rate was fixed and the waning depths were fitted such that each waning scenario had the same average age at first infection. The paralysis to infection ratio (PIR) was determined for each serotype in 1955 using available data (Nathanson & Kew, 2010).
Table 2.
Parameters and values (Koopman et al., 2017).
| Parameter | Parameter value | Parameter description |
|---|---|---|
| N | varies | total population (individuals) |
| β | varies | infection rate (effective contacts/individual/year) |
| γ | 13 | recovery rate ((year)−1) |
| ω | fast (slow) [intermediate] waning rate ((year)−1) | |
| shallow (deep) [intermediate] waning depth | ||
| b | 0.02 | birth rate ((total population)−1) |
| μ | 0.02 | natural death rate ((total population)−1) |
| PIR | serotype 1 (2) [3] paralysis to infection ratio |
Finally, at any time , we associate independent exponential waiting times with the events , respectively and set . With these ingredients at hand, we can specify the simulation algorithm that generates the dynamics in the population vector, . We terminate each simulation either when the infected population reaches zero or after fifteen years has elapsed, whichever comes first.
2.2. Algorithm description
The method of simulation was motivated by the Gillespie algorithm (Gillespie, 1976). The steps of the algorithm are as follows:
-
1.
Initialize with such that the proportion of individuals in the states S, , R, P, and is the same as the equilibrium proportions for the differential equation system (see Appendix) associated with the directed graph in Fig. 1.
-
2.
Generate a time when a first event in is to occur by using a deviate from the exponential distribution . Observe that is the minimum of the waiting times associated with the individual events .
-
3.At time , generate a uniform random deviate, r, and introduce the following decision rule:
- Select event if
- for
- Select if
-
4.
Update based on the index selected in step 4. The possible specifications for are given in Table 1, where the compartments specified under movement are updated appropriately and all other compartments stay fixed.
-
5.
If the index that was chosen in step 4 was “first infection” then generate a second uniform random deviate, , on . If PIR then we declare an incidence of paralysis to have occurred. Record this time of occurrence.
-
6.
Go back to step 2 initializing with . Notice that the rates are now .
This process repeats until the stochastic process is killed. The simulation was killed when there were no longer infected individuals in the population or 15 years had elapsed, whichever came first.
To investigate the impact of overlooking paralytic cases, we modified step 5 in the algorithm. In step 5, if the event that is chosen in step 3 corresponds to a fully susceptible individual becoming infected, then a uniformly distributed random number () is generated such that if is less than the serotype-specific paralysis to infection ratio (PIR) then a paralytic case of polio is detected. If an incidence of paralysis occurred, the time at which this event took place was recorded. To vary the detection rate, we multiplied the PIR by the appropriate multiplier (i.e. 0.75 for a detection rate) and checked that the generated random number was less than this new paralysis to infection ratio. Varying the detection rate simulated missing a paralytic case. In all simulations, we use the serotype 1 specific paralysis incidence rate.
3. Results
Simulations were run 1000 times, initialized at the endemic equilibrium of the related differential equations model. The related differential equations model is represented by the diagram in Fig. 1. The system of ordinary differential equations is presented in the Appendix. We do not use these equations for our analytical purposes, as we require a stochastic model to capture the fluctuations in the populations of small size that are the focus of the present paper. The rate of paralytic case detection was varied, the values were varied, the population sizes were varied, and the type of waning immunity (fast-shallow, intermediate, slow-deep) was varied. Note that only those simulations in which 2 or more paralytic cases occurred were used to find a distribution of times between detected paralytic cases. A sample of these results at the largest and the smallest population sizes are presented in Fig. 2, Fig. 3. Table 3, Table 4 give the proportion of inter-paralytic case periods of at least 3 years with and detection rates, respectively.
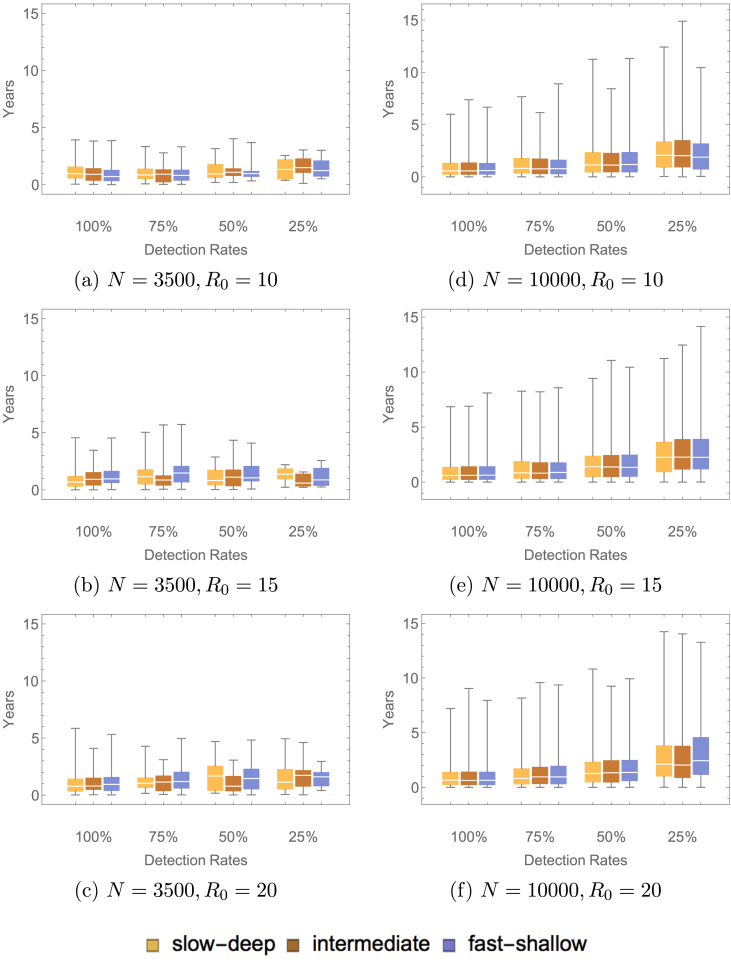
Fig. 2.
These plots show the distribution of time between detected paralytic cases with varying population sizes, varying values and varying waning immunity scenarios. These simulations ended when either there were no longer infected individuals remaining in the population or 15 years had elapsed.
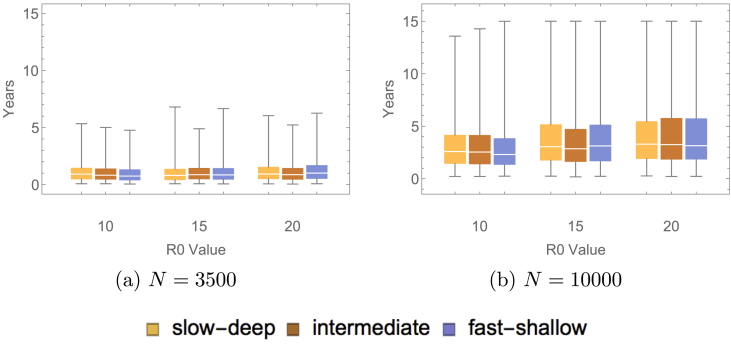
Fig. 3.
These plots show the distribution for the duration of a silent circulation with varying population sizes, varying values and varying waning immunity scenarios. The simulations were ended when either there were no longer infected individuals in the population or the time exceeded 15 years.
Table 3.
This table shows the proportion of simulations with time between detected paralytic cases greater than 3 years in a natural transmission setting (i.e. no modification to detection rates). The number in the parentheses gives the proportion of simulations with 2 or more paralytic cases detected.
| Value | Type of Waning Immunity | Population Size |
|||
|---|---|---|---|---|---|
| N = 3500 | N = 5000 | N = 7000 | N = 10,000 | ||
| 10 | fast-shallow | 6.25% (0.064) | 6.71% (0.164) | 10.63% (0.320) | 12.98% (0.578) |
| intermediate | 8.06% (0.062) | 11.36% (0.176) | 10.88% (0.340) | 13.76% (0.603) | |
| slow-deep | 2.62% (0.076) | 10.88% (0.173) | 9.54% (0.346) | 13.40% (0.597) | |
| 15 | fast-shallow | 6.06% (0.066) | 12.15% (0.181) | 14.62% (0.390) | 18.21% (0.692) |
| intermediate | 1.96% (0.051) | 11.32% (0.159) | 16.04% (0.374) | 17.74% (0.620) | |
| slow-deep | 3.03% (0.066) | 10.60% (0.151) | 14.17% (0.367) | 18.26% (0.657) | |
| 20 | fast-shallow | 7.23% (0.083) | 15.45% (0.220) | 22.27% (0.476) | 22.03% (0.749) |
| intermediate | 4.35% (0.069) | 10.73% (0.205) | 12.34% (0.397) | 17.10% (0.696) | |
| slow-deep | 3.33% (0.060) | 15.00% (0.180) | 15.18% (0.415) | 15.89% (0.711) | |
Table 4.
This table shows the proportion of simulations with time between detected paralytic cases greater than 3 years with a detection rate. The number in the parentheses gives the proportion of simulations with 2 or more paralytic cases detected.
| Value | Type of Waning Immunity | Population Size |
|||
|---|---|---|---|---|---|
| N = 3500 | N = 5000 | N = 7000 | N = 10,000 | ||
| 10 | fast-shallow | 4.76% (0.021) | 8.70% (0.046) | 15.97% (0.144) | 31.45% (0.337) |
| intermediate | 5.26% (0.019) | 11.86% (0.059) | 21.57% (0.153) | 32.08% (0.346) | |
| slow-deep | 4.35% (0.023) | 14.71% (0.068) | 32.89% (0.149) | 38.46% (0.364) | |
| 15 | fast-shallow | 8.70% (0.023) | 23.19% (0.069) | 26.37% (0.182) | 41.49% (0.417) |
| intermediate | 10.00% (0.020) | 9.68% (0.062) | 26.11% (0.157) | 40.09% (0.424) | |
| slow-deep | 0% (0.023) | 17.33% (0.075) | 26.35% (0.167) | 38.69% (0.429) | |
| 20 | fast-shallow | 11.54% (0.026) | 26.92% (0.078) | 36.24% (0.229) | 52.02% (0.519) |
| intermediate | 4.76% (0.021) | 12.73% (0.055) | 34.83% (0.178) | 48.08% (0.468) | |
| slow-deep | 10.00% (0.020) | 20.93% (0.086) | 32.06% (0.209) | 43.79% (0.459) | |
Changing the value of and varying the population size (N) had a dramatic impact on the length of time between detected paralytic cases. As and N increased, the time between detected paralytic cases increased. However, as the population size increased, the variance in the time between detected paralytic cases decreased. The variance also decreased as the detection rate increased. In both cases, this was due to the range in the number of paralytic cases detected. This implies that two villages of small population sizes can have drastically different dynamics in terms of the duration of a silent circulation as measured by detection of paralytic cases. An elimination or eradication criterion that is appropriate for one village may not be applicable to another even if it is of comparable size. Although a village with a population size of will have, on average, longer times between detected paralytic cases than a village with a population size of 3500, the large variance seen in the dynamics for the smaller population sizes may make these villages more dangerous because they have less predictability. It is important to note that the waning immunity scenario imposed on the population had little impact on the time between detected paralytic cases.
Table 3 shows the natural process of paralytic cases of poliovirus type 1. The high proportions of inter-paralytic intervals exceeding three years seen in the larger population sizes implies that AFPS alone cannot be an adequate surveillance scheme for declaring elimination to have occurred in the absence of vaccination. ES would be essential if there is to be confidence in elimination claims for small communities. Additionally, a large proportion of the simulations in Table 3 had 2 or more detected paralytic cases. In spite of this, up to of the simulations, depending upon the parameter sweep, had a time between detected paralytic cases greater than 3 years. This demonstrates that even in the case where there are paralytic cases occurring in regions with perfect detection and no vaccination, the time between these cases can exceed 3 years. This may lead to a false declaration of elimination in these areas based upon the WHO criteria of three years without a detected paralytic case (Henderson, 1989).
As shown in Fig. 3, the duration of a silent circulation, as measured by the infected population reaching zero, increased as the population size and increased. The duration of a silent circulation was not affected by the type of waning immunity. As increased and as the population size increased, the variance in the length of a silent circulation increased. As increases, the contact rates increase, which allows for an increased probability in a susceptible individual contacting an infected individual and becoming infected. As a result of stochastic effects, the larger populations at the larger values are subject to an increased probability of infection, thus prolonging the silent circulation. These effects do not appear to be as significant in the case of the smaller population sizes considered.
The increase in the time to elimination and in the time between paralytic cases as both the population size and increased was due to the large fluctuations of the infected population. These large fluctuations were induced by the substantial number of births in the larger population sizes as compared to the smaller population sizes. In addition, as increased, the height of the fluctuations increased. These large fluctuations allowed for the prolonged silent circulation that was observed in the larger populations at higher values (refer to Fig. 4). A protracted time until elimination provides the potential for long times between paralytic cases. This indicates that, in order to prevent long durations of silent circulation, it is necessary to inhibit large influxes of naive susceptible individuals. Furthermore, this demonstrates that first infections make a significant contribution to prolonging a silent circulation. For this reason, the waning immunity dynamics did not impact the length of a silent circulation.
Fig. 4.
These plots show the count of the total infected population at every 100 event steps averaged over all 1000 simulations. The population considered was of size 10,000 with fast-shallow waning immunity dynamics.
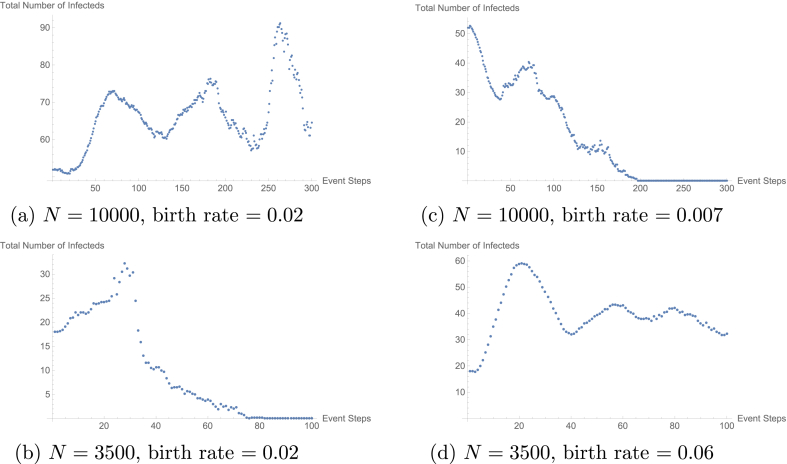
To justify the high rate of naive suceptibles produced per year in the larger populations as the explanation for the fluctuations, we modified the birth rates in both the larger and small populations. As an example, consider the plots given in Fig. 5. In this example, we reduced the naive suceptibles produced per year in the 10,000 population to be equal to that of the 3500 population. This gave a birth rate of 0.007 individuals per year. Similarly, we increased the naive susceptible produced per year in the 3500 population to be equal to that of the 10,000 population. This gave a birth rate of 0.06. These simulations were run as previously described. By modifying the birth rate, we were able to change the dynamics of the infected population. Specifically, in the case of the 10,000 population, with a reduced birth rate, we observed dynamics similar to that of the 3500 without modified birth rate and vice versa.
Fig. 5.
These plots demonstrate the effect of modifying the birth rate on the count of the total number of infected individuals in the populations. All populations considered had with fast-shallow waning immunity dynamics. Plots (a) and (b) give the count of the total infected individuals with no modification to the birth rate. In the case of Plot (a), there are an average of 200 naive susceptibles produced per year and in the case of Plot (b), there are an average of 70 naive suceptibles produced per year. Plots (c) and (d) give the count of the total infected population with modification to the birth rate. In the case of Plot (c) the birth rate was modified such that the average number of naive susceptibles produced per year was 70 and in the case of Plot (d) the birth rate was modified such that the average number of naive susceptibles produced per year was 200.
4. Discussion and conclusion
The microsimulation model that is presented in this paper was used to examine the conditions under which a small population could sustain a silent circulation of poliovirus in the absence of vaccination. A silent circulation either ends when there are no longer infected individuals in the population or a paralytic case of polio is detected. Due to the predominately asymptomatic spread of polio, it is not reasonable to be able to detect when there are no infected individuals remaining in the population. We must rely on the detection of paralytic cases as a surrogate. For this reason, one part of the criterion for declaring a region polio-free is the absence of a paralytic case of polio for at least three years (Henderson, 1989). This motivated the question: in the absence of vaccination, how long can a silent circulation persist in small populations? In our analysis, we used both the time between detected paralytic cases as well as the time at which the infected population reached zero to determine the duration of a silent circulation. Since we have the benefit of simulation, the latter results are attainable.
If we were to rely solely on detecting paralytic cases to establish the end of a silent circulation then, depending on the parameter sweep, a silent circulation could last between 1 and 4 years, with an upper bound of 15 years between two successive paralytic cases. Our results imply that three years without a detected paralytic case does not guarantee elimination. If we were to rely solely on the population of infected individuals reaching zero to declare elimination then, depending on the parameter sweep, a silent circulation could persist between 2 and 7 years, with an upper bound of 15 years. The duration of a silent circulation in either case was not affected by the type of waning immunity imposed. These results apply to small populations that are not vaccinated.
The most striking feature of these simulations is that even if every paralytic case of polio that occurs is detected, the time between detected paralytic cases can be long depending on the parameters considered. In a natural transmission setting (i.e. detection) without vaccination, there is up to a chance that a silent circulation lasts beyond 3 years. Furthermore, there is evidence that there exist areas in which detection rates are dramatically reduced. In May of 2016, the accessibility of Borno State, Nigeria to special vaccination teams was (Nnadi et al., 2017). Though it has since increased to (Nnadi et al., 2017), it is not unreasonable to suspect that this inaccessibility may have an effect on detection or reporting rates of AFP. This indicates that a system in which detecting paralytic cases of polio is the primary method of surveillance is not sufficient to prevent prolonged periods of silent circulation in the absence of intervention. Thus, it is necessary to implement other methods such as ES to supplement AFPS. This will help to detect circulating poliovirus before a paralytic case occurs with the intention of preventing prolonged periods of silent circulation.
Acknowledgements
This research was supported in part by the Army Research Office under MURI grant 558153-MA-MUR, Prime Award W91 INF-11-1-0036.
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
Contributor Information
Celeste Vallejo, Email: cvallejo@ufl.edu.
James Keesling, Email: kees@ufl.edu.
James Koopman, Email: jkoopman@umich.edu.
Burton Singer, Email: bhsinger@epi.ufl.edu.
Appendix A.
The equations in (A.1) give the system of related differential equations that was used to formulate the transition rates for the stochastic microsimulation model. The endemic equilibrium of the system was used to initialize the microsimulation model.
| (A.1) |
References
- Callaway E. Polio's moving target. Nature. 2013;496(7445):290–292. doi: 10.1038/496290a. [DOI] [PubMed] [Google Scholar]
- Diekmann O., Heesterbeek J.A.P., Roberts M.G. The construction of next-generation matrices for compartmental epidemic models. Journal of the Royal Society Interface. 2010;7(47):873–885. doi: 10.1098/rsif.2009.0386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dietz K. Transmission and control of arbovirus diseases. In: Ludwig D., Cooke K., editors. Epidemiology. SIAM; Philadelphia, PA: 1975. pp. 104–121. [Google Scholar]
- Famulare M., Chabot-Couture G., Eckhoff P.A., Lyons H., McCarthy K.A., Selinger C. How polio vaccination affects poliovirus transmission. bioRxiv. 2016:084012. [Google Scholar]
- Fine P.E., Carneiro I.A.M. Transmissibility and persistence of oral polio vaccine viruses: Implications for the global poliomyelitis eradication initiative. American Journal of Epidemiology. 1999;150(10):1001–1021. doi: 10.1093/oxfordjournals.aje.a009924. [DOI] [PubMed] [Google Scholar]
- Gillespie D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. Journal of Computational Physics. 1976;22:403–434. [Google Scholar]
- Grassly N.C., Jafari H., Bahl S., Sethi R., Deshpande J.M., Wolff C. Waning intestinal immunity after vaccination with oral poliovirus vaccines in India. The Journal of Infectious Diseases. 2012;205:1554–1562. doi: 10.1093/infdis/jis241. [DOI] [PubMed] [Google Scholar]
- Henderson R. The world health organization's plan of action for global eradication of poliomyelitis by the year 2000. Annals of the New York Academy of Sciences. 1989;569(1):69–85. doi: 10.1111/j.1749-6632.1989.tb27359.x. [DOI] [PubMed] [Google Scholar]
- Koopman J., Henry C.J., Park J.H., Eisenberg M.C., Ionides E.L., Eisenberg J.N. Dynamics affecting the risk of silent circulation when oral polio vaccination is stopped. Epidemics. 2017;20:21–36. doi: 10.1016/j.epidem.2017.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayer B.T., Eisenberg J.N.S., Henry C.J., Gomes M.G.M., Ionides E.L., Koopman J.S. Successes and shortcomings of polio eradication: A transmission modeling analysis. American Journal of Epidemiology. 2013;177(11):1236–1245. doi: 10.1093/aje/kws378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Millennium Villages Project: Pampaida, Nigeria (2006). http://millenniumvillages.org/the-villages/pampaida-nigeria/. (Accessed 21 September 2016).
- MM B., Ayivor M. Polio vaccination in Nigeria: The ‘Good’, the ‘Bad’ and the ‘Ugly’. Journal of Antivirals & Antiretrovirals. 2012;S15 [Google Scholar]
- Molineauz L., Gramiccia G. World Health Organization; Geneva: 1980. The Garki project: Research on the epidemiology and control of malaria in the Sudan savanna of West Africa. [Google Scholar]
- Nathanson N., Kew O.M. From emergence to eradication: The epidemiology of poliomyelitis deconstructed. American Journal of Epidemiology. 2010;172(11):1213–1229. doi: 10.1093/aje/kwq320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nnadi C., Damisa E., Esapa L., Braka F., Waziri N., Siddique A. Centers for Disease Control and Prevention; 2017. Continued endemic wild poliovirus transmission in security-compromised areas – Nigeria, 2016. Morbidity and mortality weekly report. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ofosu-Amaah S., Kratzer J.H., Nicholas D.D. Is poliomyelitis a serious problem in developing countries? - lameness in Ghanaian schools. British Medical Journal. 1977;1:1012–1014. doi: 10.1136/bmj.1.6067.1012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paul J.R., Horstmann D.M. A survey of poliomyelitis virus antibodies in French Morocco. The American Journal of Tropical Medicine and Hygiene. 1955;4(3):512–524. doi: 10.4269/ajtmh.1955.4.512. [DOI] [PubMed] [Google Scholar]
- Paul J.R., Melnick J.L., Barnett V.H., Goldblum N. A survey of neutralizing antibodies to poliomyelitis virus in Cairo, Egypt. American Journal of Hygiene. 1952;55:402–413. doi: 10.1093/oxfordjournals.aje.a119532. [DOI] [PubMed] [Google Scholar]
- Tebbens R.J.D., Pallansch M.A., Kalkowska D.A., Wassilak S.G.F., Cochi S.L., Thompson K.M. Characterizing poliovirus transmission and evolution: Insights from modeling experiences with wild and vaccine-related polioviruses. Risk Analysis. 2013;33(4):703–749. doi: 10.1111/risa.12044. [DOI] [PubMed] [Google Scholar]
- Thompson K.M., Pallansch M.A., Tebbens R.J.D., Wassilak S.G., Cochi S.L. Modeling population immunity to support efforts to end the transmission of live polioviruses. Risk Analysis. 2013;33(4):647–663. doi: 10.1111/j.1539-6924.2012.01891.x. [DOI] [PMC free article] [PubMed] [Google Scholar]