Spatio-temporal spread of infectious pathogens of humans

Abstract

Spatio-temporal aspects in the propagation of infectious pathogens of humans are reviewed. Mathematical modelling of these issues using metapopulation models is presented.

1. Introduction

Define mobility as the collection of processes through which individuals change their current location. Under such a general definition, human mobility is multi-modal and happens in colossal volumes. We give here a very brief and partial review of mobility, focusing on its link with the spread of infectious pathogens of humans. We present a modelling technique, metapopulations, that can be used when considering such issues. The presentation builds on previous work of the author and collaborators, in particular Arino (2009). Note that we assume here that the reader is familiar with the basic steps involved in the study of a model in mathematical epidemiology.

2. Range and duration of mobility

Call place of residence where an individual resides. In modern days, this may be for instance where their fiscal residence is located. In view of the definition above, a mobility event is any activity that takes an individual away from their place of residence. It is often useful to distinguish between temporary mobility and relocation, which results in a change of the place of residence. Mobility can be characterized using two main features, duration and range.

2.1. Duration of mobility

The duration of mobility is the length of time an individual spends away from their place of residence during a mobility event; it varies from minutes to years. A simple arbitrary classification follows. Long-term mobility involves durations longer than six months and typically concerns relocation (immigration, move) or long term displacement from the place of residence (refugees). Six months is chosen as a cut point because public health authorities typically require that individuals affiliate with them if they spend this amount of time in their midst. Medium-term mobility involves events lasting from 1 to 6 months, typically related to domestic and foreign migrant workers, with individuals often maintaining two places of residence. Short-term mobility ranges from over 1 day to 1 month and corresponds to travel away from and back to the place of residence for work or leisure. Finally, instantaneous mobility involves events lasting no more than one day. These events can be daily commute but also work-related travel.

2.2. Range of mobility

We call range of mobility the distance away from the place of residence that an individual travels for a mobility event. Ranges vary from metres (local) to thousands of kilometres (intercontinental). Human mobility has evolved greatly over the course of human history. For many years, long range mobility was mainly linked to trade. Most humans were mobile only very locally (within a village or to neighbouring villages). It is only since the beginning of the 20th century that travel for leisure has become more prevalent and that as a consequence, more and more humans undertake short-duration long-range trips.

2.3. Coexistence of ranges and durations for a given individual

Different durations and ranges of mobilities can occur simultaneously for a given individual. For instance, a migrant worker can be at the same time undertaking a long-term and long-range mobility event while commuting daily to work from their temporary place of residence.

2.4. Time to achieve a range

Another important factor in mobility is the time it takes to achieve mobility on a certain range. For instance, long-range continental and even intercontinental mobility has been going on for centuries. However, as technology evolves, the time it takes to achieve a certain range decreases.

3. Volume of mobility

Together with the evolution of range, duration and speed, the number of mobility events taking place has increased many folds over the course of human history, not only because of global population increase but also because the per capita rate at which individuals undertake mobility has greatly changed. The total number of mobility events occurring nowadays on a daily basis is enormous. The number of events is also difficult to apprehend. Indeed, while a lot of data is available concerning the number of mobility events, this data is often incomplete concerning the nature of the events themselves. Take for instance the traffic data used in Arino and Portet (2015) to parametrize a movement model. While the number of vehicles passing through counting stations is precise, it is impossible to tease out from this data whether passengers are undertaking local or long distance trips. Traffic utilization surveys are then useful complements to raw traffic data. The following examples serve to provide some sense of the number of mobility events.

3.1. Migrations

Migration usually results in a change of the place of residence. Migration has always existed; it is through migration that earth was populated. The International Organization for Migration (IOM) defines a migrant as a person living in a country that is not their country of birth and under this definition, estimates that there are more than 200 million migrants around the world today, with 60% of these migrants living in developed countries. For instance, from 1980 to 2015, there were 7.4 million new Permanent Residents to Canada, out of an estimated total population in 2015 of 35.8 millions (Government of Canada, 2015). There is also a sizeable migration from rich countries; e.g., the French population registered at a foreign embassy was 1.7 million on December 31st, 2015 (Ministère des Affaires étrangères et du Développement international, 2016). Finally, refugees constitute an important factor of international migration, particularly relevant in the context of public health as they represent populations often in precarious health conditions. UNHCR estimates there were 15 million refugees (mid-2015), 1.2 million asylum-seekers (end 2014), 38 million internally displaced persons (end 2014) and 10 million stateless persons.

3.2. Medium-term mobility

In today's globalized world, an important source of mobility is that of migrant workers, who spend extensive periods of time working in a location that is not their primary place of residence. It is estimated that in China alone, there were 273.95 million migrant workers in 2014 (National Bureau of Statistics of the People's Republic of China, 2015). Agricultural workers are another source of temporary migrance, often involving temporary work in richer countries. For instance, there are about 45,000 people per year coming to Canada to work in farms (Government of Canada, 2017).

3.3. Short-term and instantaneous mobility

In China, the Chunyun period is a 40 days movement period around Chinese New Year. Estimates are it involved 3.6 billion people-trips in 2014 (Wang, Liu, Mao, Hu, & Gu, 2014). The yearly pilgrimage to Mecca involves an average 2.5 million people (including 1.7 million non-Saudis) (Khan et al., 2010). Instantaneous mobility, such as one's daily commute to work, occurs in numbers that are difficult to evaluate but can safely be estimated to represent tens to hundreds of billions of people-kilometres each day.

4. Spatio-temporal spread of pathogens

Let us state a tautology: pathogens of humans follow humans. Indeed, whatever the modalities and characteristics of mobility, all migrants or travellers carry with them their “health history”, which may include latent or active infections (TB, H1N1, polio, HIV), immunizations (schedules vary by country), health/nutrition practices or treatment methods. Thus, as the way humans utilize space evolves, so does the spread of pathogens they carry. In earlier times, human pathogens followed well-defined human trade routes. For instance, the Black Death followed the Silk Route into Europe (Benedictow, 2004). As long range mobility becomes more of a mix between trade and leisure and trade routes evolve, the picture has become increasingly complex. (See, for instance, the animated influenza incidence maps of Réseau Sentinelles at http://www.sentiweb.fr)

In modern days, problems in the spatio-temporal spread of pathogens of humans can be seen as articulating along two main axes. The first concerns the fast spatial spread of an emerging or re-emerging pathogen, the second interactions of health systems.

4.1. Fast spatial spread – the case of SARS

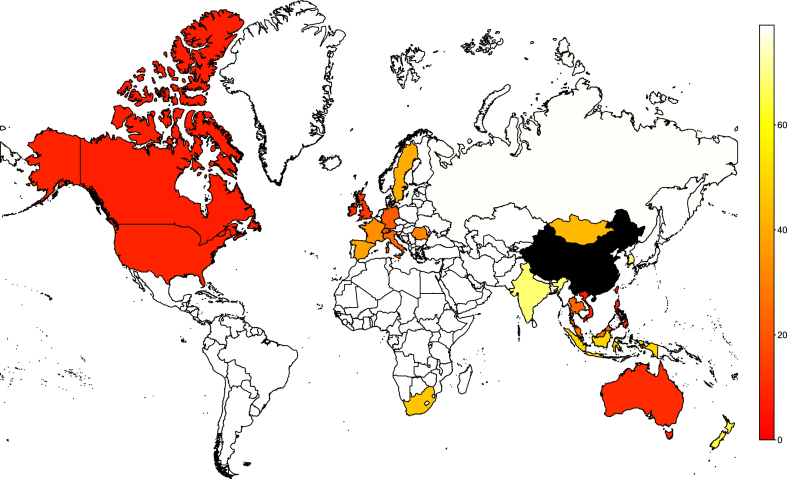
The severe acute respiratory syndrome (SARS) propagated worldwide in 2002–2003. Although it caused only 8273 cases in 28 countries, SARS illustrated the capacity for modern transportation methods to facilitate the rapid and global spread of an infectious pathogen. SARS also inflamed imaginations because its case fatality ratio was high (it caused 775 deaths, i.e., a CFR of 9.4%). The spatial extent and temporal organization of that spread is shown in Fig. 1.

Fig. 1.

Time in days to first confirmed case of SARS, with time 0 the time at which the first international spreading event took place in Hong Kong. China is represented differently as the epidemic was ongoing there at the time. The data was compiled from the WHO website and is available as an electronic appendix.

4.2. Interactions between health systems – polyomyelitis

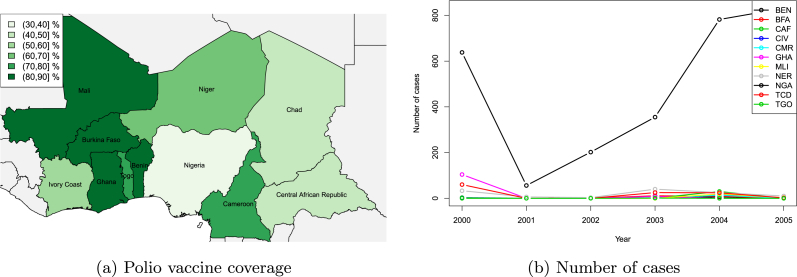
Public health systems are typically administered at political geography levels: counties, provinces, states or countries. However, pathogens ignore borders and thus mobility-induced interconnections between administrative units have consequences. One striking example is that of poliomyelitis in Nigeria in 2004. Because of a vaccine scare that started in 2002 (Raufu, 2002), authorities in the northern Nigeria state of Kano interrupted polio vaccination in 2004 (Olusanya, 2004). This occurred in a context where neighbouring countries had polio vaccine coverage that was not ideal; see Fig. 2a.

Fig. 2.

(Left) Estimated percentage of the population having, in 2004, received the third dose of polio vaccine in several African countries (WHO). (Right) Annual number of polio cases in countries shown left.

Vaccinations resumed in July the same year (Fleck, 2004), but between the official interruption and the longer lasting public distrust, the damage was done: cases spiked in Nigeria (Cheng, 2008) but also in close countries such as Cameroon (Endegue-Zanga et al., 2016). The effect is clearly visible in Fig. 2b.

5. Metapopulation models – general introduction

From the discussion above, formulating mathematical models to help understand the spatio-temporal spread of infectious diseases is very important. Many different methods are available. We focus here on metapopulation models, but stress that understanding complex phenomena such as these requires a multi-faceted approach and the interested reader would benefit greatly from looking into other alternatives. For partial differential equations models, see for instance (Rass & Radcliffe, 2003) and the references therein. Also, the early paper (Bailey, 1980) is worth reading. Concerning the spread of diseases on networks, a standard reference is Newman (2002).

In metapopulation models, space is discrete and consists of individual spatial units called patches. Patches range in spatial extent from a house or neighbourhood all the way up to countries or even continents. There are several types of metapopulation models. We focus here on models with explicit movement, in which each patch contains a dynamical system describing the dynamics of the disease in the populations present within the patch and a coupling function describes the explicit movement of individuals between patches. Other model types, not considered here, assume that there is an implicit coupling between patches and do not incorporate movement explicitly.

Assume geographical locations are elements of a set $\mathcal{P}$ with cardinality $\left|\mathcal{P}\right|$ (the number of patches). Each patch is a vertex in a directed graph (digraph). In each patch, there are individuals from a variety of compartments in the sense of Jacquez and Simon (1993). A compartment could contain for instance individuals susceptible to the disease, another individuals infected with the disease; there could be compartments for the different species affected by the disease, etc. We denote $\mathcal{C}$ the set of all compartments that exist in the general system and ${\mathcal{C}}_p\subseteq \mathcal{C}$ those compartments present in patch $p\in \mathcal{P}$.

Individuals in a given compartment may move between patches, with $m_{cqp}$ the rate of movement of individuals in compartment $c\in \mathcal{C}$ from patch $p\in \mathcal{P}$ to patch $q\in \mathcal{P}\setminus \left\{p\right\}$. This defines a digraph ${\mathcal{G}}^c$ with arcs ${\mathcal{A}}^c$ for each compartment $c\in \mathcal{C}$, with an arc from p to q if $m_{cqp}>0$ and no arc otherwise. Because there are $\left|\mathcal{C}\right|$ compartments in the overall system (whether they are present in each patch or not), each pair $\left(p,q\right)$ of patches is joined in each direction by at most $\left|\mathcal{C}\right|$ arrows, so the general context is that of a multi-digraph.

In turn, each patch $p\in \mathcal{P}$ is endowed with a dynamical system describing the evolution of numbers or densities of individuals in the compartments in ${\mathcal{C}}_p$. Usually, all the patches are equipped with the same type of system; this is what we describe here. Also, we assume here that movement is instantaneous between patches and that individuals do not change compartments as they move, so that, for instance, an individual leaves their patch of origin and arrives in the destination patch while susceptible. Some models have assumed that infection can happen during transport, e.g., (Arino, Sun, & Yang, 2016); others have considered the role of travel time, e.g., Liu, Wu and Zhou (2008). Such models are beyond the scope of this introductory review.

The general form of a metapopulation model is then, $\forall c\in \mathcal{C}$ and $\forall p\in \mathcal{P}$,

$$x_{cp}^{\prime }=f_{cp}\left(X_p\right)+\sum _{q\in \mathcal{P}}{m}_{cpq}{x}_{cq}\text{,}$$ (1)

where $X_p={\left(x_{1p},\dots ,x_{\left|\mathcal{C}\right|p}\right)}^T\in {\mathrm{ℝ}}^{\left|\mathcal{C}\right|}$ is the distribution of individuals of the different compartments present in the patch and

$$m_{cpp}=-\sum _{q\in \mathcal{P}\setminus \left\{p\right\}}{m}_{cqp}\text{,}$$ (2)

is used to make the notation more compact. The function $f_{cp}\left(X_p\right)$ indicates that processes are localized to the patch where they take place. This excludes for example the model in Arino and van den Driessche (2003), wherein birth occurs in the patch of residence but depends on the total resident population of that patch. If it is important to take into account individuals from the same compartment present in other patches, we define $X^c={\left(x_{c1},\dots ,x_{c\left|\mathcal{P}\right|}\right)}^T\in {\mathrm{ℝ}}^{\left|\mathcal{P}\right|}$ and use $f_{cp}\left(X_p,X^c\right)$. However, to simplify the discussion, we assume the form in (1) from now on.

The general form (1) can be used to summarize many different types of metapopulation models, not only ones for the spread of infectious pathogens. (Metapopulations have a rich history in their originating field of Ecology; see, e.g., Hanski and Gilpin (1997).) To focus on epidemiology, we let $\mathcal{U}\mathrm{⊊}\mathcal{C}$ and $\mathcal{I}\mathrm{⊊}\mathcal{C}$ be uninfected and infected compartments, respectively, with $\mathcal{U}\cap \mathcal{I}=\varnothing$ and $\mathcal{U}\cup \mathcal{I}=\mathcal{C}$. Let $s_{kp}$ and $i_{\ell p}$ be the number or density of individuals in uninfected and infected compartments, respectively, with $k\in \mathcal{U}$, $\ell \in \mathcal{I}$ and $p\in \mathcal{P}$. Then for all $k\in \mathcal{U}$, $\ell \in \mathcal{I}$ and $p\in \mathcal{P}$, (1) can be written

$$s_{kp}^{\prime }=f_{kp}\left(S_p,I_p,N_p\right)+\sum _{q\in \mathcal{P}}{m}_{kpq}{s}_{kq}$$ (3a)

$$i_{\ell p}^{\prime }=g_{\ell p}\left(S_p,I_p,N_p\right)+\sum _{q\in \mathcal{P}}{m}_{\ell pq}{i}_{\ell q},$$ (3b)

where $S_p=\left(s_{1p},\dots ,s_{\left|\mathcal{U}\right|p}\right)$, $I_p=\left(i_{1p},\dots ,i_{\left|\mathcal{I}\right|p}\right)$ and $N_p=\sum _{u\in \mathcal{U}}{s}_{up}+\sum _{\ell \in \mathcal{I}}{i}_{\ell p}$.

6. Metapopulation models – an example

To illustrate the type of results that can be obtained about metapopulation epidemic models, we consider a $\left|\mathcal{P}\right|$-SLIRS model. To that end, we start with a classic SLIRS (SEIRS) model,

$$S^{\prime }=b-\text{Φ}-dS+\nu R$$ (4a)

$$L^{\prime }=\text{Φ}-\left(\epsilon +d\right)L$$ (4b)

$$I^{\prime }=\epsilon L-\left(\gamma +d\right)I$$ (4c)

$$R^{\prime }=\gamma I-\left(\nu +d\right)R,$$ (4d)

with the incidence function $\text{Φ}$ taking the form

$$\text{Φ}=\beta \frac{SI}{N^{\eta }},\eta \in \left\{\mathrm{0,1}\right\}\text{.}$$ (4)

This model is classic so we do not discuss it at length here. S, L, I and R are, respectively, the numbers of susceptible, latently infected (incubating), infectious and immune individuals in the population, with $N=S+L+I+R$ the total population. Birth is into the susceptible compartment (there is no vertical transmission of the disease) at the rate b. Death is per capita in all compartments. Infection occurs when infecting contacts take place between infectious and susceptible individuals, with β the disease transmission coefficient and $\eta \in \left\{\mathrm{0,1}\right\}$ to indicate mass action when $\eta =0$ or standard incidence when $\eta =1$. Newly infected individuals incubate in the L compartment for an average $1/\epsilon$ time units then progress to an active infection in the I compartment. The active phase lasts an average $1/\gamma$ time units, after which individuals progress to the immune stage, where they remain for an average $1/\nu$ time units.

To transform (4) into a metapopulation model, all variables and parameters are given an index, p, to indicate which patch $p\in \mathcal{P}$ is under consideration. The base SLIRS is then replicated in each patch and movement terms are added. As a consequence, the $\left|\mathcal{P}\right|$-SLIRS metapopulation extension of (4) is the following system, considered for all $p\in \mathcal{P}$,

$$S_p^{\prime }=b_p-{\text{Φ}}_p-d_p{S}_p+{\nu }_p{R}_p+\sum _{q\in \mathcal{P}}{m}_{Spq}{S}_q$$ (5a)

$$L_p^{\prime }={\text{Φ}}_p-\left({\epsilon }_p+d_p\right)L_p+\sum _{q\in \mathcal{P}}{m}_{Lpq}{L}_q$$ (5b)

$$I_p^{\prime }={\epsilon }_p{L}_p-\left({\gamma }_p+d_p\right)I_p+\sum _{q\in \mathcal{P}}{m}_{Ipq}{I}_q$$ (5c)

$$R_p^{\prime }={\gamma }_p{I}_p-\left({\nu }_p+d_p\right)R_p+\sum _{q\in \mathcal{P}}{m}_{Rpq}{R}_q,$$ (5d)

with the incidence function ${\text{Φ}}_p$ taking the form

$${\text{Φ}}_p={\beta }_p\frac{S_p{I}_p}{N_p^{{\eta }_p}},{\eta }_p\in \left\{\mathrm{0,1}\right\}\text{.}$$ (5)

Note that ${\eta }_p$ in (5e) needs not be equal in all patches, allowing to consider a system with some patches having standard incidence and others mass action incidence. Such issues were considered for instance in Arino and Portet, 2015, Fromont et al., 2003.

In the notation of Section 5, $\mathcal{C}=\left\{S,L,I,R\right\}$, $\mathcal{U}=\left\{S,R\right\}$, $\mathcal{I}=\left\{L,I\right\}$. System (5) has $4\left|\mathcal{P}\right|$ equations. However, it is easier to study than this high dimensionality typically entails, since it possesses a lot of “structure”: there are $\left|\mathcal{P}\right|$ linearly coupled copies of individual units, each comprising 4 equations, the dynamics of which is well understood. In a sense, this is a “good case” of a large-scale system. We show in the following sections how to exploit this structure.

6.1. Behaviour of the total population

Consider the total population $N_p=S_p+L_p+I_p+R_p$ in (5). We have

$$N_p^{\prime }=b_p-d_p{N}_p+\sum _{X\in \left\{S,L,I,R\right\}}\sum _{q\in \mathcal{P}}{m}_{Xpq}{X}_q\text{.}$$ (6)

Writing $X\in \left\{S,L,I,R\right\}$, let $\mathbf{b}={\left(b_1,\dots ,b_{\left|\mathcal{P}\right|}\right)}^T,\mathbf{N}={\left(N_1,\dots ,N_{\left|\mathcal{P}\right|}\right)}^T,\mathbf{X}={\left(X_1,\dots ,X_{\left|\mathcal{P}\right|}\right)}^T\in {\mathrm{ℝ}}^{\left|\mathcal{P}\right|}$ be vectors and $\mathbf{d}=\mathsf{diag}\left(d_1,\dots ,d_{\left|\mathcal{P}\right|}\right)$, ${\mathcal{M}}^X$ be $\left|\mathcal{P}\right|\times \left|\mathcal{P}\right|$-matrices, with

$${\mathcal{M}}^X=\left(\begin{array}{ccc}-\sum _{q\in \mathcal{P}}{m}_{Xq1}& m_{X12}& m_{X1\left|\mathcal{P}\right|}\\ m_{X21}& -\sum _{q\in \mathcal{P}}{m}_{Xq2}& m_{X2\left|\mathcal{P}\right|}\\ m_{X\left|\mathcal{P}\right|1}& m_{X\left|\mathcal{P}\right|2}& -\sum _{q\in \mathcal{P}}{m}_{Xq\left|\mathcal{P}\right|}\end{array}\right).$$ (7)

Then (6) can be written as

$$N^{\prime }=\mathbf{b}-\mathbf{d}\mathbf{N}+\sum _{X\in \left\{S,L,I,R\right\}}{\mathcal{M}}^X\mathbf{X}\text{.}$$ (8)

It is useful to derive some properties of the movement matrix (7). For a matrix M, define $\sigma \left(M\right)=\{\lambda \in \mathrm{ℂ};Av=\lambda v,v\ne 0\}$, the spectrum of $\mathcal{M}$, $\tau \left(\mathcal{M}\right)=\text{max}\{\mathrm{\Re }\left(\lambda \right);\lambda \in \sigma \left(\mathcal{M}\right)\}$ the spectral absissa of $\mathcal{M}$ and $\rho \left(\mathcal{M}\right)=\text{max}\left\{\right|\lambda |;\lambda \in \sigma \left(M\right)\}$ the spectral radius of $\mathcal{M}$. Furthermore, we use the same notation as Berman and Plemmons (1994) for matrices and vectors: $M\ge 0$ if $m_{ij}\ge 0$ for all $i,j$; $M>0$ if $M\ge 0$ and $\exists \left(i,j\right)$ such that $m_{ij}>0$; $M\gg 0$ if $m_{ij}>0$ for all $i,j$.

Lemma 1

Let ${\mathcal{M}}^c$ be a $\left|\mathcal{P}\right|\times \left|\mathcal{P}\right|$-movement matrix for compartment $c\in \mathcal{C}$. Then the following hold true:

• 1.$-{\mathcal{M}}^c$ is a singular M-matrix.
• 2.$\tau \left({\mathcal{M}}^c\right)=0$.
• 3.$\tau \left({\mathcal{M}}^c\right)\in \sigma \left({\mathcal{M}}^c\right)$.
• 4.One of the left eigenvectors associated to the eigenvalue $\tau \left({\mathcal{M}}^s\right)=0$ is the vector $1_{\left|\mathcal{P}\right|}^T=\left(1,\dots ,1\right)$.
• 5.If additionally, ${\mathcal{M}}^c$ is irreducible, then $\tau \left({\mathcal{M}}^c\right)=0$ has multiplicity 1, $1_{\left|\mathcal{P}\right|}^T$ is (to a multiple) the only strongly positive left eigenvector associated with ${\mathcal{M}}^c$ and there is a strongly positive eigenvector $v^{\text{*}}$ corresponding to $\tau \left({\mathcal{M}}^c\right)$.
• 6.Let $\mathbf{D}>0$ be a diagonal matrix. If $\mathbf{D}\gg 0$, then $\mathbf{D}-{\mathcal{M}}^c$ is a nonsingular M-matrix and ${\left(\mathbf{D}-{\mathcal{M}}^c\right)}^{-1}>0$. If ${\mathcal{M}}^c$ is irreducible, then $\mathbf{D}-{\mathcal{M}}^c$ is a nonsingular M-matrix and ${\left(\mathbf{D}-{\mathcal{M}}^c\right)}^{-1}\gg 0$.

PROOF. Points 1–5 are shown for example in Arino and Portet (2015). To prove 6, first consider the case $\mathbf{D}\gg 0$. Define $\underset{¯}{d}={\text{min}}_{p\in \mathcal{P}}\left\{d_{pp}\right\}>0$. Then $-{\mathcal{M}}^c\le \underset{¯}{d}\mathbb{I}-{\mathcal{M}}^c\le \mathbf{D}-{\mathcal{M}}^c$. From Fiedler (2008, Theorem 5.2.5), $\underset{¯}{d}\mathbb{I}-{\mathcal{M}}^c$ is an M-matrix. Since $\tau \left({\mathcal{M}}^c\right)=0$, using a “spectrum shift” (Horn & Johnson, 2013, Problem 1.2.P8), all eigenvalues of $\underset{¯}{d}\mathbb{I}-{\mathcal{M}}^c$ have real parts larger than $\underset{¯}{d}$, so $\underset{¯}{d}-{\mathcal{M}}^c$ is a nonsingular M-matrix. In turn, Fiedler (2008, Theorem 5.1.1.4) implies that $\mathbf{D}-{\mathcal{M}}^c$ is a nonsingular M-matrix and Fiedler (2008, Theorem 5.1.1.11) allows to conclude. Suppose now that ${\mathcal{M}}^c$ is irreducible. Let $\overline{d}={\text{max}}_{p\in \mathcal{P}}\left\{d_{pp}\right\}>0$. Then $\mathbf{D}-{\mathcal{M}}^c$ is irreducibly diagonally dominant with all columns $k\in \mathcal{P}$ such that $d_{kk}=\overline{d}$ satisfying the strict diagonal dominance requirement. As a consequence, Varga (2004, Theorem 1.11) implies that $\mathbf{D}-{\mathcal{M}}^c$ is nonsingular and inverse positivity follows from Fiedler (2008), Theorem 5.2.10).

Note also that for each compartment, $-{\mathcal{M}}^c$ is a nonsymmetric Laplacian matrix. This implies that additional results are available about the spectrum of ${\mathcal{M}}^c$; see, e.g., Agaev and Chebotarev (2005). We characterize the relations between movement matrices as follows. We say movement is equal for all compartments if ${\mathcal{M}}^S={\mathcal{M}}^L={\mathcal{M}}^I={\mathcal{M}}^R=:\mathcal{M}$; movement is similar for all compartments if the zero/nonzero patterns in all matrices are the same but not the entries. Finally, movement is dissimilar across compartments if there are two movement matrices with different zero/nonzero patterns.

Case of movement equal for all compartments. Equation (8) reduces to

$$N^{\prime }=\mathbf{b}-\mathbf{d}\mathbf{N}+\mathcal{M}\mathbf{N}\text{,}$$ (9)

giving the equilibrium solution ${\mathbf{N}}^{\text{*}}={\left(\mathbf{d}-\mathcal{M}\right)}^{-1}\mathbf{b}$, which, by 6 in Lemma 1, exists if all death rates are positive or $\mathcal{M}$ is irreducible. Assume either of these properties holds. To show that ${\mathbf{N}}^{\text{*}}$ attracts all solutions of (9), consider $Df$, the Jacobian of $f\left(\mathbf{N}\right):=\mathbf{b}-\mathbf{d}\mathbf{N}+\mathcal{M}\mathbf{N}$. We have $Df=\mathcal{M}-\mathbf{d}$. Since $\mathbf{d}$ is nonsingular, we have $\tau \left(\mathcal{M}-\mathbf{d}\right)<0$, so ${\text{lim}}_{t\to \infty }\mathbf{N}\left(t\right)={\left(\mathbf{d}-\mathcal{M}\right)}^{-1}\mathbf{b}$. This is summarized as follows.

Theorem 2

Suppose that movement is equal for all compartments and that all death rates are positive or the (common) movement matrix $\mathcal{M}$ is irreducible. Then

$${\mathbf{N}}^{\text{*}}:=\underset{t\to \infty }{\text{lim}}\mathbf{N}\left(t\right)\gg 0.$$

It is actually quite “difficult” to be in a situation where : if $\mathbf{b}\gg 0$ and $\mathbf{d}-\mathcal{M}$ is a nonsingular M-matrix, then strong positivity of ${\mathbf{N}}^{\text{*}}$ is guaranteed. Thus, except if $\mathbf{d}=0$ or $\mathbf{b}\ge 0$ with some zero entries, ${\mathbf{N}}^{\text{*}}\gg 0$.

Case of unequal movement. When movement is not equal for all compartments, the problem is more complicated and, to the best of our knowledge, still open in general. To operate within a manageable context, assume movement rates are similar for all compartments. This situation might arise for instance in the case where infectious individuals are less prone to travel. Let

$$\underset{¯}{\mathcal{M}}={\left[\underset{X\in \left\{S,L,I,R\right\}}{\text{min}}{m}_{Xpq}\right]}_{pq,p\ne q}\underset{¯}{\mathcal{M}}={\left[\underset{X\in \left\{S,L,I,R\right\}}{\text{max}}{m}_{Xpq}\right]}_{pq,p=q}$$

and

$$\overline{\mathcal{M}}={\left[\underset{X\in \left\{S,L,I,R\right\}}{\text{max}}{m}_{Xpq}\right]}_{pq,p\ne q}\overline{\mathcal{M}}={\left[\underset{X\in \left\{S,L,I,R\right\}}{\text{min}}{m}_{Xpq}\right]}_{pq,p=q}.$$

Using these matrices in (8) gives the following inequality:

$$\mathbf{b}-\mathbf{d}\mathbf{N}+\underset{¯}{\mathcal{M}}\mathbf{N}\le N^{\prime }\le \mathbf{b}-\mathbf{d}\mathbf{N}+\overline{\mathcal{M}}\mathbf{N}\text{.}$$

here, $\underset{¯}{\mathcal{M}}$ and $\overline{\mathcal{M}}$ are obtained from movement matrices but are not movement matrices in the sense of Lemma 1; in particular, their column sums are not all zero. It follows that the upper bound grows unbounded and the lower bound does not guarantee nonnegativity.

Note that this does not preclude conducting an analysis of the system. Indeed, some authors have considered models with movement similar for all compartments or even dissimilar across compartments (as might arise if infectious individuals are not allowed some movements – as has been the case with HIV positive individuals travelling to some countries, for instance). However, in this case, results such as Theorem 2 are not readily available and the analysis typically relies on properties of the system embedded in the patches.

6.2. The disease free equilibrium (DFE)

Assume (5) is at equilibrium with $L_p=I_p=0$ for $p\in \mathcal{P}$. Then ${\text{Φ}}_p=0$ and for all $p\in \mathcal{P}$,

$$0=b_p-d_p{S}_p+{\nu }_p{R}_p+\sum _{q\in \mathcal{P}}{m}_{pq}^S{S}_q$$

$$0=-\left({\nu }_p+d_p\right)R_p+\sum _{q\in \mathcal{P}}{m}_{pq}^R{R}_q\text{,}$$

which we must solve for $S_p,R_p$. Here again, we write the problem in vector form. We have

$$0=\mathbf{b}-\mathbf{d}{\mathbf{S}}^{\text{*}}+\mathit{\nu }{\mathbf{R}}^{\text{*}}+{\mathcal{M}}^S{\mathbf{S}}^{\text{*}}$$

$$0=-\left(\mathit{\nu }+\mathbf{d}\right){\mathbf{R}}^{\text{*}}+{\mathcal{M}}^R{\mathbf{R}}^{\text{*}}\text{,}$$

where ${\mathbf{S}}^{\text{*}},{\mathbf{R}}^{\text{*}},\mathbf{b}\in {\mathrm{ℝ}}^{\left|\mathcal{P}\right|}$ and $\mathbf{d},\mathit{\nu }=\mathsf{diag}\left({\nu }_1,\dots ,{\nu }_{\left|\mathcal{P}\right|}\right),{\mathcal{M}}^S,{\mathcal{M}}^R$ are $\left|\mathcal{P}\right|\times \left|\mathcal{P}\right|$-matrices. We have

$$0=-\left(\mathit{\nu }+\mathbf{d}\right){\mathbf{R}}^{\text{*}}+{\mathcal{M}}^R{\mathbf{R}}^{\text{*}}\iff \left({\mathcal{M}}^R-\mathit{\nu }-\mathbf{d}\right){\mathbf{R}}^{\text{*}}=0\text{,}$$

so the solution ${\mathbf{R}}^{\text{*}}=0$ is unique if ${\mathcal{M}}^R-\mathit{\nu }-\mathbf{d}$ is invertible. This is similar to the proof of Theorem 2 and uses Lemma 1. We thus find that ${\text{lim}}_{t\to \infty }\mathbf{R}\left(t\right)=0$ provided that $\mathit{\nu }+\mathbf{d}\gg 0$ or ${\mathcal{M}}^r$ irreducible. Provided this is true, at the DFE, there holds that ${\mathbf{L}}^{\text{*}}={\mathbf{I}}^{\text{*}}={\mathbf{R}}^{\text{*}}=0$ and $\mathbf{b}-\mathbf{d}\mathbf{S}+{\mathcal{M}}^S{\mathbf{S}}^{\text{*}}=0$, i.e., ${\mathbf{S}}^{\text{*}}={\left(\mathbf{d}-{\mathcal{M}}^S\right)}^{-1}\mathbf{b}$. To summarize, provided all death rates are positive or ${\mathcal{M}}^R$ and ${\mathcal{M}}^S$ irreducible, then the DFE takes the form

$$\left({\mathbf{S}}^{\text{*}},{\mathbf{L}}^{\text{*}},{\mathbf{I}}^{\text{*}},{\mathbf{R}}^{\text{*}}\right)=\left({\left(\mathbf{d}-{\mathcal{M}}^S\right)}^{-1}\mathbf{b},\mathrm{0,0,0}\right).$$

Note that ${\mathbf{S}}^{\text{*}}={\mathbf{N}}^{\text{*}}$ at the DFE.

6.3. Computation of ${\mathcal{R}}_0$ and local stability of the DFE

Use the next generation method (van den Driessche & Watmough, 2002) with infected variables L and I ordered as

$${\mathcal{X}}_{\mathcal{I}}=\left\{L_1,\dots ,L_{\left|\mathcal{P}\right|},I_1,\dots ,I_{\left|\mathcal{P}\right|}\right\}\text{.}$$

Write the dynamics of the subsystem of (5) in the variables ${\mathcal{X}}_{\mathcal{I}}$ as ${\mathcal{X}}_{\mathcal{I}}^{\prime }=\mathcal{F}-\mathcal{V}$, with $\mathcal{F}={\left({\text{Φ}}_1,\dots ,{\text{Φ}}_{\left|\mathcal{P}\right|},0,\dots ,0\right)}^T$ and $\mathcal{V}$ having all other flows (with a negative sign). Differentiating $\mathcal{F}$ with respect to ${\mathcal{X}}_{\mathcal{I}}$, first note that whenever $k\ne p$,

$$\frac{\partial {\text{Φ}}_p}{\partial L_k}=\frac{\partial {\text{Φ}}_p}{\partial I_k}=0\text{,}$$

since there are no contacts between individuals not located in the same patch. Thus,

$$D\mathcal{F}=\left(\begin{array}{cc}\mathsf{diag}\left(\frac{\partial {\text{Φ}}_1}{\partial L_1},\dots ,\frac{\partial {\text{Φ}}_{\left|\mathcal{P}\right|}}{\partial L_{\left|\mathcal{P}\right|}}\right)& \mathsf{diag}\left(\frac{\partial {\text{Φ}}_1}{\partial I_1},\dots ,\frac{\partial {\text{Φ}}_{\left|\mathcal{P}\right|}}{\partial I_{\left|\mathcal{P}\right|}}\right)\\ 0& 0\end{array}\right)\text{.}$$

Suppose that ${\text{Φ}}_p={\beta }_p{S}_p{I}_p$, i.e., ${\eta }_p=0$. Then $\partial {\text{Φ}}_p/\partial L_p=0$ and $\partial {\text{Φ}}_p/\partial I_p={\beta }_p{S}_p$. At the DFE, $\partial {\text{Φ}}_p/\partial I_p={\beta }_p{N}_p^{\text{*}}$. Suppose that ${\text{Φ}}_p={\beta }_p{S}_p{I}_p/N_p$, i.e., ${\eta }_p=1$. Then $\partial {\text{Φ}}_p/\partial L_p=-{\beta }_p{S}_p{I}_p/N_p^2$ and $\partial {\text{Φ}}_p/\partial I_p={\beta }_p{S}_p/N_p-{\beta }_p{S}_p{I}_p/N_p$. Thus, at the DFE, $\partial {\text{Φ}}_p/\partial L_p=0$ and $\partial {\text{Φ}}_p/\partial I_p={\beta }_p$. Thus,

$$\frac{\partial {\text{Φ}}_p}{\partial L_p}{|}_{DFE}=0\text{and}\frac{\partial {\text{Φ}}_p}{\partial I_p}{|}_{DFE}={\beta }_p{\left(N^{\text{*}}\right)}^{1-{\eta }_p}\text{.}$$

As a consequence,

$$F=D\mathcal{F}{|}_{DFE}=\left(\begin{array}{cc}0& \mathsf{diag}\left(\frac{\partial {\text{Φ}}_1}{\partial I_1}{|}_{DFE},\dots ,\frac{\partial {\text{Φ}}_{\left|\mathcal{P}\right|}}{\partial I_{\left|\mathcal{P}\right|}}{|}_{DFE}\right)\\ 0& 0\end{array}\right)=:\left(\begin{array}{cc}0& F_{12}\\ 0& 0\end{array}\right).$$ (10)

On the other hand,

$$V=\mathcal{D}\mathcal{V}{|}_{DFE}=\left(\begin{array}{cc}\mathsf{dia}{\mathsf{g}}_p\left({\epsilon }_p+d_p\right)-{\mathcal{M}}^L& 0\\ -\mathsf{dia}{\mathsf{g}}_p\left({\epsilon }_p\right)& \mathsf{dia}{\mathsf{g}}_p\left({\gamma }_p+d_p\right)-{\mathcal{M}}^I\end{array}\right)\text{,}$$

where the notation $\mathsf{dia}{\mathsf{g}}_p\left(z_p\right)=\mathsf{diag}\left(z_1,\dots ,z_{\left|\mathcal{P}\right|}\right)$ is used for simplicity. Thus, using the formula for the inverse of a $2\times 2$ block matrix (Horn & Johnson, 2013), Section 7.3,

$$V^{-1}=(\begin{array}{cc}{\left(\mathsf{dia}{\mathsf{g}}_p\left({\epsilon }_p+d_p\right)-{\mathcal{M}}^L\right)}^{-1}& 0\\ {\tilde{V}}_{21}^{-1}& {\left(\mathsf{dia}{\mathsf{g}}_p\left({\gamma }_p+d_p\right)-{\mathcal{M}}^I\right)}^{-1}\end{array})\text{,}$$

where

$${\tilde{V}}_{21}^{-1}={\left(\mathsf{dia}{\mathsf{g}}_p\left({\epsilon }_p+d_p\right)-{\mathcal{M}}^L\right)}^{-1}\mathsf{dia}{\mathsf{g}}_p\left({\epsilon }_p\right){\left(\mathsf{dia}{\mathsf{g}}_p\left({\gamma }_p+d_p\right)-{\mathcal{M}}^I\right)}^{-1}\text{.}$$ (11)

So we obtain the next generation matrix

$$F{V}^{-1}=\left(\begin{array}{cc}0& F_{12}\\ 0& 0\end{array}\right)\left(\begin{array}{cc}{\tilde{V}}_{11}^{-1}& 0\\ {\tilde{V}}_{21}^{-1}& {\tilde{V}}_{22}^{-1}\end{array}\right)=\left(\begin{array}{cc}{F}_{12}{\tilde{V}}_{21}^{-1}& F_{12}{\tilde{V}}_{22}^{-1}\\ 0& 0\end{array}\right)\text{,}$$

where ${\tilde{V}}_{ij}^{-1}$ is the block $ij$ in $V^{-1}$. So ${\mathcal{R}}_0=\rho \left(F_{12}{\tilde{V}}_{21}^{-1}\right)$. It is difficult to go further without more information. However, given parameter values, ${\mathcal{R}}_0$ is easy to compute numerically. In terms of the local asymptotic stability of the DFE, (van den Driessche & Watmough, 2002), Theorem 2 gives the following result.

Theorem 3

Define ${\mathcal{R}}_0$ for the $\left|\mathcal{P}\right|$-SLIRS (5) as

$${\mathcal{R}}_0=\rho \left(F_{12}{\tilde{V}}_{21}^{-1}\right),$$ (12)

with $F_{12}$ and ${\tilde{V}}_{21}^{-1}$ defined by (10) and (11), respectively. Then the DFE

$$\left({\mathbf{S}}^{\text{*}},{\mathbf{L}}^{\text{*}},{\mathbf{I}}^{\text{*}},{\mathbf{R}}^{\text{*}}\right)=\left({\left(\mathbf{d}-{\mathcal{M}}^S\right)}^{-1}\mathbf{b},\mathrm{0,0,0}\right)$$

is locally asymptotically stable if ${\mathcal{R}}_0<1$ and unstable if ${\mathcal{R}}_0>1$.

7. Further considerations

Because of space, we have focused on the mathematical properties that are required in order to conduct a basic analysis of metapopulation epidemic models. Several additional fascinating problems exist which we now briefly present.

7.1. Global stability of the DFE

Several methods are available to consider global stability properties of the DFE in metapopulation models and have been used successfully in many cases. Note that it has also been shown that metapopulation models can exhibit backward bifurcations (Arino, Ducrot, & Zongo, 2012), so proving the global asymptotic stability of the DFE will not always be possible.

7.2. Existence and stability of an endemic equilibrium point (EEP)

The problem of existence and stability of an endemic equilibrium point where the disease is present in all patches is more complex and cannot yet be attacked in full generality. Some interesting examples are those in Iggidr et al., 2012, Li and Shuai, 2009.

7.3. Inheritance of dynamical properties

Most of the problems mentioned above are solved by exploiting the fact that metapopulations are linearly coupled copies of constituting units whose behaviour is known. This poses a very interesting problem, the inheritance problem. Consider model (3) with no movement,

$$s_{kp}^{\prime }=f_{kp}\left(S_p,I_p,N_p\right)$$ (13a)

$$i_{\ell p}^{\prime }=g_{\ell p}\left(S_p,I_p,N_p\right),$$ (13b)

where $k\in \mathcal{U}$, $\ell \in \mathcal{I}$ and $p\in \mathcal{P}$. Think of (13) as representing any model for a single population found in the literature. Within a given patch p, suppose some dynamical properties are known about (13). Which of these properties also hold for the general system with mobility (3)? It is relatively easy to show that such things as existence and boundedness of solutions is preserved. As shown in this article, the same is true to some extent of existence and local asymptotic stability of the DFE. As we have just seen, global asymptotic stability is not as easy to settle. Techniques such as the one in Li and Shuai (2010) allow to envision a general treatment of this issue when a Lyapunov function is known for the isolated model.

7.4. Metapopulation specific behaviour – mixed equilibria

A problem essentially dual to that of inheritance consists in seeking properties that hold for the metapopulation system (3) but not for uncoupled population level model (13). A prototypical example here is the problem of mixed equilibria, first considered in Arino and van den Driessche (2003). Consider a metapopulation such as (3) in which, when there is no movement, i.e., in the case of (13), some patches are at the DFE while others are at an EEP. It is shown in Arino (2009) that for such mixed equilibria to persist in the presence of movement, movement must be dissimilar between uninfected and infected compartments.

7.5. Deterministic simulations

It is worth noting that numerical simulations of metapopulation models such as (5) are simple to set up and not extremely onerous on modern computers for systems with a reasonable number of patches. Sample code in R and MatLab is provided as electronic appendices to the present paper to illustrate this.

7.6. Stochastic simulations

When dealing with problems related to the fast spatial spread of a pathogen such as SARS (Section 4.1), systems of ordinary differential equations allow to investigate an average behaviour but do not capture the range of potential outcomes that occur in an actual “real life” crisis. For this reason, stochastic simulations of metapopulation models have been carried out; see, e.g., Arino et al., 2011, Colizza and Vespignani, 2008.

Appendix A. Supplementary data

The following are the supplementary data related to this article: