In-host modeling

Abstract

Understanding the mechanisms governing host-pathogen kinetics is important and can guide human interventions. In-host mathematical models, together with biological data, have been used in this endeavor. In this review, we present basic models used to describe acute and chronic pathogenic infections. We highlight the power of model predictions, the role of drug therapy, and advantage of considering the dynamics of immune responses. We also present the limitations of these models due in part to the trade-off between the complexity of the model and their predictive power, and the challenges a modeler faces in determining the appropriate formulation for a given problem.

1. Introduction

Mathematical models of in-host pathogen kinetics have improved our understanding of the mechanistic interactions that govern chronic infections with pathogens such as HIV (Arinaminpathy, Metcalf, & Grenfell, 2014, pp. 81–96; Ciupe et al., 2006, Frascoli et al., 2013, Heffernan and Wahl, 2005, Heffernan and Wahl, 2006, Ho et al., 1995, Nowak and May, 2001, Perelson and Nelson, 1999, Perelson and Ribeiro, 2013, Perelson et al., 1996, Schwartz et al., 2016, Smith and Wahl, 2004, Stafford et al., 2000, Wang et al., 2009, Wei et al., 1995), hepatitis B (Ciupe et al., 2007a, Ciupe et al., 2007b, Dahari et al., 2009, Lewin et al., 2001, Nowak and May, 2001, Nowak et al., 1996, Qesmi et al., 2010, Qesmi et al., 2011, Ribeiro et al., 2010a, Tsiang et al., 1999, Whalley et al., 2001, Wodarz, 2005, Wodarz, 2014), hepatitis C (Canini and Perelson, 2014, Dahari et al., 2011, Guedj et al., 2010, Herrmann et al., 2000, Neumann et al., 1998a, Neumann et al., 1998b, Neumann et al., 2000, Qesmi et al., 2010, Qesmi et al., 2011, Reluga et al., 2009, Rong et al., 2013, Snoeck et al., 2010, Wodarz, 2005), tuberculosis (Du et al., 2017, Gammack et al., 2004, Gong et al., 2015, Guirado and Schlesinger, 2013, Linderman and Kirschner, 2015, Marino and Kirschner, 2004, Wigginton and Kirschner, 2001); as well as acute infections such as influenza (Arinaminpathy et al., 2014, pp. 81–96; Baccam et al., 2006, Beauchemin and Handel, 2011, Beauchemin et al., 2008, Cao et al., 2015, Dobrovolny et al., 2013, Hadjichrysanthou et al., 2016, Handel et al., 2010, Murillo et al., 2013, Pawelek et al., 2012, Price et al., 2015, Smith et al., 2013), dengue (Ben-Shachar and Koelle, 2015, Clapham et al., 2014, Nikin-Beers and Ciupe, 2015, Nikin-Beers and Ciupe, 2016), and malaria (Childs and Buckee, 2015, De Leenheer and Pilyugin, 2008, Simpson et al., 2014). Analytical investigation of these models has helped quantify the in-host basic reproduction numbers ($R_0$), which estimate the number of secondary infections that arise from one infected cell over the course of its life-span at the beginning of infection when cells susceptible to infection are not depleted. Numerical investigation and data fitting of in-host models have also helped uncover important biological parameters, including the pathogen and infected cell half-lives and the daily pathogen production. Most importantly, such models have been used to estimate the efficacy of different drug therapies, the strength of the immune responses (innate and/or adaptive immune responses), and to ultimately make predictions of disease outcome.

In this paper, we provide a review of in-host mathematical models. We present model variations of chronic and acute infections, changes observed through the incorporation of different components of the immune response and drug therapy, and the role of the data in validating the theoretical results. We conclude with a discussion on the trade-off between model complexity and its power to inform outcomes.

2. Basic model of pathogen dynamics

Depending on the pathogen being studied, the basic model of pathogen dynamics must include certain characteristics that are ‘basic’ to the disease dynamics in-host. These include, for example, the cells that the pathogen infects, the existence of the pathogen in the host (i.e. in what areas of the body pathogen particles may reside in), the time-scale of the infection of the host (i.e. long-lived and persistent (chronic) or short-lived (acute) infections) and the life-cycle of the pathogen (which includes all of the different methods by which the pathogen can produce progeny). Taking these points into consideration, one would thus expect that the basic model of infection with different pathogen types (i.e., virus, bacteria, parasite) would vary. It is interesting to note, however, that the format of the basic model for each type is very similar and may differ in very few respects. In this section we outline the basic models of pathogen dynamics that encapsulate the aforementioned ‘basic’ characteristics of infection in-host. These models are termed ‘target cell-limitation’ models because they do not explicitly incorporate the effects of the immune responses, and the pathogen decay from the peak infection is due to infection and depletion of the majority of target cells. We begin with the most famous and widely used basic model, the basic model of chronic virus infections.

2.1. Chronic virus infections

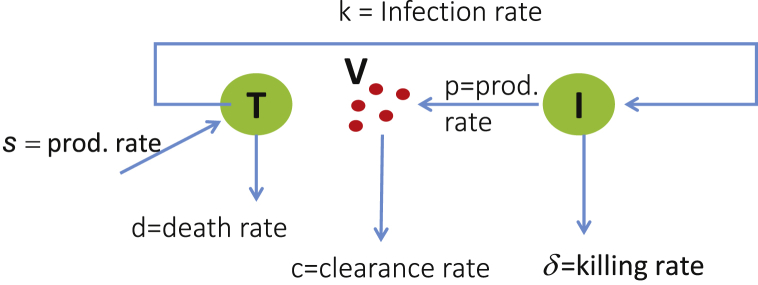
First used to model HIV in-host viral kinetics (Ho et al., 1995, Perelson et al., 1993, Perelson et al., 1996), the basic model describing the interaction between uninfected target cells T, infected cells I, and the virus V, is presented in the diagram from Fig. 1 and governed by the following system of differential equations:

$$\begin{array}{ll}\frac{dT}{dt}& =s-dT-\beta TV,\\ \frac{dI}{dt}& =\beta TV-\delta I,\\ \frac{dV}{dt}& =pI-cV.\end{array}$$ (1)

Fig. 1.

Model diagram for Eq. (1).

Briefly, uninfected target cells are produced by the body at a constant rate (s), and have a natural death rate d where $1/d$ is the expected lifetime of an uninfected target cell. Uninfected target cells T can be infected by virus particles V at rate β, producing infected target cells I. It is assumed that infected target cells have a death rate $\delta \ge d$, depending on the pathogen being considered. Finally, infected target cells produce virus particles V at rate p and these are either degraded or cleared by the immune system at rate c.

Analysis of Eq. (1) shows that there are two different equilibria, a disease free equilibrium ($E_0$), and one where the patient is chronically infected ($E_1$). The disease free and infected equilibria are given by:

$$E_0=\left(\frac{s}{d},\mathrm{0,0}\right),$$

and

$$E_1=\left(\frac{c\delta }{p\beta },\frac{p\beta s-c\delta d}{p\delta \beta },\frac{p\beta s-c\delta d}{c\delta \beta }\right).$$

We note here that the infected equilibrium cannot exist if

$$R_0<1,$$

where

$$R_0=\frac{p\beta T_0}{\delta c},$$ (2)

and $T_0=s/d$ is the target cell count at the disease free equilibrium $E_0$. $R_0$ given by Eq. (2) is called the basic reproduction number (or basic reproductive ratio), which is defined as the number of infected cells (or virus particles) that are produced by one infected cell (or virus particle), when the virus it is introduced into a population of uninfected target cells $T_0$. Local stability analysis of Eq. (1) shows that $E_0$ is locally asymptotically stable when $R_0<1$ (the infection dies out), and $E_1$ is locally asymptotically stable when $R_0>1$ (the infection takes off and leads to chronic infections). Additionally, it has been shown that $E_0$ and $E_1$ are globally asymptotically stable when $R_0\le 1$ and $R_0>1$, respectively. For further information computing the basic reproduction number see (van den Driessche and Watmough, 2002, Roberts and Heesterbeek, 2003, Heffernan et al., 2005, Diekmann et al., 1990) and on global stability analysis see (Korobeinikov, 2004, Smith and De Leenheer, 2003).

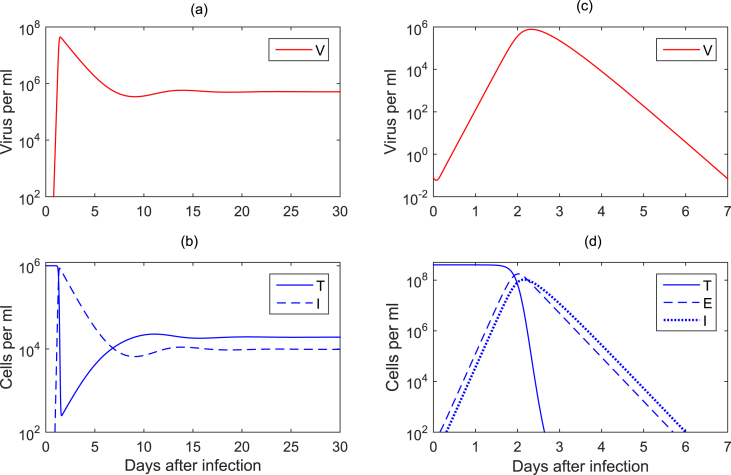
Eq. (1) has been used extensively to model HIV pathogenesis (Nowak and May, 2000, Perelson, 2002, Perelson and Ribeiro, 2013, Wodarz, 2014). For HIV infection, variables T and I represent the uninfected and infected CD4 T cells, which are the main driver of the adaptive immune responses. T are produced by the thymus at constant rate s per ml per day, die at per capita rate d, and become infected at rate β. Infected CD4 T cells I die at increased per capita rate $\delta >d$, and produce an average of p virions per day. Virus V is cleared at per capita rate c. The dynamics of variable V given by Eq. (1) encapsulate the exponential growth of HIV population, followed by the decay to a persistent equilibrium value (Fig. 2a). Variations of the model have considered HIV bursting, with $p=N\delta$ accounting for N virions being produced over the infected cell life-span $1/\delta$ (Ciupe et al., 2006). Fitting of variable V given by Eq. (1) to longitudinal HIV patient data have provided estimates of the infected cell and virus particle death and clearance rates, and of the virus production rates (Ho et al., 1995, Perelson and Ribeiro, 2013, Perelson et al., 1997, Wei et al., 1995, Wodarz, 2014). The model has also been used to determine the basic reproduction number $R_0$. Current estimates of $R_0$ are $R_0=8$ (2.3 if an eclipse phase is considered) (Kakizoe et al., 2015, Petravic et al., 2014, Ribeiro et al., 2010b) for HIV1-B and $R_0=5.3$ for HIV1-C (Shet, Nagaraja, & Dixit, 2016).

Fig. 2.

(a)–(b) Virus and cell dynamics for a chronic virus infection given by Eq. (1) for parameters $\left(s,d,\beta ,\delta ,p,c\right)=\left({10}^4,0.01,{10}^{-6},\mathrm{1,1200,23}\right)$ and initial conditions $\left(T,I,V\right)\left(0\right)=\left({10}^6,0,{10}^{-6}\right)$ as in (Stafford et al., 2000); (c)–(d) Virus and cell dynamics for a chronic virus infection given by Eq. (6) for parameters $\left(\beta ,k,\delta ,p,c\right)=\left(3.2\times {10}^{-5},\mathrm{4,5.2},4.6\times {10}^{-2},5.2\right)$ and initial conditions $\left(T,E,I,V\right)\left(0\right)=\left(4\times {10}^8,\mathrm{0,0,7.5}\times {10}^{-2}\right)$ as in (Baccam et al., 2006).

Eq. (1) has been adapted to other chronic infections with viruses such as hepatitis B and hepatitis C. In both of these infections, T and I account for uninfected and infected liver cells (hepatocytes). In order to model the liver's ability to regenerate, two logistic growth terms have been added to Eq. (1) for the proliferation of uninfected and infected hepatocytes, respectively (Ciupe et al., 2007a, Ciupe et al., 2007b, Ciupe et al., 2011a, Dahari et al., 2009, Lewin et al., 2001, Ribeiro et al., 2010a). They are $r_{T}T\left(1-\frac{T+I}{T_m}\right)$ and $r_{I}I\left(1-\frac{T+I}{T_m}\right)$, where $r_T$ and $r_I$ are maximal per capita division rate of uninfected and infected hepatocytes and $T_m$ is the liver carrying capacity. Moreover, in the case of hepatitis B infection, a cure of infected hepatocytes has been considered, with a fraction $\rho I$ moving from the infected class to the uninfected class (Ciupe et al., 2007a, Dahari et al., 2009, Lewin et al., 2001). When cell proliferation and cell cure are included in the model, Eq. (1) becomes:

$$\begin{array}{ll}\frac{dT}{dt}& =s+r_{T}T\left(1-\frac{T+I}{T_m}\right)-dT-\beta TV+\rho I,\\ \frac{dI}{dt}& =\beta TV+r_{I}I\left(1-\frac{T+I}{T_m}\right)-\delta I-\rho I,\\ \frac{dV}{dt}& =pI-cV.\end{array}$$ (3)

The analysis of these systems predicts two outcomes of infection – virus clearance described by a disease free steady state

$$E_0=\left(T_0,\mathrm{0,0}\right),$$

where

$$T_0=\frac{T_m}{2r_T}\left(r_T-d+\sqrt{{\left(r_T-d\right)}^2+\frac{4s{r}_T}{T_m}}\right),$$

$r_T>d$ (and $s\le d{T}_m$ to have a physiologically realistic number of target cells given a carrying capacity $T_m$); and a virus persistence described by a chronically infected steady state (Dahari et al., 2009)

$$E_1=\left(\overline{T},\overline{I},\overline{V}\right),$$

where:

$$\overline{V}=\frac{p\overline{I}}{c}\text{ and }\overline{I}=\left(\frac{\beta p{T}_m}{r_{Y}c}-1\right)\overline{T}-T_m\left(\frac{\delta +\rho }{r_Y}-1\right),$$

and $\overline{T}$ is the positive solution of

$$s+r_T\overline{T}\left(1-\frac{\overline{T}+\overline{I}}{T_m}\right)-dT-\frac{\beta p}{c}\overline{T}\overline{I}+\rho \overline{I}=0.$$

Similar to the analysis of Eq. (1), it can be shown that the virus is cleared when $R_0<1$, and it persists when $R_0>1$, for a modified $R_0$ given by:

$$R_0=\frac{p\beta T_0}{c[\rho +\delta +r_Y\left(\frac{T_0}{T_m}-1\right)]},$$ (4)

which simplifies to $R_0=\frac{p\beta T_0}{c{\delta }_1}$ when $T_0=T_m=s/d$, ${\delta }_1=\delta +\rho$. Current estimates for the basic reproduction numbers are $R_0=5$ for hepatitis B (Whalley et al., 2001) and $=7.2$ for hepatitis C (Snoeck et al., 2010).

2.2. Acute virus infections

Unlike chronic infections, acute infections with pathogens such as influenza, dengue, and Zika viruses are very fast and of short duration, with all infections resolving over the course of one to three weeks (depending on the pathogen characteristics). When viral resolution is fast (i.e., recovery/clearance of infection is gained over a short period of time), the target cell production and death rates can be ignored in Eq. (1). A model of acute infections can thus be described by:

$$\begin{array}{ll}\frac{dT}{dt}& =-\beta TV,\\ \frac{dI}{dt}& =\beta TV-\delta I,\\ \frac{dV}{dt}& =pI-cV.\end{array}$$ (5)

Eq. (5) has a single disease free steady state $E_0=\left(N,\mathrm{0,0}\right)$, where N is a constant. The basic reproduction number $R_0$ is the same as that in Eq. (2) (for a known initial target cell population $T_0$), and the acute infection is experienced by a host only when $R_0>1$. This means that the virus and infected target cell populations increase and then decrease, eventually reaching the disease free steady state. This model is mainly used to model dengue virus infections (Ben-Shachar and Koelle, 2015, Clapham et al., 2014, Nikin-Beers and Ciupe, 2015, Nikin-Beers and Ciupe, 2016).

Most models of influenza infection consider an additional latent (or eclipse) phase of infection. In this scenario, target epithelial cells T become infected at rate β, undergo a latent phase E, and, after an interval of time $1/k$, become infectious cells I, who start producing virus (Baccam et al., 2006, Beauchemin and Handel, 2011, Beauchemin et al., 2008, Pawelek et al., 2012, Smith et al., 2013). Such a model can be described by the following system of differential equations:

$$\begin{array}{ll}\frac{dT}{dt}& =-\beta TV,\\ \frac{dE}{dt}& =\beta TV-kE,\\ \frac{dI}{dt}& =kE-\delta I,\\ \frac{dV}{dt}& =pI-cV.\end{array}$$ (6)

Like Eq. (5), Eq. (6) has only the disease free equilibrium $E_0=\left(N,\mathrm{0,0,0}\right)$, with N being a constant. The basic reproduction number $R_0$ also remains the same, for a known initial target cell population $T_0$. We note here that the variable V given by both models (5) and (6) can reproduce the dynamics seen in acute influenza viral infections, where the virus reaches a peak 2–3 days post infection and resolves 7 days post infection (Fig. 2c). The variable V given in Eq. (6), however, represents the timeframe of the biological processes behind target cell infection and virus production more adequately. The basic reproduction number of influenza has been estimated to be $R_0=22$ for H1N1 infections (Baccam et al., 2006), and $R_0=49$ for the 1918 influenza pandemic (Smith et al., 2011). The estimates for the basic reproduction number in all virus infection studies are subject to uncertainty due to intra-patient and viral subtype variability.

2.3. Self-replicating pathogens

Some pathogens contain everything that they need to reproduce themselves (i.e., bacterial infections). In such cases a pathogen can replicate through division/proliferation and through target-cell infection. For example, the persistence of Mycobacterium tuberculosis (MTB) (the bacteria that cause tuberculosis (TB)) inside an individual includes: (i) the infection of target cells which manufacture MTB bacteria and subsequent MTB release into the body, and (2) MTB division every 16–20 h. The basic model for self-replicating pathogens can simply be represented by extending the basic model given by Eq. (1) to include pathogen self-replication. An example of such a model is:

$$\begin{array}{ll}\frac{dT}{dt}& =s-dT-\beta TV,\\ \frac{dI}{dt}& =\beta TV-\delta I,\\ \frac{dV}{dt}& =f\left(V\right)+pI-cV,\end{array}$$ (7)

where $f\left(V\right)$ is a replication function that is deemed appropriate for the pathogen being studied. For example, it may be assumed that pathogen growth can be approximated using logistic growth, i.e. $f\left(V\right)=rV\left(1-V/K\right)$, where r is the growth rate and K is the carrying capacity of pathogen load in a defined volume.

The steady states of Eq. (7), $\left(\overline{T},\overline{I},\overline{V}\right)$, are given by:

$$\begin{array}{ll}\overline{T}& =\frac{s}{d+\beta \overline{V}},\\ \overline{I}& =\frac{\beta s\overline{V}}{\left(d+\beta \overline{V}\right)\delta },\end{array}$$ (8)

and $\overline{V}$ satisfies:

$$f\left(\overline{V}\right)+\frac{p\beta s\overline{V}}{\left(d+\beta \overline{V}\right)\delta }-c\overline{V}=0.$$ (9)

When $f\left(V\right)=rV\left(1-V/K\right)$, Eq. (9) becomes:

$$\overline{V}\left(-r\beta \delta {\overline{V}}^2+\left(r\delta K\beta -rd\delta -c\beta k\delta \right)\overline{V}+rd\delta K+p\beta sK-cd\delta K\right)=0.$$ (10)

Eq. (10) has two real roots. The first real root, $\overline{V}=0$, corresponds to a disease free equilibrium $E_0=\left(s/d,\mathrm{0,0}\right)$. The other real root satisfies:

$$-r\beta \delta {\overline{V}}^2+\left(r\delta K\beta -rd\delta -c\beta k\delta \right)\overline{V}+rd\delta K+p\beta sK-cd\delta K=0,$$

and corresponds to an infected equilibrium $E_1$. It is important to note that there is only one real root of this equation, and this root only exists when

$$rd\delta +p\beta s-cd\delta <0.$$ (11)

The derivation of the basic reproduction number for Eq. (7) is not as straight forward as the derivations for Eqs. (1), (5), (6). The main difficulty comes from the fact that the derivation of $R_0$ depends on whether infection was initiated by one infectious pathogen particle, or one infected cell. Given an initial pathogen particle and $f\left(V\right)=rV\left(1-V/K\right)$, the basic reproduction number is:

$$R_{0,V}=\frac{r}{c}+\frac{p\beta T_0}{c\delta },$$ (12)

where the first term gives the total number of new pathogen particles produced by division/proliferation and the second term gives the number of new pathogens produced through the infection of target cells. However, if infection is initiated with one infected cell, the basic reproduction number would be given by

$$R_{0,I}=\frac{p}{\delta }\frac{\beta T_0}{c-r},$$ (13)

where $p/\delta$ is the number of new pathogen particles produced by an infected cell, and $\beta T_0/\left(c-r\right)$ is the number of new infected cells produced by these new particles in their average life-span $1/\left(c-r\right)$. We note, however, that Eqs. (12), (13) provide the same threshold condition that ensures the existence of the infected equilibria $E_1$ and define the local stability of the disease free and infected equilibria. Here, $E_0$ is locally asymptotically stable when $R_0<1$, and $E_1$ is locally asymptotically stable when $R_0>1$.

Eq. (7) provides the simplest model structure for a self-replicating pathogen. Recently, Yu et al. (Du et al., 2017) derived a system of four equations that can be used to model all of the disease outcomes observed from MTB infection: clearance, fast progression, slow progression, and latency. Compared to Eq. (7) it includes an equation to model immune system interference, and assumed a logistic growth term for the MTB population. While this model is by no means ‘basic’ (in that complex interaction terms were needed to represent the interactions between the immune system and the pathogen population), this model provides a drastic dimension reduction from other models of MTB infection (Gammack et al., 2004, Marino and Kirschner, 2004, Wigginton and Kirschner, 2001).

2.4. Considering a term for pathogen loss

In general, pathogen replication involves the infection of target cells. Within the infection process the pathogen particles lose their infectiousness as they are either (1) absorbed into the cell, or (2) have injected proteins needed to induce the cell to produce new particles and are, in turn, degraded. Both infection processes, thus, render the pathogen non-existent in the future. Pathogen loss due to infection is not reflected in the basic models of pathogen dynamics (Eqs. (1), (2), (3), (4), (5), (6), (7)). To appropriately capture this feature, a pathogen loss term can be included into the pathogen equation. The basic model (i.e., Eq. (1)) with the pathogen loss term becomes:

$$\begin{array}{ll}\frac{dT}{dt}& =s-dT-\beta TV,\\ \frac{dI}{dt}& =\beta TV-\delta I,\\ \frac{dV}{dt}& =pI-cV-{\beta }_{I}TV,\end{array}$$ (14)

where s, and d are chosen so as to appropriately reflect the timescale of the infection, and ${\beta }_I\ge \beta$ is the rate at which the pathogen particles are lost due to the ‘infection’ of target cells. Often it is assumed, however, that ${\beta }_I=\beta$ so that the mathematical analysis is much simpler. Here, we assume that ${\beta }_I=\beta$.

Eq. (14) has two equilibria. The uninfected equilibrium is similar to that of the basic models presented above, and is $E_0=\left(s/d,\mathrm{0,0}\right)$. The infected equilibrium $E_1=\left(\overline{T},\overline{I},\overline{V}\right)$ is described by

$$\begin{array}{ll}\overline{T}& =\frac{c\delta }{\beta \left(p-\delta \right)},\\ \overline{I}& =\frac{s\beta \left(p-\delta \right)-dc\delta }{\beta \delta \left(p-\delta \right)},\\ \overline{V}& =\frac{s\beta \left(p-\delta \right)-dc\delta }{c\beta \delta }.\end{array}$$ (15)

As before, the existence of the infected equilibrium $E_1$ and the local asymptotic stability of both equilibria $E_0$ and $E_1$ depends on the size of $R_0$ compared to unity. For Eq. (14),

$$R_{0,loss}=\frac{\beta T_0}{c+\beta T_0}\frac{p}{\delta }.$$ (16)

We note that the analysis of an extended version of Eq. (14), which includes pathogen self-replication, may become quite complex. For such an extension, there may be more than one infected equilibrium; $R_{0,I,loss}$ and $R_{0,V,loss}$ are different; and the basic reproduction numbers may not provide the full criteria for the existence and local stability of the uninfected and infected equilibria (i.e., a backward bifurcation may exist). We leave exploration of this to the reader.

Eq. (14) can be approximated by Eq. (1) if $\beta T\ll c$. In fact, this is generally assumed to be the case. However, this may not be true. For example, in a study of influenza infection in-vitro, Beauchemin et al. (2008) found that the virus loss due to infection had a similar magnitude to virus clearance, and that a model that included the virus loss term better fitted the data. Moreover, when one models the beginning of an infection where the target cell population is large, the $\beta T_0$ and c terms may also have similar magnitudes.

Mathematically there is great benefit in ignoring the virus loss term, but the modeling results may lead to misinterpretation and overestimation. As an example we compare the first terms in $R_{0,loss}$ and $R_0$, which are used to represent the two biological processes that are needed for pathogen replication using target cells, $\beta T_0/\left(c+\beta T_0\right)$ and $\beta T_0/c$. Here, $\beta T_0/\left(c+\beta T_0\right)$ gives the probability that a pathogen particle infects a cell, but $\beta T_0/c$ is interpreted as the number of infected cells that one pathogen particle makes in its lifetime $1/c$. Clearly, since a pathogen particle can only infect one cell, $R_{0,loss}$ provides a better representation and interpretation of the underlying biology than $R_0$. Also, at the beginning of an infection, if $\beta T_0$ and c have similar magnitude, then $R_{0,loss}$ would be the appropriate expression for the basic reproduction number, and $R_0$ would provide an overestimate of the number of new infected cells (or virus particles) produced by an infected cell (or virus particle) which invaded naive target population.

Finally, we note that studies of in-host pathogenesis that include stochasticity and/or stochastic dynamics (i.e., stochastic models), must include the pathogen loss term so as to appropriately capture the inherent variability in the pathogen and target cell populations seen in infected hosts. Studies by Heffernan and Wahl (2006) also show that the covariance between the target cell and virus population must also be included if it is significantly large compared to $\beta TV$. When covariance must be considered, the basic model becomes:

$$\begin{array}{ll}\frac{dT}{dt}& =s-dT-\beta TV+\beta cov\left(T,V\right),\\ \frac{dI}{dt}& =\beta TV-\beta cov\left(T,V\right)-\delta I,\\ \frac{dV}{dt}& =pI-cV-{\beta }_{I}TV+{\beta }_{I}cov\left(T,V\right).\end{array}$$ (17)

where $cov\left(T,V\right)$ is the covariance measure between the T and V populations. Covariance provides a measure of the strength of the correlation between these two populations. If the two populations are independent of each other, then $cov\left(T,V\right)=0$, and the basic model of virus dynamics with the virus loss term (Eq. (14)) is recovered. Through the infection process, however, it is evident that the T and V populations both decrease when a virus particle infects a target cell. Therefore, $cov\left(T,V\right)\ne 0$, but the magnitude of $cov\left(T,V\right)$ may be very small. Eq. (17) can be derived from first principles using probability generating functions or moment generating functions. Comparisons of model results, between the basic model with (Eq. (17)) and without (Eq. (14)) the covariance terms, and/or between the basic model (Eq. (14)) and a stochastic simulation allow one to determine when the covariance term cannot be ignored. We refer the reader to Heffernan and Wahl (2006) and Yuan and Allen (2011) for example derivations of the basic model from first principles, and example comparisons between models that ignore or include the covariance term.

3. Models of disease control

An important question that arises from the study of in-host pathogen dynamics is in determining the type of control mechanisms that can affect disease progression and persistence. This has been addressed through modeling therapeutics and immune modulatory mechanisms, which we will detail in the next sections.

3.1. Incorporating drug therapy

Effects of drug therapy have been incorporated from the early stages of in-host dynamics, when antiretroviral combination therapy (ART) against HIV was added to Eq. (1). Briefly, ART has been modeled as a reduction of the virus infectivity in the presence of reverse transcriptase inhibitors to $\beta \left(1-\eta \right)$ and a reduction in the production of infectious virions in the presence of protease inhibitors to $p\left(1-\mathit{\varepsilon }\right)$. Here $0\le \mathit{\varepsilon },\eta \le 1$ are the drug efficacies (Perelson et al., 1996, Perelson et al., 1997). The model in the presence of ART becomes:

$$\begin{array}{ll}\frac{dT}{dt}& =s-dT-\left(1-\eta \right)\beta T{V}_I,\\ \frac{dI}{dt}& =\left(1-\eta \right)\beta T{V}_I-\delta I,\\ \frac{d{V}_I}{dt}& =\left(1-\varepsilon \right)pI-c{V}_I,\\ \frac{d{V}_U}{dt}& =\varepsilon pI-c{V}_U,\end{array}$$ (18)

where $V_I$ and $V_U$ account for infectious and non-infectious viral particles. This model gives estimates for the minimal drug efficacy that can lead to virus clearance. Indeed if

$${\mathit{\varepsilon }}_{tot}=1-\left(1-\mathit{\varepsilon }\right)\left(1-\eta \right)>1-1/R_0,$$ (19)

then the virus will be removed. This and modifications of this approach have been used for the study of drug therapy in HIV, hepatitis C, hepatitis B, influenza and TB (see (Baccam et al., 2006, Beauchemin and Handel, 2011, Bonhoeffer et al., 1997, Canini and Perelson, 2014, Dahari et al., 2009, Dahari et al., 2011, Dobrovolny et al., 2013, Du et al., 2017, Eftimie et al., 2016, Forde et al., 2016, Guedj et al., 2010, Heffernan and Wahl, 2005, Heffernan and Wahl, 2006, Lau et al., 2000, Lewin et al., 2001, Linderman and Kirschner, 2015, Neumann et al., 1998a, Nowak and May, 2000, Pawelek et al., 2012, Perelson and Ribeiro, 2013, Rong and Perelson, 2010, Rong et al., 2013, Schwartz et al., 2016, Simpson et al., 2014, Smith and Wahl, 2004, Snoeck et al., 2010, Tsiang et al., 1999) for examples).

More realism can be incorporated into models like Eq. (18) if one considers that drug efficacy varies with time. Under this hypothesis, a ‘pharamacodynamics (PD)’ model can be added to the ‘pharmacokinetic (PK)’ model (18), describing drug effectiveness over time $\mathit{\varepsilon }\left(t\right)$ to be:

$$\mathit{\varepsilon }\left(t\right)=\frac{C{\left(t\right)}^n}{C{\left(t\right)}^n+E{C}_{50}^n},$$ (20)

where $C\left(t\right)$ is the drug concentration at time t, $E{C}_{50}$ is the drug concentration in the blood where the drug is half-maximal, and n is a Hill coefficient (Holford & Sheiner, 1981). Variations of such PK-PD models have been used in the investigation of drug efficacy in infections with hepatitis C (Canini and Perelson, 2014, Canini et al., 2015, Dahari et al., 2010, Shudo et al., 2008, Talal et al., 2006), influenza (Beauchemin et al., 2008, Canini et al., 2014), and HIV (Mohanty & Dixit, 2008).

3.2. Models of immune responses to virus infections

The immune system is the first line of defense against pathogens, and works to eliminate pathogens from the body in many different ways. The immune response is made of a combination of non-specific and specific reactions to pathogens that allow for effective detection and clearance/elimination of the pathogen from all regions in the body. In times where the immune response fails to control the pathogen on its own, human interventions can be used to aid the immune system through preventive or therapeutic vaccines (which induce immunity and memory) or through drug therapies. In this section we provide some examples of basic models of in-host dynamics including the innate (non-specific) and adaptive (including B-cells, antibodies and/or T-cells) immune responses.

3.2.1. Innate immune responses

While the kinetics described in Fig. 2c are a good indicator of the viral data in most acute infections, the virus RNA follow a bimodal decay in some patients infected with influenza. To describe this behaviour, mathematical models that included innate immune responses, in particular type-1 interferon (IFN), have been developed. Interferon responses are detected as early as 24 h post influenza infections (Lamb, Krug, & Knipe, 2001). They interfere with RNA synthesis and/or translation. A number of papers have used mathematical models to describe the influenza kinetics in the presence of innate immune responses (see (Beauchemin and Handel, 2011, Smith and Perelson, 2011, Smith and Ribeiro, 2010) for recent reviews). They involve an inclusion into Eq. (6) of an equation for the IFN, F, dynamics:

$$\frac{dF}{dt}=\alpha I\left(t-\tau \right)-d_{F}F,$$ (21)

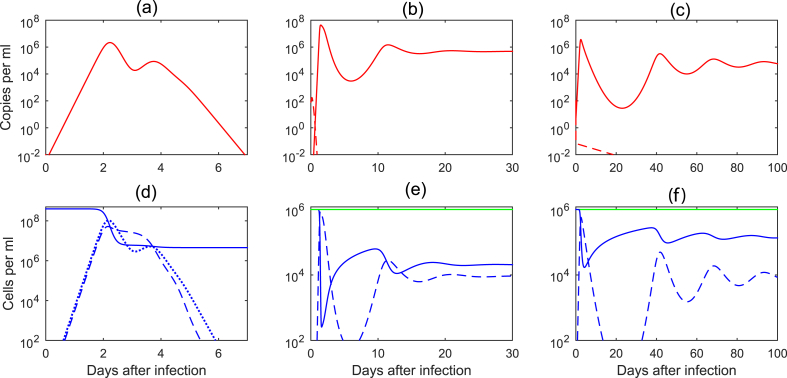
where α is the IFN production by infectious cells, $d_F$ is the IFN degradation, and τ is the delay in IFN production. The effect of IFN virus production has been modeled as a decrease in infectivity rate to ${\beta }_1=\frac{\beta }{1+{\mathit{\varepsilon }}_{1}F}$ and a decrease in the production rate $p_1=\frac{p}{1+{\mathit{\varepsilon }}_{2}F}$ (Baccam et al., 2006, Pawelek et al., 2012). With this change, the model correctly incorporated the bimodal viral peak and predicted that the first viral peak is due to delay in IFN production. When target cell depletion happens, virus decays and, consequently, both infected cells and IFN level drop. The fall of IFN leads to increased production of virions from the remaining infected cells. Hence, the second viral peak is observed (see Fig. 3a). Most importantly, this model is no longer a ’target limited model’, as the target population is not depleted by the virus (see Fig. 3d).

Fig. 3.

Virus and cell dynamics for: (a)–(d) innate immune responses to acute virus infection given by Eqs. (6), (7), (8), (9), (10), (11), (12), (13), (14), (15), (16), (17), (18), (19), (20), (21), parameters $\left(\beta ,\delta ,p,c,\alpha ,k,\tau ,d_F,{\mathit{\varepsilon }}_1,{\mathit{\varepsilon }}_2\right)=\left(4.2\times {10}^{-6},\mathrm{7,0.32},13.4,\mathrm{1,26.6},0.5,5.2,3.5\times {10}^{-6},3\times {10}^{-7}\right)$ and initial conditions $\left(T,E,I,V,F\right)\left(0\right)=\left(4\times {10}^8,\mathrm{0,0},{10}^{-2},1\right)$ as in (Baccam et al., 2006, Pawelek et al., 2012); (b)–(e) cellular immune responses to chronic virus infection given by Eq. (23) for parameters $\left(s,d,\beta ,\delta ,p,c,\mu ,d_E\right)=\left({10}^4,0.01,{10}^{-6},\mathrm{1,1200,23}\right)$, $\left(s_E,\alpha ,\mu ,d_E\right)=\left(\mathrm{0,0,0,0}\right)$ (solid lines), $\left(s_E,\alpha ,\mu ,d_E\right)=\left(300,{10}^{-5},\mathrm{1,0.5}\right)$ (dashed lines), and initial conditions $\left(T,I,V,E\right)\left(0\right)=\left({10}^6,\mathrm{0,100,10}\right)$; (c)–(f) humoral immune responses to chronic virus infection given by Eq. (25) for parameters $\left(s,d,\beta ,\delta ,p,c\right)=\left({10}^4,0.01,{10}^{-6},\mathrm{1,1200,23}\right)$, $\left(\alpha ,c_A,d_A,s_A\right)=\left(\mathrm{0,0,0,0}\right)$ (solid lines), $\left(\alpha ,c_A,d_A,s_A\right)=\left({10}^{-6},\mathrm{92,0.07},1\right)$ (dashed lines) and initial conditions $\left(T,I,V,A\right)\left(0\right)=\left({10}^6,\mathrm{0,100,14}\right)$.

3.2.2. Cellular immune responses

Cytotoxic T-lymphocytes (CTL, also known as activated CD8 T-cells) contribute to the immune response by increasing the killing of infected target cells, or through production of cytokines that purge the pathogen from an infected cell without killing it. The cytotoxic effect is an effect that has been addressed the most through modeling, either indirectly or directly; in an implicit or explicit manner (see (Wodarz, 2007)). In an implicit formulation/inclusion of the CTL we can simply assume that the infected cell death rate δ is greater than the death rate of the uninfected cells d, $\delta >d$. This consideration (in most models) is due to both direct pathogen induced killing of an infected cell, but also due to increased killing by cytotoxic immune effects and can be modeled directly, for example, using

$$\delta ={\delta }_0+{\delta }_{1}f\left(t-\tau \right),$$ (22)

where ${\delta }_0$ is the death rate associated to the viral effects, and ${\delta }_{1}f\left(t-\tau \right)$ represents the temporal CTL effects including a delay τ in CTL response. Such a model has been used to model HIV primary infection (Stafford et al., 2000).

An explicit CTL formulation includes an equation for the CTL effector cell dynamics E, such that the basic model becomes:

$$\begin{array}{l}\frac{dT}{dt}=s-dT-\beta TV,\\ \frac{dI}{dt}=\beta TV-\delta I-\mu IE,\\ \frac{dV}{dt}=pI-cV,\\ \frac{dE}{dt}=g\left(I\left(t-\tau \right),E\left(t-\tau \right)\right)-d_{E}E,\end{array}$$ (23)

where μ is the killing rate of the infected target cells, $g\left(I\left(t-\tau \right),E\left(t-\tau \right)\right)$ is a function that describes the delay in activation and expansion into the CTL class of the CD8 T cells, and $1/d_E$ is the CD8 T cell life-span. The function $g\left(I\left(t-\tau \right),E\left(t-\tau \right)\right)$ is often assumed to be a constant $g\left(I\left(t-\tau \right),E\left(t-\tau \right)\right)=\alpha$, or a mass-action type interaction $g\left(I\left(t-\tau \right),E\left(t-\tau \right)\right)=\alpha I\left(t-\tau \right)E\left(t-\tau \right)$ (Ciupe et al., 2006, Nowak and May, 2001, Wodarz, 2007). The non-cytotoxic CD8 T cell effects (modeled mostly for hepatitis B infections), assume a transition term $\rho IE$ from the infected class into the uninfected class, or into a class temporary immune to reinfection (Ciupe et al., 2007a, Ciupe et al., 2007b, Ciupe et al., 2014).

Eq. (23) predicts two outcomes: either block of infection when enough CTL are present at the time of infection, or virus persistence at a lower level when CTL is generated after the start of infection. For $g\left(I\left(t-\tau \right),E\left(t-\tau \right)\right)=s_E+\alpha IE$, the infection dies out when

$$\frac{p\beta T_0}{\left(\delta +\mu s_E/d_E\right)c}<1,$$ (24)

and persists otherwise (see Fig. 3b, dashed versus solid lines). As in the case of innate immune response (described in section 3.2.1), these models are no longer ’target cell limited’. Indeed virus decay from the peak is immune cell-mediated rather than due to target cell depletion (see Fig. 3e).

Many viruses that induce chronic infections, do so through the evasion of immune response through generation of escape variants, or through the induction of T cell tolerance and exhaustion. Virus evolution and mutation away from the immune system has been discussed in detail in two books (Nowak and May, 2001, Wodarz, 2007). Examples of models of T (B) cell exhaustion have been developed in the context of LCMV (Johnson et al., 2011), hepatitis B (Ciupe and Hews, 2012, Ciupe et al., 2014) and HIV (Conway and Perelson, 2015, Iwami et al., 2009) infections.

3.2.3. Antibody mediated immune responses

Humoral immune responses are immune responses initiated by B cells, who upon encountering virus, expand, mutate inside germinal centers and produce antibody particles. Antibody binds the virus and either neutralizes it, or activates a cellular immune response against virus-antibody immune complexes through antibody-dependent cell-mediated cytotoxicity (ADCC) or antibody-dependent cell-mediated virus inhibition (ADCVI). The neutralizing effect of antibody has been modeled through a decrease of virus infectivity from β to $\beta /\left(1+\alpha A\left(t\right)\right)$. The ADCC and ADCVI effects have been modeled as an increase of viral clearance from c to $c+c_{A}A\left(t\right)$ (Ciupe and Schwartz, 2014, Ciupe et al., 2011b, Ciupe et al., 2014, Liu et al., 2011, Nikin-Beers and Ciupe, 2015, Tabei et al., 2012, Tomaras et al., 2008). An example of a model of antibody immune responses with both effects is:

$$\begin{array}{l}\frac{dT}{dt}=s-dT-\frac{\beta }{1+\alpha A}TV,\\ \frac{dI}{dt}=\frac{\beta }{1+\alpha A}TV-\delta I,\\ \frac{dV}{dt}=pI-cV-c_{A}VA,\\ \frac{dA}{dt}=h\left(V\left(t-\tau \right),A\left(t-\tau \right)\right)-d_{A}A,\end{array}$$ (25)

where $A\left(t\right)$ is the antibody population, $h\left(V\left(t-\tau \right),A\left(t-\tau \right)\right)-d_{A}A$ describes the dynamics of the antibody response, and α and $c_A$ are the neutralization and non-neutralization effects. For antibody dynamics without delay

$$\frac{dA}{dt}=k_{p}AV+s_A-d_{A}A,$$ (26)

one can show that the virus is cleared when

$$\frac{p\beta T_0}{\left(1+\alpha s_A/d_A\right)\left(c+c_A{s}_A/d_A\right)\delta }<1,$$ (27)

and persists otherwise (see Fig. 3c, dashed versus solid lines). As in the case of innate and cellular immune responses (described in sections 3.2.1, 3.2.2), these models are not ‘target cell limited’ - virus decay from the peak is immune cell-mediated, and not due to target cell depletion (see Fig. 3f).

4. Data and data fitting

Deciding which model to use and what biological considerations to assume largely depends on the question at hand and is usually motivated by the available data. As such, in most studies, data comes in the form of pathogen time-series, sometimes accompanied by immune response measurements (CTL or antibody time series), the time when a therapy is started, and the change in pathogen dynamics in the presence of therapy. Using the model in tandem with data has led to estimates of drug efficacy, pathogen and infected cell half-lives and predictions regarding the role and timing of immune responses in the control of the infection.

It is important to note that data is usually sparse. Determining parameters using sparse data generally leads to over fitting and uncertainty in the model structure and the parameter values. Tools to help compensate for these shortcomings come from uncertainty and sensitivity analysis, model identifiability and model comparison.

Uncertainty analysis is used to determine the range of possible outcomes that a set of possible inputs (where each input has some uncertainty, i.e. each parameter has a range of values that it can take, or it can be described by a certain probability distribution of values). This allows for the identification of parameter sets that can produce ‘realistic’ outcomes (as understood by the modeler and collaborators) and identify a ‘realistic parameter space’. Relationships between the parameters can then be studied.

Sensitivity analysis is performed in order to describe how sensitive the outcome variables are to variation in individual input parameters. Since there are multiple input parameters in a mathematical model (i.e., death rates, killing rates, production rates), a sensitivity analysis can aid in the determination of the parameters that most affect model outcomes. This can then allow for parameter reduction of the mathematical model, so that a reduction in the uncertainty of the model fit can be achieved. However, one must be careful not to over-simplify as then the model will not provide any results of merit (we delay discussion of model complexity and results to section 5). In the field of pathogen dynamics, a sensitivity analysis is usually performed using Partial Rank Correlation Coefficients (PRCC) analysis. PRCC is used to determine the statistical relationships between each input parameter and each outcome variable. A detailed description of sensitivity and uncertainty analysis, including the use of PRCC is provided in (Blower and Dowlatabadi, 1994, Marino et al., 2008).

It is important to note that one dataset including pathogen load and cell count over time really only represents one ‘realization’ of what could happen in a patient (or experiment). Also, the methods of measuring said cell counts and pathogen load can introduce uncertainty into these biological measurements. Gathering multiple datasets and performing the fitting routines over multiple patients (or experiments) can aid in reducing the uncertainty in the model structure and parameter values, however, variation with-in one patient and between patients must also be accounted for.

In short, while data fitting is used in many pathogen dynamics studies, uncertainty underlies all of these studies: noise in the data, the model structure, and the estimated parameter values. An important task of all modelers is to perform uncertainty and sensitivity analysis so that such issues can be addressed (to a point). These tools, however, allow for the identification of important model components and parameters that most affect model outcomes. These results can, in turn, inform immuno- and drug-therapy development.

5. Biological complexity vs. mathematical complexity

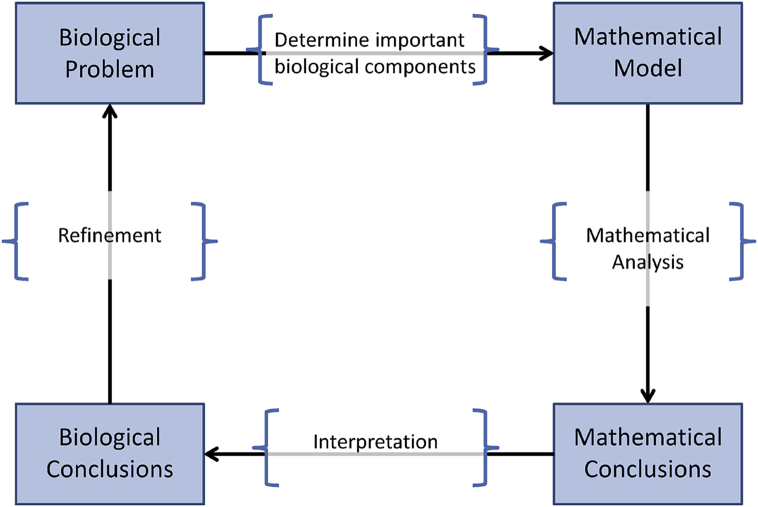
A great number of mathematical modeling textbooks, books and review articles provide a ‘pathway’ or guideline for mathematical modelers to follow to develop relevant mathematical models that can be used to address a biological question at hand. Fig. 4 provides a synopsis of these pathways. In general, given a biological problem, the task of the modeler is to (1) determine an appropriate mathematical model that incorporates the necessary and important components of the biological processes related to the biological question, (2) analyze the model (i.e., using theoretical and computational approaches, and sensitivity analysis), (3) determine a mathematical conclusion, and (4) interpret this conclusion to the related biological mechanisms. Issues that reside in this pathway, however, lie in the decision making process of which biological mechanisms must or should be included in the mathematical model, what modeling tools should be used, and how to interpret the results in a biologically meaningful way.

Fig. 4.

Modeling pathway.

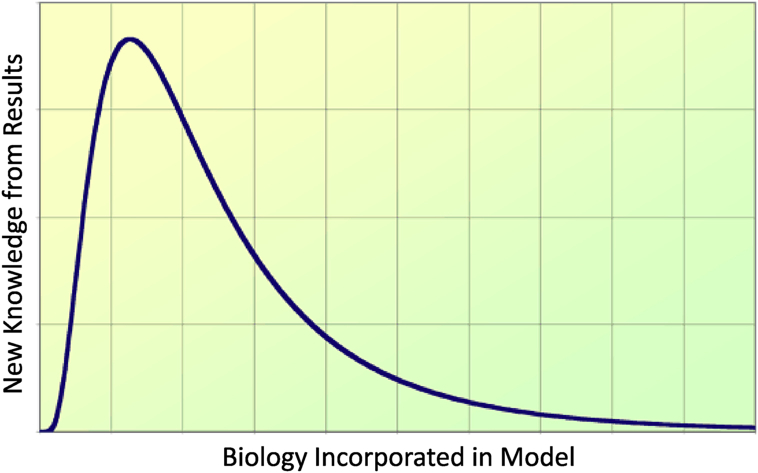
It can be very easy (and very enticing) to incorporate too much biological complexity into the mathematical model. This is a result of a desire to describe the biology in a very detailed way, but can introduce much uncertainty and complexity into the model, especially given the availability of data (see Section 4). On the other hand, it can also be very easy to oversimplify the biology. This is often a result of the modeling process whereby very simple models are required to reduce mathematical and/or computational complexity, but are often too simple to address the biological question at hand. When too much or too little biological complexity is incorporated into a model, modeling results may be sub-optimal and riddled with uncertainty. A goal of a mathematical modeler, therefore, is to optimize the level of biology that is incorporated in the model so that uncertainty is minimized, mathematical and computational complexity is manageable, and new knowledge can be produced (see Fig. 5).

Fig. 5.

Tradeoff between the incorporation of biological complexity and the applicability of model results to the biological questions at hand. The goal is to maximize new knowledge from results.

The vast majority of mathematical models that have been developed to study the in-host dynamics of infectious diseases have consisted of systems of ordinary differential equations (ODEs), the derivation of the basic reproduction number $R_0$, perhaps some simple analysis showing existence, uniqueness and local stability, and some computer/numerical simulation. A benefit to using ODEs is that there is a large library of mathematical and computational tools needed to analyze these systems, and such models/analysis have been shown to be very useful in uncovering characteristics of pathogens and immune systems dynamics (see Sections above). However, it has to be noted that the use of ODEs implicitly implies that (1) the system is ‘well-mixed’ (spatial aspects are ignored, as well as age), (2) the system is memoryless (the Markov property - exponential distributions are assumed), and (3) the system is deterministic (the same outcome is always achieved and there is no randomness). When confronted with a biological question where such assumptions are not at all representative of what is needed in a model, other more complex tools can be used. For example, if the current state of the populations should depend on something that happened in the past, then systems of delay differential equations (DDEs, or functional differential equations) can be used. If some characteristics depend on the age of a cell or pathogen particle (for example, this can be important to consider when intracellular processes operate on different timescales than the processes outside of the cell), then systems of partial differential equations (PDEs) or integral differential equations (IDEs) can be used. PDEs, IDEs and DDEs may also be needed to capture heterogeneity in distributions of infectivity, viral infectivity, the evolution of the virus, and distributions in the responsiveness of the immune reponse. Also, if sharp transitions in a state are needed, then impulsive differential equations (ImDEs) can be used. Finally, stochastic differential equations (SDEs), Monte Carlo simulations, Gillespie simulations or individual based models can be used to capture the inherent stochastic nature of host-pathogen dynamics and provide more realistic results. The mathematical complexity of systems of DDEs, PDEs, IDEs, ImDEs, SDEs is greater than that of systems of ODEs and the number of analytical tools at the hands of the modeler are limited. Thus, many modelers will turn to computer simulation and/or numerical analysis in many cases, which may result in weaker but more realistic results. Discretization of these more complex mathematical frameworks can also be conducted to obtain systems of ODEs that provide approximations to the model. However, these systems can become quite large and very complex as well, especially when levels of viral fitness, immune responsiveness and cell infection age are wanted in the model structure. The tradeoff between using systems of ODEs and other more realistic but complex models must be considered.

One method of determining whether extra complexity is needed or desired in a model is to perform an uncertainty or sensitivity analysis, whereby changes in model outcomes and changes in model parameter values are highly correlated. This allows the modeler to determine what variables and parameters are most important to the underlying dynamics and infection outcomes, and allows the modeler to perform dimension reduction, when high dimensional models are reduced to include only those variables and parameters that are needed.

Complexity in models, provided by the biology or the mathematical methods, will be an issue that needs to be considered by all modelers for all projects in the present and the future. Determining the ‘right’ level of complexity will take time, but the determination can be made easier through discussions with applied scientists, medical experts, and other mathematical modelers. We leave this discussion of complexity with two pieces of advice: (1) modelers should discuss their work and assumptions with virologists, immunologists, pathologists, etc, (but be sure to not be enticed into incorporating even more biology unless it is well justified) and (2) modelers should not be wary of trying many different mathematical and computational methods for one project to see if the complexity introduced into the model is needed, or can be simplified but still be representative of the biological processes under consideration.

6. Conclusion

In-host models can serve as powerful tools to predict and understand the dynamics of infectious diseases. These models have been used to gain new knowledge in the pathogenesis of disease in-host (including characteristics of the pathogen life-cycle), inform medicine and public health, and aid in the development of effective drug therapies and vaccines. Uncertainty and sensitivity analysis can also uncover important relationships between different pathogen and immune system components, uncover new targets for immuno- and drug-therapies, and provide direction for new experimental protocols that can provide new data to further educate models and model development. In all cases, the goal has been to identify key components of a biological process so that mathematical modeling studies can be used to provide new knowledge.