Mathematical model of Zika virus with vertical transmission

Abstract

Zika is a flavivirus transmitted to humans through either the bites of infected Aedes mosquitoes or sexual transmission. Zika has been linked to congenital anomalies such as microcephaly. In this paper, we analyze a new system of ordinary differential equations which incorporates human vertical transmission of Zika virus, the birth of babies with microcephaly and asymptomatically infected individuals. The Zika model is locally and globally asymptotically stable when the basic reproduction number is less than unity. Our model shows that asymptomatic individuals amplify the disease burden in the community, and the most important parameters for ZIKV spread are the death rate of mosquitoes, the mosquito biting rate, the mosquito recruitment rate, and the transmission per contact to mosquitoes and to adult humans. Scenario exploration indicates that personal-protection is a more effective control strategy than mosquito-reduction strategy. It also shows that delaying conception reduces the number of microcephaly cases, although this does little to prevent Zika transmission in the broader community. However, by coupling aggressive vector control and personal protection use, it is possible to reduce both microcephaly and Zika transmission. 2000 Mathematics Subject Classifications: 92B05, 93A30, 93C15.

1. Introduction

Zika virus (ZIKV) is a mosquito-borne disease transmitted to humans through the bites of infected Aedes mosquitoes, including Aedes aegypti, Aedes africanus, Aedes apicoargenteus, Aedes furcifer, Aedes hensilli, Aedes luteocephalus and Aedes vitattus. First identified in a rhesus macaque population in 1947 in the Zika forest of Uganda, ZIKV is from the Spondweni serocomplex of the Flaviviridae family of viruses. Historically, ZIKV was thought to cause mild symptoms in humans, including headaches, maculopapular rash, fever, malaise, conjunctivitis, and arthralgia, occurring three to twelve days after the bite from an infected mosquito. Recently, however, there have been reported increases in congenital anomalies (such as microcephaly), Guillain-Barre syndrome, and other neurological and autoimmune disorders in regions where ZIKV has been newly introduced (Cao-Lormeau et al., 2016, World Health Organization, 2015). Many researchers believe that ZIKV is responsible for these increases, suggesting that ZIKV is a more serious disease than initially realized.

In December 2015, the European Centre for Disease Prevention and Control issued a comprehensive update on the possible association between ZIKV, congenital microcephaly and Guillain-Barre (European Centre for Disease Prevention and Control, 2015). Most evidence, however, is correlative. In Brazil, for example, 2782 cases of microcephaly were reported in the year following ZIKV introduction, as compared with 147 cases and 167 cases in the two years prior to ZIKV arrival (Romero, 2015). Retrospective analysis of data from French Polynesia similarly uncovered an unusual number of babies born with neural defects during the height of the ZIKV outbreak (Vogel, 2016). Over this same period, French Polynesia also saw a spike in Guillain-Barre syndrome (FauciMorens, 2016, Oehler et al., 2014), as well as increases in a range of other neurologic conditions including meningitis, meningoencephalitis, and myelitis (Talan, 2016). More recently, a series of Latin American countries, including Brazil, Colombia, and Venezuela have observed similar upticks in the incidence of Guillain-Barre (World Health Organization, 2016a, World Health Organization, 2016b), consistent with the proposed relationship between this disorder and ZIKV infection.

In addition to correlative support, several clinical and lab-based findings hint at potential mechanisms to explain the link between ZIKV and neural complications (Mlakar et al., 2016). In 1952, for example, Dick et al (Dick, Kitchen, & Haddow, 1952). demonstrated ZIKV tropism to the brain in intraperitoneally infected mice. Expanding on this finding, Bell, and colleagues (Bell, Field, & Narang, 1971) later showed that both neurons and glia could be infected by ZIKV. More recently, a number of studies, have demonstrated evidence of intrauterine infection with ZIKV (Oliveira Melo et al., 2016), including infection of the fetal brain (Martines, 2015, Rubin et al., 2016). This latter finding, in particular, provides a direct path from maternal ZIKV infection to microcephaly – a rare neurological condition in which an infant's brain develops abnormally in the womb or does not grow as it should after birth (Mayo Foundation for Medical Education and Research, 2016). Ultimately, microcephaly results in an infant's head size being significantly smaller than the heads of other children of the same age and sex (Mayo Foundation for Medical Education and Research, 2016). Although microcephaly can range from mild to severe, cases currently associated with the ZIKV outbreak in Brazil are notable for the level of damage observed in the brains of affected infants (da Silva et al., 1953, Talan, 2016). Furthermore, congenital Zika usually come with a wide spectrum of clinical features (da Silva et al., 1953).

In this paper, we develop and analyze a mathematical model for ZIKV. Our focus is multi-fold. First, we consider overall ZIKV transmission in the adult population. Second, we consider ZIKV transmission to infants, either directly by mosquitoes or else prior to birth through vertical transmission from the mother. Infant ZIKV cases may be particularly severe because central nervous system (CNS) infections in young children can cause long-term damage to the developing brain (Bundy, 2014, p. 221). Finally, we consider microcephaly rates, which we assume occur as a result of vertical transmission of ZIKV to the fetus during the early stages of pregnancy. The paper is organized as follows. The model is formulated in Section 2 and we investigate the theoretical properties of the Zika model with mother-to-child vertical transmission in Section 3. In Section 4, we assess the impact of the asymptomatic classes and identify key parameters with the most impact on disease burden in Section 5. We conduct numerical exploration of three control strategies in Section 6. The study results are discussed in Section 7.

2. Model formulation

We model the transmission dynamics of ZIKV using a compartmental framework. We consider two human populations consisting of adults and newly born babies as well as the vector population. The population of newly born babies consists of susceptible $\left(S_B\left(t\right)\right)$, exposed $\left(E_B\left(t\right)\right)$, asymptomatic $\left(A_B\left(t\right)\right)$, symptomatic newly born without microcephaly, newly born with microcephaly $\left(I_{BM}\left(t\right)\right)$ and recovered newly born babies $\left(R_B\left(t\right)\right)$. The total population of adults, $N_W\left(t\right)$, at time t is split into mutually exclusive sub-populations of individuals who are susceptible $\left(S_W\left(t\right)\right)$, exposed $\left(E_W\left(t\right)\right)$, asymptomatic $\left(A_W\left(t\right)\right)$, symptomatic $\left(I_W\left(t\right)\right)$, adult with microcephaly $\left(I_{WM}\left(t\right)\right)$ and recovered adults $\left(R_W\left(t\right)\right)$. The population of the mosquitoes include the susceptible $\left(S_V\left(t\right)\right)$, exposed $\left(E_V\left(t\right)\right)$ and infected mosquitoes $\left(I_V\left(t\right)\right)$. The total population for each group is given as:

$$\begin{array}{l}{N}_B\left(t\right)=S_B\left(t\right)+E_B\left(t\right)+A_B\left(t\right)+I_B\left(t\right)+I_{BM}\left(t\right)+R_B\left(t\right),\\ N_W\left(t\right)=S_W\left(t\right)+E_W\left(t\right)+A_W\left(t\right)+I_W\left(t\right)+I_{WM}\left(t\right)+R_W\left(t\right),\\ N_V\left(t\right)=S_V\left(t\right)+E_V\left(t\right)+I_V\left(t\right)\text{.}\end{array}$$

and total human population is $N_H\left(t\right)=N_B+N_W$. Equations representing the mathematical model are given below. The flow diagram of the model is depicted in Fig. 1, and the associated state variables and parameters are described in Table 1.

$$\begin{array}{l}{S}_B^{\prime }\left(t\right)={\pi }_B-q_A{\pi }_B{A}_W\left(t\right)-q_I{\pi }_B{I}_W\left(t\right)-q_R{\pi }_B{R}_W\left(t\right)-{\lambda }_B\left(I_V,N_B\right)S_B\left(t\right)-\left(\alpha +{\mu }_B\right)S_B\left(t\right)\\ E_B^{\prime }\left(t\right)={\lambda }_B\left(I_V,N_B\right)S_B\left(t\right)-\left(\alpha +{\sigma }_B+{\mu }_B\right)E_B\left(t\right)\\ A_B^{\prime }\left(t\right)=q_A{\pi }_B{A}_W\left(t\right)+\left(1-p\right){\sigma }_B{E}_B\left(t\right)-\left(\alpha +{\gamma }_B+{\mu }_B\right)A_B\left(t\right)\\ I_B^{\prime }\left(t\right)=q_I{\pi }_B{I}_W\left(t\right)+p{\sigma }_B{E}_B\left(t\right)-\left(\alpha +{\gamma }_B+{\mu }_B\right)I_B\left(t\right)\\ I_{BM}^{\prime }\left(t\right)=r{q}_R{\pi }_B{R}_W\left(t\right)-\left(\alpha +{\mu }_B\right)I_{BM}\left(t\right)\\ R_B^{\prime }\left(t\right)=\left(1-r\right)q_R{\pi }_B{R}_W\left(t\right)+{\gamma }_B{A}_B\left(t\right)+{\gamma }_B{I}_B\left(t\right)-\left(\alpha +{\mu }_B\right)R_B\left(t\right)\\ S_W^{\prime }\left(t\right)=\alpha S_B\left(t\right)-{\lambda }_W\left(I_V,N_W\right)S_W\left(t\right)-{\mu }_W{S}_W\left(t\right)\\ E_W^{\prime }\left(t\right)={\lambda }_W\left(I_V,N_W\right)S_W\left(t\right)-\left({\sigma }_W+{\mu }_W\right)E_W\left(t\right)\\ A_W^{\prime }\left(t\right)=\left(1-p\right){\sigma }_W{E}_W\left(t\right)-\left({\gamma }_W+{\mu }_W\right)A_W\left(t\right)\\ I_W^{\prime }\left(t\right)=p{\sigma }_W{E}_W\left(t\right)-\left({\gamma }_W+{\mu }_W\right)I_W\left(t\right)\\ I_{WM}^{\prime }\left(t\right)=\alpha I_{BM}\left(t\right)-{\mu }_W{I}_{WM}\left(t\right)\\ R_W^{\prime }\left(t\right)=\alpha R_B\left(t\right)+{\gamma }_W{A}_W\left(t\right)+{\gamma }_W{I}_W\left(t\right)-{\mu }_W{R}_W\left(t\right)\\ S_V^{\prime }\left(t\right)={\pi }_V-{\lambda }_V\left(A_B,I_B,A_W,I_W,N_B,N_W\right)S_V\left(t\right)-{\mu }_V{S}_V\left(t\right)\\ E_V^{\prime }\left(t\right)={\lambda }_V\left(A_B,I_B,A_W,I_W,N_B,N_W\right)S_V\left(t\right)-\left({\mu }_V+{\sigma }_V\right)E_V\left(t\right)\\ I_V^{\prime }\left(t\right)={\sigma }_V{E}_V\left(t\right)-{\mu }_V{I}_V\left(t\right)\text{.}\end{array}$$ (2.1)

where, (′) represent derivative with respect to t, and

$$\begin{array}{l}{\lambda }_W\left(I_V,N_W\right)=\frac{{\beta }_W{b}_V{I}_V}{N_W},{\lambda }_B(I_V,N_B)=\frac{\eta {\beta }_B{b}_V{I}_V}{N_B},\\ {\lambda }_V\left(A_B,I_B,A_W,I_W,N_B,N_W\right)={\beta }_V{b}_V\left[\frac{I_W+{\rho }_W{A}_W+\eta \left(I_B+{\rho }_B{A}_B\right)}{N_W+\eta N_B}\right]\text{,}\end{array}$$

are the disease forces of infection rates, and all other parameters are as defined in Table 1. In particular, ${\beta }_W,{\beta }_B$ and ${\beta }_V$ are the transmission probability per contact in adults, newly born babies and mosquitoes, $b_V$ is the mosquito biting rate, ${\rho }_W$ and ${\rho }_B$ are modification parameters modeling the infectivity of the asymptomatic babies and adults. The parameter η is a modification parameter that indicates that babies' exposure rate is different from that of adults. For instance, they may be protected from mosquito bites, making they less likely to get the infections, on the other hand, they may receive more mosquito bites if left unprotected; we assume that $\eta >0$. We assume that the infection in the asymptomatic individuals might not be high enough to infect the susceptible mosquitoes or is the same level as for the infectious individuals, in which case the modification parameters are taken as $0\le {\rho }_B,{\rho }_W\le 1$.

Fig. 1.

Flow diagram of the Zika transmission model.

Table 1.

Description of the state variables and parameters of the Zika model (2.1).

Variable	Description
$S_B\left(t\right)$, $S_W\left(t\right)$	Susceptible newly born babies and adults
$E_B\left(t\right)$, $E_W\left(t\right)$	Exposed newly born babies and adults
$A_B\left(t\right)$, $A_W\left(t\right)$	Asymptomatic newly born babies and adults
$I_B\left(t\right)$, $I_W\left(t\right)$	Symptomatic newly born without microcephaly and adults
$I_{BM}\left(t\right)$, $I_{WM}\left(t\right)$	Microcephalic newly born babies and adults
$R_B\left(t\right)$, $R_W\left(t\right)$	Recovered newly born babies and adults
$S_V\left(t\right)$	Susceptible female mosquitoes
$E_V\left(t\right)$	Exposed female mosquitoes
$I_V\left(t\right)$	Infected female mosquitoes
Parameter	Description
${\pi }_B$	Birth rate newly born babies
p	Fraction of adults and newly born babies who are asymptomatic
$1-p$	Remaining fraction of adults and newly born babies who are infectious
α	Maturation rate
$r,q_A,q_I,q_R$	Fractions of newly born babies who are infected and have microcephaly
$1-r$	Remaining fraction of newly born babies who have microcephaly
η	Modification parameter
${\beta }_W,{\beta }_B$	Transmission probability per contact of adults and newly born babies
${\rho }_W$, ${\rho }_B$	Infectivity modification parameters in asymptomatic adults and newly born babies
${\sigma }_W,{\sigma }_B$	Progression rate of exposed adults and newly born babies
${\gamma }_W,{\gamma }_B$	Recovery rate of asymptomatic and symptomatic adults and newly born babies
${\mu }_W,{\mu }_B$	Natural death rate of adults and newly born babies
${\pi }_V$	Recruitment rate of mosquitoes
${\beta }_V$	Transmission probability per contact of susceptible mosquitoes
$b_V$	Mosquito biting rate
${\sigma }_V$	Progression rate of exposed mosquitoes
${\mu }_V$	Natural death rate of mosquitoes

Zika virus is passed prenatally from a pregnant woman to her unborn fetus (Moore et al., 2017). For example, during the 2015 Zika outbreak in Brazil, Zika virus RNA was found in the amniotic fluid of two women whose fetuses were determined via prenatal ultrasound to have microcephaly (Schuler-Faccini et al., 2016). Depending on timing of infection in the womb, newborn babies can also be infected from birth (Besnard, Lastere, Teissier, Cao-Lormeau, & Musso, 2014). Thus, we assume that some babies are born with infected with the virus. The parameters $q_A,q_I,$ $q_R$ represent fractions of newly born babies who are infected due to vertical transmission. So that the fraction ${\pi }_B\left(1-q_A{A}_W-q_I{I}_W-q_R{R}_W\right)$ are babies born healthy by infected and recovered mothers and the remaining fraction $q_A{\pi }_B{A}_W,q_I{\pi }_B{I}_W,q_R{\pi }_B{R}_W$ are born infected.

Despite the fact that there is sufficient evidence to conclude that intrauterine Zika virus infection is a cause of microcephaly (Moore et al., 2017), not all newly born babies are born with microcephaly, although they may have other congenital abnormalities (da Silva et al., 1953). We assume that some babies are born recovered from the virus. Thus, the parameter r correspond to the fraction of the $q_R{\pi }_B{R}_W$ recovered babies born by recovered mothers, while the remaining portion $\left(1-r\right)q_R{\pi }_B{R}_W$ are newly born babies who have microcephaly. The parameter p represent the fraction of adults and newly born babies who are asymptomatic and the remaining fraction $\left(1-p\right)$ are adults and newly born babies who are infectious. The parameter α denotes the maturation rate. Microcephalic individuals experience profound developmental delay (Carter, Mirzaa, McDonell, & Boycott, 2013); although their lifespan is not known, they live for a short period due to severe neurologic impairments (some have been known to live up to 9 years) (Carter et al., 2013). As a result, we assume that microcephalic adults do not reproduce.

2.1. Basic properties

We shall now explore the basic dynamical features of model (2.1). Since the model (2.1) describes both human and mosquito populations during a Zika epidemic, it will only be epidemiologically meaningful if all state variables are non-negative for $t\ge 0$. That is, its solution with positive initial data will remain positive for all time $\left(t>0\right)$.

Lemma 1

Let the initial data $F\left(0\right)\ge 0$, where $F\left(t\right)=(S_B,E_B,A_B,I_B,I_{BM},S_W,E_W,A_W,I_W,R_W,I_{WM},R_B,S_V,E_V,I_V)$. Then the solutions $F\left(t\right)$ of model (2.1) are non-negative for all time $t>0$. Furthermore

$$\underset{t\to \infty }{\text{lim}\text{sup}}{N}_H\left(t\right)\le \frac{{\pi }_B}{{\mu }_H},\underset{t\to \infty }{\text{lim}\text{sup}}{N}_V\left(t\right)=\frac{{\pi }_V}{{\mu }_V}\text{,}$$

where ${\mu }_H=\text{min}\left\{{\mu }_B,{\mu }_W\right\}\text{.}$

with,

$$\begin{array}{l}{N}_B\left(t\right)=S_B\left(t\right)+E_B\left(t\right)+A_B\left(t\right)+I_B\left(t\right)+I_{BM}\left(t\right)+R_B\left(t\right),\\ N_W\left(t\right)=S_W\left(t\right)+E_W\left(t\right)+A_W\left(t\right)+I_W\left(t\right)+I_{WM}\left(t\right)+R_W\left(t\right),\\ N_V\left(t\right)=S_V\left(t\right)+E_V\left(t\right)+I_V\left(t\right)\text{.}\end{array}$$

The proof of Lemma 1 is given in Appendix A.

Invariant regions

Model (2.1) will be analyzed in a biologically-feasible region as follows. Consider the feasible region

$$\text{Γ}={\text{Γ}}_H\times {\text{Γ}}_V\subset {\mathrm{ℝ}}_{+}^{12}\times {\mathrm{ℝ}}_{+}^3$$

with,

$$\begin{array}{l}{\text{Γ}}_H=\{S_B\left(t\right),E_B\left(t\right),A_B\left(t\right),I_B\left(t\right),I_{BM}\left(t\right),R_B\left(t\right),S_W\left(t\right),E_W\left(t\right),A_W\left(t\right),I_W\left(t\right),I_{WM}\left(t\right),R_W\left(t\right)\\ :N_H\left(t\right)=\frac{{\pi }_B}{{\mu }_H},\},\\ {\text{Γ}}_V=\{S_V\left(t\right),E_V\left(t\right),I_V\left(t\right):N_V\left(t\right)=\frac{{\pi }_V}{{\mu }_V}\}\text{.}\end{array}$$

Lemma 2

The region $={\text{Γ}}_H\times {\text{Γ}}_V\subset {\mathrm{ℝ}}_{+}^{12}\times {\mathrm{ℝ}}_{+}^3$ is positively invariant for the basic model (2.1) with non-negative initial conditions in ${\mathrm{ℝ}}_{+}^{15}$

The proof of Lemma 2 is given in Appendix B.

In the next section the conditions for the stability of the disease-free equilibrium of model (2.1) are explored.

3. Analysis of the model

Model (2.1) with endogenous reactivation and exogenous reinfection is now analyzed to gain insight into its dynamical features.

3.1. Local stability of the disease-free equilibrium

The disease free equilibrium (DFE) of model (2.1), which is obtained by setting the right hand sides of the model equations to zero is given by:

$$\begin{array}{l}{\mathcal{E}}_0=\left(S_B^{\text{*}},E_B^{\text{*}},A_B^{\text{*}},I_B^{\text{*}},I_{BM}^{\text{*}},R_B^{\text{*}},S_W^{\text{*}},E_W^{\text{*}},A_W^{\text{*}},I_W^{\text{*}},I_{WM}^{\text{*}},R_W^{\text{*}},S_V^{\text{*}},E_V^{\text{*}},I_V^{\text{*}}\right)\\ =\left(\frac{{\pi }_B}{\alpha +{\mu }_B},\mathrm{0,0,0,0,0},\frac{\alpha {\pi }_B}{{\mu }_W\left(\alpha +{\mu }_B\right)},\mathrm{0,0,0,0,0},\frac{{\pi }_V}{{\mu }_V},\mathrm{0,0}\right)\text{.}\end{array}$$ (3.1)

The local asymptotic stability of ${\mathcal{E}}_0$ can be established using the next generation operator method on the system (2.1). Taking the infected compartments $\left(E_B^{\text{*}},A_B^{\text{*}},I_B^{\text{*}},I_{BM}^{\text{*}},E_W^{\text{*}},A_W^{\text{*}},I_W^{\text{*}},I_{MW}^{\text{*}},E_V^{\text{*}},I_V^{\text{*}}\right)$ at the DFE and using the notation in (van den Driessche & Watmough, 2002), the Jacobian matrices F and V for the new infection terms and the remaining transfer terms are respectively given by,

$$F=\left(\begin{array}{ccccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 0& 0& \frac{\eta {\beta }_B{b}_V{S}_B^{\text{*}}}{N_B^{\text{*}}}\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& \frac{{\beta }_W{b}_V{S}_W^{\text{*}}}{N_W^{\text{*}}}\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& \frac{\eta {\rho }_B{\beta }_V{b}_V{S}_V^{\text{*}}}{S_W^{\text{*}}+\eta S_B^{\text{*}}}& \frac{\eta {\beta }_V{b}_V{S}_V^{\text{*}}}{S_W^{\text{*}}+\eta S_B^{\text{*}}}& 0& 0& \frac{{\rho }_W{\beta }_V{b}_V{S}_V^{\text{*}}}{S_W^{\text{*}}+\eta S_B^{\text{*}}}& \frac{{\beta }_V{b}_V{S}_V^{\text{*}}}{S_W^{\text{*}}+\eta S_B^{\text{*}}}& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right)$$

and

$$V=\left(\begin{array}{cccccccccc}{k}_2& 0& 0& 0& 0& 0& 0& 0& 0& \text{0}\\ -\left(1-p\right){\sigma }_B& k_3& 0& 0& 0& -q_A{\pi }_B& 0& 0& 0& 0\\ -p{\sigma }_B& 0& k_4& 0& 0& 0& -q_I{\pi }_B& 0& 0& 0\\ 0& 0& 0& k_5& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& k_8& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& -\left(1-p\right){\sigma }_W& k_9& 0& 0& 0& 0\\ 0& 0& 0& 0& -p{\sigma }_W& 0& k_{10}& 0& 0& 0\\ 0& 0& 0& -\alpha & 0& 0& 0& k_{12}& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& k_{14}& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& -{\sigma }_V& {\mu }_V\end{array}\right)\text{,}$$

where $k_1=\alpha +{\mu }_B,k_2=\alpha +{\sigma }_B+{\mu }_B,k_3=\alpha +{\gamma }_B+{\mu }_B,k_4=\alpha +{\gamma }_B+{\mu }_B,k_5=\alpha +{\mu }_B,k_6=\alpha +{\mu }_B,k_7={\mu }_W,k_8={\sigma }_W+{\mu }_W,k_9={\gamma }_W+{\mu }_W,k_{10}={\gamma }_W+{\mu }_W,k_{11}={\mu }_W,k_{12}={\mu }_W,k_{13}={\mu }_V,k_{14}={\mu }_V+{\sigma }_V\text{.}$

It follows that the basic reproduction number of model (2.1), denoted by ${\mathrm{ℛ}}_0$, is given by;

$${\mathrm{ℛ}}_0=\rho \left(F{V}^{-1}\right)=\sqrt{{\mathrm{ℛ}}_V\left({\mathrm{ℛ}}_W+{\mathrm{ℛ}}_B\right)}$$ (3.2)

where

$$\begin{array}{l}{\mathrm{ℛ}}_V=\frac{S_V^{\text{*}}{\beta }_V{b}_V{\sigma }_V}{k_{14}{\mu }_V},\\ {\mathrm{ℛ}}_B=\frac{{\eta }^2{\beta }_B{b}_V{\sigma }_B[{\rho }_B\left(1-p\right)k_4+p{k}_3]}{k_2{k}_3{k}_4\left(S_W^{\text{*}}+\eta S_B^{\text{*}}\right)}\\ {\mathrm{ℛ}}_W=\frac{{\beta }_W{b}_V{\sigma }_W}{k_8\left(S_W^{\text{*}}+\eta S_B^{\text{*}}\right)}[\frac{\left(1-p\right)\left(k_3{\rho }_W+\eta {\rho }_B{q}_A{\pi }_B\right)}{k_3{k}_9}+\frac{p\left(k_4+\eta q_I{\pi }_B\right)}{k_4{k}_{10}}]\text{.}\end{array}$$

The following result is established using Theorem 2 in (van den Driessche & Watmough, 2002).

Lemma 3

The DFE of model (2.1), given by ${\mathcal{E}}_0$, is locally asymptotically stable (LAS) if ${\mathrm{ℛ}}_0<1$, and unstable if ${\mathrm{ℛ}}_0>1$.

The epidemiological quantity, ${\mathrm{ℛ}}_0$ gives the average number of ZIKV cases generated by a typical infected individual introduced into an entirely susceptible human population (Anderson and May, 1991, Diekmann et al., 1990, Hethcote, 2000, van den Driessche and Watmough, 2002). Furthermore, the expression ${\mathrm{ℛ}}_B$ is the number of secondary infections in newly born babies by one introduced infectious mosquito, while the expression ${\mathrm{ℛ}}_W$ is the number of secondary infections in adults by one infectious mosquito. The expression ${\mathrm{ℛ}}_W$ consists of infections from newly born babies due to vertical transmission (mother-to-child infection) and infections due to horizontal transmissions from adults and infections from infants that have matured into adults. Lastly, the expression ${\mathrm{ℛ}}_V$ is the number of secondary infections in mosquitoes resulting from a newly introduced infectious adult woman and newly born baby. ZIKV can be adequately controlled in the community with adults and newly born babies if the threshold quantity $\left({\mathrm{ℛ}}_0\right)$ can be reduced to (and maintained at) a value less than unity (i.e. ${\mathrm{ℛ}}_0<1$).

3.2. Global asymptotic stability of the disease-free equilibrium

For Zika elimination to be independent of the initial sizes of the sub-populations of the model, the global asymptotic stability of the DFE must be established. This is what we consider next. Consider the feasible region

$${\text{Γ}}_1=\left\{X\in \text{Γ}:S_B\le S_B^{\text{*}},S_W\le S_W^{\text{*}},S_V\le S_V^{\text{*}}\right\}\text{,}$$

where, $X=R_W,S_B,E_B,A_B,I_B,I_{BM},S_W,E_W,A_W,I_W,I_{WM},R_B,S_V,E_V,I_V$.

Lemma 4

The region ${\text{Γ}}_1$ is positively invariant for model (2.1)

The proof of Lemma 4 is given in Appendix C.

Theorem 1

The DFE, ${\mathcal{E}}_0$, of model (2.1), is globally asymptotically stable (GAS) in ${\text{Γ}}_1$ whenever ${\mathrm{ℛ}}_0\le 1$.

The proof of Theorem 1 is given in Appendix D.

The above result shows that ZIKV will be eliminated from the community if the threshold quantity ${\mathrm{ℛ}}_0$ can be brought to a value less than unity.

4. Assessing the impact of the asymptomatic classes

In this section we shall explore the impact of the asymptomatically infected individuals since an estimated 80% of Zika infections do not show symptoms (Centers for Disease Control and Prevention, 2016, Duffy et al., 2009, Oster, 2016), and when infections lead to illness, the symptoms are usually mild.

Note, that we have elected to work with the square of the reproduction number, so our results remain tractable. The conclusion is not altered if the actual expression for the reproduction number is used.

Thus, differentiating the square of the basic reproduction number, ${\mathrm{ℛ}}_0^2$, given in (3.2), partially with respect to the asymptomatic modification parameters ${\rho }_B$ and ${\rho }_W$, gives

$$\frac{\partial {\mathrm{ℛ}}_0^2}{\partial {\rho }_B}=\frac{{\sigma }_V{\beta }_V{b}_V^2{S}_V^{\text{*}}\eta \left(1-p\right)\left(\eta {\sigma }_B{k}_8{k}_9+q_A{\pi }_B{\sigma }_W{\beta }_W{k}_2\right)}{k_{14}{\mu }_V{k}_2{k}_3{k}_8{k}_9\left(S_W^{\text{*}}+\eta S_B^{\text{*}}\right)}>0\text{,}$$

and

$$\frac{\partial {\mathrm{ℛ}}_0^2}{\partial {\rho }_W}=\frac{{\sigma }_V{\beta }_V{b}_V^2{S}_V^{\text{*}}\left(1-p\right){\beta }_W{\sigma }_W}{k_{14}{\mu }_V{k}_8{k}_9\left(S_W+\eta S_B^{\text{*}}\right)}>0.$$

This, implies, the square of basic reproduction number, ${\mathrm{ℛ}}_0^2$, is an increasing function of the parameters ${\rho }_B$ and ${\rho }_W$. Thus, the disease burden in the community will increase as the infectivity of the asymptomatic individuals increases.

Furthermore, if we take the limit of ${\mathrm{ℛ}}_0^2$, as ${\rho }_B\to 1$ and ${\rho }_W\to 1$ (meaning, that infectivity of the asymptomatic individuals is the same as that of the infectious individuals), we have

$$\underset{{\rho }_B\to 1,{\rho }_W\to 1}{\text{lim}}{\mathrm{ℛ}}_0={\sigma }_V{\beta }_V{b}_V^2{S}_V^{\text{*}}\{{\sigma }_W{\beta }_W{k}_2{k}_3{k}_9(k_4+\eta q_I{\pi }_B)p+{\sigma }_W{\beta }_W{k}_2{k}_4{k}_{10}\left(k_3+\eta q_A{\pi }_B\right)\left(1-p\right)+{\eta }^2{\sigma }_B{\beta }_B{k}_8{k}_9{k}_{10}[p{k}_3+(1-p)k_4]\}/\left[k_{14}{\mu }_V{k}_2{k}_3{k}_4{k}_8{k}_9{k}_{10}(S_W^{\text{*}}+\eta S_B^{\text{*}})\right]>0.$$

Thus, as the infectivity of the asymptomatic individuals increases, the disease burden increases, thereby increasing the number of Zika infected individuals in the community.

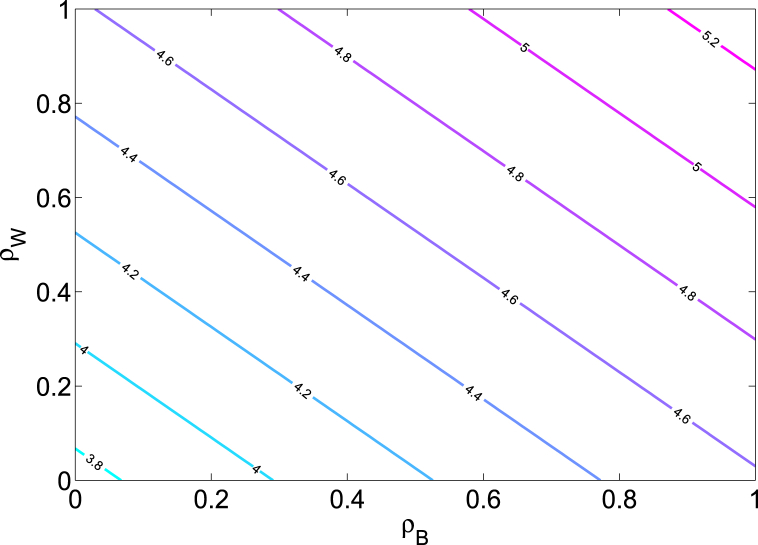
Fig. 2 shows a contour plot of the reproduction number ${\mathrm{ℛ}}_0$, as a function of the asymptomatic modification parameters ${\rho }_B$ and ${\rho }_W$. This figure indicates that Zika burden in the community gets amplified as the level of infectivity of the asymptomatic individuals increases toward that of the infectious individuals.

Fig. 2.

Contour plot of the reproduction number $\left({\mathrm{ℛ}}_0\right)$ of the Zika model (2.1) as a function of the asymptomatic modification parameters ${\rho }_B$ and ${\rho }_W$. Parameter values used are as given in Table 3.

The impact of the asymptomatic classes is further assessed by simulating the model (2.1) using various values for the modification parameters ${\rho }_B$ and ${\rho }_W$ and the same parameters in Table 1. The results obtained, depicted in Fig. 3, show, as expected, that the cumulative number of new cases generated by infectious mosquitoes to susceptible humans increases with increasing values of ${\rho }_B$ and ${\rho }_W$ (see Fig. 3(a)). Similarly, the cumulative number of new cases generated by infectious humans to susceptible mosquitoes increases with increasing values of the modification parameters (see Fig. 3(b)). Notice that 3(a) and 3(b) differ in the direction of spread, since one is infection from mosquito to host and the other is from host to mosquito.

Fig. 3.

Simulations of the Zika model (2.1) with different values of ${\rho }_B={\rho }_W=\mathrm{0,0.25},0.5,0.75,1.0$ (a). Cumulative number of new cases generated by infectious mosquitoes transmitting to susceptible humans. (b). Cumulative number of new cases generated by infectious humans transmitting to susceptible mosquitoes. Parameter values used are as given in Table 3.

Next, we evaluate the contributions of the asymptomatic and infectious individuals to the disease burden in the community. We observed from Table 2, that the percentage contributed by asymptomatic humans goes up as $p_W$ and $p_B$ go up.

Table 2.

Contribution of the asymptomatic and infectious individuals to the mosquitoes' cumulative infections with various values of ${\rho }_B$ and ${\rho }_W$.

${\rho }_W,{\rho }_B$	0.25	0.50	0.75	1.0
Asymptomatic	$20.5\text{\%}$	$34.1\text{\%}$	$43.7\text{\%}$	$50.9\text{\%}$
Infectious	$79.5\text{\%}$	$65.9\text{\%}$	$56.3\text{\%}$	$49.1\text{\%}$

5. Sensitivity analysis

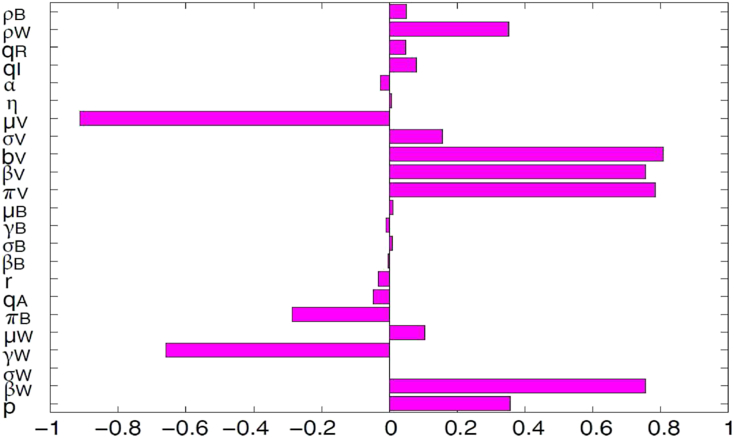
The outputs of deterministic models are governed by the model input parameters, which may exhibit some uncertainty in their determination or selection. We employed a global sensitivity analysis to assess the impact of uncertainty and the sensitivity of the outcomes of the numerical simulations to variations in each parameter of the model (2.1) using Latin Hypercube Sampling (LHS) and partial rank correlation coefficients (PRCC). LHS is a stratified sampling without replacement technique which allows for an efficient analysis of parameter variations across simultaneous uncertainty ranges in each parameter (Blower and Dowlatabadi, 1994, Marino et al., 2008, McKay et al., 2000, Sanchez and Blower, 1997). PRCC measures the strength of the relationship between the model outcome and the parameters, stating the degree of the effect that each parameter has on the outcome (Blower and Dowlatabadi, 1994, Marino et al., 2008, McKay et al., 2000, Sanchez and Blower, 1997). Thus, sensitivity analysis determines the parameters with the most significant impact on the outcome of the numerical simulations of the model (Blower and Dowlatabadi, 1994, Marino et al., 2008, McLeod et al., 2006). To generate the LHS matrices, we assume that all the model parameters are uniformly distributed. Then a total of 1000 simulations of the models per LHS run were carried out, using the ranges and baseline values tabulated in Table 3 (with the basic reproduction number, ${\mathrm{ℛ}}_0$, as the response function). From Fig. 4 it follows that the parameters that have the most influence on Zika transmission dynamics are the death rate of the mosquitoes $\left({\mu }_V\right)$, the mosquito biting rate $\left(b_V\right)$, mosquito recruitment rate $\left({\pi }_V\right)$, the transmission probability per contact to mosquitoes $\left({\beta }_V\right)$ and to adult humans $\left({\beta }_W\right)$, and the adult recovery rate $\left({\gamma }_W\right)$. Identification of these key parameters is important to the formulation of effective control strategies for combating the spread of disease. In particular, the results of this sensitivity analysis suggest that a strategy that reduces the transmission probability per contact to mosquitoes or to adult humans (i.e., reduces ${\beta }_V$ or ${\beta }_W$ respectively), will adequately reduce the spread of ZIKV in the community. Furthermore, a strategy that reduces the mosquito recruitment rate or the mosquito biting rate (i.e., reduces ${\pi }_V$ or $b_V$, respectively) or else increases the death rate of the mosquitoes (i.e., increases ${\mu }_V$) will be effective in curtailing the spread of ZIKV in the community.

Table 3.

Parameter values of model (2.1).

Parameter	Values	Range	References
α	$\frac{1}{16\times 365}$	$\frac{1}{18\times 365}$–$\frac{1}{15\times 365}$	Assumed
${\rho }_B,{\rho }_W$	0.5	0.1–1	Assumed
$p,r,q_A,q_I,q_R$	0.5	0.1–1	Assumed
${\beta }_W$	0.33	0.10–0.75	(Manore et al., 2014, Newton and Reiter, 1992, Paupy et al., 2010)
${\sigma }_W$	$\frac{1}{7.5}$	$\frac{1}{12}$–$\frac{1}{3}$	(Bewick, Fagan, Calabrese, & Agusto, 2016)
${\gamma }_W$	$\frac{1}{8.5}$	$\frac{1}{14}$–$\frac{1}{3}$	(Bewick et al., 2016)
${\mu }_W$	$\frac{1}{70\times 365}$	$\frac{1}{76\times 365}$–$\frac{1}{68\times 365}$	(Manore et al., 2014)
${\pi }_B$	$\frac{1}{15\times 365}$	$\frac{1}{18\times 365}$–$\frac{1}{12\times 365}$	(Wikipedia, 2015)
${\beta }_B$	0.33	0.001–0.54	(Dumont and Chiroleu, 2010, Dumont et al., 2008, Manore et al., 2014, Poletti et al., 2011, Turell et al., 1992)
${\sigma }_B$	$\frac{1}{7.5}$	$\frac{1}{12}$–$\frac{1}{3}$	(Bewick et al., 2016)
${\gamma }_B$	$\frac{1}{8.5}$	$\frac{1}{14}$–$\frac{1}{3}$	(Bewick et al., 2016)
${\mu }_B$	$\frac{1}{18.60\times 365}$	$\frac{1}{14.88\times 365}$–$\frac{1}{22.32\times 365}$	(World Health Organization, 2016a, World Health Organization, 2016b)
${\pi }_V$	500	50–5000	(Bewick et al., 2016)
${\beta }_V$	0.33	0.10–0.75	(Manore et al., 2014, Newton and Reiter, 1992, Paupy et al., 2010)
$b_V$	0.5	0.33–1.0	(Manore et al., 2014, Putnam and Scott, 1995, Trpis and Haussermann, 1986)
${\sigma }_V$	$\frac{1}{3.5}$	$\frac{1}{6}$–$\frac{1}{2}$	(Dubrulle et al., 2009, Dumont and Chiroleu, 2010, Moulay et al., 2011, Sebastian et al., 2009)
${\mu }_V$	$\frac{1}{21}$	$\frac{1}{42}$–$\frac{1}{8}$	(Sheppard et al., 1969, Trpis and Haussermann, 1986, Trpis et al., 1995)

Fig. 4.

PRCC values for the Zika model (2.1), using as response functions the reproduction number ${\mathrm{ℛ}}_0$. Parameter values (baseline) and ranges used are given in Table 3.

6. Assessment of control strategies

Motivated by the sensitivity analysis in the previous section, we now explore some of the key model parameters to determine their effectiveness as targets for control strategies. In particular, we consider mosquito recruitment rate $\left({\pi }_V\right)$, which can be modified with larvicides or through effective management of mosquito breeding sites. We also consider the mosquito death rate, $\left({\mu }_V\right)$, which can be modified with adulticides, and the mosquito biting rates, $\left(b_V\right)$, which can be modified using repellants or behavioral avoidance (e.g, remaining in buildings with screened windows and air-conditioning). We then consider a combined strategy where all three management strategies are employed simultaneously. Finally, we consider delayed pregnancy, because this is a recommendation put forward by several Latin American and Caribbean governments as a means of reducing microcephaly.

For our analysis, moderate control levels correspond to the baseline parameter values used in our sensitivity analysis (Table 3, column 2) whereas low and high control levels correspond to the extreme parameter values (Table 3, column 3). The parameter values and initial conditions used in these simulations are theoretical in the sense that they are similar to comparable parameters for other mosquito-transmitted diseases, but are not specific to ZIKV, which is only poorly studied. The goal is thus to illustrate the control strategies proposed in this paper for relatively broad, generic parameter ranges. These predictions should then be retested as more information becomes available that is specific to ZIKV.

6.1. Epidemiological consequences of mosquito-reduction strategies

We consider the following control levels for this strategy:

• 1.Low mosquito-reduction strategy: ${\pi }_V=500/day\text{,}$ ${\mu }_V=\frac{1}{21}/day$;
• 2.Moderate mosquito-reduction strategy: ${\pi }_V=250/day\text{,}$ ${\mu }_V=\frac{1}{14}/day$;
• 3.High mosquito-reduction strategy: ${\pi }_V=125/day\text{,}$ ${\mu }_V=\frac{1}{8}/day$.

This strategy combines the larviciding and adulticiding strategies discussed in Appendices E and F, respectively.

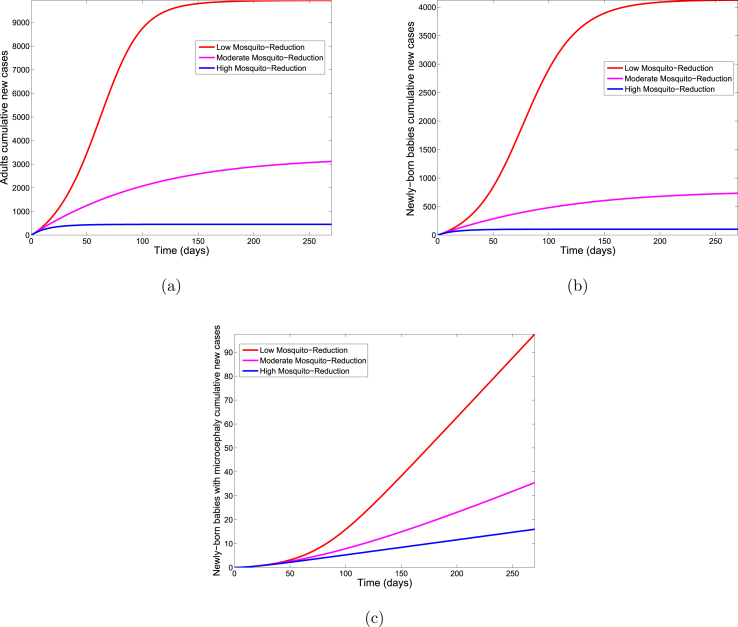
Fig. 5 shows for each of the three control levels, the cumulative number of new infections in adults, new infections in newly born babies and newly born babies with microcephaly. Comparing the three control levels in Table 4 shows a decrease in the cumulative number of new cases with increasing control.

Fig. 5.

Simulation of the Zika model (2.1) for various control levels of the mosquito reduction control strategy. (a). The cumulative number of new Zika cases in adults. (b). The cumulative number of new Zika cases in newly born babies. (c). The cumulative number of new cases of newly born babies with microcephaly. Parameter values used are as given in Table 3.

Table 4.

Simulation results of the Zika model (2.1) using the mosquito reduction control strategy.

Humans	Low-Control	Moderate-Control	High-Control
Adults	$2.1\times {10}^6$	$5.8\times {10}^5$	$1.2\times {10}^5$
Newly born babies	$7.7\times {10}^5$	$1.4\times {10}^5$	$2.8\times {10}^4$
Newly born with microcephaly	$10.0\times {10}^3$	$3.9\times {10}^3$	$2.0\times {10}^3$

6.2. Epidemiological consequences of the personal protection strategy

Personal protection reduces mosquito biting rates $\left(b_V\right)$. Similar to mosquito control, we consider three different levels of protection:

• 1.Low-effectiveness personal-protection strategy: $b_V=0.5/day$;
• 2.Moderate-effectiveness personal-protection strategy: $b_V=0.250/day$;
• 3.High-effectiveness personal-protection strategy: $b_V=0.125/day$.

Fig. 6 shows the cumulative number of new infections in adults, new infections in newly born babies and newly born babies with microcephaly for each of the three protection levels. The high effectiveness personal-protection strategy lead to a considerable reduction in the number of new cases compared to the moderate-effectiveness level (see Table 5) at the same time period. The low-effectiveness level performed the poorest producing the most number of new cases.

Fig. 6.

Simulation of the Zika model (2.1) for various control levels of the personal-protection strategy. (a). The cumulative number of new Zika cases in adults. (b). The cumulative number of new Zika cases in newly born babies. (c). The cumulative number of new cases of newly born babies with microcephaly. Parameter values used are as given in Table 3.

Table 5.

Simulation results of the cumulative number of new cases for the Zika model (2.1) using the personal-protection strategy.

Humans	Low Control	Moderate Control	High Control
Adults	$2.1\times {10}^6$	$5.4\times {10}^5$	$9.5\times {10}^4$
Newly born babies	$7.7\times {10}^5$	$1.2\times {10}^5$	$2.1\times {10}^4$
Newly born with microcephaly	$10.0\times {10}^3$	$3.4\times {10}^3$	$1.9\times {10}^3$

6.3. Combined mosquito control and personal protection strategy

The combined strategy (where both the mosquito reduction and personal protection strategies are implemented simultaneously) was assessed for the following three control levels:

• 1.Low-control strategy: ${\pi }_V=500/day,{\mu }_V=\frac{1}{21}/day\text{,}$ $b_V=0.5/day$;
• 2.Moderate-control strategy: ${\pi }_V=250/day\text{,}$ ${\mu }_V=\frac{1}{14}/day,b_V=0.25/day$;
• 3.High-control strategy: ${\pi }_V=125/day,{\mu }_V=\frac{1}{8}/day\text{,}$ $b_V=0.125/day$.

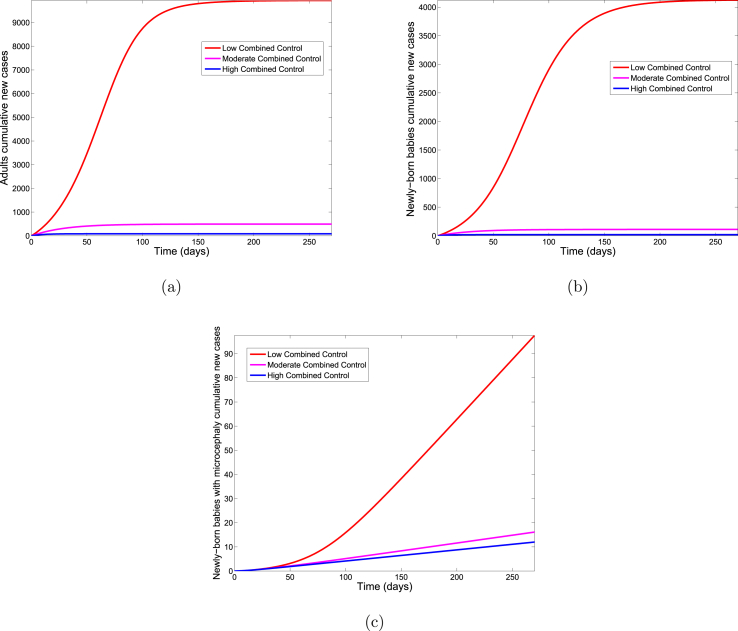
Fig. 7 shows the cumulative number of new infections in adults, new infections in newly born babies, and babies with microcephaly for each control strategy. A comparison of the three control levels in Table 6 shows that higher levels of combined control are more effective for preventing new ZIKV cases.

Fig. 7.

Simulation of the Zika model (2.1) for various control levels of the combined control strategy. (a). The cumulative number of new Zika cases in adults. (b). The cumulative number of new Zika cases in newly born babies. (c). The cumulative number of new cases of newly born babies with microcephaly. Parameter values used are as given in Table 3.

Table 6.

Simulation results of the cumulative number of new cases for the Zika model (2.1) using the combined control strategy.

Humans	Low Control	Moderate Control	High Control
Adults	$2.1\times {10}^6$	$1.2\times {10}^5$	$2.2\times {10}^4$
Newly born babies	$7.7\times {10}^5$	$2.6\times {10}^4$	$4.9\times {10}^3$
Newly born with microcephaly	$10.0\times {10}^3$	$2.0\times {10}^3$	$1.6\times {10}^3$

A comparison across control strategies (larviciding, adulticiding, mosquito-reduction, personal-protection, and the combined strategy) in each group (see Table 7) shows, as expected, that the combined strategy is more effective than the other strategies implemented separately. Indeed, combining strategies results in anywhere from a 43% reduction to a 94% reduction as compared to single control strategies. With respect to single control strategies, personal protection is more effective than mosquito-reduction for reducing ZIKV and also for preventing microcephaly in newborns.

Table 7.

Comparison of the cumulative number of new cases for the high-control levels of the various control strategies for the Zika model (2.1).

Humans	Larviciding Control	Adulticiding Control	Mosquito Reduction	Personal Protection	Combined Control
Adults	$7.5\times {10}^5$	$2.6\times {10}^5$	$1.2\times {10}^5$	$9.5\times {10}^4$	$2.2\times {10}^4$
Newly born babies	$1.8\times {10}^5$	$5.9\times {10}^4$	$2.6\times {10}^4$	$2.1\times {10}^4$	$4.9\times {10}^3$
Newly born with microcephaly	$4.4\times {10}^3$	$2.7\times {10}^3$	$2.0\times {10}^3$	$1.9\times {10}^3$	$1.6\times {10}^3$

6.4. Delayed pregnancy

In light of the warnings issued by the Brazilian, Colombian, El Salvadorian, and Jamaican governments for reproductive women to delay conceiving (Ahmed, 2016, Darlington, 2016), we explore the impact that this will have on ZIKV transmission and the number of babies born with microcephaly. To consider delayed pregnancy, we adjusted the human birth rate ${\pi }_B$. As above, we consider three levels of delayed pregnancy:

• 1.No women delay: ${\pi }_B=\frac{1}{15\times 365}$ day⁻¹;
• 2.Some women delay: ${\pi }_B=\left(\frac{1}{15\times 365}\right)/2$ day⁻¹;
• 3.Many women delay: ${\pi }_B=\left(\frac{1}{15\times 365}\right)/10$ day⁻¹.

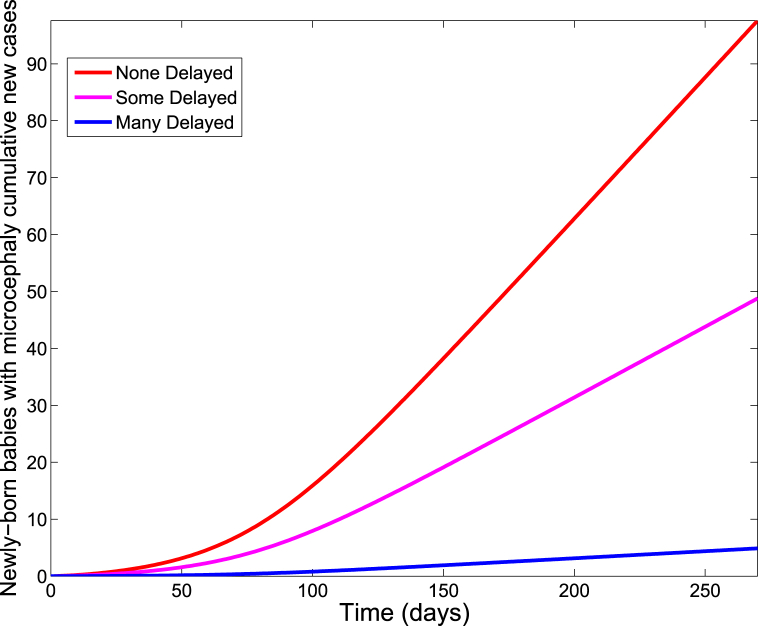
As expected, for all three scenarios, we observed a negligible difference in the cumulative number of new cases of ZIKV infections among adults and newly born babies. Indeed, there was even a small increase in the number of infected infants when pregnancy was delayed. However, there was a significant impact on the cumulative number of babies born with microcephaly, with the highly delayed rate producing the least number of babies with microcephaly (see Fig. 8). This is further demonstrated in Table 8, where we compared the three delayed conception rates levels.

Fig. 8.

Simulation of the Zika model (2.1) showing the cumulative number of new cases in newly born babies with microcephaly for various rates of delaying conception. Parameter values used are as given in Table 3.

Table 8.

Simulation results of the cumulative number of new cases for the Zika model (2.1) with various rates of delaying conception.

Humans	None-delayed	Some-delayed	Many-delayed
Adults	$2.1\times {10}^6$	$2.1\times {10}^6$	$2.1\times {10}^6$
Newly born babies	$7.7\times {10}^5$	$7.8\times {10}^5$	$7.8\times {10}^5$
Newly born with microcephaly	$10.0\times {10}^3$	$5.0\times {10}^3$	499

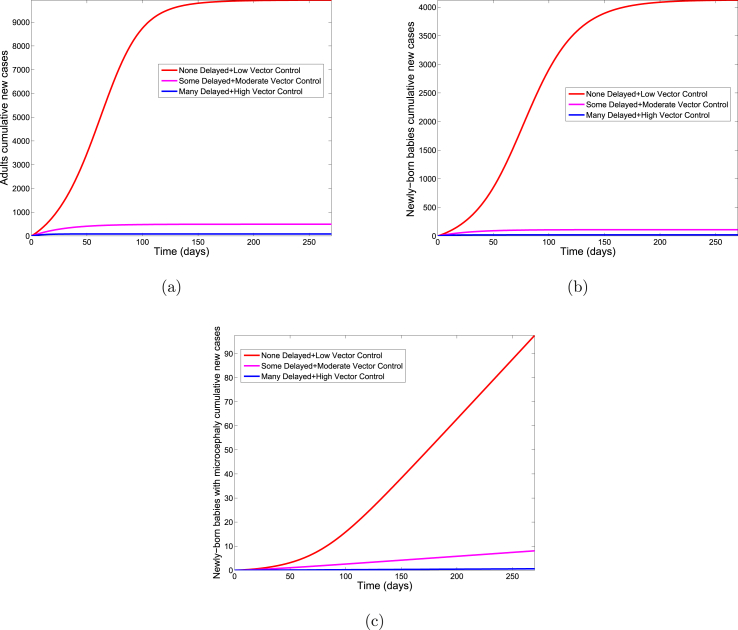
As a final scenario, we implement delayed conception simultaneously with the combined mosquito control and personal protection strategies (see Section 6.3). Again, we consider low, moderate and high levels of mosquito control, personal-protection, and pregnancy delays. Unlike the findings with delayed pregnancy alone (see above), delayed pregnancy in combination with other control strategies result in an appreciable benefit on ZIKV transmission in adult and new-born populations (see Fig. 9 and Table 9). However, when large numbers of women delay conception, and this is combined with high levels of mosquito control and personal protection, there is a dramatic reduction in babies born with microcephaly (see Table 10). Thus, delayed pregnancy, particularly when combined with mosquito control and personal protection, appears to be beneficial for reducing microcephaly rates in regions with ongoing ZIKV outbreaks.

Fig. 9.

Simulation of the Zika model (2.1) showing the cumulative number of new cases in newly born babies with microcephaly for various levels of delayed pregnancy. Parameter values used are as given in Table 3.

Table 9.

Simulation results of the cumulative number of new cases for the Zika model (2.1) using various rates of delaying conception, combined mosquito control and personal protection strategies.

Humans	None-delayed & Low-Control	Some-delayed & Moderate-Control	Many-delayed & High-Control
Adults	$2.1\times {10}^6$	$1.2\times {10}^5$	$2.2\times {10}^4$
Newly born babies	$7.7\times {10}^5$	$2.6\times {10}^4$	$4.8\times {10}^3$
Newly born with microcephaly	$10.0\times {10}^3$	$1.0\times {10}^3$	78.2

Table 10.

Comparison of the combined control strategies (involving mosquito reduction and personal protection), and delayed pregnancy for the Zika model (2.1).

Humans	Combined Control	Delayed Pregnancy	Delayed Pregnancy + Combined Control
Adults	$2.2\times {10}^4$	$2.1\times {10}^6$	$2.2\times {10}^4$
Newly born babies	$4.9\times {10}^3$	$7.8\times {10}^5$	$4.8\times {10}^3$
Newly born with microcephaly	$1.6\times {10}^3$	500	78.2

7. Discussion and conclusion

In this paper, we develop a new deterministic model to study the transmission dynamics of Zika virus. Our model incorporates mother-to-child transmission as well as the development of microcephaly in newly born babies. The analysis shows that the disease-free equilibrium of the model is locally and globally asymptotically stable whenever the associated reproduction number $\left({\mathrm{ℛ}}_0\right)$, is less than unity and unstable otherwise. Sensitivity analysis further identifies parameters with the strongest impact on model outcome (i.e., the basic reproduction number). These are the mosquito biting rate, the transmission probability per contact to mosquitoes and to human adults, the mosquito recruitment rate, and the mosquito death rate. Identification of these key parameters is vital to the formulation of effective ZIKV control strategies.

Based on our analysis, we consider various control strategies aimed at reducing mosquito biting rates, mosquito recruitment rates, and mosquito death rates to examine if these strategies will be effective in curtailing ZIKV spread in the community. We lack methods for reducing viral transmission probabilities; however, these would also be effective targets for control if management strategies existed. Specifically, we implement a mosquito-reduction strategy, a personal-protection strategy, and a combined strategy each with three different control levels (low, moderate, high). Our results show that the cumulative number of new ZIKV cases generally decreases with increasing control as does the number of cases of microcephaly. As expected, the combined strategy is most effective across the board; this is followed by the personal protection strategy.

Some countries in the Western Hemisphere currently affected by ZIKV (including Brazil, El Salvador, Colombia and Jamaica (Ahmed, 2016, Darlington, 2016)) have issued warnings against women of reproductive age becoming pregnant. Using our model to numerically explore the effect of delayed pregnancy on disease transmission and microcephaly, we find that this strategy is highly effective for reducing the number of microcephaly cases, but does not impact levels of ZIKV transmission among either infants or adults. Coupling delayed pregnancy with mosquito control and personal protection, however, results in a considerable reduction in both ZIKV transmission and microcephaly. Thus, it appears that attacking ZIKV from all fronts, including aggressive mosquito control, strong adherence to repellant use, and delayed pregnancy, provides the best solution for ZIKV management, at least over the near term.

The issue of near-term versus long-term ZIKV management strategies is an important point that warrants further discussion. The model presented in the current paper is a highly detailed study of short-term ZIKV transmission. In particular, we restrict our analysis to a 9-month window beginning at the start of a ZIKV outbreak. Consequently, any babies born from women who are or who have ever been infected by ZIKV are at high-risk for microcephaly during this window. Over longer periods, however, ZIKV infection could occur prior to pregnancy. Consequently, a history of infection (i.e., recovery adults) in mothers would not necessarily indicate high-risk pregnancy. Quite the opposite - women who acquire infection before becoming pregnant may actually be protected during pregnancy. Thus, long-term predictions may differ substantially from predictions of the current model, and this is something that we explore in a separate paper (Bewick et al., 2016).

In this paper, we formulated and analyzed a system of ordinary differential equations for transmission dynamics of ZIKV. Some of our theoretical and epidemiological findings are summarized below:

• (i).Model (2.1) is locally and globally asymptotically stable when ${\mathrm{ℛ}}_0<1$ and unstable when ${\mathrm{ℛ}}_0>1$;
• (ii).Disease burden in the community increases infectivity of the asymptomatic individuals. Similarly, the cumulative infections to mosquitoes from the asymptomatic increases as their infectivity level increases.
• (iii).Sensitivity analysis shows that the most important parameters for ZIKV spread are the death rate of the mosquitoes $\left({\mu }_V\right)$, the mosquito biting rate $\left(b_V\right)$, mosquito recruitment rate $\left({\pi }_V\right)$, the transmission probability per contact to mosquitoes and to adult humans (${\beta }_V$ and ${\beta }_W$ respectively) and the adult recovery rate $\left({\gamma }_W\right)$;
• (iv).Numerical simulations using mosquito control indicate that personal protection is a better and more effective strategy than the mosquito-reduction in reducing the disease burden in the population. As expected, a combined strategy is the most effective for reducing the ZIKV disease burden in the community.
• (v).Additional numerical simulations suggest that delaying conception reduces the number of cases of microcephaly, although it does little to prevent ZIKV transmission in the broader community. Coupled with aggressive mosquito control level and personal-protection; however, it is possible to both reduce microcephaly and prevent ZIKV transmission.

Appendix A. Proof of Lemma 1

Lemma 1

Let the initial data $F\left(0\right)\ge 0$, where $F\left(t\right)=(S_B,E_B,A_B,I_B,I_{BM},S_W,E_W,A_W,I_W,R_W,I_{WM},R_B,S_V,E_V,I_V)$. Then the solutions $F\left(t\right)$ of model (2.1) are non-negative for all time $t>0$. Furthermore

$$\underset{t\to \infty }{\text{lim}\text{sup}}{N}_H\left(t\right)=\frac{{\pi }_B}{{\mu }_H},\underset{t\to \infty }{\text{lim}\text{sup}}{N}_W\left(t\right)=\frac{{\pi }_V}{{\mu }_V}\text{,}$$

where. ${\mu }_H=\text{min}\left\{{\mu }_B,{\mu }_W\right\}\text{.}$

with,

$$\begin{array}{l}{N}_B\left(t\right)=S_B\left(t\right)+E_B\left(t\right)+A_B\left(t\right)+I_B\left(t\right)+I_{BM}\left(t\right)+R_B\left(t\right),\\ N_W\left(t\right)=S_W\left(t\right)+E_W\left(t\right)+A_W\left(t\right)+I_W\left(t\right)+I_{WM}\left(t\right)+R_W\left(t\right),\\ N_V\left(t\right)=S_V\left(t\right)+E_V\left(t\right)+I_V\left(t\right)\text{.}\end{array}$$

Proof. Let $t_1=sup\left\{t>0:F\left(t\right)>0\right\}$. Thus, $t_1>0$. Then it follows from the first equation of the Zika model (2.1) that

$$\frac{d{S}_B}{dt}={\pi }_B[1-q_A{A}_W\left(t\right)-q_I{I}_W\left(t\right)-q_R{R}_W\left(t\right)]-{\lambda }_B\left(I_V,N_B\right)S_B\left(t\right)-\left(\alpha +{\mu }_B\right)S_B\left(t\right)\text{.}$$

which can be re-written as

$$\frac{d}{dt}\{S_B\left(t\right)exp[\underset{0}{\overset{t_f}{\int }}{\lambda }_B\left(I_V\left(u\right),N_H\left(u\right)\right)du+\left(\alpha +{\mu }_B\right)t]\}={\int }_0^{t_f}[{\pi }_B-q_A{\pi }_B{A}_W\left(u\right)+-q_I{\pi }_B{I}_W\left(u\right)-q_R{\pi }_B{R}_W\left(u\right)]\times \text{exp}[\underset{0}{\overset{t_f}{\int }}{\lambda }_B\left(I_V\left(u\right),N_H\left(u\right)\right)du+\left(\alpha +{\mu }_B\right)t]\text{.}$$

So that,

$$S_B\left(t_1\right)exp[\underset{0}{\overset{t_1}{\int }}{\lambda }_B\left(I_V\left(u\right),N_H\left(u\right)\right)du+{\mu }_{W}t]-S_B\left(0\right)={\int }_0^{t_f}[{\pi }_B-q_A{\pi }_B{A}_W\left(t\right)-q_I{\pi }_B{I}_W\left(t\right)-q_R{\pi }_B{R}_W\left(t\right)]\times \text{exp}[\underset{0}{\overset{t_f}{\int }}{\lambda }_B(I_V\left(u\right),N_H\left(u\right))du+(\alpha +{\mu }_B)t]\text{.}$$

Hence,

$$S_B\left(t_1\right)=S_B\left(0\right)exp[-\underset{0}{\overset{t_1}{\int }}{\lambda }_B\left(I_V\left(u\right),N_H\left(u\right)\right)du-\left(\alpha +{\mu }_B\right)t_1]={\int }_0^{t_f}[{\pi }_B-q_A{\pi }_B{A}_W\left(u\right)-q_I{\pi }_B{I}_W\left(u\right)-q_R{\pi }_B{R}_W\left(u\right)]\times exp[-\underset{0}{\overset{t_1}{\int }}{\lambda }_B(I_V\left(u\right),N_H\left(u\right))du-(\alpha +{\mu }_B)t_1].>0.$$

It can similarly be shown that $F>0$ for all $t>0$. For the second part of the proof, it should be noted that $0<S_B\left(t\right)\le N_H\left(t\right),0<E_B\left(t\right)\le N_H\left(t\right),0<A_B\left(t\right)\le N_H\left(t\right),0<I_B\left(t\right)\le N_H\left(t\right),0<I_{BM}\left(t\right)\le N_H\left(t\right),0<R_B\left(t\right)\le N_H\left(t\right),0<S_W\left(t\right)\le N_H\left(t\right),0<E_W\left(t\right)\le N_H\left(t\right),0<A_W\left(t\right)\le N_H\left(t\right),0<I_W\left(t\right)\le N_H\left(t\right),0<I_{WM}\left(t\right)\le N_H\left(t\right),0<R_W\left(t\right)\le N_H\left(t\right),0<S_V\left(t\right)\le N_V\left(t\right),0<E_V\left(t\right)\le N_V\left(t\right),0<I_V\left(t\right)\le N_V\left(t\right)$.

Adding the components of the model (2.1) gives

$$\begin{array}{l}\frac{d{N}_H\left(t\right)}{dt}={\pi }_B-{\mu }_B{N}_B\left(t\right)-{\mu }_W{N}_W\left(t\right)\\ \frac{d{N}_V\left(t\right)}{dt}={\pi }_V-{\mu }_V{N}_V\left(t\right)\text{.}\end{array}$$

Thus,

$$\begin{array}{l}\frac{d{N}_H\left(t\right)}{dt}={\pi }_B-{\mu }_H{N}_H\left(t\right),\\ \frac{d{N}_V\left(t\right)}{dt}={\pi }_V-{\mu }_V{N}_V\left(t\right)\text{.}\end{array}$$

where ${\mu }_H=\text{min}\left\{{\mu }_B,{\mu }_W\right\}$.

Hence,

$$\begin{array}{l}\frac{{\pi }_B}{{\mu }_H}=\underset{t\to \infty }{\text{lim}\text{inf}}{N}_H\left(t\right)=\underset{t\to \infty }{\text{lim}\text{sup}}{N}_H\left(t\right)\le \frac{{\pi }_B}{{\mu }_H},\\ \frac{{\pi }_V}{{\mu }_V}=\underset{t\to \infty }{\text{lim}\text{inf}}{N}_V\left(t\right)\le \underset{t\to \infty }{\text{lim}\text{sup}}{N}_V\left(t\right)=\frac{{\pi }_V}{{\mu }_V}\text{,}\end{array}$$

as required.

Appendix B. Proof of Lemma 2

Lemma 2

The region $={\text{Γ}}_H\times {\text{Γ}}_V\subset {\mathrm{ℝ}}_{+}^{12}\times {\mathrm{ℝ}}_{+}^3$ is positively invariant for the basic model (2.1) with non-negative initial conditions in ${\mathrm{ℝ}}_{+}^{15}$

Proof. The following steps are followed to establish the positive invariance of $\text{Γ}$ (i.e., solutions in $\text{Γ}$ remain in $\text{Γ}$ for all $t>0$). The rate of change of the total population is obtained by adding the components of the model (2.1) to give

$$\frac{d{N}_H\left(t\right)}{dt}={\pi }_B-{\mu }_B{N}_B\left(t\right)-{\mu }_W{N}_W\left(t\right)$$

$$\frac{d{N}_V\left(t\right)}{dt}={\pi }_V-{\mu }_V{N}_V\left(t\right)\text{.}$$

Thus,

$$\frac{d{N}_H\left(t\right)}{dt}={\pi }_B-{\mu }_H{N}_H\left(t\right)\text{,}$$

$$\frac{d{N}_V\left(t\right)}{dt}={\pi }_V-{\mu }_V{N}_V\left(t\right)\text{.}$$

where ${\mu }_H=\text{min}\left\{{\mu }_B,{\mu }_W\right\}$. A standard comparison theorem (Lakshmikantham, Leela, & Martynyuk, 1989) can then be used to show that $N_H\left(t\right)\le N_H\left(0\right)e^{-{\mu }_{H}t}+\frac{{\pi }_B}{{\mu }_H}\left(1-e^{-{\mu }_{H}t}\right)$, in particular, $N_H\left(t\right)\le \frac{{\pi }_B}{{\mu }_H}$, if $N_H\left(0\right)\le \frac{{\pi }_B}{{\mu }_B}$. And lastly, $N_V\left(t\right)\le N_V\left(0\right)e^{-{\mu }_{V}t}+\frac{{\pi }_V}{{\mu }_V}\left(1-e^{-{\mu }_{V}t}\right)$, in particular, $N_V\left(t\right)\le \frac{{\pi }_V}{{\mu }_V}$, if $N_V\left(0\right)\le \frac{{\pi }_V}{{\mu }_V}$.

Thus, the region $\text{Γ}$ is positively invariant. Hence, it is sufficient to consider the dynamics of the flow generated by (2.1) in $\text{Γ}$. In this region, the model is epidemiologically and mathematically well-posed (Hethcote, 2000). Thus, every solution of the model (2.1) with initial conditions in $\text{Γ}$ remains in $\text{Γ}$ for all $t>0$. Therefore, the $\text{Γ}$-limit sets of the system (2.1) are contained in $\text{Γ}$. This result is summarized below.

Appendix C. Proof of Lemma 4

Lemma 4

The region ${\text{Γ}}_1$ is positively invariant for model (2.1)

Proof. It follows from the first equation of Zika model (2.1), (where $S_B^{\text{*}}=\frac{{\pi }_B}{\alpha +{\mu }_B}$), so that

$$\begin{array}{l}\frac{d{S}_B\left(t\right)}{dt}={\pi }_B-q_A{\pi }_B{A}_W\left(t\right)-q_I{\pi }_B{I}_W\left(t\right)-q_R{\pi }_B{R}_W\left(t\right)-\frac{\eta {\beta }_B{b}_V{S}_B{I}_V}{N_H}-\left(\alpha +{\mu }_B\right)S_B\left(t\right)\\ \le {\pi }_B-\left(\alpha +{\mu }_B\right)S_B\left(t\right)\\ \le \left(\alpha +{\mu }_B\right)[\frac{{\pi }_B}{\left(\alpha +{\mu }_B\right)}-S_B\left(t\right)]\\ =\left(\alpha +{\mu }_B\right)[S_B^{\text{*}}-S_B\left(t\right)]\text{.}\end{array}$$ (C-1)

Thus,

$$S_B\left(t\right)\le S_B^{\text{*}}-[S_B^{\text{*}}-S_B\left(0\right)]e^{-\left(\alpha +{\mu }_B\right)t}\text{.}$$

Thus, if $S_B\left(0\right)\le S_B^{\text{*}}$ for all $t\ge 0$, then $S_B\left(t\right)\le S_B^{\text{*}}$ for all $t\ge 0$.

Similarly, it follows from the sixth equation of the Zika model (2.1) (where $S_W^{\text{*}}=\frac{\alpha {\pi }_B}{\left(\alpha +{\mu }_B\right){\mu }_W}$), that

$$\begin{array}{l}\frac{d{S}_W\left(t\right)}{dt}=\alpha S_B-\frac{{\beta }_W{b}_V{S}_W{I}_V}{N_H}-{\mu }_W{S}_W\left(t\right),\\ \le \alpha S_B-{\mu }_W{S}_W\left(t\right),\\ \le {\mu }_W[\frac{\alpha S_B^{\text{*}}}{{\mu }_W}-S_W\left(t\right)],\\ ={\mu }_W[\frac{\alpha {\pi }_B}{{\mu }_W\left(\alpha +{\mu }_B\right)}-S_W\left(t\right)]\\ ={\mu }_W[S_W^{\text{*}}-S_W\left(t\right)]\text{.}\end{array}$$ (C-2)

Hence,

$$S_W\left(t\right)\le S_W^{\text{*}}-[S_W^{\text{*}}-S_W\left(0\right)]e^{-{\mu }_{W}t}.$$

Thus, if $S_W\left(0\right)\le S_W^{\text{*}}$ for all $t\ge 0$, then $S_W\left(t\right)\le S_W^{\text{*}}$ for all $t\ge 0$.

Finally, it follows from the twelfth equation of the Zika model (2.1), that

$$\begin{array}{l}\frac{d{S}_V\left(t\right)}{dt}={\pi }_V-{\beta }_V{b}_V\left[\frac{A_W+I_W+\eta \left(A_B+I_B\right)}{N_H}\right]S_M-{\mu }_M{S}_M\left(t\right),\\ \le {\pi }_V-{\mu }_V{S}_V\left(t\right),\\ \le {\mu }_V[\frac{{\pi }_V}{{\mu }_V}-S_V\left(t\right)],\\ ={\mu }_V[S_V^{\text{*}}-S_V\left(t\right)]\text{.}\end{array}$$ (C-3)

Thus,

$$S_V\left(t\right)\le S_V^{\text{*}}-[S_V^{\text{*}}-S_V\left(0\right)]e^{-{\mu }_{V}t}\text{.}$$

Hence, if $N_M^{\text{*}}=\frac{{\pi }_V}{{\mu }_V}$ and $S_V\left(0\right)\le S_V^{\text{*}}$ for all $t\ge 0$, then $S_V\left(t\right)\le S_V^{\text{*}}$ for all $t\ge 0$.

Thus, in summary, it has been shown that the region ${\text{Γ}}_1$ is positively invariant and attracts all solutions in ${\mathrm{ℝ}}_{+}^{14}$ for the Zika model (2.1).

Appendix D. Proof of Theorem 1

Theorem 1

The DFE, ${\mathcal{E}}_0$, of model (2.1), is globally asymptotically stable (GAS) in ${\text{Γ}}_1$ whenever ${\mathrm{ℛ}}_0\le 1$.

Proof. To prove the global stability of the disease-free equilibrium, we will following the approach in (Agusto et al., 2013).

Let $X=\left(S_W,R_W,S_B,R_B,S_V\right)$ and $Z=\left(E_B,A_B,I_B,I_{BM},E_W,A_W,I_W,I_{WM},E_V,I_V\right)$ and group the system (2.1) into

$$\begin{array}{l}\frac{dX}{dt}=F\left(X,0\right)\\ \frac{dZ}{dt}=G\left(X,Z\right)\text{,}\end{array}$$ (D-1)

where $F\left(X,0\right)$ is the right hand side of $\dot{S_W},\dot{R_W},\dot{S_B},\dot{R_B}$ and $\dot{S_V}$ with $E_B=A_B=I_B=I_{BM}=E_W=A_W=I_W=I_{WM}=E_V=I_V=0$ and $G\left(X,Z\right)$ is the right hand side of $\dot{E_W},\dot{A_W},\dot{I_W},\dot{E_B},\dot{A_B},\dot{I_B},\dot{I_{BM}}\text{,}$ $\dot{E_V}$ and. $\dot{I_V}.$

Next, consider the reduced system: $\frac{dX}{dt}=F\left(X,0\right)$ given as:

$$\begin{array}{l}\frac{d{S}_B}{dt}={\pi }_B-q_R{\pi }_B{R}_W\left(t\right)-\left(\alpha +{\mu }_B\right)S_{B}B\left(t\right)\\ \frac{d{R}_B}{dt}=\left(1-r\right)q_R{\pi }_B{R}_W\left(t\right)-\left(\alpha +{\mu }_B\right)R_B\left(t\right)\\ \frac{d{S}_W}{dt}=\alpha S_B\left(t\right)-{\mu }_W{S}_W\left(t\right)\\ \frac{d{R}_W}{dt}=\alpha R_B\left(t\right)-{\mu }_W{R}_W\left(t\right)\\ \frac{d{S}_V}{dt}={\pi }_V-{\mu }_V{S}_V\left(t\right)\text{.}\end{array}$$ (D-2)

Let

$$X^{\text{*}}=\left(S_B^{\text{*}},R_B^{\text{*}},S_W^{\text{*}},R_W^{\text{*}},S_V^{\text{*}}\right)=\left(\frac{{\pi }_B}{\alpha +{\mu }_B},0,\frac{\alpha {\pi }_B}{{\mu }_W\left(\alpha +{\mu }_B\right)},0,\frac{{\pi }_V}{{\mu }_V}\right)\text{.}$$

be an equilibrium of the reduced system (D-2), we show that $X^{\text{*}}$ is a globally stable equilibrium in ${\text{Γ}}_1$.

To do this, solve the first and second equations of (D-2), this gives

$$S_B\left(t\right)=[{\int }_0^t{e}^{\left(\alpha +{\mu }_B\right)u}{\pi }_B[1-q_R{R}_W\left(u\right)]du+S_B\left(0\right)]e^{-\left(\alpha +{\mu }_B\right)t}$$ (D-3)

$$R_B\left(t\right)=\left[{\int }_0^t\left(1-r\right)q_R{\pi }_W{R}_W\left(u\right)e^{\left(\alpha +{\mu }_B\right)u}du+R_B\left(0\right)\right]e^{-\left(\alpha +{\mu }_B\right)t}\text{.}$$

Integrating $S_B\left(t\right)$ in (D-3) gives:

$$S_B\left(t\right)=\frac{{\pi }_B[1-e^{\left(\alpha +{\mu }_B\right)t}]}{\left(\alpha +{\mu }_B\right)}-[\underset{0}{\overset{t}{\int }}{e}^{\left(\alpha +{\mu }_B\right)u}{\pi }_B{q}_R{R}_W\left(u\right)du+S_B\left(0\right)]e^{-\left(\alpha +{\mu }_B\right)t}\text{.}$$ (D-4)

Taking the limit of $S_B\left(t\right)$ in (D-4) and $R_B\left(t\right)$ in (D-3) as $t\to \infty$, we have

$$\underset{t=\to \infty }{\text{lim}}{S}_B\left(t\right)=\frac{{\pi }_B}{\left(\alpha +{\mu }_B\right)}\text{and}\underset{t\to \infty }{\text{lim}}{R}_B\left(t\right)=0.$$

Next, solving the third and fourth equations of (D-2) $S_W\left(t\right)$ and $R_W\left(t\right)$ gives

$$S_W\left(t\right)=\left[\underset{0}{\overset{t}{\int }}\alpha S_B\left(z\right)e^{{\mu }_{W}z}dz+S_W\left(0\right)\right]e^{-{\mu }_{W}t}\text{and}{R}_W\left(t\right)=\left[\underset{0}{\overset{t}{\int }}{R}_B\left(z\right)e^{{\mu }_{B}z}dz+R_W\left(0\right)\right]e^{-{\mu }_{W}t}\text{.}$$

Integrating $S_W\left(t\right)$ and $R_W\left(t\right)$ and substituting $S_B\left(t\right)$ in (D-4) and $R_B\left(t\right)$ in (D-3) gives

$$S_W\left(t\right)=\left\{\underset{0}{\overset{t}{\int }}\alpha [\frac{{\pi }_B\left(1-e^{k_{1}u}\right)}{k_1}-\left(\underset{0}{\overset{t}{\int }}{e}^{k_{1}z}{\pi }_{B}qr{R}_W\left(z\right)dz\right)+S_B\left(0\right)]e^{-k_{1}u}{e}^{k_{7}t}dt+S_W\left(0\right)\right\}{e}^{-k_{7}t}\text{,}$$

$$R_W\left(t\right)=\left\{\underset{0}{\overset{t}{\int }}\left[\alpha \left(\underset{0}{\overset{s}{\int }}Rq{\pi }_W{R}_W\left(u\right)e^{k_{6}u}du+R_B\left(0\right)\right)e^{-k_{6}u}{e}^{k_{12}s}\right]dt+R_W\left(0\right)\right\}{e}^{-k_{12}t}\text{,}$$

where, $k_1=\alpha +{\mu }_B,k_6=\alpha +{\mu }_B,k_7={\mu }_W,k_{12}={\mu }_W\text{.}$

Taking the limit as $t\to \infty$,

$$\underset{t=\to \infty }{\text{lim}}{S}_W\left(t\right)=\frac{\alpha {\pi }_B}{{\mu }_W\left(\alpha +{\mu }_B\right)}\text{and}\underset{t\to \infty }{\text{lim}}{R}_B\left(t\right)=0.$$

Similarly, solving for $S_V\left(t\right)$ in (D-2) gives $S_V\left(t\right)=\frac{{\pi }_V}{{\mu }_V}+e^{-{\mu }_{V}t}[S_V\left(0\right)-\frac{{\pi }_V}{{\mu }_V}]$ which converges to $\frac{{\pi }_V}{{\mu }_V}$, as $t\to \infty$.

These asymptotic dynamics are independent of initial conditions in $\text{Γ}$. Hence, the convergence of solutions of (D-2) is global in ${\text{Γ}}_1$. Next, following (Castillo-Chavez, Blower, van den Driessche, Kirschner, & Yakubu, 2002), we require $G\left(X,Z\right)$ to satisfy the two stated conditions:

• (i).$G\left(X,0\right)=0$ and
• (ii).$G\left(X,Z\right)=D_{Z}G\left(X^{\text{*}},0\right)Z-\hat{G}\left(X,Z\right)$, $\hat{G}\left(X,Z\right)\ge 0$,

where $\left(X^{\text{*}},0\right)=\left(\frac{{\pi }_B}{\alpha +{\mu }_B},0,\frac{\alpha {\pi }_B}{{\mu }_W\left(\alpha +{\mu }_B\right)},0,\frac{{\pi }_V}{{\mu }_V},\mathrm{0,0,0,0,0,0,0,0,0,0}\right)$ and $D_{Z}G\left(X^{\text{*}},0\right)$ is the Jacobian of $G\left(X,Z\right)$ taken with respect to $\left(E_B,A_B,I_B,I_{BM},E_W,A_W,I_W,I_{WM},E_V,I_V\right)$ and evaluated at $\left(X^{\text{*}},0\right)$, which is an M-matrix (the diagonal elements are nonnegative). Thus,

$$D_{Z}G\left(X^{\text{*}},0\right)=\left(\begin{array}{cccccccccc}-k_2& 0& 0& 0& 0& 0& 0& 0& 0& \eta {\text{Ψ}}_B\\ \left(1-p\right){\sigma }_B& -k_3& 0& 0& 0& q{\pi }_W& 0& 0& 0& 0\\ p{\sigma }_B& 0& -k_4& 0& 0& 0& q{\pi }_W& 0& 0& 0\\ 0& 0& 0& -k_5& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& -k_8& 0& 0& 0& 0& {\text{Ψ}}_W\\ 0& 0& 0& 0& \left(1-p\right){\sigma }_W& -k_9& 0& 0& 0& 0\\ 0& 0& 0& 0& p{\sigma }_W& 0& -k_{10}& 0& 0& 0\\ 0& 0& 0& \alpha & 0& 0& 0& -k_{12}& 0& 0\\ 0& \eta {\rho }_B{\text{Ψ}}_V& \eta {\text{Ψ}}_V& 0& 0& {\rho }_W{\text{Ψ}}_V& {\text{Ψ}}_V& 0& -k_{14}& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& {\sigma }_V& -{\mu }_V\end{array}\right)\text{,}$$

where, ${\text{Ψ}}_B={\beta }_B{b}_V\frac{S_B^{\text{*}}}{N_B^{\text{*}}},{\text{Ψ}}_W=\frac{{\beta }_W{b}_V{S}_W^{\text{*}}}{N_W^{\text{*}}}$, ${\text{Ψ}}_V=\frac{{\beta }_V{b}_V{S}_V^{\text{*}}}{N_H^{\text{*}}}$ and

$$\hat{G}\left(X,Z\right)=\left(\begin{array}{c}{\text{Φ}}_B{I}_V\\ 0\\ 0\\ 0\\ {\text{Φ}}_W{I}_V\\ 0\\ 0\\ 0\\ \eta {\rho }_B{\text{Φ}}_V{A}_W+\eta {\text{Φ}}_V{I}_W+{\rho }_W{\text{Φ}}_V{A}_B+{\text{Φ}}_V{I}_B\\ 0\end{array}\right)$$

where, ${\text{Φ}}_B=\frac{{\beta }_B{b}_V{S}_B^{\text{*}}}{N_B^{\text{*}}}\left(1-\frac{S_B}{N_B}\frac{N_B^{\text{*}}}{S_B^{\text{*}}}\right)\text{,}$ ${\text{Φ}}_W=\frac{{\beta }_W{b}_V{S}_W^{\text{*}}}{N_W^{\text{*}}}\left(1-\frac{S_W}{N_W}\frac{N_W^{\text{*}}}{S_W^{\text{*}}}\right)$ and ${\text{Φ}}_V=\frac{{\beta }_V{b}_V{S}_V^{\text{*}}}{N_H^{\text{*}}}\left(1-\frac{S_V}{N_H}\frac{N_H^{\text{*}}}{S_V^{\text{*}}}\right)$.

Furthermore, $S_W^{\text{*}}=\frac{\alpha {\pi }_B}{{\mu }_W\left(\alpha +{\mu }_B\right)},S_B^{\text{*}}=\frac{{\pi }_B}{\alpha +{\mu }_B},N_H^{\text{*}}=S_W^{\text{*}}+\eta S_B^{\text{*}}$ and $S_V^{\text{*}}=\frac{{\pi }_V}{{\mu }_V}$. We have in ${\text{Γ}}_1$ that, $S_W\le S_W^{\text{*}},S_B\le S_B^{\text{*}}$, and $S_V\le S_V^{\text{*}}$. Therefore, it follows that $N_H\le N_H^{\text{*}}$.

Hence, if the human population is at equilibrium level, we have that $\left(1-\frac{N_W^{\text{*}}}{S_W^{\text{*}}}\frac{S_W}{N_W}\right)>0\text{,}$ $\left(1-\frac{N_B^{\text{*}}}{S_B^{\text{*}}}\frac{S_B}{N_B}\right)>0$ and $\left(1-\frac{S_V{N}_H^{\text{*}}}{N_H{S}_V^{\text{*}}}\right)>0$; thus, $\hat{G}\left(X,Z\right)\ge 0$.

Thus,

$$G\left(X,Z\right)=\left(\begin{array}{cccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 0& {\text{Φ}}_B{I}_V\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& {\text{Φ}}_W{I}_V\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& \eta {\rho }_B{\text{Φ}}_V{A}_W& \eta {\text{Φ}}_V{I}_W& 0& 0& {\rho }_W{\text{Φ}}_V{A}_B& {\text{Φ}}_V{I}_B& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right)$$

Therefore, the disease-free equilibrium is globally asymptotically stable by the theorem in (Castillo-Chavez et al., 2002) (page 246).

E. Mosquito-Larviciding Strategy

We consider the following three control levels:

• 1.Low mosquito-larviciding strategy: ${\pi }_V=500/day$;
• 2.Moderate mosquito-larviciding strategy: ${\pi }_V=250/day$;
• 3.High mosquito-larviciding strategy: ${\pi }_V=125/day$.

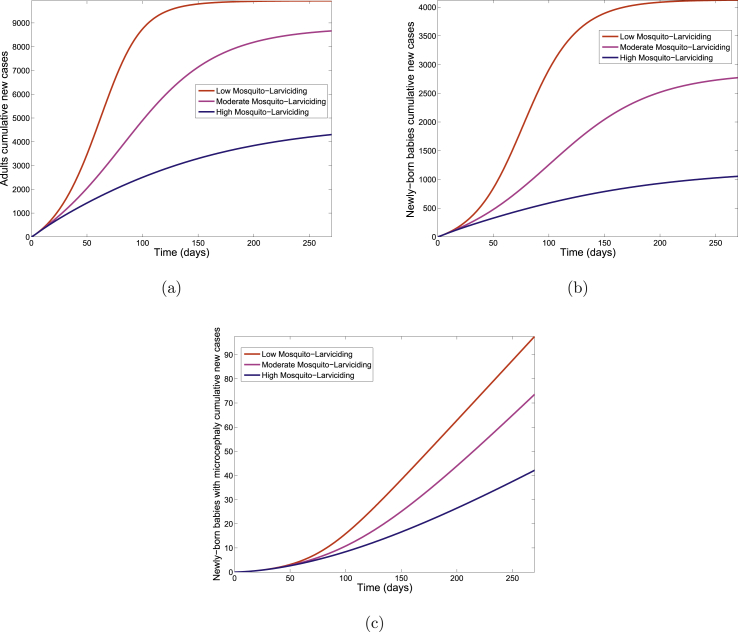
Fig. 10 shows the cumulative number of new infections in adults, new infections in newly born babies and newly born babies with microcephaly for each of the three control levels. Table 11 shows a clear decrease in the cumulative number of new cases with increasing control when comparing the three control levels.

Table 11.

Simulation results of the cumulative number of new cases days for the Zika model (2.1) using mosquito-larviciding strategy.

Humans	Low-Control	Moderate-Control	High-Control
Adults	$2.1\times {10}^6$	$1.5\times {10}^6$	$7.5\times {10}^5$
Newly born babies	$7.7\times {10}^5$	$4.4\times {10}^5$	$1.8\times {10}^5$
Newly born with microcephaly	$10.0\times {10}^3$	$7.1\times {10}^3$	$4.4\times {10}^3$

Fig. 10.

Simulation of the Zika model (2.1) for various control levels of the larviciding strategy. (a). The cumulative number of new cases in adults (b). The cumulative number of new cases in newly born babies. (c). The cumulative number of new cases of newly born babies with microcephaly. Parameter values used are as given in Table 3.

F. Mosquito-Adulticiding Strategy

• 1.Low mosquito-adulticiding strategy: ${\mu }_V=\frac{1}{21}/day$;
• 2.Moderate mosquito-adulticiding strategy: ${\mu }_V=\frac{1}{14}/day$;
• 3.High mosquito-adulticiding strategy: ${\mu }_V=\frac{1}{8}/day$.

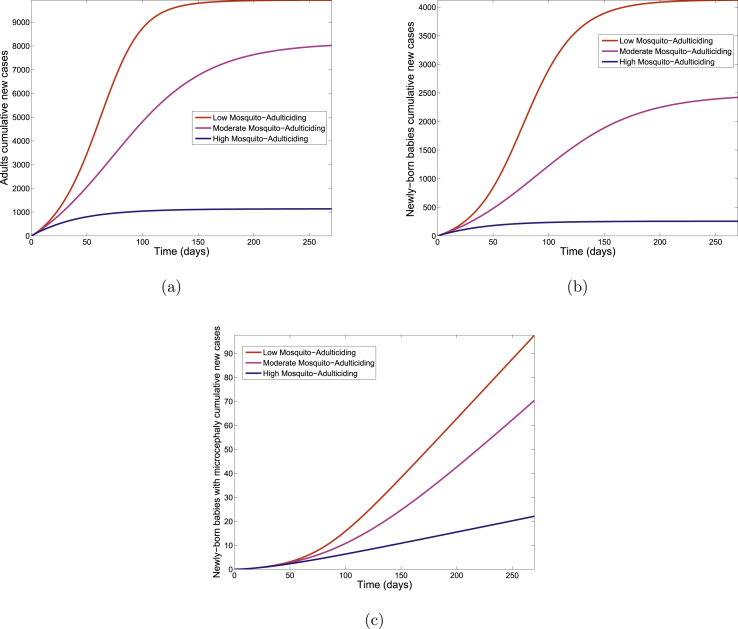
The cumulative number of new infections in adults, new infections in newly born babies and newly born babies with microcephaly for each of the three control levels is depicted in Fig. 11. A comparison of the three control levels in Table 12 shows a decrease in the cumulative number of new cases with increasing control.

Fig. 11.

Simulation of the Zika model (2.1) for various control levels of the adulticiding strategy. (a). The cumulative number of new cases in adults (b). The cumulative number of new cases in newly born babies. (c). The cumulative number of new cases of newly born babies with microcephaly. Parameter values used are as given in Table 3.

Table 12.

Simulation results of the cumulative number of new cases for the Zika model (2.1) using mosquito-adulticiding strategy.

Humans	Low-Control	Moderate-Control	High-Control
Adults	$2.1\times {10}^6$	$1.4\times {10}^6$	$2.6\times {10}^5$
Newly born babies	$7.7\times {10}^5$	$4.0\times {10}^5$	$5.8\times {10}^4$
Newly born with microcephaly	$10.0\times {10}^3$	$6.9\times {10}^3$	$2.7\times {10}^3$