How heterogeneous susceptibility and recovery rates affect the spread of epidemics on networks

Abstract

In this paper, an extended heterogeneous SIR model is proposed, which generalizes the heterogeneous mean-field theory. Different from the traditional heterogeneous mean-field model only taking into account the heterogeneity of degree, our model considers not only the heterogeneity of degree but also the heterogeneity of susceptibility and recovery rates. Then, we analytically study the basic reproductive number and the final epidemic size. Combining with numerical simulations, it is found that the basic reproductive number depends on the mean of distributions of susceptibility and disease course when both of them are independent. If the mean of these two distributions is identical, increasing the variance of susceptibility may block the spread of epidemics, while the corresponding increase in the variance of disease course has little effect on the final epidemic size. It is also shown that positive correlations between individual susceptibility, course of disease and the square of degree make the population more vulnerable to epidemic and avail to the epidemic prevalence, whereas the negative correlations make the population less vulnerable and impede the epidemic prevalence.

1. Introduction

The method of establishing the network-based models, which incorporates the contact patterns among people as static or dynamic networks into epidemiology modeling, has become an essentially important research method to study the role of nodes standing for individuals or edges denoting the interaction between individuals in the spreading process (Dorogovtsev et al., 2008, Jin et al., 2014, Luo et al., 2017, Pastor-Satorras et al., 2015). The frequently investigated and most classical epidemiological models as the basic conceptual tools in understanding the epidemic spreading and the related effective strategies for epidemic controlling are the SIS model and the SIR model. As is well known that the most valuable result in the standard SIS model (Boguná and Pastor-Satorras, 2002, Boguná et al., 2003, Luo et al., 2014, Pastor-Satorras and Vespignani, 2001) or SIR (May and Lloyd, 2001, Moreno et al., 2002, Newman, 2002) model is that the basic reproductive numbers of an infection $R_0$ is always larger than 1 for the scale-free networks in the thermodynamic limit, which implies that the heterogeneity of node's degree can reduce or even eliminate the existence of an epidemic threshold.

In most epidemiological models (Anderson et al., 1992, Jin et al., 2011, Keeling and Rohani, 2008, Li et al., 2014, Li et al., 2017, Peng et al., 2016), all individuals are assumed to be homogeneous, e.g., all susceptible individuals acquire the disease with the same probability whenever in contact with an infected individual, and all infected individuals recover, or go back to being susceptible, with the same rate. Such consideration is, however, far from the actual situation. The individual variations of infectivity (Lloyd Smith et al., 2005, Riley et al., 2003), susceptibility (Boon et al., 2011, Hardie et al., 2008, Li et al., 2010a, Zhang et al., 2014, Zhang et al., 2016) and recovery rates or infectious period are as widespread as network heterogeneity. These internal properties of individuals varying across a population result from genetic (Segal & Hill, 2003) and immunogenetic (Fryer et al., 2010) factors, differences in age, previous disease history, history of drug abuse, or differences in healthcare quality and can exert a non-negligible influence on the epidemic spreading process.

Recently, several authors have applied the percolation theory to explore the effects of individual heterogeneity in the context of network epidemics (Kenah and Robins, 2007, Miller, 2007, Miller, 2009, Neri et al., 2010, Neri et al., 2011). For instance, Kenah and Robins (Kenah & Robins, 2007) showed that the bond percolation model failed to predict the correct outbreak size distribution and probability of an epidemic when there was a nondegenerate infectious period distribution. Miller (Miller, 2007) showed that an epidemic was most likely if infectivity was homogeneous and least likely if the variance of infectivity was maximized. Similarly, the attach rate was largest if susceptibility was homogeneous and smallest if the variance was maximized. Later, Miller (Miller, 2009) showed that heterogeneity infectiousness was the dominant factor controlling the probability of an epidemic and heterogeneity in susceptibility was the dominant factor controlling the size of an epidemic.

There are some other works to study the effects of individual heterogeneity on the epidemic spreading process on networks. Karrer and Newman (Karrer & Newman, 2010) introduced the message passing approach to study a generalized SIR model that allowed for arbitrary distribution of transmission and recovery times. Using the message passing approach, Sherborne et al. (Sherborne et al., 1611) derived a new pairwise-like model for epidemics with Markovian transmission and arbitrary recovery period; and they also presented a novel extension of the edge-based compartmental model for epidemics with arbitrary distributions of transmission and recovery times. Li et al. (Li, Liu, Kim, Min, & Zhang, 2010) studied the network epidemic dynamics with both individual mobility and heterogeneity and showed that the heterogeneity of individual susceptibility and infectivity increased the epidemic threshold, and the positive correlation of individual susceptibility and infectivity availed to the epidemic prevalence. Wu et al. (Wu & Zhang, 2016) investigated the epidemic spreading on random and regular networks through a pairwise-type model to evaluate the influence of individual infectivity and susceptibility which were functions of individual activity. Smilkove et al. (Smilkov, Hidalgo, & Kocarev, 2014) found that heterogeneous susceptibility can make networks more vulnerable to the spread of epidemics if the correlation between a node's degree and susceptibility were positive. Yang et al., (Yang, Tang, & Gross, 2015) using the pairwise approximation method, showed that these correlations naturally arised in the adaptive network through considering a plausible scenario where people had intrinsic differences in susceptibility and adapted their social network structure to the presence of the disease. Abbas et al. (Abbas, Bhatia, Vorobeychik, & Koutsoukos, 2014) incorporated node properties into a node-based SIRS model for infection propagation and proposed new heuristics to curb the spread of infection in heterogeneous networks.

Although the studies mentioned above can explain how the individual heterogeneity influences the epidemic spreading process on networks to some extent, this complex phenomenon is still poorly understood and some questions remain open. Especially, there is less work to explore the effect of the heterogeneity of individual susceptibility and recovery rates at the same time on the dynamic behaviors of epidemics spreading on networks. And this invites us to follow the precious works and investigate how the heterogeneous susceptibility and recovery rates of individuals, combining with the network heterogeneity, influence the epidemic spreading process. We are interested in using or generalizing the heterogeneous mean-field theory to address this problem. Meantime, the incorporation of differential susceptibility and recovery rates into epidemic models does introduce a new dimension to epidemic modeling, since there are multiple ways for individuals with differences in susceptibility and recovery rates to be arranged in a network. Therefore, we should consider not only variations in the susceptibility and recovery rates of individuals, but also the correlations between individual susceptibility, recovery rates and connectivity to do a complete study.

In this paper, we establish an extended heterogeneous SIR epidemic model defined on networks with arbitrary network topology and analytically study the basic reproductive number $R_0$ and the final epidemic size $R\left(\infty \right)$ for this model. Our findings show that the spread of epidemics is closely correlated to the structure of population in terms of individual susceptibility and course of disease. When individual degree, susceptibility and recovery rate are independent, $R_0$ and $R\left(\infty \right)$ are increasing with the increment of the average susceptibility and the average course of disease of the entire networks. And if averages of susceptibility and disease course are identical, increasing the variance of susceptibility may block the spread of epidemics, while increasing the variance of disease course has little effect on the final epidemic size. Focusing on the individual level correlations between the two of the susceptibility, the course of disease, and the square of the degree or connectivity of individuals, we show that positive correlations between them make the network more vulnerable to epidemics (increasing $R_0$) and avail to the epidemic prevalence (increasing $R\left(\infty \right)$); whereas negative correlations make the network less vulnerable (decreasing $R_0$) and impede the epidemic prevalence (decreasing $R\left(\infty \right)$).

This paper is organized as follows: in Section 2, we propose our extended heterogeneous SIR model. And in Section 3, there are some analytical results of our extended model. Some numerical simulations are presented in Section 4. The paper concludes in the last section with discussion of results and possible applications of this work.

2. The extended heterogeneous SIR model

In this section, we outline our extended heterogeneous SIR model that incorporates not only individual distinct susceptibility and recovery rates but the topology of networks to provide more accurate descriptions of the epidemic spreading process.

In this paper, we assume that all individuals once infected are equally infectious. In order to introduce differential susceptibility and recovery rates, we assume the population can be divided into m subgroups according to the susceptibility to infection, and the susceptibility of individuals in the $ith$ subgroup is ${\beta }_i,i=\mathrm{1,2},\dots ,m\text{.}$ For each subgroup in which individual susceptibility is identical, we further divide them into n subgroups according to individual recovery rate, and the recovery rate of individuals in the $jth$ subgroup is ${\gamma }_j,j=\mathrm{1,2},\dots ,n\text{,}$ correspondingly their course of disease is ${\gamma }_j^{-1}$. For each individual, we set a pair fixed values, i.e., ${\beta }_i$ and ${\gamma }_j$ as individual internal property, that don't change over time, to depict the heterogeneity of individual susceptibility and recovery rates. To further clarity, for the susceptible individuals with susceptibility ${\beta }_i$ and recovery rate ${\gamma }_j$, they will be infected when they have contact with an infected individual with the probability ${\beta }_i$ and recover with the rate ${\gamma }_j$ if they are infected. For the infected individuals with susceptibility ${\beta }_i$ and recovery rate ${\gamma }_j$, they have been infected by one existing infectious individual with the probability ${\beta }_i$ and will recover with the rate ${\gamma }_j$. And for the recovered individuals with susceptibility ${\beta }_i$ and recovery rate ${\gamma }_j$, they were once infected by one existing infectious individuals with the probability ${\beta }_i$ and recovered with the rate ${\gamma }_j$.

To take the topology of networks into account at the same time, it is necessary to traditionally denote the number of edges attached to the nodes in a network as degree k. As a result, we denote the numbers of the susceptible, infected and recovered nodes with susceptibility ${\beta }_i$, recovery rate ${\gamma }_j$ and degree k, in a network with arbitrary network topology as $S_{i,j,k}$, $I_{i,j,k}$ and $R_{i,j,k}$ respectively. The corresponding total number of nodes with susceptibility ${\beta }_i$, recovery rate ${\gamma }_j$ and degree k is

$$N_{i,j,k}=S_{i,j,k}+I_{i,j,k}+R_{i,j,k}\text{,}$$

and the total nodes of the network is

$$N=\sum _{k=1}^M\sum _{j=1}^n\sum _{i=1}^m{N}_{i,j,k}\text{,}$$

where M is the maximum degree of nodes. The joint distribution

$$P\left(i,j,k\right)\triangleq \frac{N_{i,j,k}}{N}$$

is the proportion of nodes with susceptibility ${\beta }_i$, recovery rate ${\gamma }_j$ and degree k in the total number of nodes, which implies the structure of network in terms of node's susceptibility and recovery rates, as well as node's degree.

It is straightforward that the joint distribution

$$P_{sr}\left(i,j\right)=\sum _{k=1}^{M}P\left(i,j,k\right)$$

represents the structure of network in terms of node's susceptibility and recovery rates; the joint distribution

$$P_{sd}\left(i,j\right)=\sum _{j=1}^{n}P\left(i,j,k\right)$$

represents the structure of network in terms of node's susceptibility and degree; the joint distribution

$$P_{rd}\left(i,j\right)=\sum _{i=1}^{m}P\left(i,j,k\right)$$

represents the structure of network in terms of node's recovery rates and degree.

On the other hand, we can get some features of the topology of network and disease. We can deduce the degree distribution $P_d\left(k\right)$ to represent the topology of network, which is obtained by

$$P_d\left(k\right)=\sum _{j=1}^n\sum _{i=1}^{m}P\left(i,j,k\right)\text{.}$$

Hence, the average degree $\langle k\rangle$ is given by

$$\langle k\rangle =\sum _{k=1}^{M}k{P}_d\left(k\right)=\sum _{k=1}^M\sum _{j=1}^n\sum _{i=1}^{m}kP\left(i,j,k\right)\text{.}$$

About the features of disease, the susceptibility distribution can be denoted as

$$P_s\left(i\right)=\sum _{k=1}^M\sum _{j=1}^{n}P\left(i,j,k\right)\text{,}$$

and the average susceptibility of the entire network is

$$\langle \beta \rangle \triangleq \sum _{i=1}^m{\beta }_i{P}_s\left(i\right)=\sum _{k=1}^M\sum _{j=1}^n\sum _{i=1}^m{\beta }_{i}P\left(i,j,k\right)\text{.}$$

The distribution of recovery rates is denoted as

$$P_r\left(j\right)=\sum _{k=1}^M\sum _{i=1}^{m}P\left(i,j,k\right)\text{,}$$

and the average recovery rate of the entire network is

$$\langle \gamma \rangle \triangleq \sum _{j=1}^n{\gamma }_j{P}_r\left(j\right)=\sum _{k=1}^M\sum _{j=1}^n\sum _{i=1}^m{\gamma }_{j}P\left(i,j,k\right)\text{.}$$

In particularly, it is necessary to introduce the average course of disease of the entire network, namely the average of all individuals’ course of disease ${\gamma }_j^{-1}$

$$\langle {\gamma }^{-1}\rangle \triangleq \sum _{j=1}^n{\gamma }_j^{-1}{P}_r\left(j\right)=\sum _{k=1}^M\sum _{j=1}^n\sum _{i=1}^m{\gamma }_j^{-1}P\left(i,j,k\right)\text{.}$$

The transmission of epidemics at time t is determined by the edges that link a susceptible node with an infected node at that time. So we use $\left[S_{i,j,k}{I}_{i^{\prime },j^{\prime },k^{\prime }}\right]$ to indicate the number of the edges that link a susceptible node whose susceptibility, recovery rate and degree are ${\beta }_i$, ${\gamma }_j$ and k with an infected node whose susceptibility, recovery rate and degree are ${\beta }_{i^{\prime }}$, ${\gamma }_{j^{\prime }}$ and $k^{\prime }$ at time t. We assume that the time scale of the disease is much smaller than the lifespan of individuals and do not account for the birth or natural death of individuals or nodes. What's more, we assume that the nodes with the same degree, susceptibility and recovery rate show the identical dynamical characteristic, which generalizes the heterogeneous mean-field (HMF) theory (Moreno et al., 2002, Pastor-Satorras and Vespignani, 2001). The HMF theory just assumes that the nodes of the same degrees will show the same dynamical characteristic. Therefore, we can establish the following extended heterogeneous SIR model to precisely describe the spread of epidemics on a network:

$$\{\begin{array}{l}\frac{d{S}_{i,j,k}}{dt}=-{\beta }_i\sum _{k^{\prime }=1}^M\sum _{j^{\prime }=1}^n\sum _{i^{\prime }=1}^m\left[S_{i,j,k}{I}_{i^{\prime },j^{\prime },k^{\prime }}\right]\text{,}\hfill \\ \frac{d{I}_{i,j,k}}{dt}={\beta }_i\sum _{k^{\prime }=1}^M\sum _{j^{\prime }=1}^n\sum _{i^{\prime }=1}^m\left[S_{i,j,k}{I}_{i^{\prime },j^{\prime },k^{\prime }}\right]-{\gamma }_j{I}_{i,j,k}\text{,}\hfill \\ \frac{d{R}_{i,j,k}}{dt}={\gamma }_j{I}_{i,j,k}\text{.}\hfill \end{array}$$ (2.1)

Duo to the existence of the term $\left[S_{i,j,k}{I}_{i^{\prime },j^{\prime },k^{\prime }}\right]$ in model (2.1), this model isn't closed and we can't directly analyse its dynamic behaviors. Therefore, we introduce a generalized correlation coefficient to get some analytical results in the next section.

3. Analytical results

In this section, we consider the effect of the differences in susceptibility and recovery rates, combining with the topology of networks, on the spread of epidemics involving their respective basic reproductive number $R_0$ and the final epidemic size $R\left(\infty \right)$. The basic reproductive number as epidemic thresholds sometimes has an important ramifications in many real-world scenarios. Theoretically speaking, it characterizes the critical condition above which a global epidemic occurs. Practically speaking, quantifying it allows us to determine the effectiveness of a given immunization strategy. In addition, knowing the final epidemic size helps us evaluate the severity of the epidemic spreading.

Attempting to generalize the Correlation $C_{AB}$ between nodes of type A and B (Keeling, 1999), we shall define $C_{S_{i,j,k}{I}_{i^{\prime },j^{\prime },k^{\prime }}}$ to be the correlation between nodes of the susceptible one whose susceptibility, recovery rate and degree are ${\beta }_i$, ${\gamma }_j$ and k and the infected one whose susceptibility, recovery rate and degree ${\beta }_{i^{\prime }}$, ${\gamma }_{j^{\prime }}$ and $k^{\prime }$,

$$C_{S_{i,j,k}{I}_{k^{\prime },i^{\prime },j^{\prime }}}=\frac{\langle k\rangle N}{k{k}^{\prime }}\frac{\left[S_{i,j,k}{I}_{i^{\prime },j^{\prime },k^{\prime }}\right]}{S_{i,j,k}{I}_{i^{\prime },j^{\prime },k^{\prime }}}\text{.}$$

We say they are uncorrelated, if $C_{S_{i,j,k}{I}_{i^{\prime },j^{\prime },k^{\prime }}}=1$. In this case, we have

$$\left[S_{i,j,k}{I}_{i^{\prime },j^{\prime },k^{\prime }}\right]=\frac{k{k}^{\prime }}{\langle k\rangle N}{S}_{i,j,k}{I}_{i^{\prime },j^{\prime },k^{\prime }}=\frac{k{k}^{\prime }}{\langle k\rangle }{S}_{i,j,k}P\left(i^{\prime },j^{\prime },k^{\prime }\right){\rho }_{i^{\prime },j^{\prime },k^{\prime }}\text{.}$$

where ${\rho }_{i^{\prime },j^{\prime },k^{\prime }}=\frac{I_{i^{\prime },j^{\prime },k^{\prime }}}{N_{i^{\prime },j^{\prime },k^{\prime }}}$ indicates the relative density of susceptible nodes with susceptibility ${\beta }_{i^{\prime }}$, recovery rate ${\gamma }_{j^{\prime }}$ and degree $k^{\prime }$. Similarly, $s_{i,j,k}=\frac{S_{i,j,k}}{N_{i,j,k}}$ and $r_{i,j,k}=\frac{R_{i,j,k}}{N_{i,j,k}}$ represent the relative densities of infected and recovered nodes with susceptibility ${\beta }_i$, recovery rate ${\gamma }_j$ and degree k respectively.

On the base of the above work, under the generalized uncorrelation we deduce the following system according to system (2.1):

$$\{\begin{array}{l}\frac{d{s}_{i,j,k}}{dt}=-k{\beta }_i{s}_{i,j,k}\sum _{k^{\prime }=1}^M\sum _{j^{\prime }=1}^n\sum _{i^{\prime }=1}^m\frac{k^{\prime }P\left(i^{\prime },j^{\prime },k^{\prime }\right)}{\langle k\rangle }{\rho }_{i^{\prime },j^{\prime },k^{\prime }}\text{,}\hfill \\ \frac{d{\rho }_{i,j,k}}{dt}=k{\beta }_i{s}_{i,j,k}\sum _{k^{\prime }=1}^M\sum _{j^{\prime }=1}^n\sum _{i^{\prime }=1}^m\frac{k^{\prime }P\left(i^{\prime },j^{\prime },k^{\prime }\right)}{\langle k\rangle }{\rho }_{i^{\prime },j^{\prime },k^{\prime }}-{\gamma }_j{\rho }_{i,j,k}\text{,}\hfill \\ \frac{d{r}_{i,j,k}}{dt}={\gamma }_j{\rho }_{i,j,k}\text{.}\hfill \end{array}$$ (3.1)

For convenience, we use $S_{i,j,k}$, $I_{i,j,k}$ and $R_{i,j,k}$ to represent $s_{i,j,k}$, ${\rho }_{i,j,k}$ and $r_{i,j,k}$ respectively, and these variables obey the normalization condition $S_{i,j,k}+I_{i,j,k}+R_{i,j,k}=1$. Finally the spread of epidemics on the network can be described by the following system:

$$\{\begin{array}{l}\frac{d{S}_{i,j,k}}{dt}=-k{\beta }_i{S}_{i,j,k}\sum _{k^{\prime }=1}^M\sum _{j^{\prime }=1}^n\sum _{i^{\prime }=1}^m\frac{k^{\prime }P\left(i^{\prime },j^{\prime },k^{\prime }\right)}{\langle k\rangle }{I}_{i^{\prime },j^{\prime },k^{\prime }}\text{,}\hfill \\ \frac{d{I}_{i,j,k}}{dt}=k{\beta }_i{S}_{i,j,k}\sum _{k^{\prime }=1}^M\sum _{j^{\prime }=1}^n\sum _{i^{\prime }=1}^m\frac{k^{\prime }P\left(i^{\prime },j^{\prime },k^{\prime }\right)}{\langle k\rangle }{I}_{i^{\prime },j^{\prime },k^{\prime }}-{\gamma }_j{I}_{i,j,k}\text{,}\hfill \\ \frac{d{R}_{i,j,k}}{dt}={\gamma }_j{I}_{i,j,k}\text{.}\hfill \end{array}$$ (3.2)

In this paper, we give the initial conditions as $S_{i,j,k}\left(0\right)\approx 1,I_{i,j,k}\left(0\right)\approx 0,R_{i,j,k}\left(0\right)=0\text{,}$ indicating the initial relative densities of susceptible, infected and recovered nodes with susceptibility ${\beta }_i$, recovery rate ${\gamma }_j$ and degree k.

3.1. The basic reproductive number

In order to compute the basic reproductive number, we have attempted to apply the method of the next generation matrix (Van den Driessche & Watmough, 2002), actually we do obtain the same result, but it's a boringly tedious work. Fortunately, we also can obtain the basic reproductive number according to whether the number of infected individuals increases monotonically at the initial moment, which is excitingly easier.

On both sides of the second equation in system (3.2) multiplied $\frac{kP\left(i,j,k\right)}{{\gamma }_j}$ and summing over $i,j$ and k, with defining

$$\varphi \left(t\right)=\sum _{k=1}^M\sum _{j=1}^n\sum _{i=1}^m\frac{kP\left(i,j,k\right)I_{i,j,k}\left(t\right)}{{\gamma }_j}\text{,}$$

we obtain

$${\varphi }^{\prime }\left(t\right)=\left(\stackrel{M}{\sum _{k=1}}\stackrel{n}{\sum _{j=1}}\stackrel{m}{\sum _{i=1}}\frac{{\beta }_i{k}^{2}P\left(i,j,k\right)S_{i,j,k}\left(t\right)}{\langle k\rangle {\gamma }_j}-1\right)\stackrel{M}{\sum _{k^{\prime }=1}}\stackrel{n}{\sum _{j^{\prime }=1}}\stackrel{m}{\sum _{i^{\prime }=1}}{k}^{\prime }P\left(i^{\prime },j^{\prime },k^{\prime }\right)I_{i^{\prime },j^{\prime },k^{\prime }}\left(t\right)\text{.}$$ (3.3)

According to the definition of the basic reproductive number, we just need to judge whether the number of infected individuals increases monotonically at the initial moment. Note that whether the number of infected individuals increases monotonically at the initial moment is equal to whether $\varphi \left(t\right)$ increases monotonically. According to equation (3.3), with

$$\sum _{k^{\prime }=1}^M\sum _{j^{\prime }=1}^n\sum _{i^{\prime }=1}^m{k}^{\prime }P\left(i^{\prime },j^{\prime },k^{\prime }\right)I_{i^{\prime },j^{\prime },k^{\prime }}\left(0\right)>0\text{,}$$

${\varphi }^{\prime }\left(0\right)>0$ is equal to

$$\sum _{k=1}^M\sum _{j=1}^n\sum _{i=1}^m\frac{{\beta }_i{k}^{2}P\left(i,j,k\right)S_{i,j,k}\left(0\right)}{{\gamma }_j\langle k\rangle }>1.$$

Finally, we obtain the basic reproductive number $R_0$,

$$R_0=\sum _{k=1}^M\sum _{j=1}^n\sum _{i=1}^m\frac{{\beta }_i{k}^{2}P\left(i,j,k\right)S_{i,j,k}\left(0\right)}{{\gamma }_j\langle k\rangle }\text{.}$$

Because $S_{i,j,k}\left(0\right)\approx 1$, we have

$$R_0=\sum _{k=1}^M\sum _{j=1}^n\sum _{i=1}^m\frac{{\beta }_i{k}^{2}P\left(i,j,k\right)}{{\gamma }_j\langle k\rangle }\text{.}$$ (3.4)

From equation (3.4), we can conclude that the basic reproductive number is closely correlated with the joint distribution $P\left(i,j,k\right)$. In other words, the structure of networks with the respect of individual susceptibility and recovery rates, as well as individual degree has a significant influence on the vulnerability of networks to epidemics. Clearly, we also want to emphasize that if $m=n=1$, our extended heterogeneous SIR model will specialize to the standard SIR model (Moreno et al., 2002).

To further probe into the profound meaning of the basic reproductive number $R_0$, we discuss the following four special cases:

Case 1: Individual degree, susceptibility and recovery rate are all independent, namely $P\left(i,j,k\right)=P_s\left(i\right)P_r\left(j\right)P_d\left(k\right)$. In this case, we have

$$R_0=\frac{\langle k^2\rangle }{\langle k\rangle }\langle \beta \rangle \langle {\gamma }^{-1}\rangle \text{,}$$

where $\langle k^2\rangle$ is the average of the degrees squared.

Case 2: Individual degree is independent to individual susceptibility and recovery rate, namely $P\left(i,j,k\right)=P_d\left(k\right)P_{sr}\left(i,j\right)$. In this case, we have

$$R_0=\frac{\langle k^2\rangle }{\langle k\rangle }\langle \frac{\beta }{\gamma }\rangle =\frac{\langle k^2\rangle }{\langle k\rangle }[\langle \beta \rangle \langle {\gamma }^{-1}\rangle +Corr\left(\beta ,{\gamma }^{-1}\right){\sigma }_{\beta }{\sigma }_{{\gamma }^{-1}}]\text{,}$$

where $-1\le Corr\left(\beta ,{\gamma }^{-1}\right)\le 1$ is the Pearson correlation coefficient between individual susceptibility and course of disease, ${\sigma }_{\beta }$ and ${\sigma }_{{\gamma }^{-1}}$ are their respective standard deviation.

Case 3: Individual recovery rate is independent to individual degree and susceptibility, namely $P\left(i,j,k\right)=P_r\left(j\right)P_{sd}\left(i,k\right)$. In this case, we have

$$R_0=\frac{\langle {\gamma }^{-1}\rangle }{\langle k\rangle }\langle k^2\beta \rangle =\frac{\langle {\gamma }^{-1}\rangle }{\langle k\rangle }[\langle k^2\rangle \langle \beta \rangle +Corr\left(k^2,\beta \right){\sigma }_{k^2}{\sigma }_{\beta }]\text{,}$$

where $-1\le Corr\left(k^2,\beta \right)\le 1$ is the Pearson correlation coefficient between individual degree squared and susceptibility, ${\sigma }_{k^2}$ is the standard deviation of the degrees squared.

Case 4: Individual susceptibility is independent to individual degree and recovery rate, namely $P\left(i,j,k\right)=P_s\left(i\right)P_{rd}\left(j,k\right)$. In this case, we have

$$R_0=\frac{\langle \beta \rangle }{\langle k\rangle }\langle \frac{k^2}{\gamma }\rangle =\frac{\langle \beta \rangle }{\langle k\rangle }[\langle k^2\rangle \langle {\gamma }^{-1}\rangle +Corr\left(k^2,{\gamma }^{-1}\right){\sigma }_{k^2}{\sigma }_{{\gamma }^{-1}}]\text{,}$$

where $-1\le Corr\left(k^2,{\gamma }^{-1}\right)\le 1$ is the Pearson correlation coefficient between individual degree squared and course of disease.

According to the above discussion, we can get the following conclusions. Firstly, if individual degree, susceptibility and recovery rate are all independent, the vulnerability of networks to epidemic is determined by the topology of the network and the average susceptibility and the average course of disease of the entire networks. Secondly, positive correlation between individual susceptibility and course of disease makes the network more vulnerable to epidemic (increasing $R_0$), whereas the negative correlation makes the population less vulnerable (decreasing $R_0$). Thirdly, if individual susceptibility and course of disease have the larger standard deviations, the vulnerability of networks to epidemic will be increased or decreased to a larger degree even though there are the same level of positive or negative correlations between individual degree, susceptibility and course of disease. Fourthly, it is straightforward that heterogeneous susceptibility can make networks more vulnerable to epidemic when individual degree and susceptibility are positively correlated, and less vulnerable when individual degree and susceptibility are negatively correlated. And the effects of heterogeneous recovery rates lie in the fact that the networks are more vulnerable to diseases when individual degree and course of disease are positively correlated, and less vulnerable if they are negatively correlated. Noteworthily, even small correlations between individual degree and either individual susceptibility or course of disease can lead to significant discrepancy of $R_0$ when variation in connectivity, as measured by ${\sigma }_{k^2}$, is large compared to the average degree $\langle k\rangle$, which results from networks’ high heterogeneity of individual degree.

3.2. The final epidemic size

First, we show that for system (3.2) the disease will eventually die out, i.e., $I_{i,j,k}\left(\infty \right)=0$ for any $i,j,k$.

One can find that all solutions of system (3.2) remain non-negative and bounded in the set defined by $S_{i,j,k},I_{i,j,k},R_{i,j,k}\mathrm{\ge }0$ and $S_{i,j,k}+I_{i,j,k}+R_{i,j,k}=1$. Observing that

$$\frac{d}{dt}\left(S_{i,j,k}\left(t\right)+I_{i,j,k}\left(t\right)\right)=-{\gamma }_j{I}_{i,j,k}\left(t\right)\text{.}$$ (3.5)

We see that $S_{i,j,k}\left(t\right)+I_{i,j,k}\left(t\right)$ is decreasing whenever $I_{i,j,k}\left(t\right)>0$. However, $S_{i,j,k}\left(t\right)+I_{i,j,k}\left(t\right)$ is bounded below by 0; hence, it has a limit. Moreover, system (3.2) implies that $S_{i,j,k}^{\prime }\left(t\right)+I_{i,j,k}^{\prime }\left(t\right)$ is bounded, because $I_{i,j,k}\left(t\right)$ is bounded. Hence, $\underset{t\to \infty }{\text{lim}}\left(S_{i,j,k}^{\prime }\left(t\right)+I_{i,j,k}^{\prime }\left(t\right)\right)=0$, so $I_{i,j,k}\left(\infty \right)=0$. Therefore, duo to the arbitrariness of $i,j,k$, the disease will eventually die out for system (3.2).

If we integrate the third equation of system (3.2) from $t=0$ to $\infty$, we have

$$R_{i,j,k}\left(\infty \right)-R_{i,j,k}\left(0\right)={\gamma }_j{\int }_0^{\infty }{I}_{i,j,k}\left(s\right)ds\text{.}$$

Note that $R_{i,j,k}\left(0\right)=0$, hence we have

$$R_{i,j,k}\left(\infty \right)={\gamma }_j{\int }_0^{\infty }{I}_{i,j,k}\left(t\right)dt\text{.}$$

Integrating equation (3.5) from $t=0$ to $\infty$, we have

$$S_{i,j,k}\left(0\right)+I_{i,j,k}\left(0\right)=S_{i,j,k}\left(\infty \right)+R_{i,j,k}\left(\infty \right)\text{.}$$ (3.6)

Now we can work out the relative final size relation of the recovered. Integration of the first equation of system (3.2) from 0 to t gives

$$\text{ln}\frac{S_{i,j,k}\left(t\right)}{S_{i,j,k}\left(0\right)}=-k{\beta }_i\stackrel{M}{\sum _{k^{\prime }=1}}\stackrel{n}{\sum _{j^{\prime }=1}}\stackrel{m}{\sum _{i^{\prime }=1}}\frac{k^{\prime }P\left(i^{\prime },j^{\prime },k^{\prime }\right)R_{i^{\prime },j^{\prime },k^{\prime }}\left(t\right)}{\langle k\rangle {\gamma }_{j^{\prime }}}\text{.}$$

Hence,

$$S_{i,j,k}\left(t\right)=S_{i,j,k}\left(0\right)\text{exp}[-k{\beta }_i\sum _{k^{\prime }=1}^M\sum _{j^{\prime }=1}^n\sum _{i^{\prime }=1}^m\frac{k^{\prime }P\left(i^{\prime },j^{\prime },k^{\prime }\right)R_{i^{\prime },j^{\prime },k^{\prime }}\left(t\right)}{\langle k\rangle {\gamma }_{j^{\prime }}}]\text{.}$$

Letting $t\to \infty$, it arrives at

$$S_{i,j,k}\left(\infty \right)=S_{i,j,k}\left(0\right)\text{exp}[-k{\beta }_i\sum _{k^{\prime }=1}^M\sum _{j^{\prime }=1}^n\sum _{i^{\prime }=1}^m\frac{k^{\prime }P\left(i^{\prime },j^{\prime },k^{\prime }\right)R_{i^{\prime },j^{\prime },k^{\prime }}\left(\infty \right)}{\langle k\rangle {\gamma }_{j^{\prime }}}]\text{.}$$

Duo to equation (3.6), we have

$$R_{i,j,k}\left(\infty \right)=\{1-\text{exp}[-k{\beta }_i\stackrel{M}{\sum _{k^{\prime }=1}}\stackrel{n}{\sum _{j^{\prime }=1}}\stackrel{m}{\sum _{i^{\prime }=1}}\frac{k^{\prime }P\left(i^{\prime },j^{\prime },k^{\prime }\right)R_{i^{\prime },j^{\prime },k^{\prime }}\left(\infty \right)}{\langle k\rangle {\gamma }_{j^{\prime }}}]\}\times S_{i,j,k}\left(0\right)+I_{i,j,k}\left(0\right)\text{.}$$ (3.7)

The equation (3.7) provides the relative final size relation of the recovered, but we can't directly ascertain the existence of $R_{i,j,k}\left(\infty \right)$. Therefore, we provide the condition of this existence by the following theorem.

Theorem 3.1

If $R_0>1$, then the non-zero final size for the recovered population exists.

Proof. Let us define

$${\phi }_{\infty }=\sum _{k=1}^M\sum _{j=1}^n\sum _{i=1}^m\frac{kP\left(i,j,k\right)R_{i,j,k}\left(\infty \right)}{\langle k\rangle {\gamma }_j}\text{.}$$

Note that the positivity of ${\phi }_{\infty }$ implies the existence of the non-zero final size for the recovered population.

On both sides of equation (3.7) multiplied $\frac{kP\left(i,j,k\right)}{\langle k\rangle {\gamma }_j}$ and summing over $i,j$ and k obtains

$${\phi }_{\infty }=\stackrel{M}{\sum _{k=1}}\stackrel{n}{\sum _{j=1}}\stackrel{m}{\sum _{i=1}}\frac{kP\left(i,j,k\right)S_{i,j,k}\left(0\right)}{\langle k\rangle {\gamma }_j}+\stackrel{M}{\sum _{k=1}}\stackrel{n}{\sum _{j=1}}\stackrel{m}{\sum _{i=1}}\frac{kP\left(i,j,k\right)I_{i,j,k}\left(0\right)}{\langle k\rangle {\gamma }_j}-\stackrel{M}{\sum _{k=1}}\stackrel{n}{\sum _{j=1}}\stackrel{m}{\sum _{i=1}}\frac{kP\left(i,j,k\right)S_{i,j,k}\left(0\right)}{\langle k\rangle {\gamma }_j}\text{exp}\left(-k{\beta }_i{\phi }_{\infty }\right)\text{.}$$

Substituting the initial condition $S_{i,j,k}\left(0\right)\approx 1,I_{i,j,k}\left(0\right)\approx 0$ into the above equation, we obtain the following self-consistent equation for ${\phi }_{\infty }$:

$${\phi }_{\infty }=\sum _{k=1}^M\sum _{j=1}^n\sum _{i=1}^m\frac{kP\left(i,j,k\right)}{\langle k\rangle {\gamma }_j}[1-\text{exp}\left(-k{\beta }_i{\phi }_{\infty }\right)]\text{.}$$ (3.8)

The value ${\phi }_{\infty }=0$ is always a solution. In order to have a non-zero solution, the condition

$$\frac{d}{d{\phi }_{\infty }}\left(\sum _{k=1}^M\sum _{j=1}^n\sum _{i=1}^m\frac{kP\left(i,j,k\right)}{\langle k\rangle {\gamma }_j}[1-\text{exp}\left(-k{\beta }_i{\phi }_{\infty }\right)]\right){|}_{{\phi }_{\infty }=0}>1.$$ (3.9)

must be fulfilled. This relation implies

$$\sum _{k=1}^M\sum _{j=1}^n\sum _{i=1}^m\frac{{\beta }_i{k}^{2}P\left(i,j,k\right)}{\langle k\rangle {\gamma }_j}=R_0>1.$$ (3.10)

Therefore, if $R_0>1$, the non-zero final size for the recovered population exists.

According to Theorem 3.1, if $R_0>1$, the epidemic will outbreak. And combining with the equation (3.7), if the epidemic outbreaks, namely ${\phi }_{\infty }>0$, $R_{i,j,k}\left(\infty \right)>0$. Hence, we do want to stress that in general $R_0>1$ does guarantee a macroscopic outbreak and a prevalent infection in the entire network. However, if ${\beta }_i$ is small enough, we have $R_{i,j,k}\left(\infty \right)\approx I_{i,j,k}\left(0\right)$, which means that there hardly are epidemic outbreak in the corresponding subgroups. Interestingly, if we compute the derivation of the equation (3.7) about ${\beta }_i$, we have

$$\frac{d}{d{\beta }_i}{R}_{i,j,k}\left(\infty \right)=S_{i,j,k}\left(0\right)k{\phi }_{\infty }\text{exp}\left(-k{\beta }_i{\phi }_{\infty }\right)>0.$$

This result shows that the larger ${\beta }_i$ usually means the relatively larger $R_{i,j,k}\left(\infty \right)$ under the condition $R_0>1$.

Furthermore, we have to state that if the epidemic outbreaks, the final epidemic size $R\left(\infty \right)$ can be obtained by the computation:

$$R\left(\infty \right)=\sum _{k=1}^M\sum _{j=1}^n\sum _{i=1}^m{R}_{i,j,k}\left(\infty \right)P\left(i,j,k\right)\text{.}$$ (3.11)

From equations (3.7), (3.11), we can conclude that the final epidemic size has a close correlation with the structure of the networks in terms of nodes’ degree, susceptibility, and recovery rates. This point will be illustrated clearly in Section 4 by some numerical simulations.

Until now, we have put forward the formulas to compute the basic reproductive number $R_0$ and the total final size for the recovered population $R\left(\infty \right)$. However, these formulas have little practical application duo to the absence of complete information about the network topology and the distribution of individual susceptibility and recovery rates. In real case, we can divide population coarsely into some subgroups with $\beta ={\beta }_{low},{\beta }_{medium}$ and ${\beta }_{high}$ corresponding to low, medium and high susceptibility respectively. Similarly, $\gamma ={\gamma }_{low},{\gamma }_{medium}$ and ${\gamma }_{high}$ corresponding to low, medium and high recovery rate respectively. Obviously, the more subgroups we have, we can work out results which are closer to actual ones.

4. Numerical simulations

In this section, we directly take the value of individual course of disease and set its distribution to explore the effect of differential recovery rates on the spread of epidemics. Actually, we take individual susceptibility m values uniformly from 0 to 1, which means we divide the population into m subgroups according to individual susceptibility. And we take individual course of disease n values uniformly from 1 to 100, hence we divide the population into n subgroups according to individual course of disease. The fraction of initially infective individuals is ${10}^{-6}$.

We first assume that the degree, susceptibility, and recovery rate are independent, and will later discuss the case where the correlation of them is taken into account. In reality, individuals susceptibility and recovery rates, correspondingly their course of disease may have some different distribution characteristics, for example, the small or large average and variance. So in the following subsections, we choose to adopt both Poisson and power-law distributions to describe individual variant susceptibility and course of disease, and observe the behaviors of $R_0$ and $R\left(\infty \right)$ to discover the effect of the uncorrelated individual susceptibility and recovery rate, different levels of heterogeneity of individual susceptibility and course of disease, and the correlated individual degree, susceptibility and recovery rate on the spread of epidemics. Necessarily illustrating, in this paper we say the susceptibility follows Poisson distribution when setting the fraction of individuals with the i-th susceptibility as $p_s\left(i\right)=e^{\mathrm{-}\lambda }\frac{{\lambda }^{\left(i\mathrm{-1}\right)}}{\left(i\mathrm{-1}\right)!},i=\mathrm{1,2},\dots ,m,$ and the course of disease follows Poisson distribution when setting the fraction of individuals with the j-th course of disease as $p_r\left(j\right)=e^{\mathrm{-}\lambda }\frac{{\lambda }^{\left(j\mathrm{-1}\right)}}{\left(j\mathrm{-1}\right)!},j=\mathrm{1,2},\dots ,n,$ where λ is the sufficiently small parameters.

4.1. The effects of the uncorrelated individual susceptibility and recovery rate

To begin with, we show how the uncorrelated individual susceptibility and recovery rate affect the spread of epidemics. Here, we just consider the following two cases: individual susceptibility and course of disease both follow Poisson distribution or power-law distribution.

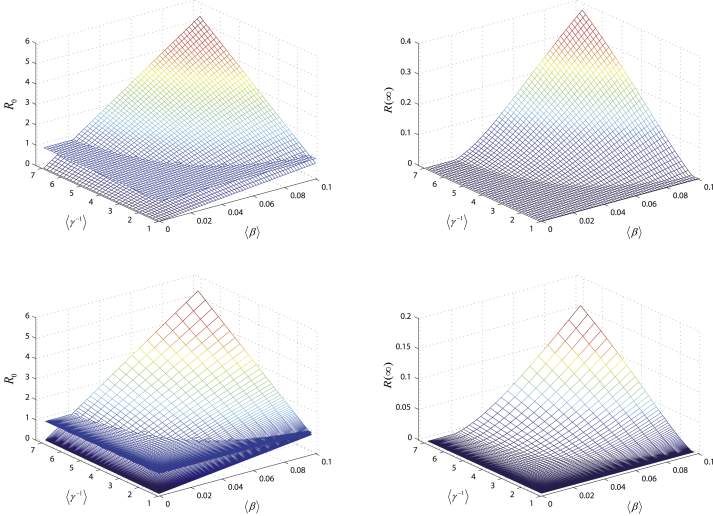
$R_0$ and $R\left(\infty \right)$ are plotted as the functions of $\langle \beta \rangle$ and $\langle {\gamma }^{-1}\rangle$ in Fig. 1. In a good agreement, when $R_0\le 1$, $R\left(\infty \right)=0$, and when $R_0>0$, $R\left(\infty \right)>0$. And $R_0$ and $R\left(\infty \right)$ congruously change with rebuilding the structure of population. On the whole, $R_0$ and $R\left(\infty \right)$ are increasing with the increment of $\langle \beta \rangle$ and $\langle {\gamma }^{-1}\rangle$. In the left two panels in Fig. 1, $R_0$ is equal, although individual susceptibility and course of disease follow different distributions. This accords with our theoretical analysis that when individual susceptibility and recovery rate are independent, the vulnerability of networks to epidemic reflected by $R_0$ is mainly determined by the average susceptibility and the average course of disease of the entire networks. From Fig. 1, it is not difficult to conclude that the structure of population in terms of individual susceptibility and course of disease have a non-negligible impact on the vulnerability of network to disease and the prevalence of the epidemic. Lowering the average susceptibility and the average course of disease of the entire networks will effectively control the outbreak and prevalence of the epidemic.

Fig. 1.

The effects of the structure of population. We plot $R_0$ and $R\left(\infty \right)$ as functions of $\langle \beta \rangle$ and $\langle {\gamma }^{-1}\rangle$. Here, $m=n=30$, and individual degree satisfies power-law distribution with exponent $\mu =2.5$ and $M=100$. Individual susceptibility and course of disease follow Poisson distributions in the top two panels and power-law distributions in the bottom two panels.

4.2. The effects of different levels of heterogeneity of individual susceptibility and course of disease

As shown in the right two panels in Fig. 1, there is relatively lower final size of the recovered in the bottom right subgraph. This invites us to explore the effect of different levels of heterogeneity of individual susceptibility and course of disease on the spread of epidemics which are measured by the variances of them, i.e., $Var\left(\beta \right)$ and $Var\left({\gamma }^{-1}\right)$.

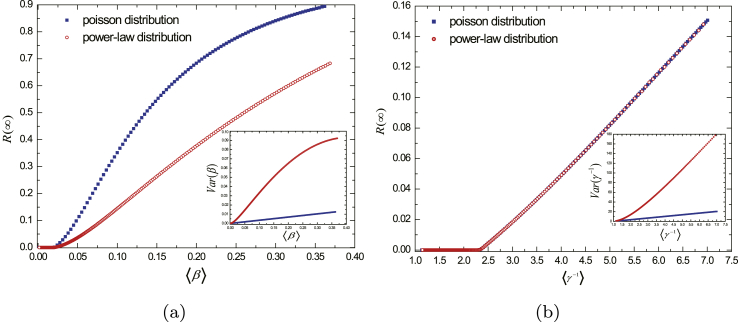
Considering the susceptibility, we plot $R\left(\infty \right)$ and $Var\left(\beta \right)$ (inset) as the functions of $\langle \beta \rangle$ when it follows Poisson distribution (blue squares) and power-law distribution (red circles) with fixing the distribution of individual course of disease as Poisson distribution with $\langle {\gamma }^{-1}\rangle =6.5000$, $Var\left({\gamma }^{-1}\right)=18.7757$, as shown in Fig. 2a. For individual course of disease, we simulate $R\left(\infty \right)$ and $Var\left({\gamma }^{-1}\right)$ (inset) as a function of $\langle {\gamma }^{-1}\rangle$ when it follows Poisson distribution (blue squares) and power-law distribution (red circles) with fixing the distribution of susceptibility as Poisson distribution with $\langle \beta \rangle =0.0556$, $Var\left(\beta \right)=0.0019$, as shown in Fig. 2b.

Fig. 2.

The effects of different levels of heterogeneity of individual susceptibility and course of disease. In (a), we plot $R\left(\infty \right)$ and $Var\left(\beta \right)$ (inset) as a function of $\langle \beta \rangle$, where the distribution of susceptibility is tuned as Poisson distribution (blue squares) and power-law distribution (red circles), individual course of disease satisfies Poisson distribution with $\langle {\gamma }^{-1}\rangle =6.5000$, $Var\left({\gamma }^{-1}\right)=18.7757$. In (b), we plot $R\left(\infty \right)$ and $Var\left({\gamma }^{-1}\right)$ (inset) as a function of $\langle {\gamma }^{-1}\rangle$, where the distribution of individual course of disease is tuned as Poisson distribution (blue squares) and power-law distribution (red circles), the susceptibility satisfies Poisson distribution with $\langle \beta \rangle =0.0556$, $Var\left(\beta \right)=0.0019$. Here, $m=n=30$, and individual degree satisfies power-law distribution with exponent $\mu =2.5$ and $M=100$.

As visualized in Fig. 2a, the $R\left(\infty \right)$ of the network with power-law distributed susceptibility is smaller than the one of the network with Poisson distributed susceptibility, while the former network has a larger $Var\left(\beta \right)$. Differently, there is no deviation of $R\left(\infty \right)$ between the two case where the distribution of individual course of disease is power-law distribution and Poisson distribution, even though there are two distinctly different variances, as shown in Fig. 2b.

From Fig. 2, it is straightforward to conclude that increasing the variance of individual susceptibility may block the spread of epidemic intensely (decreasing $R\left(\infty \right)$). However, increasing the variance of individual course of disease has little effect on the epidemic. This is instinctively understandable. Since individual susceptibility is differential, there are susceptible individuals with lower susceptibility than the average susceptibility, who are less likely acquiring disease when in contact with infectious individuals. Furthermore, the bigger variance of the power-law distributed susceptibility indicates that there are more susceptible individuals with poor susceptibility. As a consequence, the final epidemic size becomes smaller. To understand the invalidation of the increasing of the variance of individual course of disease, we can regard individual course of disease as the residence time of the disease in the individual. The length of different residence time in any individual doesn't lead to the difference of the final epidemic size under the condition that the average course of disease of the entire networks is fixed.

4.3. The effects of the correlated individual degree, susceptibility and recovery rate

Note that we have not considered so far the correlation of individual degree, susceptibility and recovery rate in the previous numerical simulations, where we assumed the degree, susceptibility and recovery rate of each individual are independent. However, a complete study of differential susceptibility and recovery rates should consider not only variations in the susceptibility and recovery rates of individuals, but also the correlations between individual degree, susceptibility and recovery rate. In the following simulations, we carry on the exchanging processes (Li, Liu et al., 2010) to fulfill both the positive and negative correlation between the susceptibility, the course of disease and the degrees squared.

4.3.1. The correlated individual susceptibility and recovery rate

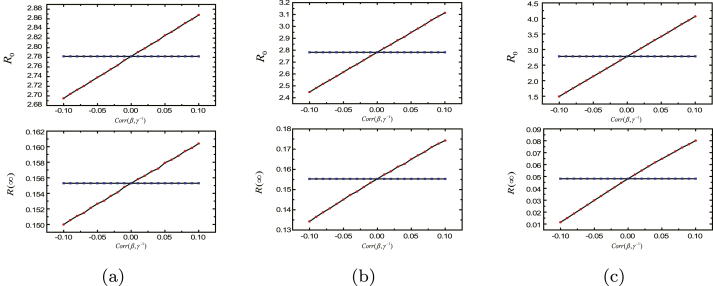
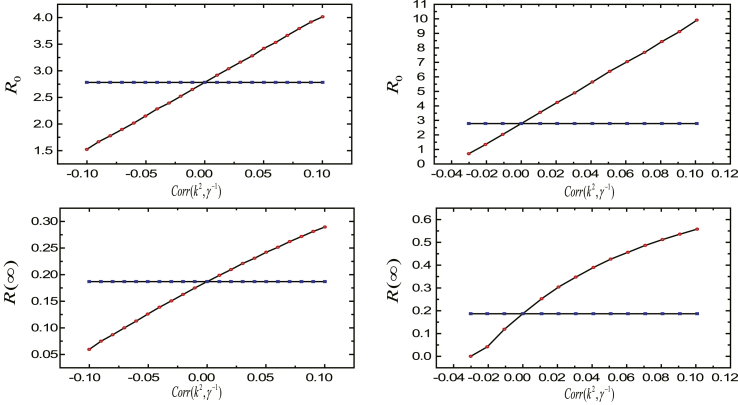
Firstly, we explore the effect of correlated individual susceptibility and recovery rate through showing the relations of $R_0$ and $R\left(\infty \right)$ to the Pearson correlation coefficient between individual susceptibility and course of disease $Corr\left(\beta ,{\gamma }^{-1}\right)$. For convenience, we assume that individual degree is independent to individual susceptibility and recovery rates. $R_0$ and $R\left(\infty \right)$ (red circles) are plotted as the function of the correlation coefficient $Corr\left(\beta ,{\gamma }^{-1}\right)$ in Fig. 3. As shown in the picture, $R_0$ and $r\left(\infty \right)$ are both increasing with the increment of $Corr\left(\beta ,{\gamma }^{-1}\right)$. Comparing Fig. 3a,b,3c, the increasing or decreasing of $R_0$ and $R\left(\infty \right)$ in Fig. 3b is larger than the change in Fig. 3a; and in Fig. 3c, the correlation makes $R_0$ and $R\left(\infty \right)$ grow up or down more apparently. For comparison, we also compute $R_0$ and $R\left(\infty \right)$ (blue squares) when the susceptibility and recovery rate are independent with the same distributions correspondingly. Taking them as a standard, it is easy to find that $R_0$ and $R\left(\infty \right)$ become bigger when there is positive correlation, while $R_0$ and $R\left(\infty \right)$ become smaller when there is negative correlation.

Fig. 3.

The effects of the correlated individual susceptibility and recovery rate. We show $R_0$ and $R\left(\infty \right)$ (red circles) as the function of $Corr\left(\beta ,{\gamma }^{-1}\right)$, and the results are obtained by 500 independent realizations for each value of $Corr\left(\beta ,{\gamma }^{-1}\right)$. Here, $m=50$, $n=50$, and individual degree follows power-law distribution with exponent $\mu =2.5$ and $M=100$. In (a), individual susceptibility and course of disease follow Poisson distribution with $\langle \beta \rangle =0.0556$, $Var\left(\beta \right)=5.6\times {10}^{-4}$, $\langle {\gamma }^{-1}\rangle =6.5000$ and $Var\left({\gamma }^{-1}\right)=5.5000$; in (b), individual susceptibility follows Poisson distribution with $\langle \beta \rangle =0.0556$, $Var\left(\beta \right)=5.6\times {10}^{-4}$, and individual course of disease follows power-law distribution with $\langle {\gamma }^{-1}\rangle =6.5000$ and $Var\left({\gamma }^{-1}\right)=173.2610$; in (c), individual susceptibility and course of disease follow power-law distribution with the same averages $\langle \beta \rangle =0.0556$ and $\langle {\gamma }^{-1}\rangle =6.5000$, yet much bigger variances $Var\left(\beta \right)=0.0177$ and $Var\left({\gamma }^{-1}\right)=173.2610$. For comparison, we also compute $R_0$ and $R\left(\infty \right)$ (blue squares) when the susceptibility and recovery rates are independent correspondingly.

From Fig. 3, we can come to some conclusions. Firstly, the positive correlation of individual susceptibility and course of disease makes the population more vulnerable to epidemic (increasing $R_0$), and avails to the epidemic prevalence (increasing $R\left(\infty \right)$), whereas the negative correlation makes the population less vulnerable (decreasing $R_0$) and impedes the epidemic prevalence (decreasing $R\left(\infty \right)$). Instinctively understanding, it is natural that individuals with larger susceptibility and with smaller recovery rate at the same time are more likely to be infected by the infectious individuals and last longer time in infected state once he acquired the epidemic. As a consequence, the positively correlated individual susceptibility and course of disease promote the vulnerability of population to epidemic. To the contrary, the negatively correlated individual susceptibility and course of disease will cripple the vulnerability of population to epidemic. This result derives from the fact individuals with larger susceptibility and larger recovery rate who are more likely to be infected by the infected but last shorter time in infected state are disable to facilitate the spread of epidemics.

Secondly, the existence of the correlation between individual susceptibility and course of disease makes the heterogeneous recovery rates play a totally different role on epidemic as increasing the variance of the course of disease with fixing the same average does accelerate the variation of $R_0$ and $R\left(\infty \right)$. This result is so different from the result obtained when we assume the individual susceptibility and recovery rate are independent. This result suggests we can't ignore the effect of the heterogeneity of individual course of disease on the spread of epidemics when it is correlated to individual susceptibility.

4.3.2. The correlated individual degree and susceptibility

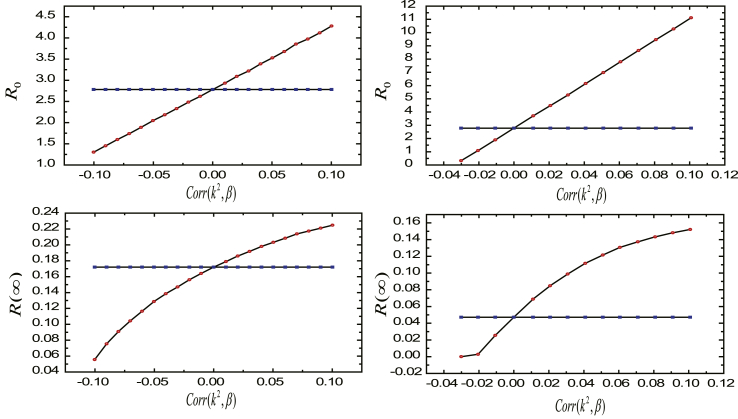
Then, we explore the effects of the correlated individual degree and susceptibility through uncovering the relations of $R_0$ and $R\left(\infty \right)$ to the Pearson correlation coefficient between individual degree squared and susceptibility $Corr\left(k^2,\beta \right)$. In our simulations, we set individual degree satisfying power-law distribution with the power-law exponent $\mu =2.5$ and $M=100$; individual course of disease is set as a constant value ${\gamma }^{-1}=6.5000$. $R_0$ and $R\left(\infty \right)$ (red circles) are plotted as the function of $Corr\left(k^2,\beta \right)$ in Fig. 4. On the left, individual susceptibility follows Poisson distribution, while on the right it follows power-law distribution. It can be found that $R_0$ and $R\left(\infty \right)$ are increasing functions of $Corr\left(k^2,\beta \right)$. Similarly, $R_0$ and $R\left(\infty \right)$ is larger than the standard obtained when we assume individual degree and susceptibility are independent if the correlations are positive, $R_0$ and $R\left(\infty \right)$ is smaller than the standard if the correlations are negative.

Fig. 4.

The effects of the correlated individual degree and susceptibility. We show $R_0$ and $R\left(\infty \right)$ (red circles) as the function of $Corr\left(k^2,\beta \right)$, and the results are obtained by 500 independent realizations for each value of $Corr\left(k^2,\beta \right)$. Here, $m=100$, the course of disease of all individuals is set as a constant value ${\gamma }^{-1}=6.5000$, and individual degree follows power-law distribution with exponent $\mu =2.5$ and $M=100$. On the left, the susceptibility follows Poisson distribution with $\langle \beta \rangle =0.0556$, $Var\left(\beta \right)=5.6\times {10}^{-4}$; on the right it follows power-law distribution with $\langle \beta \rangle =0.0556$, $Var\left(\beta \right)=0.0177$. For comparison, we also compute $R_0$ and $R\left(\infty \right)$ (blue squares) when the degree and susceptibility are independent correspondingly.

Therefore, we can conclude that individual level correlations between degree and susceptibility will promote the vulnerability of the networks to epidemic and the epidemic prevalence when the correlation is positive; and cripple the vulnerability and the epidemic prevalence when the correlation is negative. This result uncover a scenario of important significance in the process of the spread of the disease that the individuals with high degree and large susceptibility make for the spread of disease, while ones with high degree yet small susceptibility impede the contagion of disease.

4.3.3. The correlated individual degree and recovery rate

Finally, we explore the effects of the correlated individual degree and recovery rate through revealing the relations of $R_0$ and $R\left(\infty \right)$ to the Pearson correlation coefficient between the square of the degree and individual course of disease $Corr\left(k^2,{\gamma }^{-1}\right)$. In our simulations, we also set individual degree satisfying power-law distribution with the power-law exponent $\mu =2.5$ and $M=100$; individual susceptibility is set as a constant value $\beta =0.0556$. We plot $R_0$ and $R\left(\infty \right)$ (red circles) as functions of $Corr\left(k^2,{\gamma }^{-1}\right)$ in Fig. 5. On the left, individual course of disease follows Poisson distribution, while on the right it follows power-law distribution. It can be seen that $R_0$ and $R\left(\infty \right)$ are increasing as $Corr\left(k^2,{\gamma }^{-1}\right)$ increases. Without surprise, if the correlations are positive, $R_0$ and $R\left(\infty \right)$ is again larger than the standard obtained when we assume individual degree and recovery rate are independent; if the correlations are negative, $R_0$ and $R\left(\infty \right)$ is smaller than the standard.

Fig. 5.

The effects of the correlated individual degree and recovery rate. We show $R_0$ and $R\left(\infty \right)$ (red circles) as the function of $Corr\left(k^2,{\gamma }^{-1}\right)$, and the results are obtained by 500 independent realizations for each value of $Corr\left(k^2,{\gamma }^{-1}\right)$. Here, $n=100$, individual susceptibility is set as a constant value $\beta =0.0556$, and the degree of individuals follows power-law distribution with $\mu =2.5$ and $M=100$. On the left, individual course of disease follows Poisson distribution with $\langle {\gamma }^{-1}\rangle =6.5000$, $Var\left({\gamma }^{-1}\right)=5.5000$; on the right it follows power-law distribution with $\langle {\gamma }^{-1}\rangle =6.5000$, $Var\left({\gamma }^{-1}\right)=173.2610$. For comparison, we also compute $R_0$ and $R\left(\infty \right)$ (blue squares) when the degree and recovery rate are independent correspondingly.

From Fig. 5, one can come to the parallel conclusion that the positive correlations between individual degree and course of disease will increase the vulnerability of the networks to epidemic and the epidemic prevalence, while the negative correlation will decrease the vulnerability and the epidemic prevalence. We want to highlight the fact the infected individuals who recover slowly and are prone to have plentiful neighbors boost the outbreak of disease, while individuals recovering slowly and tending to possess scanty neighbors don't facilitate the existence of epidemic.

In summery, the positive correlations of the susceptibility, the course of disease, and the square of the degree of individual can make the networks more vulnerable to epidemic and avail to the epidemic prevalence, whereas the negative correlations make the networks less vulnerable and impede the epidemic prevalence. These results suggest that we should reduce the susceptibility probability of the people who recover slowly or have many neighbors and cure the infected who have acquired the disease with high probability or possess plentiful neighbors as soon as possible.

5. Discussion

In this paper we extend the traditional SIR epidemic model to incorporate not only the topology of networks but individual heterogeneous susceptibility and recovery rates. We put forward the formulas to compute the basic reproductive number and the final epidemic size and show that they both are altering with tuning the structure of population. Therefore, the spread of epidemics has a close connection with the structure of population, which is induced by the heterogeneity of individual susceptibility and recovery rates. Additionally, we also show that increasing the variance of individual susceptibility may block the spread of epidemics prominently, while increasing the variance of individual course of disease has little effect on the final epidemic size. Furthermore, we uncover some significant scenarios in the process of spread of disease through investigating the effect of the individual level correlations between individual connectivity, susceptibility and course of disease. Individuals with larger susceptibility but smaller recovery rates are more likely to be infected by the infectious individuals and last longer time in infected state once they acquired the epidemic, and they will promote the vulnerability of population to epidemic and the epidemic prevalence. And the individuals possessing plentiful neighbors who are more likely to be infected or recover more slowly once infected will accelerate the spread of epidemics. Therefore, it is not enough to only take into account network heterogeneity to make an appropriate and fruitful immunization strategy. In fact, a good vaccination campaign should target the most highly connected people who with high susceptibility are easier to be infected or with lower recovery rate may be in the infected state for a long time once infected.

Nevertheless, the formulas we provide to compute $R_0$ and $R\left(\infty \right)$ have little practical use in absence of complete information about the network topology and the distribution of individual susceptibility and recovery rates (or course of disease). As a consequence, it perfectly motivates our works to explore the significant but insufficient information of individuals in population. However, it still inspires and guides our practical application in the prevention and control of epidemic. As some possible application, we can more accurately estimate the vulnerability of networks to epidemic and the severity of the epidemics if it outbreaks through coarsely dividing population into some subgroups according to individual different susceptibility and recovery rates. It is a pity that our work carried out on the uncorrelated network, which is far from real world. Actually, we don't know what will happen with taking link level correlations in the degree, susceptibility and recovery rates of nodes into consideration. It will be an attractive option for future studies.