Modelling of ciprofloxacin killing enhanced by hyperbaric oxygen treatment in Pseudomonas aeruginosa PAO1 biofilms

Abstract

Outline

In chronic lung infections by Pseudomonas aeruginosa (PA) the bacteria thrive in biofilm structures protected from the immune system of the host and from antibiotic treatment. Increasing evidence suggests that the susceptibility of the bacteria to antibiotic treatment can be significantly enhanced by hyperbaric oxygen treatment. The aim of this study is to simulate the effect of ciprofloxacin treatment in a PAO1 biofilm model with aggregates in agarose when combined with hyperbaric oxygen treatment. This is achieved in a reaction-diffusion model that describes the combined effect of ciprofloxacin diffusion, oxygen diffusion and depletion, bacterial growth and killing, and adaptation of the bacteria to ciprofloxacin. In the model, the oxygen diffusion and depletion use a set of parameters derived from experimental results presented in this work. The part of the model describing ciprofloxacin killing uses parameter values from the literature in combination with our estimates (Jacobs, et al., 2016; Grillon, et al., 2016). Micro-respirometry experiments were conducted to determine the oxygen consumption in the P. aeruginosa strain PAO1. The parameters were validated against existing data from an HBOT experiment by Kolpen et al. (2017). The complete oxygen model comprises a reaction-diffusion equation describing the oxygen consumption by using a Michaelis-Menten reaction term. The oxygen model performed well in predicting oxygen concentrations in both time and depth into the biofilm. At 2.8 bar pure oxygen pressure, HBOT increases the penetration depth of oxygen into the biofilm almost by a of factor 4 in agreement with the scaling that follows from the stationary balance between the consumption term and diffusion term.

Conclusion

In the full reaction-diffusion model we see that hyperbaric oxygen treatment significantly increases the killing by ciprofloxacin in a PAO1 biofilm in alignment with the experimental results from Kolpen et al. (Kolpen, et al., 2017; Kolpen, et al. 2016). The enhanced killing, in turn, lowers the oxygen consumption in the outer layers of the biofilm, and leads to even deeper penetration of oxygen into the biofilm.

Introduction

Pseudomonas aeruginosa is a gram-negative bacterium associated with the lung disease cystic fibrosis (CF) [5]. CF is an autosomal recessive disease caused by a defect in the cystic fibrosis transmembrane conductance regulator gene (CFTR) [6]. CFTR is a chloride ion channel that reduces the mucus volume of the epithelial lining fluid leading to dehydration and mucociliary dysfunction [7, 8]. The stagnation of mucus contributes to accumulation of bacteria, including Pseudomonas aeruginosa. Consequently, a sustained inflammatory response results in a gradual decline in lung function ultimately causing death for CF patients [9, 10].

Microscopical examinations indicate that P. aeruginosa resides in microcolonies, also known as biofilms, surrounded by numerous polymorphonuclear leukocytes (PMN) in the endobronchial mucus in lungs from CF patients with chronic lung infection [11]. In vivo measurements have revealed intense depletion of oxygen (O₂) in the endobronchial mucus in CF patients with chronic lung infection [12]. The extreme depletion of O₂ is reproduced in newly expectorated endobronchial secretions as steep oxyclines [13, 14] and is predominately caused by O₂ consumption for production of reactive O₂ and nitrogen species by the PMNs [15–17]. Consequently, O₂ consumption by aerobic respiration is very small and anaerobic bacterial respiration is favoured in the O₂ depleted parts of endobronchial secretions from CF patients [13, 18]. The ability of the O₂ consumption by the accumulated PMNs to restrict P. aeruginosa is further evidenced by the inhibition of aerobic growth of P. aeruginosa by the PMNs in the endobronchial mucus in CF lungs [19].

Studies suggest that O₂ limitation in the adhered biofilm resulting in low metabolic activity is correlated with high survival rates of P. aeruginosa’s during antibiotic treatment [20]. The biofilms in CF lungs are, however, not adhered to solid surfaces, but are embedded as small aggregates in the viscous endobronchial mucus [21]. To mimic the organisation of P. aeruginosa in small aggregates surrounded by viscous mucus we have embedded P. aeruginosa in agarose allowing us to confirm that the killing of P. aeruginosa biofilm by ciprofloxacin is oxygen dependent and to demonstrate that hyperbaric oxygen treatment (HBOT) increases the killing of P. aeruginosa by ciprofloxacin [4]. To further approach the situation in the infected CF lungs we mimicked the PMN-mediated low availability of oxygen for aerobic bacterial respiration by culturing the biofilms embedded in agarose for three days before assessing the effect of HBOT on the killing of P. aeruginosa during treatment with ciprofloxacin [3]. In this way we could demonstrate that when aerobic respiration was enabled by reoxygenation during HBOT, P. aeruginosa became susceptible to ciprofloxacin, thus confirming the contribution of bacterial respiration to increased bacterial killing by antibiotics [22]. P. aeruginosa is known to have five terminal oxidases in the electron transport chain which directly consume oxygen by reduction [23]. Although less efficient, P. aeruginosa is also capable of anaerobic respiration with N-oxides as terminal electron acceptors, leaving its overall metabolism complex [24, 25].

CF patients are treated with a wide range of antibiotics [26, 27]. The killing effect of some antibiotics, e. g. fluoroquinolones, aminoglycosides, and beta-lactams is enhanced under aerobic conditions due to formation of reactive oxygen species (ROS) [4, 28], hence oxygen availability and aerobic respiration are relevant for treatment. Two antibiotics used to treat P. aeruginosa biofilm infections in CF are tobramycin and ciprofloxacin [26]. Tobramycin has shown a considerable time delay for the penetration into biofilms which probably increases the adaptive response in the bacteria [29]. Several simulation studies of the bacterial killing of P. aeruginosa with and without adaptation have been carried out with various antibiotics, including ciprofloxacin, illuminating their pharmacokinetic and dynamic properties on P. aeruginosa infection and how time kill-curves evolve during treatment [30–32]. However, none have yet linked the observed increased killing from HBOT to an antibiotic adaptation model.

This paper investigates the dynamics of O₂ treatment and the resulting O₂ concentration profiles in a biofilm model of P. aeruginosa. The model parameters are determined in respirometry experiments and from the O₂ penetration and unloading dynamics reported by Kolpen et al. [3] and shown in Fig 1. Using the oxygen model in combination with a modified version of an existing antibiotic model with ciprofloxacin treatment by Jacobs et al. (2016) [1] and Gregoire et al. (2010) [30], the dynamics of bacterial killing in a biofilm is investigated and the limitations of this and existing models are discussed.

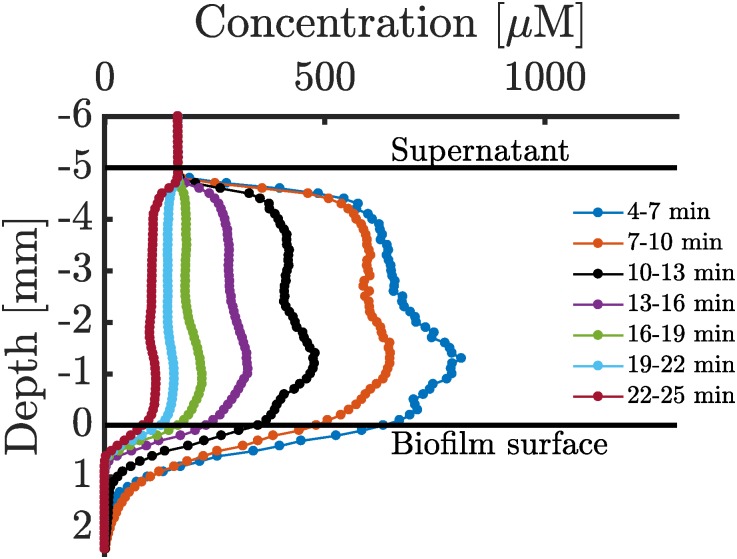
Fig 1. Oxygen profiles sampled after 90 minutes of HBOT.

Oxygen profiles are recorded after 90 minutes of HBOT applied to a 5 mm thick agarose biofilm, hence an unloading process of an already oxygen penetrated biofilm is observed. Oxygen profiling was initiated 4 minutes after the 90 minutes HBOT and every profile takes approximately 3 minutes to record. Horizontal black bars represent supernatant and biofilm surfaces, respectively. The concentration of oxygen in the supernatant immediately after treatment is approximately 1000 μM as the chamber has to be decompressed to 1 atm. The biofilm is present for depth 0 mm to 5 mm while the supernatant is present in the region from −5 mm to 0 mm. The supernatant is displayed primarily to verify that the mixing is strong in this region. Figure modified from [3].

Materials and methods

Bacterial strain and growth media

The standard laboratory P. aeruginosa strain PAO1 was obtained from Stover et al. [33]. Growth was established in Lysogeny broth (LB) [5 g/L yeast extract (Oxoid, Basingstoke, UK), 10 g/L tryptone (Oxoid) and 10g/L NaCl (Merck, Rahway, NJ), pH 7.5], incubated overnight at 37°C and shaken at 150 rpm. Overnight cultures were used in micro-respirometry experiments to estimate O₂ consumption in stationary cultures. For O₂ consumption experiments in exponential cultures, the overnight culture was diluted in LB to OD₆₀₀ = 0.01 and grown until OD₆₀₀ = 0.4. Bacterial CFU counts were determined on solid lactose agar plates (‘Blue plates’ based on a modified Conradi–Drigalski medium containing 10 g/L detergent, 1 g/L Na₂S₂O₃ ⋅ H₂O, 0.1 g/L bromothymolblue, 9 g/L lactose and 0.4 g/L glucose, pH 8.0; Statens Serum Institut, Copenhagen, Denmark) to select for Gram-negative bacteria. All plates were incubated overnight at 37°C.

Oxygen depletion measurements

For bulk O₂ depletion experiments in planktonic cultures respiration vials (OXVIAL4) with integrated stripes of the O₂ sensitive REDFLASH-indicators glued to the inner wall (Pyro-Science, GmbH) were positioned on top of a magnetic stirring head connected to a magnetic stirrer (Model 300, Rank Brothers, Cambridge, UK). The O₂ concentration measurements were recorded with separately available adaptor rings (ADVIAL4, Pyro-Science) to allow easy fixation of bare optical fibers (SPFIB-BARE, Pyro-Science) which connect the respiration vials to an optical oxygen meter (FireStingO₂, FSO2-4, Pyro Science). The software Pure Oxygen Logger (v.3.206 with FireStingO₂ (Firmware 3.07), Pyro-Science) measured O2 in continuous mode with sampling every 1 s. The used channels were activated; the respective sensor code, output unit, as well as environmental conditions for the sample temperature ([°C]), pressure ([mbar]), and salinity ([g/L]) were entered. The temperature was fixed at 37°C and the pressure was fixed at 1013 mbar. The factory calibration was used to calibrate the sensors (OXVIAL4) according to the manufacturer’s recommendation. O₂ concentrations were measured in both stationary and exponential cultures diluted 10 times in LB.

For vertical space-time profiles in biofilms we used the data reported by Kolpen et al. [3]. For completeness, we provide brief experimental details for these data: PAO1 biofilms were grown and treated under anoxic conditions in an anaerobic growth chamber. The optical density at 600 nm (OD₆₀₀) of overnight cultures of PAO1 was adjusted to 0.4 before 100-fold dilution in LB medium supplemented with 2% 2-hydroxyethyl-agarose (Sigma-Aldrich, Brøndby, Denmark) and 1 mL was loaded into 24-well microtiter plates to achieve a cell loading of ∼10⁶ cells/ml. The biofilm size was 5.7 mm high and 15 mm wide. The medium was supplemented with anoxic NaNO₃ (1 mM) to enable anaerobic respiration. The supernatant was replaced daily with 1 mL of LB medium supplemented with 1 mM NaNO3. Microtiter plates were covered with Parafilm and lid and were incubated under anoxic conditions at 37°C for 3 days. The 3 day old biofilm was treated for 90 min with HBOT (100% O₂ at 2.8 bar). Less than 1 minute after ending the treatment, the microtiter plate was positioned on a heated metal rack and kept at 37°C. The vertical O₂ profiles were recorded with a fiber-optic O₂ microsensor positioned with a micromanipulator (50 μm tip diameter, FireSting2, Profix version 4.51; Pyro-Science GmbH, Germany). The microsensor was calibrated according to the manufacturer’s recommendations (air saturated and O₂-free water). The microsensor was positioned at the base of the biofilm sample and profiles were recorded while moving the sensor in vertical steps of 100 μm through the biofilm sample.

Analysis

Overview of Analysis: First we model the oxygen consumption in a well mixed culture as described in “Reaction model”. This serves to determine the basic parameters needed to describe the oxygen consumption. Next, in “Reaction-diffusion model for oxygen”, we combine the obtained oxygen consumption model with a simple diffusion model. This allows us to verify that the hyperbaric oxygen penetration into a biofilm model reported by [3] and shown in Fig 1 are qualitatively described. Finally, in “Ciprofloxacin model with oxygen consumption”, a full model describing the killing by ciprofloxacin in combination with hyperbaric oxygen treatment is constructed. This model includes a mechanism for reversible adaptive oxygen-dependent killing. This enables us to give predictions for the combined effect of HBOT and ciprofloxacin treatment.

Reaction model

A simple reaction model using a Michaelis-Menten reaction term is presented in Eq (1) where c is the molar concentration of oxygen. The model includes two parameters, namely K_m and R_max. The latter is the maximum consumption rate and has in other studies [34–37] been decomposed into a subset of parameters as seen in Eq (2), where μ_max is the maximum specific growth rate with units of h⁻¹, ε_c is the dimensionless volume fraction occupied by cells, ρ_x is the intrinsic cellular oxidase density with units μM, and Y_x,o is the dimensionless oxygen yield coefficient. Importantly, Eq (1) reveals that the overall consumption in a biofilm scales linearly in the volume fraction occupied by cells.

$$\begin{array}{c}\hfill \frac{dc}{dt}=-R_{\text{max}}\frac{c}{K_m+c}\end{array}$$ (1)

$$\begin{array}{c}\hfill R_{\text{max}}=\frac{{\mu }_{\text{max}}{\epsilon }_c{\rho }_x}{Y_{x,o}}\end{array}$$ (2)

The parameter K_m acts as a cut-off value, indicating the oxygen concentration below which limitation sets in. Even though PA has five terminal oxidases which reduce oxygen [24], we shall describe the process using just one value for K_m. This works well, since the individual cutoffs all lie within an order of magnitude from K_m = 4 μM [23]. Our maximal oxygen reaction velocity therefore represents the sum of contributions from all oxidases.

The solution to Eq (1) is obtained by integration as presented in Eq (3) where c(0) is the initial concentration of oxygen.

$$\begin{array}{c}\hfill c\left(t\right)=K_m\text{W}({\displaystyle \frac{c\left(0\right)}{K_m}}exp\left({\displaystyle \frac{c\left(0\right)-R_{\text{max}}t}{K_m}}\right))\end{array}$$ (3)

The solution involves the Lambert W function, which is the inverse of x → xe^x [38]. Estimates of R_max and K_m may now be established by fitting the experimental data as illustrated in Fig 2. Experimental data is obtained from respirometry experiments as described in Materials and Methods.

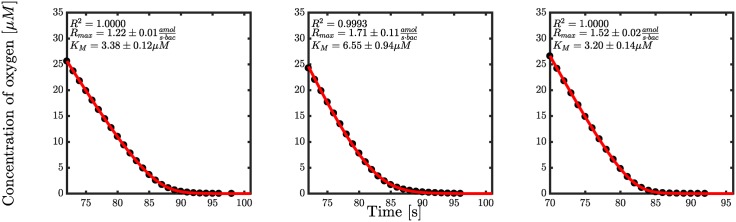
Fig 2. Oxygen consumption for overnight cultures of PAO1.

Dots represent experimental data and the red lines are the solution from Eq (3) with respective parameters.

In Fig 2, three typical respirometry profiles and fits with Eq (3) are shown. Using the solution from Eq (3), the value of K_m was determined from a total of 14 respirometry experiments shown in S1–S4 Figs. The parameter values providing the best fit were computed using the Levenberg-Marquardt algorithm in MATLAB with an integer weighting to compensate for the statistical underrepresentation of data in the tail.

The average K_m for the first batch of experiments with six similar cultures is 3.4 μM (see S1 and S2 Figs). In Fig 2, three of these are shown. Additionally, another batch of eight respirometry experiments were conducted where an average K_m of 0.62 μM was observed (see S3 and S4 Figs). Clearly, K_m is very low and the bacteria can thus easily be saturated with oxygen. The variation in K_m probably arises from the interactivity of the five terminal oxidases present in P. aeruginosa [39]. A study by Arai et al. [23] determined K_m for each oxidase to be between 0.23-4.3 μM corresponding well to the respirometry results.

The estimate of R_max in Fig 2 is centered around 1.5 attomol per second per bacteria but some variation of this parameter was seen across the 14 different profiles. The mean value of R_max was calculated to be $2.57\frac{\text{amol}}{\text{s}·\text{bac}}$ and ranges from a minimum value of $1.22\frac{\text{amol}}{\text{s}·\text{bac}}$ to a maximum value of $5.70\frac{\text{amol}}{\text{s}·\text{bac}}$. Interestingly, it was observed that the cultures that exhibited exponential growth had an average R_max value of $4.48\frac{\text{amol}}{\text{s}·\text{bac}}$ which would indicate a shift in consumption rate per bacteria when entering a stationary phase. However, the number of profiles of exponentially growing cultures was low (n = 3) and further respirometry experiments are therefore required to confirm this.

Reaction-diffusion model for oxygen

As a first attempt to understand the effect of HBOT in biofilm, oxygen profiles were sampled immediately after HBOT by Kolpen et al. (2017) in [3] as reproduced in Fig 1. In the experiment, a series of oxygen profiles were sampled after 90 minutes of HBOT as the oxygen level returned to normoxic. By modelling the oxygen profiles one should be able to predict the condition of the biofilm during treatment. Assuming that the underlying oxygen consumption mechanism is similar to that in the planktonic cells in the respirometry experiments, the data can be described by adding a diffusion term to the rhs of Eq (1). We then get a 1-dimensional reaction-diffusion equation as seen in Eq (4).

$$\begin{array}{c}\hfill \frac{\partial c}{\partial t}=D_{{\text{O}}_2}\frac{{\partial }^{2}c}{\partial z^2}-R_{\text{max}}\frac{c}{K_m+c}\end{array}$$ (4)

When the concentration of oxygen is large, c ≫ K_m, the penetration depth of oxygen scales in proportion to the square root of the oxygen concentration at the boundary.

When the oxygen concentration is below K_m, the reaction-diffusion equation is reduced to:

$$\begin{array}{c}\hfill \frac{\partial c}{\partial t}=D_{{\text{O}}_2}\frac{{\partial }^{2}c}{\partial z^2}-\frac{R_{\text{max}}}{K_m}c\end{array}$$ (5)

with the steady state solution

$$\begin{array}{c}\hfill c\left(z\right)=c_0{\text{e}}^{-{\mathrm{\lambda }}_{z}z}\end{array}$$ (6)

for thick biofilms.

The first-order assumption gives the relationships between K_m and R_max:

$$\begin{array}{ccc}\hfill R_{\text{max}}=K_m{D}_{{\text{O}}_2}{\mathrm{\lambda }}_z^2& & {\mathrm{\lambda }}_t=D_{{\text{O}}_2}{\mathrm{\lambda }}_z^2\hfill \end{array}$$ (7)

These relationships make it possible to estimate R_max. Although estimates of this parameter were already made in the previous analysis of the respirometry experiments, it would be appropriate to compare the maximum consumption in a biofilm culture with the planktonic cultures used in the respirometry experiments. The fit was made on the tail of the last oxygen profile in Fig 1 such that a steady-state approximation was appropriate, and for data points below 4 μM such that a first-order reaction could be assumed. The fit was done with the Levenberg-Marquardt method in MATLAB R2016b. The result of the interpolation and fit is shown in S5 Fig. Prior to fitting the data were smoothed using cubic spline in interp1 in MATLAB R2016b and an offset correction was included in the fit.

The resulting estimate of R_max is 81 μM/min in the upper part of the biofilm. This value was calculated by choosing a representative value for K_m of 3.8 μM, the mean of the cutoffs obtained by Arai et al. (2014) [23] of the bo₃, CIO, and aa₃ enzymes, which are the ones we expect to dominate the oxygen consumption during HBOT [23]. As noted, the oxidase regulation of the five oxidases is quite complex [39] and may influence the value of K_m.

In the experiment reported by Kolpen et al. [3], where the supernatant is replaced and contains fresh nutrient as well as NaNO₃ during the anaerobic phase, the cell density is higher in the top of the biofilm after the three days of anaerobic growth. We may estimate the cell density from the fitted reaction velocity, R_max = 81 μM/min and the consumption per bacteria, ∼3 amol/s/cell and arrive at 5 ⋅ 10⁸ CFU/mL near the surface of the biofilm. This is significantly higher than the average density in the biofilm in [3] which is in the order of 10⁷ CFU/mL. The elevated value is a consequence of unevenly distributed growth in the biofilm resulting from oxygen during aerobic growth and NaNO₃ during anaerobic growth, both being supplied from the biofilm interface. Bearing in mind the uneven cell distribution in the experiment, we expect only a qualitative agreement between the model and the data.

The reaction-diffusion equation in Eq (4) was solved with the numerical solver pdepe in MATLAB that uses an implementation by Skeel et al. [40]. Since the supernatant appears to be only moderately mixed we adapted a pragmatic approach where the boundary concentrations at the surface of the biofilm are controlled by a polynomial spline fitted to the experimental data. Similarly the initial concentration of oxygen in the biofilm is constructed as a polynomial spline through the first oxygen profile in Fig 1. The algorithm chosen to fit the parameters in Eq (3) was the Levenberg-Marquardt algorithm in MATLAB.

Ciprofloxacin model with oxygen consumption

The reaction-diffusion model provides a suitable basis for investigating the effect of oxygen when treating PAO1 biofilms with antibiotics. A generic model is presented here, containing mechanisms that introduce oxygen-induced antibiotic killing.

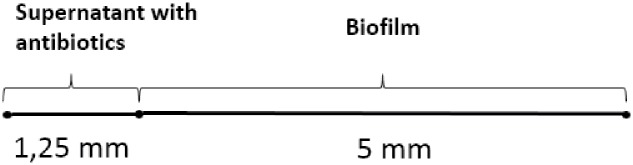
The geometry of such a model is seen in Fig 3 showing one domain for introduction of antibiotics, i.e. the supernatant and another for the biofilm [3]. The model is intended to provide a qualitative prediction for an experiment in a microtiter plate filled with 5 mm biofilm containing agarose with 1.25 mm well mixed liquid supernatant. Ciprofloxacin and oxygen levels are controlled in the supernatant from where it diffuses into the biofilm. Reflective boundary conditions at the bottom are assumed for oxygen and ciprofloxacin.

Fig 3. Geometry of ciprofloxacin model coupled with oxygen treatment.

Sketch of the 1-dimensional model implemented in MATLAB. The origin is placed at the interface between the supernatant and the biofilm domains, hence the top of the supernatant has coordinate z = −1.25 mm, the top of the biofilm has z = 0 mm, and the bottom of the biofilm has coordinate z = 5 mm.

Adaptation of bacteria to the antibiotic can be modelled in several ways. However, model 5 from Jacobs et al. (2016) [1] fits well in this context as it contains one bacterial population with a reversible adaptation to antibiotics. In order to make the ciprofloxacin killing dependent on the growth rate, we multiply the killing term by the normalised growth rate as seen in the last term in Eq (10). The resulting model is displayed in Eqs (8)–(13), where z is the depth into the biofilm.

Inside the biofilm, i. e. for z > 0, the model reads

Oxygen:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial c}{\partial t}}=D_{{\text{O}}_2}{\displaystyle \frac{{\partial }^{2}c}{\partial z^2}}-R_{\text{max}}{\displaystyle \frac{c}{K_m+c}}{\displaystyle \frac{\epsilon }{{\epsilon }_{\text{norm}}}}\end{array}$$ (8)

Ciprofloxacin:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial u}{\partial t}}=D_{\text{cip}}{\displaystyle \frac{{\partial }^{2}u}{\partial z^2}}\end{array}$$ (9)

Bacteria:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial \epsilon }{\partial t}}=\mu \left(c\right)(1-{\displaystyle \frac{\epsilon }{{\epsilon }_{\text{max}}}})\epsilon -K_{\text{max}}{\displaystyle \frac{\mu \left(c\right)}{{\mu }_{\text{max}}}}{\displaystyle \frac{u^{\gamma }}{{\mathit{\text{KC}}}_{50S}^{\gamma }+u^{\gamma }}}\epsilon \end{array}$$ (10)

Adaptation:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial \beta }{\partial t}}=({\displaystyle \frac{S_{\text{max}}u}{S{C}_{50}+u}}-\beta )k_{\text{out}}\end{array}$$ (11)

Functions:

$$\begin{array}{c}\hfill {\mathit{\text{KC}}}_{50S}={\mathit{\text{KC}}}_{50,\text{base}}(1+\beta )\end{array}$$ (12)

$$\begin{array}{c}\hfill \mu \left(c\right)={\mu }_{\text{max}}\frac{c}{K_m+c}\end{array}$$ (13)

Eq (8) is the oxygen model from Eq (4) but the reaction term is scaled to be proportional to the fraction of live bacteria in the biofilm. Eq (9) describes the diffusion of ciprofloxacin from the supernatant into the biofilm. Eq (10) describes the change in bacterial concentration within the biofilm and is separated into two terms describing the oxygen-dependent growth and the oxygen-dependent killing effect of ciprofloxacin, respectively. The growth term in Eq (10) is assumed to follow a local logistic growth model with an oxygen dependent specific growth rate following Monod kinetics as shown in Eq (13). This is a fair assumption since the volume fraction occupied by cells is well below 1% in the studied biofilms.

The initial bacterial concentration in the biofilm is set to 5 ⋅ 10⁸ CFU/mL so the simulation captures the estimated oxygen consumption in the top of the biofilm, as observed in the experiments by Kolpen et al. [3, 4]. This is about an order of magnitude lower than in a fully developed biofilm. To ensure an oxygen-dependent killing, the killing term is scaled by the normalised oxygen-dependent growth (μ(c)/μ_max). A similar strategy for incorporating oxygen-dependent killing was used by Stewart (1994) [34] in a model without adaptation. The effect of an adaptive susceptibility to antibiotics has been shown to be considerable [30, 32]. Eq (11) includes both an up and down regulation of adaptation.

The combined oxygen and ciprofloxacin model in Eqs (8)–(13) was solved with pdepe using a 1-dimensional model presented in Fig 3 assuming radial and axial symmetry. We use the estimated oxygen consumption parameters, diffusion parameters, and kinetic parameter values suggested in the literature as detailed in Table 1. Both oxygen and ciprofloxacin are assumed to be well mixed in the supernatant domain and this was implemented in pdepe by setting an artificially high diffusion constant, hence it remains nearly uniformly distributed in the supernatant domain throughout the simulation. As an alternative to using a unit step function to connect the variables across the interface we use a fast shifting logistic function.

Table 1. Parameter values used for simulation of the oxygen and ciprofloxacin models.

Parameter	Symbol	Value	Reference
Diffusion constant of oxygen	DO2	9.44 mm2/h	[41]
Maximum oxygen reaction velocity	Rmax	81 μM/min	CSab
Oxygen concentration for half-maximum reaction velocity	Km	3.8 μM	[23], CS
Diffusion constant ciprofloxacin	Dcip	1.44mm2/h	[42]
Maximum effect of ciprofloxacin	Kmax	8 h−1	[3], CSc
Maximum specific growth rate	μmax	0.40 h−1	[37]
Maximum adaptation	Smax	4	[1]
Initial half-maximum killing rate concentration of ciprofloxacin	KC50,base	0.2 μg/mL	[2]
Antibiotic concentration that yields 50% of Smax	SC50	1.06 μg/mL	[1]
Turnover rate constant for adaptation	kout	0.05 h−1	[1]
Hill coefficient	γ	1.2	[30]
Maximum population density	εmax	109.5 CFU/mL	[1]
Normalisation constant	εnorm	5 ⋅ 108 CFU/mL	CS

^a Current Study

^b Estimated from fit of λ_t and respirometry experiments.

^c Estimated from time-kill curves by Kolpen and coworkers.

The initial conditions in the biofilm are c₀ = 0, u₀ = 0, ε₀ = 10⁶ CFU/mL, and β₀ = 0, and the initial conditions in the supernatant domain are c₀ = the applied oxygen concentration, u₀ = the actual dose, ε₀ = 0 CFU/mL, and β₀ = 0. Hence, the introduction of antibiotics is implemented as a uniform initial condition in the supernatant.

Results and discussion

Oxygen model

Using the estimated parameters for R_max and K_m, the reaction-diffusion equation, Eq (4), was simulated and compared with the experimental oxygen profiles in Fig 1 as shown in Fig 4.

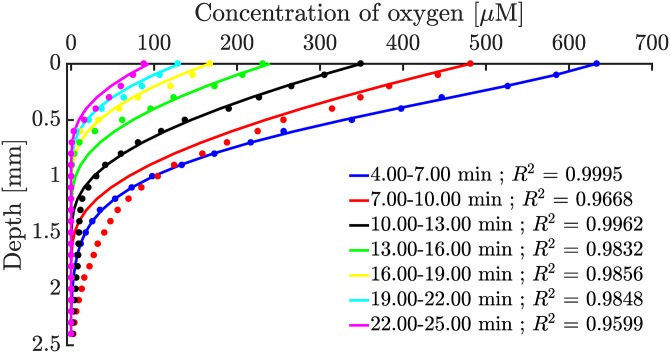
Fig 4. Numerical solutions of the reaction-diffusion equation with a michaelis-menten reaction term.

Dots are experimental data from Fig 1 and the coloured lines are matching numerical solutions to Eq (4). The biofilm extends from depth 0 mm to 5 mm, but only the part with measurable oxygen concentration is shown in the figure.

Looking at Fig 4, the dynamics of the oxygen profiles are qualitatively described by a reaction-diffusion model with a Michaelis-Menten reaction term. As mentioned, R_max is proportional to the CFU unit count in the biofilm and is thus scaled linearly with the live cell-to-volume fraction in Eq (2). A more detailed model could include a reaction velocity scaled to per bacteria such that the units of R_max would be in amol⋅s⁻¹ bac⁻¹. Such a model would be able to describe oxygen consumption across a larger range of bacterial concentrations instead of relying on an estimate of R_max for a specific cell density as done here. In S1 and S2 Figs it is observed that there is a difference between zero-growth and exponential-growth PAO1 cultures. Generally, the larger R_max values suggest that exponential-growth cultures are consuming oxygen at a higher capacity per bacterium than zero-growth bacteria. However, further studies are needed to accurately estimate at which bacterial concentration the shift from exponential capacity to stationary capacity happens.

Also, K_m may vary between different experiments depending on their growth conditions prior to starting HBOT because of the five terminal oxidases that respond to different regulatory mechanisms as described by [39].

Antibiotic model

As mentioned, it has been thoroughly investigated by Kolpen et al. [3, 4] that treatment of P. aeruginosa with fluoroquinolones like ciprofloxacin shows a time-dependent increased killing when supplementing treatment with high concentrations of oxygen. We have proposed a pharmacodynamic biofilm model accounting for this increased killing, as seen in Eqs (8)–(13).

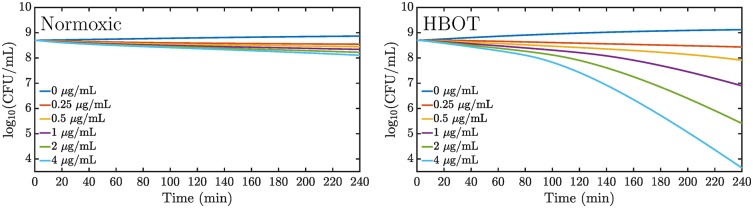
The simulations show an oxygen-dependent increased killing as seen in Fig 5 where the volume averaged CFU counts are displayed. At the largest ciprofloxacin dose, we observe 2 orders of magnitude decrease in the CFU after about 2 hours of combined ciprofloxacin and HBOT treatment.

Fig 5. Predicted volume-averaged time kill curves for normoxic oxygen treatment and HBOT.

Different dosing schemes over 4 hours of treatment simulated in a 5 mm biofilm model. The initial ciprofloxacin concentrations in the 1.25 mm supernatant are displayed in the figures while the fully equilibrated concentrations are 5 times lower. Left: Normoxic treatment. Right: Hyperbaric oxygen treatment.

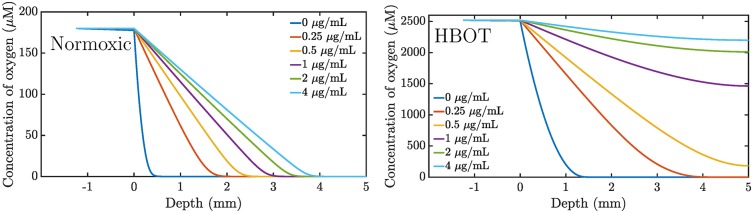
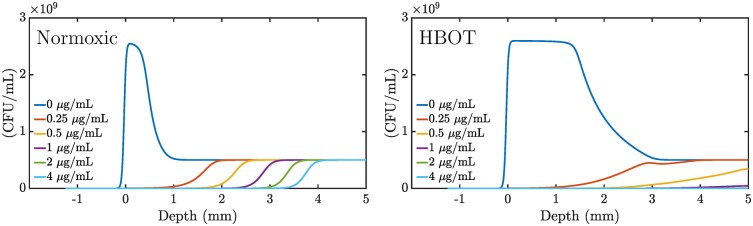
HBOT increases the penetration depth as seen in Fig 6. This leads to faster growth and metabolic activity, thus making the bacteria more susceptible to antibiotic treatment. However, Fig 5 indicates that the opposing growth is still large enough to compensate the oxygen-dependent killing for initial doses below 1 μg/mL (0.2 μg/mL equilibrated concentration). Fig 7 reveals the distribution of live bacteria in the biofilm: bacteria survive near the bottom and die at the top.

Fig 6. Oxygen penetration.

Simulation of oxygen penetration in a 5 mm biofilm following a 4 hour treatment scheme with six different ciprofloxacin dosings. The initial concentration ciprofloxacin in the supernatant is indicated in the figure. The equilibrated concentration is 5 times lower. Left: Normoxic treatment. Right: Hyperbaric oxygen treatment.

Fig 7. Bacterial killing along the depth dimension of the biofilm.

Simulation of a 4 hour treatment scheme with six different doses of ciprofloxacin in a 5 mm biofilm model. The initial concentration ciprofloxacin in the supernatant is indicated in the figure while the equilibrated concentration is 5 times lower. Bacterial density is measured in (CFU/mL). Left: Normoxic treatment. Right: Hyperbaric oxygen treatment.

The combined oxygen model with antibiotic killing provides a mechanism for oxygen enhanced killing. The model has a number of opposing effects such as bacterial growth, oxygen-dependent killing, antibiotic adaptation, and oxygen consumption that all contribute to the killing of bacteria. The HBOT makes the culture metabolically active deep into the biofilm. At sufficiently high concentrations of antibiotics the metabolic activity is suppressed and the oxygen is allowed to penetrate even deeper into the biofilm. This, in turn, allows killing even below the normal penetration depth for the oxygen. In this sense, the effect is self-perpetuating. Of course, the parameter values have a significant influence on the simulation and the above dynamics. In further studies it would be interesting to challenge the model against experimental data to see if our model that incorporates oxygen-dependent killing suffices in describing the already observed increased bacterial killing under oxygen treatment by [3, 4].

Conclusion

A reaction-diffusion model with a Michaelis-Menten reaction term adequately describes P. aeruginosa’s oxygen consumption in an artificial PAO1 biofilm. Important model parameters, K_m and R_max, have been determined by performing respirometry experiments and fitting data to an existing PAO1 experiment with HBOT, respectively. Furthermore, we constructed an antibiotic model that included a mechanism for adaptive oxygen-dependent killing of P. aeruginosa by introducing a normalised oxygen-growth rate into the antibiotic killing. The increase of the penetration depth of oxygen caused by the HBOT is further boosted by the killing effect from the antibiotics, thus causing the effect to be more efficient than would be naively expected.

In the model, oxygen limitation allows P. aeruginosa to survive in biofilms in a dormant state. Hyperbaric oxygen treatment induces metabolic activity and growth, thus increasing the susceptibility for antibiotics leading to a more efficient killing of bacteria. In the specific geometry studied, we find that 4 hours of combined treatment with HBOT and ciprofloxacin at initial concentration 1 μg/mL, results in an equilibrated ciprofloxacin concentration of 0.2 μg/mL and full penetration of oxygen. This, in turn, ensures efficient killing.

The oxygen model presented here describes the oxygen consumption in PAO1 biofilms qualitatively and it is clear that HBOT has the potential to play an important role in the treatment of P. aeruginosa biofilm infections with selected antibiotics.

Supporting information

S1 Fig. Fit of the last oxygen profile from Fig 1.

Interpolation (black dots) of last oxygen profile (blue dots) from in vitro experiment with PAO1 biofilm after HBOT by Kolpen et al. (2016) and subsequent fit of interpolated data (red line).

(EPS)

S2 Fig. Oxygen consumption for exponential PAO1 culture.

Dots represent experimental data and the red line is the fit. CFU from left to right: 2.2, 2.40, and 2.80 ⋅ 10⁷ mL⁻¹.

(EPS)

S3 Fig. Oxygen consumption for stationary PAO1 culture.

Dots represent experimental data and the red line is the fit. CFU is 1.8 ⋅ 10⁹ mL⁻¹ for all three.

(EPS)

S4 Fig. Oxygen consumption for stationary PAO1 culture.

Dots represent experimental data and the red line is the fit. CFU = 1.7 ⋅ 10⁸ mL⁻¹.

(EPS)

S5 Fig. Oxygen consumption for stationary PAO1 culture.

Dots represent experimental data and the red line is the fit. CFU = 2.3 ⋅ 10⁸ mL⁻¹.

(EPS)

S6 Fig. Concentration of ciprofloxacin in the supernatant and the biofilm 2, 4, 6, and 8 hours after introduction of 4 μg/mL in the supernatant.

(EPS)

Data Availability

All relevant data are within the paper and its Supporting Information files.

Funding Statement

This work was supported by grants from University of Copenhagen, Center for Antimicrobial Research, UC-CARE, http://uc-care.ku.dk, Award Number: 50061804231-F16 | Recipient: Mette Kolpen; Danish Council for Independent Research, Technology and Production Sciences, FTP, http://dff.ufm.dk, Award Number: DFF–4184-00515 | Recipient: Peter Østrup Jensen; and Cystic Fibrosis Foundation, USA, http://www.cff.org, Award Number: HOIBY05A0 | Recipient: Niels Høiby. The funders played no role in experimental design, data analysis and interpretation, nor the decision to submit the work for publication.