A primer on stochastic epidemic models: Formulation, numerical simulation, and analysis

Abstract

Some mathematical methods for formulation and numerical simulation of stochastic epidemic models are presented. Specifically, models are formulated for continuous-time Markov chains and stochastic differential equations. Some well-known examples are used for illustration such as an SIR epidemic model and a host-vector malaria model. Analytical methods for approximating the probability of a disease outbreak are also discussed.

1. Introduction

The intent of this primer is to provide a brief introduction to the formulation, numerical simulation, and analysis of stochastic epidemic models for a newcomer to this field. A background in modeling with ordinary differential equations (ODEs) is assumed. The ODE epidemic models serve as a framework for formulating analogous stochastic models and as a source of comparison with the stochastic models. This primer is restricted to two types of stochastic settings, continuous-time Markov chains (CTMCs) and stochastic differential equations (SDEs). Some well-known examples are used for illustration such as an SIR epidemic model and a host-vector malaria model. For additional examples and information on stochastic epidemic models and stochastic modeling in general, consult the textbooks and papers listed in the references, e.g., (Allen, 2007, Allen, 2008, Allen, 2010, Allen, 2015, Allen et al., 2008, Andersson and Britton, 2000, Bailey, 1975, Britton, 2010, Daley and Gani, 1999, Durrett, 1999, Greenwood et al., 2009, Isham et al., 2005, Jagers, 1975, Karlin and Taylor, 1975, Karlin and Taylor, 1981).

Stochastic modeling of epidemics is important when the number of infectious individuals is small or when the variability in transmission, recovery, births, deaths, or the environment impacts the epidemic outcome. The variability associated with individual dynamics such as transmission, recovery, births or deaths is often referred to as demographic variability. The variability associated with the environment such as conditions related to terrestrial or aquatic settings is referred to as environmental variability. Environmental variability is especially important in modeling zoonotic infectious diseases, vector-borne diseases, and waterborne diseases (e.g., Ebola, avian influenza, malaria, and cholera) (Altizer et al., 2013, Jutla et al., 2013, Wu et al., 2016). In this primer, the emphasis is on demographic variability.

In CTMCs and SDEs, the time variable is continuous, $t\in [0,\infty )$, but the state variables are either discrete (CTMC) or continuous (SDEs). In the following sections, these two stochastic processes are formulated for the well-known SIR (Susceptible-Infectious-Recovered) epidemic model and the Ross malaria host-vector model. The Gillespie algorithm and the Euler-Maruyama numerical method are described for the two types of stochastic processes. In addition, some analytical methods from branching processes that are related to the CTMC models are used to approximate the probability of an outbreak. In the last section, some stochastic methods for modeling environmental variability are presented.

2. SIR deterministic epidemic model

In the SIR deterministic model, $S\left(t\right)$, $I\left(t\right)$, and $R\left(t\right)$ are the number of susceptible, infectious, and recovered individuals, respectively. In the simplest model, there are no births and deaths, only infection and recovery:

$$\begin{array}{l}\frac{dS}{dt}=-\beta I\frac{S}{N}\\ \frac{dI}{dt}=\beta I\frac{S}{N}-\gamma I\\ \frac{dR}{dt}=\gamma I\text{,}\end{array}$$ (1)

where the total population size is constant, $S\left(t\right)+I\left(t\right)+R\left(t\right)=N$. The disease-free equilibrium is $S=N$ and $I=R=0$. The basic reproduction number ${\mathcal{R}}_0=\beta /\gamma$ which is equal to the ratio of the transmission rate β and the recovery rate γ, determines the epidemic outcome when $S\left(0\right)\approx N$. If $I\left(0\right)>0$ and ${\mathcal{R}}_{0}S\left(0\right)/N>1$, then the number of infectious individuals increases, an outbreak, and if ${\mathcal{R}}_{0}S\left(0\right)/N<1$, the number of infectious individuals decrease. As $R\left(t\right)=N-S\left(t\right)-I\left(t\right)$, system (1) can be simplified to two equations for $S\left(t\right)$ and $I\left(t\right).$

The stochastic formulation of the CTMC and SDE models requires defining two random variables for S and I whose dynamics depend on the probabilities of the two events: infection and recovery. For simplicity, the same notation is used in the stochastic and the deterministic formulations.

3. SIR continuous time Markov chain

3.1. Formulation

The discrete random variables for the SIR CTMC model satisfy

$$S\left(t\right),I\left(t\right)\in \left\{\mathrm{0,1,2},\dots ,N\right\}\text{,}$$

where $t\in [0,\infty )$. The lower case s and i denote the values of the discrete random variables from the set $\left\{\mathrm{0,1,2},\dots ,N\right\}$. The transition probabilities associated with the stochastic process are defined for a small period of time $\Delta t>0$:

$$p_{\left(s,i\right),\left(s+k,i+j\right)}(\Delta t)=\mathrm{\mathbb{P}}((S(t+\Delta t),I(t+\Delta t))=(s+k,i+j)|(S\left(t\right),I\left(t\right))=(s,i))\text{.}$$

The transition probabilities depend on the time between events $\Delta t$ but not on the specific time t, a time-homogeneous process. In addition, given the current state of the process at time t, the future state of the process at time $t+\Delta t$, for any $\Delta t>0$, does not depend on times prior to t, known as the Markov property. For comparison purposes, the transition probabilities are defined in terms of the rates in the SIR ODE model:

$$p_{\left(s,i\right),\left(s+k,i+j\right)}\left(\Delta t\right)=\{\begin{array}{ll}\beta i\frac{s}{N}\Delta t+o\left(\Delta t\right)\text{,}& \left(k,j\right)=\left(-1,+1\right)\\ \gamma i\Delta t+o\left(\Delta t\right)\text{,}& \left(k,j\right)=\left(0,-1\right)\\ 1-\left(\beta i\frac{s}{N}+\gamma i\right)\Delta t& \\ +o\left(\Delta t\right)\text{,}& \left(k,j\right)=\left(\mathrm{0,0}\right)\\ o\left(\Delta t\right)\text{,}& otherwise\text{.}\end{array}$$ (2)

Summarized in Table 1 are the changes, $\Delta S\left(t\right)=S\left(t+\Delta t\right)-S\left(t\right)$ and $\Delta I\left(t\right)=I\left(t+\Delta t\right)-I\left(t\right)$, associated with the two events, infection and recovery.

Table 1.

SIR CTMC model assumptions.

Event	Change $\left(\Delta S,\Delta I\right)$	Probability
Infection	$\left(-1,+1\right)$	$\beta i\frac{s}{N}\Delta t+o\left(\Delta t\right)$
Recovery	$\left(0,-1\right)$	$\gamma i\Delta t+o\left(\Delta t\right)$

Given $S\left(0\right)=N-i$ and $I\left(0\right)=i>0$, the epidemic ends at time t, when $I\left(t\right)=0$. The states $\left(S,I\right)$, where $I=0$ are referred to as absorbing states; the epidemic stops when an absorbing state is reached. The absorbing states are the states $\left(s,i\right)$ with $i=0$.

3.2. Kolmogorov differential equations

Differential equations for the transition probabilities can be derived from (2). These differential equations are often referred to as the forward or the backward Kolmogorov differential equations. The forward equations, also referred to as the “master equations”, are used to predict the future dynamics, whereas the backward equations are used to study the end of the epidemic, such as estimating the probability of reaching an absorbing state.

Note that there are $\left(N+1\right)\left(N+2\right)/2$ ordered pairs of states $\left(s,i\right)$, e.g., $\left(s,i\right)\in \left\{\left(N,0\right),\left(N-\mathrm{1,1}\right),\dots ,\left(\mathrm{0,0}\right)\right\}$, where $s+i\le N$. The general form of the Kolmogorov differential equations can be expressed in a simple form, if the transition probabilities are denoted as $p_{a,b}\left(t\right)$, where a and b are two ordered pairs from the set of $\left(N+1\right)\left(N+2\right)/2$ ordered pairs. The general form for the forward Kolmogorov differential equations are

$$\frac{d{p}_{a,b}\left(t\right)}{dt}=\sum _{k\ne a}{p}_{a,k}\left(t\right)q_{k,b}-q_{a,a}{p}_{a,b}\left(t\right)$$ (3)

and the backward Kolmogorov differential equations are

$$\frac{d{p}_{a,b}\left(t\right)}{dt}=\sum _{k\ne a}{q}_{a,k}{p}_{k,b}\left(t\right)-q_{a,a}{p}_{a,b}\left(t\right)\text{,}$$ (4)

where the values of $q_{k,b}$, $q_{a,a}$, and $q_{a,k}$ are defined from the transition rates in Equation (2).

In the forward equations, the transition rates depend on the future state $b=\left(s,i\right)$. If a is any state, for the process to be in state $b=\left(s,i\right)$ at time $t+\Delta t$, one of the following events occurs: (1) the process transitions from a to $\left(s+1,i-1\right)$ in time t and an infection occurs with transition probability $\beta \left(s+1\right)\left(i-1\right)\Delta t/N+o\left(\Delta t\right)$, or (2) the process transitions from a to $\left(s,i+1\right)$ in time t and a recovery occurs with transition probability $\gamma \left(i+1\right)\Delta t+o\left(\Delta t\right)$, or (3) the process transitions from a to $\left(s,i\right)$ in time t and no change occurs with probability $1-\left(\beta si/N+\gamma i\right)\Delta t+o\left(\Delta t\right)$. That is,

$$p_{a,\left(s,i\right)}\left(t+\Delta t\right)=p_{a,\left(s+1,i-1\right)}\left(t\right)\frac{\beta \left(s+1\right)\left(i-1\right)}{N}\Delta t+p_{a,\left(s,i+1\right)}\left(t\right)\gamma \left(i+1\right)\Delta t+p_{a,\left(s,i\right)}\left(t\right)[1-\left(\beta si/N+\gamma i\right)\Delta t]+o\left(\Delta t\right)\text{,}$$

where all terms of order $\Delta t$ are included in the last term $o\left(\Delta t\right)$. Subtracting $p_{a,\left(s,i\right)}\left(t\right)$ from both sides, dividing by $\Delta t$, and letting $\Delta t\to 0$, leads to the forward Kolmogorov differential equations:

$$\frac{d{p}_{a,\left(s,i\right)}\left(t\right)}{dt}=p_{a,\left(s+1,i-1\right)}\left(t\right)\frac{\beta }{N}\left(s+1\right)\left(i-1\right)+p_{a,\left(s,i+1\right)}\left(t\right)\gamma \left(i+1\right)-p_{a,\left(s,i\right)}\left(t\right)[\frac{\beta }{N}si+\gamma i]\text{.}$$

A similar derivation applies to the backward equations. However, the transition rates depend on the initial state $a=\left(s,i\right)$. A transition occurs in time $\Delta t$, either infection, recovery or no change, and in the remaining time t, there is a transition to state b. The backward equations (4) are

$$\frac{d{p}_{\left(s,i\right),b}\left(t\right)}{dt}=\frac{\beta si}{N}{p}_{\left(s-1,i+1\right),b}\left(t\right)+\gamma i{p}_{\left(s,i-1\right),b}\left(t\right)-[\frac{\beta }{N}si+\gamma i]p_{\left(s,i\right),b}\left(t\right)\text{.}$$

For a more thorough derivation of these equations, consult the references, e.g., (Allen, 2010, Karlin and Taylor, 1975, Ross, 2014).

If the $\left(N+1\right)\left(N+2\right)/2$ ordered pairs $\left(s,i\right)$ are labeled in a specific order from $k=1$ to $k=\left(N+1\right)\left(N+2\right)/2$, then a matrix of transition rates Q can be defined. Matrix Q has dimension $\left(N+1\right)\left(N+2\right)/2\times \left(N+1\right)\left(N+2\right)/2$ and is known as the infinitesimal generator matrix. Matrix Q is straightforward to define for a single random variable whose states are already linearly ordered from 0 to N (e.g., (Allen, 2010, Karlin and Taylor, 1975, Karlin and Taylor, 1981, Ross, 2014)). But for a bivariate process with states $\left(s,i\right)$ the form of matrix Q depends on how the set of ordered pairs are linearly ordered. In general, matrix Q has negative diagonal entries and nonnegative off-diagonal entries. In addition, matrix Q has the property that the row sums are zero. It follows from Equations (3), (B.1), (B.2), (B.3), (B.4), (C.1), (4) that the forward and the backward Kolmogorov differential equations can be written as systems of matrix differential equations, $dP\left(t\right)/dt=P\left(t\right)Q$ and $dP\left(t\right)/dt=QP\left(t\right)$, respectively, where $P\left(t\right)$ is the matrix of transition probabilities. Matrix $P\left(t\right)$ has diagonal entries $p_{a,a}\left(t\right)$, where a is one of the linearly ordered states. The formal solution of these equations is $P\left(t\right)=e^{Qt}$, where $P\left(0\right)=I$ is the identity matrix. Note that sometimes the transition probabilities are written in the reverse order, $p_{\left(s+k,i+j\right),\left(s,i\right)}\left(t\right)=\mathrm{\mathbb{P}}((S\left(t\right),I\left(t\right))=(s+k,i+j)|(S\left(0\right),I\left(0\right))=(s,i))$. In this case, the transpose of these equations is applied with matrix $Q^T$ instead of Q (Allen, 2008, Allen, 2010).

3.3. Branching process approximation

In this brief introduction, we study the stochastic behavior near the disease-free equilibrium to determine whether an epidemic (major outbreak) occurs when a few infectious individuals are introduced into the population. The probability of no major outbreak (a minor outbreak) for the CTMC model near the disease-free equilibrium is approximated by applying branching process theory and techniques from probability generating functions (pgfs). Most important is the fact that when I hits zero, it stays in state zero. The state I has reached an absorbing state and disease transmission stops. In the limit, of course, the infectious individuals in the stochastic and deterministic models always approach zero, $I\left(t\right)\to 0$ as $t\to \infty$. But finite time extinction of I occurs in the stochastic model. We are interested in the stochastic dynamics at the initiation of an epidemic, when almost everyone in the population is susceptible. (The duration of the epidemic, once initiated, is another interesting stochastic problem, not considered here, see e.g., (Barbour, 1975, Daley and Gani, 1999)).

The branching process is the linear approximation of the SIR stochastic process near the disease-free equilibrium. For a few initial infectious individuals, the branching process either grows exponentially or hits zero. These two phenomena are captured in the branching process approximation of the CTMC model near the disease-free equilibrium. If the number of infectious individuals increases substantially to a large number of cases, then there is a major outbreak. However, if there are only a few additional cases, above the initial number of cases, then there is a minor outbreak. The branching process is a good approximation of the CTMC model, if the susceptible population size is sufficiently large. Then the two outcomes, either a major or minor outbreak, are clearly distinguishable.

The branching process is a birth and death process for I; the variables S and R are not considered in this approximation. The term $\beta i$ is the infection rate (birth) and $\gamma i$ is the recovery rate (death). The process begins with just a few infectious individuals. The branching process approximation is a CTMC, but near the disease-free equilibrium, the rates are linear (Table 2).

Table 2.

Branching process approximation of the SIR CTMC model near the disease-free equilibrium.

Change $\Delta I$	Probability
$+1$	$\beta i\Delta t+o\left(\Delta t\right)$
$-1$	$\gamma i\Delta t+o\left(\Delta t\right)$

Three important assumptions underlie the branching process approximation:

• (1)Each infectious individual behavior is independent from other infectious individuals.
• (2)Each infectious individual has the same probability of recovery and the same probability of transmitting an infection.
• (3)The susceptible population is sufficiently large.

Assumption (1) is reasonable if a small number of infectious individuals is introduced into a large homogeneously-mixed population (assumption (3)). Assumption (2) is also reasonable in a homogeneously-mixed population with constant transmission and recovery rates, β and γ.

Two probability generating functions (pgfs) are used in the study of the probability of extinction. The first one applies to each infectious individual, known as the offspring pgf, and the second one applies to the entire infectious class $I\left(t\right)$ at time t. For our purposes, the offspring pgf is the most important one. In general, an offspring pgf has the form:

$$f\left(u\right)=\sum _{j=0}^{\infty }{p}_j{u}^j,u\in \left[\mathrm{0,1}\right]\text{,}$$

where $p_j$ is the probability of one individual generating j new individuals of the same type, e.g., one infectious individual generates j infectious individuals. The pgf has some properties that are useful in the analysis. For example, $f\left(1\right)=1$ and the “mean” number of offspring generated from one individual is defined as

$$f\text{'}\left(1\right)=\sum _{j=1}^{\infty }j{p}_j\text{.}$$

The offspring pgf for one infectious individual, $I\left(0\right)=1$, is defined from Table 2:

$$f\left(u\right)=\frac{\gamma }{\beta +\gamma }+\frac{\beta }{\beta +\gamma }{u}^2,u\in \left[\mathrm{0,1}\right]\text{.}$$ (5)

The first term in $f\left(u\right)$ is the probability that an infectious individual recovers and the coefficient of the second term is the probability that an infectious individual infects another individual. The power to which u is raised is the number of infectious individuals generated from one infectious individual. If an individual recovers, then no new infections are generated $\left(u^0\right)$ and if the infection is transmitted to another individual, there are now two individuals infectious $\left(u^2\right)$. This offspring pgf differs from a discrete-time branching process, where the “parent” dies and is replaced by the offspring in the next generation. The difference is due to the fact that in a small period of time, in a continuous-time process, the infectious individual that infects another person is counted as still being infectious (two infectious individuals). This infectious individual has the same probability of infecting another individual $\beta /\left(\beta +\gamma \right)$ and the same probability of recovery, $\gamma /\left(\beta +\gamma \right)$.

The offspring pgf (5) satisfies $f\left(1\right)=1$ and the mean value is

$$f\text{'}\left(1\right)=\frac{2\beta }{\beta +\gamma }\text{.}$$

This latter expression is not the same as the basic reproduction number, the average number of infectious individuals generated by one infectious individual during the period of infectivity. However, $f^{\prime }\left(1\right)$ is a threshold parameter, similar to ${\mathcal{R}}_0$. In particular, $f^{\prime }\left(1\right)>1$ if and only if ${\mathcal{R}}_0>1$.

It is well-known from the theory of branching processes that a fixed point of the offspring pgf yields the asymptotic probability of extinction (Athreya and Ney, 1972, Dorman et al., 2004, Harris, 1963, Jagers, 1975). It is shown in Appendix B that the fixed points of f are the stationary solutions (time-independent solutions) of the branching process approximation for the probability of extinction of the infectious class $I\left(t\right)$. Solving for the fixed points of f in (5), $f\left(u\right)=u$ for $u\in \left[\mathrm{0,1}\right]$, yields two solutions, namely, $u=1$ $\left(f\left(1\right)=1\right)$, and $u=\gamma /\beta =1/{\mathcal{R}}_0$ (if ${\mathcal{R}}_0>1$). It is shown in Appendix B that if ${\mathcal{R}}_0<1$, then the fixed point $u=1$ is stable and if ${\mathcal{R}}_0>1$, the fixed point $u=1/{\mathcal{R}}_0$ is stable. When $I\left(0\right)=i>1$, the assumption of independence of infectious individuals, implies the probability of no outbreak is either 1 or ${\left(1/{\mathcal{R}}_0\right)}^i$.

The preceding results were first applied to the stochastic SIR epidemic model by Whittle in 1955 (Whittle, 1955). More precisely, he used the terminology, “the probability of a minor outbreak” is ${\left(1/{\mathcal{R}}_0\right)}^i$ and “the probability of a major outbreak” is $1-{\left(1/{\mathcal{R}}_0\right)}^i$. As these estimates for extinction (no outbreak) are asymptotic approximations from the branching process, they are more accurate for a large susceptible population size N and a few infectious individuals. The results are summarized below:

$$\begin{array}{l}{\mathrm{\mathbb{P}}}_{\text{minor}\text{outbreak}}=\{\begin{array}{ll}{\left(\frac{1}{{\mathcal{R}}_0}\right)}^i\text{,}& {\mathcal{R}}_0>1\\ 1\text{,}& {\mathcal{R}}_0<1\text{,}\end{array}\\ {\mathrm{\mathbb{P}}}_{\text{major}\text{outbreak}}=\{\begin{array}{ll}1-{\left(\frac{1}{{\mathcal{R}}_0}\right)}^i\text{,}& {\mathcal{R}}_0>1\\ 0\text{,}& {\mathcal{R}}_0<1.\end{array}\end{array}$$

3.4. Numerical simulation

In general, for multivariate processes, it is difficult to find analytical solutions for the transition probabilities from the forward and backward Kolmogorov differential equations. For multivariate processes, it is often simpler to numerically simulate stochastic realizations (sample paths) of the process. A numerical method for simulation of CTMC models was developed by Gillespie (Gillespie, 1977). This method is known as the Gillespie algorithm or the Stochastic Simulation algorithm. To numerically simulate the change in state, two uniform random numbers, $u_1,u_2\in U\left[\mathrm{0,1}\right]$, are required for each change, one for the interevent time and a second one for the particular event.

The Markov property implies that the interevent time T has an exponential distribution $T\sim \lambda e^{-\lambda t}$, where the parameter λ is the sum of the rates for all possible events. For the SIR CTMC model,

$$\lambda =\beta si/N+\gamma i\text{,}$$

where $\left(s,i\right)$ is the particular value for the state of $\left(S\left(t\right),I\left(t\right)\right)$ at a given time t. To compute a value for the interevent time τ from the exponential distribution, the first uniform random number $u_1$ yields

$$\tau =-\frac{\text{ln}{u}_1}{\lambda }\text{.}$$ (6)

(See Appendix A for the derivation of the interevent time.) The second random number $u_2$ tells which particular event occurs. In general, given n events, the interval $\left[\mathrm{0,1}\right]$ is subdivided according to the probability of each event, $[0,p_1],(p_1,p_1+p_2],\dots ,(p_1+\cdots p_{n-1},1]$, ${\sum }_{i=1}^n{p}_i=1$. If $u_2$ lies in the kth subinterval, then the kth event occurs. For the SIR CTMC model, there are only two events with corresponding probabilities

$$p_1=\frac{\beta si/N}{\beta si/N+\gamma i}\text{and}{p}_2=\frac{\gamma i}{\beta si/N+\gamma i}\text{.}$$

If $i=0$, an absorbing state has been reached and the process stops.

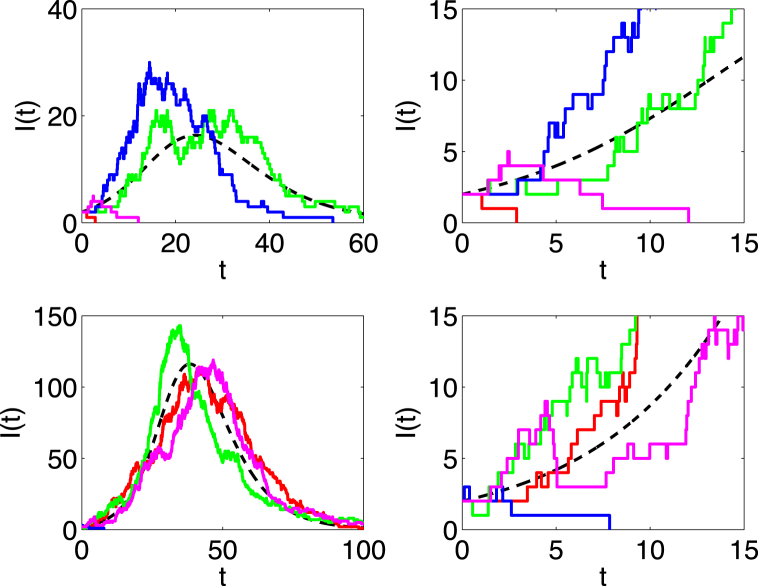
Four sample paths of the SIR CTMC model are plotted in Fig. 1 for $N=100$ (top two graphs) and $N=750$ (bottom two graphs). The close-up of the dynamics on the right side illustrates exponential growth at the initiation of an outbreak, the region where the branching process approximation is applicable.

Fig. 1.

The dashed curve is the ODE solution of $I\left(t\right)$ in the SIR model and the other curves are four sample paths of the SIR CTMC model. Parameter values are $\beta =0.3$, $\gamma =0.15$, and either $N=100$ (top graphs) or $N=750$ (bottom graphs). The initial conditions are $S\left(0\right)=98$ and $I\left(0\right)=2$. The graphs on the right are a close-up view on the time interval $\left[\mathrm{0,15}\right]$ of the graphs on the left. The value $\mathrm{\mathbb{P}}=0.25$ is the estimate for the probability of a minor outbreak. On average, one sample path out of four hits zero, given ${\mathcal{R}}_0=2$ and $I\left(0\right)=2$.

4. SIR stochastic differential equations

4.1. Formulation

Stochastic differential equations for the SIR epidemic model follow from a diffusion process. The random variables are continuous,

$$S\left(t\right),I\left(t\right)\in [0,N]\text{.}$$

Forward and backward Kolmogorov partial differential equations for the transition probability density functions can be derived and they in turn lead directly to the SDEs, e.g., (Allen, 2007, Allen, 2008, Allen et al., 2008, Kurtz, 1970, Kurtz, 1971, Kurtz, 1972). The SDEs are useful in simulating sample paths of the continuous-state process. In addition, the SDEs are much easier to solve numerically than the Kolmogorov differential equations and faster than simulating sample paths of the CTMC model. A heuristic derivation of the SDEs corresponding to the SIR epidemic model is described below.

Divide the time interval $[0,t]$ into small subintervals of length $\Delta t$. Let $\Delta X\left(t\right)={\left(\Delta S\left(t\right),\Delta I\left(t\right)\right)}^T$. Subdivide $\Delta t$ further into smaller subintervals of length $\Delta t_i=t_i-t_{i-1}$, $i=1,\dots ,n$ with $t_0=t$, $t_n=t+\Delta t$, and ${\sum }_{i=1}^n\Delta t_i=\Delta t$.

$$\Delta X\left(t\right)=\sum _{i=1}^n\Delta X\left(t_i\right)\text{.}$$

For $\Delta t_i$ sufficiently small, it is reasonable to assume that the random variables $\left\{\Delta X\left(t_i\right)\right\}$ on the interval $\Delta t$ are independent and identically distributed. For n sufficiently large, the Central Limit Theorem implies that $\Delta X\left(t\right)$ has an approximate normal distribution with mean $\mathbb{E}\left(\Delta X\left(t\right)\right)$ and covariance matrix $CV\left(\Delta X\left(t\right)\right)$, e.g., (Allen, 2007, Allen et al., 2008, Kurtz, 1970, Kurtz, 1971, Kurtz, 1972). Thus,

$$\Delta X\left(t\right)-\mathbb{E}(\Delta X\left(t\right))\approx \text{Normal}(0,CV(\Delta X(t)),$$

where 0 is the zero vector. The expectation of $\Delta X$ to order $\Delta t$ is the change that occurs ($+1$ or $-1$) times the probability:

$$\mathbb{E}\left(\Delta X\right)\approx \left(\begin{array}{c}-\beta SI/N\\ \beta SI/N-\gamma I\end{array}\right)\Delta t=f\Delta t$$

and the covariance matrix of $\Delta X$ to order $\Delta t$ is

$$CV\left(\Delta X\right)\approx \mathbb{E}\left(\Delta X{\left(\Delta X\right)}^T\right)=\mathbb{E}\left(\begin{array}{cc}{\left(\Delta S\right)}^2& \Delta S\Delta I\\ \Delta S\Delta I& {\left(\Delta I\right)}^2\end{array}\right)=\left(\begin{array}{cc}\beta SI/N& -\beta SI/N\\ -\beta SI/N& \beta SI/N+\gamma I\end{array}\right)\Delta t=C\Delta t\text{.}$$

To write the SDEs for the SIR stochastic process, either the square root of the covariance matrix $C\Delta t$ is required, or alternately, a matrix G so that $G{G}^T=C$ (Allen, 2007, Allen et al., 2008). The following matrix G has this latter property (G is not unique) (Allen, 2007, Allen et al., 2008). Matrix G is straightforward to compute as each column represents the square root of the rates as given in Table 1,

$$G=\left(\begin{array}{cc}-\sqrt{\beta SI/N}& 0\\ \sqrt{\beta SI/N}& -\sqrt{\gamma I}\end{array}\right)\text{.}$$

Then $\Delta X\left(t\right)\approx f\left(X\left(t\right)\right)\Delta t+G\left(X\left(t\right)\right)\Delta W\left(t\right)$, where $\Delta W\left(t\right)={\left(\Delta W_1\left(t\right),\Delta W_2\left(t\right)\right)}^T$ and $\Delta W_i\left(t\right)\sim \text{Normal}\left(0,\Delta t\right)$. Letting $\Delta t\to 0$, leads to the following system of SDEs:

$$dX\left(t\right)=f\left(X\left(t\right)\right)dt+G\left(X\left(t\right)\right)dW\left(t\right)\text{,}$$

where $W\left(t\right)={\left(W_1\left(t\right),W_2\left(t\right)\right)}^T$ is a vector of two independent Wiener processes. That is, $W_i\left(t\right)\sim \text{Normal}\left(0,t\right)$ is a normally distributed random variable with mean zero and variance t or $d{W}_i\left(t\right)\sim \text{Normal}\left(0,dt\right)$. The notation $B\left(t\right)=W\left(t\right)$ is also employed, where $B\left(t\right)$ denotes Brownian motion, e.g., (Oksendal, 2000). This stochastic differential equation is known as an Itô SDE because the right side is evaluated at time t (Allen, 2007, Allen et al., 2008).

Rewriting the expression $dX\left(t\right)$ in terms of the random variables $S\left(t\right)$ and $I\left(t\right)$ leads to the following system of Itô SDEs:

$$\begin{array}{l}dS\left(t\right)=-\left[\beta S\left(t\right)I\left(t\right)/N\right]dt-\sqrt{\beta S\left(t\right)I\left(t\right)/N}d{W}_1\left(t\right)\\ dI\left(t\right)=\left[\beta S\left(t\right)I\left(t\right)/N-\gamma I\left(t\right)\right]dt+\sqrt{\beta S\left(t\right)I\left(t\right)/N}d{W}_1\left(t\right)-\sqrt{\gamma I\left(t\right)}d{W}_2\left(t\right)\text{.}\end{array}$$ (7)

Note that if $I\left(t\right)=0$, then the epidemic stops. The Itô SDEs reduce to the original ODE model (1), if the two Wiener processes are neglected.

4.2. Numerical simulation

The Euler-Maruyama method is a simple numerical method that can be used to simulate sample paths of SDEs. The Euler-Maruyama method is of order $\Delta t$ and follows directly from the derivation of the SDE, where $\Delta W\left(t\right)=W\left(t+\Delta t\right)-W\left(t\right)\sim \text{Normal}\left(0,\Delta t\right)$. In general, for a system of SDEs of the form,

$$dX\left(t\right)=f\left(X\left(t\right),t\right)dt+G\left(X\left(t\right),t\right)dW\left(t\right)\text{,}$$

the Euler-Maruyama method is a finite-difference approximation,

$$X\left(t+\Delta t\right)=X\left(t\right)+f\left(X\left(t\right),t\right)\Delta t+G\left(X\left(t\right),t\right)\eta \sqrt{\Delta t}\text{,}$$

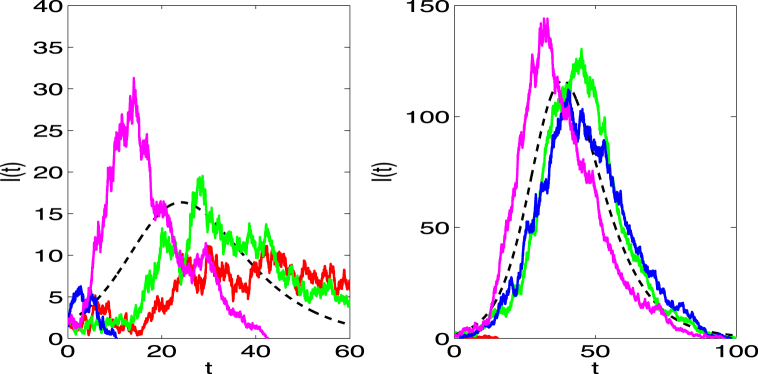
$t=0,\Delta t,2\Delta t,\dots$, where $\Delta t$ is chosen sufficiently small to ensure convergence. For k independent Wiener processes $W\left(t\right)={\left(W_1\left(t\right),\dots ,W_k\left(t\right)\right)}^T$, the vector $\eta =\left({\eta }_1,\dots ,{\eta }_k\right)$ is k independent standard normal random numbers ${\eta }_i\in \text{Normal}\left(\mathrm{0,1}\right)$. Sample paths of the SIR SDE model are illustrated in Fig. 2. The sample paths are continuous, but not differentiable (a property of the Wiener process).

Fig. 2.

The dashed curve is the ODE solution of $I\left(t\right)$ in the SIR model and the other solid curves are four sample paths of the SIR SDE model. Parameter values and initial conditions are the same as for the CTMC model in Fig. 1 for $N=100$ (left) and $N=750$ (right).

Numerical simulation of sample paths for SDE models is faster and simpler than computing sample paths for CTMC models when the population size is large. The time step in SDE models is chosen small but it has a fixed length, whereas in CTMC models the interevent time τ must be computed for each change $\Delta X$ and the interevent time decreases as the population size increases (see Equation (6)). Numerical methods with greater accuracy than the Euler-Maruyama method are discussed in the references, e.g., (Kloeden and Platen, 1992, Kloeden et al., 1997). In addition, methods have been developed to speed up the stochastic simulation (see, e.g., StochSS: Stochastic Simulation Service, www.StochSS.org, Petzold, UC Santa Barbara).

5. Malaria deterministic model

Malaria infection is caused by a Plasmodium parasite. An infectious mosquito transmits the parasite to a susceptible host through a mosquito bite. It is the female mosquito that bites the host to acquire blood for reproduction. According to the website of the World Health Organization (World Health Organization, 2015) there were approximately 214 million new cases of malaria and 438,000 deaths worldwide in 2015. Most cases were reported in the African region. Sir Ronald Ross was one of the first scientists to formulate mathematical models for the spread of malaria between insect vectors and human hosts (Ross, 1909, Ross, 1911, Smith et al., 2012) and for his work on malaria he was awarded the Nobel Prize in Physiology or Medicine in 1902.

In the Ross malaria model, the total number of vectors M and hosts H are constant. The variables S and I are the number of susceptible and infectious hosts, respectively, and U and V are the number of healthy and infectious vectors, respectively. A female mosquito requires a certain number of blood meals for reproduction and it is assumed that a single mosquito takes k bites per unit time to fulfill this blood requirement. Another important assumption is that the total number of bites by the mosquito population is dependent on the total number of mosquitoes but it is not dependent on the number of human hosts (only the proportion of human hosts). The probability per bite that an infectious mosquito transmits malaria is p and the probability per bite that a healthy mosquito acquires infection is q. Parameter $\alpha =kp$ is the transmission rate from an infectious mosquito to a human and $\beta =kq$ is the acquisition rate from an infectious host to a healthy mosquito. The host recovery rate is γ and the mosquito death rate is μ. The birth rate and death rate of the mosquito population are equal. The natural birth and death rates of humans are negligible with respect to the modeling time frame and are assumed to be zero. With the preceding assumptions, the malaria model takes the form:

$$\begin{array}{l}\frac{dS}{dt}=-\alpha V\frac{S}{H}+\gamma I\\ \frac{dI}{dt}=\alpha V\frac{S}{H}-\gamma I\\ \frac{dU}{dt}=-\beta U\frac{I}{H}+\mu M-\mu U\\ \frac{dV}{dt}=\beta U\frac{I}{H}-\mu V\end{array}$$ (8)

The disease-free equilibrium for this model is $S=H$, $U=M$ and $I=0=V$. Linearization of the differential equations for I and V about the disease-free equilibrium yields the matrices from the next generation matrix approach (van den Driessche & Watmough, 2002):

$$F-V=\left(\begin{array}{cc}0& \alpha \\ \beta \frac{M}{H}& 0\end{array}\right)-\left(\begin{array}{cc}\gamma & 0\\ 0& \mu \end{array}\right)\text{.}$$ (9)

The spectral radius of $F{V}^{-1}$ is often defined as the basic reproduction number (van den Driessche & Watmough, 2002):

$$\rho \left(F{V}^{-1}\right)=\sqrt{\frac{\alpha \beta \left(M/H\right)}{\mu \gamma }}\text{.}$$

An equivalent form in terms of the threshold of one, is defined as the product of the transmission from vector to host and from host to vector:

$${\mathcal{R}}_0=\left(\frac{\alpha }{\mu }\right)\left(\frac{\beta \left(M/H\right)}{\gamma }\right)$$ (10)

(e.g., (Heffernan et al., 2005, Lloyd et al., 2007)). This latter expression is used in the following discussion of the basic reproduction number. For model (8), the disease dies out if ${\mathcal{R}}_0<1$ and a stable endemic equilibrium exists if ${\mathcal{R}}_0>1$.

6. Malaria continuous time Markov chain

6.1. Formulation

The malaria CTMC model is a time-homogeneous process with the Markov property. There are six events corresponding to transmission from host to vector and vector to host, recovery of humans, death of healthy and infectious mosquitoes, and birth of mosquitoes. Table 3 is a summary of these events and their probabilities. In the malaria CTMC model, given $\left(S\left(t\right),I\left(t\right),U\left(t\right),V\left(t\right)\right)=\left(s,i,u,v\right)$, the exponential distribution for the interevent time $T\sim \lambda e^{-\lambda t}$ has parameter

$$\lambda =\gamma i+\alpha v\left(s/H\right)+\beta u\left(i/H\right)+\mu \left(M+u+v\right)\text{.}$$

Table 3.

Ross malaria CTMC model assumptions

$\left(\Delta S,\Delta I\right)$	Probability	$\left(\Delta U,\Delta V\right)$	Probability
$\left(+1,-1\right)$	$\gamma i\Delta t+o\left(\Delta t\right)$	$\left(-\mathrm{1,1}\right)$	$\beta u\left(i/H\right)\Delta t+o\left(\Delta t\right)$
$\left(-1,+1\right)$	$\alpha v\left(s/H\right)\Delta t+o\left(\Delta t\right)$	$\left(+\mathrm{1,0}\right)$	$\mu M\Delta t+o\left(\Delta t\right)$
		$\left(-\mathrm{1,0}\right)$	$\mu u\Delta t+o\left(\Delta t\right)$
		$\left(0,-1\right)$	$\mu v\Delta t+o\left(\Delta t\right)$

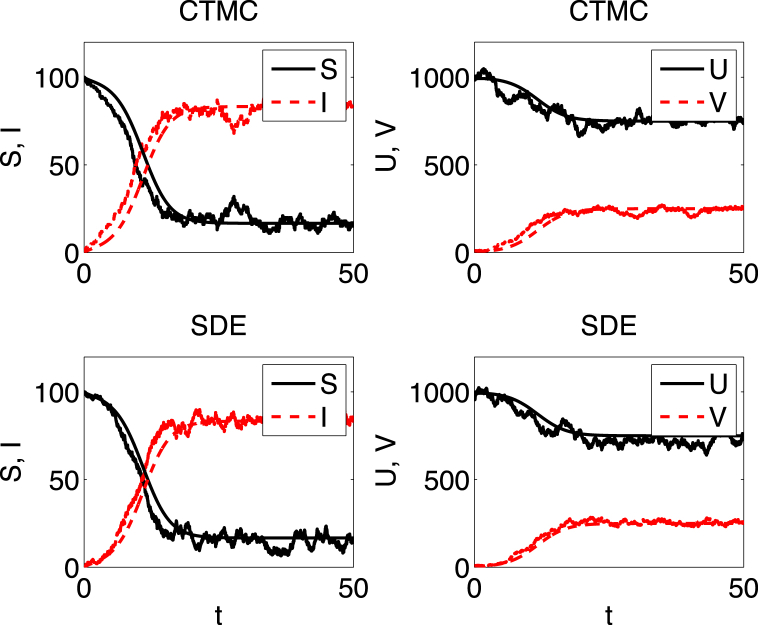
A sample path of the CTMC model is graphed in Fig. 3. A stable endemic equilibrium exists in the ODE model if ${\mathcal{R}}_0>1$ and the sample path of the CTMC model fluctuates around this endemic equilibrium.

Fig. 3.

The smooth curve in each figure is the solution of the host-vector ODE model. The other curves are one sample path of the CTMC model (top two figures) and one sample path of the SDE model (bottom two figures). The parameters are $H=100,M=1000$, $\alpha =0.2$, $\gamma =0.1$, $\beta =0.2$, and $\mu =0.5$. Initial conditions are $I\left(0\right)=0$, $V\left(0\right)=10$, $S\left(0\right)=100$ and $U\left(0\right)=990.$ The value of ${\mathcal{R}}_0=8$ with $q_1=1/6$ and $q_2=3/4$. The probability of extinction in the CTMC is approximately $\mathrm{\mathbb{P}}\approx 0.06$. The stable endemic equilibrium in the ODE model is $\left(\overline{S},\overline{I},\overline{U},\overline{V}\right)$ = (16.7, 83.3, 750, 250).

6.2. Branching process approximation

Approximation of the CTMC near the disease-free equilibrium, leads to a multitype branching process in two variables $I\left(t\right)$ and $V\left(t\right)$. Table 4 is a summary of the changes in I and V near the disease-free equilibrium when $S\approx H$ and $U\approx M$.

Table 4.

Branching process approximation of the malaria model near the disease-free equilibrium

Change $\left(\Delta I,\Delta V\right)$	Probability
$\left(+\mathrm{1,0}\right)$	$\alpha v\Delta t+o\left(\Delta t\right)$
$\left(0,+1\right)$	$\beta i\left(M/H\right)\Delta t+o\left(\Delta t\right)$
$\left(-\mathrm{1,0}\right)$	$\gamma i\Delta t+o\left(\Delta t\right)$
$\left(0,-1\right)$	$\mu v\Delta t+o\left(\Delta t\right)$

Next, two offspring pgfs are defined, one for a host and one for a mosquito. Each offspring pgf has the general form:

$$\sum _{j,k}\mathrm{\mathbb{P}}((I,V)=(j,k))u_1^j{u}_2^k,u_i\in [\mathrm{0,1}],i=\mathrm{1,2.}$$

For one infectious host, there are only two events, either recovery of the host or infection of a mosquito. The offspring pgf for I, given $I\left(0\right)=1$ and $V\left(0\right)=0$ is

$$f_1\left(u_1,u_2\right)=\frac{\gamma }{\gamma +\beta \left(M/H\right)}+\frac{\beta \left(M/H\right)}{\gamma +\beta \left(M/H\right)}{u}_1{u}_2\text{.}$$ (11)

That is, one infectious host recovers with probability $\gamma /\left(\gamma +\beta \left(M/H\right)\right)$ or infects a mosquito with probability $\beta \left(M/H\right)/\left(\gamma +\beta \left(M/H\right)\right).$ Note the term $u_1{u}_2$ in (11) means one infectious host generates one infectious mosquito ($u_2$ raised to the power one) and remains infectious ($u_1$ raised to the power one). The offspring pgf for V, given $V\left(0\right)=1$ and $I\left(0\right)=0$, is

$$f_2\left(u_1,u_2\right)=\frac{\mu }{\mu +\alpha }+\frac{\alpha }{\mu +\alpha }{u}_1{u}_2\text{.}$$ (12)

That is, one infectious mosquito dies with probability $\mu /\left(\mu +\alpha \right)$ or infects a host with probability $\alpha /\left(\mu +\alpha \right)$.

To find the probability of extinction (no outbreak), we compute the fixed points of the system on the unit square $\left[\mathrm{0,1}\right]\times \left[\mathrm{0,1}\right]$, $f_1\left(u_1,u_2\right)=u_1$ and $f_2\left(u_1,u_2\right)=u_2$, e.g., (Allen and van den Driessche, 2013, Athreya and Ney, 1972, Dorman et al., 2004, Harris, 1963). The two solutions of this system are (1,1) and $\left(q_1,q_2\right)$, where

$$q_1=\frac{\gamma }{\gamma +\beta \left(M/H\right)}+\frac{\beta \left(M/H\right)}{\gamma +\beta \left(M/H\right)}\left(\frac{1}{{\mathcal{R}}_0}\right)$$ (13)

$$q_2=\frac{\mu }{\mu +\alpha }+\frac{\alpha }{\mu +\alpha }\left(\frac{1}{{\mathcal{R}}_0}\right)$$ (14)

(e.g., (Allen & Lahodny, 2012)). The fixed point $\left(q_1,q_2\right)$ exists in the unit square provided ${\mathcal{R}}_0>1$. Equivalent expressions were derived by Bartlett in 1964, but they were not written in terms of ${\mathcal{R}}_0$ (Bartlett, 1964). Another equivalent set of expressions for $q_1$ and $q_2$ were derived by Lloyd et al. assuming geometric offspring pgfs (Lloyd et al., 2007). The expression for $q_1$ in (13) has a biological interpretation. Beginning from one infectious host, there is no outbreak if the infectious host recovers with probability $\gamma /\left(\gamma +\beta \left(M/H\right)\right)$ or if there is no successful transmission to a susceptible mosquito with probability $\beta \left(M/H\right)/\left(\gamma +\beta \left(M/H\right)\right)[1/{\mathcal{R}}_0]$.

The stability of the fixed points is determined from the spectral radius of the Jacobian matrix of the offspring pgfs, evaluated at $\left(\mathrm{1,1}\right)$, e.g., (Allen and van den Driessche, 2013, Athreya and Ney, 1972, Dorman et al., 2004, Harris, 1963). If the spectral radius is less than one, then $\left(\mathrm{1,1}\right)$ is stable and if it is greater than one, (1,1) is unstable and $\left(q_1,q_2\right)$ is stable. (See Appendix C.) The Jacobian matrix of the offspring pgfs evaluated at $\left(\mathrm{1,1}\right)$ is

$$\mathbb{M}=\left(\begin{array}{cc}\frac{\beta M/H}{\gamma +\beta M/H}& \frac{\beta M/H}{\gamma +\beta M/H}\\ \frac{\alpha }{\mu +\alpha }& \frac{\alpha }{\mu +\alpha }\end{array}\right)\text{.}$$

In general, it can be shown that

$$\mathbb{W}\left(\mathbb{M}-I\right)=F-V\text{,}$$ (15)

where F and V are computed from the next generation matrix approach, Equation (9), $\mathbb{W}$ is a diagonal matrix of interevent time parameters, $\mathbb{W}=\text{diag}\left(\gamma +\beta M/H,\mu +\alpha \right)$, and I is the identity matrix (Allen & van den Driessche, 2013). In addition, there is an important relation between ${\mathcal{R}}_0$ and matrix $\mathbb{M}$:

$${\mathcal{R}}_0>1\text{if}\text{and}\text{only}\text{if}\rho \left(\mathbb{M}\right)>1$$

which follows from the identity (15) (Allen & van den Driessche, 2013).

Therefore, the probability of extinction (no outbreak) is one, if ${\mathcal{R}}_0<1$, but less than one, if ${\mathcal{R}}_0>1$. Given $I\left(0\right)=i$ and $V\left(0\right)=v$, it follows from the independent assumption in the branching process approximation that the probabilities of a major or a minor outbreak are:

$${\mathrm{\mathbb{P}}}_{\text{minor}\text{outbreak}}=\{\begin{array}{ll}{q}_1^i{q}_2^v\text{,}& {\mathcal{R}}_0>1\\ 1\text{,}& {\mathcal{R}}_0<1\text{,}\end{array}{\mathrm{\mathbb{P}}}_{\text{major}\text{outbreak}}=\{\begin{array}{ll}1-q_1^i{q}_2^v\text{,}& {\mathcal{R}}_0>1\\ 0\text{,}& {\mathcal{R}}_0<1\end{array}\text{.}$$

Alternate forms for the offspring pgf have been proposed that differ from the assumptions in the underlying SIR CTMC epidemic model (Table 1) or in the host-vector CTMC model (Table 3), e.g., (Antia et al., 2003, Blumberg and Lloyd-Smith, 2013, Lloyd et al., 2007, Lloyd-Smith et al., 2005). Offspring pgfs have been assumed to have geometric, Poisson, gamma, or negative binomial distributions (Antia et al., 2003, Blumberg and Lloyd-Smith, 2013, Lloyd et al., 2007, Lloyd-Smith et al., 2005). But they are often applied in the discrete-time case. The geometric distribution and the forms in (5), (11), (12) preserve the Markov property of an exponentially distributed lifetime (Dorman et al., 2004). Branching process approximations can be extended to more complex epidemic models with multiple groups (Allen and Lahodny, 2012, Allen and van den Driessche, 2013).

7. Malaria stochastic differential equations

A derivation of the SDEs for the host-vector model follows in a similar manner as for the SIR model. For simplicity, denote the change of the system variables as $\Delta X={\left(\Delta S,\Delta I,\Delta U,\Delta V\right)}^T$ and the right side of the host-vector ODE model as $g_i$, $i=\mathrm{1,2,3,4}$, i.e., $dS/dt=g_1$. Then the Itô SDEs for the malaria model are computed from the expectation and covariance of $\Delta X$ based on the six events in Table 3. The system of SDEs has the form $dX\left(t\right)=f\left(X\left(t\right)\right)dt+G\left(X\left(t\right)\right)dW\left(t\right)$, where G is a $4\times 6$ matrix satisfying $G{G}^T=C$, where to order $\Delta t$, $C\Delta t$ is the approximate covariance matrix,

$$G=\left(\begin{array}{cccccc}-\sqrt{\alpha VS/H}& \sqrt{\gamma I}& 0& 0& 0& 0\\ \sqrt{\alpha VS/H}& -\sqrt{\gamma I}& 0& 0& 0& 0\\ 0& 0& -\sqrt{\beta UI/H}& \sqrt{\mu M}& -\sqrt{\mu U}& 0\\ 0& 0& \sqrt{\beta UI/H}& 0& 0& -\sqrt{\mu V}\end{array}\right)\text{,}$$

and $W\left(t\right)$ is a vector of six independent Wiener processes, corresponding to the six events represented in Table 3 (Allen, 2007, Allen et al., 2008). More explicitly, the system of Itô SDEs for the host-vector model is

$$\begin{array}{l}dS=g_{1}dt-\sqrt{\alpha VS/H}d{W}_1+\sqrt{\gamma I}d{W}_2\\ dI=g_{2}dt+\sqrt{\alpha VS/H}d{W}_1-\sqrt{\gamma I}d{W}_2\\ dU=g_{3}dt-\sqrt{\beta UI/H}d{W}_3+\sqrt{\mu M}d{W}_4-\sqrt{\mu U}d{W}_5\\ dV=g_{4}dt+\sqrt{\beta UI/H}d{W}_3-\sqrt{\mu V}d{W}_6\text{,}\end{array}$$

where the dependence on time t is omitted. For $I\left(t\right)=0$ and $V\left(t\right)=0$, the epidemic stops.

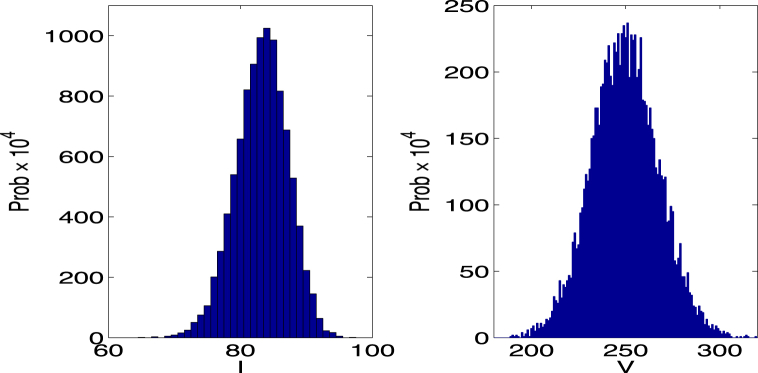
The Euler-Maruyama method is used to compute sample paths of the host-vector SDE model (see Fig. 3) and to approximate the probability density for large time (see probability histogram in Fig. 4). The probability density appears to be approximately stationary as solutions fluctuate near the endemic equilibrium of the ODE model. How much fluctuation occurs in the disease dynamics depends on the transmission processes (demographic variability). In a more realistic host-vector model, the disease dynamics are also affected by environmental conditions. Environmental variability is especially important in a vector-borne disease, where the vector life cycle is intimately connected to temperature and moisture levels.

Fig. 4.

The two histograms (computed from 10,000 sample paths of the host-vector SDE model) approximate the probability density for I and V at $t=50$. Parameter values are the same as in Fig. 3 but with initial conditions sufficiently large such that the probability of hitting zero is close to zero. The computed mean values and standard deviations are ${\mu }_I=83.2$, ${\mu }_V=249.6$, ${\sigma }_I=3.94$, and ${\sigma }_V=17.8$. The mean values are close to the endemic equilibrium values of the host-vector ODE model: $\left(\overline{I},\overline{V}\right)=\left(83.3,250\right)$.

8. Environmental variability

For the SIR epidemic model or the malaria host-vector model, changes in the environment may impact the parameters for birth, death, recovery, or transmission. For example, if birth, death, or transmission rates fluctuate with changes in the environmental conditions, then a stochastic differential equation for the model parameter can be formulated as a mean-reverting process (fluctuation about some average value) (E. Allen, 2016).

For example, a mean-reverting Ornstein-Uhlenbeck (OU) process for the parameter α is modeled by the SDE:

$$d\alpha \left(t\right)=r\left(\overline{\alpha }-\alpha \left(t\right)\right)dt+\sigma dW\left(t\right)\text{,}$$

where $\overline{\alpha }$ is the mean value and ${\sigma }^2$ is proportional to the variance. In particular, for the OU process, $\alpha \left(t\right)$ has a normal distribution with mean

$$\mathbb{E}\left(\alpha \left(t\right)\right)=\overline{\alpha }+\left(\alpha \left(0\right)-\overline{\alpha }\right)e^{-rt}$$

and variance

$$Var\left(\alpha \left(t\right)\right)=\frac{{\sigma }^2}{2r}\left(1-\text{exp}\left(-2rt\right)\right)$$ (16)

(Allen, 2016, Oksendal, 2000). In the limit, as $t\to \infty$, the mean is $\overline{\alpha }$ and variance is ${\sigma }^2/\left(2r\right)$. The mean agrees with the solution of the ODE: $d\alpha \left(t\right)/dt=r\left(\overline{\alpha }-\alpha \left(t\right)\right)$.

In another example, if the carrying capacity $K\equiv K\left(t\right)$ varies both seasonally and randomly, a biologically reasonable model for $K\left(t\right)$ has the form (Allen, E. Allen, & Jonsson, 2006):

$$dK\left(t\right)=r\left(\overline{K}-K\left(t\right)\right)dt+\hat{r}\text{cos}\left(\omega t\right)dt+\sigma dW\left(t\right)\text{.}$$ (17)

The mean of K is

$$\mathbb{E}\left(K\left(t\right)\right)=\overline{K}+[K\left(0\right)-\overline{K}-\frac{r\hat{r}}{{\omega }^2+r^2}]e^{-rt}+\frac{\hat{r}}{{\omega }^2+r^2}[\omega \text{sin}\left(\omega t\right)+r\text{cos}\left(\omega t\right)]$$

and variance has the same expression as in (16). (See Fig. 5.) The parameter K can also be modeled as a discrete random variable. Other mean-reverting stochastic processes that have the additional desirable property of being nonnegative are discussed in (E. Allen, 2016).

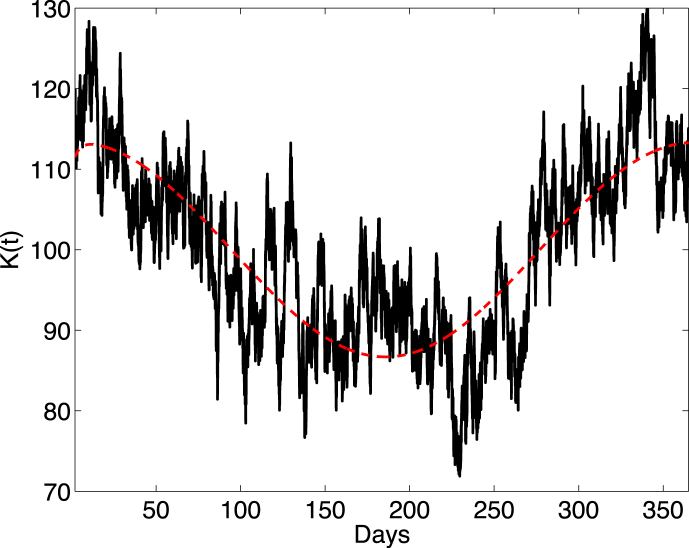
Fig. 5.

The smooth curve is the ODE solution of $K\left(t\right)$ (Wiener process neglected in (17)) and the random curve is one sample path of the SDE model (17). Parameter values are $\overline{K}=100$, $r=0.3$, $\hat{r}=4$, $\omega =2\pi /365$, and $\sigma =5$. The initial condition is $K\left(0\right)=110.$

9. Summary

The intent of this primer is to introduce the topic of stochastic epidemic modeling from the perspective of an ODE epidemic framework. The emphasis is on continuous-time Markov chains and stochastic differential equations. Many topics of relevance to stochastic epidemic modeling have been omitted, e.g., epidemic duration, discrete-time Markov chains, stochastic spatial models, and parameter estimation for stochastic models. The references provide a wealth of information on these and other topics in stochastic epidemic modeling.

Appendix A. Interevent time in the CTMC model

Let $F\left(t\right)=1-e^{-\lambda t}=\mathrm{\mathbb{P}}(T\le t)$ be the cumulative distribution for the interevent time T. Let U denote the uniform distribution on $\left[\mathrm{0,1}\right]$. Properties of U and the fact that F is strictly increasing on $[0,\mathrm{\infty })$, yields

$$F\left(t\right)=\mathrm{\mathbb{P}}(U\le F\left(t\right))=\mathrm{\mathbb{P}}(F^{-1}\left(U\right)\le t)\text{.}$$

But this implies $T=F^{-1}\left(U\right)$. Calculation of the inverse function and using the fact that $1-U$ has the same distribution as U leads to the formula for τ in Equation (6):

$$F^{-1}\left(U\right)=-\frac{\text{ln}\left(1-U\right)}{\lambda }=-\frac{\text{ln}\left(U\right)}{\lambda }\text{.}$$

Appendix B. PGF for the SIR branching approximation

For the SIR CTMC model, the pgf $G_i$ for the infectious class $I\left(t\right)$, given $I\left(0\right)=i$, is defined in terms of the transition probabilities, $p_{i,j}\left(t\right)=\mathrm{\mathbb{P}}(I\left(t\right)=j|I\left(0\right)=i)$:

$$G_i(u,t)=\mathbb{E}\left(u^{I\left(t\right)}\right|I\left(0\right)=i)=\sum _{j=0}^{\infty }{p}_{i,j}\left(t\right)u^j=p_{i,0}\left(t\right)+p_{i,1}\left(t\right)u+p_{i,2}\left(t\right)u^2+\cdots \text{.}$$ (B.1)

Note that $G_i\left(0,t\right)=p_{i,0}\left(t\right)$ is the probability of disease extinction by time t: $I\left(t\right)=0$, given $I\left(0\right)=i$. From the independent assumptions, it follows that $G_i$ is the product of i generating functions for $I\left(0\right)=1$:

$$G_i\left(u,t\right)={\left[G_1\left(u,t\right)\right]}^i\text{.}$$ (B.2)

The backward Kolmogorov differential equations for the branching process approximation of $I\left(t\right)$ are as follows:

$$\frac{d{p}_{i,k}}{dt}=\beta i{p}_{i+1,k}+\gamma i{p}_{i-1,k}-\left(\beta +\gamma \right)i{p}_{i,k}\text{.}$$ (B.3)

A differential equation is derived for $p_{\mathrm{1,0}}\left(t\right)$ based on the identities (B.1) and (B.2), and the backward Equation (B.3). Differentiate (B.2) with respect to t, solve for $\partial G_1/\partial t$, then replace $\partial G_i/\partial t$ with an equivalent expression from definition (B.1):

$$\frac{\partial G_1}{\partial t}=\frac{1}{i{\left(G_1\right)}^{i-1}}\frac{\partial G_i}{\partial t}=\frac{1}{i{G}_{i-1}}\left(\sum _{k=0}^{\infty }\frac{d{p}_{i,k}}{dt}{u}^k\right)\text{.}$$

Substitution of $d{p}_{i,k}/dt$ from the backward Kolmogorov differential Equation (B.3) leads to

$$\begin{array}{l}\frac{\partial G_1}{\partial t}=\frac{1}{G_{i-1}}\sum _{k=0}^{\infty }[\beta p_{i+1,k}+\gamma p_{i-1,k}-\left(\beta +\gamma \right)p_{i,k}]u^k\\ =\beta \frac{G_{i+1}}{G_{i-1}}+\gamma \frac{G_{i-1}}{G_{i-1}}-\left(\beta +\gamma \right)\frac{G_i}{G_{i-1}}\\ =\left(\beta +\gamma \right)[\frac{\beta }{\beta +\gamma }{\left(G_1\right)}^2+\frac{\gamma }{\beta +\gamma }-G_1]\\ =\left(\beta +\gamma \right)[f\left(G_1\right)-G_1]\text{,}\end{array}$$

where the offspring pgf f is defined in (5). Since the right side of the differential equation is independent of u, the differential equation also applies to $G_1\left(0,t\right)=p_{\mathrm{1,0}}\left(t\right).$ That is,

$$\frac{d{p}_{\mathrm{1,0}}\left(t\right)}{dt}=\left(\beta +\gamma \right)[f\left(p_{\mathrm{1,0}}\left(t\right)\right)-p_{\mathrm{1,0}}\left(t\right)],p_{\mathrm{1,0}}\left(t\right)\in \left[\mathrm{0,1}\right]\text{.}$$ (B.4)

From the theory of autonomous differential equations, the steady-states of (B.4) are the stationary solutions of the process: solutions u of $f\left(u\right)=u$. From the offspring pgf in (5), there are two possible steady-state solutions, either $u=1$ or $u=\gamma /\beta =1/{\mathcal{R}}_0.$ It is easy to check if ${\mathcal{R}}_0<1$, then $u=1$ is the stable steady-state and if ${\mathcal{R}}_0>1$, then $u=1/{\mathcal{R}}_0$ is the stable steady-state. If more than one individual is infectious, $I\left(0\right)=i>1$, then the asymptotic steady-states are either 1 or ${\left(1/{\mathcal{R}}_0\right)}^i$.

Appendix C. PGF for the host-vector branching approximation

In a manner similar to the derivation for the stochastic SIR model, differential equations for the probabilities of extinction can be derived for the branching process approximation in the host-vector model. Let $p_{\left(i,v\right),\left(l,m\right)}\left(t\right)$ be the transition probabilities for $I\left(t\right)$ and $V\left(t\right)$ in the branching process approximation. The generating function $G_{\left(i,v\right)}$ is defined as

$$G_{\left(i,v\right)}\left(u_1,u_2,t\right)=\sum _{l,m}{p}_{\left(i,v\right),\left(l,m\right)}\left(t\right)u_1^l{u}_2^m\text{.}$$

In the branching process approximation, assume

$$G_{\left(i,v\right)}\left(u_1,u_2,t\right)={\left[G_{\left(\mathrm{1,0}\right)}\left(u_1,u_2,t\right)\right]}^i{\left[G_{\left(\mathrm{0,1}\right)}\left(u_1,u_2,t\right)\right]}^v.$$ (C.1)

Below are the backward Kolmogorov differential equations for I and V, where the transition probabilities $p_{a,b}\left(t\right)\equiv p_{\left(i,v\right),b}\left(t\right)$, $a=\left(i,v\right)$, and $b=\left(l,m\right)$:

$$\frac{d{p}_{\left(i,v\right),b}}{dt}=\alpha v{p}_{\left(i+1,v\right),b}+\beta i\frac{M}{H}{p}_{\left(i,v+1\right),b}+\gamma i{p}_{\left(i-1,v\right),b}+\mu v{p}_{\left(i,v-1\right),b}-[\alpha v+\beta i\frac{M}{H}+\gamma i+\mu v]p_{\left(i,v\right),b}\text{.}$$

Differentiate the identity in (C.1) with respect to t for two cases: $v=0$ and $i=0$.

$$\begin{array}{l}\frac{\partial G_{\left(\mathrm{1,0}\right)}}{\partial t}=\frac{1}{i{\left[G_{\left(\mathrm{1,0}\right)}\right]}^{i-1}}\frac{\partial G_{\left(i,0\right)}}{\partial t}=\frac{1}{i{G}_{\left(i-\mathrm{1,0}\right)}}\sum _b\frac{d{p}_{\left(i,0\right),b}}{dt}{u}_1^l{u}_2^m\\ \frac{\partial G_{\left(\mathrm{0,1}\right)}}{\partial t}=\frac{1}{v{\left[G_{\left(\mathrm{0,1}\right)}\right]}^{v-1}}\frac{\partial G_{\left(0,v\right)}}{\partial t}=\frac{1}{v{G}_{\left(0,v-1\right)}}\sum _b\frac{d{p}_{\left(0,v\right),b}}{dt}{u}_1^l{u}_2^m\text{.}\end{array}$$

Substitute the backward Kolmogorov differential equations into the right side, apply the identity (C.1), and simplify. This leads to the following differential equations for $G_{\left(\mathrm{1,0}\right)}$ and $G_{\left(\mathrm{0,1}\right)}$:

$$\begin{array}{l}\frac{\partial G_{\left(\mathrm{1,0}\right)}}{\partial t}=\left(\gamma +\beta \frac{M}{H}\right)[f_1\left(G_{\left(\mathrm{1,0}\right)},G_{\left(\mathrm{0,1}\right)}\right)-G_{\left(\mathrm{1,0}\right)}]\\ \frac{\partial G_{\left(\mathrm{0,1}\right)}}{\partial t}=\left(\mu +\alpha \right)[f_2\left(G_{\left(\mathrm{1,0}\right)},G_{\left(\mathrm{0,1}\right)}\right)-G_{\left(\mathrm{0,1}\right)}]\text{.}\end{array}$$

Since $p_{\left(\mathrm{1,0}\right),\left(\mathrm{0,0}\right)}\left(t\right)=G_{\left(\mathrm{1,0}\right)}\left(\mathrm{0,0},t\right)$ and $p_{\left(\mathrm{0,1}\right),\left(\mathrm{0,0}\right)}\left(t\right)=G_{\left(\mathrm{0,1}\right)}\left(\mathrm{0,0},t\right)$, the preceding differential equations can be expressed in terms of the two probabilities of extinction. The steady-states of this system are the fixed points of the offspring pgfs (11), (12). The stability of these steady-states is determined by the eigenvalues of the Jacobian matrix $\mathbb{W}\left(\mathbb{M}-I\right)$. The steady-state (1,1) is stable if the eigenvalues of the Jacobian matrix have negative real part if and only if $\rho \left(\mathbb{M}\right)<1$ if and only if ${\mathcal{R}}_0<1$ (Allen & van den Driessche, 2013).