Reproduction numbers of infectious disease models

Abstract

This primer article focuses on the basic reproduction number, ${\mathrm{ℛ}}_0$, for infectious diseases, and other reproduction numbers related to ${\mathrm{ℛ}}_0$ that are useful in guiding control strategies. Beginning with a simple population model, the concept is developed for a threshold value of ${\mathrm{ℛ}}_0$ determining whether or not the disease dies out. The next generation matrix method of calculating ${\mathrm{ℛ}}_0$ in a compartmental model is described and illustrated. To address control strategies, type and target reproduction numbers are defined, as well as sensitivity and elasticity indices. These theoretical ideas are then applied to models that are formulated for West Nile virus in birds (a vector-borne disease), cholera in humans (a disease with two transmission pathways), anthrax in animals (a disease that can be spread by dead carcasses and spores), and Zika in humans (spread by mosquitoes and sexual contacts). Some parameter values from literature data are used to illustrate the results. Finally, references for other ways to calculate ${\mathrm{ℛ}}_0$ are given. These are useful for more complicated models that, for example, take account of variations in environmental fluctuation or stochasticity.

1. Introduction

Infectious diseases continue to debilitate and to cause death in humans and animals, with new disease-causing pathogens emerging and old pathogens reemerging or evolving. For example, viruses give rise to influenza, measles and West Nile virus, bacteria give rise to anthrax, salmonella, chlamydia and cholera, and protozoa give rise to malaria and trypanosomiasis (sleeping sickness). Disease may be passed directly from person to person by respiratory droplets (e.g., measles), via body secretions (e.g., chlamydia), by biting tsetse flies (e.g., trypanosomiasis) or mosquitoes (e.g., malaria), or by ingestion in food or water (e.g., cholera). Some diseases can be controlled by vaccines, antibiotics, antiviral drugs, reduction in vector populations, increased sanitation or behavioral changes. In order to consider control strategies for a particular disease, it is essential to know features of the pathogen, the mode of transmission and other epidemiological details, since as indicated by the above examples, these differ greatly between diseases.

Mathematical modelling can play an important role in helping to quantify possible disease control strategies by focusing on the important aspects of a disease, determining threshold quantities for disease survival, and evaluating the effect of particular control strategies. A very important threshold quantity is the basic reproduction number, sometimes called the basic reproductive number or basic reproductive ratio (Heffernan, Smith, & Wahl, 2005), which is usually denoted by ${\mathrm{ℛ}}_0$. The epidemiological definition of ${\mathrm{ℛ}}_0$ is the average number of secondary cases produced by one infected individual introduced into a population of susceptible individuals, where an infected individual has acquired the disease, and susceptible individuals are healthy but can acquire the disease.

In reality, the value of ${\mathrm{ℛ}}_0$ for a specific disease depends on many variables, such as location and density of population. For a few specific diseases, Table 1 gives estimates of ${\mathrm{ℛ}}_0$ gleaned from data in the literature.

Table 1.

Estimated Mean Values of ${\mathrm{ℛ}}_0$ from Data.

Disease outbreak and location	${\mathrm{ℛ}}_0$	Reference
Smallpox in Indian subcont. (1968–73)	4.5	Anderson and May (1991)
Poliomyelitis in Europe (1955–60)	6	Anderson and May (1991)
Measles in Ghana (1960–68)	14.5	Anderson and May (1991)
SARS epidemic in (2002–03)	3.5	Gumel et al. (2004)
1918 Spanish influenza in Geneva
Spring wave	1.5	Chowell, Ammon, Hengartner, and Hyman (2006)
Fall wave	3.8	Chowell et al. (2006)
H2N2 influenza pandemic in US (1957)	1.68	Longini, Halloran, Nizam, and Yang (2004)
H1N1 influenza in South Africa (2009)	1.33	White, Archer, and Pagano (2013)
Ebola in Guinea (2014)	1.51	Althaus (2014)
Zika in South America (2015–16)	2.06	Gao et al. (2016)

The aim of this review is to elaborate on mathematical ways of finding ${\mathrm{ℛ}}_0$ for ODE disease models in a population, bearing in mind the epidemiological meaning of ${\mathrm{ℛ}}_0$, and to demonstrate how this and other reproduction numbers can be used to guide control strategies. Section 2 introduces simple models that establish notation and serve as background for later sections. The next generation matrix method to theoretically calculate ${\mathrm{ℛ}}_0$ for ODE models is presented in Section 3. In Section 4, the use of ${\mathrm{ℛ}}_0$ and other reproduction numbers to guide control strategies is shown by defining elasticity indices, and type and target reproduction numbers. Sections 5, 6, 7 apply these ideas to models specific for West Nile virus in birds, cholera in humans, and anthrax in animals, respectively. As suggested by a referee, Zika models are briefly discussed in Section 8. For these diseases, numerical values for model parameters are taken from the literature, with references given for these and for proofs (which are not detailed here). A final section, Section 9, gives references to other approaches for calculating ${\mathrm{ℛ}}_0$, in particular for models formulated in other ways. Inevitably the reference list is incomplete as there have recently been many articles on infectious diseases (it has been said that there is an epidemic of disease models), many of which determine a basic or control reproduction number.

2. Simple compartmental disease models

2.1. SIR epidemic model

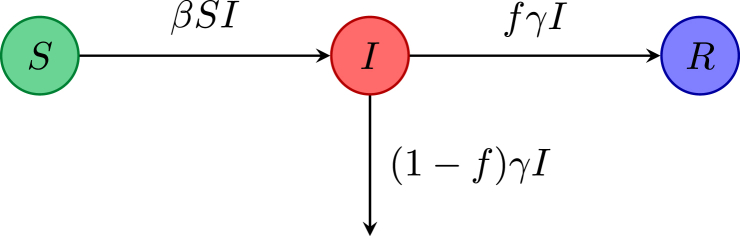
To begin with a simple model, assume that each member of a population is either susceptible, infectious (infected with the disease) or recovered from the disease with life-long immunity. If the disease is short lived compared with the population lifetime, then demography can be ignored. Such a model may be appropriate as a very simple model for seasonal influenza, ignoring features such as immunity from past infections. Let $S,I,R$ denote the number of susceptible, infectious, recovered individuals at time t. Transmission of influenza is airborne or by respiratory secretions on hands, so this is often modeled by mass action, namely a term $\beta SI$, where β is the disease transmission rate constant and $\beta I$ is the force of infection. Let $1/\gamma$ denote the mean infectious time (about 5 days for influenza), thus $\gamma >0$ is the recovery rate, and let f denote the fraction of infectious individuals who recover from the disease (thus the fraction $1-f$ die from the disease). The flow diagram for the disease dynamics with compartments S, I and R is given in Fig. 1.

Fig. 1.

Flow diagram for the $SIR$ model.

Ordinary differential equations (ODEs) for this $SIR$ model are given by

$$\frac{dS}{dt}=-\beta SI,\frac{dI}{dt}=\beta SI-\gamma I,\frac{dR}{dt}=f\gamma I\text{.}$$

Initially $S\left(0\right)=S_0,I\left(0\right)>0$ with $I\left(0\right)\ll S\left(0\right)$, and $R\left(0\right)=0$. There is a disease free equilibrium (DFE) with $\left(S,I,R\right)=\left(S_0,\mathrm{0,0}\right)$. Focusing on the I equation, the initial behavior is governed by the sign of $\beta S_0-\gamma$, or equivalently $\frac{\beta S_0}{\gamma }-1$. This leads to the definition of ${\mathrm{ℛ}}_0=\frac{\beta S_0}{\gamma }$, with the DFE locally asymptotically stable (LAS) if ${\mathrm{ℛ}}_0<1$, but unstable if ${\mathrm{ℛ}}_0>1$. This ${\mathrm{ℛ}}_0$ is the product of the transmission rate, the mean infectious time and $S_0$, and clearly fits with the epidemiological definition of ${\mathrm{ℛ}}_0$ given in the Introduction. Note that ${\mathrm{ℛ}}_0$ is independent of the fraction dying from the disease. From the dynamics of the system, if ${\mathrm{ℛ}}_0<1$, then the number of infectious individuals decreases monotonically to 0; whereas if ${\mathrm{ℛ}}_0>1$, then this number first increases (before tending to zero); thus ${\mathrm{ℛ}}_0=1$ acts as a sharp threshold between the disease dying out or causing an epidemic.

If ${\mathrm{ℛ}}_0>1$, then initially $I\left(t\right)$ is approximately $I\left(0\right)\text{exp}\left[\gamma \left({\mathrm{ℛ}}_0-1\right)t\right]$. With a knowledge of the mean infectious time, it may be possible to use this formula with initial data from an epidemic to estimate the value of ${\mathrm{ℛ}}_0$. If ${\mathrm{ℛ}}_0>1$ and $f=1$ (no death due to disease), then the fraction of susceptibles at the end of the epidemic, $s\left(\infty \right)=S\left(\infty \right)/N$ where N is the total population, is given by the unique root between 0 and 1 of the final size equation

$$\text{ln}s\left(\infty \right)=-{\mathrm{ℛ}}_0\left(1-s\left(\infty \right)\right)\text{.}$$

If data on this fraction are available, then this equation can be used to estimate ${\mathrm{ℛ}}_0$ after the epidemic has passed.

If a vaccine that is perfect is available, and a fraction p of the population is vaccinated, then the disease will not spread if $\left(1-p\right){\mathrm{ℛ}}_0<1$, that is a fraction $p>1-1/{\mathrm{ℛ}}_0$ is vaccinated, giving herd immunity. So this simple model predicts that diseases with large values of ${\mathrm{ℛ}}_0$ require a large proportion of the population to be successfully vaccinated (compare ${\mathrm{ℛ}}_0$ values for smallpox and measles as given in Table 1). Interestingly, the disease that has historically caused the most human deaths, namely smallpox, is the only human disease that currently has been declared eradicated (due largely to vaccination campaigns).

Simple demography can be included in this $SIR$ model with $A>0$ denoting the input of individuals (all susceptible) per unit time, and $d>0$ denoting the natural death rate. The equation for the infectious individuals then becomes

$$\frac{dI}{dt}=\beta SI-\left(d+\gamma \right)I\text{,}$$

giving ${\mathrm{ℛ}}_0=\frac{\beta S_0}{d+\gamma }$ with $S_0=\frac{A}{d}$.

2.2. $SEIR$ Compartmental model

In many infectious diseases there is an exposed period also called a latent period after transmission of infection but before the infected individual can transmit the infection. During this time the pathogen is in the host, but in low numbers so that the host is not yet infectious. If the exposed period is relatively long, then an exposed compartment should be included to give an $SEIR$ model. Let E denote the number of exposed individuals, and the mean exposed period be $1/\kappa$ where $\kappa >0$ is the rate of loss of latency. To include simple demography, let A be the input of individuals per unit time, and d be the natural death rate. Assuming that the disease does not cause death, the disease evolves according to the equations

$$\begin{array}{l}\frac{dS}{dt}=A-dS-\beta SI\\ \frac{dE}{dt}=\beta SI-\left(d+\kappa \right)E\\ \frac{dI}{dt}=\kappa E-\left(d+\gamma \right)I\\ \frac{dR}{dt}=\gamma I-dR\text{,}\end{array}$$

with nonnegative initial conditions. The flow for this model is depicted in Fig. 2. The DFE is given by $\left(S_0,E,I,R\right)=\left(\frac{A}{d},\mathrm{0,0,0}\right)$. There are now two infected compartments (E and I), and linearizing about the DFE it can be seen that only the equations in these two variables determine the stability of the DFE. From these two equations, the Jacobian matrix at the DFE gives the characteristic equation

$$z^2+\left(2d+\kappa +\gamma \right)z+\left(d+\kappa \right)\left(d+\gamma \right)-\kappa \beta S_0=0.$$

Fig. 2.

Flowchart for the $SEIR$ model.

This equation has all roots with negative real parts (thus the DFE is linearly stable) if and only if each coefficient is positive, i.e., $\left(d+\kappa \right)\left(d+\gamma \right)>\kappa \beta S_0$. Writing this condition in non-dimensional form as $\kappa \beta S_0/\left(d+\kappa \right)\left(d+\gamma \right)<1$ is more epidemiologically meaningful. In fact $\kappa /\left(d+\kappa \right)$ is the fraction of individuals progressing from exposed to infectious, and $1/\left(d+\gamma \right)$ is the average infectious time taking death into account. From the biological definition,

$${\mathrm{ℛ}}_0=\frac{\kappa }{\left(d+\kappa \right)}\frac{\beta S_0}{\left(d+\gamma \right)}$$

for this $SEIR$ model. Note that if $d=0$ this simplifies to the ${\mathrm{ℛ}}_0$ for the $SIR$ model obtained in Section 2.1. If ${\mathrm{ℛ}}_0<1$, then the disease dies out; whereas if ${\mathrm{ℛ}}_0>1$, the quadratic has a positive root, and the disease invades the population. In fact the disease then tends to an endemic state with $I^{\text{*}}=\frac{A\kappa \left(1-1/{\mathrm{ℛ}}_0\right)}{\left(d+\kappa \right)\left(d+\gamma \right)}$. This endemic equilibrium exists only for ${\mathrm{ℛ}}_0>1$, and there is a forward bifurcation at ${\mathrm{ℛ}}_0=1$. A mathematical way to determine ${\mathrm{ℛ}}_0$ for this and more complex models is given in the next Section.

3. Computation of ${\mathrm{ℛ}}_0$ by the next generation matrix method

The Jacobian method used for the $SEIR$ model yields a biologically reasonable ${\mathrm{ℛ}}_0$, but for more complex compartmental models, especially those with more infected compartments, the method is hard to apply as it relies on the algebraic Routh-Hurwitz conditions for stability of the Jacobian matrix. An alternative method proposed by Diekmann, Heesterbeek, and Metz (1990) and elaborated by van den Driessche and Watmough (2002) gives a way of determining ${\mathrm{ℛ}}_0$ for an ODE compartmental model by using the next generation matrix. Here an outline of this method is given, the proofs and further details can be found in van den Driessche and Watmough (2002) and van den Driessche and Watmough (2008).

Let $x={\left(x_1,x_2,\dots ,x_n\right)}^T$ be the number of individuals in each compartment, where the first $m<n$ compartments contain infected individuals. Assume that the DFE $x_0$ exists and is stable in the absence of disease, and that the linearized equations for $x_1,\dots ,x_m$ at the DFE decouple from the other equations. The assumptions are given in more details in the references cited above. Consider these equations written in the form $\frac{d{x}_i}{dt}={\mathcal{F}}_i\left(x\right)-{\mathcal{V}}_i\left(x\right)$ for $i=\mathrm{1,2},\dots ,m$. In this splitting, ${\mathcal{F}}_i\left(x\right)$ is the rate of appearance of new infections in compartment i, and ${\mathcal{V}}_i\left(x\right)$ is the rate of other transitions between compartment i and other infected compartments. It is assumed that ${\mathcal{F}}_i$ and ${\mathcal{V}}_i\in {\mathcal{C}}^2$, and ${\mathcal{F}}_i=0$ if $i\in \left[m+1,n\right]$.

Now define $F=\left[\frac{\partial {\mathcal{F}}_i\left(x_0\right)}{\partial x_j}\right]$ and $V=\left[\frac{\partial {\mathcal{V}}_i\left(x_0\right)}{\partial x_j}\right]$ for $1\le i,j\le m.$ From the biological meanings of F and V, it follows that F is entrywise non-negative and V is a non-singular M-matrix (see Berman and Plemmons (1994)), so $V^{-1}$ is entrywise non-negative. Let $\psi \left(0\right)$ be the number of initially infected individuals. Then $F{V}^{-1}\psi \left(0\right)$ is an entrywise non-negative vector giving the expected number of new infections. Matrix $F{V}^{-1}$ has $\left(i,j\right)$ entry equal to the expected number of secondary infections in compartment i produced by an infected individual introduced in compartment j. Thus $F{V}^{-1}$ is the next generation matrix and

$${\mathrm{ℛ}}_0=\rho \left(F{V}^{-1}\right)\text{,}$$

where $\rho$ denotes the spectral radius. The linear stability of the DFE is determined from the Jacobian matrix by $s\left(F-V\right)$, where s denotes the maximum real part of the eigenvalues sometimes called the spectral bound. Using the above notation, the relation between this quantity and ${\mathrm{ℛ}}_0$ is given in the following result, the proof of which uses properties of M-matrices; see the references cited above.

Theorem 1

If $x_0$ is a DFE of the system $\frac{d{x}_i}{dt}={\mathcal{F}}_i\left(x\right)-{\mathcal{V}}_i\left(x\right)$, then $x_0$ is locally asymptotically stable if ${\mathrm{ℛ}}_0=\rho \left(F{V}^{-1}\right)<1$, but unstable if ${\mathrm{ℛ}}_0>1$, i.e. sign $s\left(F-V\right)=$ sign $\left({\mathrm{ℛ}}_0-1\right).$

This next generation matrix approach is now illustrated by returning to the $SEIR$ Model of Section 2.2. The infected compartments are E and I. At the DFE matrices F and V are

$$F=\left[\begin{array}{cc}0& \beta S_0\\ 0& 0\end{array}\right],V=\left[\begin{array}{cc}d+\kappa & 0\\ -\kappa & d+\gamma \end{array}\right]\text{,}$$

giving

$$F{V}^{-1}=\left[\begin{array}{cc}\frac{\kappa \beta S_0}{\left(d+\kappa \right)\left(d+\gamma \right)}& \frac{\beta S_0}{d+\gamma }\\ 0& 0\end{array}\right]\text{.}$$

So $F{V}^{-1}$ has eigenvalues 0 and ${\mathrm{ℛ}}_0$ where

$${\mathrm{ℛ}}_0=\frac{\kappa \beta S_0}{\left(d+\kappa \right)\left(d+\gamma \right)}\text{,}$$

as deduced biologically in Section 2.2. Here $\beta S_0$ is the infection rate in a population of $S_0$ susceptibles, $\kappa /\left(d+\kappa \right)$ is the fraction progressing from E to I, $1/\left(d+\gamma \right)$ is the mean time in I, thus the $\left(\mathrm{1,1}\right)$ entry of $F{V}^{-1}$ is the expected number of secondary infections produced in compartment E by an infected person originally in E.

As an extension of this $SEIR$ model, suppose that individuals in E are mildly infectious at a reduced rate $\mathit{\epsilon }\beta SE$ with $0<\epsilon <1$. This could also be thought of as an initial infectious class before the pathogen has fully developed in the host. Proceeding as previously yields

$$F=\left[\begin{array}{cc}\mathit{\epsilon }\beta S_0& \beta S_0\\ 0& 0\end{array}\right]$$

with V unchanged. Thus

$${\mathrm{ℛ}}_0=\frac{\kappa \beta S_0}{\left(d+\kappa \right)\left(d+\gamma \right)}+\frac{\mathit{\epsilon }\beta S_0}{\left(d+\kappa \right)}\text{.}$$

The first term gives contributions from the infectious compartment I as before, whereas the second term gives contributions from the mildly infectious E compartment, thus increasing the value of ${\mathrm{ℛ}}_0$.

As another extension of the $SEIR$ model (with the E compartment assumed not infectious), suppose that a fraction p of individuals are vaccinated at recruitment into the susceptible population. This is an approximation for vaccination of babies against childhood diseases. In addition, suppose that the vaccine is perfectly effective, so everyone receiving the vaccine is protected from the disease. With input $A=dN$, keeping the total population $N=S+E+I+R$ constant, $\left(1-p\right)dN$ enter S and $pN$ enter the R compartment. The DFE then becomes $\left(S,E,I,R\right)=\left(\left(1-p\right)N,\mathrm{0,0},pN\right)$ and the vaccination reproduction number also called a control reproduction number, denoted here by ${\mathrm{ℛ}}_V$, is given by

$${\mathrm{ℛ}}_V=\frac{\kappa \beta \left(1-p\right)N}{\left(d+\kappa \right)\left(d+\gamma \right)}\text{.}$$

This gives the fraction that need to be vaccinated as $p>1-1/{\mathrm{ℛ}}_0$ (with $S_0=N$) to bring ${\mathrm{ℛ}}_V$ below the threshold value of one, as determined to give herd immunity (see Section 2.1).

The examples given above each have the rank of the next generation matrix equal to one, so the reproduction number is easy to calculate as the trace of this matrix. A more complicated model in which this occurs is when the next generation matrix is separable, i.e., $K=F{V}^{-1}$ has $\left(i,j\right)$ entry $k_{ij}=a_i{b}_j$. Assume that $b_j=c_j$ and $a_i=c_i{N}_i/\sum _{\ell }{c}_{\ell }{N}_{\ell }$ with $\sum _k{N}_k=1$ as given in Diekmann, Heesterbeek, and Britton (2012, Exercise 7.18) for a sexually transmitted disease in groups, with populations given by $N_j$ and the total population normalized to 1. Then ${\mathrm{ℛ}}_0=\sum _j{a}_j{b}_j=\sum _j{c}_j^2{N}_j/\sum _{\ell }{c}_{\ell }{N}_{\ell }=\langle c\rangle +Var\left[c\right]/\langle c\rangle$, where $\langle c\rangle$ denotes the mean value of c and $Var\left[c\right]$ denotes the variance of c.

Remark 2

As a cautionary remark, note that Theorem 1 assures local stability if ${\mathrm{ℛ}}_0<1$. For many models, global stability can be proved by comparison theorems (see, for example, Castillo-Chávez, Feng, and Huang (2002)) or Lyapunov functions (see, for example, Shuai and van den Driessche (2013)). However, in some models that have more complicated structure (e.g., include vaccination that is not perfect (Arino et al., 2003, Brauer, 2004, Kribs-Zaleta and Velasco-Hernandez, 2000)) multigroup models (Hadeler & Castillo-Chávez, 1995) endemic equilibria may exist near the DFE for ${\mathrm{ℛ}}_0<1$, and there is a backward bifurcation at ${\mathrm{ℛ}}_0=1$, with the DFE locally but not globally stable in a range of ${\mathrm{ℛ}}_0$ values below 1. In such a situation, the initial numbers in the infected compartments determine whether or not the disease persists; see for example, Castillo-Chávez and Song (2004) and Martcheva (2015, Section 7.5). So for disease control, ${\mathrm{ℛ}}_0$ may have to be decreased further below 1.

4. Use of reproduction numbers to suggest control strategies

Related reproduction numbers, and elasticity indices of ${\mathrm{ℛ}}_0$ are now defined, and then in later sections applied to specific disease models.

4.1. Type and target reproduction numbers

Herd immunity is applicable if a control strategy is aimed at all individuals in a population, but if the population has several host types, then a control strategy may be aimed at only one host population. For example, in a vector-host model for malaria, spraying may be targeted at the mosquito vectors. To address this Roberts and Heesterbeek (2003) and Heesterbeek and Roberts (2007) introduced the concept of a type reproduction number denoted by $\mathcal{T}$. In general such a strategy influences one row or one column of the next generation matrix, depending on whether the control influences susceptibility or infectivity. This concept was further generalized by Shuai, Heesterbeek, and van den Driessche (2013) by singling out sets of entries for control, leading to the definition of a target reproduction number. For example, in a cholera outbreak, the prevention of contacts among children could be a reduction strategy; an age structured model would then target a specific entry of the next generation matrix.

To describe this algebraically, let $K=\left[k_{ij}\right]$ be the order n next generation matrix (i.e., $K=F{V}^{-1}$) and suppose that the entries in a set S are to be targeted with a control strategy (this can be either a decrease or an increase in entries of S). The target matrix $K_S$ has $\left(i,j\right)$ entry equal to $k_{ij}$ if entry $\left(i,j\right)\in S$, and 0 otherwise. If $\rho \left(K-K_S\right)<1$, then the target reproduction number ${\mathcal{T}}_S$ is defined as

$${\mathcal{T}}_S=\rho \left(K_S{\left(Id-K+K_S\right)}^{-1}\right)$$

where $Id$ is the identity matrix of order n. When all entries in one or more rows (or columns) of K are targeted, then the target reproduction number reduces to the type reproduction number as defined by Roberts and Heesterbeek (2003) and Heesterbeek and Roberts (2007). If a fraction at least $1-1/{\mathcal{T}}_S$ of the contributions due to the set S can be prevented, then the disease will die out. Note that if K is irreducible, then ${\mathcal{T}}_S=1\left(>1\right)$ if and only if ${\mathrm{ℛ}}_0=1\left(>1\right)$ (Roberts and Heesterbeek, 2003, Shuai et al., 2013).

4.2. Sensitivity and elasticity

To determine best control measures, knowledge of the relative importance of the different factors responsible for transmission is useful. Initially disease transmission is related to ${\mathrm{ℛ}}_0$ and sensitivity predicts which parameters have a high impact on ${\mathrm{ℛ}}_0$. The sensitivity index of ${\mathrm{ℛ}}_0$ with respect to a parameter ω is $\frac{\partial {\mathrm{ℛ}}_0}{\partial \omega }.$ Another measure is the elasticity index (normalized sensitivity index) that measures the relative change of ${\mathrm{ℛ}}_0$ with respect to ω, denoted by ${\mathrm{\Upsilon }}_{\omega }^{{\mathrm{ℛ}}_0}$, and defined as

$${\mathrm{\Upsilon }}_{\omega }^{{\mathrm{ℛ}}_0}=\frac{\partial {\mathrm{ℛ}}_0}{\partial \omega }\times \frac{\omega }{{\mathrm{ℛ}}_0}\text{.}$$

The sign of the elasticity index tells whether ${\mathrm{ℛ}}_0$ increases (positive sign) or decreases (negative sign) with the parameter; whereas the magnitude determines the relative importance of the parameter. These indices can guide control by indicating the most important parameters to target, although feasibility and cost play a role in practical control strategy. If ${\mathrm{ℛ}}_0$ is known explicitly, then the elasticity index for each parameter can be computed explicitly, and evaluated for a given set of parameters. The magnitude of the elasticity indices depends on these parameter values, which are probably only estimates. To help identify the robustness of ${\mathrm{ℛ}}_0$ to the parameters, Latin Hypercube Sampling maximin criteria can be used; see, for example, Blower and Dowlatabadi (1994). Another technique to investigate this is to compute ${\mathrm{ℛ}}_0$ over the feasible region of a given parameter while keeping the other parameters fixed at baseline values; see for example Manore, Hickmann, Xu, and Hyman (2014).

5. A model for West Nile virus

Some diseases, for example, West Nile virus, dengue fever, malaria, Zika virus are transmitted through a vector (for these diseases the vectors are various species of mosquitoes), rather than directly from person to person. Female mosquitoes bite to obtain a blood meal that is essential for reproduction, so only female mosquitoes need be considered. West Nile virus can kill birds and humans, but infected mosquitoes remain infectious for life and do not die of the virus. Birds can transmit the virus back to mosquitoes, whereas humans appear to be dead end hosts, and so may be excluded from a simple model. Since the life-cycle of mosquitoes is much shorter than that of birds, mosquito demography should be included in a model, but bird demography can be ignored. For a simple mosquito-bird (vector-host) model, take S and I compartments in each population, giving a system of four ODEs as formulated by Wonham and Lewis (2008). The equations for this system with nonnegative initial conditions are

$$\begin{array}{l}\frac{d{S}_B}{dt}=-{\alpha }_B\beta \frac{S_B{I}_M}{S_B+I_B}\\ \frac{d{I}_B}{dt}={\alpha }_B\beta \frac{S_B{I}_M}{S_B+I_B}-{\delta }_B{I}_B\\ \frac{d{S}_M}{dt}=b_M\left(S_M+I_M\right)-d_M{S}_M-{\alpha }_M\beta \frac{S_M{I}_B}{S_B+I_B}\\ \frac{d{I}_M}{dt}={\alpha }_M\beta \frac{S_M{I}_B}{S_B+I_B}-d_M{I}_M\text{,}\end{array}$$

where the variables and parameters are defined as

• •$S_B,S_M$: number of susceptible birds, mosquitoes
• •$I_B,I_M$: number of infectious birds, mosquitoes
• •${\alpha }_B,{\alpha }_M$: probability per bite of virus transmission to bird, mosquito
• •β: biting rate of mosquitoes on birds
• •${\delta }_B$: bird death rate from virus
• •$b_M,d_M$: mosquito birth, natural death rate

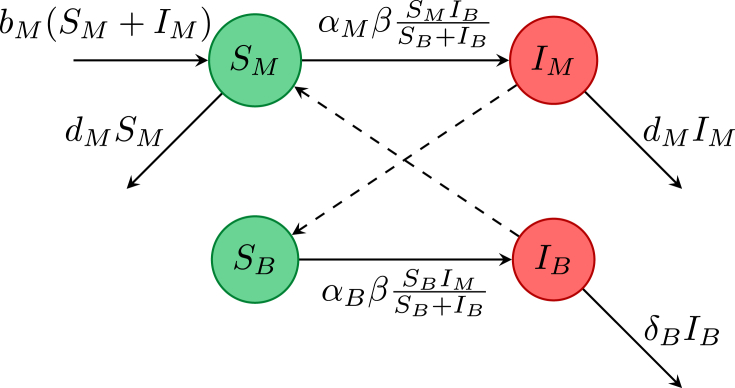
The disease is transferred by an infectious mosquito biting a susceptible bird, or by a susceptible mosquito biting an infectious bird, This cross infection between mosquitoes and birds is illustrated in the flow diagram in Fig. 3. The transmission is assumed to be frequency dependent; see Wonham and Lewis (2008) for more discussion on the model and transmission assumptions.

Fig. 3.

Flowchart for the West Nile virus model by Wonham and Lewis (2008).

Assuming that $b_M=d_M$ so the bird population is constant, there is a DFE with all birds and mosquitoes susceptible, with populations denoted by $S_B=S_{B0}$, $S_M=S_{M0}$ and $I_B=I_M=0$. Using the next generation matrix at the DFE

$$F=\left[\begin{array}{cc}0& {\alpha }_B\beta \\ {\alpha }_M\beta \frac{S_{M0}}{S_{B0}}& 0\end{array}\right],V=\left[\begin{array}{cc}{\delta }_B& 0\\ 0& d_M\end{array}\right],F{V}^{-1}=\left[\begin{array}{cc}0& \frac{{\alpha }_B\beta }{d_M}\\ \frac{{\alpha }_M\beta S_{M0}}{{\delta }_B{S}_{B0}}& 0\end{array}\right]\text{,}$$

giving

$${\mathrm{ℛ}}_0=\sqrt{\left(\frac{{\alpha }_B\beta }{d_M}\right)\left(\frac{{\alpha }_M\beta S_{M0}}{{\delta }_B{S}_{B0}}\right)}\text{.}$$

The first ratio under the square root represents the number of bird infections caused by one infectious mosquito, and the second represents the number of mosquito infections caused by one infected bird. The square root represents a geometric mean. In the literature the square root is often omitted, giving the same threshold for stability at 1, but taking the average number of secondary infected humans resulting from a single infected human; see, for example, Roberts and Heesterbeek (2003).

The relative importance of each parameter for control can be estimated by computing elasticity indices. For this model, ${\mathrm{\Upsilon }}_{{\alpha }_B}^{{\mathrm{ℛ}}_0}={\mathrm{\Upsilon }}_{{\alpha }_M}^{{\mathrm{ℛ}}_0}=\frac{1}{2},{\mathrm{\Upsilon }}_{\beta }^{{\mathrm{ℛ}}_0}=1,{\mathrm{\Upsilon }}_{d_M}^{{\mathrm{ℛ}}_0}={\mathrm{\Upsilon }}_{{\delta }_B}^{{\mathrm{ℛ}}_0}=-\frac{1}{2}$. Thus reducing the biting rate of mosquitoes has the largest proportional effect on reducing ${\mathrm{ℛ}}_0$.

Targeting the mosquito to bird transmission, the target reproduction number has $S=\left\{\left(\mathrm{1,2}\right)\right\}$, thus

$${\mathcal{T}}_S=\rho \left(\left[\begin{array}{cc}0& {\alpha }_B\frac{\beta }{d_M}\\ 0& 0\end{array}\right]{\left[\begin{array}{cc}1& 0\\ -\frac{{\alpha }_M\beta S_{M0}}{{\delta }_S{S}_{B0}}& 1\end{array}\right]}^{-1}\right)={\mathrm{ℛ}}_0^2\text{.}$$

If the transmission from mosquitoes to birds can be reduced by a fraction at least $1-1/{\mathrm{ℛ}}_0^2$, then the vector-host disease will die out.

This simple model has in particular neglected the period during which mosquitoes are in the larval stage, and also the exposed period of infected mosquitoes during which the viral load becomes sufficiently high for bites to be able to transmit the disease. Both these periods are significant fractions of the mosquito life-span. Including the two extra compartments of larval and exposed mosquitoes, gives a 6-dimensional ODE system, as formulated in Wonham and Lewis (2008). The resulting ${\mathrm{ℛ}}_0$ is not changed by the larval stage, but the exposed class reduces ${\mathrm{ℛ}}_0$ by a factor that is the square root of the probability of an exposed mosquito becoming infectious. Numerical model simulations in Wonham and Lewis (2008) show that the inclusion of these classes delays the disease outbreak.

Jiang, Qiu, Wu, and Zhu (2009) consider a bird-mosquito West Nile virus model (proposed by Bowman, Gumel, van den Driessche, Wu, and Zhu (2005)) and find that backward bifurcation is possible for some parameter values, thus the initial numbers of mosquitoes and birds are important in determining whether or not the disease dies out, even if ${\mathrm{ℛ}}_0<1$. More complicated vector-host models require appropriate parameter values to estimate elasticity indices and so to guide control planning; see, for example, Manore et al. (2014) for a comparison of dengue and chikungunya dynamics, and Cai, Li, Tuncer, Martcheva, and Lashari (2017) for a malaria model that may also exhibit backward bifurcation. Temperature plays an important role in the reproduction of many vectors that transmit vector-borne diseases. Thus climate change and variations in temperature may have an important influence on ${\mathrm{ℛ}}_0$ and disease persistence. A detailed study of this effect for Lyme Disease, which is transmitted by ticks, using data from northeastern North America is given by Ogden et al. (2014), and concludes that climate warming may have partly driven the emergence of Lyme disease in this region. More recently, Wang and Zhao (2017) develop a periodic time-delayed model of Lyme disease, compute ${\mathrm{ℛ}}_0$ from data, and show that ${\mathrm{ℛ}}_0$ can be driven below 1 if the recruitment rate of tick larvae is reduced.

6. Cholera models

Cholera is an infection of the small intestine caused by the bacterium Vibrio cholerae. Infection causes mild diarrhea in most cases, but some cases develop severe diarrhea and vomiting, which if untreated may lead to death within a few hours due to dehydration and electrolyte imbalance. Cholera can be transmitted indirectly to humans via water infected with the bacterium that is shed from infected humans, or directly from human to human (without differentiating between males and females). The relative importance of these two transmission paths is a key factor in designing control strategies as illustrated by the following models of cholera from the literature.

6.1. Direct and indirect transmission, Tien and Earn (2010)

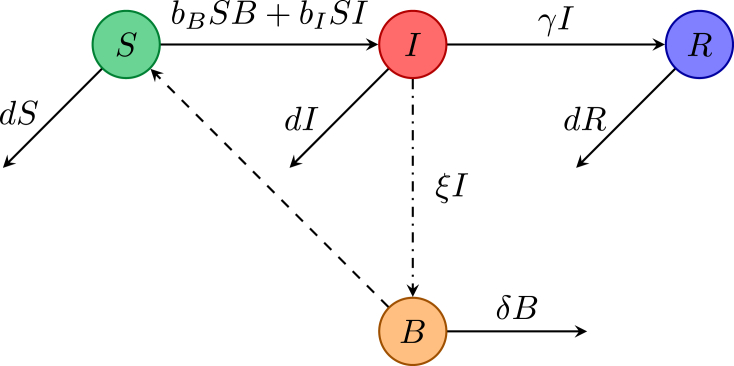
The same notation is used as previously, augmented by a variable B measuring the concentration of bacterium in the water, with δ the removal rate of the bacterium, and ξ the shedding rate of bacterium by infectious humans. The model formulated by Tien and Earn (2010) incorporates both direct and indirect transmission by using mass action terms with transmission rate constants $b_I$ and $b_B$. Their model assumes that there is no death due to cholera, so that the human population $N=S+I+R$ remains constant. The flow for this model of cholera dynamics is given in Fig. 4. The equations governing the dynamics are

$$\begin{array}{l}\frac{dS}{dt}=dN-b_{B}SB-b_{I}SI-dS\\ \frac{dI}{dt}=b_{B}SB+b_{I}SI-\left(d+\gamma \right)I\\ \frac{dR}{dt}=\gamma I-dR\\ \frac{dB}{dt}=\xi I-\delta B\text{,}\end{array}$$

with nonnegative initial conditions having $0<I\left(0\right)+B\left(0\right)\ll S\left(0\right)$ and $R\left(0\right)=0$. The DFE is given by $\left(S,I,R,B\right)=\left(N,\mathrm{0,0,0}\right)$, and assuming that shedding is not a new infection (i.e., goes into the V matrix), the next generation matrix has rank 1 and gives

$${\mathrm{ℛ}}_0=\frac{{\beta }_B+{\beta }_I}{d+\gamma }\text{where}{\beta }_B=\frac{b_{B}N\xi }{\delta },{\beta }_I=b_{I}N\text{.}$$

Fig. 4.

Flowchart of the cholera model by Tien and Earn (2010).

The two routes of transmission enter ${\mathrm{ℛ}}_0$ in an additive way, thus ${\mathrm{ℛ}}_0={\mathrm{ℛ}}_{0B}+{\mathrm{ℛ}}_{OI}$, with ${\mathrm{ℛ}}_{0B}={\beta }_B/\left(d+\gamma \right)$ and ${\mathrm{ℛ}}_{0I}={\beta }_I/\left(d+\gamma \right)$. If either the indirect or direct reproduction number is greater than one, then ${\mathrm{ℛ}}_0>1$, emphasising the fact that both transmission routes must be controlled to eliminate cholera.

However, if shedding is regarded as a new infection, then this alternative splitting gives

$$\tilde{F}=\left[\begin{array}{cc}{b}_{I}N& b_{B}N\\ \xi & 0\end{array}\right],\tilde{V}=\left[\begin{array}{cc}d+\gamma & 0\\ 0& \delta \end{array}\right],\tilde{F}{\tilde{V}}^{-1}=\left[\begin{array}{cc}\frac{b_{I}N}{d+\gamma }& \frac{b_{B}N}{\delta }\\ \frac{\xi }{d+\gamma }& 0\end{array}\right]\text{.}$$

This splitting gives a next generation matrix of rank 2, so ${\widetilde{\mathrm{ℛ}}}_0=\rho \left(\tilde{F}{\tilde{V}}^{-1}\right)$ is the positive root of the quadratic equation

$$G\left(z\right)=z^2-\frac{{\beta }_I}{d+\gamma }z-\frac{{\beta }_B}{d+\gamma }=0.$$

From the signs of the coefficients, this quadratic has a unique positive root, ${\widetilde{\mathrm{ℛ}}}_0$; and if $G\left(1\right)>0\left(<0\right)$, then ${\widetilde{\mathrm{ℛ}}}_0<1\left(>1\right)$. But $G\left(1\right)=1-\frac{{\beta }_I}{d+\gamma }-\frac{{\beta }_B}{d+\gamma }$, giving the same threshold as derived for ${\mathrm{ℛ}}_0$ above. However, it is hard to interpret ${\widetilde{\mathrm{ℛ}}}_0$ biologically.

For qualitative control, both splittings suggest vaccination to reduce the susceptible population at the DFE, however current vaccines are only $50-60\text{\%}$ effective for a short duration. More importantly, provision of clean water, which reduces indirect transmission (decreases $b_B$), water treatment to increase the bacterium decay rate δ, improvement in sanitation by disposal of human faeces (decreases ξ), and improvement in hygiene (decreases $b_I$), all combined in the acronym WASH, may be more beneficial in controlling cholera.

For this cholera model with shedding not a new infection, elasticity indices of ${\mathrm{ℛ}}_0$ can be calculated explicitly as

$${\mathrm{\Upsilon }}_{{\beta }_B}^{{\mathrm{ℛ}}_0}=\frac{{\mathrm{ℛ}}_{0B}}{{\mathrm{ℛ}}_0},{\mathrm{\Upsilon }}_{{\beta }_I}^{{\mathrm{ℛ}}_0}=\frac{{\mathrm{ℛ}}_{0I}}{{\mathrm{ℛ}}_0},{\mathrm{\Upsilon }}_{\gamma }^{{\mathrm{ℛ}}_0}=-\frac{\gamma }{d+\gamma }\text{.}$$

The parameter estimates for the 2006 cholera outbreak in Angola as reported in Table 1 of Eisenberg, Robertson, and Tien (2013) with time unit one day, namely ${\beta }_B=1.21,{\beta }_I=0.264,\gamma =0.25,d\approx 0$, give

$${\mathrm{ℛ}}_{0B}=4.84,{\mathrm{ℛ}}_{0I}=1.05,\text{thus}{\mathrm{ℛ}}_0=5.89\text{,}$$

$${\mathrm{\Upsilon }}_{{\beta }_B}^{{\mathrm{ℛ}}_0}=0.82,{\mathrm{\Upsilon }}_{{\beta }_I}^{{\mathrm{ℛ}}_0}=0.18,{\mathrm{\Upsilon }}_{\gamma }^{{\mathrm{ℛ}}_0}=-1.$$

This latter result means that if the recovery rate is increased, then ${\mathrm{ℛ}}_0$ decreases by the same relative amount. From these elasticity indices for the normalized transmission rates, it follows that the indirect transmission has the larger effect on ${\mathrm{ℛ}}_0$. Note that ${\beta }_B$ depends on the water transmission rate as well as the shedding rate and pathogen decay rate. However, Eisenberg et al. (2013) find that both transmission pathways are needed to explain the data well, and both should be considered in formulating public health policies to reduce the impact of cholera.

Taking the next generation matrix $K=\tilde{F}{\tilde{V}}^{-1}$, type and target reproduction numbers can be calculated; see Shuai et al. (2013). If direct transmission is targeted (for example, by improving hygiene or isolation), then $S=\left\{\left(\mathrm{1,1}\right)\right\}$, and the formula in Section 4.1 gives this target reproduction number as ${\mathcal{T}}_S={\mathrm{ℛ}}_{0I}/\left(1-{\mathrm{ℛ}}_{0B}\right)$ provided that ${\mathrm{ℛ}}_{0B}<1$, i.e., cholera cannot be maintained by only indirect transmission. If adequate clean water is provided, then the target reproduction number with $S=\left\{\left(\mathrm{1,2}\right)\right\}$ gives ${\mathcal{T}}_S={\mathrm{ℛ}}_{0B}/\left(1-{\mathrm{ℛ}}_{0I}\right)$ provided that cholera cannot be maintained by direct transmission alone. Thus if clean water is provided to at least a proportion $\left({\mathrm{ℛ}}_0-1\right)/{\mathrm{ℛ}}_{0B}$ of the population, then cholera will die out.

6.2. A random network model, Li, Ma, and van den Driessche (2015).

To take account of realistic heterogeneity in human contacts, network models have been introduced; see, for example, Newman (2003). The network consists of nodes as humans and edges as contacts. Miller (2011) showed that an $SIR$ model on a configuration type random network can be represented by a 2-dimensional ODE system. Li et al. (2015) extended this model to a random network of humans with each connected to a single infectious water node, as is appropriate for cholera.

Assume that the human to human network is generated by the probability generating function $\psi \left(x\right)={\sum }_{k=0}^{\infty }{x}^k{p}_k$ where $p_k$ is the degree distribution and k is the node degree. Let ${\beta }_I$ be the transmission rate along a human to human edge, and let ${\beta }_W=b_W\xi /\delta$ with $b_W$ the rate of transmission along the water to human edges caused by a unit concentration of bacterium in the water. Parameters $\gamma ,\xi ,\delta$ are as in the previous model (Section 6.1). The dynamics of this network cholera model are then given by a 3-dimensional ODE system, see Li et al. (2015) for details, which has the next generation matrix at the DFE given by

$$F{V}^{-1}=\left[\begin{array}{ccc}{\mathrm{ℛ}}_p& {\mathrm{ℛ}}_w& {\mathrm{ℛ}}_w\\ 0& 0& 0\\ {\mathrm{ℛ}}_i& {\mathrm{ℛ}}_w& {\mathrm{ℛ}}_w\end{array}\right]\text{,}$$

where ${\mathrm{ℛ}}_w=\frac{{\beta }_W}{\gamma }$, ${\mathrm{ℛ}}_i=\frac{{\beta }_I}{{\beta }_I+\gamma }\psi \text{'}\left(1\right)$ and ${\mathrm{ℛ}}_p=\frac{{\beta }_I}{{\beta }_I+\gamma }\frac{{\psi }^{″}\left(1\right)}{{\psi }^{\prime }\left(1\right)}$ are the basic reproduction numbers for the human to water to human, the water infected human to human, and the human infected human to human infected individuals, respectively. Note that $\psi \text{'}\left(1\right)$ is the average degree of the network. Since $F{V}^{-1}$ has rank 2 (the second row and column can be ignored in calculating the spectral radius) the basic reproduction number ${\mathrm{ℛ}}_0$ is given by the largest positive root of the quadratic equation

$$z^2-\left({\mathrm{ℛ}}_w+{\mathrm{ℛ}}_p\right)z+{\mathrm{ℛ}}_w\left({\mathrm{ℛ}}_p-{\mathrm{ℛ}}_i\right)=0\text{,}$$

with the disease threshold given by ${\mathrm{ℛ}}_0=1$. For a Poisson network, the variance is equal to the mean, i.e., ${\psi }^{\text{″}}\left(1\right)={\left[\psi \text{'}\left(1\right)\right]}^2$, giving ${\mathrm{ℛ}}_p={\mathrm{ℛ}}_i$, thus ${\mathrm{ℛ}}_0={\mathrm{ℛ}}_w+{\mathrm{ℛ}}_p$ as in the compartmental model of Section 6.1. However, for other networks this additive result of indirect and direct transmission does not hold. For example, on a scale-free network, the variance is greater than the mean, so ${\mathrm{ℛ}}_p>{\mathrm{ℛ}}_i$ and ${\mathrm{ℛ}}_0<{\mathrm{ℛ}}_w+{\mathrm{ℛ}}_p$. Thus the network structure is important in considering ways to control cholera by bringing ${\mathrm{ℛ}}_0$ below the threshold value of 1.

If ${\mathrm{ℛ}}_0>1$, then target reproduction numbers can help guide strategies for control. For example, if ${\mathrm{ℛ}}_p<1$, i.e., cholera cannot be sustained in the population just by the human to human transmission, then the type reproduction on the water transmission is given by

$${\mathcal{T}}_w=\rho \left(\left[\begin{array}{cc}0& 0\\ {\mathrm{ℛ}}_i& {\mathrm{ℛ}}_w\end{array}\right]{\left[\begin{array}{cc}\left(1-{\mathrm{ℛ}}_p\right)& -{\mathrm{ℛ}}_w\\ 0& 1\end{array}\right]}^{-1}\right)={\mathrm{ℛ}}_w+\frac{{\mathrm{ℛ}}_w{\mathrm{ℛ}}_i}{1-{\mathrm{ℛ}}_p}\text{.}$$

Preventing a fraction of at least $1-1/{\mathcal{T}}_w$ contributions from human infections due to water infection would cause cholera to die out.

For a Poisson network, the elasticity indices with respect to the transmission parameters are

$${\mathrm{\Upsilon }}_{{\beta }_W}^{{\mathrm{ℛ}}_0}=\frac{{\mathrm{ℛ}}_w}{{\mathrm{ℛ}}_0}\text{and}{\mathrm{\Upsilon }}_{{\beta }_I}^{{\mathrm{ℛ}}_0}=\frac{\gamma {\mathrm{ℛ}}_i}{\left(\beta +\gamma \right){\mathrm{ℛ}}_0}\text{.}$$

For other networks, the elasticity indices can be found by implicitly differentiating the quadratic in z.

7. A model for anthrax transmission

Anthrax is caused by a spore forming bacterium Bacillus anthracis. It is mainly a disease of animals, but humans can become infected by contact with infected animals, their hides, wool or meat. Infected animals may recover from anthrax (usually carnivores) or die from the disease (usually herbivores) (WHO, 2016). Transmission to animals may occur from eating infected carcasses or by inhalation of spores, and rarely by direct transmission. A model including these first two important models of transmission in animals can be formulated as a system of four ODEs, and is a special case of the model in Saad-Roy, van den Driessche, and Yakubu (2017) where direct transmission is also included. Let $S,I,C$ denote the number of susceptible animals, infected animals and infected carcasses, and A denote the grams of anthrax spores in the environment. It is assumed that animals follow logistic growth with birth rate r and carrying capacity K, with all newborn animals being susceptible. Spores grow at rate β per carcass and decay at rate α. Transmission rates from infected carcasses and from spores are denoted by ${\eta }_c$ and ${\eta }_a$, respectively. Parameters $d,\gamma ,\tau ,\delta ,$ and κ denote the animal natural death rate, death rate due to anthrax, recovery rate of infected animals, carcass consumption rate and carcass decay rate, respectively. The dynamics of the model are given by the system

$$\begin{array}{l}\frac{dS}{dt}=r\left(S+I\right)\left(1-\frac{\left(S+I\right)}{K}\right)-{\eta }_{a}AS-{\eta }_{c}CS-dS+\tau I\\ \frac{dI}{dt}={\eta }_{a}AS+{\eta }_{c}CS-\left(\gamma +d+\tau \right)I\\ \frac{dA}{dt}=-\alpha A+\beta C\\ \frac{dC}{dt}=\left(\gamma +d\right)I-\delta \left(S+I\right)C-\kappa C\end{array}$$

Assuming that $r>d$, the total animal population persists and there is a DFE $\left(S,I,A,C\right)=\left(S_0,\mathrm{0,0,0}\right)$ with $S_0=K\left(1-d/r\right)$. Taking the infected compartments as $I,A$, and C and assuming that the transmission terms, spore growth rate and death of infected animals give rise to new infections (as in Friedman and Yakubu (2013)), the Jacobian matrix at the DFE is decomposed as $\hat{F}-\hat{V}$

$$\hat{F}=\left[\begin{array}{ccc}0& {\eta }_a{S}_0& {\eta }_c{S}_0\\ 0& 0& \beta \\ \gamma +d& 0& 0\end{array}\right],\hat{V}=\left[\begin{array}{ccc}\gamma +d+\tau & 0& 0\\ 0& \alpha & 0\\ 0& 0& \delta S_0+\kappa \end{array}\right]\text{,}$$

where $\hat{F}$ is a nonnegative matrix and $\hat{V}$ is a nonsingular M-matrix. Thus,

$${\hat{\mathcal{R}}}_0=\rho \left(\hat{F}{\hat{V}}^{-1}\right)=\rho \left[\begin{array}{ccc}0& \frac{{\eta }_a{S}_0}{\alpha }& \frac{{\eta }_c{S}_0}{\delta S_0+\kappa }\\ 0& 0& \frac{\beta }{\delta S_0+\kappa }\\ \frac{\gamma +d}{\gamma +d+\tau }& 0& 0\end{array}\right]\text{.}$$

This gives ${\widehat{\mathrm{ℛ}}}_0$ as the positive root of the cubic polynomial

$$G\left(z\right)=z^3-{\mathrm{ℛ}}_{0c}z-{\mathrm{ℛ}}_{0a}=0$$

where ${\mathrm{ℛ}}_{0c}=\frac{\gamma +d}{\gamma +d+\tau }\frac{{\eta }_c{S}_0}{\delta S_0+\kappa }$ and ${\mathrm{ℛ}}_{0a}=\frac{\gamma +d}{\gamma +d+\tau }\frac{\beta {\eta }_a{S}_0}{\alpha \left(\delta S_0+\kappa \right)}$.

Alternatively, taking spore growth rate and death of infected animals as transfer, the Jacobian is split in a different way, giving

$$F=\left[\begin{array}{ccc}0& {\eta }_a{S}_0& {\eta }_c{S}_0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right],V=\left[\begin{array}{ccc}\gamma +d+\tau & 0& 0\\ 0& \alpha & -\beta \\ -\left(\gamma +d\right)& 0& \delta S_0+\kappa \end{array}\right]\text{,}$$

and ${\mathrm{ℛ}}_0={\mathrm{ℛ}}_{0a}+{\mathrm{ℛ}}_{0c}$, which is the sum of infections from spores in the environment (${\mathrm{ℛ}}_{0a}$) and from feeding on carcasses $\left({\mathrm{ℛ}}_{0c}\right)$. Note that $G\left(1\right)=1-{\mathrm{ℛ}}_0$, showing that ${\widehat{\mathrm{ℛ}}}_0=1$ if and only if ${\mathrm{ℛ}}_0=1$. Thus ${\widehat{\mathrm{ℛ}}}_0$ gives the same threshold as the more biologically meaningful basic reproduction number ${\mathrm{ℛ}}_0$ for anthrax to die out or persist.

For values of the growth parameters $K=100,r=1/300$ and $d=1/600$ giving $S_0=50$, Table 2 gives baseline parameter values from Saad-Roy et al. (2017), elasticity indices of ${\mathrm{ℛ}}_0$ and numerical values for these indices. These baseline parameters give ${\mathrm{ℛ}}_{0a}=0.114$, ${\mathrm{ℛ}}_{0c}=1.137$, thus ${\mathrm{ℛ}}_0=1.251$. Note that the model in Saad-Roy et al. (2017) includes a small amount of direct transmission between animals. Also in the caption of Table 2 in Saad-Roy et al. (2017) the values of ${\mathrm{ℛ}}_{0a}$ and ${\mathrm{ℛ}}_{0c}$ are erroneously switched: the correct values given here result in switching of the elasticity indices of ${\eta }_a$ and ${\eta }_c$, and the elasticity index of α should be $-0.0880$ in Saad-Roy et al. (2017).

Table 2.

Baseline Parameter Values and Elasticity Indices for the Anthrax Model.

Parameter	Value	Elasticity	Numerical Elasticity
δ	0.05	${\mathrm{\Upsilon }}_{\delta }^{{\mathrm{ℛ}}_0}\mathrm{=-}\frac{\delta S_0}{\delta S_0+\kappa }$	$-0.962$
${\eta }_c$	0.1	${\mathrm{\Upsilon }}_{{\eta }_c}^{{\mathrm{ℛ}}_0}=\frac{{\mathrm{ℛ}}_{0c}}{{\mathrm{ℛ}}_0}$	0.909
τ	0.1	${\mathrm{\Upsilon }}_{\tau }^{{\mathrm{ℛ}}_0}=-\frac{\tau }{\gamma +d+\tau }$	$-0.409$
γ	0.143	${\mathrm{\Upsilon }}_{\gamma }^{{\mathrm{ℛ}}_0}=-\frac{\gamma \tau }{\left(\gamma +d+\tau \right)\left(\gamma +d\right)}$	0.404
${\eta }_a$	0.5	${\mathrm{\Upsilon }}_{{\eta }_a}^{{\mathrm{ℛ}}_0}=\frac{{\mathrm{ℛ}}_{0a}}{{\mathrm{ℛ}}_0}$	0.091
β	0.5	${\mathrm{\Upsilon }}_{{\eta }_a}^{{\mathrm{ℛ}}_0}=\frac{{\mathrm{ℛ}}_{0a}}{{\mathrm{ℛ}}_0}$	0.091
α	0.1	${\mathrm{\Upsilon }}_{\alpha }^{{\mathrm{ℛ}}_0}=-\frac{{\mathrm{ℛ}}_{0a}}{{\mathrm{ℛ}}_0}$	$-0.091$
κ	0.1	${\mathrm{\Upsilon }}_{\kappa }^{{\mathrm{ℛ}}_0}=-\frac{\kappa }{\delta S_0+\kappa }$	$-0.038$

For these baseline parameter values, the elasticity indices show that the carcass decay rate and transmission rate from infected carcasses have the largest relative influence on ${\mathrm{ℛ}}_0$. Thus a control strategy that increases carcass decay rate or decreases carcass transmission is likely to be successful. This can be further explored by calculating the type reproduction number focussing on the removal of infected carcasses on death. Taking $S=\left\{\left(\mathrm{3,1}\right)\right\}$ in $\hat{F}{\hat{V}}^{-1}$, gives ${\mathcal{T}}_S={\mathrm{ℛ}}_0$. Thus for eradication at least a fraction $1-1/{\mathrm{ℛ}}_0$ of infected carcasses need to be removed, which is about $20\text{\%}$ for the baseline parameters in Table 2. Further discussion on removal of carcasses at any time after death is given in Sections 5.1 and 6.1 of Saad-Roy et al. (2017).

8. Modelling Zika transmission

An outbreak of Zika virus started in Brazil in early 2015, and since then has spread to many parts of the Americas. Although Zika symptoms are usually mild, it is of great concern as serious brain anomalies, such as microcephaly, can occur in fetuses of infected pregnant females. Zika is transmitted to humans by mosquitoes and also sexually by an infected male to a susceptible female. These two modes of transmission are included in models in the recent literature; see, for example, Brauer et al., 2016, Gao et al., 2016, Saad-Roy et al., 2016. Neglecting the exposed compartments, a simplified version of the model in Brauer et al. (2016) is

$$\begin{array}{l}\frac{d{S}_H}{dt}=-{\beta }_H{S}_H\frac{I_M}{N_M}-\alpha S_H\frac{I_H}{N_H}\\ \frac{d{I}_H}{dt}={\beta }_H{S}_H\frac{I_M}{N_M}+\alpha S_H\frac{I_H}{N_H}-\gamma I_H\\ \frac{d{S}_M}{dt}=d_M{N}_M-d_M{S}_M-{\beta }_M{S}_M\frac{I_H}{N_H}\\ \frac{d{I}_M}{dt}={\beta }_M{S}_M\frac{I_H}{N_H}-d_M{I}_M\text{.}\end{array}$$

For this system, the human population $N_H$ is divided into $S_H$ susceptible humans, $I_H$ infectious humans and $R_H$ recovered humans (this equation uncouples); the constant mosquito population $N_M$ is divided into $S_M$ susceptible mosquitoes and $I_M$ infectious mosquitoes. The positive parameters are γ the rate of human recovery, $d_M$ the birth and death rate of mosquitoes, ${\beta }_H$ the biting rate times the probability of transmission from mosquito to human, ${\beta }_M$ the biting rate times the probability of transmission from human to mosquito, and α the direct sexual transmission from human to human.

Using the next generation matrix method with all infection terms in matrix F, the basic reproduction number is the positive root of the quadratic equation $z^2-{\mathcal{R}}_{d}z-{\mathcal{R}}_v=0$, with ${\mathrm{ℛ}}_d=\frac{\alpha }{\gamma }$ and ${\mathrm{ℛ}}_v=\frac{{\beta }_H{\beta }_M}{\gamma d_M}$, accounting for the direct sexual transmission and vector transmission, respectively. Note that in this model the transmission term from mosquito to human is normalized differently than that from mosquito to bird in the West Nile virus model of Section 5, and also note similarity between this model and the cholera model in Section 6.1 with direct and indirect transmission. Brauer et al. (2016) show different splittings for matrices F and V leading to different expressions for the basic reproduction number, one such splitting giving ${\mathrm{ℛ}}_0={\mathrm{ℛ}}_d+{\mathrm{ℛ}}_v$. This point about multiple expressions for the basic reproduction number (in both discrete and continuous time models) is elaborated by Cushing and Diekmann (2016).

In their Zika model, Gao et al. (2016) include exposed compartments and also divide the infected human compartment into symptomatically, convalescent and asymptomatically infected. Their global sensitivity analysis shows that their basic reproduction number is most sensitive to mosquito biting and death rates. Saad-Roy et al. (2017) divide the human population in two regions (a source and import region) into sexually actives males and females and sexually inactive humans. Sexually active males are further divided into two stages, since Zika can be transmitted from males to females by blood and by semen, with the virus staying longer in the semen. Sexual contacts between males and females are represented by a random bipartite directed (male to female) network, with homogeneous mixing between mosquitoes and humans. Input parameter values are used to compute ${\mathrm{ℛ}}_0$ from a matrix of order 14, and a value of ${\mathrm{ℛ}}_0\approx 1.4$ is found. This model predicts that by the time one microcephaly case is detected, a sizable fraction of the population has been infected with Zika, emphasizing the need for surveillance of this disease.

9. Other approaches to obtain ${\mathrm{ℛ}}_0$

This concluding section gives a glimpse of other results about the basic reproduction number, including calculating it for models given by systems other than ODEs, and estimating its magnitude from data. A few relevant references are given so that a reader can follow up on these glimpses to obtain more details.

9.1. Next generation operator to calculate ${\mathrm{ℛ}}_0$

The method of computing ${\mathrm{ℛ}}_0$ as the spectral radius of the next generation matrix given in Section 3 assumes that the population is divided into discrete compartments or states. However, if these are continuous, as for example in an age structured model, then the next generation operator K specifies how the disease evolves in a generation, namely $\left(K\varphi \right)\left(x\right)=\underset{\text{Ω}}{\int }k\left(x,y\right)\varphi \left(y\right)dy$, where $k\left(x,y\right)$ is the kernel of the linear positive operator K, and $\text{Ω}$ is a subset of $R^n$; see Diekmann et al. (1990) and Diekmann et al. (2012, Section 7.3). The kernel $k\left(x,y\right)$ gives the expected number of new cases with state x caused by an infectious individual in state y during its period of infectiousness. Then the basic reproduction number ${\mathrm{ℛ}}_0$ is defined as the spectral radius of the positive operator K. If the range of K is one dimensional, then ${\mathrm{ℛ}}_0$ is the unique non-zero eigenvalue; see Diekmann et al. (2012, Section 7.4) for some examples, and see Section 4 in Thieme (2009) for discussion of an $SIR$ model with variable susceptibility.

9.2. ${\mathrm{ℛ}}_0$ in a periodic environment

The method of Section 3 assumes that the environment is constant, but in reality environmental parameters are changing, for example temperature changes periodically. The models then become non-autonomous dynamical systems. In the past twenty or so years, many authors have extended the definition of ${\mathrm{ℛ}}_0$ to periodic environments; see for example, Bacaër and Ait Dads, 2011, Inaba, 2012, Thieme, 2009, Wang and Zhao, 2017, Zhao, 2013, Chapter 11) and references therein. Inaba (2012) introduces a new definition of ${\mathrm{ℛ}}_0$ in a heterogeneous environment based on the generation evolution operator as a generalization of previous definitions.

9.3. Survival function method to compute ${\mathrm{ℛ}}_0$

Let $F\left(a\right)$ denote the infection survival probability, that is the probability that a newly infected individual remains infected (and infectious) for at least time a, and $b\left(a\right)$ denote the average number of newly infected individuals that an infectious individual produces per unit time. Using these functions, ${\mathrm{ℛ}}_0={\int }_0^{\infty }b\left(a\right)F\left(a\right)da$. For the $SIR$ model of Section 2.1, the infectious period is assumed to have a negative exponential distribution. Thus $F\left(a\right)=e^{-\gamma a}$ and $b\left(a\right)=\beta S_0$. Then ${\mathrm{ℛ}}_0={\int }_0^{\infty }\beta S_0{e}^{-\gamma a}da=\frac{\beta S_0}{\gamma }$, as determined in Section 2.1.

This method can be used for models that take account of the fact that infectivity (the probability of transmission from a contact) varies with time since infection, rather than being constant throughout the infectious period. In such an age of infection SIR model, with a the time since first infection, $b\left(a\right)=\beta \left(a\right)S_0$ where $S_0$ is the DFE equilibrium. This method is not restricted to models described by ODEs and can be extended to a series of states, for example to a vector-host system; see, for example, Heffernan et al. (2005, Section 2.1).

9.4. Calculation of ${\mathrm{ℛ}}_0$ for discrete time systems

There are many discrete time epidemic models in the literature; see, for example, Allen (1994) and Yakubu (2010). Care must be taken in formulating these discrete time models so that the number of individuals in each compartment does not go negative.

The next generation matrix approach can also be used for discrete time epidemic models; see Allen and van den Driessche (2008) and references therein. To describe this briefly, assume that the equations of the epidemic model are given by $x\left(t+1\right)=G\left(x\left(t\right)\right)$ where $x\left(t\right)$ denotes the population states at time t, with $x_1,\dots ,x_m$ infected and the remaining states uninfected. Assuming that there is a unique DFE, then linearizing the infected state equations about this DFE gives $y\left(t+1\right)=\left(F+T\right)y\left(t\right)$ where F and T are nonnegative matrices evaluated at the DFE. Here F is the matrix of new infections that survive the time interval, and T is the transition matrix with $\rho \left(T\right)<1$. Then matrix $Q=F{\left(Id-T\right)}^{-1}$ is the next generation matrix for this discrete system, and the basic reproduction number ${\mathrm{ℛ}}_0=\rho \left(Q\right)$. Allen and van den Driessche (2008) give details of the assumptions and show that the DFE is locally asymptotically stable if ${\mathrm{ℛ}}_0<1$ but unstable if ${\mathrm{ℛ}}_0>1$. The assumed order of events within each time step is important, since different assumptions can yield different ${\mathrm{ℛ}}_0$ values; see Lewis, Rencławowicz, van den Driessche, and Wonham (2006) for an illustration of this on discrete time West Nile virus models.

A graph theoretic method to determine the net reproductive rate for discrete time systems was developed by de-Camino-Beck and Lewis (2008) and applied to the control of invasive species. They use graph reduction rules on the life-cycle graph to calculate ${\mathrm{ℛ}}_0$. An analogous method for continuous time models given by ODEs is described in de-Camino-Beck, Lewis and van den Driessche (2009), where an algorithm to compute ${\mathrm{ℛ}}_0$ by reduction on the digraph associated with the matrix $F{\mathrm{ℛ}}_0^{-1}-V$ is given.

9.5. Stochastic models

An excellent introduction to stochastic epidemic models formulated as discrete time Markov chains, continuous time Markov chains, and stochastic differential equations is given in Allen (2010, Chapter 3), where some numerical examples of stochastic sample paths and corresponding deterministic solutions are given. Also, Keeling and Rohani (2008, Chapter 6) give three methods for approximating stochasticity into disease transmission and recovery. The probability of an outbreak depends on the value of ${\mathrm{ℛ}}_0$ and also on the initial number of infected individuals, $i_0$. If the population size is large, then this probability is approximately 0 if ${\mathrm{ℛ}}_0\le 1$, but $1-{\left(1/{\mathrm{ℛ}}_0\right)}^{i_0}$ if ${\mathrm{ℛ}}_0>1$. This estimate applies to the stochastic $SIS$ and $SIR$ models only for a finite time range, since as $t\to \infty$ the probability of an outbreak is zero (an absorbing state). Thus, one difference between stochastic and deterministic models is that stochastic sample paths can converge to the disease free state, whereas the corresponding deterministic solution converges to an endemic equilibrium. Thus in a vaccination program, stochasticity may lead to disease extinction before the herd immunity level of vaccination is reached.

9.6. Estimation of ${\mathrm{ℛ}}_0$ from data

As described in previous sections, the magnitude of ${\mathrm{ℛ}}_0$ is important in determining the severity of a disease and for designing control strategies. Early in an outbreak of some diseases, for example seasonal influenza, it may be fairly easy to estimate the average length of infection and the initial number of infectious individuals, thus an estimate of ${\mathrm{ℛ}}_0$ can be obtained from the formula $I\left(0\right)\text{exp}\left[\gamma \left({\mathrm{ℛ}}_0-1\right)t\right]$ given in Section 2.1. If the exponential growth rate of the initial phase of the outbreak, usually denoted by r, is observed from data, then ${\mathrm{ℛ}}_0=1+\frac{r}{\gamma }$. However, this formula is based on a simple $SIR$ model, and so has limited applicability. A recent paper by Sanches and Massad (2016) compares three methods to estimate ${\mathrm{ℛ}}_0$ for dengue fever, without this assumption of initial exponential growth. Ma, Dushoff, Bolker, and Earn (2014) use maximum likelihood to compare four commonly used phenomenological models (exponential, Richards, logistic, delayed logistic) in estimating initial growth rates of simulated epidemic models. Moreover, in a series of recent papers, Chowell and collaborators assume sub-exponential initial growth given by

$$\frac{dC\left(t\right)}{dt}=r{C}^p\left(t\right)\text{ with }r>0\text{and }0<p<1\text{;}$$

see Chowell and Viboud, 2016, Chowell et al., 2016a, Chowell et al., 2016b, Chowell et al., 2016c, and Viboud, Simonsen, and Chowell (2016). They find that the suboptimal growth model outperforms the exponential model (with $p=1$) for several infectious disease datasets, and that the effective reproduction number declines within 3–5 disease generations (rather than maintaining a constant ${\mathrm{ℛ}}_0$).

Most other methods to estimate ${\mathrm{ℛ}}_0$ require data over a longer time period or until the outbreak is over. For example, after an epidemic when the proportion of susceptibles who did not catch the disease is known (assuming that all individuals are originally susceptible), ${\mathrm{ℛ}}_0$ may be estimated from the final size equation, giving ${\mathrm{ℛ}}_0=\frac{-\text{ln}\left(s\left(\infty \right)\right)}{1-s\left(\infty \right)}$; see Section 2.1. Using standard optimization techniques, parameters in a model can be estimated from data points at successive times during an outbreak. However, this means that some time must have elapsed for sufficient data to be collected, and so gives a delay in estimating ${\mathrm{ℛ}}_0$, especially for an emerging disease. In addition, stochastic effects are important, particularly near the beginning of an outbreak. For more details on estimating ${\mathrm{ℛ}}_0$ and fitting models to data, see Chowell and Brauer (2009, Sections 8, 9), Diekmann et al. (2012, Chapter 13), and Martcheva (2015, Chapter 6).