Abstract
Emerging data suggest that the genetic regulation of the biological response to inflammatory stress may be fundamentally different to the genetic underpinning of the homeostatic control (resting state) of the same biological measures. In this paper, we interrogate this hypothesis using a single-SNP score test and a novel class-level testing strategy to characterize protein-coding gene and regulatory element-level associations with longitudinal biomarker trajectories in response to stimulus. Using the proposed class-level association score statistic for longitudinal data, which accounts for correlations induced by linkage disequilibrium, the genetic underpinnings of evoked dynamic changes in repeatedly measured biomarkers are investigated. The proposed method is applied to data on two biomarkers arising from the Genetics of Evoked Responses to Niacin and Endotoxemia study, a National Institutes of Health-sponsored investigation of the genomics of inflammatory and metabolic responses during low-grade endotoxemia. Our results suggest that the genetic basis of evoked inflammatory response is different than the genetic contributors to resting state, and several potentially novel loci are identified. A simulation study demonstrates appropriate control of type-1 error rates, relative computational efficiency, and power.
Keywords: Score test, Genome-wide association studies (GWAS), single nucleotide polymorphisms (SNPs), Long non-coding RNAs (lncRNAs), Protein coding gene-level testing, Inflammatory biomarkers, Longitudinal data analysis
1. Introduction
Advancing our knowledge of the molecular and physiological underpinnings of complex diseases will deepen insight into disease etiology while providing opportunity to develop targeted interventions and lessen disease morbidity and mortality. In this paper, we develop and evaluate a method, termed classlevel association score statistic for longitudinal data (CLASS-LD), to reveal and characterize novel regulatory and protein-coding gene (PCG)-based determinants of inflammatory biomarkers that change over time in response to stimulus. The data motivating our research arise from the Genetics of Evoked Responses to Niacin and Endotoxemia (GENE) study, a National Institutes of Health-sponsored investigation of the genomics of inflammatory and metabolic responses during low-grade endotoxemia [1–3]. The aim of this investigation is to identify PCGs and regulatory elements that impact the time-varying trajectory of inflammatory biomarkers interleukin-6 (IL-6) and C-reactive protein (CRP) in direct response to stimulus. Because activation of innate immunity is a fundamental pathophysiological process in complex cardiometabolic disease, for example, atherosclerosis and type 2 diabetes, as well as complex inflammatory disorders, for example, response to sepsis and trauma, our understanding of the genetic basis of these evoked inflammatory biomarkers in the GENE study provides clinically relevant impact toward development of novel prognostic markers and therapeutic targets in complex diseases [1, 3–7]. In the GENE study, we recently identified and replicated a genome-locus significant on chromosome 7 for the febrile response to lipopolysaccharides (LPS) and found that this chromosome 7 locus had no association with body temperature at rest in the same individuals [3]. In this paper, we further investigate, using more sophisticated analytic tools, the concept and emerging data [3, 8] that the genetic regulation of the biological and biomarker response to inflammatory stress may be fundamentally different to the genetic underpinning of the homeostatic control of the same biomarkers.
We focus our interrogation on known canonical PCGs [9–11] and well-annotated human long noncoding RNAs (lncRNAs) [12–14]; however, the methodological framework allows for interrogation of alternative taxonomies, or what we refer to generally as ‘classes’, such as gene sets annotated in the Molecular Signatures Database (MSigDB), larger emerging sets of multi-exon human lncRNAs [12–14], super-enhancer elements [15], and splicing codes. We note that the term class is similar to a single nucleotide polymorphism (SNP) set as described, for example, in [16, 17]. The aim of our proposed method is to characterize SNP-level and genomic class associations with longitudinal biomarker trajectories in response to stimulus for the setting in which classes can potentially influence an overall shift in the biomarker level as well as the rate of change in the biomarker over time. In order to accommodate the large number of highly correlated SNPs within a class, we fit separate models for each SNP, a strategy most commonly applied for cross-sectional investigations [18], and then derive the covariance structure analytically for corresponding score tests to account for the within-class linkage disequilibrium (LD) structure.
The application of mixed effects models to repeated measures data is well described [19, 20]. Moreover, methods for testing genetic association in longitudinal studies, including applications of a mixed modeling framework, are presented in a few notable publications (e.g., [21–27]). These include a twostage approximation method to address the computational burden of fitting a linear mixed effects model for analysis of single-SNP associations [24, 25]; a set-based test for genetic association with longitudinal data based on a genetic random field model [23]; linear mixed effects penalized-spline models for single and multi-allelic markers [21]; application of a linear mixed effects model to differentiate genetic and environmental contributions to the variability in longitudinal data [22]; flexible semiparametric models to account for repeated measurements nested within individuals and subjects nested within families [27]; generalized estimating equations for rare variant and gene–environment interactions using longitudinal data [26]. Finally, the sequence kernel association test uses a mixed effects model (with random SNP level effects) and a score-based statistic to analyze regional association in the cross-sectional data setting [17]. To our knowledge, combining a score-based testing strategy with a mixed effects modeling framework for repeated measures data to characterize single-SNP and class-level association has not been described. Incorporation of orthogonal polynomials in the design matrix further allows for modeling nonlinear trends and meaningful SNP by time interactions. As described in [17], while conservative, the score test only requires fitting a reduced model and is thus computationally efficient for single-SNP analysis, as we demonstrate in our simulation study.
To begin, we describe a simple modeling framework for modeling nonlinear repeated measures data, emphasizing that the proposed approach is flexible with respect to the specific choice of components for this model (Section 2.1). We then describe a score test approach for evaluating single-SNP associations (Section 2.2), define a class-based test statistic, and approximate its distribution analytically, taking into account the within-class correlation of statistics due to LD (Section 2.3). Simulation studies are presented to characterize type-1 error rates, computational efficiencies, and power (Section 3). The approach is then applied to the GENE study data in order to identify PCGs and lncRNAs that associate with inflammatory biomarker trajectories (Section 4). Finally, we offer a discussion of this testing strategy and potential further extensions (Section 5).
2. Approach
2.1. Model
Consider a general form of the linear mixed effects model [19] given by
| (1) |
where Y is of length n and represents a quantitative trait, X0 is the fixed effects design matrix for intercept, time and potentially additional covariates, Xs is the fixed effects design matrix involving the SNP data, Z is the random effects design matrix, b ~ N(0,D), , and Z ⊂ X0. Using the notation of [28], we further let and define Vλ = In + λZΩZT. The mixed effects model is a well-established and fully described modeling framework that accounts for within-individual correlations while offering flexibility for unbalanced data in the context of longitudinal data [19,29,30]. In subsequent sections, we refer to the model of Equation (1) as the full model.
We use the general framework of Equation (1) in the single-SNP score test (Section 2.2) and in the derivation of the distribution of the class-level statistic (Section 2.3) such that the specifications of X0, Xs, and Z are generic. As an example, in Section 4, we define X0 = [1n, t(1),…, t(K)] and Xs = [xs, t(1)xs,…, t(K)xs], where 1n is an n × 1 vector of 1’s, t(k) is the kth order orthogonal polynomial of time for k = 1,…,K, and xs is a vector of the number of variant alleles at SNP s (assuming a standard additive genetic model) for the individuals in the study. In this case, Xs = ΔsX0 where Δs = diag(xs). The precise form of the design matrices, including inclusion of relevant covariates and additional polynomials, can be determined for each specific outcome under study using standard modeling fitting procedures [19, 31]. A broad range of alternative model formulations within this framework are also tenable, including a piecewise linear mixed effects model [19, 32].
2.2. Score test for single-SNP association
In the model of Equation (1), the parameter γ represents the SNP association with the outcome, Y, and generally, interest is in testing H0 : γs = 0 against H1 : γs ≠ 0 without specifying β. For example, in the setting described in Section 4, in which Xs = [xs, t(1)xs,…, t(K)xs], a test of H0 : γs = 0 is an overall test of no main effect of SNP s nor any SNP s by time interactions on the response Y. This null hypothesis corresponds to the reduced model given by
| (2) |
Letting the log likelihood of the parameters be denoted l = log{L(θ)}, we have
| (3) |
The score function and information matrix are respectively given by
| (4) |
| (5) |
and
| (6) |
Defining , it follows from [33] (Section 9.3) that Σ(β, γs) is the asymptotic covariance matrix of Uγs(β, γs). The score test statistic for H0 : γs = 0 against H1 : γs ≠ 0 without specifying β is thus given by
| (7) |
where is the estimate of β under the null hypothesis. As Eβ,γs [U(β, γs)] = 0 for all β, γs, under the null hypothesis, the score test statistic, S, has a central χ2 distribution with q degrees of freedom, where q is the length of the parameter vector γs.
2.3. Class-level test of association
Within a genomic class with m SNPs, we have S = (S1, S2,…, Sm)T, a vector of m potentially correlated central χ2-statistics, each corresponding to a single-SNP score test statistic with q degrees of freedom. We define a class-level test statistic as
| (8) |
where ωj are pre-specified weights such that . In our data example of Section 4, equal weights (ωj = 1/m, for all j = 1,…,m) are applied in the absence of prior biological information regarding single SNPs and because the analysis is focused on common variants. In the simulation study of Section 3, alternative weights allowing for a greater influence of less common variants as described by Wu et al. [17] are also considered. Notably, 𝒞 can be expressed as a quadratic form, given by
| (9) |
where , for j = 1,…,m, and . Moreover, Y ~ MVN(μY, ΣY), where under the null, μY = X0β and .
Under the null hypothesis, 𝒞 is a weighted sum of correlated chi-square statistics, whose distribution is difficult to track analytically. Given that 𝒞 can be expressed as a quadratic form (as given in Equation (9)), we adopt the method in [34] to closely approximate the distribution of 𝒞 with a chi-square distribution. This computationally efficient approximation method, which searches for the distribution matching the first four moments of the quadratic form, turns out to work well in our setting in which accurate control of type-1 error rates at the 5 × 10−6 level is required. Specifically, using the result of [34] we have
| (10) |
where μχ = l + δ, , t* = (t − μ𝒞)/σ𝒞, μ𝒞 = c1, , and
| (11) |
where Ak = A(A)k−1 for k ≥ 1, A0 = I and tr[·] is the trace of a matrix. Finally, if , δ = s1a3 − a2, and l = a2 − 2δ. Otherwise, if , a = 1/s1, δ = 0, and . An estimate of ck is given by replacing μY and ΣY in Equation (11) by their estimates under the reduced model of Equation (2).
2.4. A note on approximating the distribution of 𝒞
As an alternative strategy, we could instead apply the results of [35, 36] and [37] and approximate 𝒞 by where we set E(𝒞) = E(ℛ) and Var(𝒞) = Var(ℛ). In our setting, E(𝒞) = q = E(ℛ) = aν and therefore a = q/ν and . Moreover, Var(ℛ) = a2(2ν) and thus Var(𝒞) = (q2/ν2)(2ν) = 2q2/ν. Finally, this yields
| (12) |
In order to derive the covariance, Cov(Sj, Sk) of Equation (12), we again note that we can write Sj = YTAjY and Sk = YTAkY, where Aj and Ak are as defined earlier. Under H0, E(Y) = X0 β̃, and , and therefore, using the established result for quadratic forms, we have
| (13) |
where again tr(·) is the trace of a matrix. An estimate of Cov(Sj, Sk) is given by replacing the variance components with their estimates under the reduced model of Equation (2). Finally, we estimate ν with ν̂, which is calculated by replacing Cov(Sj, Sk) of Equation (12) with its estimate.
While this approximation approach ensures the correct mean and variance of the test statistic distribution, the precision at the tail of the distribution in not well established.We evaluated this precision in our setting using a simulation study with 1 × 108 replications. Estimated type-1 error rates are 1.17 × 10−2, 1.55 × 10−3, 2.42 × 10−4, 3.4 × 10−5, and 8.0 × 10−6 at α = 1 × 10−2, 1 × 10−3, 1 × 10−4, 1 × 10−5, and 1 × 10−6, respectively. These results suggest that the type-1 error rate is relatively accurate when the α-level is large (e.g., 1 × 10−2), but the precision declines as α decreases. Importantly, this implies that this alternative approximation may be appropriate for a single candidate class analysis but is not optimal in the context of multiple testing in which precision at smaller p-values is required. The approach we describe in Section 2.3, on the other hand, offers reasonable precision up to α = 10−6 as reported in Table I. Interestingly, the approach of Section 2.3 is also computationally more efficient than this alternative strategy, as the approach of Section 2.3 does not require the extensive matrix multiplication needed to calculate the within-class pairwise covariances of the SNP-level score statistics (Equation (13)).
Table I.
Estimated type-1 error rates for SNP and class-level tests.
| SNP-level analysis§ | Type-1 error threshold (α) | ||||
|---|---|---|---|---|---|
|
|
|||||
| Total sample size (n) | 1.000 × 10−4 | 1.000 × 10−5 | 1.000 × 10−6 | 1.000 × 10−7 | 5.0 × 10−8 |
| 150 | 0.892 × 10−4 | 0.837 × 10−5 | 0.810 × 10−6 | 0.850 × 10−7 | 4.5 × 10−8 |
| 500 | 0.970 × 10−4 | 0.942 × 10−5 | 0.980 × 10−6 | 0.810 × 10−7 | 4.0 × 10−8 |
| Class-level analysis‡ | Type-1 error threshold (α) | ||||
|
|
|||||
| Total sample size (n) | 1.000 × 10−2 | 1.000 × 10−3 | 1.000 × 10−4 | 1.00 × 10−5 | 1.00 × 10−6 |
| 150 | 0.934 × 10−2 | 0.944 × 10−3 | 0.975 × 10−4 | 1.05 × 10−5 | 1.06 × 10−6 |
| 500 | 0.993 × 10−2 | 1.060 × 10−3 | 1.180 × 10−4 | 1.33 × 10−5 | 1.19 × 10−6 |
Estimated type-1 error rates for the single nucleotide polymorphism (SNP)-level analysis are based on 1 × 109 simulations of complete data (t = 0, 1, 2, 4, 6, 12) for n = 150 and 500 individuals using reduced model estimates for interleukin-6 provided in Table III.
Estimated type-1 error rates for the class-level analysis are based on 1×108 simulations of complete data (t = 0, 6, 12, 24) for n = 150 and 500 individuals using reduced model estimates for C-reactive protein provided in Table III.
3. Simulation studies
We perform simulation studies to characterize type-1 error, computational efficiency, and power. For the SNP-level test, repeated measures data at t = 0, 1, 2, 4, 6, 12 h for sample sizes of n = 150 (close to our example data sample size of n = 174) and n = 500 individuals are generated independent of genotype, using the reduced model estimates for IL-6 reported in Section 4 and Table III. Type-1 error rates for the SNP-level score test are estimated using randomly generated SNPs with minor allele frequencies ranging from 0.10 to 0.40. P-value thresholds of α = 1.0 × 10−4 to 5.0 × 10−8 are considered, and estimated error rates based on 1 × 109 simulations are provided in Table I. For the class-level analysis, we generate correlated SNPs on seven SNPs that map to the inhibitor of kappa light polypeptide gene enhancer in B-cells, kinase epsilon (IKBKE) gene identified as associated with the CRP trajectory (see Section 4 and Table V). SNPs are generated by sampling with replacement from the n = 174 individuals in our study, preserving the within-individual link to maintain the observed LD structure within IKBKE. Repeated measures data at t = 0, 6, 12, 24 h for sample sizes of n = 150 and n = 500 individuals are generated independent of genotype, using the reduced model estimates for CRP reported in Section 4 and Table III. A class-level test statistic is calculated according to Equation (8) using equal weights (ωj = 1/m, for all j = 1,…,m), and a corresponding p-value is calculated using the approximation of Equation (10). P-value thresholds of α = 1 × 10−2 to 1 × 10−6 are considered, and estimated error rates based on an additional 1 × 108 simulations are provided in Table I. These results suggest reasonable precision for our observed sample size of n = 174 individuals at the Bonferroni-corrected thresholds for both the SNP-level (p ≤ 5.0 × 10−8) and class-level (p ≤ 5 × 10−6) analyses.
Table III.
Reduced model estimates for interleukin-6 (IL-6) and C-reactive protein (CRP).
| log(IL-6)‡ | log(CRP)‡ | |||||
|---|---|---|---|---|---|---|
|
| ||||||
| Est | SE | t-value | Est | SE | t-value | |
| Fixed effects (β) | ||||||
| (Intercept) | 2.50 | 0.04 | 59.35 | 1.21 | 0.05 | 22.78 |
| poly(time, 5)1§ | −2.65 | 0.74 | −3.58 | 31.78 | 0.61 | 52.19 |
| poly(time, 5)2 | −27.11 | 0.74 | −36.67 | −10.64 | 0.61 | −17.47 |
| poly(time, 5)3 | 30.21 | 0.74 | 40.87 | −4.53 | 0.61 | −7.44 |
| poly(time, 5)4 | 7.00 | 0.74 | 9.47 | — | — | — |
| poly(time, 5)5 | −16.12 | 0.74 | −21.81 | — | — | — |
| Variance components | ||||||
| 0.22 | 0.39 | |||||
| 0.55 | 0.37 | |||||
Natural log transformation is applied to each biomarker prior to model fitting.
Orthogonal polynomials for time of degree five (for IL-6) and of degree three (for CRP) are considered as predictor variables to model each biomarker trajectory over time.
Table V.
Class level associations with IL-6 and CRP induced response
| Interleukin 6 (IL-6) | Class-level score test | SNP-level score p-value | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|||||||||||||
| Class | Chr | Start♯ | Stop♯ | 𝒞 | t̃‡ | l | δ | p-value | Min | Median | Max | minP rs§ | # SNPs |
| ENSG00000229401.1* | 6 | 10434548 | 10457014 | 38.52 | 47.40 | 11.55 | 0 | 2.81E-06 | 1.00E-04 | 2.62E-04 | 6.60E-01 | rs303064 | 7 |
| EIF3A∘ | 6 | 24544331 | 24646383 | 28.28 | 59.85 | 19.21 | 0 | 4.65E-06 | 3.58E-08 | 2.06E-02 | 9.94E-01 | rs2760166 | 27 |
| RBP3 | 10 | 48381486 | 48390991 | 44.24 | 45.74 | 10.95 | 0 | 3.46E-06 | 3.60E-07 | 6.94E-03 | 2.70E-02 | rs4922515 | 3 |
| EBF3∘,¶ | 10 | 131633495 | 131762091 | 24.69 | 87.78 | 32.18 | 0 | 4.71E-07 | 5.25E-09 | 1.80E-01 | 9.80E-01 | rs4751138 | 26 |
| MED21 | 12 | 27175454 | 27183606 | 48.73 | 41.98 | 8.61 | 0 | 2.37E-06 | 5.52E-07 | 3.47E-06 | 5.71E-01 | rs7298467 | 3 |
| PCGF2 | 17 | 36890149 | 36904561 | 53.92 | 39.36 | 7.29 | 0 | 2.21E-06 | 1.15E-07 | 7.21E-03 | 1.44E-02 | rs3785457 | 2 |
| SLC9A8∘,¶ | 20 | 48429249 | 48508779 | 41.28 | 53.94 | 12.49 | 0 | 4.15E-07 | 1.33E-08 | 4.17E-03 | 1.91E-01 | rs17786105 | 10 |
| C-reactive protein (CRP) | Class-level score test | SNP-level score p-value | |||||||||||
|
|
|||||||||||||
| Class | Chr | Start♯ | Stop♯ | 𝒞 | t̃t‡ | l | δ | p-value | Min | Median | Max | minP rs§ | # SNPs |
|
| |||||||||||||
| IKBKE¶ | 1 | 206643585 | 206670223 | 49.34 | 39.51 | 7.04 | 0 | 1.63E-06 | 5.93E-06 | 2.11E-03 | 1.14E-01 | rs4844539 | 7 |
| ENSG00000261000.1* | 1 | 206677280 | 206677789 | 80.45 | 30.23 | 4.00 | 0 | 4.40E-06 | 1.62E-06 | 9.42E-06 | 1.72E-05 | rs2871360 | 2 |
| ENSG00000224165.1* | 2 | 25194258 | 25262563 | 67.58 | 32.52 | 4.58 | 0 | 2.95E-06 | 1.77E-06 | 1.77E-06 | 6.01E-01 | rs4665750 | 16 |
| XLOC_002310*∘,¶ | 2 | 128193815 | 128228064 | 66.14 | 36.94 | 4.96 | 0 | 5.86E-07 | 4.36E-08 | 5.40E-05 | 4.71E-01 | rs11900469 | 12 |
| ENSG00000231731.3*,¶ | 2 | 128221217 | 128263373 | 59.89 | 35.71 | 5.37 | 0 | 1.62E-06 | 2.57E-07 | 5.40E-05 | 9.74E-01 | rs3889307 | 8 |
| ENSG00000272789.1* | 2 | 128383571 | 128384423 | 82.25 | 31.61 | 4.02 | 0 | 2.35E-06 | 1.78E-06 | 5.10E-06 | 8.41E-06 | rs13015157 | 2 |
| COL5A2∘,¶ | 2 | 189896640 | 190044605 | 112.49 | 56.22 | 4.46 | 0 | 3.48E-11 | 1.24E-10 | 2.02E-08 | 2.24E-06 | rs10931393 | 7 |
| XLOC_002433*,¶ | 2 | 190202502 | 190305828 | 91.57 | 35.49 | 4.03 | 0 | 3.82E-07 | 1.75E-07 | 1.75E-07 | 2.93E-05 | rs1520855 | 7 |
| WDR75¶ | 2 | 190306158 | 190340264 | 94.93 | 35.54 | 4.00 | 0 | 3.61E-07 | 1.75E-07 | 5.98E-07 | 1.02E-06 | rs13032853 | 2 |
| FAM134A | 2 | 220042938 | 220050197 | 78.80 | 30.10 | 4.01 | 0 | 4.73E-06 | 9.73E-07 | 2.23E-05 | 2.23E-05 | rs2385394 | 5 |
| TPRG1∘ | 3 | 188889762 | 189041271 | 30.44 | 57.91 | 17.04 | 0 | 2.38E-06 | 9.38E-09 | 1.87E-01 | 8.89E-01 | rs1515078 | 37 |
| ENSG00000248425.1* | 4 | 14392062 | 14395616 | 36.87 | 48.94 | 12.74 | 0 | 3.73E-06 | 1.57E-05 | 3.85E-02 | 2.24E-01 | rs2191685 | 7 |
| TCF21¶ | 6 | 134210258 | 134213393 | 64.02 | 41.16 | 5.60 | 0 | 1.74E-07 | 3.78E-07 | 3.13E-05 | 7.40E-01 | rs41286216 | 11 |
| C11orf95¶ | 11 | 63527363 | 63536113 | 100.93 | 37.42 | 4.00 | 4.21E-08 | 1.47E-07 | 1.47E-07 | 1.47E-07 | 1.47E-07 | rs2509744 | 2 |
| B3GAT1 | 11 | 134248397 | 134281812 | 34.07 | 51.13 | 14.15 | 0 | 4.39E-06 | 5.25E-07 | 3.30E-01 | 9.65E-01 | rs1866768 | 9 |
| TMEM132B¶ | 12 | 125811161 | 126143589 | 24.56 | 82.79 | 29.09 | 0 | 4.73E-07 | 1.19E-07 | 4.09E-01 | 9.99E-01 | rs7955449 | 84 |
| VASN¶ | 16 | 4421848 | 4433529 | 83.06 | 38.55 | 4.53 | 0 | 1.67E-07 | 4.46E-07 | 1.27E-05 | 2.50E-05 | rs3810818 | 2 |
| XLOC_012931*,¶ | 19 | 6656384 | 6662832 | 76.65 | 33.61 | 4.32 | 0 | 1.32E-06 | 4.89E-07 | 1.03E-04 | 2.05E-04 | rs344569 | 2 |
| CNBD2¶ | 20 | 34556528 | 34618622 | 78.90 | 33.07 | 4.11 | 0 | 1.33E-06 | 6.31E-07 | 5.79E-06 | 1.26E-04 | rs2590965 | 4 |
| ENSG00000226527.1*,¶ | 21 | 34484004 | 34496009 | 52.84 | 43.70 | 7.75 | 0 | 5.11E-07 | 8.68E-06 | 3.77E-03 | 6.56E-02 | rs11088239 | 6 |
Classes with at least two single nucleotide polymorphisms (SNPs) and a class-level score statistic p-value ≤ 5 × 10−6 are reported.
C11orf95 is also called ENSG00000188070.8 and ENSG00000224165.1 is also called XLOC_001398.
Classes additionally meeting the Bonferroni-corrected threshold of p ≤ 0.05/22, 949 = 2.18 × 10−6.
Class boundaries are extended by 5 Kb up and down stream from indicated start and stop locations in order to capture potentially associated regulatory elements.
t̃ = t* σχ + μχ.
lncRNAs while all other classes are protein-coding genes.
minP rs is the identifier for the SNP within the class with the smallest SNP-level score test p-value.
Classes that were identified as significantly associated with the corresponding biomarker based on the SNP-level score test as described in Table IV including extended boundaries (minimum SNP-level score p-value ≤ 5 × 10−8).
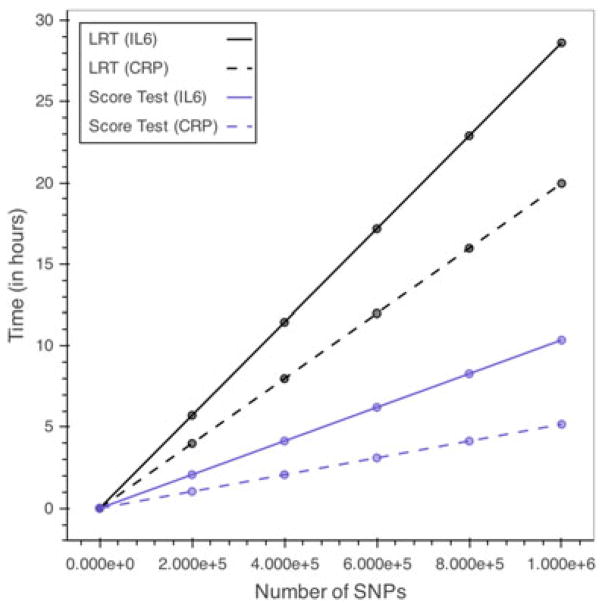
The computational performances of the single-SNP score-based test and the likelihood ratio test (LRT) are also compared through a simulation study. Complete repeated measures data on n = 150 individuals at six time points for IL-6 and three time points for CRP are simulated using the model estimates of Section 4 and Table III, and SNPs are generated with minor allele frequencies ranging from 0.10 to 0.40. The LRT is performed by fitting the full and reduced models described in Section 2.1 with the lmer() function, and models are compared with the anova() function in R. For the score test, the reduced model is fitted for the first SNP iteration, and subsequently, the score statistic is calculated in R using the formula of Equation (7). The per SNP computation is estimated on the basis of the average of 100 simulations on a MacBook pro using a single 2.5 GHz Intel Core i7 processor and then extrapolated to give the expected computation time for up to 106 SNPs. The results are illustrated in Figure 1 and suggest that the score test is approximately 2.8 times more efficient than the LRT for both the IL-6 and CRP analyses.
Figure 1.
Expected computation times for single-SNP analysis using LRT and score-based test. Estimated computation times are based on a MacBook Pro using a single 2.5 GHz Intel Core i7 processor assuming complete data on n = 150 individuals. Full and reduced models are fitted using the lmer() function of the lme4 package, and the LRT is performed using the anova() function in R version 3.3.0. The score test statistic is calculated on the basis of the formula of Equation (7). SNP, single nucleotide polymorphism; LRT, likelihood ratio test; IL-6, interleukin-6; CRP, C-reactive protein. [Colour figure can be viewed at wileyonlinelibrary.com]
Power analysis is performed to evaluate performance under example conditions that are consistent with the observed data. We select four genes as the basis for analysis, two of which are reported as significant findings in Tables IV and V based on both the single-SNP and class-level analyses (EBF3 for IL-6 and TPRG1 for CRP) and two with more moderate class-level associations, one of which has a significant single-SNP association (SLC6A7 for IL-6 with a class-level score test p-value = 6.72E-06 and minimum single-SNP score test p-value = 8.84E-06 and MREG for CRP with a class-level score test p-value 1.44E-05 and minimum single-SNP score test p-value= 4.890E-08). In addition to having a range of associations with the repeatedly measured biomarkers, these genes were chosen to demonstrate power for a variety of LD structures and numbers of SNPs per class. The observed numbers of SNPs within the class, the proportion of these SNPs with LD >0.3 with at least one other SNP within the same class, and the proportion with LD >0.6 with at least one other SNP within the same class are respectively 26, 0.46, 0.38 for EBF3; 11, 0.64, 0.36 for SLC6A7; 37, 0.68, 0.51 for TPRG1; and 22, 0.41, 0.18 for MREG. For the simulation study, complete genotype data for each of these four genes are sampled with replacement from the GENE study data, preserving the within-individual links and LD structure.
Table IV.
Single SNP associations with IL-6 and CRP induced response.
| Interleukin 6 (IL-6) | Score† | Univariate | ||||||
|---|---|---|---|---|---|---|---|---|
|
|
|
|||||||
| Class | Chr | Start♯ | Stop♯ | SNP | Stat | p-value | Baseline§ | Change‡ |
| ENSG00000248869.1* | 4 | 137717876 | 138133953 | rs13101322 | 52.731 | 1.33E-09 | 1.69E-01 | 7.18E-06 |
| rs17239822 | 53.546 | 9.11E-10 | 3.47E-01 | 2.80E-05 | ||||
| EIF3A | 6 | 24544331 | 24646383 | rs2760166 | 45.586 | 3.58E-08 | 1.60E-03 | 2.50E-03 |
| rs2744542 | 45.586 | 3.58E-08 | 1.60E-03 | 2.50E-03 | ||||
| LRRC16A | 6 | 25279655 | 25620758 | rs67394187 | 48.023 | 1.17E-08 | 2.66E-01 | 2.51E-06 |
| ENSG00000232104.2* | 9 | 3526722 | 3671646 | rs10814395 | 45.227 | 4.22E-08 | 3.25E-03 | 7.17E-04 |
| C10orf71 | 10 | 50507186 | 50535537 | rs11101093 | 44.717 | 5.33E-08 | 3.30E-01 | 1.35E-04 |
| rs11101094 | 44.717 | 5.33E-08 | 3.30E-01 | 1.35E-04 | ||||
| rs10857469 | 44.717 | 5.33E-08 | 3.30E-01 | 1.35E-04 | ||||
| EBF3 | 10 | 131633495 | 131762091 | rs10734092 | 48.245 | 1.06E-08 | 7.00E-01 | 1.63E-04 |
| rs10734091 | 48.080 | 1.14E-08 | 7.35E-01 | 1.78E-04 | ||||
| rs4751138 | 49.759 | 5.25E-09 | 3.28E-01 | 1.32E-04 | ||||
| ENSG00000226130.1* | 17 | 14629045 | 14633003 | rs9899891 | 48.376 | 9.94E-09 | 4.61E-01 | 7.12E-05 |
| SLC9A8 | 20 | 48429249 | 48508779 | rs17786105 | 47.748 | 1.33E-08 | 1.22E-01 | 3.17E-04 |
| PARVB | 22 | 44420156 | 44565112 | rs2272940 | 49.790 | 5.18E-09 | 1.15E-02 | 1.50E-02 |
| C-reactive protein (CRP) | Score† | Univariate | ||||||
|
|
|
|||||||
| Class | Chr | Start♯ | Stop♯ | SNP | Stat | p-value | Baseline§ | Change‡ |
|
| ||||||||
| NKAIN1 | 1 | 31652591 | 31712734 | rs10914330 | 41.417 | 2.20E-08 | 5.90E-01 | 5.75E-03 |
| ENSG00000232451.1* | 2 | 23240996 | 23421927 | rs17044637 | 40.732 | 3.05E-08 | 3.60E-05 | 3.99E-01 |
| rs4665538 | 40.732 | 3.05E-08 | 3.60E-05 | 3.99E-01 | ||||
| PROC | 2 | 128175995 | 128186822 | rs10928765 | 39.986 | 4.36E-08 | 2.64E-05 | 5.25E-01 |
| XLOC_002310* | 2 | 128193815 | 128228064 | rs11900469 | 39.986 | 4.36E-08 | 2.64E-05 | 5.25E-01 |
| RAB3GAP1 | 2 | 135809834 | 135928279 | rs935614 | 41.346 | 2.28E-08 | 4.66E-04 | 6.17E-01 |
| ZRANB3 | 2 | 135957573 | 136288806 | rs1463136 | 45.330 | 3.39E-09 | 6.48E-04 | 7.31E-02 |
| COL5A2 | 2 | 189896640 | 190044605 | rs13429993 | 42.826 | 1.12E-08 | 2.59E-05 | 8.29E-01 |
| rs10931393 | 52.225 | 1.24E-10 | 8.86E-07 | 8.19E-01 | ||||
| rs10195023 | 40.949 | 2.75E-08 | 3.75E-05 | 8.71E-01 | ||||
| rs10181597 | 43.895 | 6.75E-09 | 3.11E-06 | 8.80E-01 | ||||
| rs1356165 | 41.601 | 2.02E-08 | 2.79E-06 | 4.08E-01 | ||||
| MREG | 2 | 216807313 | 216878346 | rs10211101 | 39.739 | 4.90E-08 | 1.99E-03 | 4.98E-03 |
| PDIA5 | 3 | 122785855 | 122880953 | rs938392 | 40.782 | 2.98E-08 | 4.83E-06 | 7.66E-01 |
| TPRG1 | 3 | 188889762 | 189041271 | rs9848261 | 42.669 | 1.21E-08 | 3.29E-04 | 1.71E-01 |
| rs1515078 | 43.205 | 9.38E-09 | 1.44E-04 | 3.07E-01 | ||||
| rs17422816 | 42.969 | 1.05E-08 | 1.54E-04 | 3.02E-01 | ||||
| rs9867318 | 41.396 | 2.23E-08 | 1.90E-04 | 3.37E-01 | ||||
| KIAA1239 | 4 | 37246689 | 37451087 | rs6531533 | 42.311 | 1.44E-08 | 1.89E-04 | 1.36E-01 |
| ENSG00000248457.1* | 5 | 12914179 | 13032998 | rs1438297 | 41.458 | 2.16E-08 | 1.46E-04 | 2.55E-01 |
| ENSG00000189238.4* | 12 | 127210815 | 127230798 | rs4765449 | 41.018 | 2.67E-08 | 2.03E-04 | 5.24E-01 |
Single nucleotide polymorphism (SNP)-level score test is based on overall test of main effect of the SNP and the SNP by time interactions where an additive model for each SNP is assumed; that is, SNPs are coded as 0, 1, or 2 for number of minor alleles present. Corresponding reduced models are as described in Table III.
lncRNAs while all other classes are protein-coding genes.
p-value for baseline analysis corresponds to test of additive association based on a linear model for the natural log transformation of the corresponding biomarker value at t = 0.
p-value for change analysis corresponds to test of additive association based on a linear model of the natural log transformation of the difference in biomarker response between baseline (t = 0) and peak, corresponding to 2 h for interleukin-6 (IL-6) and 24 h for C-reactive protein (CRP).
Class boundaries are extended by 5 Kb up and down stream from indicated start and stop locations in order to capture potentially associated regulatory elements.
Next, we simulate repeatedly measured biomarker responses under a collection of alternatives. Because of the high degree of collinearity among SNPs within a gene, we first apply an LD pruning strategy [38] to fit full models and obtain data-driven parameter estimates. We note that our proposed strategy as described in Section 2.3 only requires fitting the null model thus overcoming the challenges inherent with the presence of high within-class LD; however, for the purpose of simulating realistic biomarker trajectories, we need to fit a full model involving multiple SNP signals within a class. The LD pruning approach involves iteratively retaining the strongest signal SNP (smallest p-value based on a score test of SNP and SNP by time interactions) and eliminating all remaining SNPs within the class that have a pairwise LD of ≥ 0.3with this strongest signal SNP. The process is repeated until all SNPs have a pairwise LD < 0.3. After LD pruning, we have a subset of quasi-independent SNPs for each gene, totaling 15 out of the original 26 for EBF3; 5 of 11 for SLC6A7; 14 of 37 for TPRG; and 1 and 14 of 22 for MREG.
Models of association, under which biomarker response data are simulated, are listed in Table II, and include (a) a model with main effects of SNPs and linear time; (b) a model with main effects of SNPs and orthogonal polynomials for time. Here, five polynomials for IL-6 and three for CRP are used to be consistent with the example of Section 4. (c) a model with interactions between SNPs and linear time. The natural logarithm of IL-6 and CRP are both simulated according to these models. In each case, a mixed effects model with random individual-level intercepts are fitted to the GENE study data to arrive a parameter estimates. As one example, model (a) for IL-6 based on the SLC6A7 gene includes main effects for five SNPs and a linear time component. The fitted model based on the GENE study data is ŷ = 2.379 − 0.020 * time + 0.010x1 + 0.148x2 + 0.024x3 + 0.050x4 + 0.027x5, where x1,…, x5 correspond to the five SNPs in SLC6A7 after LD pruning. Simulated response trajectories based on this model include random person-specific effects and random measurement errors, which are assumed to arise from independent normal distributions.
Under each condition, 1000 simulations are conducted and power is defined as the proportion of these that correctly results in detecting a class-level association. In each scenario, we report power assuming the same model of association (e.g., linear versus nonlinear time trend) used to generate the data. While this can result in higher power estimates than if an incorrect model were specified, we assume that appropriate model fitting techniques are applied a priori as we do in the example of Section 4. For comparison, power is also reported for the minP SNP-level score test approach and the minP univariate approach based on the change from baseline to peak, corresponding to 2 h for IL-6 and 24 h for CRP. Details of these alternative approaches are given in Section 4. Bonferroni adjustments are applied for the minP approaches according to the number of SNPs within the class. Finally, three sets of weights are considered for the class-level test of association: (1) ωj = 1/m for all j = 1,…,m; (2) ; and (3) , where m is the number of SNPs in the class. In case (1), we apply equal weights, as carried out in the example of Section 4. The two alternatives are suggested by Wu et al. [17], where we additionally scale the weights to sum to 1 within a class. In case (2), we are weighting by the inverse of the variance of the SNP, given by 1/MAFj(1−MAFj). This results in slightly higher weights for the less common variants. Finally, case (3) up weights rare variants and down weights more common variants. Because we do not have rare variants (MAFj ≥ 0.01 for all j), scheme (2) does not result in the extreme weighting described in [17], and we expect scheme (3) to result in lower power.
The power results are provided in Table II and, as expected, suggest that the class-level score test yields a range of powers depending on the underlying model of association, the within-class LD structure, the number of SNPs, and the sample size (n). Assuming equal weights and a sample size of n = 150, the power for the class-level test ranged from 30.0% for MREG with CRP as the outcome assuming model (a) to a maximum of 95.8% also for MREG with CRP as the outcome, assuming model (c). In all cases, the minP score had lower power, ranging from 18.3% to 87.2% for a sample size of n = 150, and power for the change analysis is substantially smaller. The choice of weights also dramatically impacts power with drastically lower power observed for the extreme choice of weights of scheme (3). This result is expected as these data do not include rare variants, and the lower frequency variants, which obtain a relatively large proportion of the weight, are not necessarily the drivers of association. For example, under weighting scheme (3) and model (a), rs451139 in EBF3 (MAFj = 0.12) has a corresponding ωj = 0.82 and a model coefficient βj = −0.060, while rs451138 (MAFj = 0.36) has a corresponding ωj = 1.8 × 10−7 and a model coefficient βj = 0.231 (the largest effect of all SNPs within this gene). Thus, while the influence of rs451138 is substantial in the true model, the contribution of this SNP to the overall score test is practically 0. On the other hand, under weighting scheme (2), the corresponding weights are ωj = 0.071 and ωj = 0.033 for rs451139 and rs451138, respectively, which is consistent with the relatively high power for weighting scheme (2) compared with (3) −79.2% vs. 29.2% power for a sample size of n = 150. The difference in power between weighting schemes (1) and (2) is relatively small, and without prior information to suggest that less frequent variants are more influential, we elect to use equal weights in the example of Section 4. Finally, we note that the estimated type-1 error rate of the class-level score test for the four genes and two outcomes (eight combinations), assuming a model with polynomials for time and no SNP-level effect, averaged 0.050, 0.048, and 0.047 for weighting schemes (1), (2), and (3), respectively.
Table II.
Estimated power§ under a range of observed data conditions.
| Interleukin 6 (IL-6) | Class-level score test (alternative specifications of ωj)▽
|
||||||
|---|---|---|---|---|---|---|---|
| Data generating model* | Gene | n | (1) | (2) | (3) | minP score♯ | Change‡ |
| (a) SNPs + time | SLC6A7 | 150 | 0.489 | 0.440 | 0.105 | 0.377 | 0.140 |
| 300 | 0.771 | 0.772 | 0.169 | 0.690 | 0.005 | ||
| EBF3 | 150 | 0.779 | 0.792 | 0.292 | 0.526 | 0.079 | |
| 300 | 0.984 | 0.989 | 0.524 | 0.923 | 0.093 | ||
| (b) SNPs + poly(time, 5) | SLC6A7 | 150 | 0.640 | 0.606 | 0.175 | 0.545 | 0.208 |
| 300 | 0.913 | 0.916 | 0.245 | 0.869 | 0.441 | ||
| EBF3 | 150 | 0.933 | 0.933 | 0.447 | 0.789 | 0.316 | |
| 300 | 1.000 | 1.000 | 0.743 | 0.995 | 0.678 | ||
| (c) SNPs + time + SNPs * time | SLC6A7 | 150 | 0.430 | 0.349 | 0.115 | 0.297 | 0.021 |
| 300 | 0.721 | 0.685 | 0.186 | 0.586 | 0.017 | ||
| EBF3 | 150 | 0.673 | 0.639 | 0.213 | 0.417 | 0.095 | |
| 300 | 0.970 | 0.977 | 0.441 | 0.843 | 0.087 | ||
| C-reactive protein (CRP) | Class-level score test (alternative specifications of ωj)▽
|
||||||
| Data generating model* | Gene | n | (1) | (2) | (3) | minP score♯ | Change‡ |
|
| |||||||
| (a) SNPs + time | MREG | 150 | 0.300 | 0.358 | 0.146 | 0.258 | 0.13 |
| 300 | 0.741 | 0.725 | 0.272 | 0.681 | 0.291 | ||
| TPRG1 | 150 | 0.380 | 0.386 | 0.222 | 0.183 | 0.105 | |
| 300 | 0.732 | 0.704 | 0.386 | 0.479 | 0.183 | ||
| (b) SNPs + poly(time, 3) | MREG | 150 | 0.358 | 0.335 | 0.145 | 0.289 | 0.191 |
| 300 | 0.713 | 0.747 | 0.259 | 0.650 | 0.398 | ||
| TPRG1 | 150 | 0.379 | 0.349 | 0.196 | 0.188 | 0.132 | |
| 300 | 0.720 | 0.680 | 0.358 | 0.453 | 0.278 | ||
| (c) SNPs + time + SNPs * time | MREG | 150 | 0.958 | 0.965 | 0.538 | 0.872 | 0.502 |
| 300 | 1.000 | 1.000 | 0.884 | 0.999 | 0.863 | ||
| TPRG1 | 150 | 0.949 | 0.930 | 0.442 | 0.823 | 0.159 | |
| 300 | 0.999 | 0.999 | 0.759 | 0.996 | 0.331 | ||
Power is defined as the proportion of 1000 simulations for which we correctly reject the null hypothesis.
Weights are defined as follows: (1) ωj = 1/m; (2) ; and (3) , where m is the number of single nucleotide polymorphisms (SNPs) within the corresponding class.
Mixed effects models with person-specific intercept terms are used to generate repeated natural log biomarker response data.
Power for minP score corresponds to the proportion of minimum p-values of SNP-level score tests within the class that are significant after applying a Bonferroni adjustment for the number of SNPs within the class.
Power for the change analysis corresponds to the proportion of significant tests of additive association, after a Bonferroni adjustment for the number of SNPs within the class, based on a linear model of the natural log transformation of the difference in biomarker response between baseline (t = 0) and peak, corresponding to 2 h for interleukin-6 (IL-6) and 24 h for C-reactive protein (CRP).
4. Example: genetics of inflammatory response to stimulus
As mentioned in Section 1, the data motivating our research arise from the GENE study, a National Institutes of Health-sponsored investigation of the genomics of inflammatory and metabolic responses during low-grade endotoxemia [1–3]. Eligible participants (n = 294) participated in five separate visits, including three outpatient visits and two inpatient visits that addressed separate hypotheses: (i) an endotoxin challenge visit (1 ng/kg Escherichia coli-derived LPS) (GENE-LPS) and (ii) a niacin challenge visit (GENE-niacin). Findings from the GENE-LPS component are the focus of our present investigation. The GENE inpatient LPS visit lasted approximately 40 h, with a 10-h overnight acclimatization phase and a 30-h post-LPS phase, as described [1–3]. Multiple clinical variables were assessed regularly during the visit, including temperature and serial blood draws (−15 and −5 min and 1, 2, 4, 6, 12, 18, and 24 h post LPS) and subsequent measurement of levels of tumor necrosis factor alpha, IL-6, interleukin-1 receptor agonist, serum amyloid A, and high-sensitivity CRP. Herein, we are interested in testing the single-SNP and genomic class modulation of the response trajectories for each of the two inflammatory biomarkers, IL-6 and CRP. We focus our interrogation on the large subgroup of Caucasians (n = 174) as genotypes, and response patterns are expected to differ across race and ethnicity [3].
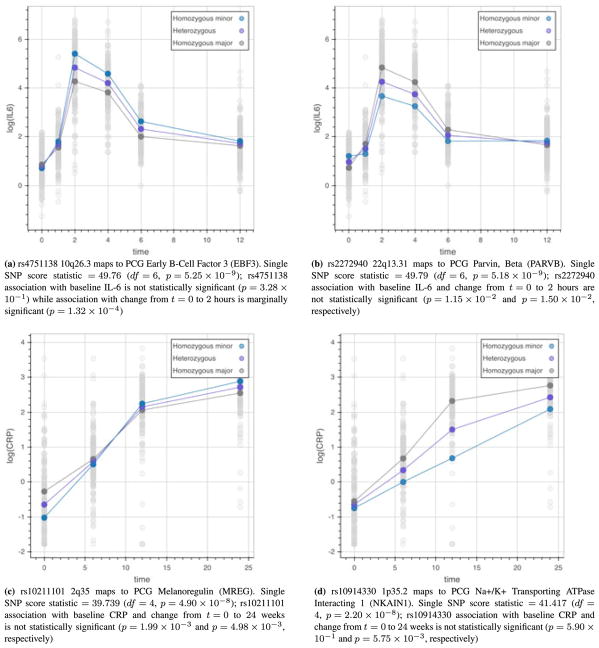
After acute stimulation with LPS, we generally see two nonlinear trends over time, as illustrated in Figure 2 for two exemplar biomarkers, IL-6 [Figure 2(a) and (b)] and CRP [Figure 2(c) and (d)]. Tumor necrosis factor alpha and interleukin-1 receptor agonist (not shown) behave similar to IL-6, while serum amyloid A (not shown) follows a trend similar to CRP. Standard model fitting procedures were applied, resulting in a model for IL-6 with five polynomials for time and a model for CRP with three polynomials for time. Both models include a random person-specific intercept term ( ). The resulting parameter estimates, standard errors, and t-values are provided in Table III.
Figure 2.
Sample time-varying interleukin-6 (IL-6) and C-reactive protein (CRP) trajectories by genotype. Non-linear trends in IL-6 and CRP over time are modified by single nucleotide polymorphisms (SNPs); these modifications vary across SNPs, and SNPs influencing the trajectories differ from those impacting resting state. [Colour figure can be viewed at wileyonlinelibrary.com]
The SNP-level score-based test is applied to 353,561 filtered SNPs mapping to 28,496 classes (16,416 PCGs and 12,080 lncRNAs) to test for association with IL-6 and CRP. For this analysis, we extended the upstream and downstream boundaries of the classes by 5Kb in order to capture any potentially associated strong promoter and 3′ untranslated region (UTR) regulatory regions and considered SNPs with complete data. A Bonferroni-corrected threshold of 5 × 10−8 based on one million independent signals on the genome is used to determine statistical significance. P-value precision at this small threshold value is evaluated through simulation studies in Section 3. For each SNP, a single overall test for the SNP main effect and interactions of the SNP with orthogonal polynomials for time is calculated and reported. Fifth-order polynomials for time are considered for IL-6 analysis (six observed time points), and third-order polynomials for time are considered in the CRP analysis (four observed time points). A total of 15 SNPs across three lncRNAs and six PCGs were identified as associated with IL-6 and 21 SNPs across four lncRNAs, and nine PCGs were identified as associated with CRP, as listed in Table IV. Sample estimated IL-6 and CRP response trajectories by genotype based on the corresponding full models are provided in Figure 2.
Interestingly, the majority of SNPs identified as associated with IL-6 and CRP trajectories are not statistically associated with resting state (p-values indicated in the second to last columns of Table IV). Indeed, among all detected SNPs for the biomarker trajectories (p < 5×10−8), only three SNPs within the collagen, type V, alpha 2 (COL5A2) gene (rs10931393, p = 8.86 × 10−7; rs10181597, p = 3.11 × 10−6; and rs1356165, p = 2.79 × 10−6) and one SNP in the protein disulfide isomerase family A, member 5 (PDIA5) gene (rs938392, p = 4.83 × 10−6) appear potentially associated with CRP at baseline with a liberal threshold of < 5 × 10−6, and no SNPs appear to be statistically associated with baseline IL-6 values. The COL5A2 SNP rs10931393 is also the strongest resting state signal for CRP. On the other hand, the strongest resting state signal for IL-6 is rs7331544 mapping to PCG microtubule associated tumor suppressor candidate 2 (MTUS2) (p = 1.29 × 10−6), which is not statistically associated with the IL-6 trajectory (SNP-level score = 15.499, df = 6, p = 1.67×10−2). In addition to a striking complement to the knowledge extracted from baseline analysis, applying a score test with polynomial regression modeling of the biomarker trajectories also identified genetic loci for the response to inflammatory stress not found by simply analyzing change in biomarker from baseline to peak (p-values indicated in the last column of Table IV). Thus, the application of appropriate modeling strategies appears to be critical to derive the optimal clinical and biological inference.
For the IL-6 response, in addition to several novel lncRNAs, the findings include loci with promising protein coding candidates involved in cytoskeletal and cell adhesion functions (leucine-rich repeat-containing 16A – LRRC16A, parvin beta – PARVB, eukaryotic translation initiation factor 3 subunit A – EIF3A), tumor suppression (early B-cell factor 3 – EBF3), and solute exchange (solute carrier family 9 member A8 – SLC9A8). For example, LRRC16A at chromosome 6 regulates capping protein, a critical determinant of actin assembly and actin-based cell motility and has been implicated recently in platelet formation and the platelet-dependent inflammatory pathophysiology of adult respiratory distress syndrome [39]. For CRP, several lncRNA loci were identified in addition to signals that overlap novel protein coding candidates for inflammatory response. For example, COL5A2, which encodes an alpha chain for one of the low abundance fibrillar collagens that is causal in Ehlers–Danlos syndrome, was recently implicated through whole-exome sequencing in the autoimmune disorder systemic sclerosis [40].
The results of our class-level interrogation of PCGs and lncRNA associations with IL-6 and CRP are highlighted in Table V. This analysis is based on the 22,949 classes (13,664 PCGs and 9285 lncRNAs) with at least two SNPs and assumes equal weights (ωj = 1, ∀j) across SNPs. All classes with p ≤ 5×10−6 are included in Table V. We apply a threshold that is larger than the Bonferroni-corrected threshold of p ≤ 0.05/22949 = 2.18 × 10−6 in order to additionally report suggestive results in this relatively small sample size setting. In total, the class-level approach identified 7 suggestive classes (six PCGs and one lncRNA) for IL-6 and 20 classes (11 PCGs and 9 lncRNAs) for CRP. Several identified loci are common to the individual SNP analysis, for example, EBF3 and SLC9A8 for IL-6 trajectories, yet the class-level analysis appears to uncover many additional associations for IL-6 and CRP responses not identified through single-SNP interrogation.
For IL-6 responses, for example, polycomb group gene transcription repression (polycomb group RING finger 2 – PCGF2) [41] and novel innate immune scavenger receptors (scavenger receptor cysteine-rich family, 5 domains – SSC5D) [42] both have evidence to support candidacy in modulating proteomic responses in response to LPS-induced inflammatory stress and in inflammatory disorders. Similarly, for CRP trajectories, multiple lincRNA and PCG loci have been uniquely identified via class-level testing, including, for example, I-kappa-B signaling (IKBKE) [43] and glycotransferases (beta-1, 3-glucuronyltransferase 1 – B3GAT1) [44], which have evidence for actions in immune and inflammatory response. In addition to classes with prior and consistent evidence of association, both the single-SNP and class-level testing revealed multiple novel loci and pathways, previously not prioritized for mechanistic and translational study in acute and chronic inflammatory disease, yet warranting further interrogation.
Finally, we additionally applied a class-level analysis to the baseline level of each biomarker using Genetic Class Association Testing [45], which, similar to the class-level test described herein, combines SNP-level tests of association in a manner that accounts for within-class LD structure but is limited to cross-sectional analysis. Considering the same 22,949 PCGs and lncRNAs, this analysis yielded no findings for baseline IL-6 and one finding for CRP (COL5A2, Cs = 30.0, p = 1.36×10−6) based on a p ≤ 5 × 10−6 threshold. Consistent with single-SNP analyses, we identify many more significant class-level associations for the LPS-induced biomarker trajectories than for the baseline level of the same biomarker. Finally, we note that there is no overlap of our findings for LPS-evoked inflammatory trajectories in plasma IL-6 and CRP with findings for published large-scale population-based genetic association studies of resting levels of plasma IL-6 and CRP with the one exception that EBF3 is potentially in the same locus as Janus kinase and microtubule interacting protein 3 (JAKMP3), which has been reported previously as associated with IL-6 [46].
5. Discussion
In this paper, we describe an SNP and class-level score-based test for evaluating genetic association with nonlinear time-varying biomarker responses. One attractive feature of our proposed class-level test is that it allows efficient computation of p-values (without the need for permutation, etc.). The simulation study showed that the p-values for class-level tests are accurate when the sample size is moderate or large. Biologically, the findings from this analysis are significant as they reveal distinct and substantially more genomic loci associated with change in IL-6 and CRP response to LPS relative to resting state levels of the same biomarker at baseline. Indeed, in this sample, which is small for genetic studies of resting biomarkers, there are multiple significant findings for biomarker responses but no genome-wide statistically significant SNP-level associations and only one class-level association with baseline level of either biomarker. These findings may be relevant to acute and chronic inflammatory disease driven by genetic regulation of dynamic rather than static inflammatory programs. Although our class-based findings for biomarker trajectories require additional genomic and functional validations as candidates for inflammatory diseases, many promising new lncRNA and PCG loci have been identified for further interrogation.
We also demonstrate the computational advantages of the SNP-level score test relative to the LRT at the genome-wide level. The class-level analysis maintains the same advantage over the LRT of not requiring fitting models under the alternative. Moreover, estimating the distribution of the class-level statistic as described in Section 2.3 is computationally efficient as direct estimation of pairwise correlations of within-class test statistics is not required. The class-level analysis was performed on the Massachusetts Green High Performance Computing Cluster and took approximately 5 h to run across 2000 cores for CRP with 22,949 classes of size 2 to a maximum of 1036 SNPs (median = 6, IQR = 3–12). As the number of SNPs in a class contributes considerably to the computation time, through increasing the dimensions of Xs, Aj, and Bj, one alternative strategy is to apply a first stage LD pruning strategy [18, 38]. For example, pruning could be applied genome-wide using a moving window or within-individual classes so that the class-level analysis is limited to SNPs with LD ≤ 0.30. The class-level test as described would then still account for residual correlations that could exist between SNP-level score statistics while reducing the computational burden. The disadvantage of LD pruning is the potentially substantial loss of information resulting from eliminating SNPs with moderate LD, and thus, a careful balance must be achieved in the trade-off between computational efficiency and maintaining meaningful data.
Finally, we emphasize the overall versatility of the CLASS-LD approach described herein. Another of the important features of this approach is that the class-level score test does not depend on whether the pattern of association is the same for all SNPs within a class. For example, the major allele of one SNP and the minor allele of another SNP within the same class may both contribute to the response over time, and/or one SNP may influence the overall shift in the biomarker response, while another SNP influences the early or late stage change over time in the response. In all of these scenarios, the class-level statistic is capturing the degree of statistical significance, and differences in the precise pattern of association do not negatively impact the ability to detect overall associations. Additionally, while this paper is not focused on rare variant analysis, the advantage of a score test approach for rare variant analysis has been described previously for regional association in the cross-sectional setting [17], and further investigation of the versatility of CLASS-LD for rare variant analysis is warranted. The moderate number of findings that are statistically significant after conservative correction for multiple testing, with a relatively small sample size of n = 174 individuals, suggest reasonable power for identifying associations. This is further supported by our power analysis results. Finally, we emphasize that this approach is relatively simple to implement using existing R tools, and the linear mixed modeling framework is a natural and established setting for analysis of longitudinal data. Thus, implementation of alternative model formulations, for example, a piecewise linear change point model or inclusion of additional polynomials for time, is relatively straightforward. All coding scripts for the examples and simulation study are available upon request.
Acknowledgments
Support for this research was provided by NHLBI R01-HL107196 (J. Q., S. N., M. P. R., and A. S. F.), K24-HL107643 (M. P. R.), and R01-HL113147 (M. P. R.). Simulation studies and genome-wide analysis were performed using the Massachusetts Green High Performance Computing Center (MGHPCC) in Holyoke, MA.
References
- 1.Ferguson JF, Patel PN, Shah RY, Mulvey CK, Gadi R, Nijjar PS, Usman HM, Mehta NN, Shah R, Master SR, Propert KJ, Reilly MP. Race and gender variation in response to evoked inflammation. Journal of Translational Medicine. 2013;11:63. doi: 10.1186/1479-5876-11-63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ferguson JF, Ryan MF, Gibney ER, Brennan L, Roche HM, Reilly MP. Dietary isoflavone intake is associated with evoked responses to inflammatory cardiometabolic stimuli and improved glucose homeostasis in healthy volunteers. Nutrition, Metabolism & Cardiovascular Diseases. 2014;24(9):996–1003. doi: 10.1016/j.numecd.2014.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ferguson JF, Meyer NJ, Qu L, Xue C, Liu Y, DerOhannessian SL, Rushefski M, Paschos GK, Tang S, Schadt EE, Li M, Christie JD, Reilly MP. Integrative genomics identifies 7p11.2 as a novel locus for fever and clinical stress response in humans. Human Molecular Genetics. 2015 Mar;24(6):1801–1812. doi: 10.1093/hmg/ddu589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mehta NN, McGillicuddy FC, Anderson PD, Hinkle CC, Shah R, Pruscino L, Tabita-Martinez J, Sellers KF, Rickels MR, Reilly MP. Experimental endotoxemia induces adipose inflammation and insulin resistance in humans. Diabetes. 2010;59(1):172–181. doi: 10.2337/db09-0367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.de la Llera Moya M, McGillicuddy FC, Hinkle CC, Byrne M, Joshi MR, Nguyen V, Tabita-Martinez J, Wolfe ML, Badellino K, Pruscino L, Mehta NN, Asztalos BF, Reilly MP. Inflammation modulates human HDL composition and function in vivo. Atherosclerosis. 2012 Jun;222(2):390–394. doi: 10.1016/j.atherosclerosis.2012.02.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Meyer NJ, Ferguson JF, Feng R, Wang F, Patel PN, Li M, Xue C, Qu L, Liu Y, Boyd JH, Russell JA, Christie JD, Walley KR, Reilly MP. A functional synonymous coding variant in the IL1RN gene is associated with survival in septic shock. American Journal of Respiratory and Critical Care Medicine. 2014;190(6):656–664. doi: 10.1164/rccm.201403-0586OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Walley KR, Thain KR, Russell JA, Reilly MP, Meyer NJ, Ferguson JF, Christie JD, Nakada TA, Fjell CD, Thair SA, Cirstea MS, Boyd JH. PCSK9 is a critical regulator of the innate immune response and septic shock outcome. Science Translational Medicine. 2014;6(258):258ra143. doi: 10.1126/scitranslmed.3008782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Franco LM, Bucasas KL, Wells JM, Nino D, Wang X, Zapata GE, Arden N, Renwick A, Yu P, Quarles JM, Bray MS, Couch RB, Belmont JW, Shaw CA. Integrative genomic analysis of the human immune response to influenza vaccination. Elife. 2013;2:e00299. doi: 10.7554/eLife.00299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hsu F, Kent WJ, Clawson H, Kuhn RM, Diekhans M, Haussler D. The UCSC known genes. Bioinformatics. 2006;22(9):1036–1046. doi: 10.1093/bioinformatics/btl048. [DOI] [PubMed] [Google Scholar]
- 10.Karolchik D, Barber GP, Casper J, Clawson H, Cline MS, Diekhans M, Dreszer TR, Fujita PA, Guruvadoo L, Haeussler M, Harte RA, Heitner S, Hinrichs AS, Learned K, Lee BT, Li CH, Raney BJ, Rhead B, Rosenbloom KR, Sloan CA, Speir ML, Zweig AS, Haussler D, Kuhn RM, Kent WJ. The UCSC genome browser database: 2014 update. Nucleic Acids Research. 2014;42(Database issue):D764–770. doi: 10.1093/nar/gkt1168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Subramanian A, Tamayo P, Mootha VK, Mukherjee S, Ebert BL, Gillette MA, Paulovich A, Pomeroy SL, Golub TR, Lander ES, Mesirov JP. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proceedings of the National Academy of Sciences of the United State of America. 2005;102:15545–15550. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mattick JS, Rinn JL. Discovery and annotation of long noncoding RNAs. Nature Structural & Molecular Biology. 2015;22(1):5–7. doi: 10.1038/nsmb.2942. [DOI] [PubMed] [Google Scholar]
- 13.Derrien T, Johnson R, Bussotti G, Tanzer A, Djebali S, Tilgner H, Guernec G, Martin D, Merkel A, Knowles DG, Lagarde J, Veeravalli L, Ruan X, Ruan Y, Lassmann T, Carninci P, Brown JB, Lipovich L, Gonzalez JM, Thomas M, Davis CA, Shiekhattar R, Gingeras TR, Hubbard TJ, Notredame C, Harrow J, Guigó R. The GENCODE v7 catalog of human long noncoding RNAs: analysis of their gene structure, evolution, and expression. Genome Research. 2012;22(9):1775–1789. doi: 10.1101/gr.132159.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hangauer MJ, Vaughn IW, McManus MT. Pervasive transcription of the human genome produces thousands of previously unidentified long intergenic noncoding RNAs. PLOS Genetics. 2013;9(6):e1003569. doi: 10.1371/journal.pgen.1003569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hnisz D, Abraham BJ, Lee TI, Lau A, Saint-Andre V, Sigova AA, Hoke HA, Young RA. Super-enhancers in the control of cell identity and disease. Cell. 2013;155(4):934–947. doi: 10.1016/j.cell.2013.09.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lin X, Lee S, Christiani DC, Lin X. Test for interactions between a genetic marker set and environment in generalized linear models. Biostatistics. 2013;14(4):667–681. doi: 10.1093/biostatistics/kxt006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wu MC, Lee S, Cai T, Li Y, Boehnke M, Lin X. Rare-variant association testing for sequencing data with the sequence kernel association test. The American Journal of Human Genetics. 2011;89(1):82–93. doi: 10.1016/j.ajhg.2011.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Reed E, Nunez S, Kulp D, Qian J, Reilly MP, Foulkes AS. A guide to genome-wide association analysis and post-analytic interrogation. Statistics in Medicine. 2015;34(28):3769–3792. doi: 10.1002/sim.6605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fitzmaurice GM, Laird NM, Ware JH. Applied Longitudinal Analysis. John Wiley & Sons; Hoboken: 2004. [Google Scholar]
- 20.Verbeke G, Molenberghs G. Linear Mixed Models for Longitudinal Data. Springer; New York: 2000. [Google Scholar]
- 21.Fan R, Zhang Y, Albert PS, Liu A, Wang Y, Xiong M. Longitudinal association analysis of quantitative traits. Genetic Epidemiology. 2012;36(8):856–869. doi: 10.1002/gepi.21673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Furlotte NA, Eskin E, Eyheramendy S. Genome-wide association mapping with longitudinal data. Genetic Epidemiology. 2012;36(5):463–471. doi: 10.1002/gepi.21640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.He Z, Zhang M, Lee S, Smith JA, Guo X, Palmas W, Kardia SL, Diez Roux AV, Mukherjee B. Set-based tests for genetic association in longitudinal studies. Biometrics. 2015;71(3):606–615. doi: 10.1111/biom.12310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sikorska K, Rivadeneira F, Groenen PJ, Hofman A, Uitterlinden AG, Eilers PH, Lesaffre E. Fast linear mixed model computations for genome-wide association studies with longitudinal data. Statistics in Medicine. 2013;32(1):165–180. doi: 10.1002/sim.5517. [DOI] [PubMed] [Google Scholar]
- 25.Sikorska K, Montazeri NM, Uitterlinden A, Rivadeneira F, Eilers PH, Lesaffre E. GWAS with longitudinal phenotypes: performance of approximate procedures. European Journal of Human Genetics. 2015;23(10):1384–1391. doi: 10.1038/ejhg.2015.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sitlani CM, Rice KM, Lumley T, McKnight B, Cupples LA, Avery CL, Noordam R, Stricker BH, Whitsel EA, Psaty BM. Generalized estimating equations for genome-wide association studies using longitudinal phenotype data. Statistics in Medicine. 2015;34(1):118–130. doi: 10.1002/sim.6323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wang Y, Huang C, Fang Y, Yang Q, Li R. Flexible semiparametric analysis of longitudinal genetic studies by reduced rank smoothing. Journal of the Royal Statistical Society: Series C (Applied Statistics) 2012;61(1):1–24. doi: 10.1111/j.1467-9876.2011.01016.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Crainiceanu CM, Ruppert D. Likelihood ratio tests in linear mixed models with one variance component. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2004;66(1):165–185. [Google Scholar]
- 29.Verbeke G, Molenberghs G. Linear Mixed Models for Longitudinal Data. Springer-Verlag Inc; 2000. [Google Scholar]
- 30.McCulloch CE, Searle SR. Generalized, Linear, and Mixed Models. John Wiley & Sons; Hoboken: 2001. [Google Scholar]
- 31.Herrell F. Regression Modeling Strategies:With Applications to Linear Models, Logistic Regression, and Survival Analysis. Cham: 2001. Springer Series in Statistics. [Google Scholar]
- 32.Naumova EN, Must A, Laird NM. Tutorial in biostatistics: evaluating the impact of ‘critical periods’ in longitudinal studies of growth using piecewise mixed effects models. International Journal of Epidemiology. 2001;30(6):1332–1341. doi: 10.1093/ije/30.6.1332. [DOI] [PubMed] [Google Scholar]
- 33.Cox DR, Hinkley DV. Theoretical Statistics. Chapman & Hall/CRC; London: 1974. [Google Scholar]
- 34.Liu H, Tang Y, Zhang HH. A new chi-square approximation to the distribution of non-negative definite quadratic forms in non-central normal variables. Computational Statistics & Data Analysis. 2009;53(4):853–856. [Google Scholar]
- 35.Makambi K. Weighted inverse chi-square method for correlated significance tests. Journal of Applied Statistics. 2003;30(2):225–234. [Google Scholar]
- 36.Brown MB. 400: a method for combining non-independent, one-sided tests of significance. Biometrics. 1975;31(4):987–992. [Google Scholar]
- 37.Chuang L-L, Shih Y-S. Approximated distributions of the weighted sum of correlated chi-squared random variables. Journal of Statistical Planning and Inference. 2012;142(2):457–472. [Google Scholar]
- 38.Laurie CC, Doheny KF, Mirel DB, Pugh EW, Bierut LJ, Bhangale T, Boehm F, Caporaso NE, Cornelis MC, Edenberg HJ, Gabriel SB, Harris EL, Hu FB, Jacobs KB, Kraft P, Landi MT, Lumley T, Manolio TA, McHugh C, Painter I, Paschall J, Rice JP, Rice KM, Zheng X, Weir BS GENEVA Investigators. Quality control and quality assurance in genotypic data for genome-wide association studies. Genetic Epidemiology. 2010;34(6):591–602. doi: 10.1002/gepi.20516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wei Y, Wang Z, Su L, Chen F, Tejera P, Bajwa EK, Wurfel MM, Lin X, Christiani DC. Platelet count mediates the contribution of a genetic variant in LRRC16A to ARDS risk. Chest. 2015;147(3):607–617. doi: 10.1378/chest.14-1246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mak AC, Tang PL, Cleveland C, Smith MH, Connolly MK, Katsumoto TR, Wolters PJ, Kwok PY, Criswell LA. Whole exome sequencing for identification of potential causal variants for diffuse cutaneous systemic sclerosis. Arthritis Rheumatol. 2016;68(9):2257–2262. doi: 10.1002/art.39721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Morey L, Santanach A, Blanco E, Aloia L, Nora EP, Bruneau BG, Di Croce L. Polycomb regulates mesoderm cell fate-specification in embryonic stem cells through activation and repression mechanisms. Cell Stem Cell. 2015;17(3):300–315. doi: 10.1016/j.stem.2015.08.009. [DOI] [PubMed] [Google Scholar]
- 42.Miro-Julia C, Escoda-Ferran C, Carrasco E, Moeller JB, Vadekaer DF, Gao X, Paragas N, Oliver J, Holmskov U, Al-Awqati Q, Lozano F. Expression of the innate defense receptor S5D-SRCRB in the urogenital tract. Tissue Antigens. 2014;83(4):273–285. doi: 10.1111/tan.12330. [DOI] [PubMed] [Google Scholar]
- 43.Sacre SM, Andreakos E, Feldmann M, Foxwell BM. Endotoxin signaling in human macrophages: signaling via an alternate mechanism. Journal of Endotoxin Research. 2004;10(6):445–452. doi: 10.1179/096805104225005878. [DOI] [PubMed] [Google Scholar]
- 44.Górska A, Gruchała-Niedoszytko M, Niedoszytko M, Maciejewska A, Chełmińska M, Skrzypski M, Wasa̧g B, Kaczkan M, Lange M, Nedoszytko B, Pawłowski R, Małgorzewicz S, Jassem E. The role of TRAF4 and B3GAT1 gene expression in the food hypersensitivity and insect venom allergy in mastocytosis. Archivum Immunologiae Et Therapiae Experimentalis (Warsz) 2016;64(6):497–503. doi: 10.1007/s00005-016-0397-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Qian J, Nunez S, Reed E, Reilly MP, Foulkes AS. A simple test of class-level genetic association can reveal novel cardiometabolic trait loci. PLoS ONE. 2016;11(2):e0148218. doi: 10.1371/journal.pone.0148218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kim DK, Cho MH, Hersh CP, Lomas DA, Miller BE, Kong X, Bakke P, Gulsvik A, Agusti A, Wouters E, Celli B, Coxson H, Vestbo J, MacNee W, Yates JC, Rennard S, Litonjua A, Qiu W, Beaty TH, Crapo JD, Riley JH, Tal-Singer R, Silverman EK ECLIPSE Investigator, ICGN Investigator & COPDGene Investigator. Genome-wide association analysis of blood biomarkers in chronic obstructive pulmonary disease. American Journal of Respiratory and Critical Care Medicine. 2012;186(12):1238–1247. doi: 10.1164/rccm.201206-1013OC. [DOI] [PMC free article] [PubMed] [Google Scholar]