Abstract
Introduction
Protein function is determined by protein structure which is in turn determined by the corresponding protein sequence. If the rules that cause a protein to adopt a particular structure are understood, it should be possible to refine or even redefine the function of a protein by working backwards from the desired structure to the sequence. Automated protein design attempts to calculate the effects of mutations computationally with the goal of more radical or complex transformations than are accessible by experimental techniques.
Areas covered
The authors give a brief overview of the recent methodological advances in computer-aided protein design, showing how methodological choices affect final design and how automated protein design can be used to address problems considered beyond traditional protein engineering, including the creation of novel protein scaffolds for drug development. Also, the authors address specifically the future challenges in the development of automated protein design.
Expert opinion
Automated protein design holds potential as a protein engineering technique, particularly in cases where screening by combinatorial mutagenesis is problematic. Considering solubility and immunogenicity issues, automated protein design is initially more likely to make an impact as a research tool for exploring basic biology in drug discovery than in the design of protein biologics.
Keywords: Protein design, automated protein design, ab initio design, scoring function, protein folding, conformational search
1. Automated protein design: radical protein engineering by computer
Proteins play multiple important roles in living organisms [1]. As functional biomolecules, proteins catalyze metabolic reactions, transport molecules and metabolites, coordinate response to stimuli, have vital roles in the transfer of biological information (i.e. for DNA/RNA replications, transcriptions, and translations), and are at the heart of many other specific biological processes, which make them critical for regulatory systems and communication between cells. As structural scaffolding, proteins also form rigid but flexible supports for different functions, such as in the cytoskeleton of eukaryotic cells [2], or in motor proteins in muscle cells [3,4].
The diverse range of functions are indebted to the peculiar construction of proteins in comparison to other polymers: each protein consists of single or multiple polyamide chains made out of a unique combination of 20 different amino acid residues. Each residue is characterized by different chemical functional groups. The group’s rotational degrees of freedom allow a protein to attain a conformation that yields attractive physical forces and chemical interactions that stabilize the protein structure in a global sense. At the same time, they also have the local flexibility to selectively bind and to specifically recognize other molecules for carrying out certain biological functions.
Thus, the holy grail of protein science is to understand the interplay between amino acid sequences with their corresponding spatial structures, which in return, determines their functions. The first protein sequencing was done in 1949 by Sanger [5], while the first protein structure elucidation by X-ray crystallography was made in the late 1950s by Kendrew and Perutz [6,7]; both leading to the rise of question of protein folding as famously addressed by Levinthal in 1969 [8]. Since then, there have been an enormous number of protein sequence-structure studies done from a physics, chemistry, biology, and informatics point of view – a quest that still continues to the present day. After 50 years of studies, our understanding is still far from complete. Nevertheless, the knowledge accumulated from these studies has given rise to interesting questions: (1) Is it possible to infer protein structure and functions solely from the amino acid sequence? (2) Is it possible to build a protein with a novel (de novo) sequence, while still having control toward the outcome of the structural topology, stability and function?
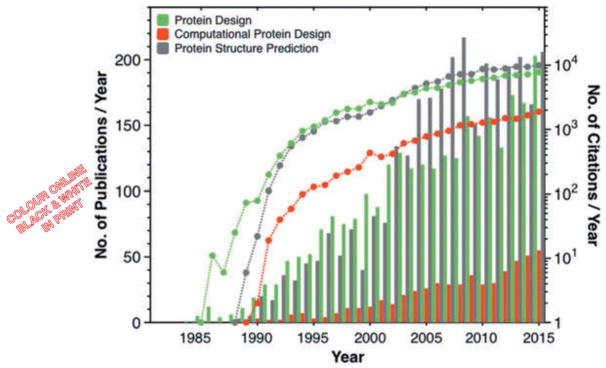
The first question gave rise to the field of protein structure prediction [9,10], while the second gave rise to the field of protein design, both of which emerged concurrently (Figure 1). In protein structure prediction, the aim is to deduce the three-dimensional structure of an amino acid sequence; while, in protein design, having a specific, known function or protein structure as a target, the aim is to figure out which amino acid sequences will lead to successful, correct folding, and biological activity. One may think of the protein design problem as the inverse of the protein structure prediction problem [11], or as an inverted-folding problem [12].
Figure 1.
Number of publications (bar graphs) and cumulative number of citations from the previous years (dots) related to the topics of protein design and computational protein design. The term ‘computational protein design’ here also including similar terms such as ‘automated,’ ‘computer-aided,’ ‘ab initio’ and ‘first principle’ protein design while the term ‘de novo’ protein design is excluded, as it is not necessarily referring to ‘automated protein design.’ Data is taken from web of science.
The possibility of predictive control in refining or even redefining protein functions has become the main driving force for the field of protein design. The vast possibilities of amino acid sequence combinations opened up by substantial sequence rewrites poses a problem. Protein design is a combinatorial problem in the order of 20L, where L is the number of amino acids in a target protein. Even a small protein with L = 30 will possess 1.07 × 1039 different possible combinations to be checked. By comparison, the age of universe is estimated to be 4.32 × 1017s, assuming 13.7 billion years since the Big Bang. To complicate the problem more, the readily gigantic ‘sequence space’ search must be solved altogether with solving the ‘spatial space’ search problem, i.e. the protein’s fold and shape in three-dimensional space are determined by the L-amino acids’ backbone and side-chain conformations, which are governed by numerous weak chemical interactions between themselves or with the environment. In light of this, the search for the most energetically favorable de novo protein also requires a good approximation toward a true free energy surface potential, after which protein design turns into an optimization problem. Considering the search space dimensions, all of these aims will require the implementation of an efficient computational algorithm combined with robust and elegant statistical and mathematical tricks and techniques.
The term protein design is, on many occasion, used interchangeably with the term protein engineering. Most protein engineering is achieved either through rational design, the evaluation of a few human selected mutations guided by comprehensive structural and biochemical knowledge, or by directed evolution by display technologies which evaluate very large mutant libraries generated by random mutagenesis at specific positions with the protein chains [11]. The success of this strategy is long and varied; nearly all protein therapeutics have been developed using some combination of the two strategies. The methods work in most cases because protein–protein interactions and enzymatic active sites are often relatively localized; evaluating one mutation site often only requires consideration of a few other sites in the immediate vicinity of the mutation – a mutation on side of the protein surface usually does not impact the effect of a mutation on the other side. As long as the effect of the mutations is relatively localized, directed evolution by random mutagenesis can be an efficient way for searching for optimal protein structures as a large area can be covered by independent screens.
However, there are applications in which direct application of the traditional methods of display technology and rational engineering are challenging and computer-aided or automatic protein design is required. One of the primary examples is when the number of mutations that must be considered exceeds the size of even the largest display libraries. While the library sizes of 1015 that are achieved by techniques like ribosome display [13] may seem large, in reality 1015 mutants only corresponds to ~12 designated positions and can quickly be exceeded if the mutations cannot be considered to act independently of each other. Such a situation often occurs in the redesign of the hydrophobic core of the protein for increased stability [14,15], where tight packing requires the consideration of how each mutation affects the other and subtle steric clashes can be difficult for humans to evaluate.
Another interesting application in this vein is the creation of water soluble versions of membrane proteins [16,17]. Membrane proteins are an essential component of the cellular signaling network. Because of their central role in cell signaling and regulation, they are highly overrepresented in both current drug targets and in estimates of future ones [18]. While this obviously stimulates a great interest in the structural biology and biophysical characterization of these proteins for structure based rational drug design [19], the intrinsic properties of membrane proteins make such studies difficult. Membrane proteins are notoriously difficult to express and purify in an active state. Even if expressed properly in sufficient amounts, the requirement of a membrane system for stability poses unique challenges for most biophysical techniques [20,21]. Removal of the protein into a detergent system amenable to crystallization or NMR studies often results in either aggregation of the protein or creation of an inactive state and requires careful consideration of experimental conditions. As an alternate approach, the exterior of the protein can be redesigned to switch the hydrophobic, membrane-favorable residues with more polar ones, increasing the solubility of the protein and therefore allowing the well-established methods developed for use for soluble proteins to be used for membrane proteins. Slovic et al. created a water-soluble version of the KcsA potassium ion channel by redesigning the surface using a statistical potential to replace hydrophobic residues with those expected to be present on the surface of a water-soluble protein. The resulting design mutates 29 out of 104 on the surface of the protein to create a soluble protein that could be expressed in high yield [22]. The resulting structure closely resembles that of the original membrane protein and retains the potassium ion selectivity of the native protein [23]. Water soluble analogs of other membrane proteins have been developed by this method including the mu opioid receptor [24]. The need for computational design is clear here: a large number of mutations are needed to achieve solubility and optimization is difficult to achieve through iterative rounds of direct evolution.
Simultaneous multiparameter optimization can also cause difficulty for display based screening. A prominent example occurs in the engineering of bispecific antibodies. Antibodies are normally symmetric homodimers where each of the two chains binds the same target. This poses a problem in some contexts where simultaneous binding to two separate targets is desired. In cancer immunotherapy, for example, the activation of cytotoxic T cells against the tumor requires binding to both a tumor-associated antigen on the tumor cell and binding to the CD3 antigen on the T-cell [25,26]. Since both proteins bind to the same loops in the complementarity determining region, engineering such simultaneous engagement is difficult using normal monoclonal antibodies. Bispecific antibodies solve this problem by using a chimeric protein to create a heterodimer where each chain binds a different target [27]. Bispecific antibodies can be created by random recombination of individual antibody chains but the process is inefficient and requires an affinity purification process for production that is difficult to scale up to manufacturing scale [28].
Redesigning the interface between the two CH3 domains of the antibody to enforce complementarity can greatly increase the yield of functional bispecific antibodies [29]. The dual functional nature of bispecific antibodies does not lend itself well to traditional protein engineering high-throughput approaches using directed evolution without modification to enforce a logical AND gate [30]. Computational approaches can create a small set of mutations (typically several hundred) [31] which have a high probability of success that can therefore be screened by lower throughput methods. This technology was used by Xencor to create two bispecific antibodies, XmAb14045 and XmAb13676, that have entered Phase 1 clinical trials for acute myeloid leukemia and non-Hodgkin’s lymphoma, respectively, in 2016 and 2017. The previous examples are some of the applications of protein design to pharmaceutical research and are not meant as an exhaustive list. The field is developing at a rapid pace and further applications can be found in recent reviews [32–34]. It is important to note here that computational design is not exclusive of other protein engineering techniques and a protein typically go through several rounds of protein design followed by experimental optimization [35].
2. The scope of automated protein design
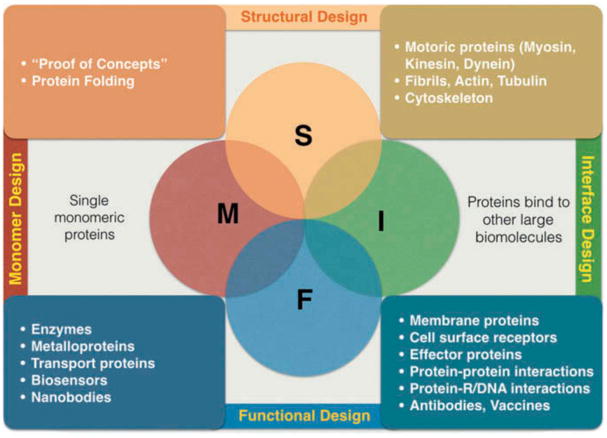
Protein design problems can be classified into two major design types (Figure 2): (1) structural design, pertaining to either the design of new structural topologies as a proof of concept with no specific biological function considered particularly or, more relevant to drug development, optimizing the biophysical properties such as solubility and thermodynamic stability, and (2) functional design, which involves consideration of tuning and optimizing a certain biological function without radically altering the protein structure. Each class can be divided into two different design subclasses: (1) monomer design, where a monomer protein can function by itself or (2) complex/interface design, where a protein needs to form a complex with other proteins (as homomers or heteromers), or form a protein–protein interacting assembly for exerting a function. Due to space limitation, we will only briefly describe each of the subclass as they are relevant to our next discussion about the challenges in automated design. For in-depth review articles and books discussing most recent progress in computational protein design projects in general, readers are encouraged to check the referred publications [36–39].
Figure 2.
General classification of protein design.
2.1. Structural protein design – the creation of novel protein scaffolds
The main objective of protein design for this subclass is both as a ‘proof of concept,’ i.e. to show a proposed design methodology works well, and to create a scaffold with favorable pharmacokinetic and biophysical properties onto which a binding loop can be grafted. Earlier we have mentioned some examples from Richardson [40] and from Mayo [41], while another recent prominent examples was made by Baker and coworkers with the design of the Top7 protein [42]. Top7 is an exceptionally stable 93-residue globular protein (ΔGfolding = −13.2 kcal mol−1 at 25°C), in which a novel α/β fold either is not naturally present in nature or at least has not yet been discovered experimentally. The Top7 protein was a landmark in theoretical protein design research as it showed it was no longer necessary to keep to the templates provided by nature for protein engineering.
Further work along this vein aimed at defining the rules that defined designable structures with the goal of eventually expanding the repertoire of protein therapeutics beyond the scaffolds in current use. Almost all protein therapeutics currently used are antibodies constructed from the immunoglobulin (Ig) scaffold. Antibodies possess a unique advantage over other protein scaffolds in that polyclonal antibodies against a wide range of targets can be generated by immunization of animals, from which highly specific monoclonal anti-bodies can be made by hybridoma screening. The long history of antibodies in the pharmaceutical industry has generated a vast knowledge bank of the pharmacokinetics, immunogenicity, and clinical safety profiles of monoclonal antibodies [43]. The Ig scaffold is modular with a conserved Fc domain linked to the variable Fad domain that binds the target. This multidomain structure allows the antibody to be screened at the cellular level and then purified on an industrial scale using proteins that recognize the conserved Fc domain [44]. The large size of the multi-domain structure limits glomerular and renal clearance giving rise to long half-lives, which is favorable in many clinical situations [45,46]. The conserved Fc domain of the antibody can also bind the FcγR receptor to activate the cellular component of the immune response. By contrast, most other naturally occurring potential scaffolds have a single binding site, limiting their mode of action to sequestration unless fused to another protein or a second effector site is engineered onto the scaffold.
Antibodies also have a number of disadvantages for certain applications. The classic Ig scaffold is dependent on disulfide bonds, which limits the use of bacterial expression for manufacturing. Their large size and consequent slow diffusivity may limit penetration into solid tumors, which reduces their potential effectiveness in cancer immunotherapy [45]. In imaging applications, a long half-life is often problematic and smaller a scaffold with more rapid renal clearance may be desired [46]. These limitations have led to the search for alternative scaffolds for protein engineering. The most radical option is to move away from proteins entirely and build on a non-protein scaffold [47,48]. Aptamers, oligonucleotide polymers, can be produced rapidly and, in the case of DNA aptamers, at a cost far below that of antibodies. The reversible nature of oligonucleotide denaturation means DNA and RNA can be stored at room temperature indefinitely, in contrast to protein-based therapeutics which are sensitive to heat induced denaturation and have a limited shelf-life [49]. However, the oligonucleotide backbone is vulnerable to degradation from nucleases in vivo [49]. The very short in vivo half-life of oligonucleotide aptamers (sometimes less than 10 min)[50] has led to the search for new protein scaffolds which possess the compactness and thermal stability of aptamers but with higher in vivo stability [46,51]. Computational design has played a prominent role in this search [52–54]. A particular focus has been on miniproteins, which at the 30–50 amino acid range, lie at the edge between proteins and peptides [55,56]. The interest in miniproteins has been sparked by the possibility of limited oral bioavailability for some folded peptides, as exemplified by modified formulations of the 39-amino acid helical peptide drug exenatide [57], and even the possibility for intracellular targeting which is not possible for antibody and aptamer based designs [55,58], A miniprotein drug would likely require remodeling the protein surface to accommodate a binding site for the target protein. Unfortunately, the number of naturally occurring miniprotein scaffolds is limited and unlikely to meet the needs of the pharmaceutical industry. With the aim of expanding this repertoire, Baker et al. constructed a new set of disulfide stabilized, cyclic miniproteins by de novo computational design that may serve as new scaffolds for protein therapeutics. Computationally designed peptide scaffolds based on this concept are beginning to enter the clinic. PG-200, an orally available interleukin-23 receptor antagonist [59] from Protagonist Therapeutics created from the computational selection of disulfide stabilized peptide scaffolds [60–62], is entering Phase I clinical trials for Crohn’s disease.
2.2. Design of novel and improved protein functions – novel enzymes and biosensors
2.2.1. Monomer design
Included into this subclass are enzymes, metalloproteins, and other proteins that bind small molecules. Enzymes are an interesting design target from either a scientific and economic perspective. The first computationally designed enzyme was pioneered by Bolon and Mayo in 2001 [63], with the design of hydrolase over a largely catalytically inert thioredoxin scaffold. The breakthrough with de novo enzyme design showing significant catalytic activities was made by Baker and coworkers between 2008 and 2010, through the design of a Kemp-elimination reaction [64], retro-aldol reaction [65], and Diels-Alder reaction [66], for which active site designs were also done on top of catalytically inert scaffolds. In the context of drug discovery, these designs are particularly interesting as no natural analog exists for the Kemp eliminase and Diels-Alderase enzymes, opening up the possibility of enzymes being used for more diverse roles in drug synthesis [67]. A computationally designed α-gliadin peptidase that survives gastric conditions for the treatment of celiac disease is under preclinical development by PvP Biologics [68,69].
The main challenge is dealing with the (many) transition states and intermediates involved in a catalytic cycle, which require a hybrid quantum mechanics and molecular mechanics approach using (QM/MM) modeling [70] and molecular dynamics (MD) simulations [71]. In 2012, Mayo and coworkers demonstrated an iterative design guided by MD simulations and experiments, giving a major improvement in the design of Kemp-elimination enzyme [72].
Similar in concept to enzyme design is the design of biosensors [12,73], including metalloproteins [37], and single chain anti-bodies called nanobodies [74]. For these classes, specificity and regulation of affinity by external cues, e.g. environmental pH or substrate concentrations, need to be considered carefully [75,76]. In order to design specificity, there are two general paradigm to be used: positive design (i.e. by stabilizing the protein–substrate binding complex) and negative design (i.e. by destabilizing competing protein–substrate binding complexes) [32].
2.2.2. Complex/interface design
Many diseases are either related to inappropriate protein–protein interactions or the absence of them [77–80]. Many cell surface receptors and their effector proteins are involved in signaling pathways, where activity is regulated by a small molecular stimulus. In cancer, the protein–protein interactions either promote proliferation or inhibit the apoptotic pathway [78]. From protein design point of view, it is then desirable to design protein inhibitors which will disrupt such interactions [79,81]. The main challenge of designing a protein inhibitor of a protein–protein interaction is optimizing the interface [82], which is confounded by potential conformational changes within the protein upon binding [83], the need to simultaneously balance affinity and specificity [84], positioning bridging waters at the interface [85], and possibly allosteric effects of the non-binding surface [86,87].
Membrane proteins, which encompass a large class of proteins, interact directly with both non-polar lipids bilayer and polar intra/extra-cellular matrix environment. Due to this, design and experimental validations (i.e. expressions, crystallizations) are usually difficult and the scoring functions, which are designed for soluble environments, must be reparameterized to reflect the environment of the membrane [88]. Recently, Barth and coworkers demonstrated a successful transmembrane design (i.e. engineering) of a GPCR protein, which shows how a protein design algorithm may guide the alteration of transmembrane proteins affinity toward a certain ligand [89]. However, due to the complexity of transmembrane proteins as mentioned before, the design procedure was limited to rely mostly on homology modeling and ligand docking [90].
3. Challenges in automated protein design
Challenges in automated protein design include: (i) the enormous search spaces for the optimal sequence and conformation given a defined structure or function, (ii) the development of fast, approximate yet accurate scoring functions that mimic ‘true’ folding and/or molecular interaction potentials, and (iii) the choice and improvement of an efficient optimization algorithm.
3.1. Challenge I: sequence and spatial search space
The full-optimization of protein’s geometry with respect to every sequence possibility is an combinatorial NP-hard (Non-deterministic Polynomial problem in the language of computational complexity theory) [91] which means there are, so far, no known polynomial-time and polynomial-space algorithms are available to solve the problem which require at most, time- and memory-wise, a factor equal to polynomial of the input data size. As a result, approximations and simplifications need to be made.
3.1.1. Use of amino acid sequences evolutionary information
A major simplification can be made by either considering the conformational search separately from the sequence search or ruling out certain mutations without a calculation intensive conformational check. Although sequence and spatial conformations are intertwined, early protein designs tried to simplify the search problem by considering only the amino acid sequence [11], as shown in the successful design of a collagen-based, fibrous protein based on the highly conserved Gly-Pro-X motif [40]. Previous work in protein structure prediction has shown that evolutionary information can be used to infer the importance of certain interactions. Since structure follows sequence, a high degree of sequence conservation at a site relative to the rest of the sequence usually implies an important structural or functional roles for that residue in catalysis, folding, or interaction with other proteins [92,93]. Amino acids that evolve together are likely to be either contact with each other or have a catalytic role in the active site [94].
Mutations at conserved positions are generally destabilizing and a non-homologous mutation may abrogate function [95]. This asserts the idea of limiting the sequence search to those readily explored by natural evolution. The sequence search can be limited strictly by only considering the amino acids observed at that position in homologs of the template sequence [96], or exclude conserved residues entirely and focus on optimization of the areas of the protein that are less conserved. Structural motifs that have been found to be stable [97] in wide variety of contexts may also be used. Alternatively, co-evolving residue pairs outside the main interacting surface may be an indication that long-range electrostatics are important and the scope of the design should be expanded [98].
However, the major weakness of only considering evolutionary information is that the search space is confined to known, evolved proteins [99], lowering the chance of designing novel protein folds that have not been sampled through evolution or incorporating novel binding activities. Recently, the reverse idea has also been shown to be successful: Instead of using evolutionary information of evolved proteins, the design of a novel beta-propeller protein was accomplished based on a predicted ancestor protein sequence, which aims to recover protein functions lost during the evolutionary process [100]. Reliance on evolutionary information also restricts the use of non-natural amino acids, such as with D-amino acids [101] Non-natural amino acids can convey many advantages over natural ones. In peptide drug designs, for example, the use of D- instead of L-amino acids increases peptide stability toward degradations by proteases [78].
3.1.2. Restriction of the backbone
To fully optimize a protein geometry, a total of (3N-6) parameters including interatomic-bond lengths, angles, and dihedral angles but excluding the translational and rotational degree of freedom of the proteins need to be considered where N is the total number of atoms in a protein. In computational protein design, however, instead of optimizing protein’s geometry fully each of the bond lengths and angles is usually fixed into a predetermined, idealized value obtained either from averaged experimental values or from high-level QM calculations. The problem can be reduced into the language of two molecular building blocks: a protein residue’s backbone and side-chain, each of which can be treated separately.
Each residue’s backbone and side-chain conformation will govern the total conformation of the protein in three-dimensional space, which will in turn determine its functions. Although searching for the optimal sequence and spatial configuration restricts the exploration to (1) the amino acid residue types, (2) residue backbone torsional bond angles, and (3) side-chain torsional bond angles, the combinatorial space problem is still too difficult to solve without additional approaches.
3.1.2.1. Fixed backbone design
One popular approach to reduce the geometric search space is done by fixing the protein backbone, administered by restraining backbone torsional angles ψ (N(i-1)-Ci-Cαi-Ni), φ (Ci-Cαi-Ni-C(i+1)), and ω (Cαi-Ni-C(i+1)-Cα(i+1), the rotational (dihedral) angles for the amide bonds, which is either ~0° (cis-conformation, e.g. prolines) or ~180° (trans-conformation, e.g. all other natural amino acids)). This allows the side-chains to adopt only a discrete set of conformations (i.e. rotamers), while fixing all interatomic-bond distances and angles to idealized values. Termed as fixed-backbone protein design [102], it finds most of its uses and successes in re-designing native proteins with resolved structures. The aim is that to make the re-designed protein to have superior properties, e.g. stronger binding affinity, or better enzymatic activity, with respect to the wild type. Placing different (mutant) amino acids on a native protein backbone may put additional steric tension among the atoms, as the available enclave space is not optimized for the mutated amino acids, e.g. due to rotamer optimization problems (Section 3.1.3). Even if continuous side-chain optimization is considered, one still need to be concerned with the fact that the native backbone is identified as an ideal conformation in a non-native environment (e.g. the crystalline structure of a protein is an averaged ensemble over many confined conformations that possesses crystal contacts that may not exist in vivo).
Most scoring functions in protein design algorithms at least implicitly take into consideration the dynamic motions of the protein to get a realistic model of the protein in living cells (Section 3.2). Thus, allowing some flexibility to the backbone become one critical step in ‘fixed’ backbone protein design. Flexibility provides a mechanism to relieve minor steric clashes, which in turn may stabilize the designed protein [103]. Backbone flexibility is especially important for enzyme design, or for any functions that require high adaptability with regard to the environment or receptors. With this approach, the relaxed backbone should not differ significantly from the initial backbone framework and the torsional backbone angles should still be acceptable within the Ramachandran set [104].
Backbone flexibility, including loop flexibility, is modeled based on statistical observations of alternative conformations in protein crystal structures [105]. Some models may utilize either small, discrete search around the target backbone topology, using predetermined backbone libraries, or a heuristic search with continuous global backbone movements [106].
3.1.2.2. ‘De novo’ backbone design
Relaxing the backbone in fixed backbone design usually refers to insubstantial backbone relaxation, which will not extensively change the protein fold or topology. It will be interesting however to have the ability to design novel protein folds whose topologies have not been seen in nature (de novo backbone) [99]. Having this capability may allow the introduction of new structure and functions never seen before.
Different approaches have been made. Kim and coworkers pioneered the design of trimers and tetramers of right-handed super-coiled α-helical proteins through hydrophobic-polar residues patterning, which were guided by scrutinizing the unfolding free energies for each residue candidate [107]. Meanwhile, Baker and coworkers designed the Top7 protein as mentioned earlier, by iterating consecutively between sequence design and the corresponding structure prediction [42]. More recently, but still based on similar principles, Baker and coworkers tried to formulate basic rules that may govern the folding of a protein into their native state, bridging the intuition between secondary to tertiary protein structure [108]. These rules, which make use of a discrete model of protein local geometry and restriction within the Ramachandran space, significantly reduce the geometric space search for the backbone and were later used to design completely novel protein folds [109]. Similar to the fixed-backbone design, the de novo backbone optimization also may include in its process, the refinement step utilizing the relaxed backbone design scheme to obtain best ‘aqueous conformation’ of the protein.
3.1.3. Search for optimal side-chain conformations
Taking (N-1) idealized values of inter-atomic bond lengths and (N-2) idealized angles leaves us with (N-3) rotational degree of freedom (torsional bond angles, Section 3.1). Depending on the type of amino acid i, each may have different number t of torsional bond angles, χit, t ≤ 5: χi1 (Ci-Cαi-Cβi-Cγi), χi2 (Cαi-Cβi-Cγi-Cδi), χi3 (Cβi-Cγi-Rδi-Cεi), χi4 (Cγi-Cδi-Cεi-Cζi); n = 5 for i = Arg, Lys; n = 4 for i = Met; n = 3 for i = Glu, Gln.
To search for the best torsional conformations, it is impractical to implement a continuous geometric search. The alternative is doing a discrete, instead of continuous, search [105] which still increases the number of parameters to search from (N-3) to [(N-3) × (360°/a°)], where a is the angular step size for the torsional angles.
3.1.3.1. Rotamers
Another approach is to use rotamers, by taking idealized values of torsional angles instead of ‘continuously’ optimizing them. In this approach, a set of rotamers (rotamer library) is used in an iterative search for the best idealized, torsional conformation of amino acid i at one position in the backbone.
A rotamer is obtained by screening a protein structural library (e.g. crystal PDB database), and represents frequently observed torsion angle conformations for each individual amino acid. The rotamers correspond to low-energy conformations in the protein crystal structure, supported by the fact that residue side-chain torsional angles tend to cluster into particular χit values centered on a probabilistic density distribution [110,111]. Dunbrack and Karplus later noticed that there are significant dependencies of rotamers with respect to its local [φ,ψ] backbone conformations [112], from which the backbone-dependent rotamer libraries were built. One possible advantage of using this approach is to have the possibility modeling a water bridge, i.e. a water molecule chelated between two residues via hydrogen bond interactions, which is important in protein–protein interactions [113,114].
3.1.3.2. Non-rotameric rotamers
Rotamers however may not be the best representation to describe conformational space in general. Residues that possess tautomeric, partial double bonds or aromatic characteristics, such as in Asn, Asp, Gln, Glu, Phe, Tyr, His, and Trp (termed as non-rotameric), yield asymmetric probability density distributions. The latest version of Dunbrack’s rotamer libraries tries to tackle this issue by using better statistical estimate models for estimating these non-rotameric cases [115].
3.1.3.3. Dynamical rotamers
Yet another drawback with the rotamer based approach is with the sampling database: the PDB crystal database may largely omit dynamic, floppy conformations which yield low electronic densities and thus low accuracy or missing atomic positions. The crystal structure itself is not always a good representative of the actual protein conformations in its native biological environment. In this case, rotamers with important functional conformations may not be correctly sampled. In this respect it will be interesting to see rotamer libraries built from protein structures elucidated from NMR, which sample low-lying conformational states absent in crystal structures that may be useful in imparting a degree of flexibility to the design [116,117]. However, NMR may suffer still from the difficulties in resonance assignment within highly flexible regions. In the future, cryo-EM based structures which can give atomic resolutions may be used for this purpose [118,119]. Currently, to sample dynamic rotamer conformations one may resort to MD simulations to sample over a set of representative proteins [120,121].
For design involving protein–protein interactions, one needs to take into consideration the effect of binding induced conformational changes. Rotamers obtained from a database of protein monomeric structures may not serve this purpose. Also, the high representation of monomeric structures and non-interacting regions within the PDB make rotamers associated with functional conformations underrepresented in the rotamer library.
Thus, the challenge is to accurately model protein conformational changes upon binding or close contact with other molecules, which is important for estimating how a mutant in the designed protein will affect intra- or intermolecular interactions [122], or how the designed protein responds to the environment. One approach is to relax and do ‘continuous’ optimization of the rotamers, so that the final result may correspond to low-energy conformations in its native environment [123]. Sampling from MD simulations, using a reliable force field, e.g. using a reaction force field for the case involving chemical reactions, may give rise to a set of rotamers fit for this purpose. In addition, backbone conformations associated with loop motions and large domain (secondary or tertiary structures) movement [124], might also be modeled in this way, and complemented using mode vibrations simulations from QM, hybrid QM/MM, or semi-empirical QM methods [125].
3.1.3.4. Reduced representation approach
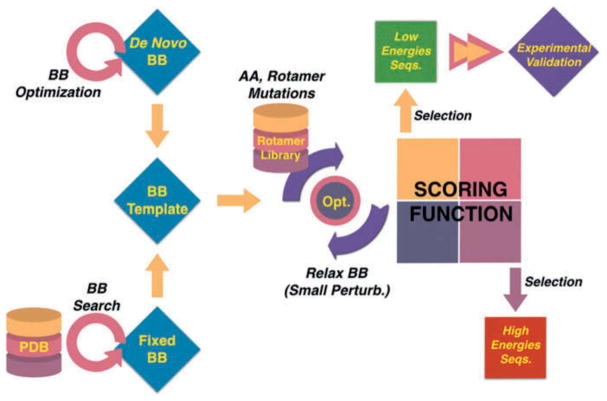
Further reduction in search space can be obtained by implicit atomic representations, e.g. molecular framework poses or functional groups of atoms might be converted into centroid, coarse-grained or pseudo-atomistic models [126,127]. For example, in terms of rotamers, each rotamer pose and type can be represented as a one coarse-grained bead. Loss of inter-atomic interactions details might be compensated with some empirical approximations [128,129]. This approach is ideally implemented in a recursive, two-step optimization process in flexible backbone design with iterations between backbone optimization and side-chain optimization, see Figure 3).
Figure 3.
General scheme for an automated protein design. AA refers to amino acids; BB refer to protein’s backbone; opt. refer to optimization processes or algorithm; seqs. refer to amino acid sequences.
3.2. Challenge II: scoring function development
In protein design, one of the important goals is to develop a ‘realistic’ scoring (or free energy) function, which can accurately describe the physical and chemical interactions among atoms in proteins and its surrounding environment. The scoring function will form a potential which can guide protein conformational change in a design simulation in response to a mutation (Challenge I). The scoring function approximates the true free energy G, which accounts for the electronic energy E, molecular enthalpy H, and entropy S. The protein ‘energy scores,’ either EP or GP, will be used to estimate the protein stability (ΔGfolding) and/or protein interaction (ΔΔGinteraction) with the surroundings or other molecules.
| (1) |
| (2) |
Unlike in full-scale MD simulations, the approaches generally used in protein design consider only protein conformations singly (i.e. a snapshot of folded/unfolded, bound/unbound). This is a particular problem for free energy calculations of protein stability which requires an energy of the unfolded state. Since there are currently no available structures for the corresponding unfolded chain of amino acids (although it is theoretically possible through NMR studies [130,131]), a hypothetical model of unfolded chain must be constructed and used as a reference [122,129].
Analogous to natural protein evolution, the scoring function, along with the optimization algorithm (Challenge III), act as a guide for selecting the best sequence for a target feature (i.e. ‘natural selection,’ Figure 3). Getting a good scoring function, which can discriminate the lowest energy scoring sequence from other competing low-energy scoring states, is thus essential and extremely critical. Due to the size of proteins, a good scoring function for protein design implies the use of approximations to achieve a reasonable balance between speed and accuracy [132,133], which may satisfy the need for huge number of iterations or samplings in the optimization algorithm.
3.2.1. Physics-based scoring functions
3.2.1.1. Molecular mechanics-based force-fields
QM-based simulation methods, including QM/MM and semi-empirical QM methods are still too expensive for protein design simulations, even with current progress in computational technologies. For protein simulations, MM-based methods pioneered by Levitt, Warshel, and Karplus have then become a clear alternative [134], which are parametrized from either thermodynamics, crystallographic, spectroscopic data or high-level QM calculations. The MM force field in its general form introduces covalent bond energy potentials (harmonic oscillator model of bond strain, bend, and torsional vibrations) and non-covalent bond potentials (van der Waals and electrostatic forces). Thus, within the force field, the internal energy of a molecular protein or protein–ligand complex in a single conformational state is represented as:
| (3) |
3.2.1.2. Physics-based energy functions for protein design
Incorporate the non-covalent part of the MM force field while dropping the covalent part. This is done due to the fact that the design simulation samples only an idealized protein geometry constructed from backbone and side-chain rotamers for a particular state (i.e. a snapshot), instead of sampling the dynamics, as in MD simulations. An advantage of physics-based methods is that the energy terms are intuitive and give a direct translation to real physical energy quantities. The terms are usually designed to be pairwise decomposable, which assumes that the total energy of a protein conformation EP (van der Waals, electrostatic, and hydrogen bond) is additive across atomic pairs. A pairwise decomposable scoring function is a requirement for the dead-end elimination (DEE) rotamer searching algorithm. Since the DEE is essential to prevent combinatorial explosion, in practice protein design scoring functions are required to be pairwise decomposable, ruling out polarizable and other non-local force-fields.
Physics-based scoring functions often take the form:
| (4) |
The van der Waals (vdW) term reflects both the weak attractive force from the correlated transient motion of electrons and induced dipoles and the strong, but short ranged, repulsive force from the Pauli Exclusion Principle. In standard MM force-fields it is modeled with a Lennard–Jones potential with a 6th-degree polynomial modeling the attractive potential and a 12th-degree polynomial modeling the repulsive part:
| (5) |
where d is the separation between the two atoms and r is the distance at which the potential is at a minimum (the atomic radii). While the Lennard–Jones approximates the true potential reasonably well, the discrete rotamer and limited backbone flexibility approximations required to make the conformational search computationally tractable means that some steric clashes will inevitably exist. If unadjusted, this can lead to an inappropriately high weighting of the repulsive part of the potential and poor packing of the sidechains. To address this problem, a softened repulsive term is often used which replaces the 12th degree polynomial with another term that is more tolerant of small overlaps. The repulsive part of the Lennard–Jones potential can be replaced with either a linear term (EGAD) [135], or a term that becomes linear after a specified cut-off value (ROSETTA) [136]. Alternatively, the functional form can be kept the same and the effective atomic radii r shrunk. Softening the repulsion term in either manner assumes that the structure can relax sufficiently to eliminate small clashes, for example by backbone rub motions or small deviations from ideal rotamer geometry for the side-chains. The reduced repulsion also allows closer approach then is normally possible for polar atoms which can bring about inappropriately large hydrogen bonding values which must be reparameterized to appropriate values [137].
As the parametrization of MM force-fields is based on gas phase properties, a solvation free energy term ΔGsolvation also needs to be included to model the electrostatic and entropic changes that occur when the protein interacts with water. Because consideration of the effects of explicit water molecules is difficult, protein design scoring functions usually rely upon an implicit solvation model such as the Lazaridis–Karplus (EEF1) [138], Generalized Born [139], or Poisson-Boltzmann methods [140,141]. Implicit models treat water molecules as a continuum, approximating the energy of solvation as a linear function of the accessible surface area. Since solvation is primarily an entropic effect, the ‘energy’ function actually refers to a free energy calculation. All the models approximate the largely entropic hydrophobic effect as being directly proportional to the solvent accessible surface area (SASA). The calculation of the SASA can be made pairwise decomposable [142], allowing it to be used with DEE and other algorithms that require precomputation of energies.
The models differ in their treatment of electrostatic interactions. The electrostatic energy of a protein system properly contains terms from the interactions of charges and dipoles within the protein itself, the interaction of solvent dipoles with protein charges and dipoles, and the screening effect of the solvent dipoles on the protein internal electrostatics. The Poisson-Boltzmann method attempts to calculate the electrostatic potential of a protein of arbitrary shape exactly within a mean field approximation, using a single dielectric constant for the protein and ignoring ion volume effects [143,144]. The equation must be solved numerically and gridding errors have been suggested to be a major source of error [35]. If the protein is modeled as a set of spheres, the resulting equation can be solved analytically to generate the Generalized Born model. The radii of the spheres in the model (Born radii) are not true distances but are adjusted to approximate the results of the Poisson-Boltzmann equation as closely as possible [145]. The Generalized Born method used in EGAD [146] and PROTEUS [147] is faster, immune to gridding numerical artifacts, but is sensitive to the choice of the Born radii. The Lazaridis–Karplus method takes abstraction a step further and calculates the solvation energy as the simply the sum of coulombic contributions from functional groups parameterized from small molecules with a distance dependent dielectric [148]. This is the electrostatic term used in ORBIT [149], FoldX [122], and Evodesign [150].
An additional HBond term is added to account for the specific characteristic of hydrogen bonds [151], as each has partial covalent and electrostatic characteristic. A purely electrostatic term misses the orientational dependence that arises from the partly covalent nature of the hydrogen bond, which can be captured by a MM approach with the terms parameterized by high level QM calculations on small molecules [152]. A purely covalent term misses the long-range polarizing effects of hydrogen bonds and improve the formation of hydrogen bond networks [153]. An additional electrostatic term can be added to reflect these contributions. Since hydrogen bonds are also calculated in the electrostatic term, one must also be careful of not over-counting its contributions [153,154].
Finally, it is important to note that the free energy of stability is a free energy change that is defined with respect to the unfolded state. A loss of stability upon mutation can result from either an increase in the free energy of the native state or a decrease in the free energy of the unfolded state. The free energy of the unfolded state is difficult to calculate as there is no single conformation to base the calculation on. One method is to simply ignore it, which amounts to assuming the energy of the denatured state is independent of sequence. Another method assumes the energy of the denatured state is dependent on local interactions only and the energy of the unfolded state depends on the overall amino acid composition but not the sequence itself. Making this assumption drastically simplifies the calculation of the unfolded state as a single reference energy can be used for any amino acid (or amino acid triplet), reducing the intractable conformational search problem to a simple lookup table. This is the approach used in most protein design programs [106,155]. However, the structure of the denatured state is known to be not entirely random and persistent structure in the unfolded state in the form of local hydrophobic clusters and residual secondary structure (SS) will reduce the accuracy of the technique [156,157]. Alternatively, the ‘unfolded’ state can be considered to be not a true random coil but rather a statistical average of the structures found in folded proteins, which can be obtained by surveying fragments from the PDB. An unfolded reference state energy for a specific amino acid taking into account local persistent structure can then be obtained by threading random sequences unto this fragment database and averaging over both sequence and fragments [135].
3.2.2. Knowledge-based scoring functions
Knowledge-based energy (scoring) function, or statistical potentials, or potentials of mean force, are based on defining, associating, and deriving the scoring (‘energy’) values as a function of the frequency distribution of a feature in a structural or sequence database. This frequency, when defined with respect to a random distribution, is assumed to be a measure of its contribution to an ‘energy’ or ‘free energy’ feature. Again, the term ‘energy’ calculated from this approach has no direct physical meaning, and its relation to the true definition of physical energy may not always clear.
Knowledge-based scoring functions are generally expressed as a pairwise sum of statistical potentials between protein atoms or moieties:
| (6) |
| (7) |
The statistical ‘energy’ function G is expressed as a linear combination of singlet (ωi) and pairwise (ωij) decomposable statistical ‘energy’ potentials in terms of a Boltzmann probability density distribution (kB is Boltzmann constant, T is ‘temperature,’ a parameter associated with the state of an ensemble not directly corresponding to a physical temperature). Singlet ‘energy’ terms are related to protein characteristics independent of other moieties, such as hydrophobicity and hydrophilicity, while pairwise terms are related to interaction-dependent features, such as inter-moiety clashes and electrostatic interactions. In the equation, the indices i, j may represent moieties such as atoms, rotamers, amino acid types, or coarse-grained beads.
The inverse (log-odds) of the Boltzmann probability distribution might also be used with the aim to make it resemble the potentials of mean force, which then may give a ‘physical flavor’ to the scoring function:
| (8) |
Another alternative is describing the potential using Bayesian statistics, which usually is expressed in its log-odds form:
| (9) |
| (10) |
Here, the potential ‘energy’ term ω is determined by the probability distribution P of rotamer ri or pair of rotamers ri and rj, when located in a certain molecular environment e in the protein. Worthy to be mentioned that in connection to the rotamer library, the selection of rotamers is also done using this type of statistical potential [115].
Statistical potentials contain mostly arithmetic operations and thus have the advantage of being fast in comparison to time-consuming physics-based potentials, which may involve solving linear algebraic equations. Within this approach however, a good selection of training set database (which becomes the ‘knowledge base’) is critical before one can get a reliable statistical potential.
3.2.3. Machine-learning-based scoring functions
Machine-learning-based scoring functions uses a variety of mostly supervised machine-learning algorithms [158,159], such as artificial neural networks [160], random forest [161–163], and support vector machine [164], to learn about a specific energetic or other structural or biological properties using a training set of protein structures. The resulting, trained, machine-learning-based function, can then be used to produce a scoring value associated with a predicted property:
Used as an input are features or descriptors, or also known as fingerprints. Each descriptor is a one-dimensional vector, where each element is a mathematical quantification of a certain structural or interaction feature. In this approach, each structural or interacting moiety is represented by a unique descriptor. For example, the EvoDesign program [165], which is a fixed-backbone protein design approach, uses amino acid counts within a seven residue window and the BLOSUM62 substitution matrix as features to quickly predict the SS, solvent accessibility (SA), and torsional backbone framework of an amino acid sequence through a back-propagated-neural-network-trained function. The propensity score is then used to judge whether or not a sequence will have similar SS as the template.
Similar to knowledge-based scoring, machine-learning-based scoring can be computationally cheap and quick. The SS/SA prediction in EvoDesign gives ~70% accuracy with a runtime on the order of microseconds, while the traditional, sequence-alignment-based SS/SA prediction may take minutes with only a slightly higher accuracy of ~80% [150].
In computational drug design, interaction fingerprints or signatures [166–168], which have emerged only recently, have been used to estimate the binding energy between protein and ligand. The same principle might also be extended for estimating the protein–protein interaction energies; and with some training via machine-learning methods, this can be used as a basis for scoring the protein intermolecular interactions efficiently.
3.2.4. Empirical (hybrid) scoring function
An empirical scoring function computes the ‘energy’ or ‘free energy’ by summing up the weighted contributions of many individual ‘energy’ representation terms, most of which try to mimic as close as possible the physical interpretation of their counterparts in a physics-based method [169]. The energy terms lean toward chemical intuition and interpretation instead of physics, e.g. the hydrophobicity, hydrophilicity, polarity, and inter-atomic clash penalty. To calculate binding affinity, a ‘free energy’ term derived from the association constant (Ka) or dissociation constant (Kd) might also be added [170]. The empirical scoring rewards term contributing to stability/binding and penalize those reducing stability/binding. The contributions are scaled or weighted according to regression analyses benchmarked against certain experimental observables:
| (12) |
Here, each ‘energy’ term might employ any of the above-mentioned scoring type: machine-learning-, physics-, or knowledge-based statistical functions. Thus, this type of scoring function is termed a hybrid scoring function. Almost every scoring function used in popular protein design algorithm, such as those used in RosettaDesign [128,153,171], FoldX [122], or OSPREY [106], falls into this category. Evodesign uses a combination of knowledge-based scores based in amino acid frequency at the corresponding location within structural related protein, machine-learning-based prediction of secondary and tertiary structure, and the physics-based FoldX force field [97,150].
The main challenge for this type of scoring function is parameter tuning to balance the terms contributing to the free energy to obtain values that are well correlated with the physically realistic energy values. While this type of scoring is easily extendable, one must consider carefully the problem of over-counting of an ‘energetic’ feature (e.g. polarity vs. electrostatic, atomic clashes vs. van der Waals), and to ensure the extension function does make sense.
3.3. Challenge III: choice of optimization algorithm
Protein design requires accurate scoring functions to score and rank sequences by how well they fold into the target structure. Considering the vast search space mentioned earlier, the challenge is to develop an efficient optimization algorithm that can handle this task in a reasonable computational time with available computational resources. Also, considering the search space dimensions, even with some approximations, the problem of optimizing the design scoring function is still categorized as an NP-hard problem [91], which can only be approximated with exponential algorithm. Several types of algorithms have been developed, following either a deterministic or stochastic approach.
3.3.1. Deterministic algorithms
Algorithms included into this class commonly implemented into protein design programs are the Dead-End Elimination (DEE) [172,173], (integer) linear programming [174,175], branch-and-bound, or divide-and-conquer [132,176], and self-consistent mean field approaches [133,177].
Notably is the DEE technique, which iteratively seeks to eliminate early rotamers and/or combinations of rotamers associated with high energy configurations by pruning [105,106,123,132,178]. The iterations continue until it converges into a single solution, which is proven to always be the Global Minimum Energy Conformation (GMEC) [172,173]. Thus, DEE when converged gives a mathematical assurance that the quality of the design is the best solution within the scope of the scoring function and/or the protein model. Therefore, in the case that the design fails when it is experimentally validated (i.e. the protein is not stable or is not showing expected activities), one can be sure that it is solely caused by the inaccuracy of the scoring function, giving clear feedback for the iterative improvement of the scoring function [132].
However, the problem with DEE is that there is no guarantee it will always converge. As a solution, searching methods employing DEE always provide a back-up algorithm in the case DEE search fails, such as using integer linear programming or branch-and-bound based methods (i.e. A* algorithm [179]), as implemented in OSPREY [106]. Other algorithms, such as FASTER [178,180], uses stochastic criteria to continue with the optimization in the case of DEE failure. However, this means that in the case of DEE non-convergence the GMEC guarantee is lost, although approaching the near-GMEC limit may still be possible [133,181].
3.3.2. Stochastic algorithms
Monte Carlo and Genetic Algorithm have also been implemented in automated protein design. Optimization utilizing Monte Carlo methods (Metropolis, Simulated Annealing, Replica Exchange/Parallel Tempering) are the most widely used for protein design [36,133]. Within the Monte Carlo scheme, sequential optimization is done by always accepting lower scoring sequences, while higher scoring sequences will be accepted with a probability equivalent to the Boltzmann probability, exp(–ΔE/kBT); where kB is Boltzman’s constant and T is temperature factor. The temperature factor allows the (Metropolis) Monte Carlo simulations to visit different local minima. To explore more local/global minima, a higher T value can be chosen and annealed in a stepwise manner (Simulated Annealing), or in a parallel manner (Replica Exchange) [182,183]. With the latter, several trajectories, each runs at a different T value, are generated so that the simulation trajectory can jump to adjacent trajectory with a higher/lower T according to Boltzman’s probability, thus allowing it to explore the global energy scoring surface in a more efficient way. Besides the memory and CPU advantages compared to deterministic techniques, replica exchange and Monte Carlo techniques have the advantage of providing Boltzmann like sampling of the conformation/sequence space near the GMEC [184]. Boltzmann sampling of rotamers for a given sequence may provide a measure of the conformational entropy of a design, a factor which has largely been neglected in energy functions to this date. Probabilistic sampling of sequence space may be a better way of identifying specific sites for experimental directed evolution by identifying residues in the sequence likely to have low-energy mutants rather than attempting to identify the GMEC. Given the known inaccuracies of protein design energy functions, such a combinatorial approach targeting protein ‘hot spots’ may be more effective then directly targeting the GMEC [185].
Genetic Algorithms are a stochastic method which is based on the natural selection principle [186], which is a selection method done in a similar manner to Simulated Annealing. The difference lies in the description of amino acids/rotamers as a bit string vector, which is then randomized and mutated by genetic operators: a mutation operator, which simply mutates the bit string value randomly, just like in Monte Carlo, and a crossover operator, which randomly fragments and recombines two bit string vectors. With the latter operator there is a possibility that one may come up with a ‘super individual,’ which is ‘genetically superior’ than the other [133].
Algorithms based on stochastic methods are significantly cheaper than those based on deterministic ones. However, designed sequences optimized with a stochastic approach do not guarantee a GMEC or near-GMEC solution. Thus, in choosing which optimization method to be used, again, one also needs to consider the tradeoff between speed, algorithm complexity, and the certainty/accuracy of the results.
3.4. Challenge IV: clinical translation
It is useful to establish a distinction between proteins designed by automated protein design as a research tools to aid the drug discovery process and the creation of therapeutic protein biologics through automated protein design.
Research tools are meant for exploratory preclinical research aimed at establishing the basic biology of the system prior to clinical development. Because they are not meant for human use and are restricted to in vitro applications or at the most animal model studies, optimization of pharmacokinetic and ADMET properties is not as critical as they are in clinical applications. An example of a research tool is the water soluble analog of the KcsA potassium ion channel described in Section 2, which is meant to further rational drug design by facilitating biophysical characterization of the drug target.
Novel designed proteins meant as therapeutics to are subject to the same toxicity and pharmacokinetic constraints as other protein biologics [187]. In addition to affinity (or catalytic rate enhancement in the case of enzymes) and thermodynamic stability, a whole host of other properties must also be tuned to acceptable ranges including in vivo half-life, ADMET, off target effects, and others [188].
Most of these issues are not specific to computationally designed proteins and the particulars of the optimization process will vary by the specifics of the protein being optimized. However, two issues deserve special attention as they are more prominent with computationally designed proteins than those built from conventional protein engineering. The solubility of designed proteins is often less then corresponding native proteins as current force-fields have a tendency to over-represent hydrophobic interactions, particularly on the surface [188]. The inappropriate clustering of hydrophobic residues on the surface may lead to aggregation unless properly accounted for. Alterations to the protein core from complete protein redesign may result in low thermodynamic stability and periodic fluctuations that expose the interior of the protein to solvent, creating a surface favorable for aggregation. Explicit consideration of solubility in design, either with a scoring term that disfavors hydrophobic patches on the surface [189], or solubility prediction based on sequence threading [190,191], may be effective in increasing protein yield and in vivo efficacy.
Immunogenicity is also of special concern for designed proteins as the introduction of non-human on a protein surface can raise an immune response. Deimmunization programs by removal of predicted T-cell epitopes will likely a prerequisite before any designed protein can be used in the clinic [192–194].
4. Conclusion
Protein design offers various opportunities, not only in terms of applications, but also a long list of challenges, due to our poor understanding of how to represent the physiochemical principles underlying protein stability, folding mechanism, and interactions with the environment or other molecules in a computationally tractable manner. In interface design in particular, current scoring functions are too biased toward hydrophobic interactions to the neglect of electrostatic and hydrogen bonding interactions, leading to aggregation prone sequences and low affinity, non-specific binding [85,129,195]. Nevertheless, recent progress in protein design shows promising results, with the demonstration of the successful expression and synthesis of proteins with novel folds, topologies, and functions when guided by computational design algorithms. Progress has accelerated at a high pace, with the wake of new computational technologies, more affordable computational resources, and most importantly, breakthroughs in the development of more accurate scoring functions and optimization algorithms. Protein design is an extremely complex problem which needs to be approached and solved in a holistic manner.
5. Expert opinion
One of the remaining challenges in protein design is to predict with certain confidence, whether a designed sequence from a simulation will yield a successful protein expression and exhibit the desired activities. This is also important for having quick feedback from the success/failure of the designs, in order to make improvements to the scoring functions.
One option to overcome the challenge is through the DEE algorithm, which, if well converged, gives mathematical assurance that the quality of the design is the best solution within the scope of the scoring function. Any errors can then be attributed to the scoring function and not due to the optimization search. Even with the DEE algorithm, one will always need to rely on experimental validations, which take time, costs, and manpower. In protein structure prediction, the methods can be benchmarked and tested based on the gold standard, i.e. the known structures from the PDB; in protein design, however, there is currently not such good standard until a biophysical or biochemical experiment is done to validate the design. Based on the fact that most mutations are destabilizing when considered individually, native sequence recovery has been proposed as method for benchmarking methods, however, protein design intrinsically assumes the wild type sequence is not unique in fitting the scaffold structure.
The ability to evaluate, pre screen and predict successful designs is important. The ability to predict whether a proposed design will eventually fold into a stable structure (foldability, stability and structure prediction), and perform the preferred function (function prediction) without requiring expression and biophysical characterization is essential. The novelty of a design sequence will pose a challenge to existing algorithms. It will require structure or function prediction algorithms which do not rely on sequence or structure homolog templates (i.e. ab initio prediction). Toward this end, in addition to physico chemical scoring terms, protein design algorithms may also incorporate scoring terms related with predicted structure or SS, rewarding scores might be given to sequences predicted to have the desired (secondary) structural feature or functions.
To facilitate the structure and function predictions, a comprehensive database, which includes failed (negative control) and successful (positive control) designs, could be constructed, and made as a basis for the predictions [72]. One of the difficulties in building the database is due to the tendency of researchers to publish only good/successful design results. It is until only recently (i.e. after 2010s), when researchers started to also include the details of failed designs as well, at least in the Supplementary/Supporting Information section. However, this is done in a scattered manner and there has not been to our knowledge a systematic effort to build a comprehensive database of successes and failures. Protein design will benefit more from the publications of both positive and negative results.
Recently Baker and coworkers demonstrated the use of an ‘on-the-fly’ successful/failed database in refining the scoring function to gain a higher success rate in protein design [95], which has been made possible by recent innovations in molecular biology. The combined cycle between computational protein design, next-generation gene synthesis, and high-throughput protease susceptibility assays, provides a framework for systematic measurements of protein stability, creating a feedback loop between computation and experiment in a short time span and low-cost manner [196].
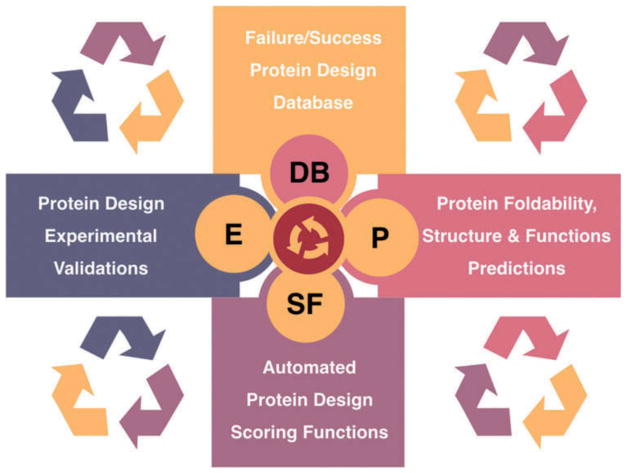
We think that the future development of accurate scoring functions for protein design will involve a collaborative effort between Protein Design, Experimental Validations, Protein Structure & Function Prediction, and Informatics/Data Science (Figure 4). This in turn will improve our understanding regarding protein folding, structure and function prediction. In other words, the field of protein design should in the future be interwoven with these other fields for a meaningful progress to be made. Less stable or unstable proteins validated by experiments (failed design) as well as successful designs, along with data science and MD simulations, may give useful feedback in studying protein stability and folding mechanism, and possibly open up new avenues beyond backbone-based protein design, e.g. intrinsically disordered protein designs.
Figure 4.
Future inter-connected solutions for the development of Scoring Functions (SF) for protein design: Collaborative approach between protein design, experimental validations (E), Proteins; foldability, structure & function Predictions (P), and informatics/data science (development and management of design results Database (DB).
Article highlights.
The idea of having control over protein function and stability has become the main driving force for the field of automated protein design.
Automated protein design is particularly useful in protein engineering where a large number of interdependent mutations must be considered or screening by directed evolution is difficult.
Challenges in automated protein design include the enormously large dimensional spaces for searching the optimal sequence and conformation within a defined structure or function and the development of a fast yet accurate scoring functions along with an efficient optimization algorithm.
One of the remaining challenges is to be able to evaluate the stability of a proposed design model quickly through computational or experimental means to iteratively improve scoring functions.
Solubility and immunogenicity issues continue to be a particular concern of proteins engineered by automated protein design and currently limit clinical development.
The future development of accurate scoring function for protein design will involve a collaborative effort between different disciplines, including informatics and data science.
In turn, this may give useful feedback to the studies of protein stability, protein folding, and protein structure and function prediction, and may open up the possibilities beyond backbone-based protein design, e.g. the design of intrinsically disordered proteins.
This box summarizes key points contained in the article.
Acknowledgments
The authors thank Dr Smita Mohanty and Dr Xiaoqiang Huang for their fruitful discussions and suggestions. We also thank Xinqiu Yao for proof-reading the manuscript.
Funding
This work was supported by the National Institute of General Medical Sciences (GM083107 and GM116960) as well the US National Science Foundation (DBI1564756).
Footnotes
Declaration of interest
The authors have no relevant affiliations or financial involvement with any organization or entity with a financial interest in or financial conflict with the subject matter or materials discussed in the manuscript. This includes employment, consultancies, honoraria, stock ownership or options, expert testimony, grants or patents received or pending, or royalties. Peer reviewers on this manuscript have no relevant financial or other relationships to disclose.
References
Papers of special note have been highlighted as either of interest
(•) or of considerable interest
(••) to readers.
- 1.Miklos GLG, Maleszka R. Protein functions and biological contexts. Proteomics. 2001;1:169–178. doi: 10.1002/1615-9861(200102)1:2<169::AID-PROT169>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- 2.Fife CM, McCarroll JA, Kavallaris M. Movers and shakers: cell cytoskeleton in cancer metastasis. Br J Pharmacol. 2014;171(24) doi: 10.1111/bph.12704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bhabha G, Johnson GT, Schroeder CM, et al. How Dynein moves along microtubules. Trends Biochem Sci. 2016;41(1):94–105. doi: 10.1016/j.tibs.2015.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hirokawa N, Noda Y, Tanaka Y, et al. Kinesin superfamily motor proteins and intracellular transport. Nat Rev Mol Cell Biol. 2009;10(10):682–696. doi: 10.1038/nrm2774. [DOI] [PubMed] [Google Scholar]
- 5.Sanger F. The terminal peptides of insulin. Biochem J. 1949;45(5):563–574. doi: 10.1042/bj0450563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kendrew JC, Bodo G, Dintzis HM, et al. A three-dimensional model of the myoglobin molecule obtained by X-ray analysis. Nature. 1958;181(4610):662–666. doi: 10.1038/181662a0. [DOI] [PubMed] [Google Scholar]
- 7.Muirhead H, Perutz MF. Structure of haemoglobin: a three-dimensional Fourier synthesis of reduced human haemoglobin at 5.5 [angst] resolution. Nature. 1963;199(4894):633–638. doi: 10.1038/199633a0. [DOI] [PubMed] [Google Scholar]
- 8.Zwanzig R, Szabo A, Bagchi B. Levinthal’s paradox. Proc Natl Acad Sci U S A. 1992;89(1):20–22. doi: 10.1073/pnas.89.1.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Baker D, Sali A. Protein structure prediction and structural genomics. Science. 2001;294(5540):93. doi: 10.1126/science.1065659. [DOI] [PubMed] [Google Scholar]
- 10.Zhang Y. Progress and challenges in protein structure prediction. Curr Opin Struct Biol. 2008;18(3):342–348. doi: 10.1016/j.sbi.2008.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Richardson JS, Richardson DC. The de novo design of protein structures. Trends Biochem Sci. 1989;14:304–309. doi: 10.1016/0968-0004(89)90070-4. [DOI] [PubMed] [Google Scholar]
- 12••.Havranek JJ, Harbury PB. Automated design of specificity in molecular recognition. Nat Struct Biol. 2003;10(1):45–52. doi: 10.1038/nsb877. A good minireview emphasizing the importance of specificity in molecular interactions for targeting a specific functions using computational protein design. [DOI] [PubMed] [Google Scholar]
- 13.He M, Taussig MJ. Ribosome display: cell-free protein display technology. Brief Funct Genomic Proteomic. 2002;1(2):204–212. doi: 10.1093/bfgp/1.2.204. [DOI] [PubMed] [Google Scholar]
- 14.Lazar GA, Handel TM. Hydrophobic core packing and protein design. Curr Opin Chem Biol. 1998;2(6):675–679. doi: 10.1016/s1367-5931(98)80102-6. [DOI] [PubMed] [Google Scholar]
- 15.Woolfson DN. Core-directed protein design. Curr Opin Struct Biol. 2001;11(4):464–471. doi: 10.1016/s0959-440x(00)00234-7. [DOI] [PubMed] [Google Scholar]
- 16.Rawlings AE. Membrane proteins: always an insoluble problem? Biochem Soc Trans. 2016;44(3):790–795. doi: 10.1042/BST20160025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Perez-Aguilar JM, Saven JG. Computational design of membrane proteins. Structure. 2012;20(1):5–14. doi: 10.1016/j.str.2011.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Overington JP, Al-Lazikani B, Hopkins AL. How many drug targets are there? Nat Rev Drug Discov. 2006;5(12):993–996. doi: 10.1038/nrd2199. [DOI] [PubMed] [Google Scholar]
- 19.Yin H, Flynn AD. Drugging membrane protein interactions. Annu Rev Biomed Eng. 2016;18:51–76. doi: 10.1146/annurev-bioeng-092115-025322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Carpenter EP, Beis K, Cameron AD, et al. Overcoming the challenges of membrane protein crystallography. Curr Opin Struct Biol. 2008;18(5):581–586. doi: 10.1016/j.sbi.2008.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sanders CR, Sonnichsen F. Solution NMR of membrane proteins: practice and challenges. Magn Reson Chem. 2006;44:S24–40. doi: 10.1002/mrc.1816. [DOI] [PubMed] [Google Scholar]
- 22.Slovic AM, Kono H, Lear JD, et al. Computational design of water-soluble analogues of the potassium channel KcsA. Proc Natl Acad Sci U S A. 2004;101(7):1828–1833. doi: 10.1073/pnas.0306417101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ma D, Tillman TS, Tang P, et al. NMR studies of a channel protein without membranes: structure and dynamics of water-solubilized KcsA. Proc Natl Acad Sci U S A. 2008;105(43):16537–16542. doi: 10.1073/pnas.0805501105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Perez-Aguilar JM, Xi J, Matsunaga F, et al. A computationally designed water-soluble variant of a G-protein-coupled receptor: the human mu opioid receptor. PLoS ONE. 2013;8(6):e66009. doi: 10.1371/journal.pone.0066009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhukovsky EA, Morse RJ, Maus MV. Bispecific antibodies and CARs: generalized immunotherapeutics harnessing T cell redirection. Curr Opin Immunol. 2016;40:24–35. doi: 10.1016/j.coi.2016.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Liu Z, Gunasekaran K, Wang W, et al. Asymmetrical Fc engineering greatly enhances antibody-dependent cellular cytotoxicity (ADCC) effector function and stability of the modified antibodies. J Biol Chem. 2014;289(6):3571–3590. doi: 10.1074/jbc.M113.513366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Byrne H, Conroy PJ, Whisstock JC, et al. A tale of two specificities: bispecific antibodies for therapeutic and diagnostic applications. Trends Biotechnol. 2013;31(11):621–632. doi: 10.1016/j.tibtech.2013.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Klein C, Sustmann C, Thomas M, et al. Progress in overcoming the chain association issue in bispecific heterodimeric IgG antibodies. MAbs. 2012;4(6):653–663. doi: 10.4161/mabs.21379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ridgway JB, Presta LG, Carter P. ‘Knobs-into-holes’ engineering of antibody CH3 domains for heavy chain heterodimerization. Protein Eng. 1996;9(7):617–621. doi: 10.1093/protein/9.7.617. [DOI] [PubMed] [Google Scholar]
- 30.Choi HJ, Kim YJ, Choi DK, et al. Engineering of immunoglobulin Fc heterodimers using yeast surface-displayed combinatorial Fc library screening. PLoS ONE. 2015;10(12):e0145349. doi: 10.1371/journal.pone.0145349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lazar GA, Dang W, Karki S, et al. Engineered antibody Fc variants with enhanced effector function. Proc Natl Acad Sci U S A. 2006;103(11):4005–4010. doi: 10.1073/pnas.0508123103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32••.Samish I, MacDermaid CM, Perez-Aguilar JM, et al. Theoretical and computational protein design. Annu Rev Phys Chem. 2011;62:129–149. doi: 10.1146/annurev-physchem-032210-103509. A book volume which provides a recent, rigorous review of popular methods employed in computational protein design, its challenges, implementations, and applications. Also includes specific examples of different protein designs and their respective experimental validation protocols. [DOI] [PubMed] [Google Scholar]
- 33.Samish I. The Framework of computational protein design. Methods Mol Biol. 2017;1529:3–19. doi: 10.1007/978-1-4939-6637-0_1. [DOI] [PubMed] [Google Scholar]
- 34••.Samish I. Achievements and challenges in computational protein design. Methods Mol Biol. 2017;1529:21–94. doi: 10.1007/978-1-4939-6637-0_2. Contains a detailed analysis of every computationally designed protein up to 2014. [DOI] [PubMed] [Google Scholar]
- 35.Whitehead TA, Chevalier A, Song Y, et al. Optimization of affinity, specificity and function of designed influenza inhibitors using deep sequencing. Nat Biotechnol. 2012;30(6):543–548. doi: 10.1038/nbt.2214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Samish I. Computational protein design. New York, NY: Humana Press; 2017. [Google Scholar]
- 37.Paladino A, Marchetti F, Rinaldi S, et al. Protein design: from computer models to artificial intelligence. Wiley Interdiscip Rev: Comput Mol Sci. 2017;7(5):e1318. [Google Scholar]
- 38.Yu F, Cangelosi VM, Zastrow ML, et al. Protein design: toward functional metalloenzymes. Chem Rev. 2014;114(7):3495–3578. doi: 10.1021/cr400458x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Pantazes RJ, Grisewood MJ, Maranas CD. Recent advances in computational protein design. Curr Opin Struct Biol. 2011;21(4):467–472. doi: 10.1016/j.sbi.2011.04.005. [DOI] [PubMed] [Google Scholar]
- 40.Hecht MH, Richardson JS, Richardson DC, et al. De novo design, expression, and characterization of felix: a four-helix bundle protein of native-like sequence. Science. 1989;249:884–891. doi: 10.1126/science.2392678. [DOI] [PubMed] [Google Scholar]
- 41.Dahiyat BI, Mayo SL. De novo protein design: fully automated sequence selection. Science. 1997;278:82–87. doi: 10.1126/science.278.5335.82. [DOI] [PubMed] [Google Scholar]
- 42.Kuhlman B, Dantas G, Ireton GC, et al. Design of a novel globular protein fold with atomic-level accuracy. Science. 2003;302(5649):1364–1368. doi: 10.1126/science.1089427. [DOI] [PubMed] [Google Scholar]
- 43.Lipman NS, Jackson LR, Trudel LJ, et al. Monoclonal versus polyclonal antibodies: distinguishing characteristics, applications, and information resources. Ilar J. 2005;46(3):258–268. doi: 10.1093/ilar.46.3.258. [DOI] [PubMed] [Google Scholar]
- 44.Godawat R, Brower K, Jain S, et al. Periodic counter-current chromatography – design and operational considerations for integrated and continuous purification of proteins. Biotechnol J. 2012;7(12):1496–1508. doi: 10.1002/biot.201200068. [DOI] [PubMed] [Google Scholar]
- 45.Ryman JT, Meibohm B. Pharmacokinetics of monoclonal antibodies. CPT Pharmacometrics Syst Pharmacol. 2017;6(9):576–588. doi: 10.1002/psp4.12224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gebauer M, Skerra A. Engineered protein scaffolds as next-generation antibody therapeutics. Curr Opin Chem Biol. 2009;13(3):245–255. doi: 10.1016/j.cbpa.2009.04.627. [DOI] [PubMed] [Google Scholar]
- 47.Valeur E, Gueret SM, Adihou H, et al. New modalities for challenging targets in drug discovery. Angew Chem Int Ed Engl. 2017;56(35):10294–10323. doi: 10.1002/anie.201611914. [DOI] [PubMed] [Google Scholar]
- 48.Goodman CM, Choi S, Shandler S, et al. Foldamers as versatile frameworks for the design and evolution of function. Nat Chem Biol. 2007;3(5):252–262. doi: 10.1038/nchembio876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Zhou J, Rossi J. Aptamers as targeted therapeutics: current potential and challenges. Nat Rev Drug Discov. 2017;16(3):181–202. doi: 10.1038/nrd.2016.199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Healy JM, Lewis SD, Kurz M, et al. Pharmacokinetics and biodistribution of novel aptamer compositions. Pharm Res. 2004;21(12):2234–2246. doi: 10.1007/s11095-004-7676-4. [DOI] [PubMed] [Google Scholar]
- 51.Wurch T, Pierre A, Depil S. Novel protein scaffolds as emerging therapeutic proteins: from discovery to clinical proof-of-concept. Trends Biotechnol. 2012;30(11):575–582. doi: 10.1016/j.tibtech.2012.07.006. [DOI] [PubMed] [Google Scholar]
- 52.Fleishman SJ, Corn JE, Strauch EM, et al. Hotspot-centric de novo design of protein binders. J Mol Biol. 2011;413(5):1047–1062. doi: 10.1016/j.jmb.2011.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Whitehead TA, Baker D, Fleishman SJ. Computational design of novel protein binders and experimental affinity maturation. Methods Enzymol. 2013;523:1–19. doi: 10.1016/B978-0-12-394292-0.00001-1. [DOI] [PubMed] [Google Scholar]
- 54.Woldring DR, Holec PV, Stern LA, et al. A gradient of sitewise diversity promotes evolutionary fitness for binder discovery in a three-helix bundle protein Scaffold. Biochemistry. 2017;56(11):1656–1671. doi: 10.1021/acs.biochem.6b01142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Craik DJ, Fairlie DP, Liras S, et al. The future of peptide-based drugs. Chem Biol Drug Des. 2013;81(1):136–147. doi: 10.1111/cbdd.12055. [DOI] [PubMed] [Google Scholar]
- 56.Bhardwaj G, Mulligan VK, Bahl CD, et al. Accurate de novo design of hyperstable constrained peptides. Nature. 2016;538(7625):329–335. doi: 10.1038/nature19791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Soudry-Kochavi L, Naraykin N, Nassar T, et al. Improved oral absorption of exenatide using an original nanoencapsulation and microencapsulation approach. J Control Release. 2015;217:202–210. doi: 10.1016/j.jconrel.2015.09.012. [DOI] [PubMed] [Google Scholar]
- 58.Daniels DS, Schepartz A. Intrinsically cell-permeable miniature proteins based on a minimal cationic PPII motif. J Am Chem Soc. 2007;129(47):14578–14579. doi: 10.1021/ja0772445. [DOI] [PubMed] [Google Scholar]
- 59.Smythe ML. Orally delivered peptides for treatment of inflammatory bowel disease. 2016. [Google Scholar]
- 60.Barkan DT, Cheng XL, Celino H, et al. Clustering of disulfide-rich peptides provides scaffolds for hit discovery by phage display: application to interleukin-23. BMC Bioinform. 2016;17(1):481. doi: 10.1186/s12859-016-1350-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Tran TT, Kulis C, Long SM, et al. Defining scaffold geometries for interacting with proteins: geometrical classification of secondary structure linking regions. J Comput Aided Mol Des. 2010;24(11):917–934. doi: 10.1007/s10822-010-9384-y. [DOI] [PubMed] [Google Scholar]
- 62.Long SM, Tran TT, Adams P, et al. Conformational searching using a population-based incremental learning algorithm. J Comput Chem. 2011;32(8):1541–1549. doi: 10.1002/jcc.21732. [DOI] [PubMed] [Google Scholar]
- 63.Bolon DN, Mayo SL. Enzyme-like proteins by computational design. Proc Natl Acad Sci U S A. 2001;98(25):14274–14279. doi: 10.1073/pnas.251555398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Rothlisberger D, Khersonsky O, Wollacott AM, et al. Kemp elimination catalysts by computational enzyme design. Nature. 2008;453(7192):190–195. doi: 10.1038/nature06879. [DOI] [PubMed] [Google Scholar]
- 65.Jiang L, Althoff EA, Clemente FR, et al. De novo computational design of retro-aldol enzymes. Science. 2008;319:1387–1391. doi: 10.1126/science.1152692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66••.Siegel JB, Zanghellini A, Lovick HM, et al. Computational design of an enzyme catalyst for a stereoselective bimolecular diels-alder reaction. Science. 2010;329:309–313. doi: 10.1126/science.1190239. One of the early successes on the design of new enzymes for reactions not catalyzed by naturally occurring biocatalysts, which demonstrate the power of combining computational design method with directed evolution. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67••.Reetz MT. What are the limitations of enzymes in synthetic organic chemistry? Chem Rec. 2016;16(6):2449–2459. doi: 10.1002/tcr.201600040. Perspective on enzyme protein engineering from the perspective of an organic chemist. [DOI] [PubMed] [Google Scholar]
- 68.Wolf C, Siegel JB, Tinberg C, et al. Engineering of Kuma030: a gliadin peptidase that rapidly degrades immunogenic gliadin peptides in gastric conditions. J Am Chem Soc. 2015;137(40):13106–13113. doi: 10.1021/jacs.5b08325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Gordon SR, Stanley EJ, Wolf S, et al. Computational design of an alpha-gliadin peptidase. J Am Chem Soc. 2012;134(50):20513–20520. doi: 10.1021/ja3094795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Senn HM, Thiel W. QM/MM methods for biomolecular systems. Angew Chem Int Ed Engl. 2009;48(7):1198–1229. doi: 10.1002/anie.200802019. [DOI] [PubMed] [Google Scholar]
- 71.Childers MC, Daggett V. Insights frommolecular dynamics simulations for computational protein design. Mol Syst Des Eng. 2017;2(1):9–33. doi: 10.1039/C6ME00083E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Privett HK, Kiss G, Lee TM, et al. Iterative approach to computational enzyme design. Proc Natl Acad Sci U S A. 2012;109(10):3790–3795. doi: 10.1073/pnas.1118082108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Tinberg CE, Khare SD, Dou J, et al. Computational design of ligand-binding proteins with high affinity and selectivity. Nature. 2013;501(7466):212–216. doi: 10.1038/nature12443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Muyldermans S. Single domain camel antibodies: current status. Rev Mol Biotechnol. 2001;74:277–302. doi: 10.1016/s1389-0352(01)00021-6. [DOI] [PubMed] [Google Scholar]
- 75.Havranek JJ. Specificity in computational protein design. J Biol Chem. 2010;285(41):31095–31099. doi: 10.1074/jbc.R110.157685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Mandell DJ, Kortemme T. Computer-aided design of functional protein interactions. Nat Chem Biol. 2009;5(11):797–807. doi: 10.1038/nchembio.251. [DOI] [PubMed] [Google Scholar]
- 77.Uversky VN. Adv Protein Chem Struct Biol. 2017. Intrinsic disorder, protein–protein interactions, and disease. [DOI] [PubMed] [Google Scholar]
- 78.Milroy LG, Grossmann TN, Hennig S, et al. Modulators of protein–protein interactions. Chem Rev. 2014;114(9):4695–4748. doi: 10.1021/cr400698c. [DOI] [PubMed] [Google Scholar]
- 79.Berg T. Inhibition of protein–protein interactions: new options for developing drugs against neglected tropical diseases. Angew Chem Int Ed Engl. 2017 doi: 10.1002/anie.201706479. [DOI] [PubMed] [Google Scholar]
- 80.Brender JR, Zhang Y. Protein–protein interactions and genetic disease. eLS. 2017 [Google Scholar]
- 81.Ivanov AA, Khuri FR, Fu H. Targeting protein–protein interactions as an anticancer strategy. Trends Pharmacol Sci. 2013;34(7):393–400. doi: 10.1016/j.tips.2013.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Moal IH, Moretti R, Baker D, et al. Scoring functions for protein–protein interactions. Curr Opin Struct Biol. 2013;23(6):862–867. doi: 10.1016/j.sbi.2013.06.017. [DOI] [PubMed] [Google Scholar]
- 83.Dagliyan O, Proctor EA, D’Auria KM, et al. Structural and dynamic determinants of protein–peptide recognition. Structure. 2011;19(12):1837–1845. doi: 10.1016/j.str.2011.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Karanicolas J, Kuhlman B. Computational design of affinity and specificity at protein–protein interfaces. Curr Opin Struct Biol. 2009;19(4):458–463. doi: 10.1016/j.sbi.2009.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Stranges PB, Kuhlman B. A comparison of successful and failed protein interface designs highlights the challenges of designing buried hydrogen bonds. Protein Sci. 2013;22(1):74–82. doi: 10.1002/pro.2187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Khersonsky O, Fleishman SJ. Incorporating an allosteric regulatory site in an antibody through backbone design. Protein Sci. 2017;26(4):807–813. doi: 10.1002/pro.3126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Kastritis PL, Rodrigues JP, Folkers GE, et al. Proteins feel more than they see: fine-tuning of binding affinity by properties of the non-interacting surface. J Mol Biol. 2014;426(14):2632–2652. doi: 10.1016/j.jmb.2014.04.017. [DOI] [PubMed] [Google Scholar]
- 88.Ghirlanda G. Design of membrane proteins: toward functional systems. Curr Opin Chem Biol. 2009;13(5–6):643–651. doi: 10.1016/j.cbpa.2009.09.017. [DOI] [PubMed] [Google Scholar]
- 89.Barth P, Senes A. Toward high-resolution computational design of the structure and function of helical membrane proteins. Nat Struct Mol Biol. 2016;23(6):475–480. doi: 10.1038/nsmb.3231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Feng X, Ambia J, Chen KM, et al. Computational design of ligand-binding membrane receptors with high selectivity. Nat Chem Biol. 2017;13(7):715–723. doi: 10.1038/nchembio.2371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Pierce NA, Winfree E. Protein design is NP-hard. Protein Eng. 2002;15:779–782. doi: 10.1093/protein/15.10.779. [DOI] [PubMed] [Google Scholar]
- 92.Roy A, Yang J, Zhang Y. COFACTOR: an accurate comparative algorithm for structure-based protein function annotation. Nucleic Acids Res. 2012;40(WebServer issue):W471–7. doi: 10.1093/nar/gks372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Socolich M, Lockless SW, Russ WP, et al. Evolutionary information for specifying a protein fold. Nature. 2005;437(7058):512–518. doi: 10.1038/nature03991. [DOI] [PubMed] [Google Scholar]
- 94.Morcos F, Pagnani A, Lunt B, et al. Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proc Natl Acad Sci U S A. 2011;108(49):E1293–301. doi: 10.1073/pnas.1111471108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95••.Rocklin GJ, Chidyausiku TM, Goreshnik I, et al. Global analysis of protein folding using massively parallel design, synthesis, and testing. Science. 2017;357:168–175. doi: 10.1126/science.aan0693. Computational protein design guided by iterative feedback provided from high-throughput protein expressions made possible by the next generation gene synthesis opened a major breakthrough in increasing de novo protein stability and improving understanding of how sequence affects folding and stability in uncharted space. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Brender JR, Shultis D, Khattak NA, et al. An evolution-based approach to De Novo protein design. Methods Mol Biol. 2017;1529:243–264. doi: 10.1007/978-1-4939-6637-0_12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Mackenzie CO, Grigoryan G. Protein structural motifs in prediction and design. Curr Opin Struct Biol. 2017;44:161–167. doi: 10.1016/j.sbi.2017.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Burton DR, Weiss RA. A boost for HIV vaccine design. Science. 2010;329:770–773. doi: 10.1126/science.1194693. [DOI] [PubMed] [Google Scholar]
- 99.Huang PS, Boyken SE, Baker D. The coming of age of de novo protein design. Nature. 2016;537(7620):320–327. doi: 10.1038/nature19946. [DOI] [PubMed] [Google Scholar]
- 100.Voet AR, Noguchi H, Addy C, et al. Computational design of a self-assembling symmetrical beta-propeller protein. Proc Natl Acad Sci U S A. 2014;111(42):15102–15107. doi: 10.1073/pnas.1412768111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Durani S. Protein design with L- and D-α-amino acid structures as the alphabet. Acc Chem Res. 2008;41(10):1301–1308. doi: 10.1021/ar700265t. [DOI] [PubMed] [Google Scholar]
- 102••.Mandell DJ, Kortemme T. Backbone flexibility in computational protein design. Curr Opin Biotechnol. 2009;20(4):420–428. doi: 10.1016/j.copbio.2009.07.006. A good article showing the importance of backbone flexibility in functional protein design by taking into account the role of conformational variability in controlling biological processes. [DOI] [PubMed] [Google Scholar]
- 103.Davis IW, Arendall WB, 3rd, Richardson DC, et al. The backrub motion: how protein backbone shrugs when a sidechain dances. Structure. 2006;14(2):265–274. doi: 10.1016/j.str.2005.10.007. [DOI] [PubMed] [Google Scholar]
- 104.Ramachandran GN, Ramakrishnan C, Sasisekharan V. Stereochemistry of polypeptide chain configurations. J Mol Biol. 1963;7(1):95–99. doi: 10.1016/s0022-2836(63)80023-6. [DOI] [PubMed] [Google Scholar]
- 105••.Gainza P, Nisonoff HM, Donald BR. Algorithms for protein design. Curr Opin Struct Biol. 2016;39:16–26. doi: 10.1016/j.sbi.2016.03.006. A good review covering the advantages and weaknesses of recent methods and algorithms developed and employed for computational protein design since 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Gainza P, Roberts KE, Georgiev I, et al. OSPREY: protein design with ensembles, flexibility, and provable algorithms. Methods Enzymol. 2013;523:87–107. doi: 10.1016/B978-0-12-394292-0.00005-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Harbury PB, Plecs JJ, Tidor B, et al. High-resolution protein design with backbone freedom. Science. 1998;282:1462–1467. doi: 10.1126/science.282.5393.1462. [DOI] [PubMed] [Google Scholar]
- 108.Koga N, Tatsumi-Koga R, Liu G, et al. Principles for designing ideal protein structures. Nature. 2012;491(7423):222–227. doi: 10.1038/nature11600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109••.Lin Y-R, Koga N, Tatsumi-Koga R, et al. Control over overall shape and size in de novo designed proteins. Proc Natl Acad Sci U S A. 2015;112:E5478–85. doi: 10.1073/pnas.1509508112. An important paper showing an approach to designing ideal protein structures stabilized by peptide building blocks governed by completely consistent local and non-local interactions, which may become the foundation for designing de novo protein topologies. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Janin J, Wodak S, Levitt M, et al. Conformation of amino acid side-chains in proteins. J Mol Biol. 1978;125:357–386. doi: 10.1016/0022-2836(78)90408-4. [DOI] [PubMed] [Google Scholar]
- 111.Ponder JW, Richards FM. Tertiary templates for proteins: use of packing criteria in the enumeration of allowed sequences for different structural classes. J Mol Biol. 1987;193:775–791. doi: 10.1016/0022-2836(87)90358-5. [DOI] [PubMed] [Google Scholar]
- 112.Dunbrack RLJ, Karplus M. Backbone-dependent rotamer library for proteins application to side-chain prediction. J Mol Biol. 1993;230(2):543–574. doi: 10.1006/jmbi.1993.1170. [DOI] [PubMed] [Google Scholar]
- 113.Jiang L, Kuhlman B, Kortemme T, et al. A “solvated rotamer” approach to modeling water-mediated hydrogen bonds at protein–protein interfaces. Proteins. 2005;58(4):893–904. doi: 10.1002/prot.20347. [DOI] [PubMed] [Google Scholar]
- 114.Schymkowitz JW, Rousseau F, Martins IC, et al. Prediction of water and metal binding sites and their affinities by using the Fold-X force field. Proc Natl Acad Sci U S A. 2005;102(29):10147–10152. doi: 10.1073/pnas.0501980102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Shapovalov MV, Dunbrack RL., Jr A smoothed backbone-dependent rotamer library for proteins derived from adaptive kernel density estimates and regressions. Structure. 2011;19(6):844–858. doi: 10.1016/j.str.2011.03.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Brutscher B, Felli IC, Gil-Caballero S, et al. NMRmethods for the study of instrinsically disordered proteins structure, dynamics, and interactions: general overview and practical guidelines. In: Felli IC, Pierattelli R, editors. Intrinsically disordered proteins studied by NMR sPECTROSCOPY. Cham: Springer International Publishing; 2015. pp. 49–122. [DOI] [PubMed] [Google Scholar]
- 117.Schneider M, Fu XR, Keating AE. X-ray vs. NMR structures as templates for computational protein design. Proteins: Struct Funct Bioinform. 2009;77(1):97–110. doi: 10.1002/prot.22421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Bai XC, McMullan G, Scheres SH. How cryo-EM is revolutionizing structural biology. Trends Biochem Sci. 2015;40(1):49–57. doi: 10.1016/j.tibs.2014.10.005. [DOI] [PubMed] [Google Scholar]
- 119.Wang RY, Kudryashev M, Li X, et al. De novo protein structure determination from near-atomic-resolution cryo-EM maps. Nat Methods. 2015;12(4):335–338. doi: 10.1038/nmeth.3287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Towse CL, Rysavy SJ, Vulovic IM, et al. New dynamic rotamer libraries: data-driven analysis of side-chain conformational propensities. Structure. 2016;24(1):187–199. doi: 10.1016/j.str.2015.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Scouras AD, Daggett V. The dynameomics rotamer library: amino acid side chain conformations and dynamics from comprehensive molecular dynamics simulations in water. Protein Sci. 2011;20(2):341–352. doi: 10.1002/pro.565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Schymkowitz J, Borg J, Stricher F, et al. The FoldX web server: an online force field. Nucleic Acids Res. 2005;33(WebServer issue):W382–8. doi: 10.1093/nar/gki387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Gainza P, Roberts KE, Donald BR. Protein design using continuous rotamers. PLoS Comput Biol. 2012;8(1):e1002335. doi: 10.1371/journal.pcbi.1002335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Delaforge E, Milles S, Huang JR, et al. Investigating the role of large-scale domain dynamics in protein–protein interactions. Front Mol Biosci. 2016;3:54. doi: 10.3389/fmolb.2016.00054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Christensen AS, Kubar T, Cui Q, et al. Semiempirical quantum mechanical methods for noncovalent interactions for chemical and biochemical applications. Chem Rev. 2016;116(9):5301–5337. doi: 10.1021/acs.chemrev.5b00584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Kmiecik S, Gront D, Kolinski M, et al. Coarse-grained protein models and their applications. Chem Rev. 2016;116(14):7898–7936. doi: 10.1021/acs.chemrev.6b00163. [DOI] [PubMed] [Google Scholar]
- 127.Tozzini V. Coarse-grained models for proteins. Curr Opin Struct Biol. 2005;15(2):144–150. doi: 10.1016/j.sbi.2005.02.005. [DOI] [PubMed] [Google Scholar]
- 128.Leaver-Fay A, Tyka M, Lewis SM, et al. ROSETTA3: an object-oriented software suite for the simulation and design of macromolecules. Methods Enzymol. 2011;487:545–574. doi: 10.1016/B978-0-12-381270-4.00019-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Leaver-Fay A, O’Meara MJ, Tyka M, et al. Scientific benchmarks for guiding macromolecular energy function improvement. Methods Enzymol. 2013;523:109–143. doi: 10.1016/B978-0-12-394292-0.00006-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Dyson HJ, Wright PE. Unfolded proteins and protein folding studied by NMR. Chem Rev. 2004;104:3607–3622. doi: 10.1021/cr030403s. [DOI] [PubMed] [Google Scholar]
- 131••.Petrov D, Zagrovic B. Are current atomistic force fields accurate enough to study proteins in crowded environments? PLoS Comput Biol. 2014;10(5):e1003638. doi: 10.1371/journal.pcbi.1003638. Using a series of Molecular Dynamics simulations, the article shows the weaknesses of current atomistic force fields in capturing protein behavior in a biologically relevant, crowded, high protein concentration environments, which is argued is due to a general overestimation of the potential energy of protein–protein interactions at the expense of water–water and water–protein interactions. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Traore S, Roberts KE, Allouche D, et al. Fast search algorithms for computational protein design. J Comput Chem. 2016;37(12):1048–1058. doi: 10.1002/jcc.24290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Voigt CA, Gordon DB, Mayo SL. Trading accuracy for speed: a quantitative comparison of search algorithms in protein sequence design. J Mol Biol. 2000;299(3):789–803. doi: 10.1006/jmbi.2000.3758. [DOI] [PubMed] [Google Scholar]
- 134.Karplus M, Lavery R. Significance of molecular dynamics simulations for life sciences. Isr J Chem. 2014;54(8–9):1042–1051. [Google Scholar]
- 135.Pokala N, Handel TM. Energy functions for protein design: adjustment with protein–protein complex affinities, models for the unfolded state, and negative design of solubility and specificity. J Mol Biol. 2005;347(1):203–227. doi: 10.1016/j.jmb.2004.12.019. [DOI] [PubMed] [Google Scholar]
- 136.Kellogg EH, Leaver-Fay A, Baker D. Role of conformational sampling in computing mutation-induced changes in protein structure and stability. Proteins: Structure Funct Bioinform. 2011;79(3):830–838. doi: 10.1002/prot.22921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Boas FE, Harbury PB. Potential energy functions for protein design. Curr Opin Struct Biol. 2007;17(2):199–204. doi: 10.1016/j.sbi.2007.03.006. [DOI] [PubMed] [Google Scholar]
- 138.Lazaridis T, Karplus M. Effective energy function for proteins in solution. Proteins. 1999;35:133–152. doi: 10.1002/(sici)1097-0134(19990501)35:2<133::aid-prot1>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 139.Villa F, Mignon D, Polydorides S, et al. Comparing pairwise-additive and many-body generalized Born models for acid/base calculations and protein design. J Comput Chem. 2017;38(28):2396–2410. doi: 10.1002/jcc.24898. [DOI] [PubMed] [Google Scholar]
- 140.Genheden S, Ryde U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin Drug Discov. 2015;10(5):449–461. doi: 10.1517/17460441.2015.1032936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Chen F, Liu H, Sun H, et al. Assessing the performance of the MM/PBSA and MM/GBSA methods. 6. Capability to predict protein–protein binding free energies and re-rank binding poses generated by protein–protein docking. Phys Chem Chem Phys. 2016;18(32):22129–22139. doi: 10.1039/c6cp03670h. [DOI] [PubMed] [Google Scholar]
- 142.Street AG, Mayo SL. Pairwise calculation of protein solvent-accessible surface areas. Fold Des. 1998;3(4):253–258. doi: 10.1016/S1359-0278(98)00036-4. [DOI] [PubMed] [Google Scholar]
- 143.Li L, Li C, Zhang Z, et al. On the dielectric “constant” of proteins: smooth dielectric function for macromolecular modeling and its implementation in DelPhi. J Chem Theory Comput. 2013;9(4):2126–2136. doi: 10.1021/ct400065j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Grochowski P, Trylska J. Continuum molecular electrostatics, salt effects, and counterion binding–a review of the Poisson-Boltzmann theory and its modifications. Biopolymers. 2008;89(2):93–113. doi: 10.1002/bip.20877. [DOI] [PubMed] [Google Scholar]
- 145.Onufriev A, Case DA, Bashford D. Effective Born radii in the generalized Born approximation: the importance of being perfect. J Comput Chem. 2002;23(14):1297–1304. doi: 10.1002/jcc.10126. [DOI] [PubMed] [Google Scholar]
- 146.Pokala N, Handel TM. Energy functions for protein design I: efficient and accurate continuum electrostatics and solvation. Protein Sci. 2004;13(4):925–936. doi: 10.1110/ps.03486104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 147.Gaillard T, Simonson T. Pairwise decomposition of an MMGBSA energy function for computational protein design. J Comput Chem. 2014;35(18):1371–1387. doi: 10.1002/jcc.23637. [DOI] [PubMed] [Google Scholar]
- 148.Lazaridis T, Karplus M. Effective energy function for proteins in solution. Proteins. 1999;35(2):133–152. doi: 10.1002/(sici)1097-0134(19990501)35:2<133::aid-prot1>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 149.Gordon DB, Marshall SA, Mayo SL. Energy functions for protein design. Curr Opin Struct Biol. 1999;9(4):509–513. doi: 10.1016/s0959-440x(99)80072-4. [DOI] [PubMed] [Google Scholar]
- 150••.Mitra P, Shultis D, Brender JR, et al. An evolution-based approach to de novo protein design and case study on Mycobacterium tuberculosis. PLoS Comput Biol. 2013;9(10):e1003298. doi: 10.1371/journal.pcbi.1003298. Proposes a new method of protein design based on structural profiles collected from structurally similar proteins and of validating designs computationally by protein structure prediction. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Hubbard RE, Kamran Haider M. Hydrogen bonds in proteins: role and strength. 2010. [Google Scholar]
- 152.Kortemme T, Morozov AV, Baker D. An orientation-dependent hydrogen bonding potential improves prediction of specificity and structure for proteins and protein–protein complexes. J Mol Biol. 2003;326(4):1239–1259. doi: 10.1016/s0022-2836(03)00021-4. [DOI] [PubMed] [Google Scholar]
- 153.O’Meara MJ, Leaver-Fay A, Tyka MD, et al. Combined covalent-electrostatic model of hydrogen bonding improves structure prediction with Rosetta. J Chem Theory Comput. 2015;11(2):609–622. doi: 10.1021/ct500864r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Liu J, Wang R. Classification of current scoring functions. J Chem Inf Model. 2015;55(3):475–482. doi: 10.1021/ci500731a. [DOI] [PubMed] [Google Scholar]
- 155.Simonson T, Gaillard T, Mignon D, et al. Computational protein design: the proteus software and selected applications. J Comput Chem. 2013;34(28):2472–2484. doi: 10.1002/jcc.23418. [DOI] [PubMed] [Google Scholar]
- 156.Bowler BE. Residual structure in unfolded proteins. Curr Opin Struct Biol. 2012;22(1):4–13. doi: 10.1016/j.sbi.2011.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Hackel M, Konno T, Hinz HJ. A new alternative method to quantify residual structure in ‘unfolded’ proteins. Biochim Biophys Acta Protein Struct Mol Enzymol. 2000;1479(1–2):155–165. doi: 10.1016/s0167-4838(00)00051-0. [DOI] [PubMed] [Google Scholar]
- 158.Ain QU, Aleksandrova A, Roessler FD, et al. Machine-learning scoring functions to improve structure-based binding affinity prediction and virtual screening. Wiley Interdiscip Rev Comput Mol Sci. 2015;5(6):405–424. doi: 10.1002/wcms.1225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 159.Botu V, Batra R, Chapman J, et al. Machine learning force fields: construction validation, and outlook. J Phys Chem C. 2017;121(1):511–522. [Google Scholar]
- 160.Holley LH, Karplus M. Protein secondary structure prediction with a neural network. Proc Natl Acad Sci U S A. 1989;86:152–156. doi: 10.1073/pnas.86.1.152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161.Barik A, Nithin C, Karampudi NB, et al. Probing binding hot spots at protein–RNA recognition sites. Nucleic Acids Res. 2016;44(2):e9. doi: 10.1093/nar/gkv876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162.Brender JR, Zhang Y. Predicting the effect of mutations on protein–protein binding interactions through structure-based interface profiles. PLoS Comput Biol. 2015;11(10):e1004494. doi: 10.1371/journal.pcbi.1004494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 163.Zhao N, Han JG, Shyu CR, et al. Determining effects of non-synonymous SNPs on protein–protein interactions using supervised and semi-supervised learning. PLoS Comput Biol. 2014;10(5):e1003592. doi: 10.1371/journal.pcbi.1003592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164.Shen J, Zhang J, Luo X, et al. Predicting protein–protein interactions based only on sequences information. Proc Natl Acad Sci U S A. 2007;104(11):4337–4341. doi: 10.1073/pnas.0607879104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.Mitra P, Shultis D, Zhang Y. EvoDesign: de novo protein design based on structural and evolutionary profiles. Nucleic Acids Res. 2013;41(Web Server issue):W273–80. doi: 10.1093/nar/gkt384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166.Lenselink EB, Jespers W, van Vlijmen HW, et al. Interacting with GPCRs: using interaction fingerprints for virtual screening. J Chem Inf Model. 2016;56(10):2053–2060. doi: 10.1021/acs.jcim.6b00314. [DOI] [PubMed] [Google Scholar]
- 167.Pires DE, Blundell TL, Ascher DB. mCSM-lig: quantifying the effects of mutations on protein-small molecule affinity in genetic disease and emergence of drug resistance. Sci Rep. 2016;6:29575. doi: 10.1038/srep29575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168.Da C, Kireev D. Structural protein–ligand interaction fingerprints (SPLIF) for structure-based virtual screening: method and benchmark study. J Chem Inf Model. 2014;54(9):2555–2561. doi: 10.1021/ci500319f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169.Mackerell AD., Jr Empirical force fields for biological macromolecules: overview and issues. J Comput Chem. 2004;25(13):1584–1604. doi: 10.1002/jcc.20082. [DOI] [PubMed] [Google Scholar]
- 170.Selzer T, AlbecK S, Schreiber G. Rational design of faster associating and tighter binding protein complexes. Nat Struct Biol. 2000;7:537–541. doi: 10.1038/76744. [DOI] [PubMed] [Google Scholar]
- 171.Liu Y, Kuhlman B. RosettaDesign server for protein design. Nucleic Acids Res. 2006;34(Web Server issue):W235–8. doi: 10.1093/nar/gkl163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Desmet J, Maeyer MD, Hazes B, et al. The dead-end elimination theorem and its use in protein side-chain positioning. Nature. 1992;356(6369):539–542. doi: 10.1038/356539a0. [DOI] [PubMed] [Google Scholar]
- 173.Goldstein RF. Efficient rotamer elimination applied to protein side-chains and related spin glasses. Biophys J. 1994;66:1335–1440. doi: 10.1016/S0006-3495(94)80923-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 174.Zhu Y. Mixed-Integer linear programming algorithm for a computational protein design problem. Ind Eng Chem Res. 2007;46:839–845. [Google Scholar]
- 175.Saraf MC, Moore GL, Goodey NM, et al. IPRO: an iterative computational protein library redesign and optimization procedure. Biophys J. 2006;90(11):4167–4180. doi: 10.1529/biophysj.105.079277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 176.Gordon DB, Mayo SL. Branch-and-Terminate: a combinatorial optimization algorithm for protein design. Structure. 1999;7:1089–1098. doi: 10.1016/s0969-2126(99)80176-2. [DOI] [PubMed] [Google Scholar]
- 177.Koehl P, Delarue M. Appplication of a self-consistent mean field theory to predict protein side-chains conformations and estimate their conformational theory. J Mol Biol. 1994;239:249–275. doi: 10.1006/jmbi.1994.1366. [DOI] [PubMed] [Google Scholar]
- 178.Desmet J, Spriet J, Lasters I. Fast and accurate side-chain topology and energy refinement (FASTER) as a new method for protein structure optimization. Proteins. 2002;48(1):31–43. doi: 10.1002/prot.10131. [DOI] [PubMed] [Google Scholar]
- 179.Leach AR, Lemon AP. Exploring the conformational space of protein side chains using dead-end elimination and the A* algorithm. Proteins. 1998;33:227–239. doi: 10.1002/(sici)1097-0134(19981101)33:2<227::aid-prot7>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- 180.Allen BD, Mayo SL. Dramatic performance enhancements for the FASTER optimization algorithm. J Comput Chem. 2006;27(10):1071–1075. doi: 10.1002/jcc.20420. [DOI] [PubMed] [Google Scholar]
- 181.Tian Y, Huang X, Zhu1 Y. Computational design of enzyme–ligand binding using a combined energy function and deterministic sequence optimization algorithm. J Mol Model. 2015:21. doi: 10.1007/s00894-015-2742-x. [DOI] [PubMed] [Google Scholar]
- 182.Yang X, Saven JG. Computational methods for protein design and protein sequence variability: biased Monte Carlo and replica exchange. Chem Phys Lett. 2005;401(1–3):205–210. [Google Scholar]
- 183.Druart K, Bigot J, Audit E, et al. A hybrid monte carlo scheme for multibackbone protein design. J Chem Theory Comput. 2016;12(12):6035–6048. doi: 10.1021/acs.jctc.6b00421. [DOI] [PubMed] [Google Scholar]
- 184.Mignon D, Simonson T. Comparing three stochastic search algorithms for computational protein design: Monte Carlo, replica exchange Monte Carlo, and a multistart, steepest-descent heuristic. J Comput Chem. 2016;37(19):1781–1793. doi: 10.1002/jcc.24393. [DOI] [PubMed] [Google Scholar]
- 185.Saven JG. Combinatorial protein design. Curr Opin Struct Biol. 2002;12(4):453–458. doi: 10.1016/s0959-440x(02)00347-0. [DOI] [PubMed] [Google Scholar]
- 186.Jones DT. De novo protein design using pairwise potentials and a genetic algorithm. Protein Sci. 1994;3:567–574. doi: 10.1002/pro.5560030405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 187.Shah DK. Pharmacokinetic and pharmacodynamic considerations for the next generation protein therapeutics. J Pharmacokinet Pharmacodyn. 2015;42(5):553–571. doi: 10.1007/s10928-015-9447-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 188.Tobin PH, Richards DH, Callender RA, et al. Protein engineering: a new frontier for biological therapeutics. Curr Drug Metab. 2014;15(7):743–756. doi: 10.2174/1389200216666141208151524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 189.Jacak R, Leaver-Fay A, Kuhlman B. Computational protein design with explicit consideration of surface hydrophobic patches. Proteins. 2012;80(3):825–838. doi: 10.1002/prot.23241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 190.Sormanni P, Aprile FA, Vendruscolo M. The CamSol method of rational design of protein mutants with enhanced solubility. J Mol Biol. 2015;427(2):478–490. doi: 10.1016/j.jmb.2014.09.026. [DOI] [PubMed] [Google Scholar]
- 191••.Broom A, Jacobi Z, Trainor K, et al. Computational tools help improve protein stability but with a solubility tradeoff. J Biol Chem. 2017;292(35):14349–14361. doi: 10.1074/jbc.M117.784165. Examination of the solubility/stability tradeoff with common design scoring functions. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 192.Parker AS, Choi Y, Griswold KE, et al. Structure-guided deimmunization of therapeutic proteins. J Comput Biol. 2013;20(2):152–165. doi: 10.1089/cmb.2012.0251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 193.Parker AS, Zheng W, Griswold KE, et al. Optimization algorithms for functional deimmunization of therapeutic proteins. BMC Bioinform. 2010;11:180. doi: 10.1186/1471-2105-11-180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 194.King C, Garza EN, Mazor R, et al. Removing T-cell epitopes with computational protein design. Proc Natl Acad Sci U S A. 2014;111(23):8577–8582. doi: 10.1073/pnas.1321126111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 195.Sharabi O, Dekel A, Shifman JM. Triathlon for energy functions: who is the winner for design of protein–protein interactions? Proteins: Struct Funct Bioinform. 2011;79(5):1487–1498. doi: 10.1002/prot.22977. [DOI] [PubMed] [Google Scholar]
- 196••.Chevalier A, Silva DA, Rocklin GJ, et al. Massively parallel de novo protein design for targeted therapeutics. Nature. 2017;550(7674):74–79. doi: 10.1038/nature23912. An application of massively parallel protein design for creating small proteins targeting specific therapeutic targets. The design is process is guided by iterative feedback provided from high-throughput protein expressions and characterizations to improve the computational design at each design cycle. The designed proteins show high stability and activity and show to provide potent prophylactic and therapeutic protection against influenza, even after extensive repeated dosing. [DOI] [PMC free article] [PubMed] [Google Scholar]