Efficient collective swimming by harnessing vortices through deep reinforcement learning

Significance

Can fish reduce their energy expenditure by schooling? We answer affirmatively this longstanding question by combining state-of-the-art direct numerical simulations of the 3D Navier–Stokes equations with reinforcement learning, using recurrent neural networks with long short-term memory cells to account for the unsteadiness of the flow field. Surprisingly, we find that swimming behind a leader is not always associated with energetic benefits for the follower. In turn, we demonstrate that fish can improve their sustained propulsive efficiency by placing themselves at appropriate locations in the wake of other swimmers and intercepting their wake vortices judiciously. The results show that autonomous, “smart” swimmers may exploit unsteady flow fields to reap substantial energetic benefits and have promising implications for robotic swarms.

Abstract

Fish in schooling formations navigate complex flow fields replete with mechanical energy in the vortex wakes of their companions. Their schooling behavior has been associated with evolutionary advantages including energy savings, yet the underlying physical mechanisms remain unknown. We show that fish can improve their sustained propulsive efficiency by placing themselves in appropriate locations in the wake of other swimmers and intercepting judiciously their shed vortices. This swimming strategy leads to collective energy savings and is revealed through a combination of high-fidelity flow simulations with a deep reinforcement learning (RL) algorithm. The RL algorithm relies on a policy defined by deep, recurrent neural nets, with long–short-term memory cells, that are essential for capturing the unsteadiness of the two-way interactions between the fish and the vortical flow field. Surprisingly, we find that swimming in-line with a leader is not associated with energetic benefits for the follower. Instead, “smart swimmer(s)” place themselves at off-center positions, with respect to the axis of the leader(s) and deform their body to synchronize with the momentum of the oncoming vortices, thus enhancing their swimming efficiency at no cost to the leader(s). The results confirm that fish may harvest energy deposited in vortices and support the conjecture that swimming in formation is energetically advantageous. Moreover, this study demonstrates that deep RL can produce navigation algorithms for complex unsteady and vortical flow fields, with promising implications for energy savings in autonomous robotic swarms.

There is a long-standing interest for understanding and exploiting the physical mechanisms used by active swimmers in nature (nektons) (1–4). Fish schooling, in particular, one of the most striking patterns of collective behavior and complex decision-making in nature, has been the subject of intense investigation (5–9). A key issue in understanding fish-schooling behavior, and its potential for engineering applications (10), is the clarification of the role of the flow environment. Fish sense and navigate in complex flow fields full of mechanical energy that is distributed across multiple scales by vortices generated by obstacles and other swimming organisms (11, 12). There is evidence that their swimming behavior adapts to flow gradients (rheotaxis), and, in certain cases, it reflects energy-harvesting from such environments (13, 14). Hydrodynamic interactions have also been implicated in the fish-schooling patterns that form when individual fish adapt their motion to that of their peers, while compensating for flow-induced displacements. Recent experimental studies have argued that fish may interact beneficially with each other (9, 15, 16), but in ways that challenge (17) the earlier proposed mechanisms (5, 6) governing fish schooling. However, the role of hydrodynamics in fish schooling is not embraced universally (8, 18, 19), and there is limited quantitative information regarding the physical mechanisms that would explain such energetic benefits. Experimental (15, 16) and computational (20) studies of collective swimming have been hampered by the presence of multiple deforming bodies and their interactions with the flow field. Moreover, numerical simulations have demonstrated that a coherent swimming group cannot be sustained without exerting some form of control strategy on the swimmers (21, 22). Here, we use deep reinforcement learning [deep RL (23)] to discover such strategies for two autonomous and self-propelled swimmers and elucidate the physical mechanisms that enable efficient and sustained coordinated swimming.

During fish propulsion, body undulations and the sideways displacement of the caudal fin generate and inject a series of vortex rings in its wake (24–26). When fish swim in formation, these vortices may assist the locomotion of fish that intercept them judiciously, which in turn can reduce the collective swimming effort. Such vortex-induced benefits have been observed in trout, which curtail muscle use by capitalizing on energy injected in the flow by obstacles present in streams (13, 27). Here, we examine configurations of two and three self-propelled swimmers in a leader(s) –follower(s) arrangement and investigate the physical mechanisms that lead to energetically beneficial interactions by considering four distinct scenarios. Two of these involve smart followers that can make autonomous decisions when interacting with a leader’s wake and are referred to as interacting swimmers ($IS$) (e.g., the follower in Fig. 1). Additionally, we consider two distinct solitary swimmers ($SS$) that swim in isolation in an unbounded domain. In the case of interacting swimmers, ${IS}_{\eta }$ denotes swimmers that learn the most efficient way of swimming in the leader’s wake (without any positional constraints) and acquire a policy ${\pi }_{\eta }$ in the process. In turn, swimmer ${IS}_d$ attempts to minimize lateral deviations from the leader’s path, resulting in a locally optimal policy ${\pi }_d$. These autonomous swimmers take decisions by virtue of deep RL, using visual cues from their environment (Fig. 2A). The solitary swimmers ${SS}_{\eta }$ and ${SS}_d$ execute actions identical to ${IS}_{\eta }$ and ${IS}_d$, respectively, and serve as “control” configurations to assess how the absence of a leader’s wake impacts swimming-energetics.

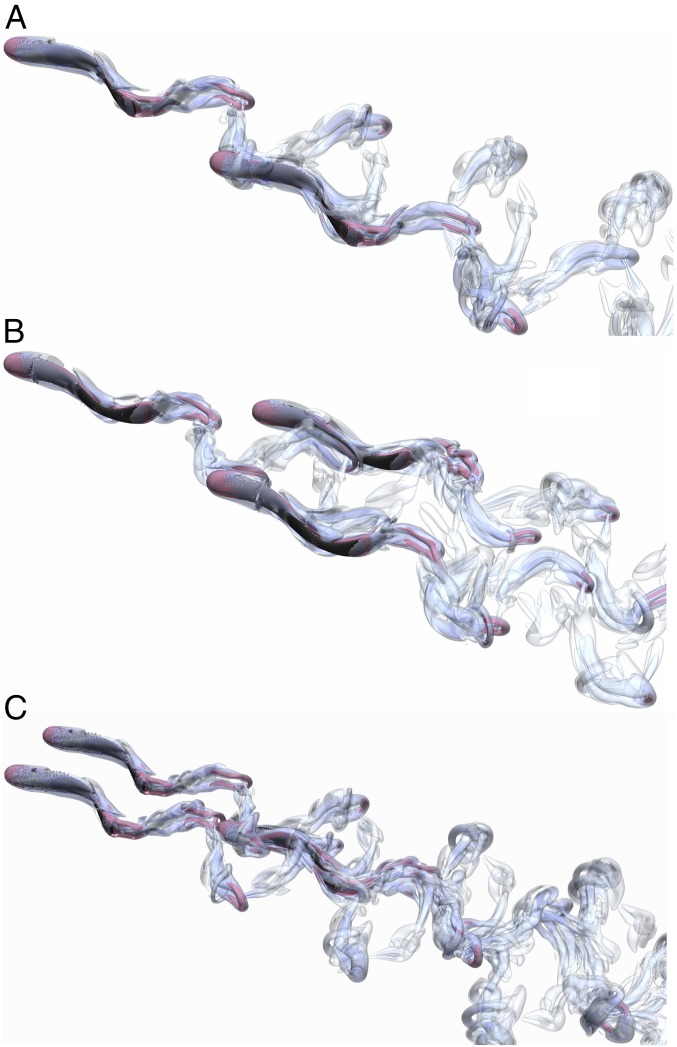
Fig. 1.

Efficient coordinated swimming of two and three swimmers. (A) DNS of two swimmers, in which the leader swims steadily and the follower maintains a specified relative position such that it increases its efficiency by interacting with one row of the vortex rings shed by the leader. The flow is visualized by isosurfaces of the Q criterion (28). (B) DNS of three swimmers, where the two followers maintain specified positions that increase their efficiency by interacting with both rows of the vortex rings shed by the leader. (C) DNS of three swimmers with the follower benefitting from one row of wake vortices generated by each leader. Animations of the 3D simulations are provided in Movies S1–S3.

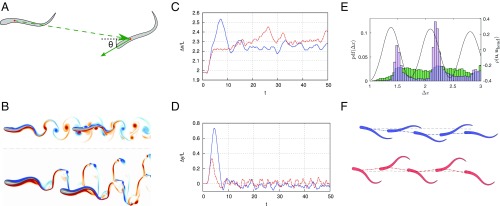
Fig. 2.

Learning efficient swimming strategies: Differences between 2D and 3D flow fields. (A) The smart swimmer relies on a predefined set of variables to identify its “observed state” (such as range and bearing relative to the leader that are depicted). Additional observed-state parameters are described in Methods. (B) Comparison of vorticity field in the wake of 2D (Upper) and cross-section of the 3D (Lower) swimmers (red, positive; blue, negative). In 2D, the leader’s wake vortices are aligned with its centerline. In contrast, in 3D flows, the wake vortices are diverging, leaving a quiescent region behind the leader. In 2D, smart followers must align with the leader’s centerline. In 3D, they must orient themselves at an angle to harness the wake vortex rings (WRs). Every half a tail-beat period, the smart follower in 2D simulations (${IS}_{\eta }$) autonomously selects the most appropriate action encoded in policy ${\pi }_{\eta }$ learned during training simulations, which allows it to maximize long-term swimming efficiency (Movie S4). The smart follower is capable of adapting to deviations in the leader’s trajectory (Movie S5), as these situations are encountered when performing random actions during training. (C) Relative horizontal displacement of the smart followers with respect to the leader, over a duration of 50 tail-beat periods starting from rest (solid blue line, ${IS}_{\eta }$; dash-dot red line, ${IS}_d$). (D) Lateral displacement of the smart followers. (E) Histogram showing the probability density function (PDF; left vertical axis) of swimmer ${IS}_{\eta }$’s preferred center-of-mass location during training. In the early stages of training (first 10,000 transitions; green bars), the swimmer does not show a strong preference for maintaining any particular separation distance. Toward the end of training (last 10,000 transitions; lilac bars), the swimmer displays a strong preference for maintaining a separation distance of either $\mathrm{\Delta }x=1.5L$ or $2.2L$. The solid black line depicts the correlation coefficient, with peaks in the black curve signifying locations where the smart follower’s head movement would be synchronized with the flow velocity in an undisturbed wake (see SI Appendix for relevant details). (F) Comparison of body deformation for swimmers ${IS}_{\eta }$ (Upper) and ${IS}_d$ (Lower), from $t=27$ to $t=29$. Their respective trajectories are shown with the dash-dot lines, whereas the dashed gray line represents the trajectory of the leader. A quantitative comparison of body curvature for the two swimmers may be found in SI Appendix, Fig. S1.

Deep RL for Swimmers

RL (29) has been introduced to identify navigation policies in several model systems of vortex dipoles, soaring birds and microswimmers (30–32). These studies often rely on simplified representations of organisms interacting with their environment, which allows them to model animal locomotion with reduced physical complexity and manageable computational cost. However, the simplifying assumptions inherent in such models often do not account for feedback of the animals’ motion on the environment. High-fidelity numerical simulations, although significantly more computationally demanding, can account for such important considerations to a greater extent, for instance, by allowing flapping or swimming motions that closely mimic the interaction of real animals with their environment. This makes them invaluable for investigating concepts that may be carried over readily to bioinspired robotic applications, with minimal modification. This consideration has motivated our present study, where we expand on our earlier work (33), combining RL with direct numerical simulations (DNSs) of the Navier–Stokes (NS) equations for self-propelled autonomous swimmers. We first investigate 2D swimmers in a tandem configuration to scrutinize the strategy adopted by the RL algorithm for attaining the specified goals. Based on the observed behavior and the physical intuition we gain from examining these smart swimmers, we formulate simplified rules for implementing active control in significantly more complex 3D systems. This reverse-engineering approach allows us to determine simple and effective control rules from a data-driven perspective, without having to rely on simplistic models which may introduce errors owing to underlying assumptions.

Efficient Autonomous Swimmers

We first analyze the kinematics of swimmers ${IS}_{\eta }$ and ${IS}_d$ (Fig. 2), which were described previously, and were trained to attain specific high-level objectives via deep RL (see Methods for details). In both cases, the swimmer trails a leader representing an adult zebrafish of length L, swimming steadily at a velocity U, with tail-beat period T [Reynolds number $Re=L^2/\left(T\nu \right)\approx 5000$]. After training, we observe that ${IS}_d$ is able to maintain its position behind the leader quite effectively ($\mathrm{\Delta }y\approx 0$; Fig. 2D), in accordance to its reward ($R_d=1-\left|\mathrm{\Delta }y\right|/L$). Surprisingly, ${IS}_{\eta }$ with a reward function proportional to swimming efficiency ($R_{\eta }=\eta$), also settles close to the center of the leader’s wake (Fig. 2D and Movie S4), although it receives no reward related to its relative position. This decision to interact actively with the unsteady wake has significant energetic implications, as described later in the text. Both ${IS}_d$ and ${IS}_{\eta }$ maintain a distance of $\mathrm{\Delta }x\approx 2.2L$ from their respective leaders (Fig. 2C). ${IS}_{\eta }$ shows a greater proclivity to maintain this separation and intercepts the periodically shed wake vortices just after they have been fully formed and detach from the leader’s tail. In addition to $\mathrm{\Delta }x=2.2L$, there is an additional point of stability at $\mathrm{\Delta }x=1.5$ (Fig. 2E). The difference $0.7L$ matches the distance between vortices in the wake of the leader. In both positions, the lateral motion of the follower’s head is synchronized with the flow velocity in the leader’s wake, thus inducing minimal disturbance on the oncoming flow field. We note that a similar synchronization with the flow velocity has been observed when trout minimize muscle use by interacting with vortex columns in a cylinder’s wake (13). ${IS}_{\eta }$ undergoes relatively minor body deformation while maneuvering (Fig. 2F), whereas ${IS}_d$ executes aggressive turns involving large body curvature. Trout interacting with cylinder wakes exhibit increased body curvature (27), which is contrary to the behavior displayed by ${IS}_{\eta }$. The difference may be ascribed to the widely spaced vortex columns generated by large-diameter cylinders used in the experimental study; weaving in and out of comparatively smaller vortices generated by like-sized fish encountered in a school (Fig. 2B) would entail excessive energy consumption.

We note that maintaining $\mathrm{\Delta }y=0$ requires significant effort by ${IS}_d$ (SI Appendix, Fig. S2D), which is expected, as this swimmer’s reward ($R_d$) is insensitive to energy expenditure. One of our previous studies (33) demonstrated that minimizing lateral displacement led to enhanced swimming efficiency (compared with the leader), albeit with noticeable deviation from $\mathrm{\Delta }y=0$. This conclusion is markedly different from our current observation and can be attributed to the use of improved learning techniques which are better able to achieve the specified goal. In the present study, recurrent neural networks augmented with “long short-term memory” cells (SI Appendix, Fig. S3) help encode time dependencies in the value function and produce far more robust smart swimmers than simpler feedforward networks (33). The performance of our deep recurrent network is compared with that of a feedforward network in SI Appendix, Fig. S4 and indicates that the deep network is better able to achieve the goal of in-line following, but at the penalty of increased energy expenditure. As a result, ${IS}_d$ succeeds in correcting for oscillations about $\mathrm{\Delta }y=0$ much more effectively by undergoing severe body undulations (Fig. 2F), leading to increased costs (SI Appendix, Fig. S2). These observations confirm that following a leader indiscriminately can be disadvantageous if energetic considerations are not taken into account. Thus, it is unlikely that strict in-line swimming is used as a collective-swimming strategy in nature, and fish presumably adopt a strategy closer to that of ${IS}_{\eta }$, by coordinating their motion with the wake flow. We note that patterns similar to the ones reported in this study have been observed in a recent experimental study (17). The behavior of swimmer ${IS}_{\eta }$ is also compared qualitatively to that of a real fish following a companion in Movie S6, and we observe that the motion of ${IS}_{\eta }$ resembles the swimming behavior of the live follower quite well.

Intercepting Vortices for Efficient Swimming

To determine the impact of wake-induced interactions on swimming performance, we compare energetics data for ${IS}_{\eta }$ and ${SS}_{\eta }$ in Fig. 3. The swimming efficiency of ${IS}_{\eta }$ is significantly higher than that of ${SS}_{\eta }$ (Fig. 3A), and the cost of transport (CoT), which represents energy spent for traversing a unit distance, is lower (Fig. 3B). Over a duration of 10 tail-beat periods (from $t=20$ to $t=30$; SI Appendix, Fig. S2) ${IS}_{\eta }$ experiences a $11\%$ increase in average speed compared with ${SS}_{\eta }$, a $32\%$ increase in average swimming efficiency and a $36\%$ decrease in CoT. The benefit for ${IS}_{\eta }$ results from both a $29\%$ reduction in effort required for deforming its body against flow-induced forces ($P_{Def}$) and a $53\%$ increase in average thrust power ($P_{Thrust}$). Performance differences between ${IS}_{\eta }$ and ${SS}_{\eta }$ exist solely due to the presence/absence of a preceding wake, since both swimmers undergo identical body undulations throughout the simulations. Comparing the swimming efficiency and power values of four distinct swimmers (SI Appendix, Fig. S2 and Table S1), we confirm that ${IS}_{\eta }$ and ${SS}_{\eta }$ are considerably more energetically efficient than either ${IS}_d$ or ${SS}_d$.

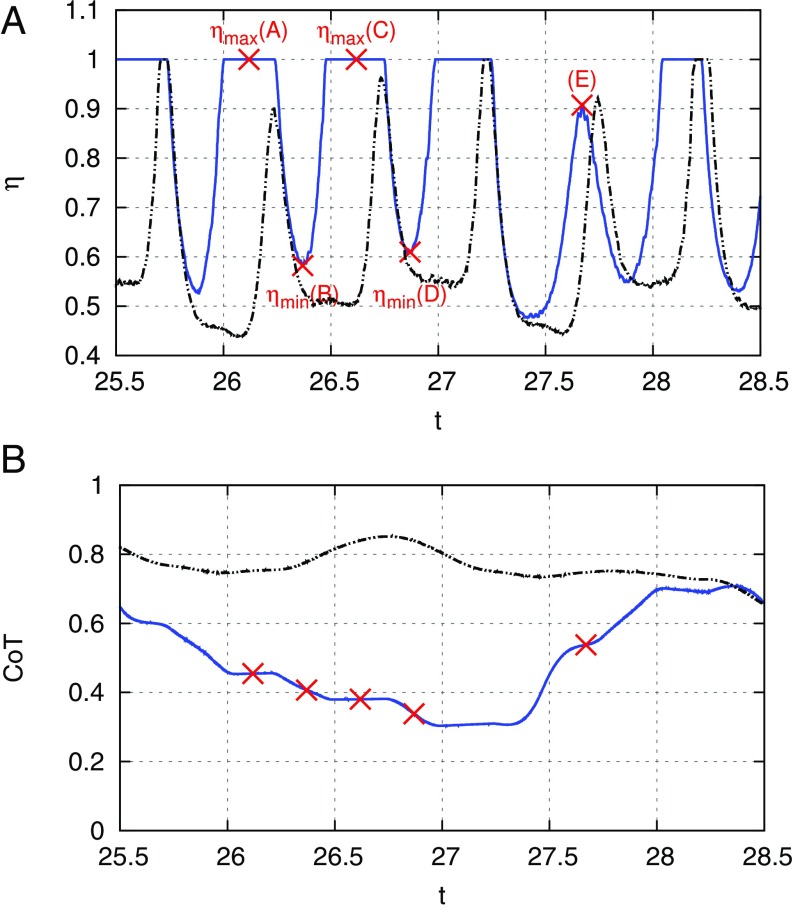
Fig. 3.

Energetics data for a smart follower maximizing its swimming efficiency. Swimming efficiency (A) and CoT (B) for ${IS}_{\eta }$ (solid blue line) and ${SS}_{\eta }$ (dash-double-dot black line), normalized with respect to the CoT of a steady solitary swimmer. Four instances of maximum and minimum efficiency, which occur periodically throughout the simulation at times $\left(n{T}_p+0.12\right)$, $\left(n{T}_p+0.37\right)$, $\left(n{T}_p+0.62\right)$, $\left(n{T}_p+0.87\right)$, have been highlighted. $T_p=1$ denotes the constant tail-beat period of the swimmers, whereas n represents an integral multiple. The decline in η at point $E$ ($t\approx 27.7$, $\eta =0.86$) results from an erroneous maneuver at $t\approx 26.5$ (Movie S7), which reveals the existence of a time delay between actions and their consequences.

The efficient swimming of ${IS}_{\eta }$ [e.g., point ${\eta }_{max}\left(A\right)$ in Fig. 3A] is attributed to the synchronized motion of its head with the lateral flow velocity generated by the wake vortices of the leader (Movie S4v). This mechanism is evidenced by the correlation curve shown in Fig. 2E and by the coalignment of velocity vectors close to the head in Fig. 4 A and B. As shown in Movie S7, ${IS}_{\eta }$ intercepts the oncoming vortices in a slightly skewed manner, splitting each vortex into a stronger ($W_{1U}$, Fig. 4A) and a weaker fragment ($W_{1L}$). The vortices interact with the swimmer’s own boundary layer to generate “lifted vortices” ($L_1$), which in turn generate secondary vorticity ($S_1$) close to the body. Meanwhile, the wake and lifted vortices created during the previous half-period, $W_{2U}$, $W_{2L}$, and $L_2$, have traveled downstream along the body. This sequence of events alternates periodically between the upper (right lateral) and lower (left lateral) surfaces, as seen in Movie S7. Interactions of ${IS}_{\eta }$ with the flow field at points ${\eta }_{min}\left(D\right)$ and $\left(E\right)$ in Fig. 3A are analyzed separately in SI Appendix, Figs. S5 and S6.

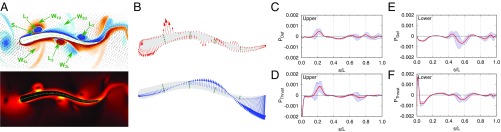
Fig. 4.

Flow field and flow-induced forces for ${IS}_{\eta }$, corresponding to maximum efficiency. (A) Vorticity field (red, positive; blue, negative) with velocity vectors shown as black arrows (Upper) and velocity magnitude shown in Lower (bright, high speed; dark, low speed). The snapshots correspond to $t=26.12$, i.e., point ${\eta }_{max}\left(A\right)$ in Fig. 3A. Demarcations are shown at every $0.2L$ along the body center line for reference. The wake vortices intercepted by the follower ($W_{1U}$, $W_{1L}$, $W_{2U}$, $W_{2L}$), the lifted vortices created by interaction of the body with the flow ($L_1$, $L_2$, and $L_3$), and secondary vorticity $S_1$ generated by $L_1$ have been annotated. (B) Flow-induced force vectors (Upper) and body deformation velocity (Lower) at $t=26.12$. (C and D) Deformation power (C) and thrust power (D) (with negative values indicating drag power) acting on the upper surface of follower. The red line indicates the average over 10 different snapshots ranging from $t=30.12$ to $t=39.12$. The envelope signifies the SD among the 10 snapshots. (E and F) Deformation power (E) and thrust power (F) on the lower (left lateral) surface of the swimmer.

We observe that the swimmer’s upper surface is covered in a layer of negative vorticity (and vice versa for the lower surface) (Fig. 4 A, Upper) owing to the no-slip boundary condition. The wake or the lifted vortices weaken this distribution by generating vorticity of opposite sign (e.g., secondary vorticity visible in narrow regions between the fish surface and vortices $L_1$, $W_{1L}$, $L_2$, and $L_3$) and create high-speed areas visible as bright spots in Fig. 4 A, Lower. The resulting low-pressure region exerts a suction force on the surface of the swimmer (Fig. 4 B, Upper), which assists body undulations when the force vectors coincide with the deformation velocity (Fig. 4 B, Lower) or increases the effort required when they are counteraligned. The detailed impact of these interactions is demonstrated in Fig. 4 C–F. On the lower surface, $W_{1L}$ generates a suction force oriented in the same direction as the deformation velocity ($0<s<0.2L$ in Fig. 4B), resulting in negative $P_{Def}$ (Fig. 4E) and favorable $P_{Thrust}$ (Fig. 4F). On the upper surface, the lifted vortex $L_1$ increases the effort required for deforming the body (positive peak in Fig. 4C at $s=0.2L$), but is beneficial in terms of producing large positive thrust power (Fig. 4D). Moreover, as $L_1$ progresses along the body, it results in a prominent reduction in $P_{Def}$ over the next half-period, similar to the negative peak produced by the lifted vortex $L_2$ ($s=0.55L$ in Fig. 4E). The average $P_{Def}$ on both the upper and lower surfaces is predominantly negative (i.e., beneficial), in contrast to the minimum swimming efficiency instance ${\eta }_{min}\left(D\right)$, where a mostly positive $P_{Def}$ distribution signifies substantial effort required for deforming the body (SI Appendix, Fig. S5). We observe noticeable drag on the upper surface close to $s=0$ (Fig. 4 B, Upper and Fig. 4D), attributed to the high-pressure region forming in front of the swimmer’s head. Forces induced by $W_{1L}$ are both beneficial and detrimental in terms of generating thrust power ($0<s<0.2L$ in Fig. 4F), whereas forces induced by $L_2$ primarily increase drag but assist in body deformation (Fig. 4E). The tail section ($s=0.8L$ to $1L$) does not contribute noticeably to either thrust or deformation power at the instant of maximum swimming efficiency.

Energy-Saving Mechanisms in Coordinated Swimming

The most discernible behavior of ${IS}_{\eta }$ is the synchronization of its head movement with the wake flow. However, the most prominent reduction in deformation power occurs near the midsection of the body ($0.4\le s\le 0.7$ in Fig. 4 C and E). This indicates that the technique devised by ${IS}_{\eta }$ is markedly different from energy-conserving mechanisms implied in theoretical (6, 34) and computational (20) work, namely, drag reduction attributed to reduced relative velocity in the flow and thrust increase owing to the “channelling effect.” In fact, the predominant energetics gain (i.e., negative $P_{Def}$) occurs in areas of high relative velocity, for instance, near the high-velocity spot generated by vortex $L_2$ (Fig. 4). This dependence of swimming efficiency on a complex interplay between wake vortices and body deformation aligns closely with experimental findings (13, 27). We remark that the majority of the results presented here are obtained with a steadily swimming leader. However, with no additional training, ${IS}_{\eta }$ is able to exploit the wake of a leader executing unfamiliar maneuvers, by deliberately choosing to interact with the unsteady wake, as seen in Movies S5 and S6. The smart follower is able to respond effectively to such unfamiliar situations, since it is exposed to a variety of perturbations while taking random actions during training. This observation demonstrates the robustness of the RL algorithm to uncertainties in the environment and further establishes its suitability for use in realistic scenarios.

Having examined the behavior and physical mechanisms associated with energy savings, we now formulate and test a simple control rule that enables efficient coordinated swimming. We remark that this is a combination of RL and DNSs in a reverse-engineering context, where: (i) We use the capability of RL to discern useful patterns from a large cache of simulation data; (ii) we analyze the physical aspects of the resulting optimal strategy, to identify the behavior and mechanisms that lead to energetic benefits, and finally; (iii) we use this understanding to devise a rule-based control algorithm for sustained energy-efficient synchronized swimming, in a notably more complex 3D setting. To the best of our knowledge, there is no work available in the literature that investigates the flow physics governing interactions among multiple independent swimmers, by using high-fidelity simulations of 3D NS equations.

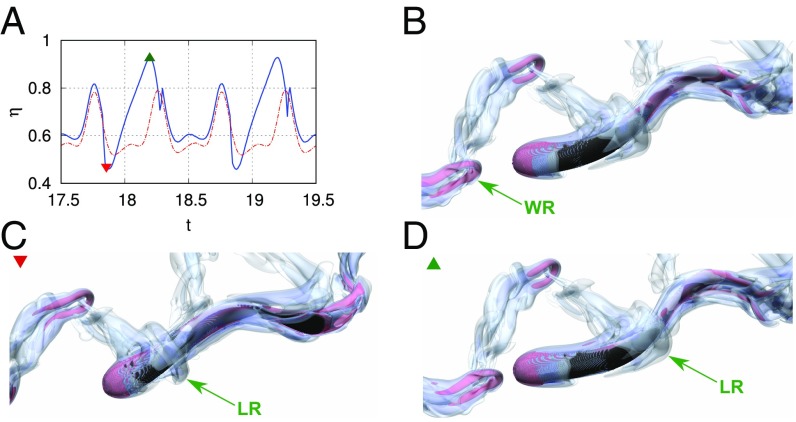
Given the head-synchronization tendency of the 2D smart swimmer ${IS}_{\eta }$, we first identify suitable locations behind a 3D leader where the flow velocity would match a follower’s head motion (SI Appendix, Fig. S7). A feedback controller is then used to regulate the undulations of two followers to maintain these target coordinates on either branch of the diverging wake, as shown in Fig. 1B and Movie S1. We note that a fish following in-line behind the leader would not benefit in the present 3D simulations, since the region behind the leader remains quiescent owing to the diverging wake. The controlled motion yields an $11\%$ increase in average swimming efficiency for each of the followers (Fig. 5A) and a $5\%$ reduction in each of their CoT. Overall, the group experiences a $7.4\%$ increase in efficiency when compared with three isolated noninteracting swimmers. The mechanism of energy savings closely resembles that observed for the 2D swimmer; an oncoming WR (Fig. 5B) interacts with the deforming body to generate a “lifted-vortex” ring (LR; Fig. 5C). As this new ring proceeds along the length of the body, it modulates the follower’s swimming efficiency as observed in Fig. 5. Remarkably, the positioning of the lifted ring at the instants of minimum and maximum swimming efficiency resembles the corresponding positioning of lifted vortices in the 2D case; a slight dip in efficiency corresponds to lifted vortices interacting with the anterior section of the body (Fig. 5C and SI Appendix, Fig. S5), whereas an increase occurs upon their interaction with the midsection (Figs. 4 and 5D).

Fig. 5.

The 3D swimmer interacting with WRs. (A) Swimming efficiency for a 3D leader (dash-dot red line) and a follower (solid blue line) that adjusts its undulations via a proportional-integrator (PI) feedback controller to maintain a specified position in the wake. After an initial transient, the patterns visible in the efficiency curves repeat periodically with $T_p$. Time instances where the follower attains its minimum and maximum swimming efficiency have been marked with an inverted red triangle and an upright green triangle, respectively. The sudden jumps at $t\approx 18.3$ and $19.3$ correspond to adjustments made by the PI controller. (B) An oncoming WR is intercepted by the head of the follower and generates a new LR (C) similar to the 2D case (Fig. 4). As this ring interacts with the deforming body, it lowers the swimming efficiency initially ($t\approx 17.8$; A and C), but provides a noticeable benefit further downstream ($t\approx 18.2$; A and D).

These results showcase the capability of machine learning, and deep RL in particular, for discovering effective solutions to complex physical problems with inherent spatial and temporal nonlinearities, in a completely data-driven and model-free manner. Deep RL is especially useful in scenarios where decisions must be taken adaptively in response to a dynamically evolving environment, and the best control strategy may not be evident a priori due to unpredictable time delay between actions and their effect. This necessitates the use of recurrent networks capable of encoding time dependencies, which can have a demonstrable impact on the physical outcome, as shown in SI Appendix, Fig. S4. In conclusion, we demonstrate that deep RL can produce efficient navigation algorithms for use in complex flow fields, which in turn can be used to formulate control rules that are effective in decidedly more complex settings and thus have promising implications for energy savings in autonomous robotic swarms.

Methods

We perform 2D and 3D simulations of multiple self-propelled swimmers using wavelet adapted vortex methods to discretize the velocity–vorticity form of the NS equations (in 2D) and their velocity pressure form along with the pressure-projection method (in 3D) using finite differences on a uniform computational grid. The swimmers adapt their motion using deep RL. The learning process is greatly accelerated by using recurrent neural networks with long short-term memory as a surrogate of the value function for the smart swimmer. Details regarding the simulation methods and the RL algorithm are provided in SI Appendix.