Electrochemical trapping of metastable Mn³⁺ ions for activation of MnO₂ oxygen evolution catalysts

Significance

Manganese oxide films are desirable oxygen evolution reaction (OER) catalysts due to their stability in acidic solutions and viability as earth-abundant materials. Enhanced catalytic activity of MnO₂ incorporated with Mn³⁺ provides an imperative for understanding the structural and electronic effects giving rise to the superior OER catalysis. We show that (i) Mn³⁺ is stabilized kinetically in tetrahedral sites and (ii) its presence strains the oxide lattice, leading to a favorable disposition of oxide-based vs. metal-based energy levels that favors enhanced OER activity. The results herein offer a design concept of exploiting ion-induced lattice strain for creating superior metal oxide OER catalysts.

Abstract

Electrodeposited manganese oxide films are promising catalysts for promoting the oxygen evolution reaction (OER), especially in acidic solutions. The activity of these catalysts is known to be enhanced by the introduction of Mn³⁺. We present in situ electrochemical and X-ray absorption spectroscopic studies, which reveal that Mn³⁺ may be introduced into MnO₂ by an electrochemically induced comproportionation reaction with Mn²⁺ and that Mn³⁺ persists in OER active films. Extended X-ray absorption fine structure (EXAFS) spectra of the Mn³⁺-activated films indicate a decrease in the Mn–O coordination number, and Raman microspectroscopy reveals the presence of distorted Mn–O environments. Computational studies show that Mn³⁺ is kinetically trapped in tetrahedral sites and in a fully oxidized structure, consistent with the reduction of coordination number observed in EXAFS. Although in a reduced state, computation shows that Mn³⁺ states are stabilized relative to those of oxygen and that the highest occupied molecular orbital (HOMO) is thus dominated by oxygen states. Furthermore, the Mn³⁺(T_d) induces local strain on the oxide sublattice as observed in Raman spectra and results in a reduced gap between the HOMO and the lowest unoccupied molecular orbital (LUMO). The confluence of a reduced HOMO–LUMO gap and oxygen-based HOMO results in the facilitation of OER on the application of anodic potentials to the δ-MnO₂ polymorph incorporating Mn³⁺ ions.

The widespread implementation of solar energy at the level needed for global energy demand (1, 2) requires its efficient storage in the form of fuels (3). The conversion of water to H₂ and O₂ is one of the most energy-dense carbon-neutral fuel schemes to store solar energy (4). Effective catalysts for the hydrogen evolution reaction and oxygen evolution reaction (OER) require a design that manages the coupling of electrons and protons so as to avoid high energy intermediates (5, 6). Of these two proton-coupled electron transfer reactions, the OER is more kinetically challenging, because it requires the management of four electrons and four protons. Oxidic catalysts of cobalt (7–11), nickel (12–16), manganese (17, 18), and other noncritical metals (19, 20) allow OER to be performed efficiently under a wide range of conditions, including nonbasic solutions, where self-healing circumvents corrosion of the catalysts (21). The manganese oxidic OER catalysts are unique, as they are distinguished by their ability to perform OER in acid (17, 18, 22–28). As clearly established by the work of Dismukes and coworkers (29, 30), the OER activity of MnO₂ polymorphs is greatly enhanced when Mn³⁺ ions are present in the lattice (31). Mn³⁺ ions may be introduced by cycling the potential of birnessite-like MnO₂ polymorphs (32, 33). Alternatively, Mn³⁺ ions may be introduced chemically by using the comproportionation of MnO₂ with Mn(OH)₂ to produce a hausmannite-like intermediate (α-Mn₃O₄) (17). On reoxidation of these films back to a predominantly MnO₂ state, ex situ X-ray photoelectron spectroscopy (XPS) studies indicate an average Mn oxidation state from +3.6 to +3.8 instead of the expected +4.0 of MnO₂, which is consistent with the presence of Mn³⁺ (32, 33). Despite the observation that electrochemical doping of Mn³⁺ enhances OER activity of MnO₂ polymorphs, the role of Mn³⁺ in such electroactivated films is not understood, and it is also not understood why such a reduced state would persist under oxidizing conditions.

X-ray absorption spectroscopy (XAS) measurements made during the electroactivation of electrochemically deposited δ-MnO₂ phase show that Mn³⁺ character remains present in OER active catalyst films and that the Mn–O bond coordination number is lowered with the formation of Mn³⁺. Computational studies, supported by extended X-ray absorption fine structure (EXAFS) results, reveal that the Mn³⁺ ions are located in a tetrahedral environment, which is kinetically stable and induces local strain of the lattice that is observed in Raman microspectroscopic spectra. This strain results in a raising of the O2p valence band above the Mn³⁺ tetrahedral (T_d) and Mn⁴⁺ octahedral (O_h) valence bands with a commensurate lowering of the metal-based conduction bands. Oxidation of tetrahedral Mn³⁺ is thus more difficult than that of oxygen. The studies herein rationalize why Mn³⁺ is observed to persist at the onset of OER in MnO₂ polymorphs and why the presence of Mn³⁺ enhances OER catalysis.

Experimental Procedures

Electrochemistry.

MnO₂ films were prepared following identical procedures as previous studies on these electrodeposited catalysts, and their chemical composition, XPS, EM, and X-ray spectra properties were identical to those of the previously reported material (17, 18, 22). MnO₂ films were electrodeposited in solutions containing 0.5 mM Mn²⁺ (prepared from MnCl₂•4H₂O, 99.995% trace metal basis; Strem) and 0.9 M KNO₃ (99.0−100.5%; Macron) at pH 8.0. Powder X-ray diffraction patterns of the amorphous films are well-defined and show that films are locally the MnO₂ polymorph of birnessite (δ-MnO₂). The electrodeposition protocol (“anodic deposition”) for producing δ-MnO₂ entailed the application of a constant potential of 1.1 V [vs. normal hydrogen electrode (NHE)] to the electrode. Potentials were converted to the NHE scale by the following relation: E_NHE = E_Ag/AgCl + 0.197 V. All Fluorinated Tin Oxide (FTO) films were sonicated in acetone and rinsed with type I water before use. The MnO₂ films activated with Mn³⁺ (generally designated as δ-MnO₂^act) were generated by multipotential steps (“multistep deposition”), where the electrode was initially held at 1.1 V for 3 s followed by the application of −0.4 V for 2 s, and this multipotential two-step series was repeated as desired. Cyclic voltammograms (CVs) were recorded using a CH Instruments potentiostat. A three-electrode cell configuration was used with a platinum mesh counterelectrode, an Ag/AgCl reference electrode, and an FTO working electrode. The FTO working electrode was sonicated in acetone and rinsed with water before each measurement. The ohmic drop of cell was compensated by using the positive feedback compensation implemented in the instrument.

The electrochemical setup for in situ XAS experiments used a Biologic SP-150 potentiostat in a three-electrode configuration. SI Appendix, Fig. S1 presents the geometry and dimensions of the cell used for XAS measurement. The 25 × 25 × ∼50-mm quartz cell consisted of three GL14 glass threaded necks (Adams & Chittenden Scientific Glass). A 5-mm hole was cut and fire-polished on one long face of the cell so that the X-ray beam could enter the cell and strike the working electrode surface. Optically transparent 128-µm-thick Polyethylene Terephthalate tape coated with a thin layer (Eastman Chemical Inc.) of conductive Indium Tin Oxide (ITO) was used as the working electrode, which is transparent to X-rays. The Polyethylene Terephthalate–ITO tape was sonicated in acetone and rinsed with type I water before being sealed to the outside of the fire-polished opening of the quartz cell with Devcon 5-min epoxy. An Ag/AgCl reference electrode (BASi; filled with saturated KCl) and a Pt mesh (99.9%; Alfa Aesar) auxiliary electrode were introduced through separate GL14 caps and septa. All experiments were conducted at ambient temperature (∼23 °C) and used automatic internal resistance compensation, where the electrode/solution resistance was determined by applying a small potential step at the open circuit potential.

XAS.

XAS measurements were conducted at beamline 4–1, Stanford Synchrotron Radiation Lightsource. Measurements were performed at the Mn K edge in a fluorescence geometry using a 30-element solid-state germanium detector. Because the in situ cell is completely absorbing, standard simultaneous energy calibration could not be performed. Instead, a Kapton foil was placed at an angle in front of the first ion chamber to scatter X-rays off-axis. An Mn reference foil and photodiode were used for simultaneous energy calibration using the scattered X-rays. The alignment of the working electrode was optimized after an initial anodic deposition of δ-MnO₂ film on the electrode. In situ XAS data were collected continuously during the initial deposition of δ-MnO₂ and subsequent activation of the film by multistep activation protocols. During multistep deposition, the two-step potential series was repeated 25 times, which we designate one multistep cycle (one multistep cycle of 25 steps is designated c1, two cycles are designated c2, etc.). Each cycle ended at an anodic potential of 1.1 V (one cycle ending on an anodic pulse is designated c1A, etc.) or at a cathodic potential of −0.4 V (one cycle ending on a cathodic pulse is designated c1C, etc.). A full XAS was collected to a wavenumber, k, of 12 Å⁻¹. Data processing and analysis were conducted using ATHENA and ARTEMIS, part of the IFEFFIT software suite (34). All spectra were calibrated, normalized, and background-subtracted per the protocols outlined in the ATHENA documentation (35). EXAFS data were fit to a birnessite reference to a k window of 3–10.5 Å⁻¹, with single scattering pathways. Given that the establishment of the local structure of the anodically deposited films is birnessite (22), EXAFS spectra of an anodically deposited film were fit with the assumption of a first shell (Mn–O) coordination number of N₁ = 6, yielding an experimental value of 5.3. This lower coordination number for the anodically deposited film was owing to deposition of an amorphous birnessite film and the presence of water in the interlayer. Using the S₀² value from an anodically deposited film, a calibration factor was used to obtain the coordination number from the fitted parameters of multicycled films.

Raman Spectroscopy.

Raman microspectroscopy was carried out at the Center for Nanoscale Systems on a Horiba LabRam Evolution system using an excitation wavelength of 532 nm (0.5 mW) and a long working distance objective (Olympus LMPLANFL 50×) with a numerical aperture of 0.5, resulting in a Gaussian excitation profile of ∼500 nm (FWHM). To average out morphological irregularities, each sample was measured at 49 different locations (55–1,765 cm⁻¹, 15-s integration time, one window, two accumulations) evenly arranged on a square grid of 60 × 60 μm². The confocal pinhole was set to 200 μm during the acquisition. Spectra were calibrated to a silicon reference sample (520.64 cm⁻¹), and each spectrum was recorded with a frequency resolution of ∼1.7 cm⁻¹. Raw spectra were averaged, multiplied by the Bose–Einstein factor (T = 298 K), baseline-corrected, and fitted to a sum of Lorentzian functions using an unconstrained nonlinear Levenberg–Marquardt optimization algorithm implemented in Labview.

Samples of δ-MnO₂ were electrodeposited onto an FTO working electrode by passing a current of 60 mC/cm², giving rise to an absorbance of 0.85 at 532 nm; subsequent activation to δ-MnO₂^act produced a film with an absorbance of 0.73 at 532 nm (SI Appendix, Fig. S2).

Calculations.

To characterize the electronic structure of the δ-MnO₂/δ-MnO₂^act (referred to as MnOx), in particular focusing on accurately reproducing the relative energy levels of the transition metal and oxygen states, we relied on hybrid density functional theory calibrated using the GW approximation (36). This methodology has been recently reported to accurately reproduce the properties of insulators (37) with mixed Mott–Hubbard and charge–transfer behavior, such as the MnOx system at hand. Specifically, we calibrated the fraction of exact Hartree–Fock exchange, α_EX, introduced into an Heyd–Scuseria–Ernzerhof type hybrid exchange–correlation functional (38) to reproduce the Kohn–Sham gap obtained from a G₀W₀ calculation:

$$E_{\mathrm{XC}}=\left(1-{\mathrm{\alpha }}_{\mathrm{EX}}\right)E_{\mathrm{x}}^{\mathrm{PBE}}+{\mathrm{\alpha }}_{\mathrm{EX}}{E}_{\mathrm{x}}^{\mathrm{HF}}+E_{\mathrm{c}}^{\mathrm{PBE}},$$ [1]

where E_XC is the exchange–correlation energy and PBE refers to the Perdew–Burke–Ernzerhof exchange–correlation functional (39). An exact exchange fraction value of α_EX = 0.35 was chosen based on a band gap of α-Mn₃O₄ (hausmannite) computed in G₀W₀ to be 3.0 eV, which is in reasonable agreement with previous calculations (40) and experiment (41–43). By calibrating to α-Mn₃O₄, we sought to capture the behavior of both tetrahedrally and octahedrally coordinated Mn, which are present in this structure. We note that the value obtained by calibration to the birnessite-type MnOOH is also α_EX = 0.35, while that obtained by calibration to the experimental band gap of α-Mn₃O₄ or the purely octahedral birnessite δ-MnO₂ structure is α_EX = 0.29. This difference, however, does not lead to any qualitative changes in the calculation outcomes to the best of our knowledge. All calibration curves are available in SI Appendix, Fig. S3.

A hausmannite (α-Mn₃O₄) structure was used as a model to investigate the redox behavior of mixed tetrahedrally and octahedrally coordinated Mn within an oxide sublattice. Hausmannite contains both octahedral and tetrahedral Mn environments and is a faithful analog of δ-MnO₂^act inasmuch as it is generated by oxidizing hausmannite, which is an overlayer on birnessite nanoparticles (22). A computational methodology previously reported for identifying defect-induced redox behavior in transition metal semiconductors was followed (44, 45). (i) Beginning with the α-Mn₃O₄ structure, electrons were removed from the system one by one, compensating for the charge with a homogeneous jellium background and allowing the system to locally relax while keeping the overall lattice fixed. (ii) The oxidation states of the Mn and O atoms in the system were then tracked by tracing the evolution of their magnetic moment, which is a precise signature of Mn²⁺, Mn³⁺, and Mn⁴⁺ as well as O²⁻ and O⁻, as calibrated to typical values observed in known manganese oxide and oxyhydroxide structures. Note that we do not observe relaxation by peroxide formation as evidenced by a lack of short O–O bonds.

All first principles calculations are performed using the Vienna Ab-Initio Simulation Package (46) using the projector-augmented wave method (47), a reciprocal space discretization of 15 Å⁻¹, and a plane-wave cutoff of 650 eV. All calculations are converged to 0.01 eV Å⁻¹ on forces and 10⁻⁸ eV on total energy to ensure that a reliable minimum is found. Structural models for Mn₃O₄ as well as MnO₂ and MnOOH used in the calibration are obtained from the Inorganic Crystal Structure Database (48), with magnetic orderings chosen based on small supercell enumerations as suggested by previous benchmarks for the MnO₂ system (49).

Results

Electrochemistry.

Fig. 1 shows the CVs of as-deposited δ-MnO₂ and δ-MnO₂^act films over a potential window that includes OER activity and/or film activation. For all CVs, the bare FTO electrode was first held at open circuit potential, and scans were initiated to positive potentials at a rate of 100 mV/s. Fig. 1A shows the CV for the OER activity of δ-MnO₂ in the absence of Mn³⁺ incorporation. Two notable features are observed, indicated by waves A and B. Wave A corresponds to the nucleation and deposition of δ-MnO₂ from Mn²⁺ as described by the half-reaction (18):

$$\text{A}:{\text{Mn}}^{2+}+2{\text{H}}_2\text{O}\rightleftharpoons {\text{MnO}}_2+4{\text{H}}^{+}+2{\text{e}}^{-}.$$ [2]

Fig. 1.

CVs of a 1-cm² FTO electrode in 0.5 mM Mn²⁺ and 0.9 M KNO₃ solution at 100-mV/s scan rate showing the first (red line) and second (blue line) cycles for (A) the as-deposited δ-MnO₂ and (B) the as-deposited film activated via the incorporation of Mn³⁺ ions by the comproportionation reaction (Eq. 4). A–D indicate the waves discussed in the text.

A limiting film thickness is obtained on the initial scan (Fig. 1A, red trace), as there is little subsequent growth on a subsequent scanning (Fig. 1A, blue trace). Wave B corresponds to the modest OER activity of birnessite:

$$\text{B}:2\hspace{0.17em}{\text{H}}_2\text{O}\rightleftharpoons {\text{O}}_2+4{\text{H}}^{+}+4{\text{e}}^{-}.$$ [3]

The second scan (Fig. 1A, blue trace) shows that the OER activity for wave B remains effectively unchanged; the OER activity does not change even after 200 scans over a potential window of 1.7–0.5 V (SI Appendix, Fig. S4).

Fig. 1B shows the CV of a film that incorporates Mn³⁺ ions by scanning cathodically to potentials of −0.4 V. Wave C corresponds to the comproportionation reaction between Mn⁴⁺ and Mn²⁺ to produce α-Mn₃O₄ (hausmannite) (22, 33):

$$\mathrm{C}:\mathrm{\delta }-{\text{Mn}}^{\text{IV}}{\text{O}}_2+2{\text{Mn}}^{\text{II}}{\left(\text{OH}\right)}_2\to \mathrm{\alpha }{-\text{Mn}}_3^{\text{II},\text{III}}{\text{O}}_4+2{\text{H}}_2\text{O}.$$ [4]

The addition of NO₃⁻ as a supporting electrolyte is needed for the incorporation of Mn³⁺ ions in the film. Under cathodic potentials, NO₃⁻ is reduced, forming hydroxide anions at the electrode surface (50), driving the production of Mn(OH)₂, and enabling comproportionation to occur. In the absence of Mn²⁺, Mn³⁺ cannot be produced, and film activation does not occur (17). No appreciable increase in OER activity is observed when an electrodeposited δ-MnO₂ film is scanned to the same limiting cathodic potential in Fig. 1B in the absence of Mn²⁺ (but in the presence of NO₃⁻ and OH⁻). After inducing the comproportionation reaction on cathodic scanning, the return trace shows a significant increase in current associated with OER (wave D corresponding to Eq. 3), which is indicative of an activated film produced on Mn³⁺ incorporation (denoted δ-MnO₂^act). As previously reported (22), the chemistry described by Eq. 4 occurs at the surface of nanosized domains of birnessite, and while there is a predominant birnessite phase, the δ-MnO₂^act surface overlayer is unique in that it is the active catalyst for OER.

The experiments in Fig. 1 taken together establish that δ-MnO₂ alone shows only modest OER activity, regardless of potential cycling of the film, and only when Mn³⁺ is introduced is enhanced OER activity observed.

In Situ X-Ray Absorption Spectroscopy.

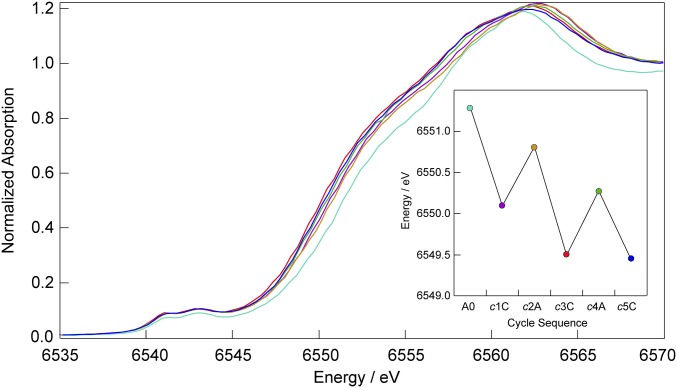
Fig. 2 shows the in situ X-ray absorption near-edge structure (XANES) spectra collected on an as-deposited δ-MnO₂ (birnessite) film activated by applying a two-step potential alternately between 1.1 and −0.4 V. The δ-MnO₂ film was electrodeposited in the in situ X-ray cell during XAS data collection. After sufficient material accrued, the film was realigned to the X-ray beam for optimal signal and then activated by applying the two-step potential 25 times. After each multistep cycle, an XAS spectrum was recorded (XANES spectra shown over a wider energy range are presented in SI Appendix, Fig. S5). The A0 XANES spectrum was collected on the as-deposited film, and subsequent spectra are shown for multiple cycles of 25 potential 1.1/−0.4 V steps terminating at the anodic potential (designated with A) or at a cathodic potential (designated with C).

Fig. 2.

In situ XANES spectra of an as-deposited δ-MnO₂ film subject to multipotential step activation. XANES spectra were collected after applying a potential between 1.1 and −0.4 V 25 times with a cycle terminating at the anodic or cathodic potential. One cycle (designated c) = 25 steps. The cycle number is designated numerically, and A and C denote cycles terminating at anodic or cathodic potential, respectively. Inset shows the energy position of the XANES edge determined from the inflection point as deduced from the maximum of the first derivative. The edge positions in Inset are color-coded to match the XANES spectra for cycles A0 (teal), c1C (purple), c2A (orange), c3C (red), c4A (green), and c5C (blue). The normalized absorption was determined from the full spectra shown in SI Appendix, Fig. S5.

The energy of the edge, determined from the inflection point as deduced from the maximum of the first derivative, shifts to lower energy on the application of the first multistep potential consistent with the generation of Mn³⁺ according to Eq. 4. Moreover, sequential spectra of cycles ending at the cathodic limiting potential exhibit a lower-energy absorption threshold than those terminating with the anodic limiting potential, giving rise to the sawtooth pattern shown in Fig. 2, Inset. Subsequent cycles ultimately converge to an absorption threshold of 6,549.75–6,550.0 eV (SI Appendix, Fig. S6), consistent with a lower average oxidation state of manganese in activated films compared with the as-deposited film (XANES spectrum A0). The indication of a lower oxidation state in SI Appendix, Fig. S6 is consistent with the lower average oxidations state of +3.6–3.8 measured previously by coulometry (17) and CV and XPS studies (32, 33).

Fitting the first two peaks of the EXAFS data shown in SI Appendix, Fig. S7 for the cycles of Fig. 2 reveals a decrease in the Mn–O coordination number from predominantly six to four with cycling (Fig. 3A, red bars). Note that the primary Mn–Mn coordination number remains at two within the error limits of the fitting. As expected, the associated Mn–O and Mn–Mn bond lengths (Fig. 3B, red and blue bars, respectively) are relatively constant given that the activated film maintains primarily birnessite character (22). Furthermore, although M–O bonds in T_d sites tend to be shorter than that of Mn in O_h sites, this trend holds for Mn in the same oxidation state. The Mn²⁺(T_d) sites in hausmannite have an Mn–O bond length of 2.043 Å, while the adjacent Mn³⁺(O_h) sites have an average bond length of 2.046 Å. In birnessite, which makes up the majority of the material, the bond length is 1.89 Å, and thus, a bond length change of from 2.05 to 1.9 Å is the largest to be expected and is entirely within the error limits of our fitting. An Mn–O coordination number of four is typical of an Mn occupying a T_d site, which is supported by the increase in intensity of the preedge features visible in the XANES data near 6,542 eV after c1C (Fig. 2). Such an increase in the preedge data has been attributed to speciation of Mn in tetrahedral coordinated sites (51).

Fig. 3.

(A) Mn–O (red) and Mn–Mn (blue) coordination numbers and (B) Mn–O (red) and Mn–Mn (blue) bond lengths as calculated from fitting parameters (SI Appendix, Table S1) of the EXAFS spectra (SI Appendix, Fig. S7). Cycle numbers are indicated as per Fig. 2.

Raman Microspectroscopy.

To gain further insight into the structural differences between δ-MnO₂ and δ-MnO₂^act films, we carried out resonance Raman microspectroscopy with an excitation wavelength of 532 nm (Fig. 4). δ-MnO₂ displays a characteristic Raman spectrum in the range from 450 to 700 cm⁻¹ with three dominant marker bands: a prominent Raman feature between 570 and 590 cm⁻¹ corresponding to an in-plane Mn–O stretching vibration along the octahedral layers in δ-MnO₂ and two bands at ∼500 and ∼630–650 cm⁻¹ associated with out-of-plane Mn–O vibrations perpendicular to the layers (52–56). All three bands are sensitive markers reporting on changes to the oxidation states of octahedral Mn cations as well as the interlayer separation and structural distortions of the involved Mn–O environments (53, 54, 57). This specificity to the local structure of the [MnO₆] octahedral framework renders Raman spectroscopy useful to the investigation of the effects of the activation protocol for electrodeposited δ-MnO₂ films.

Fig. 4.

Raman spectra of as-deposited δ-MnO₂ (red), activated δ-MnO₂^act (blue) films, and corresponding spectral fit (black dashed). Individually fitted Lorentzian functions are shown in gray, with important marker bands highlighted in green as a visual aid. Blue arrows indicate frequency shifts compared with δ-MnO₂ of these marker bands.

Fig. 4 shows the Raman spectra acquired for electrodeposited δ-MnO₂ (Fig. 4, red) and δ-MnO₂^act (Fig. 4, blue). Various polymorphs of MnOx have been extensively studied in literature, and the δ-MnO₂ Raman spectrum (Fig. 4, red) is in excellent agreement with the previous literature reports of an in-plane Mn–O stretching vibration located at 572 cm⁻¹ as well as out-of-plane Mn–O stretching vibrations at 495 and 651 cm⁻¹ for the δ-MnO₂ polymorph (52, 56, 58). In addition, we observe a moderately intense band at 606 cm⁻¹ as well as several bands with lower intensity at 148, 387, 419, and 731 cm⁻¹, all of which remain unassigned. We, therefore, concentrate only on the key marker bands in our analysis.

The δ-MnO₂^act Raman spectrum (Fig. 4, blue) is significantly altered compared with that of δ-MnO₂. The prominent feature at 573 cm⁻¹ in δ-MnO₂^act is assigned to the in-plane Mn–O stretching mode by comparison with the corresponding 572-cm⁻¹ band observed for δ-MnO₂. In contrast, the more intense out-of-plane Mn–O stretching vibration found at 651 cm⁻¹ in δ-MnO₂ red-shifts in δ-MnO₂^act to 634 cm⁻¹, and the other out-of-plane Mn–O stretching vibration blue-shifts to 502 cm⁻¹. Both out-of-plane stretching modes additionally show reduced intensity relative to the 573-cm⁻¹ in-plane Mn–O stretching mode. A reduction in intensity is also observed for the low-frequency phonon mode at ∼148 cm⁻¹, most likely indicative of a lower long-range order and higher strain present in the activated film (vide infra).

Catalyst Structure and Oxidation Configuration.

The catalysis mechanism underlying the superior performance of the activated δ-MnO₂ films (i.e., δ-MnO₂^act) can be understood by consideration of the electronic structure derived from the various local Mn–O ligand fields. The in situ XAS results reported here as well as ex situ X-ray pair distribution function analysis reported previously (22) indicate that the δ-MnO₂^act catalyst comprises both α-Mn₃O₄ hausmannite-like and δ-MnO₂ birnessite-like structures and does not contain local environments unique to any other known MnO₂ polymorph phase. Both structures comprise face-centered cubic oxygen frameworks with Mn occupying octahedral and tetrahedral interstitial sites (59) as illustrated in Fig. 5A. The XAS data presented in Fig. 2 establish the presence of Mn³⁺ and Mn⁴⁺ sites in the δ-MnO₂^act film but not the δ-MnO₂ film. Understanding the effect of Mn³⁺ on the electronic structure of δ-MnO₂^act is thus key to revealing the source of superior catalytic activity.

Fig. 5.

Electronic structure of the activated catalyst based on an oxidized α-Mn₃O₄ hausmannite structure as a model system containing both octahedral and tetrahedral Mn–O environments. (A) Schematic representation of the α-Mn₃O₄ hausmannite and δ-MnO₂ structures illustrating their common underlying face-centered cubic oxygen framework and similarity in octahedral Mn structure. The unique tetrahedral Mn sites in α-Mn₃O₄ are highlighted. (B) Evolution of oxidation states of Mn and O as electrons are removed from the α-Mn₃O₄ model system. Oxidation states are derived from the values of characteristic atom-projected magnetic moments according to typical values observed for computed manganese oxides and hydroxides. (C) Schematic of the band structure of the activated catalyst system derived from the “α-Mn₃O₄– 3e⁻” model. The T_d and O_h sections of the band diagram represent tetrahedral and octahedral Mn environments, while the Jahn–Teller orbital depicts the relative position of the O_h LUMO accounting for structural relaxation through Jahn–Teller distortion. (D) Average valence of Mn and O as a function of oxidation level as indicated by the electronically titrated α-Mn₃O₄ model.

While the exact structure of an amorphous film is not amenable to a precise atomistic description, electronic behavior of the activated catalyst can be modeled by electronic titration of hausmannite α-Mn₃O₄ from its initial Mn^2.66+ average oxidation state to Mn⁴⁺. As previously established, the activated film can only be reached via the hausmannite intermediate. Furthermore, as the α-Mn₃O₄ structure contains both the tetrahedral and octahedral Mn environments of interest (and no others), it provides a first-order approximation of the electronic structure of the catalyst, which can inform a discussion of the enhanced activity resulting from Mn³⁺ incorporation into a native Mn⁴⁺ oxidic lattice. Thus, oxidized α-Mn₃O₄ provides a tractable local environment model of the oxidized, partial tetrahedral structure of δ-MnO₂^act.

The oxidation behavior of this structural model, shown in Fig. 5B, provides a picture of the relative stability of various oxidation states in the mixed tetrahedral/octahedral δ-MnO₂^act structure. From the initial hausmannite starting point, all tetrahedral Mn exists in the 2+ oxidation state, whereas octahedral Mn exists in the 3+ oxidation state. The valence band is dominated by a tetrahedral Mn²⁺(T_d) state, while the octahedral manganese ions are in a Jahn–Teller distorted, high-spin Mn³⁺(O_h) state, as expected for hausmannite (60). As the structure is oxidized, electrons are removed from the high-energy tetrahedral Mn states forming tetrahedral Mn³⁺(T_d) alongside the octahedral Mn³⁺(O_h) states. The next oxidation step removes electrons from the octahedral manganese sites, forming Mn⁴⁺(O_h). After three electrons per formula unit are removed from the Mn₃O₄ structure, all octahedral manganese is in the Mn⁴⁺(O_h) state, while all tetrahedral manganese ions are in the Mn³⁺(T_d) state. At this point, the valence band is dominated by oxygen states rather than tetrahedral Mn³⁺(T_d) states, indicating that the oxidation of tetrahedral Mn³⁺(T_d) is more difficult than that of oxygen. Consistent with this result, on further oxidation, electrons are extracted from O2p orbitals, while the tetrahedral sites remain as Mn³⁺(T_d) (Fig. 5B). Indeed, after the onset of oxygen oxidation, some of the octahedral Mn regains some Mn³⁺(O_h) character. Thus, with the observation of the energy ordering of an O valence band to higher energy than that of manganese valence bands, we conclude that any tetrahedral Mn in the activated film would remain as Mn³⁺(T_d) even under highly oxidizing conditions, forcing oxygen electrons to the valence band edge even for an average Mn oxidation state below Mn⁴⁺ as is observed in the in situ XAS data shown in Fig. 2. This observation suggests that the activated catalyst described here operates via a similar mechanism to that proposed by Smith et al. (30): the suppression of Mn⁴⁺ formation by particular bonding structure enables the formation of oxygen holes competitively with Mn^3+/4+ oxidation.

A schematic illustration of the electronic structure of the activated film, derived from the fully oxidized α-Mn₃O₄ structural model, is given in Fig. 5C. Consistent with the results of the electronic titration calculation (Fig. 5B), the highest occupied molecular orbital (HOMO) is dominated by O2p states, while the lowest unoccupied molecular orbital (LUMO) is composed of antibonding states of tetrahedral Mn³⁺(T_d). Octahedral Mn is oxidized from Mn³⁺(O_h) to Mn⁴⁺(O_h) at a higher potential than that of the tetrahedral Mn^2+/3+(T_d) transition; the origin of this order of oxidation potentials is in the stabilization of octahedral Mn³⁺(O_h) by Jahn–Teller distortion. In the undistorted octahedral environment found with Mn⁴⁺(O_h), the unoccupied antibonding e_g* state is shifted up in energy and is above the LUMO of tetrahedral Mn³⁺(T_d). A more subtle effect on energy ordering arises from the impact of local tensile strain, as adjacent tetrahedral and octahedral environments are oxidized. As Mn³⁺(T_d) states initially form from Mn²⁺(T_d), the average T_d Mn–O bond length decreases from 2.04 to 1.98 Å. On oxidation of the nearby octahedral environments to Mn⁴⁺(O_h), the strong Mn–O bonding in the octahedra stretches the bonds in the tetrahedral environment, increasing the average T_d Mn–O bond length to 2.16 Å. This local strain confers more ionic character to the T_d Mn–O interaction and lowers the energy of the antibonding T_d LUMO, further decreasing the energy gap between the occupied O2p states and unoccupied Mn states. The red shift in the ultraviolet-visible spectrum of δ-MnO₂^act compared with δ-MnO₂ (SI Appendix, Fig. S2) is consistent with this prediction of a reduced HOMO–LUMO gap. This decrease in energy gap leads to a further facilitation of the OER, as these stabilized empty states accept the electrons released from reductive elimination of O₂.

An important feature of the electronic structure of the activated catalyst is the relative position of the HOMO oxygen band vs. that of pure δ-MnO₂. We align the band structures of the two structures using characteristic features of the Mn⁴⁺(O_h) environment present in both structures, effectively measuring the position of the occupied oxygen states with respect to the Mn(O_h) t_2g levels shared by both structures. This method yields an informative model of the differences in the electronic states of the two materials but inherently neglects the impact of structural features beyond the nearest neighbor cation–anion coordination shell. Nonetheless, based on this alignment (SI Appendix, Fig. S8), we can conclude that the activated catalyst contains higher energy oxygen states than pure δ-MnO₂ birnessite, with the oxygen band in the catalyst extending up to 0.6 eV above the Fermi level of birnessite. Note that, while the absolute values of the HOMO–LUMO gaps may be overestimated by the computational methodology used here, their relative values are reliable. The presence of these higher-energy oxygen states can be rationalized by the significant tensile strain experienced by oxygen bridging Mn³⁺ and Mn⁴⁺ environments, as this strain decreases the Mn–O orbital overlap and destabilizes the bonded state.

Discussion

The strong evidence of tetrahedral Mn in the fully oxidized and activated δ-MnO₂^act film gives valuable insight into the electronic structure of the activated catalyst and provides a rationale for superior performance in the presence of Mn³⁺ in enhancing OER catalysis with MnO₂ polymorphs. Qualitatively, Mn³⁺ is well-known to promote oxygen evolution (17, 61–64) but has been difficult to isolate in neutral and acidic conditions (65). Based on the Mn Pourbaix diagram (66), Mn₂O₃ and MnOOH may only be stable under alkaline conditions, while under acidic conditions, the only stable oxidation states of manganese are Mn²⁺ and Mn⁴⁺. Correspondingly, Mn³⁺, if formed within an oxide lattice, typically disproportionates to form Mn²⁺ and Mn⁴⁺ below pH 9 (62, 63, 65, 67). One unique result reported here is that Mn in tetrahedral sites is kinetically trapped, and in a fully oxidized structure, the tetrahedral Mn is forced to remain as Mn³⁺(T_d). Indeed, in the oxidized δ-MnO₂^act film, where all octahedral Mn is fully oxidized to Mn⁴⁺(O_h) and tetrahedral Mn is fully oxidized to Mn³⁺(T_d), no disproportionation reaction is possible, and it is not observed. This result is supported by the experimental XPS studies that show a persistent average Mn oxidation state of Mn^3.6+–3.8+ (22), with only Mn³⁺ and Mn⁴⁺ in the fully oxidized film under anodic conditions, as well as the EXAFS studies revealing a decrease in the Mn–O coordination number for the activated film.

The persistence of the metastable tetrahedral Mn species in the oxidized film is consistent with the migration behavior of Mn in rock salt-derived oxides, such as hausmannite and birnessite. Previous studies have found that Mn migration through the structure proceeds through hops between adjacent T_d and O_h sites. However, Mn²⁺ is the only species that is able to migrate between these T_d and O_h sites in the structure, while Mn³⁺ and Mn⁴⁺ are immobile (68, 69). Thus, Mn³⁺ “migrates” only by disproportionating into Mn²⁺ and Mn⁴⁺, after which the Mn²⁺ ion moves through the structure (69). As no disproportionation reaction is possible in the fully oxidized δ-MnO₂^act film, we speculate that the Mn is kinetically locked in its metastable T_d site.

The Raman data support the computational titration of hausmannite presented in Fig. 5B. Mn³⁺ is kinetically trapped in the interlayer T_d sites, with the octahedral [MnO₆] framework remaining largely that of birnessite-like octahedral Mn⁴⁺, since the 572-cm⁻¹ Mn–O stretching vibration of δ-MnO₂ (Fig. 4, red) remains unchanged on activation (Fig. 4, blue). In contrast, frequency shifts associated with out-of-plane vibrations (495 and 651 cm⁻¹) are intimately related to the interlayer geometry. Red shifts of up to 15 cm⁻¹ have been reported for the 651-cm⁻¹ mode in δ-MnO₂ and have been attributed to a contraction of the [MnO₆] interlayer spacing due to reduced interlayer repulsion of the [MnO₆] octahedra (54). Furthermore, similar spectral changes were also observed during electrochemical potential sweeps and attributed to a phase transition from initially hexagonal to monoclinic (57). The observed Raman shifts and relative intensity changes of the 502- and 634-cm⁻¹ bands in MnO₂^act, therefore, provide evidence on changes to the interlayer separation due to the existence of interlayer Mn³⁺ ions that persist even after a final anodic potential pulse, consistent with theoretical modeling.

In combination with our XAS results and theoretical modeling, we formulate a structural picture of the MnO₂^act catalyst film, in which the octahedral [MnO₆] framework is structurally largely robust when interlayer Mn³⁺ cations are present. The Raman shift of the out-of-plane modes together with the lowering of the Mn oxidation number reported by XAS supports the contention that the role of the activation procedure is to generate interlayer Mn³⁺ ions, which in turn, cause strain of the initial layered birnessite lattice. This strain establishes most likely the formation of a partial 3D hausmannite-like structure, in which Mn³⁺ ions occupy tetrahedral sites, as suggested by the lowering of the Mn–O coordination number and theoretical modeling. Consequently, the film maintains Mn³⁺(T_d) character on onset of OER.

The electronic structure of the activated film, shown in Fig. 5C, suggests a mechanistic role for Mn³⁺(T_d) states in driving oxygen evolution through both the generation of reactive oxygen states and a decreased HOMO–LUMO gap. The activated film has the general structure of a charge-transfer insulator, with the HOMO dominated by particularly weakly bound O2p states, while the LUMO consists of antibonding states within the Mn³⁺(T_d) environment. Such an electronic structure has been generally correlated to high oxygen evolution activity (70). Mechanistically, in such a structure, electronic excitations create oxygen holes (Mnⁿ–O → Mnⁿ⁻¹–O•), forming highly reactive oxyl radicals, which are known to be critical intermediates in the proton-coupled electron transfer transformation of H₂O to O₂ (71–76) and in the proposal of reductive coupling (77, 78) and excess charging in Li batteries (79). The generation of oxyl radicals resulting from a high lying O2p valence band, with the population of oxygen radicals inversely proportional to the size of the HOMO–LUMO energy gap, is an emerging precept for the origin of enhanced OER activity in oxidic metal catalysts (80). While pristine birnessite δ-MnO₂ has similar charge-transfer character to the activated film, the oxygen in δ-MnO₂ is significantly more bound than in the activated catalyst as evidenced by the lower absolute energy of the oxygen band. Furthermore, the HOMO–LUMO gap is calculated to be between 2.8 and 3.4 eV, which results in a very small population of reactive oxygen radicals. In contrast, the metastable Mn³⁺(T_d) states of δ-MnO₂^act create low-lying metal states, with a calculated HOMO–LUMO gap of 1.9 eV, which can be further decreased by local tensile strains likely present around these tetrahedral sites.

The redox behavior of the δ-MnO₂^act catalyst material is similar to that observed in disordered Li-excess materials, which have recently received significant attention as high-capacity cathodes for Li ion batteries. The competition between Mn^3+/4+ and oxygen oxidation found in the δ-MnO₂^act catalyst is analogous to the activation of oxygen redox preferentially to transition metal oxidation in Li-excess cathodes. In both cases, the redox behavior is controlled by unique local bonding environments, with strained metal–oxygen bonds in this δ-MnO₂ material and poorly hybridized Li–O–Li environments in Li-excess cathodes leading to the formation of reactive oxygen states (79, 81). Similarly, transition metal oxidation is suppressed in both cases by constraining metal–oxygen bond lengths to that of the reduced state (77, 82). The result of these mechanisms is a promotion of oxygen evolution from the disordered metastable material, thus leading to enhanced OER activity.

Conclusion

The enhanced OER activity of MnO₂ polymorph OER catalysts is known to be derived from the presence of Mn³⁺ ions, where the suppression of Mn³⁺ oxidation to Mn⁴⁺ by structural constraints has been proposed as a key step in enabling oxygen hole accumulation and the reductive elimination of O₂ (39, 40). We find that the incorporation of Mn³⁺, which typically disproportionates in oxide lattices, is enabled by the comproportionation of Mn⁴⁺ in the form of MnO₂ and Mn²⁺ in the form of Mn(OH)₂. The kinetic trapping of Mn³⁺ is thus only possible via this comproportionation effect, which requires the generation of OH⁻ and the presence of Mn²⁺. Further examination of the activated structure yields insights extending beyond the observation of Mn³⁺ valency, promoting higher catalytic turnover. Raman microspectroscopy provides evidence for a locally strained lattice due to the presence of interlayer Mn³⁺ cations. In situ XANES and EXAFS further show that Mn³⁺ is most likely coordinated by a T_d ligand field in the activated films. In combination with computational modeling, these results suggest a local 3D hausmannite-like structure that produces an HOMO level primarily dominated by O2p valence states and unoccupied metal-based LUMO states with an attenuated HOMO–LUMO gap. In this light, our activated catalyst is similar to the mechanism of Mn⁴⁺ suppression in Mn₂O₃ and γ-MnOOH as proposed by Smith et al. (30): the Mn cations trapped in T_d sites are unable to form Mn⁴⁺ and thus, induce a reordering of Mn-d and O2p states, facilitating oxygen hole formation. These factors contribute to enhanced OER activity by facilitating oxyl radical formation for reductive coupling to produce oxygen, providing crucial design principles for the improvement of OER activity in metal oxidic catalysts.