Significance
At higher temperatures, and in high magnetic fields at low temperatures, an extraordinary and unidentified electronic phase, dubbed the “pseudogap,” appears in lightly hole-doped cuprates. At high fields and low temperatures, the pseudogap phase supports quantum oscillations that have resisted quantitative theoretical explanation since their discovery, and it also exhibits an unidentified density wave state. Although the latter has typically been referred to as a “charge” density wave because of the observed charge density modulations, theory indicates that it could actually be an electron-pair density wave (PDW) state. Here we demonstrate theoretically that a biaxial PDW state with 8a periodicity may provide a compelling quantitative explanation for much of the observed quantum oscillation data.
Keywords: pair density wave, cuprate pseudogap, quantum oscillations
Abstract
There has been growing speculation that a pair density wave state is a key component of the phenomenology of the pseudogap phase in the cuprates. Recently, direct evidence for such a state has emerged from an analysis of scanning tunneling microscopy data in halos around the vortex cores. By extrapolation, these vortex halos would then overlap at a magnetic-field scale where quantum oscillations have been observed. Here, we show that a biaxial pair density wave state gives a unique description of the quantum oscillation data, bolstering the case that the pseudogap phase in the cuprates may be a pair density wave state.
The discovery of charge density wave correlations in cuprates by neutron and X-ray scattering, scanning tunneling microscopy (STM), and NMR has had a profound influence on the field of high-temperature superconductivity, but a number of observations indicate that the cuprate pseudogap phase involves more than just charge ordering (1). The pseudogap itself is characterized by a large suppression of spectral weight existing over a wide energy range around the Fermi energy (2–4), which seems incompatible with the weak short-range charge order observed by X-ray scattering. Given that the pseudogap is largest in the same region of momentum space that the d-wave superconducting gap is largest has led to numerous speculations that it is connected with pairing. Evidence for pairing correlations in the pseudogap phase has been suggested from a number of experiments, such as from the temperature dependence of the susceptibility [which has been interpreted as offering evidence for diamagnetism (5)], but alternate explanations for such data also exist. This is complicated by other experimental evidence indicating the presence of time-reversal symmetry breaking (6).
In an attempt to make sense of various conflicting interpretations of the pseudogap phase, it was speculated that a pair density wave (PDW) state, evident in numerical studies of the and Hubbard models (7, 8), could be the primary phase (with the charge modulations as a secondary effect) and also gives a natural explanation for the momentum dependence of angle-resolved photoemission data (9). More direct evidence has emerged from STM using a superconducting tip, where it was shown that the pairing order parameter was indeed modulated in space (10). This has been further bolstered by recent scanning tunneling data in a magnetic field (11). There, direct evidence was found for biaxial order in a halo surrounding the vortex cores at a wave vector that was one-half that of the charge density wave correlations, exactly as expected based on PDW phenomenology (12). This last observation leads to an obvious conjecture. One can estimate the field at which these vortex halos overlap (13), and this field is the same at which a long-range ordered charge density wave state has been seen by NMR and X-ray scattering (14).∗ Interestingly, this is virtually the same field at which quantum oscillations also become evident (15). This implies that the small electron pockets inferred from these data are due to the state contained in these vortex halos.
The most successful model for describing quantum oscillation data is that of Harrison and Sebastian (16). By assuming a biaxial charge density wave state, they are able to form nodal pockets by folding of the Fermi arcs observed by photoemission to obtain an electron diamond-shaped pocket centered on the -point side of the Fermi arc observed by angle-resolved photoemission (17). In their scenario, as this pocket grows, eventually a Lifshitz transition occurs, leading to a hole pocket centered around the point itself. A central question is whether an alternate model could have a similar phenomenology.
To explore this issue, we consider a biaxial PDW state with a wave vector of magnitude as observed in the recent STM data (11).† The secular matrix for such a state is of the form
Here, we assume a d-wave form for the PDW order parameter, , with its argument, , being the Fourier transform of the relative coordinate of the pair (the center of mass Fourier transform being ). We also ignore all of the other off-diagonal components, which arise from the secondary charge order, as they lead only to quantitative corrections to the results presented here. For we assumed the tight-binding dispersion of He et al. (18) for Bi2201. We do this for two reasons. First, this was the dispersion considered in previous work on PDWs (9). Second, there are no complications in this dispersion associated with bilayer splitting.
A few remarks are in order here. First, the above truncated matrix considers only leading-order terms that connect the electron state to the hole states determined by the four biaxial PDW wave vectors. The leading terms ignored in this approximation would be those that connect these hole states to other electron states besides . By examining these other states, we find that they should lead only to quantitative corrections, just like the neglected charge density wave (CDW) terms mentioned above (the full secular matrix for the commensurate wave vector would be of dimension 128). Second, the difference between this matrix and its CDW variant would simply involve taking away the negative signs along the diagonal (i.e., replace the four hole states by particle states instead). Of course, this difference has a profound impact on the results, as we discuss below.
To proceed, we need to define the spectral function, , as measured by angle-resolved photoemission:
Here, is the ith eigenvalue of the secular matrix, the component of the corresponding eigenvector (the analogue of the particle-like Bogoliubov component), and a phenomenological broadening parameter.
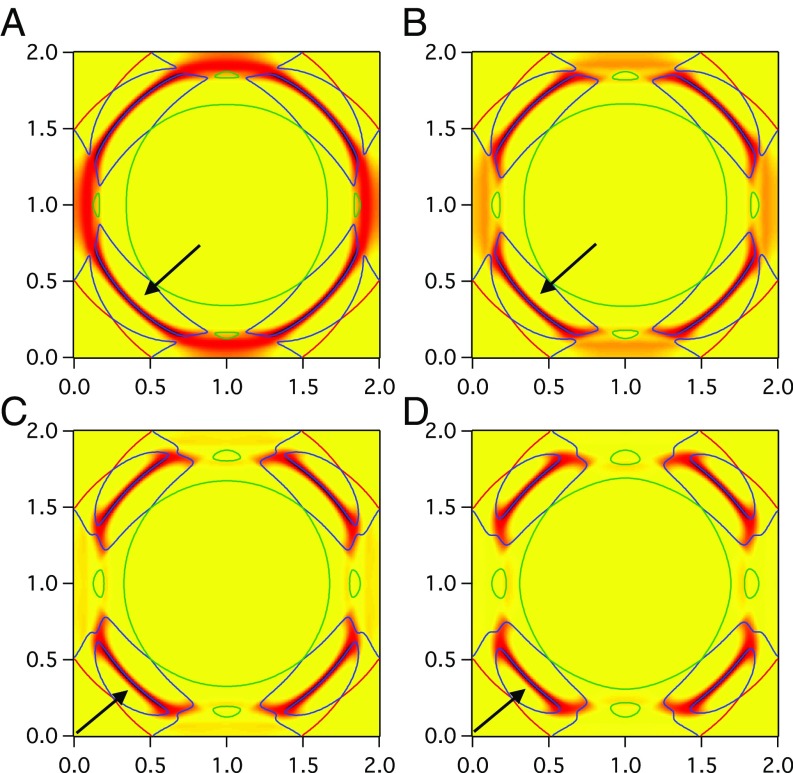
In Fig. 1, we show the spectral weight and eigenvalue contours at for four values of (the maximum energy gap of the PDW state). Deep in the pseudogap phase (large ), a small pocket centered along the diagonal is observed whose flat edge follows the spectral weight. As such, this pocket should dominate the deHaas–vanAlphen (dHvA) amplitude, unlike the other pockets which exhibit little or no spectral weight.‡ Note that the spectral weight, although small on the back side of this pocket [ is 0.0032 along the zone diagonal for Fig. 1C], is still nonzero along its entire contour. Moreover, despite the strong particle–hole mixing, this pocket is an electron-like pocket (its area increases as the chemical potential increases). This oval-shaped pocket is quite different from the electron pocket predicted in the CDW model, which is diamond-like in shape. As the hole doping increases (smaller ), this pocket undergoes a Lifshitz transition, resulting in a larger hole-like pocket also centered along the diagonal that resembles that obtained in the phenomenological Yang-Rice-Zhang (YRZ) model for the cuprates (22, 23). Although the CDW model also has a Lifshitz transition, the resulting hole pocket is quite different (a diamond-shaped pocket centered instead at the point of the zone). Once the PDW gap collapses, then we recover the much larger hole pocket centered at that is characteristic of the overdoped state (24). We remark that the biaxial nature of the PDW order is critical in forming these smaller pockets, although hints of them can be found in earlier work that assumed a uniaxial PDW instead (25–28) (the last two of these papers addressing the dHvA data).
Fig. 1.
Spectral weight and eigenvalue contours at for a PDW state with its amplitude, , being (A) 25 meV, (B) 50 meV, (C) 75 meV, and (D) 100 meV (the x and y axes are and in units of ). Arrows point to the center of the electron pocket (C and D) and the hole pocket (A and B). The normal-state dispersion is given by He et al. (18). Here, the modulus of the PDW ordering vector, , is , as observed in recent STM experiments (11). For the spectral weight, a phenomenological broadening parameter, , of 25 meV is assumed. Note the reduction of antinodal spectral weight as increases, which is completely suppressed at = 200 meV.
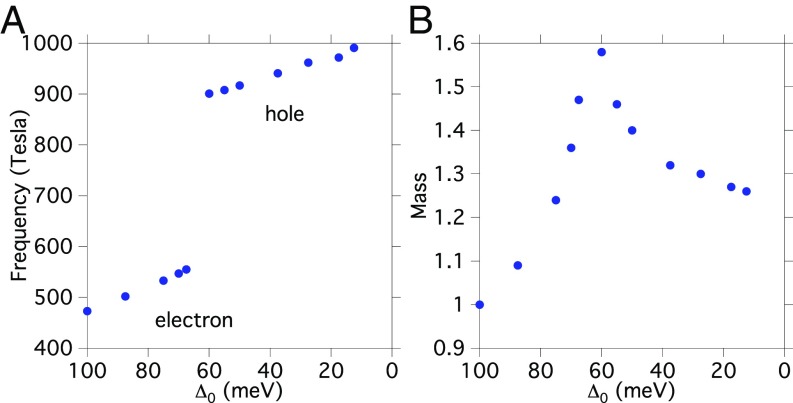
We quantify this by plotting the area of the pocket (in the dHvA units of tesla) along with the cyclotron mass as a function of in Fig. 2. We see a modest dependence of the pocket area on except for the pronounced jump at the Lifshitz transition, along with the associated mass divergence at the Lifshitz transition. These dependencies are in good accord with the measured dHvA data as a function of hole doping (29), including the mass divergence, noting that quantitative details are influenced by the dispersion and chemical potential (that is, the conversion of the x axis of Fig. 2 to doping is influenced not only by the doping dependence of , but also by the doping dependence of the band structure and chemical potential). Moreover, the results presented here offer a prediction. That is, beyond the mass divergence (as decreases), there should be a small doping range where a large hole pocket of roughly twice the size of the electron pocket occurs before the very large hole pocket in the overdoped regime forms when the gap collapses. This prediction is consistent with Hall effect data that show a region of the phase diagram between = 0.16 and = 0.19 where the Hall constant rapidly changes (30), with = 0.16 being where the mass divergence referred to above occurs and = 0.19 where the large Fermi surface is recovered (here, is the doping).
Fig. 2.
(A and B) dHvA frequency (area of the pocket) (A) and cyclotron mass vs. (B) derived from Fig. 1. Note the Lifshitz transition where the small electron pocket for large converts to a larger hole pocket for smaller . As a reference, the area of the large normal-state hole pocket centered at for is 17.68 kT with a cyclotron mass of 3.69.
We feel that the biaxial PDW scenario offered here is an attractive alternate to models based on a CDW. It is not only consistent with recent STM data in the vortex halos (11), but also consistent with magneto-transport data that indicate the presence of pairing correlations for magnetic fields not only up to but well beyond the resistive Hc2. This is in line as well with previous theoretical work on quantum oscillations in a d-wave vortex liquid (31). Certainly, we hope that the model offered here will lead to additional studies of high magnetic fields to definitively determine whether a PDW state really exists and, if so, what its characteristics and consequences are.
In summary, the work presented here bolsters the case that the enigmatic pseudogap phase in the cuprates is a PDW state.
Acknowledgments
We thank Stephen Edkins, Mohammad Hamidian, and Andrew Mackenzie for access to their vortex halo STM data in advance of publication. We also acknowledge Neil Harrison, Peter Johnson, Marc-Henri Julien, Catherine Kallin, Steve Kivelson, Patrick Lee, Brad Ramshaw, Subir Sachdev, Suchitra Sebastian, Todadri Senthil, Louis Taillefer, and Zhiqiang Wang for discussions. This work was supported by the Center for Emergent Superconductivity, an Energy Frontier Research Center funded by the US Department of Energy, Office of Science, under Award DE-AC0298CH1088.
Footnotes
The authors declare no conflict of interest.
∗The field at which the area of the halos is equal to the total area is , where is the flux quantum and the radius of the halo. For a typically observed radius of 50 Å, this field would be 26 Tesla.
†Here, we assume a homogeneous PDW order parameter and ignore any uniform superconducting component, along with any effects due to vortices and their associated phase winding. This should be justified for the high fields at which the quantum oscillations are observed.
‡It could be questioned whether these semiclassical orbits exist, since one side of the contour is particle-like and the other hole-like (19). The part of the thermodynamic potential from which the oscillations arise, though, involves only the particle-like content of the states (20). Therefore, as long as is nonzero along the entire contour, we argue that Landau levels associated with this contour exist. For the same reason, all other contours can be ignored when considering quantum oscillations (except for possible breakdown orbits) since their amplitudes will be suppressed due to their small . A similar argument applies to the overall magnitude of the specific heat. A proper treatment would require a full quantum mechanical solution of the secular matrix in the presence of a magnetic field. For a vortex lattice in a type-II superconductor (where the wave vector of its Brillouin zone plays the same role as the PDW ), the magnetization oscillations from such a calculation are closely related to those of the lowest-lying quasiparticle band, at least for the fundamental harmonic (21).
References
- 1.Fradkin E, Kivelson SA, Tranquada JM. Theory of intertwined orders in high temperature superconductors. Rev Mod Phys. 2015;87:457–482. [Google Scholar]
- 2.Timusk T, Statt B. The pseudogap in high-temperature superconductors: An experimental survey. Rep Prog Phys. 1999;62:61–122. [Google Scholar]
- 3.Norman MR, Pines D, Kallin C. The pseudogap: Friend or foe of high Tc? Adv Phys. 2005;54:715–733. [Google Scholar]
- 4.Lee PA, Nagaosa N, Wen X-G. Doping a Mott insulator: Physics of high-temperature superconductivity. Rev Mod Phys. 2006;78:17–85. [Google Scholar]
- 5.Li L, et al. Diamagnetism and Cooper pairing above Tc in cuprates. Phys Rev B. 2010;81:054510. [Google Scholar]
- 6.Fauque B, et al. Magnetic order in the pseudogap phase of high-Tc superconductors. Phys Rev Lett. 2006;96:197001. doi: 10.1103/PhysRevLett.96.197001. [DOI] [PubMed] [Google Scholar]
- 7.Corboz P, White SR, Vidal G, Troyer M. Stripes in the two-dimensional t-J model with infinite projected entangled-pair states. Phys Rev B. 2011;84:041108. [Google Scholar]
- 8.Zheng B-X, et al. Stripe order in the underdoped region of the two-dimensional Hubbard model. Science. 2017;358:1155–1160. doi: 10.1126/science.aam7127. [DOI] [PubMed] [Google Scholar]
- 9.Lee PA. Amperean pairing and the pseudogap phase of cuprate superconductors. Phys Rev X. 2014;4:031017. [Google Scholar]
- 10.Hamidian MH, et al. Detection of a Cooper-pair density wave in Bi2Sr2CaCu2O8+x. Nature. 2016;532:343–347. doi: 10.1038/nature17411. [DOI] [PubMed] [Google Scholar]
- 11.Edkins SD, et al. 2018. Magnetic-field induced pair density wave state in the cuprate vortex halo. arXiv:1802.04673.
- 12.Agterberg DF, Garaud J. Checkerboard order in vortex cores from pair-density-wave superconductivity. Phys Rev B. 2015;91:104512. [Google Scholar]
- 13.Wu T, et al. Emergence of charge order from the vortex state of a high-temperature superconductor. Nat Commun. 2013;4:2113. doi: 10.1038/ncomms3113. [DOI] [PubMed] [Google Scholar]
- 14.Gerber S, et al. Three-dimensional charge density wave order in YBa2Cu3O6.67 at high magnetic fields. Science. 2015;350:949–952. doi: 10.1126/science.aac6257. [DOI] [PubMed] [Google Scholar]
- 15.Maharaj AV, Zhang Y, Ramshaw BJ, Kivelson SA. Quantum oscillations in a bilayer with broken mirror symmetry: A minimal model for YBa2Cu3O6+δ. Phys Rev B. 2016;93:094503. [Google Scholar]
- 16.Harrison N, Sebastian SE. Protected nodal electron pocket from multiple-Q ordering in underdoped high temperature superconductors. Phys Rev Lett. 2011;106:226402. doi: 10.1103/PhysRevLett.106.226402. [DOI] [PubMed] [Google Scholar]
- 17.Norman MR, et al. Destruction of the Fermi surface in underdoped high-Tc superconductors. Nature. 1998;392:157–160. [Google Scholar]
- 18.He R-H, et al. From a single-band metal to a high-temperature superconductor via two thermal phase transitions. Science. 2011;331:1579–1583. doi: 10.1126/science.1198415. [DOI] [PubMed] [Google Scholar]
- 19.Dai Z, Zhang Y-H, Senthil T, Lee P. 2018. Pair density wave, charge density wave and vortex in high Tc cuprates. arXiv:1802.03009.
- 20.Miller P, Gyorffy BL. Theoretical investigations of the vortex lattice and de Haas-van Alphen oscillations in the superconducting state. J Phys Condens Matter. 1995;7:5579–5606. [Google Scholar]
- 21.Norman MR, MacDonald AH. Absence of persistent magnetic oscillations in type-II superconductors. Phys Rev B. 1996;54:4239–4245. doi: 10.1103/physrevb.54.4239. [DOI] [PubMed] [Google Scholar]
- 22.Yang K-Y, Rice TM, Zhang F-C. Phenomenological theory of the pseudogap state. Phys Rev B. 2006;73:174501. [Google Scholar]
- 23.Yang H-B, et al. Reconstructed Fermi surface of underdoped Bi2Sr2CaCu2O8+δ cuprate superconductors. Phys Rev Lett. 2011;107:047003. doi: 10.1103/PhysRevLett.107.047003. [DOI] [PubMed] [Google Scholar]
- 24.Vignolle B, et al. Quantum oscillations in an overdoped high-Tc superconductor. Nature. 2008;455:952–955. [Google Scholar]
- 25.Berg E, Fradkin E, Kivelson SA, Tranquada JM. Striped superconductors: How spin, charge and superconducting orders intertwine in the cuprates. New J Phys. 2009;11:115004. [Google Scholar]
- 26.Loder F, Kampf AP, Kopp T. Superconducting state with a finite-momentum pairing mechanism in zero external magnetic field. Phys Rev B. 2010;81:020511. [Google Scholar]
- 27.Zelli M, Kallin C, Berlinsky AJ. Mixed state of a -striped superconductor. Phys Rev B. 2011;84:174525. [Google Scholar]
- 28.Zelli M, Kallin C, Berlinsky AJ. Quantum oscillations in a -striped superconductor. Phys Rev B. 2012;86:104507. [Google Scholar]
- 29.Ramshaw BJ, et al. Quasiparticle mass enhancement approaching optimal doping in a high-Tc superconductor. Science. 2015;348:317–320. doi: 10.1126/science.aaa4990. [DOI] [PubMed] [Google Scholar]
- 30.Badoux S, et al. Change of carrier density at the pseudogap critical point of a cuprate superconductor. Nature. 2016;531:210–214. doi: 10.1038/nature16983. [DOI] [PubMed] [Google Scholar]
- 31.Banerjee S, Zhang S, Randeria M. Theory of quantum oscillations in the vortex-liquid state of high-Tc superconductors. Nat Commun. 2013;4:1700. doi: 10.1038/ncomms2667. [DOI] [PubMed] [Google Scholar]