Uncertainty in forecasts of long-run economic growth

Significance

This study develops estimates of uncertainty in projections of global and regional per-capita economic growth rates through 2100, comparing estimates from expert forecasts and an econometric approach designed to analyze long-run trends and variability. Estimates from both methods indicate substantially higher uncertainty than is assumed in current studies of climate change impacts, damages, and adaptation. Results from this study suggest a greater than 35% probability that emissions concentrations will exceed those assumed in the most severe of the available climate change scenarios (RCP 8.5), illustrating particular importance for understanding extreme outcomes.

Abstract

Forecasts of long-run economic growth are critical inputs into policy decisions being made today on the economy and the environment. Despite its importance, there is a sparse literature on long-run forecasts of economic growth and the uncertainty in such forecasts. This study presents comprehensive probabilistic long-run projections of global and regional per-capita economic growth rates, comparing estimates from an expert survey and a low-frequency econometric approach. Our primary results suggest a median 2010–2100 global growth rate in per-capita gross domestic product of 2.1% per year, with a standard deviation (SD) of 1.1 percentage points, indicating substantially higher uncertainty than is implied in existing forecasts. The larger range of growth rates implies a greater likelihood of extreme climate change outcomes than is currently assumed and has important implications for social insurance programs in the United States.

Projections of long-run productivity growth and economic growth are primary inputs into analyses used to support long-term planning and decision-making on many critical national priorities. These include investments in infrastructure as well as policies affecting public and private pension funds and social insurance (1). One of the most direct applications is projecting productivity growth to construct economic and geophysical models to project climate change and estimate the social cost of carbon estimates for rulemaking in the United States and around the world (2). Quantifying uncertainty in long-run economic growth has become fundamental to analysis of uncertainty in integrated assessment models and has been highlighted as a key priority by the Intergovernmental Panel on Climate Change and the National Academy of Sciences (3–5). Long-run growth scenarios are also imbedded in projections of greenhouse gas (GHG) emissions and concentrations as well as projections of temperature and other climatic outcomes (6, 7), thereby underpinning the full range of scientific research on the physical impacts (8–10) and economic damages from climate change (11, 12).

This study develops systematic and comprehensive probabilistic estimates of uncertainty in long-run growth forecasts, analogous to those for population forecasts in refs. 13 and 14. We use two approaches: (i) an expert survey* and (ii) a low-frequency statistical forecasting approach^† to estimate the distribution of the rate of growth of per-capita output^‡ to 2050 and 2100—these time frames being particularly relevant for policy decisions and long-run investments. The primary finding is that the uncertainty in long-run growth is larger than assumed in widely used models of climate change. We find that the shared socioeconomic pathways (SSPs) and representative concentration pathways (RCPs) (16), which are scenario-based projections used by the Intergovernmental Panel on Climate Change (IPCC) and underlie much research on physical impacts and economic damages, may understate the uncertainty in future economic growth and associated GHG concentrations. Our results indicate that existing scenarios miss the upper tail of productivity growth, implicitly understating the likelihood of high output growth rates and the resulting high emissions, concentrations, temperature change, and climate damages.

Quantifying the uncertainty in long-run productivity growth is challenging because it reflects so many underlying forces, including new technologies (17, 18), reforms to institutions (19), environmental and resource constraints, population pressures, and the growth of tangible, human, and intellectual capital (20). These challenges and the mixed record of long-run forecasts reinforces the importance of a systematic approach and a rigorous analysis of uncertainty. Both the expert survey and the low-frequency statistical approach yield similar results for the median global economic growth rate: ∼2% per year from 2010 to 2100. Both methodologies suggest that growth rates will be higher during the first half of the 21st century than the second, although the expert survey suggests greater uncertainty over the longer run (to 2100). Both approaches also indicate higher and more uncertain growth rates for China and low-income countries. The results indicate that the projections from the low-frequency statistical approach may be less robust for low-income countries and may miss structural shifts that expert forecasts suggest are likely to occur in the second half of the 21st century.

Quantifying Uncertainty in Long-Run Forecasts

Two approaches have been used by researchers and government agencies to develop forecasts of long-run productivity growth: (i) time series estimation using historical data and (ii) statistical estimation using expert expectations.^§ This study makes forecasts using both approaches and presents a systematic comparison of the results from both methods. This study also presents estimates of uncertainty in long-run growth forecasts, which are critical for modeling uncertainty in long-run physical and economic outcomes. We directly compare the resulting forecast distributions for six groupings: World, United States, China, High-Income Countries, Middle-Income Countries, and Low-Income Countries. For each region, we examine two forecast horizons: 2010–2050 and 2010–2100.

Expert Forecasts.

Expert surveys are widely used to develop “consensus” estimates of short-run forecasts (up to 3 y) of economic growth; they have become key inputs in financial research and monetary policy (21). Prominent economic surveys include the Livingston Survey, the Bank of England’s Inflation Report, the Blue-Chip Survey of Professional Forecasters, annual forecasts conducted by the National Association of Business Economists, and the Goldsmith-Nagan Bond Money Market Letter. These surveys combine forecasts from multiple forecasters to develop aggregate predictions because combined forecasts have been shown to have a smaller forecast error (using the mean squared error) than individual forecasts (22, 23).

One advantage of utilizing information from expert forecasts in addition to extrapolating from historical data are that they can draw upon and appropriately weight numerous sources of information and account for new trends or other factors that may lead to breaks in trends. This may be particularly important when the sample is small relative to the forecast horizon and where there may be nonstationarities in the underlying processes. Both of these are at work in long-run (decadal or century-long) future growth rates. Expert predictions have been utilized less formally to construct forecasts of long-run growth rates as part of larger climate modeling studies (24, 25). This study presents long-run forecast distributions using a systematic process of peer-nomination and is representative of a varied set of scholarship on long-run growth across economic fields.

Our expert forecast data come from the Yale Long Run Growth Survey, which was designed to elicit predictions and uncertainties about the growth in per-capita GDP and was administered in 2014–2015. Survey respondents were selected using a process of nomination by a panel of peers. The peer nomination process yielded a sample of economic experts that is widely recognized and that vary in field and methodological orientation.^¶ Survey responses were provided by 16 survey respondents and 13 experts included complete forecasts distributions that were used to estimate the combined forecast distributions. [See the footnotes (*) for a list of survey respondents. Three responses did not include comprehensive sets of estimates and were omitted from the uncertainty study.]

The survey first provided experts with historical data containing information on per-capita GDP growth rates for 1900–2010 using data from Maddison (26) Barro and Ursúa (27). (Participants were provided with information about historical per-capita GDP growth rates. See SI Appendix for details on the survey instrument.) The focal section asked participants to provide five quantile estimates (10th, 25th, 50th, 75th, and 90th percentiles) for average annual rates of growth of per-capita real GDP for the six world regions as well as over two time horizons: 2010–2050 and 2010–2100.^# This survey instrument includes a number of features that are designed to address bias from overconfidence (see discussion in SI Appendix, A.3).^‖ Consistent with the Survey of Professional Forecasters, respondents provide subjective probability distributions that explicitly characterize uncertainty and allow for a systematic analysis of patterns both within- and across-forecast distributions (28). The expert responses were then aggregated into a combined distribution by quantile (see detailed discussion of aggregation in SI Appendix, A.1, and an analysis of robustness in SI Appendix, A.3).

Low-Frequency Forecasts.

A wide range of time series methods has been used to construct macroeconomic forecasts, typically focusing on high-frequency processes [the dynamics of growth and financial markets in business cycles (29–31)]. The use of statistical forecasting techniques in long-run growth applications has been limited by inherent challenges in characterizing variability in long-run, nonstationary processes and also by the short time span of most economic measures, such as real GDP and per-capita output (32, 33). One approach for obtaining long-run estimates has been developed by the Social Security Actuary and the Congressional Budget Office for 75-y stochastic projections (34–36). The Congressional Budget Office requires estimates of uncertainty in long-run productivity growth forecasts to study the impact of uncertainty of productivity growth on revenues, expenses, and budget deficits. These projections assume that productivity growth is characterized by finite-variance shocks that are independent and identically distributed (i.i.d.). This assumption implies that uncertainty (measured, for example, as the SD of productivity shocks) declines with the square root of the time horizon. One important finding from both the expert and low-frequency approaches is that the uncertainty declines much more slowly than is consistent with i.i.d. shocks.

Recent statistical approaches to quantify the long-run uncertainty of economic variables have focused on low-frequency dynamics. Most work on variability of economic trends focuses on high-frequency dynamics, as with daily or monthly volatility of financial variables such as the stock market or business cycle frequency of output, wages, or inflation. The issues addressed here (for climate change or demographic developments) require analysis of low-frequency variability—at the timescale of a decade or more. A notable approach on which we draw is the work of Müller and Watson, or MW, which demonstrates that long-run trends in a range of time series processes can be captured by projecting the series onto a set of trigonometric functions (37, 38, 39). These studies use discrete cosine transforms to estimate low-frequency variability for several economic variables and demonstrate that the low-frequency method provides robust predictions of uncertainty for multiple macroeconomic series over the past 100 y (39). They apply their approach using annual (1901–2014) and a post-World War II time series for the United States to construct a 75-y forecasts for per-capita GDP growth, inflation, and stock returns in the United States. Low-frequency methods have not at this time been used for productivity growth outside the United States.

We implement the MW low-frequency forecasting methodology using time series data on per-capita global and regional growth rates for 1900–2010 using data from refs. 26 and 27. Global and regional growth rates are constructed using constant 2006 output shares. We adjust MW prediction intervals to match the quantiles of the forecast distribution that were specified in our expert survey, and we extend the projections to 2100. The MW method uses both frequentist and Bayesian procedures to incorporate uncertainty. We report the Bayesian estimates, which require fewer assumptions and are feasible to match to the exact quantiles from our expert forecasts.

Results

Global and Regional Growth Forecasts.

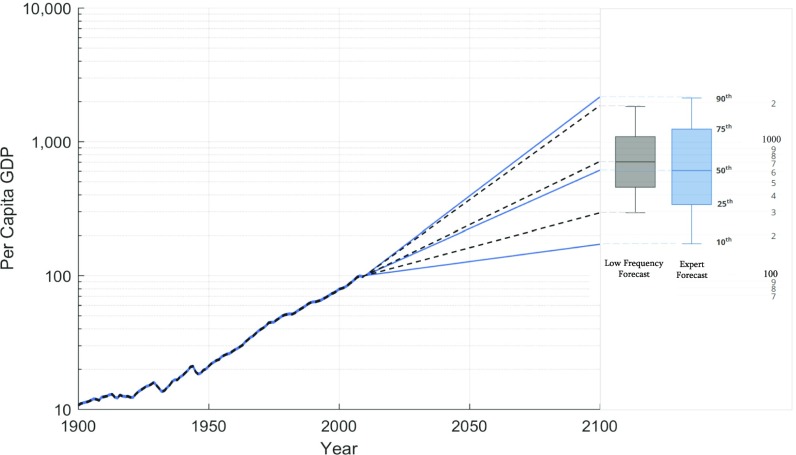
Fig. 1 and Table 1 illustrate the projections of global annual per-capita output over the 2010–2100 period for both the expert survey and the low-frequency statistical approach. A first important finding is that there is little difference in the 50th percentile results between the two approaches. The two approaches are also similar for the 75th and 90th percentiles. There is a greater difference at the 10th and 25th percentiles, with the expert survey showing lower growth (and therefore greater uncertainty) at those percentiles than the low-frequency estimates. In responses to open-ended questions regarding their reasoning, many of the experts suggest that there is a nonnegligible probability of major historical discontinuities that would depress future growth and therefore lead to greater dispersion at the low end. Global conflict and civil unrest, persistent corruption or the deterioration of institutions, and sustained disruptions to world trade are cited as the most likely negative shocks to 21st-century growth. At the upper end of the distribution, the experts refer in their qualitative responses to the possibility of an acceleration of technical change, including artificial intelligence and health technology, as most likely positive shocks to productivity growth in the 21st century.

Fig. 1.

Actual historical data and projections of global output, 1900–2100. Historical estimates of global per-capita GDP (1900–2010) use data from Barro and Ursúa (32). Projection lines for 2010–2100 show per-capita output from survey (blue lines) and low-frequency forecasts (black lines). Global aggregates are geometric means of national growth rates, weighted by share of global income in 2006. All growth data are indexed by setting output in 2010 to 100.

Table 1.

Expert and low-frequency estimates by region and time horizon

		2010–2050							2010–2100
Region	Statistic	10th	25th	50th	75th	90th	µ	σ	10th	25th	50th	75th	90th	µ	σ
World	Expert TM	1.17	1.80	2.59	3.23	3.92	2.54	1.07	0.60	1.36	2.03	2.85	3.47	2.06	1.12
	Expert (SD)	1.37	0.97	0.75	0.85	0.92	—	—	2.14	1.14	0.84	0.94	1.06	—	—
	Low freq	1.2	1.7	2.2	2.7	3.3	2.23	0.99	1.2	1.7	2.2	2.7	3.3	2.23	0.98
High	Expert TM	0.56	1.23	1.76	2.30	2.75	1.72	0.84	0.27	0.95	1.46	2.08	2.57	1.47	0.88
	Expert (SD)	1.38	0.82	0.68	0.69	0.77	—	—	1.55	0.92	0.62	0.73	0.84	—	—
	Low freq	0.7	1.4	2.0	2.5	3.0	1.90	0.99	1.0	1.5	2.0	2.4	2.8	1.92	0.89
Middle	Expert TM	0.93	1.76	2.67	3.36	4.11	2.57	1.23	0.34	1.30	1.98	2.72	3.45	1.96	1.18
	Expert (SD)	1.47	0.91	0.77	0.68	0.77	—	—	2.15	0.83	0.81	0.64	0.97	—	—
	Low freq	0.5	1.2	1.9	2.6	3.4	1.92	1.27	0.5	1.3	1.9	2.6	3.4	1.94	1.41
Low	Expert TM	1.05	2.23	3.41	4.25	5.12	3.21	1.57	0.62	1.72	2.53	3.45	4.57	2.58	1.49
	Expert (SD)	1.70	1.25	0.78	0.95	1.26	—	—	2.10	1.23	1.10	1.05	1.55	—	—
	Low freq	2.8	4.3	6.1	8.1	10.2	6.34	3.00	1.8	3.5	5.5	7.9	10.7	5.95	3.74
United States	Expert TM	0.60	1.14	1.75	2.18	2.63	1.66	0.79	0.49	0.91	1.53	2.04	2.64	1.52	0.84
	Expert (SD)	1.18	0.76	0.75	0.69	0.68	—	—	1.28	0.76	0.76	0.65	0.78	—	—
	Low freq	0.9	1.5	2.2	2.8	3.4	2.14	1.09	1.2	1.7	2.1	2.5	2.9	2.03	0.84
China	Expert TM	1.51	2.81	4.23	5.19	6.31	4.01	1.85	0.89	2.02	2.93	3.87	4.87	2.92	1.51
	Expert (SD)	1.83	1.57	1.11	1.18	1.35	—	—	2.29	1.59	1.25	1.15	1.38	—	—
	Low freq	1.6	3.9	6.6	9.5	12.7	6.93	4.61	0.7	3.1	5.7	8.9	12.7	6.33	5.36

Note: Expert and low-frequency estimates by region and time horizon. Expert TM and SD are the trimmed mean and SD of expert forecasts at each quantile. Low-frequency forecasts are Bayes estimates at each quantile. Notation is that μ and σ are the means and SDs of the respective forecast distributions. Expert μ and σ are estimated using a fitted normal distribution (see SI Appendix for details).

Table 1 provides estimates of the quantiles of the distribution of per-capita output growth for both time horizons and different regional aggregations. For the 2010–2100 period, the 50th percentile growth forecast is 2.0% per year for the expert forecast and 2.2% per year for the low-frequency forecast. For global growth, the means are within 0.05% points for both methods and both horizons. The interquartile range (IQR) of the expert forecast distribution is 1.5 percentage points, indicating that there is a 25% probability that global growth rate will be less than 1.4% per year and a 25% probability that it will exceed 2.9% per year. The IQR for the low-frequency statistical approach over 2010–2100 is significantly lower (1.0 percentage point), with most of the difference coming from the 10th and 25th percentiles, as is shown in Fig. 1. This result is a clear indication that the low-frequency approach finds lower long-run uncertainty than experts.

For the shorter time horizon, to mid-21st century, there is relatively little difference between the two methodologies in the IQR of the forecasts. Expert forecasts indicate that economic growth will follow historical trends over the next four decades but not across the entire century. In fact, 97% of the responses across regions in the expert sample have the expert’s quantile estimate to 2050 higher than the estimate to 2100 (midcentury estimates are 0.56 percentage points higher on average). Only 50% of the low-frequency forecasts for midcentury are higher than the full-century estimate (midcentury estimates are 0.16 percentage points higher on average). The primary difference between expert and low-frequency forecast distributions is in uncertainty about the low end of the growth distribution in the latter half of the century.

Table 1 also shows that the global economic growth estimates based on the low-frequency statistical approach fall within 1 SD of the expert forecast estimates for nearly all percentiles and time horizons. This result holds for most regional stratifications, but most notably does not hold in the higher percentiles for low-income countries. We also find far greater uncertainty in economic growth in low-income countries in the low-frequency forecasts than the expert forecasts. This notably contrasts with the global estimates, for which we find greater uncertainty in the expert forecasts.

The difference between the two approaches is particularly dramatic for China. For example, the 90th percentile over the 2010–2100 period indicates a growth rate in China of 12.7% per year using the low-frequency statistical approach and only 4.9% per year based on the expert surveys. This difference clearly reveals expert judgment regarding the persistence of high growth rates in China and elsewhere in the developing world. Expert forecasts predict that very high recent economic growth rates of China will not persist throughout the 21st century, marking an important difference from the low-frequency forecast. For example, we find that only 2 of 10 low-frequency forecasts for the low-income countries fall within 1 sample SD of a combined expert forecast and only 4 of 10 for China. The difference between the two approaches emphasizes the potential importance of nonstationarities in future growth patterns and the need to address potential discontinuities in long-run growth projections.

Implications for Climate Change.

The results reported in Table 1 indicate substantially higher uncertainty in long-run economic growth than has been assumed in climate–economy models, in IPCC assessment reports, and in a large body of science on the impacts of global climate change (4–7, 16, 25, 33). One common approach in climate policy analysis is based on economic growth rates defined as part of SSPs. The SSPs are five scenarios that provide 100-y forecasts for key demographic and economic variables; they are designed to provide plausible “storylines” for the evolution of these variables (16, 39). In the SSP storylines, economic growth rates vary based on structural factors that are assumed to determine productivity growth (40, 41). However, the SSPs are not based on probabilistic methods and are not structured to formally capture uncertainty in long-run productivity growth rates.** Rather, they are used to describe “uncertainty in mitigation, adaptation, and impacts associated with alternative climate and socioeconomic futures” (16).

Fig. 2A compares the per-capita GDP growth from expert and low-frequency forecast distributions (10th, 25th, 50th, 75th, and 90th percentiles) with the five reference (no policy) SSP scenarios of per-capita growth.^†† The figure reveals two important findings. First, estimates from SSP2 are consistent with median estimates of the present forecasts. SSP2 is described as a “middle of the road” scenario, with “medium” demographics, development of advanced energy technologies, frontier productivity growth, and regional convergence. SSP5, a high-growth baseline, falls closer to the 75th percentile of our two forecast distributions. Second, the range of SSPs does not reflect the uncertainties in either the expert or the low-frequency forecasts. The full set of global growth rates implied by the SSPs excludes most of the upper quartile of both of the forecast distributions, implying that the probability of high emissions and climate damages may be underestimated in current analyses based on the SSP scenarios. (Any bias in the forecasts from our expert information would reduce the uncertainty in reported forecast distributions, such that our findings should be interpreted as a lower bound on differences between the uncertainty in the expert forecast versus other estimates.)

Fig. 2.

(A) Forecast uncertainty for global output in 2100 from expert and low-frequency methods and SSPs. SSP data for SSPs are from IIASA (https://tntcat.iiasa.ac.at/SspDb/). (B) Projected CO₂ concentrations in middle for 2100. CO₂ concentrations at left use output growth based on the estimates from the expert mean and dispersion, and then project 2100 concentrations using the DICE-2016R model. Projected CO₂ concentrations for SSPs come from SSP public database, version 1.1, and RCPs at right, version 2.0, at IIASA (https://tntcat.iiasa.ac.at/SspDb/).

We can illustrate the downward tendency of the SSPs by comparing the projected CO₂ concentrations these imply with concentrations that reflect the pdfs that are derived in the present study. To obtain comparable SSPs, we take the reference SSPs that are generated by the modeling community and assume these generate 2100 CO₂ concentrations according to the MAGICC model (SSP Public Database, version 1.1: https://tntcat.iiasa.ac.at/SspDb/dsd?Action=htmlpage&page=about). For comparison, we use the distribution of CO₂ concentrations using the forecast distribution of productivity growth from the present study and the resulting CO₂ concentrations using the dynamic integrated climate–economy (DICE) integrated assessment model. We rely on the DICE model for this comparison because it is simple to adopt, is widely used by analysts, and has results that are in the middle of a range of estimates of uncertainty in a multimodel study of integrated assessment models (see SI Appendix for detailed explanation). Fig. 2B shows that the results for CO₂ concentrations show a similar pattern as that for output. The high end of CO₂ concentrations in these scenarios, given by SSP5, excludes the upper quartile of CO₂ distributions with the present findings on uncertainty in productivity growth. We emphasize that these differences are driven almost entirely by uncertainty in productivity growth. As a test of this, we extend our comparison to examine year 2100 CO₂ concentrations in models that treat productivity growth as the only uncertain parameter versus models with uncertainty in five key parameters: productivity growth, equilibrium temperature sensitivity, the damage function, the carbon cycle, and the rate of decarbonization. The results show that CO₂ concentrations are effectively unchanged when uncertainty is introduced in the other four parameters. Furthermore, differences in the upper quartile of CO₂ concentrations disappear in models with uncertainty in other key parameters but not in the productivity growth rate (see SI Appendix for multimodel and productivity-only results).

We further study the implications of uncertainty in productivity growth via comparison with the RCPs, which are a set of scenarios developed by modelers to represent the full range of projected GHG concentrations in 2100 (42). We compare the range of concentrations of the RCPs with those generated by the DICE model. The RCPs clearly understate the range of concentrations relative to projections that incorporate the uncertainty in productivity growth. RCP2.6, RCP4.5, and RCP6 are scenarios that allow climate policy to affect outcomes, complicating the comparison with our probabilistic forecast for a no-policy baseline. RCP8.5 was designed to represent “a very high baseline emissions scenario” and is intended to represent the upper bound of climate forcings available in the literature. Our results indicate that there is a greater than 35% probability that emissions concentrations will exceed those assumed in RCP8.5. This finding indicates that models in which climate models treat RCP8.5 as an upper bound on future climate forcings exclude a range of concentrations that systematic economic projections indicate are reasonably likely.

Understanding structural uncertainty is a critical component of climate research and policy. Many scientific research programs are currently focused on identifying the physical impacts, societal damages, and adaptive responses that will occur in the context of baseline productivity and emissions growth across the 21st century. The findings here indicate that current research may be based on estimates that substantially underestimate uncertainty about output growth, particularly at the upper end (43, 44). Depending upon the magnitude of the uncertainties and the rate at which they are resolved, climate policies might need to be more or less stringent to meet international objectives.

Conclusions

Public policy research on a variety of topics relies upon forecasts of productivity growth. Understanding the uncertainty in these forecasts is critical for decisions being made today, including infrastructure, investments in public and private pension funds, funding social insurance systems, and investments in mitigating and adapting to climate change. We use expert forecasts from the Yale Long Run Growth Survey and a low-frequency statistical approach to produce systematic probabilistic estimates of long-run per-capita GDP growth over the 21st century, covering six regional groupings and two time horizons.

Before summarizing the major results, we emphasize the inherent difficulties of projecting trends of economic growth into the distant future because of the variety of time-varying forces at work and the potential for unanticipated events and technologies to have impact. The combined expert forecast for the median growth rate in per-capita output is ∼2.03% per year between 2010 and 2100, with an SD of 1.1 percentage points per year. These estimates are similar for the two methods used—the expert survey and the low-frequency statistical estimation approach—with a key difference being that expert judgment finds greater uncertainty and higher likelihood of lower economic growth in the second half of the 21st century. Low-frequency forecasts are substantially different from expert forecasts for low-income countries such as China, where structural shifts may reduce the reliability of time series estimation.

One of the most important findings of this analysis is that uncertainty in per-capita GDP growth rates in the present study is substantially higher than stochastic projections embedded in multiple existing public policy applications, with direct effects on regulations in the United States and other countries. Furthermore, the emissions and concentrations scenarios that underpin the study of climate change impacts, damages, and adaptation across a range of scientific domains do not reflect the range of economic growth trajectories determined by the present study, and most omit the upper end of the output distribution. This finding has critical implications for the future development of a climate modeling program that is capable of addressing and incorporating uncertainty.

While extremely challenging, the effort to quantify uncertainty in long-run productivity growth is necessary for understanding central scientific uncertainties and forming a solid basis for key regulatory decisions in the United States and other countries. The combination of long-run time series techniques with expert forecasts allows for an analysis of areas of agreement and disagreement between these different methods, resulting in more robust forecasts. The present results present an important upward revision in the uncertainty reflected in commonly used forecasts and demonstrates important implications for climate change.