Comparison of Variable Selection Methods for Clinical Predictive Modeling

Abstract

Objective

Modern machine learning-based modeling methods are increasingly applied to clinical problems. One such application is in variable selection methods for predictive modeling. However, there is limited research comparing the performance of classic and modern for variable selection in clinical datasets.

Materials and Methods

We analyzed the performance of eight different variable selection methods: four regression-based methods (stepwise backward selection using p-value and AIC, Least Absolute Shrinkage and Selection Operator, and Elastic Net) and four tree-based methods (Variable Selection Using Random Forest, Regularized Random Forests, Boruta, and Gradient Boosted Feature Selection). We used two clinical datasets of different sizes, a multicenter adult clinical deterioration cohort and a single center pediatric acute kidney injury cohort. Method evaluation included measures of parsimony, variable importance, and discrimination.

Results

In the large, multicenter dataset, the modern tree-based Variable Selection Using Random Forest and the Gradient Boosted Feature Selection methods achieved the best parsimony. In the smaller, single-center dataset, the classic regression-based stepwise backward selection using p-value and AIC methods achieved the best parsimony. In both datasets, variable selection tended to decrease the accuracy of the random forest models and increase the accuracy of logistic regression models.

Conclusions

The performance of classic regression-based and modern tree-based variable selection methods is associated with the size of the clinical dataset used. Classic regression-based variable selection methods seem to achieve better parsimony in clinical prediction problems in smaller datasets while modern tree-based methods perform better in larger datasets.

1. INTRODUCTION

The widespread implementation of electronic health records across the healthcare system is paving the way for large-scale, data-driven clinical research [1–3]. Modern data modeling methods, mostly derived from the machine learning literature, are also becoming widely available and are starting to be used by clinical researchers [2–4]. However, there has been limited research comparing the performance of classic and modern modeling methods in clinical datasets [5].

The prediction of clinical outcomes is a common medical information need that is particularly adept to the use of large clinical datasets, making clinical predictive modeling a promising area of study in this era of digital healthcare [3]. One of the crucial steps in the development of clinical prediction models is the variable selection process, which aims at removing irrelevant input variables from the models being derived [6]. Data used to derive prediction models oftentimes contains both replicable variables with a true relationship with the outcome (also known as “signal”), and non-replicable variables with only an idiosyncratic relationship with the outcome (or “noise”). The goal of variable selection methods is to increase the signal-to-noise ratio in the data in order to develop appropriately fitted models that will make accurate predictions when new, unseen data is used as input [7, 8].

Variable selection methods are also used to reduce the complexity of the prediction models without compromising their accuracy. Sparse, less complex models that achieve good performance are said to be parsimonious [8]. Highly complex, non-parsimonious models are not only difficult to replicate in different healthcare settings but there is a real world monetary and computational cost associated with mapping and maintaining numerous variables for complex algorithms designed to run in real-time [9].

Classic variable selection methods, such as selection by subject matter experts and regression-based stepwise selection, have been commonly used in the development clinical prediction models [10–16]. An alternative to these is the use of modern variable selection methods derived from tree-based algorithms (e.g. random forest). These methods are widely used in other areas of biomedical research [17, 18], but their use in clinical prediction models has been limited so far. Furthermore, there is evidence that the size of a dataset and the event per variable ratio (that is, the number of events –or cases – in the derivation dataset for every variable included in the model) play a major role in the performance of different methods [5].

Our aim in this study was to analyze the performance of eight different variable selection methods, both regression-based and tree-based methods, in two clinical datasets of different sizes used for predictive modeling: a multicenter adult clinical deterioration cohort and a single center pediatric acute kidney injury cohort [14, 15].

2. MATERIALS AND METHODS

2.1. Clinical datasets

2.1.1. Adult clinical deterioration cohort

This is a multicenter observational cohort dataset with 269,999 patients admitted to the wards of five hospitals [14]. 6.1% of patients in the dataset had a clinical deterioration event: 424 cardiac arrests, 13,188 intensive care unit (ICU) transfers, and 2,840 deaths on the wards. The dataset was analyzed using a discrete-time survival format in 8-hour time windows. The variables extracted from the electronic health record (EHR) for predictive modeling of clinical deterioration included laboratory results, vital signs, and patient demographics (29 variables in total). Missing values were imputed using the population median, and the original dataset was divided in a 60/40 split for derivation and validation, which resulted in 356 events per variable in the derivation set.

2.1.2. Pediatric early acute kidney injury cohort

This is a single center observational cohort dataset of 6,564 critically ill children admitted to a pediatric ICU without evidence of acute kidney injury (AKI) [15]. Among the patients in the dataset, there was a 4% incidence of early AKI, which was defined as the development of new AKI by 72 hours of ICU stay. The variables extracted from the EHR for predictive modeling of early AKI included laboratory results, vital signs, medications from the first 12 hours of ICU stay as well as demographic information and admission characteristics (26 variables in total). Missing values were imputed using multiple imputation methods and the original dataset was divided in a 60/40 split for derivation and validation, which resulted in 6 events per variable in the derivation set.

2.2. Variable selection methods

2.2.1. Overview

We studied the performance of eight variable selection methods: four regression-based methods (stepwise backward selection using p-value and AIC, Least Absolute Shrinkage and Selection Operator, and Elastic Net) and four tree-based methods (Variable Selection Using Random Forest, Regularized Random Forests, Boruta, and Gradient Boosted Feature Selection) [8, 19–23]. We chose to focus our analysis on regression-based and tree-based variable selection methods given their prevalence in the medical literature [6, 16]. Furthermore, we chose four representative variable selection methods from each group to balance the comparisons and include methods with wider adoption (e.g. stepwise backward selection, random forest) and methods generating increasing interest in the literature (e.g. elastic net, gradient boosted feature selection). Here we review both types of methods in more detail.

2.2.2. Regression-based methods

2.2.2.1. Stepwise backward selection using p-values

Stepwise backward selection using p-values is a classic variable selection method that has been extensively used in the medical literature [8]. First, all the variables are tested in a regression model and subsequently the least significant variables are eliminated in a stepwise approach. Most commonly, this method uses a p-value cut-off as a stopping rule, usually keeping the subset of variables that have a significance level of p<0.05, but other levels can also be used. We implemented this method in our two cohorts using a significance level of p<0.05 to select the variables and evaluate the performance of the method in the validation set.

2.2.2.2. Stepwise backward selection using AIC

Stepwise backward selection using the Akaike Information Criterion (AIC) is a method very similar to the stepwise backward selection using p-value, except the stopping rule is based on achieving the lowest AIC. AIC penalizes the complexity of the model by decreasing the p-value threshold at which variables are dropped from the model in proportion to the number of variables selected. That is, the lower the number of variables in the model, the less restrictive the p-value threshold becomes [8].

2.2.2.3. Least Absolute Shrinkage and Selection Operator (Lasso)

Lasso is a linear regression-based model that is regularized by imposing an L1 penalty on the regression coefficients [22]. The L1 penalty forces the sum of the absolute value of the coefficients to be less than a constant. The variable selection process is embedded in this model because, given the nature of the L1 norm, some coefficients will be forced to be 0, and hence are eliminated from the model. In order to find the optimal constraint parameter in our implementation we performed 100 sequential searches over a parameter grid of 0.02 increments and calculated the area under the receiver operating characteristic curve (AUC) using ten-fold cross-validation. The model with the highest AUC was used to determine which variables were selected and to evaluate the performance of the method in the validation set.

2.2.2.4. Elastic Net

Elastic Net could be considered an extension of the Lasso where an L1 and an L2 penalty are imposed [24]. The properties of the L2 norm encourage a grouping effect so that highly correlated variables are either kept in the model or are eliminated together. It also performs variable selection in an embedded fashion similar to the Lasso. The potential advantages over the Lasso can be attributed to the grouping effect and the fact that Elastic Net can better deal with situations where the number of predictors exceeds the number of cases (p > n situations). In our implementation, the optimal parameters were found by performing 100 random searches over a parameter grid and calculated the AUC using a two-dimensional ten-fold cross-validation. The model with the highest AUC was used to determine which variables were selected and to evaluate the performance of the method on the validation set.

2.2.3. Tree-based methods

2.2.3.1. Variable Selection Using Random Forest (VSURF)

The random forest is an ensemble model of hundreds or thousands of decision trees that uses the average output of all the trees to predict an outcome [7]. Each individual decision tree is derived by performing recursive partitioning of random subsets of the input variables. The variables selected and the actual cut-points for the partition are determined based on the overall goal of splitting the data into subsets that have the most differing proportions of the outcome or information gain. VSURF takes advantage of the variable selection mechanisms embedded in the random forest algorithm and selects the smallest model with an out-of-bag error less than the minimal error augmented by its standard deviation. The method selects two variable subsets: one used for interpretation that includes all variables highly correlated with the outcome, and one more limited that only includes the smallest subset of variables that are appropriate for prediction [20]. In our implementation, the variables in the interpretation subset determined by the algorithm were considered as the variables selected by the VSURF method. To evaluate the performance of the method, the variables selected were then used to derive a random forest model using 500 trees and other default settings. The resultant model was used to test the performance on the validation set.

2.2.3.2. Regularized Random Forests (RRF)

RRF are a random forest-based method that penalize the selection of a new variable for splitting in each tree if the information gain is not superior to that of previous splits [19]. RRF therefore favors the selection of the smallest subset of variables possible to perform the prediction. In our implementation we regularized the model derivation by performing 100 searches over a randomly generated parameter grid and determined the best tuning parameter using ten-fold cross-validation. The resulting model was used to determine the variables selected and to evaluate the performance of the method on the validation set.

2.2.3.3. Boruta

Boruta is a random forest-based method that iteratively removes the features that are proven to be statistically less relevant than random probes, which are artificial noise variables introduced in the model by the algorithm [21]. In our implementation the variables rejected by the Boruta algorithm were removed from the original variable set and the remaining variables were considered as the variables selected by the method. To evaluate the performance of the method, the variables selected were then used to derive a random forest model using 500 trees and other default settings. The resultant model was used to test the performance on the validation set.

2.2.3.4. Gradient Boosted Feature Selection (GBFS)

GBFS uses the gradient boosting machine framework to select variables. GBFS derives an ensemble of limited-depth regression trees for which variables are selected sparsely by penalizing the inclusion of new variables. When a tree selects a new variable, the algorithm penalizes the model at a cost equal to the parameter lambda, while allowing the use of previously utilized variables at no added cost. Therefore, only variables producing sufficient gain in prediction accuracy to overcome the penalty will be included [23]. In our implementation, in order to find the optimal lambda we performed sequential searches over a parameter grid of 0.1 increments and determined the best lambda using ten-fold cross-validation. The resulting variables selected by the GBFS method with the optimal lambda were used to derive a gradient boosted machine model using 500 trees with interaction depth of 4 and a learning rate of 0.1, consistent with the default GBFS method. The resultant model was used to test the performance on the validation set.

2.3. Method-specific modeling approaches

2.3.1. Regression-based methods

Since the regression-based methods assume a linear relationship between the variables and the outcome, the continuous variables in the regression-based models were transformed using restricted cubic splines with three default knots [8, 25].

2.3.2. Tree-based methods

Since tree-based methods are known to underperform in highly unbalanced datasets, such as the ones used in this paper, the derivation data for both datasets were balanced using non-heuristic random sub-sampling of the majority class [26].

Otherwise the method-specific default settings were used for the rest of the modeling consistent with prior literature comparing modeling methods [5].

2.4. Method evaluation

2.4.1. Parsimony

A model is considered parsimonious when it is both sparse (i.e., it uses the least amount of variables possible) and has good prediction accuracy [7, 8]. The trade-off of sparsity and accuracy is difficult to quantify, and hence we present both performance and sparsity measures together to allow for different use case interpretation. Prediction performance was measured using the area under the ROC curve (AUC) of the model on the validation set and sparsity as the number of variables selected by the method.

2.4.2. Performance change from reference model

Three reference models for each dataset were derived using all the variables available to measure the change from the baseline performance incurred by each method. A fixed effects logistic regression model with restricted cubic splines was used as reference for the two backward selection methods (p-value and AIC), Lasso, and Elastic Net. A random forest model with 500 trees was used as reference for the VSURF, RRF, and Boruta methods. Finally, a gradient boosted machine model with 500 trees was used as reference for the GBFS method. As described above, the method-specific default settings in the corresponding statistical package were used for the three reference models, consistent with prior literature comparing modeling methods.

2.4.3. Variable importance and variable selection

Variables in each model were ranked by importance and a category from 1 to 4 was assigned to each variable based on the quartile of importance, with the 4^th quartile being the variables with the highest importance. This was done to account for the different importance metrics that each method uses and to allow for comparison between methods.

For all method evaluations, the derivation (60%) sets from the original publications were used to run the various variable selection methods and the validation (40%) sets were used to calculate resulting model accuracy.

2.5. Analysis

Data were analyzed using STATA version 13 (StatCorp, College Station, TX), MATLAB release 2015b (The MathWorks, Inc., Natick, MA), and R version 3.2.2 (R Foundation for Statistical Computing, Vienna, Austria). The following R packages were used for modeling: glmnet, VSURF, Boruta, RRF, gbm, randomForest, and caret [27].

Institutional Review Boards at the University of Chicago, NorthShore University HealthSystem, and Children’s Hospital Los Angeles granted waivers of consent for this study based on general impracticability and minimal harm.

3. RESULTS

3.1. Parsimony

Figures 1 and 2 present the parsimony measures (AUC against the number of variables selected) for the adult clinical deterioration cohort and the pediatric early acute kidney injury cohort, respectively.

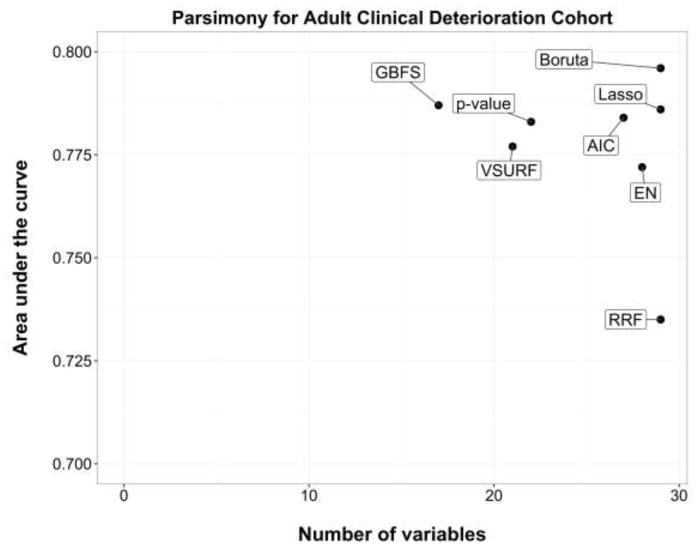
Figure 1.

Parsimony measures in the adult clinical deterioration cohort. Area under the curve is the discrimination performance on the validation set.

AIC, backward selection using Akaike Information Criterion; p-value, backward selection using p-value <0.05; EN, Elastic Net.

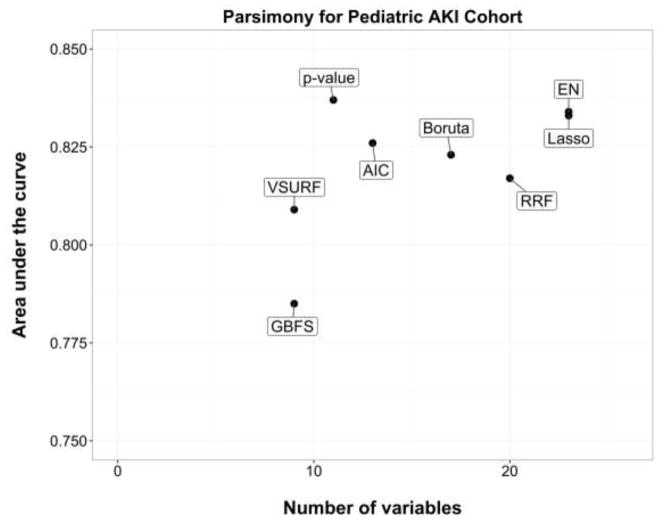
Figure 2.

Parsimony measures in the pediatric early acute kidney injury cohort.

The area under the curve is the discrimination performance on the validation set. AIC, backward selection using Akaike Information Criterion; p-value, backward selection using p-value <0.05; EN, Elastic Net.

In the adult clinical deterioration cohort, the most accurate model was Boruta (29 variables selected, AUC 0.796) and the sparsest was GBFS (17 variables selected, AUC 0.787). Overall, GBFS, backward selection using p-value, and VSURF achieved the best parsimony in that cohort (Figure 1). In the pediatric early acute kidney injury cohort, the most accurate model was backward selection using p-value (11 variables, AUC 0.837) and the sparsest were VSURF and GBFS (9 variables, AUCs 0.809 and 0.785). Overall, backward selections using p-value and AIC achieved the best parsimony in that cohort (Figure 2). RRF performed poorly in both cohorts (29 variables, AUC 0.735; and 20 variables, AUC 0.817).

3.2. Performance change from reference model

The reference models for the adult clinical deterioration cohort had a performance AUC in the validation set of 0.78 for the logistic regression, 0.80 for the random forest, and 0.79 for the gradient boosted machine. In the pediatric early acute kidney injury cohort, the reference models had an AUC of 0.82 for the logistic regression, 0.83 for the random forest, and 0.80 for the gradient boosted machine.

Figures 3 and 4 present the performance changes measure (method-based AUC minus reference model AUC) against the number of variables selected for the adult clinical deterioration cohort and the pediatric early acute kidney injury cohort, respectively.

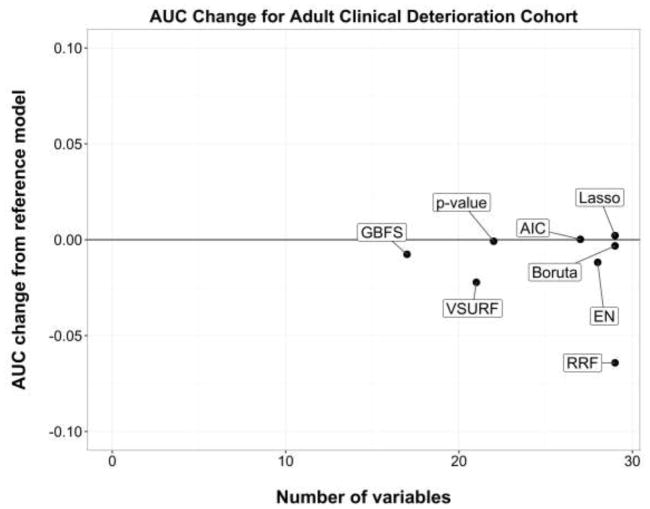
Figure 3.

Performance change from the reference model in the adult clinical deterioration cohort.

Area under the curve (AUC) is the discrimination performance on the validation set. Models above the black line represent an improvement over the reference model, whereas models below the black line represent a loss of performance. AIC, backward selection using Akaike Information Criterion; p-value, backward selection using p-value <0.05; EN, Elastic Net.

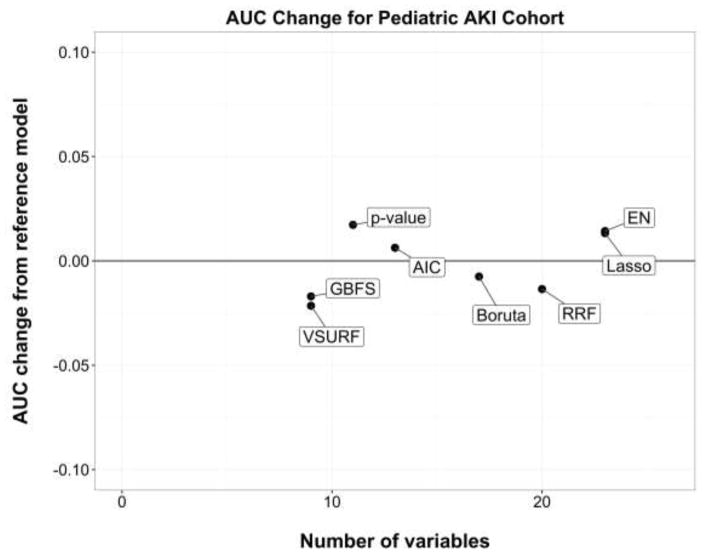
Figure 4.

Performance change from the reference model in the pediatric early acute kidney injury cohort.

Area under the curve (AUC) is the discrimination performance on the validation set. Models above the black line represent an improvement over the reference model, whereas models below the black line represent a loss of performance. AIC, backward selection using Akaike Information Criterion; p-value, backward selection using p-value <0.05; EN, Elastic Net.

In general, most regression-based methods had equal or better performance than their reference model after variable selection, whereas tree-based methods had some a loss of performance. Model sparsity had no obvious effect in this relationship, that is, methods that resulted in fewer variables still performed equally well or better than other methods in their family (e.g. backward selection using p-value vs. Lasso, or VSURF vs. RRF).

3.3. Variable importance and variable selection

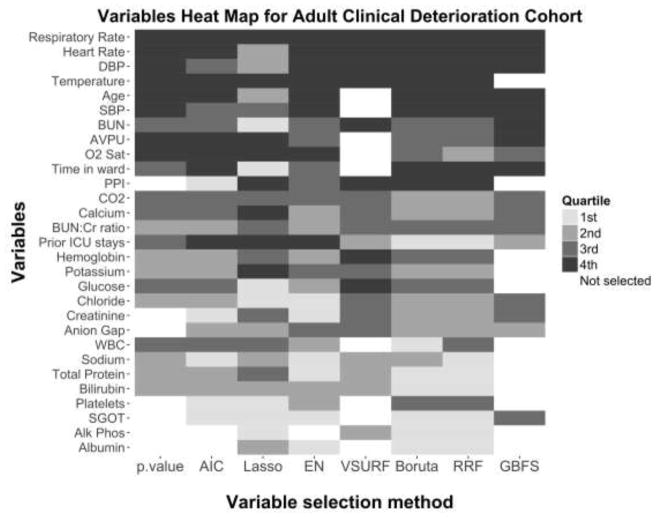
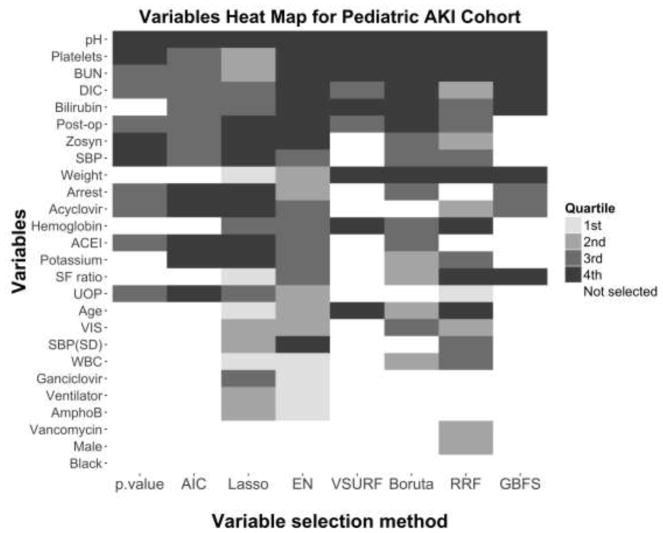
Figure 5 and 6 present the variables selected and importance ranking by quartiles from highest (4^th quartile) to lowest importance (1^st quartile) for the adult clinical deterioration cohort and the pediatric early acute kidney injury cohort, respectively. A description of the variables in each cohort can be found in the original papers [14, 15].

Figure 5.

Heat map of the variables selected and their importance quartile for each variable selection method in the adult clinical deterioration cohort.

The color of each cell represents the importance of each variable (in the vertical axis) as ranked by each variable selection method (in the horizontal axis). The importance ranking is categorized in quartiles, with darker cells denoting higher importance quartiles. White cells represent variables not selected by a particular variable selection method. Notably, only one variable, Respiratory Rate, was ranked by all methods in the top two quartiles of importance, and no variable was excluded by all methods. AIC, backward selection using Akaike Information Criterion; p-value, backward selection using p-value <0.05; EN, Elastic Net.

Figure 6.

Heat map of the variables selected and their importance quartile for each variable selection method in the pediatric early acute kidney injury cohort.

The color of each cell represents the importance of each variable (in the vertical axis) as ranked by each variable selection method (in the horizontal axis). The importance ranking is categorized in quartiles, with darker cells denoting higher importance quartiles. White cells represent variables not selected by a particular variable selection method. Notably, only one variable, pH, was ranked by all methods in the top two quartiles of importance, and only one variable, Black, was excluded by all methods. AIC, backward selection using Akaike Information Criterion; p-value, backward selection using p-value <0.05; EN, Elastic Net.

In general, the sparsest models in both cohorts were the backward selection using a p-value <0.05, VSURF and GBFS. Regression-based models were more likely to rank ordinal variables (e.g. “AVPU” or “Prior ICU stays” in the adult clinical deterioration cohort) or binary variables (e.g. “Post-op”, “Arrest”, “Acyclovir”, or “ACEI” in the pediatric early acute kidney injury cohort) as higher importance when compared to the tree-based models. The majority of the variables ranked as highly important in the tree-based methods were continuous variables. Only “respiratory rate” in the adult clinical deterioration cohort and “pH” in the pediatric early acute kidney injury cohort were ranked in the highest quartile of importance by all of the methods.

4. DISCUSSION

We present the performance of eight variable selection methods, both regression-based and tree-based, in two clinical datasets of different sizes. Tree-based variable selection methods, especially GBFS and VSURF, achieved better parsimony in the larger dataset and consistently ranked continuous variables as more important. The regression-based methods, especially the classic backward selection method using p-value <0.05 and the AIC-based method, achieved better parsimony in the smaller dataset. The tree-based methods tended to incur a loss of performance in comparison to the reference models when fewer variables were used, whereas most of regression-based methods either retained the same performance or improved compared to the reference model when fewer variables were selected. The sparsest methods in both datasets were GBFS, VSURF, and backward selection using p-value <0.05.

Prior studies have compared the performance of different variable selection methods in clinical and biomedical datasets [6, 28–33]. For example, Bagherzadeh-Khiabani and colleagues compared 19 variable selection methods, mostly regression-based, in a small cohort of pre-diabetic patients (about 12 events per variable in their best performing model) [6]. Consistent with our findings, one of the methods with best parsimony in their study was the backward selection methods using p-value <0.05, which achieved performance within 1% of the AUC of the best performing method with about a third of the variables selected. A random forest-based selection method was also amongst the sparsest methods, which is in agreement with our findings. Van der Ploeg and Steyerberg compared the performance of four variable selection methods in a small cohort of 222 clinical and environmental Legionella pneumophila strains with a large number of continuous variables as predictors (>400) [33]. In their study, the random forest-based method had the best performance followed by the Lasso. Since they did not report measure of sparsity, it is difficult to compare these results with our study, but the performance of the random forest-based method might be explained by the large number of continuous variables used, which would be in agreement with our findings. This bias of tree-based methods towards continuous variables has been previously described [34], and can be problematic in clinical datasets with a large number of categorized variables.

Our findings are consistent with the study by Van der Ploeg and colleagues who found that modern modeling methods tend to be “data hungry” [5]. In their analysis, using artificially-generated clinical databases, they found that the classic logistic regression method performed well in datasets with 20 to 50 events per variable, whereas random forest and other modern modeling methods required >200 events per variable to achieve stability. Our findings that the random forest methods performed better in the larger dataset whereas the regression-based methods performed better in the smaller AKI dataset confirm the findings by Van der Ploeg and colleagues. However, even though tree-based methods performed better than regression-based methods in the larger cohort with a higher events-per-variable ratio, it is important to note that, compared to the reference model, tree-based methods also tended to incur greater loss of performance than the regression-based methods as fewer variables were selected. This was consistent in both cohorts even though, in theory, fewer variables would improve the events-per-variable ratio. This goes against recent literature that claims that fewer variables are better [6]. While this is true in the context of regression-based methods, it doesn’t appear to be the case in tree-based methods. In fact, our results show that tree-based methods perform at their best when all variables are used in both cohorts. A possible explanation for this is that tree-based methods explicitly account for variable interactions, whereas regression-based methods do not.

While we found that the classic regression-based methods perform better in the smaller dataset, it is important to note that the events-per-variable ratios were at least 15:1 in the best models. Prior studies have demonstrated that backward selection using p-value and other classic regression-based methods tend to overestimate coefficients in cohorts with lower events-per-variable ratios, so they should be used with caution in those situations [35, 36].

Our findings highlight the importance of understanding that different modeling methods have different advantages and disadvantages. As the growth of the digital infrastructure takes hold in the healthcare environment, clinical researchers find themselves with a new set of opportunities and challenges, and top amongst these is making the best possible use of the large amounts of clinical data available to make new discoveries and improve patient care [1–3]. Using the appropriate modeling methods is a key component of this process. Consistent with Wolpert’s “No Free Lunch Theorem”, we found that algorithms that perform well on one class of problems will suffer in other cases [37]. However, at least having a general idea of the types of modeling methods more likely to succeed with specific types of problem can be useful to researchers. A generalization of our findings is that for clinical problems in smaller datasets with <20 events per variable, classic regression-based variables selection methods achieve better parsimony, whereas in prediction problems with larger datasets and >300 events per variable, tree-based variable selection methods, like GBFS or VSURF, work better. Further research will be needed to determine whether these findings are consistent in other clinical problems and types of datasets and what should be done in cases when the events-per-variable ratio falls in the mid-range.

Our results have to be interpreted understanding that in our method evaluation we valued parsimony, or the balance between performance and sparsity, as the most desirable characteristic of a variable selection method. This was based on the premise that very complex, non-parsimonious clinical prediction models are difficult to replicate in different healthcare settings. Furthermore, there is a real world cost associated with mapping and maintaining numerous variables for complex algorithms in an already strained healthcare information technology infrastructure [9]. As more clinical prediction models reach production status, it is likely that those in charge of implementing and maintaining these models will view their degree of parsimony as a key characteristic.

Our study has several limitations. First, we used the default settings of the algorithms that we tested and made no attempts to optimize the algorithms using different settings. This is consistent with prior studies [5], but we understand that some algorithms are highly customizable and this can provide a level of flexibility that might be advantageous but that we did not test in this study. In addition, we used only two clinical datasets to test the different methods. While this limits the generalizability of our findings, we did attempt to represent the two most common types of EHR-based datasets found in the literature: the very large multicenter dataset and the smaller single center dataset.

5. CONCLUSION

In conclusion, the performance of regression-based and tree-based variable selection methods is associated with the events-per-variable ratio of the clinical dataset used. Classic regression-based variable selection methods seem to achieve better parsimony in clinical prediction problems in smaller datasets with <20 events per variable, while modern tree-based methods have better parsimony in larger datasets with >300 events per variable. Further research is needed to determine whether these findings are consistent in other clinical problems and dataset sizes.

6. SUMMARY TABLE.

What was known:

1)Modern machine learning-based modeling techniques are increasingly applied to clinical problems, including variable selection methods for predictive modeling using Electronic Health Record data.

2)Prior studies have shown that modern modeling techniques are “data hungry.”

3)There is limited research comparing the performance of classic and modern modeling techniques for variable selection in clinical datasets.

What we add:

1)The performance of classic and modern variable selection methods appears to be associated with the size of the clinical dataset and the event-per-variable rate.

2)Classic regression-based variable selection methods perform better in smaller datasets, while modern tree-based methods do better in larger datasets.

Highlights.

• Modern, machine learning-based modeling techniques are increasingly applied to clinical problems, including variable selection methods for predictive modeling using Electronic Health Record data

• Prior studies have shown that modern modeling techniques are “data hungry”

• The performance of classic and modern variable selection methods appears to be associated with the size of the clinical dataset and the event-per-variable rate

• In our study, we showed that classic regression-based variable selection methods perform better in smaller datasets, while modern tree-based methods do better in larger datasets

9. APPENDIX A

9.1. Additional details of the clinical datasets

9.1.1. Adult clinical deterioration cohort

The clinical variables used and their distributions are shown in Table A.1. Variable missingness differed by data type and participating site, with vital signs having the least percent missing (all <1% except oxygen saturation [10%] and AVPU [19%]), followed by complete blood count (7–8%), electrolytes and renal function tests (11–16%), and liver function tests (48–50%). When a variable value was missing for a time interval, the previous value was carried forward. If no previous value was available, the median value for that variable was imputed under the assumption that these values were normal, as performed in similar studies. Preliminary screening for collinearity was performed using pairwise correlations between all variables. The correlation for all pairs variables used in the analyses was <0.75. A limited number of variable interactions were also explored preliminarily in a full logistic regression model. The interaction of age and time in the ward with the rest of the variables was examined, but had no effect in model performance [14].

Table A.1.

Distribution of clinical variables in the adult clinical deterioration cohort.

IQR, inter-quartile range.

Variable	Distribution
Continuous variables	Median (IQR)
Diastolic blood pressure (DBP), mmHg	68 (59, 76)
Heart rate, beats per minute	81 (71, 92)
Oxygen saturation (O2 Sat), %	97 (96, 98)
Respiratory rate, breaths per minute	18 (18, 20)
Systolic blood pressure (SBP), mmHg	124 (110, 140)
Temperature, degrees Celsius	36.6 (36.3, 36.9)
Albumin, g/dL	3 (3, 3.1)
Alkaline phosphatase (Alk Phos), units/L	80 (80, 80)
Bilirubin, mg/dL	0.7 (0.7, 0.7)
Blood urea nitrogen (BUN), mg/dL	16 (11, 24)
Calcium, mg/dL	8.5 (8.2, 8.9)
Chloride, mEq/L	104 (101, 106)
Carbon dioxide (CO2), mEq/L	26 (24, 28)
Creatinine, mg/dL	0.9 (0.7, 1.2)
Glucose, mg/dL	111 (98, 129)
Hemoglobin, g/dL	10.7 (9.5, 12)
Platelets, K/uL	215 (164, 274)
Potassium, mEq/L	4 (3.8, 4.3)
Aspartate aminotransferase (SGOT), units/L	26 (26, 26)
Sodium, mEq/L	138 (136, 139)
Total protein, g/dL	6 (6, 6)
White blood cell count (WBC), K/uL	8.4 (6.3, 10.9)
Pulse pressure index (PPI)	0.5 (0.4, 0.5)
BUN:Creatinine (BUN:Cr) ratio	15.7 (12, 21.4)
Anion gap, mEq/L	8 (6, 10)
Time in ward, hours	52 (20, 112)
Age, years	65 (50.2, 79.1)
Categorical variables	Proportion, %
Mental status per AVPU (AVPU), score
0 – Alert	97.5
1 – Responds to voice	1.6
2 – Responds to pain	0.7
3 – Unresponsive	0.2
Prior ICU stays
0	82
1	16
2	1.7
≥ 3	0.3

1.1.1. Pediatric early acute kidney injury cohort

The clinical variables used and their distribution are shown in Table A.2. Variable missingness differed by data type, with vital signs having the least percent missing (<1%), followed by electrolytes and renal function tests (1.1%), complete blood count (32.3%), bilirubin level (47.6%), and pH (90.4%). Gender and race were recorded in all cases. Other categorical variables (i.e. pre-admission cardiac arrest, postoperative recovery, and medications) that were not recorded in the EHR were assumed to be negative. Missing continuous variables were considered to be missing at random due to the short clinical time window (12 hours from ICU admission) and the likelihood that missing variables were associated with observed variables. In these cases, missing variables were imputed using multiple imputation by chain equations, as previously described [38]. Preliminary screening for collinearity was performed using pairwise correlations between all variables. The correlation for all pairs variables used in the analyses was <0.75. Interactions amongst variables were not explored in a logistic regression model given the constraints of the lower event-per-variable ratio.

Table A.2.

Distribution of clinical variables in the pediatric AKI cohort.

IQR, inter-quartile range.

Variable	Distribution
Continuous variables	Median (IQR)
Age, years	7.1 (1.6, 13.5)
pH	7.31 (7.25, 7.46)
Weight, kg	22 (10.5, 45)
Urine output (UOP), z-score	0 (0, 0)
Bilirubin, mg/dL	0.5 (0.4, 0.5)
Blood urea nitrogen (BUN), mg/dL	10 (8, 13)
Hemoglobin, g/dL	11.1 (10, 12.4)
Platelets, K/uL	226 (161, 299)
Potassium, mEq/L	4 (3.8, 4.2)
White blood cell count (WBC), K/uL	11.4 (8, 15.5)
Lowest systolic blood pressure (SBP), z-score	0 (0, 0)
Systolic blood pressure standard deviation (SBP[SD]), mmHg	10 (8, 12)
Lowest SaO2/FiO2 (SF) ratio	171 (158, 476)
Vasoactive-inotropic score (VIS)	0 (0, 0)
Disseminated intravascular coagulopathy (DIC) score	0 (0, 0)
Categorical variables	Proportion, %
On mechanical ventilation	44
Male	54
Black	7.5
Cardiac arrest pre-admission	2
Postoperative recovery	37
Received vancomycin	2.4
Received amphotericin B (ampho B)	1
Received ganciclovir	0.5
Received ACE inhibitors (ACEI)	1.8
Received acyclovir	2
Received ampicillin/tazobactam (Zosyn)	5.9