Elastic properties of 2D Ti₃C₂T_x MXene monolayers and bilayers

Nanoindentation experiments show that Ti₃C₂T_x MXenes have a higher elastic modulus than other solution-processed 2D materials.

Abstract

Two-dimensional (2D) transition metal carbides and nitrides, known as MXenes, are a large class of materials that are finding numerous applications ranging from energy storage and electromagnetic interference shielding to water purification and antibacterial coatings. Yet, despite the fact that more than 20 different MXenes have been synthesized, the mechanical properties of a MXene monolayer have not been experimentally studied. We measured the elastic properties of monolayers and bilayers of the most important MXene material to date, Ti₃C₂T_x (T_x stands for surface termination). We developed a method for preparing well-strained membranes of Ti₃C₂T_x monolayers and bilayers, and performed their nanoindentation with the tip of an atomic force microscope to record the force-displacement curves. The effective Young’s modulus of a single layer of Ti₃C₂T_x was found to be 0.33 ± 0.03 TPa, which is the highest among the mean values reported in nanoindentation experiments for other solution-processed 2D materials, including graphene oxide. This work opens a pathway for investigating the mechanical properties of monolayers and bilayers of other MXenes and extends the already broad range of MXenes’ applications to structural composites, protective coatings, nanoresonators, and membranes that require materials with exceptional mechanical properties.

INTRODUCTION

Because of its Young’s modulus of about 1 TPa (1), graphene is considered the strongest material known, which makes it relevant for applications in structural composites, protective coatings, fibers, etc. (2–4). The elastic moduli of mechanically exfoliated and chemical vapor deposition–grown transition metal dichalcogenides, such as MoS₂ and WS₂, have also been measured and found to be about a third that of graphene (5–7). Among other two-dimensional (2D) materials, only hexagonal boron nitride (h-BN) showed mechanical characteristics approaching graphene (8). However, it should be recognized that many of the record-breaking properties of graphene have been measured on small samples prepared by micromechanical exfoliation, a method relevant to fundamental studies but not to large-scale structural applications. Another limitation of pristine graphene is its poor solubility in conventional solvents, which complicates its processability and miscibility with other materials, such as polymers, for the preparation of composites.

Graphene oxide (GO) is often viewed as a low-cost and scalable alternative to pristine graphene for large-scale mechanical applications (2, 3) and can be prepared by oxidative exfoliation of graphite in acid solutions (9). GO sheets can reach hundreds of micrometers in lateral size (10), and because of their surface and edge functionalization with oxygen-containing moieties, they are highly soluble in water and other solvents and can be blended with various polymers. Despite some degradation of integrity of the graphene lattice during oxidation (11), the Young’s modulus values of GO and reduced GO (rGO) monolayers are still considerably high (>200 GPa), as determined in nanoindentation (12, 13) and wrinkling experiments (14), and are about one-fifth of the Young’s modulus of pristine graphene. GO sheets can also be processed into mechanically stable macroscopic structures, such as “graphene oxide paper” (15), or used as the reinforcement in various polymer matrix composites (3, 4).

In searches for other 2D crystals with promising elastic characteristics, it is natural to consider transition metal carbides (TMCs), which are known for their exceptional bulk mechanical properties (16). Since 2011, TMCs have been available in a 2D form, known as MXenes (17). More than 20 different MXenes have been synthesized by selective metal extraction and exfoliation of ternary TMCs and nitrides, known as MAX phases, in fluorine-containing etchants (18), and many other MXenes have been studied theoretically (18, 19). MXenes have a general formula of M_n+1X_nT_x, where M represents a transition metal (Ti, Zr, V, Nb, Ta, Cr, Mo, Sc, etc.), X is carbon or nitrogen, and n = 1, 2, or 3 (20). This chemical synthesis of MXenes adds surface functionalities such as fluorine, oxygen, and hydroxyl groups, denoted as T_x in the MXenes’ general formula. Examples of widely studied MXenes include Ti₃C₂T_x, Ti₂CT_x, Nb₂CT_x, V₂CT_x, Mo₂TiC₂T_x, and Nb₄C₃T_x, all of which have surface functional groups. Similar to GO, the synthesis of MXenes is scalable (21), and materials are processable in water and a variety of polar organic solvents (22).

Ti₃C₂T_x is the first discovered and the most widely studied MXene material to date. It shows higher electrical conductivity than solution-processed graphene (23), outstanding electrochemical properties (24), and great promise for various applications ranging from energy storage (18) to electromagnetic interference shielding (25). Large uniform monolayer Ti₃C₂T_x flakes of several square micrometers in lateral size can now be prepared in high yields (21, 23), but the mechanical properties of Ti₃C₂T_x monolayers, or any other MXenes for that matter, have not been measured yet. To date, only a few theoretical studies are available on mechanical properties of MXenes (26–30), predicting them to be stiffer than their MAX phase precursors (31) and bulk TMCs (16). MXene paper and composites have been tested (32), but their properties are determined by weak interfaces.

Here, we report mechanical measurements of the elastic modulus and breaking strength of monolayer and bilayer Ti₃C₂T_x MXene flakes by the atomic force microscopy (AFM) indentation. We also compare the MXene flakes to GO flakes, as both materials can be solution-processed because of their surface functionalization and are often discussed with regard to similar applications, such as conductive coatings, filtration membranes, composites, porous scaffolds, and energy storage (3, 18). As shown in Fig. 1A, a monolayer of Ti₃C₂T_x consists of three layers of close-packed Ti atoms stacked in the ABC ordering, with carbon atoms occupying the octahedral sites; the flakes are terminated with –F, –O, or –OH groups. Our results show that a single layer of Ti₃C₂T_x has an effective elastic modulus of 330 ± 30 GPa, which exceeds considerably the mean values previously found in the nanoindentation experiments on GO and rGO monolayers (12, 13) and other solution-processed 2D materials.

Fig. 1. Preparation of MXene membranes.

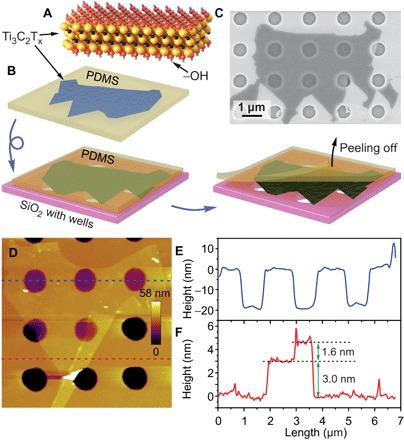
(A) Structure of a Ti₃C₂T_x monolayer. Yellow spheres, Ti; black spheres, C; red spheres, O; gray spheres, H. (B) Scheme of the polydimethylsiloxane (PDMS)–assisted transfer of MXene flake on a Si/SiO₂ substrate with prefabricated microwells. See text for details. (C) SEM image of a Ti₃C₂T_x flake covering an array of circular wells in a Si/SiO₂ substrate with diameters of 0.82 μm. (D) Noncontact AFM image of Ti₃C₂T_x membranes. (E and F) Height profiles along the dashed blue (E) and red (F) lines shown in (D).

RESULTS

The synthesis of Ti₃C₂T_x was performed by in situ hydrofluoric acid (HF) etching of aluminum from Ti₃AlC₂, as described by Alhabeb et al. (21) and Lipatov et al. (23). This method produces high-quality MXene flakes with lateral sizes up to 10 μm (23). The final product is a dark green solution of Ti₃C₂T_x flakes in water, which could be directly drop-casted on a Si/SiO₂ substrate with prefabricated microwells. However, this deposition method yields fractured and surface-contaminated flakes after drying (fig. S1). Flake fracture is caused by the hydrophilicity of Ti₃C₂T_x and the high surface tension of water, which drags MXene flakes into wells upon drying. Flakes that only partially cover microwells survive drying, but become crumpled and therefore unusable for indentation experiments.

We developed a deposition technique, which produces very clean, tautly stretched Ti₃C₂T_x membranes (Fig. 1B). First, MXene solution is drop-casted on a PDMS support and air-dried, leaving multiple MXene flakes on a surface. The surface of a PDMS support with MXene flakes is washed with running deionized (DI) water to remove possible salt contaminants from the original solution. After drying, the PDMS support is placed on a Si/SiO₂ substrate with prefabricated microwells with flakes facing down. No pressure was applied to the support to avoid damaging the flakes. Then, the PDMS film is gently peeled from the substrate, leaving some of the MXene flakes on the SiO₂ surface. The rationale behind this technique is that hydrophilic MXene flakes should have stronger attractive interaction with the hydrophilic silica surface than with the hydrophobic PDMS. This method should also be applicable to other solution-processed 2D materials, such as GO, and MXenes other than Ti₃C₂T_x. We also tested several other approaches for membrane fabrication, but all of them had certain drawbacks, while the direct PDMS transfer method consistently produced MXene membranes of excellent quality.

A representative scanning electron microscopy (SEM) image in Fig. 1C shows a transferred MXene flake that fully covers five microwells. According to noncontact AFM images (Fig. 1D), the MXene membranes are stretched across the openings and adhere to the well walls because of the attractive interaction between MXene flakes and SiO₂ (see the AFM height profile in Fig. 1E). The step height at the edge of the flake shown in Fig. 1D is about 3.0 nm (Fig. 1F), which includes trapped water molecules between the flake and the substrate. This flake folds at its edge, which adds a layer to itself, and measuring its height reveals a thickness of 1.6 nm for noncontact AFM mode (Fig. 1F), which matches the thickness that we observed in AFM measurements of Ti₃C₂T_x monolayers in our previous study (23). While the procedure that we used for the synthesis of Ti₃C₂T_x provides monolayer flakes at high yields, we also found several suspended bilayer structures, which consisted of two monolayer flakes overlapping over a well.

Since the thickness of Ti₃C₂T_x monolayers is an important parameter for analysis of the results of nanoindentation experiments, it is necessary to comment on the limitations of AFM for the determination of thicknesses of monolayers of 2D materials. For example, while the nominal thickness of graphene is 0.335 nm, in various experiments, the AFM measurements of monolayer graphene flakes produced thickness values in the range of 0.4 to 1.7 nm, as summarized by Shearer et al. (33). This inaccuracy could be affected by a number of factors that include the AFM imaging mode (tapping, contact, etc.), tip-surface interactions, presence of various surface adsorbates, and trapped interfacial molecules, among others. Therefore, nominal thicknesses, rather than AFM-measured thicknesses, were used in other works on mechanical indentation of 2D materials for calculations of mechanical characteristics (1, 5). Here, likewise, AFM produced a largely overestimated thickness value of 1.6 nm, and for the Young’s modulus calculation, we instead used the thickness of a Ti₃C₂T_x monolayer of 0.98 nm, which was determined by atomically resolved transmission electron microscopy (TEM) and supported by theoretical calculations (34, 35). It should be pointed out that high-resolution TEM is a preferred method for the determination of the thickness of a Ti₃C₂T_x monolayer compared to x-ray diffraction (XRD) analysis. When Ti₃C₂T_x is produced in a bulk form, XRD could be used to determine the interlayer spacing between the MXene sheets; this spacing can vary considerably, depending on the amount and chemical nature of species intercalated between the sheets (36). However, in the monolayer Ti₃C₂T_x membrane, there are no interlayer spacings with intercalated species, and similarly to AFM, the XRD measurements may overestimate the nominal thickness of a MXene monolayer.

The scheme of the nanoindentation experiment is shown in Fig. 2A. The surface of a substrate was scanned for MXene flakes suspended over wells using AFM in tapping mode. At least two AFM scans of the same well were performed to confirm that no drift of a sample occurred. Then, the AFM tip was positioned directly in the center of a selected well and slowly moved downward, providing controlled stretching of a MXene flake. Two to four cycles of loading and unloading were performed on the same MXene flake, with an incremental loading increase of 50 nN (see the corresponding curves in Fig. 2B). The bottom inset in Fig. 2B illustrates the behavior of the membrane in the beginning of the indentation experiment. The tip first snaps down to the membrane attracted by van der Waals forces and then begins to deflect the membrane as the tip presses downward. We extrapolate the linear force versus deflection (F-δ) dependence before snapping until it crosses the curve and consider this point as a center of origin where the force and displacement are both zero, which is necessary to obtain the correct F-δ relationship. The extension and retraction curves within each loading cycle, as well as the curves for different loads, retrace each other, indicating high elasticity of MXene flakes and that no flake detachment occurs during the measurements. The fracture of this bilayer Ti₃C₂T_x membrane occurred at a load force of about 200 nN and a deflection of 38 nm. Even at the maximum deflection, the center of the membrane is far from the bottom of the well that is ≈300 nm deep. The AFM tip punctures the membrane, leaving a small hole as seen in the top inset in Fig. 2B. Unlike in graphene membranes (1), in which the breaks extend over the entire well (fig. S3, B and C), the punctures in suspended Ti₃C₂T_x flakes were very local, in agreement with noncatastrophic fracture of MXene sheets predicted by molecular dynamics simulations (37).

Fig. 2. Elastic response and indentation test results.

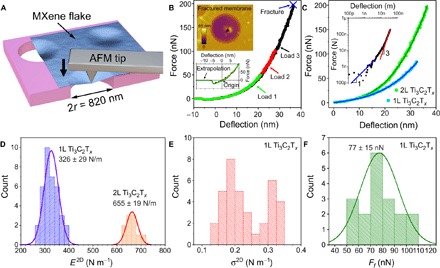
(A) Scheme of nanoindentation of a suspended Ti₃C₂T_x membrane with an AFM tip. (B) Force-deflection curves of a bilayer Ti₃C₂T_x flake at different loads. The bottom inset is a detailed view of the same curves showing the center of origin. The top inset shows AFM image of the fractured membrane. (C) Comparison of loading curves for monolayer (1L) and bilayer (2L) Ti₃C₂T_x membranes and the least squares fit to the experimental indentation curves by Eq. 1. Hole diameter is 820 nm. The inset shows the same experimental curve for bilayer Ti₃C₂T_x in logarithmic coordinates. The curve shows a linear behavior in the first 10 nm of indentation (blue line) and approaches the cubic behavior at high loads (red line). (D) Histogram of elastic stiffness for monolayer and bilayer membranes. Solid lines represent Gaussian fits to the data. (E) Histogram of pretensions of monolayer membranes. (F) Histogram and Gaussian distribution of breaking forces for monolayer membranes. Tip radius is 7 nm.

We consider the system under investigation as isotropic because of circular wells, the spherical tip, and close-packed structure of Ti₃C₂T_x. Therefore, we can parametrize the membrane using Young’s modulus E_Young, Poisson’s ratio v [0.227 for Ti₃C₂T_x (38)], and thickness h and fit the experimental F-δ data using the formula

$$\mathit{F}={\mathrm{\sigma }}_0^{2\mathrm{D}}\mathrm{\pi }\mathrm{\delta }+{\mathit{E}}^{2\mathrm{D}}\frac{{\mathit{q}}^3{\mathrm{\delta }}^3}{{\mathit{r}}^2}$$ (1)

where ${\mathrm{\sigma }}_0^{2\mathrm{D}}$ represents prestress in the membrane, E^2D is the 2D elastic modulus, and r is the radius of the well (1, 5). The dimensionless constant q is related to v as q = 1/(1.049 − 0.15v − 0.16v²) = 0.9933. The first term in Eq. 1 corresponds to the prestretched membrane regime and is valid for small loads. The second term for the nonlinear membrane behavior is characterized by a cubic F ~ δ³ relationship with a coefficient of E^2D, which dominates at large loads. The applicability of this formula is demonstrated in the inset in Fig. 2C, where the F-δ dependence for a bilayer Ti₃C₂T_x flake is shown in logarithmic scale. At small loads (less than 10 nN), the dependence is linear and shown by the blue solid line, while above 10 nN, the coefficient is 3 (red solid line), meaning that the dependence is cubic. The latter fits a considerable amount of the experimental data, confirming that most of the mechanical response is expected to be in the region characterized by a cubic F ~ δ³ relationship. It is possible to use this relationship to determine the corresponding coefficient E^2D with high precision. Other nonlinear effects in F-δ dependence can be ignored if the AFM tip radius is much smaller than the radius of a well, that is, r_tip ≪ r (1, 5). In our case, the diameter of the well measured by SEM is a = 2r = 820 nm, and according to the manufacturer’s specifications, the AFM tip radius is 7 nm, which results in r_tip/r = 0.017 ≪ 1. Figure 2C shows the experimental and fitting curves for single- and double-layer MXene flakes. Good fitting (R² > 0.995 for all measurements) is an indicator that the model is appropriate.

In our experiments, we measured 18 membranes from 16 different monolayer Ti₃C₂T_x MXene flakes. For each membrane, two curves at different loads were collected before the rupture, totaling 36 experimental points. For monolayer MXene membranes, the E^2D elasticity ranged from 278 to 393 N/m, with an average of 326 ± 29 N/m (Fig. 2D). A narrow distribution of the experimental E^2D values was achieved even though the measurements were performed on 16 different flakes. For each MXene flake that covered two wells, the nanoindentation experiments were even more reproducible. For one pair of wells covered by the same flake, we found E^2D elasticities of 344 and 341 N/m, and for another such pair of wells, we measured E^2D values of 318 and 323 N/m (fig. S2). These results show great reproducibility of data measured within the same flake. The corresponding distribution of membrane pretensions is shown in Fig. 2E. The values of ${\mathrm{\sigma }}_0^{2\mathrm{D}}$ lay in the range from 0.14 to 0.34 N/m for monolayer MXene flakes, showing strong interaction between the membrane and the well walls. These values are comparable with those obtained for graphene and MoS₂ membranes (1, 5).

The procedure used for the synthesis of Ti₃C₂T_x provides monolayer flakes (23). Two monolayer flakes may overlap or one flake may fold on top of a well, in both cases resulting in bilayer membranes. The F-δ curve for one of the bilayer Ti₃C₂T_x membranes is presented in Fig. 2C, in comparison with the curve for a monolayer MXene flake. We measured four different bilayer membranes, collecting a total of 10 experimental points, which are presented in the histogram plot in Fig. 2D. The E^2D values determined for bilayer Ti₃C₂T_x flakes ranged from 632 to 683 N/m, with an average of 655 ± 19 N/m. This number is exactly twice that determined for monolayer MXene membranes, suggesting a strong interaction between layers that is likely associated with the hydrogen bonding between the Ti₃C₂T_x surface groups. Similar effects were observed for overlapping GO membranes (12) and multilayer h-BN flakes (8), where a strong interaction between layers was caused by either hydrogen bonding or interlayer B-N interaction, respectively. In contrast, multilayer graphene exhibits lower E^2D than expected from multiplying monolayer E^2D by the number of layers due to weaker interlayer interaction and therefore a greater tendency of layers to slide relative to each other upon indentation (1, 8).

Suspended MXene membranes can be deformed elastically up to a certain stress when mechanical failure occurs. Figure 2F presents the distribution of fracture forces for monolayer MXene membranes ranging from 50 to 102 nN and averaging at F_f = 77 ± 15 nN. As shown in the inset in Fig. 2B, the fracture occurred in the center of a membrane where the stress was applied by the AFM tip. We can extract the maximum stress at the central part of the sheet using the expression for the indentation of a linearly elastic circular membrane under a spherical indenter (39)

$${\mathrm{\sigma }}_{\text{max}}^{2\mathrm{D}}=\sqrt{\frac{{\mathit{F}}_{\mathit{f}}{\mathit{E}}^{2\mathrm{D}}}{4\mathrm{\pi }{\mathit{r}}_{\text{tip}}}}$$ (2)

In our work, we used a diamond AFM tip with a radius of 7 nm, rendering ${\mathrm{\sigma }}_{\text{max}}^{2\mathrm{D}}$ to be between 14 and 20 N/m. On average, these values correspond to 5.2% of the Young’s modulus E^2D for monolayer MXene membranes, which is lower than the theoretical upper limit of a material’s breaking strength (37) due to the presence of defects in the material (40).

Considering that graphene is a benchmark 2D material, we decided to directly compare F-δ curves for suspended Ti₃C₂T_x and graphene monolayers (Fig. 3A). The elasticity of graphene in our experiment was found to be 341 ± 28 N/m, obtained from three monolayer membranes (see details in fig. S3), which is very close to the previously reported values of 340 ± 50 N/m (1) and thus reconfirms the validity of our experimental approach.

Fig. 3. Comparison of indentation tests on Ti₃C₂T_x with other 2D materials.

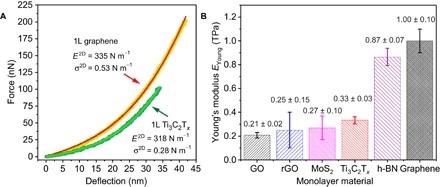
(A) Comparison of experimental F-δ curves for monolayer graphene and Ti₃C₂T_x membranes. (B) Comparison of effective Young’s moduli for several 2D materials: GO (12), rGO (13), MoS₂ (5), h-BN (8), and graphene (1). In this chart, we compare values produced on membranes of monolayer 2D materials in similar nanoindentation experiments.

DISCUSSION

The effective Young’s modulus E_Young and breaking strength σ_max can be calculated from E^2D and ${\mathrm{\sigma }}_{\text{max}}^{2\mathrm{D}}$, respectively, by dividing them by the membrane’s thickness. As we explained previously, for the Young’s modulus calculation, we used the nominal thickness of a Ti₃C₂T_x monolayer of 0.98 nm, which was obtained from high-resolution TEM analysis and theoretical calculations (34, 35); the same approach was used in other works on indentation of 2D materials (1, 5). The effective Young’s modulus for MXene membranes is 333 ± 30 GPa, and the breaking strength is 17.3 ± 1.6 GPa (taking the average tip radius of 7 nm). It is interesting to note that according to the molecular dynamics simulations, Ti₃C₂ has a Young’s modulus of 502 GPa (27). As expected, the experimentally determined value for Ti₃C₂T_x of 333 ± 30 GPa is lower because of surface functionalization and the presence of defects. However, the difference in the Young’s moduli of the “ideal” Ti₃C₂ and the experimentally realized Ti₃C₂T_x is not as dramatic as in the case of graphene and GO (1050 GPa versus 210 GPa). This could be rationalized by the fact that surface functionalization has a stronger effect on the mechanical properties of one-atom-thick monolayer graphene compared to thicker Ti₃C₂T_x flakes. In the future studies, it would be interesting to compare mechanical properties of Ti₃C₂T_x with different functional groups and, ultimately, without functionalization. It should be pointed out that in Ti₃C₂T_x monolayers used in this study, a considerable fraction of the nominal thickness of 0.98 nm is occupied by the surface functionalities (34), such as –F and –OH, and thinner flakes of pristine Ti₃C₂ are expected to have a Young’s modulus approaching the theoretically predicted value of 502 GPa (27).

Comparison of E_Young values with other benchmark 2D materials is presented in Fig. 3B. At 330 ± 30 GPa, the effective Young’s modulus of Ti₃C₂T_x MXene exceeds the previously reported mean values for GO, rGO, and MoS₂ that were produced in similar nanoindentation experiments (5, 12, 13) but is lower than those of h-BN and graphene (1, 8). While the values for graphene, h-BN, and MoS₂ were reported for defect-free flakes, the Ti₃C₂T_x MXene flakes tested here are solution-processed. There is potential to develop methods to synthesize Ti₃C₂T_x flakes of higher quality to reach a larger Young’s modulus closer to the theoretical value. In addition, Ti₃C₂T_x is just one of more than 20 synthesized MXenes, and MXenes with a different number of atomic layers or a different transition metal may have higher elasticity. This study suggests great potential of MXenes for structural composites, protective coatings, nanoresonators, membranes, textiles, and other applications that require bulk quantities of solution-processable materials with exceptional mechanical properties.

MATERIALS AND METHODS

Synthesis of Ti₃C₂T_x

MAX phase precursor, Ti₃AlC₂, was produced as described elsewhere (17, 21). Ti₃C₂T_x MXene was synthesized via selective etching of Al from Ti₃AlC₂ using in situ HF etchant solution as described elsewhere (21). The etchant solution was prepared by adding 0.8 g of LiF to 10 ml of 9 M HCl and allowing the solution to mix thoroughly at room temperature for a few minutes. After that, 0.5 g of Ti₃AlC₂ was slowly added over the course of 5 min to avoid initial overheating due to the exothermic nature of the reaction. Then, the reaction was allowed to proceed at ambient conditions (~23°C) under continuous stirring (550 rpm) for 24 hours. The resulting MXene was repeatedly washed with DI water until an almost neutral pH (≥6) was achieved. The product was then collected using vacuum-assisted filtration through a polyvinylidene difluoride membrane (0.45-μm pore size; Millipore) and dried in a vacuum desiccator at room temperature for 24 hours. To delaminate 0.2 g of Ti₃C₂T_x, a freshly produced powder was redispersed in 50 ml of DI water and stirred continuously for 1 hour. Then, the Ti₃C₂T_x solution was centrifuged at 3500 rpm, and the supernatant, a dark green colloidal solution of MXene, was collected. Previous studies have shown that this solution contains primarily monolayer flakes (23, 40).

Materials characterization

Scanning electron microscopy

SEM analysis was performed using a Zeiss Supra 40 Field-Emission SEM at an accelerating voltage of 5 kV.

Atomic force microscopy

Surface topography imaging and force-indentation curve measurements were performed on an Asylum Research MFP-3D system. Single-crystal diamond tips (D80, SCD Probes) with tip radii of 5 to 10 nm and a spring constant of ~3.5 N/m, according to the manufacturer’s specifications, were used for force-indentation experiments. The spring constant of each AFM cantilever was calibrated via thermal noise method (41) before indentation experiments. During the force-indentation experiments, the z-piezo displacement speed was controlled at a rate of 100 nm/s. Different rates ranging from 50 to 1000 nm/s were also tested and showed no clear difference for the force-indentation curves.

Analysis of force-indentation curves

During the indentation experiments, the cantilever bending and z-piezo displacement were recorded as the tip moved downward. The cantilever bending was calibrated by measuring a force-displacement curve on a hard Si/SiO₂ surface in advance. The loading force was obtained by multiplying the cantilever bending by the cantilever spring constant, and the deflection of the membrane was obtained by subtracting the cantilever bending from the z-piezo displacement.

In the real force-deflection data, there is a negative force section due to the tip jump-to-surface effect, where the tip snaps down to the membrane attracted by van der Waals forces when it is very close to the surface. We extrapolated the zero force line in the force-deflection dependence before snapping until it crossed the curve and considered this point as a center of origin where the force and displacement are both zero, which is necessary to obtain the correct force-deflection relationship.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/6/eaat0491/DC1

fig. S1. Ti₃C₂T_x MXene membranes prepared by drop-casting from an aqueous solution.

fig. S2. Mechanical properties of Ti₃C₂T_x MXene monolayer on a single flake.

fig. S3. Mechanical properties of graphene monolayers.