Abstract
Proteins fulfill versatile biological functions by interacting with each other and forming high-order complexes. Although the order in which protein subunits assemble is important for the biological function of their final complex, this kinetic information has received comparatively little attention in recent years. Here we describe a multiscale framework that can be used to simulate the kinetics of protein complex assembly. There are two levels of models in the framework. The structural details of a protein complex are reflected by the residue-based model, while a lower-resolution model uses a rigid-body (RB) representation to simulate the process of complex assembly. These two levels of models are integrated together, so that we are able to provide the kinetic information about complex assembly with both structural details and computational efficiency.
Keywords: protein complex assembly, multiscale modeling, coarse-grained simulation, protein association rate, kinetic Monte-Carlo, diffusion-reaction algorithm
1. Introduction
Proteins form high-order complexes to carry out their diverse functions in cells [1,2]. In order to maintain the proper functions, natural evolution has developed specific assembling pathways for these complexes [3,4]. Any mistake along the pathways of complex assembly can lead to severe biological consequences [5]. Moreover, in a crowded cellular environment, the assembly of protein complexes is often under kinetic, rather than thermodynamic, control [6,7]. Therefore, to study the kinetics of protein complex assembly is of paramount importance. Unfortunately, relative to the intensive studies made for the structural determination of protein complexes, the dynamic aspects of their assembling pathways have just started to be understood. Additional to the recently developed experimental techniques such as super-resolution microscopy [8], electron microscopy [9] and native mass spectrometry [10], a large variety of computational models have also been developed to simulate the association of protein complexes. However, among these models, high-resolution methods based on molecular dynamic simulations can hardly approach the fully time scale of assembly processes for large protein complexes [11–27]. In contrast, low-resolution models fail to provide a quantitative description of the structure and energetics of protein complexes [28–35].
In this chapter, we outline a computational framework to simulate the kinetics of protein complex assembly. The framework consists of models on two different scales [36]. The higher-resolution simulation uses residue-based coarse-grained (CG) models of protein structure to evaluate the binding rates between each pair of subunits in a complex, whereas the lower-resolution model uses a rigid-body (RB) representation to simulate the process of complex assembly. By feeding the binding rates calculated from the residue-based simulations into the lower-resolution simulations, two levels of models are integrated together so that assembly of specific protein complexes can be studied with both structural detail and computational efficiency.
2. Materials
2.1 Information needed as input parameters
The following information is needed as input parameters for simulations.
The structure (atomic coordinates) of the entire protein complex in PDB format.
The translational and rotational diffusion constants of each subunit in the complex. These constants can be obtained by curve fitting to the data that were calculated by a precise boundary element method [37,38].
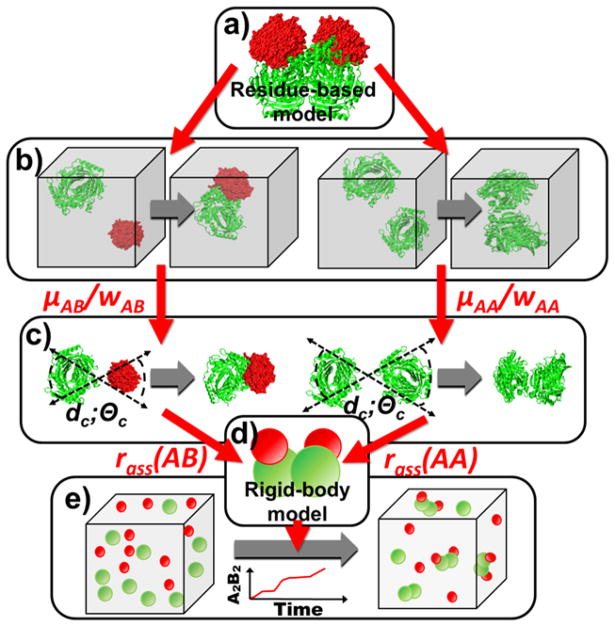
The dissociation constants (Kd) which quantify the binding stability for all pairs of individual subunits in the complex. For instance, a hetero-trimer that contains two types of subunits (A and B) includes two types of binding interfaces (Fig. 1a). One is between subunit A and B, while the other is between two subunits A. The dissociation constants through both AB and AA binding are needed.
The on rates (kon) of binding which quantify the kinetics of association for all pairs of individual protein subunits in the complex.
Figure 1.
There are two levels of models in the schematic framework of our multiscale simulation method. The structural details of each protein subunits in a complex can be reflected by the residue-based model (a). We first adjust the parameters in the energy functions of residue-based simulation to reproduce the experimentally measured values of kon for each pair of subunits (b). Given the same energy parameter, the rate of association rass for each pair of subunits is then estimated by the same residue-based model, but with a different boundary condition (c). Finally, the derived values of rass, together with the diffusion constants and binding affinities of interacting subunits, are used to guide the simulation with a rigid-body-based representation (d). The rigid body simulations which contains a large number of protein subunits in the system are able to provide the kinetic information about complex assembly, such as how many final complexes or kinetic intermediate are formed along simulation time (e).
2.2 Residue-based model for simulation protein association
2.2.1. Model representation
The atomic structure of proteins was reduced to a simplified model in which each residue is represented by two sites [39]. One is the position of its Cα atom, while the other is the representative center of a side-chain selected based on the specific properties of a given amino acid.
2.2.2. Simulation algorithm
The kinetic Monte-Carlo (KMC) simulation starts from an initial conformation in which a pair of proteins was randomly placed. The translational and rotational diffusions are then carried out within each simulation step for both proteins in the system. Specific boundary conditions are applied after the diffusions. The new binding conformation is evaluated by either GO-like potential [40], or a coarse-grained physical-based energy functions [39]. The probability of acceptance for this new conformation after diffusion depends on the calculated binding energy. At the end of each simulation step, the distances between all intermolecular interfacial pairs were calculated to determine how many native contacts were recovered. When at least three native contacts were recovered, we assumed that the two proteins formed an encounter complex and the current simulation trajectory was terminated. Otherwise, the simulation ended when it reached the predefined maximal duration (see Note 5).
2.2.3. Boundary condition
Two different boundary conditions are used in our study. The first is the periodic boundary condition. In the periodic boundary condition, two proteins are initially placed in a three-dimensional periodic box at random positions (Fig. 1b). During simulation, if one protein exists from one side of the box, it will immediately enter the opposite side. In the second boundary condition, a different initial conformation is constructed. Specifically, the binding interfaces of two proteins are placed randomly, but within the given distance cutoff dc, and the range of their packing angles is within the cutoff Θc (Fig. 1c). Consequently, in the following simulation, two molecules either formed an encounter complex or separated far away from each other by the end of each simulation trajectory.
2.2.4. Energy functions between proteins
The binding between proteins were originally evaluated by a GO-like potential [40] which gives scores for all pairs of native contact. Any pair of Cα atoms between residues i in one protein and j in the other is defined as a native contact if its corresponding distance in the native structure is smaller than 7.5 Ǻ. An adjustable parameter μ defines the energy depth of the GO potential. It can be used to control the rate of binding.
In our more recent study, the total energy of binding between two proteins is described by a simple physics-based potential function consisting of three terms [39]. The first component is the electrostatic interaction which was previously used in the Kim-Hummer model [41,42]. The second component is the hydrophobic interaction, which is calculated by summing the hydrophobic scores of all contact residue pairs. The hydrophobic scores of a contact residue pair are taken from a previous study by Kyte and Doolittle [43]. The excluded volume effect during protein binding is taken into account as the third component. Finally, a weight parameter w which determines the relative contributions between the hydrophobic and electrostatic interactions can be used to control the rate of binding.
2.3 Rigid-body model for simulation protein complex assembly
2.3.1. Model representation
In the rigid-body-based model, proteins are simplified as spherical rigid bodies with various radii (see Note 4). Multiple binding sites are assigned on the surface of each rigid body [44]. The spatial assignment of each binding site depends on the quaternary arrangement of the protein complex under study (Fig. 1d).
2.3.2. Simulation algorithm
A diffusion-reaction algorithm is developed to simulation the assembly kinetics [44]. As the initial configuration, a large number of proteins with all species of subunits in the complex are randomly distributed in a 3D simulation box (Fig. 1e). The number of subunits and the size of simulation box are determined by the concentrations and the stoichiometry of the complex. Followed by the initial conformation, the system is evolved by an iteration of diffusion-reaction process. Molecules are first chosen to undergo random diffusions with the periodic boundary condition. The amplitude of diffusions for all molecules is determined by their corresponding diffusion coefficients. If a complex is formed during the process of assembly, its all subunits will move together, with a relatively smaller diffusion coefficient. After diffusions, any pair of subunits that fulfill the binding criteria has the probability to associate together, by the corresponding on rate. In contrast, any associated pair of subunits has the probability to break into separate monomers, by the corresponding on rate and binding affinity.
3. Methods
3.1 Calibrate the energy function in residue-based simulations
For each different pair of interacting protein subunits in a complex, following steps of operation will be carried out sequentially (Fig. 1b).
-
3.1.1
104 residue-based simulation trajectories are generated with periodic boundary condition, using either GO-like or physics-based potential functions. The default value of μ in the GO-like potential or w in the physics-based energy function is used as initial condition.
-
3.1.2
The on rate kon is derived by counting how many complexes are associated from these simulation trajectories.
-
3.1.3
The calculated kon from the simulation is compared with the experimentally measured value. The value of μ or w is adjusted accordingly, if the calculated kon is either weaker or stronger than the corresponding experimental value.
-
3.1.4
The 1st step is repeated using the adjusted value of μ or w, so that the new kon is calculated.
-
3.1.5
The procedure from the 1st to the 4th step is iterated until the calculated kon fits reasonably well with the experimental value. Consequently, the calibrated parameter μ or w is used to derive the association rate rass in 3.2.
If no experimental kon is available for a specific pair of protein subunits, 3.1 will be skipped. The association rate rass for this pair of subunits is directly calculated in 3.2 by using the physics-based energy function with the default value of weight constant w (see Note 3).
3.2 Derive the association rate rass for all pairs of subunits in the complex
The rass in the rigid-body-based model is the rate of association between two interacting proteins under given binding criteria. It is a specific parameter resulting from the coarse-grained nature of rigid-body-based model and depends on the choice of different binding criteria, such as the distance and orientation between two proteins. For each different pair of interacting protein subunits in a complex, we can derive rass using the specific calibrated energy functions described above. In detail, following steps of operation will be carried out sequentially for each pair of subunits in a complex (Fig. 1c).
-
3.2.1
104 residue simulation trajectories are generated with the second type of boundary condition, in which the initial conformation is constructed by placing two proteins within the given distance cutoff dc, and the range of their packing angles within the cutoff Θc (see Note 1). Either GO-like or physics-based potential functions can be used with the calibrated parameter μ or w from 3.1. The maximal length of each trajectory equals ΔtRB, which is the simulation time step of the rigid-body-based model (see Note 2).
-
3.2.2
The dimerization probability between protein subunits ρ is calculated by counting how many complexes are associated from these simulation trajectories.
-
3.2.3
The association rate rass can be calculated as rass=ρ/ΔtRB. The values of rass for all pairs of interacting protein subunits in a given complex are derived for the simulation of complex assembly which will be introduced in 3.3.
3.3 Simulate the complex assembly by rigid-body-based model
Based on calculated rass for all pairs of subunits in the complex, following steps of rigid-body simulation will be carried out to study the kinetics of complex assembly (Fig. 1e).
-
3.3.1
The diffusion constants for all protein subunits in the complex are calculated by a precise boundary element method.
-
3.3.2
The off rate koff which characterizes the kinetics of dimer dissociation is calculated for all pairs of protein subunits in the complex using the equation koff= kon×Kd, in which kon is the on rate and Kd is the dissociation constant for a corresponding pair of protein subunits.
-
3.3.3
The radii of rigid bodies for all subunits are determined by the given three-dimensional structure of the complex.
-
3.3.4
The number of binding sites for each subunit and their relative positions are assigned on the surface of its corresponding rigid body based on the quaternary organization of the protein complex.
-
3.3.5
After determine the size of simulation box, the initial conformation of the rigid-body simulation is constructed by randomly placing rigid bodies for all types of subunits in the box. The number of rigid bodies for each type of subunit is determined by the concentrations and the stoichiometry of the complex.
-
3.3.6
The simulations are carried out by giving the desired number of trajectories and the length of simulation time for each trajectory.
-
3.3.7
Collect information from the simulation trajectories and analyze the simulation result, such as the number of protein complexes and different intermediate states formed along simulation time.
Using above framework of multi-scale simulation procedure, we can study how mutations affect the kinetics of protein complex assembly (see Note 6) and evaluate how protein complex assembly can be regulated by solvation effect (see Note 7).
Acknowledgments
This work was supported in part by the National Institutes of Health (Grant No. R01GM120238) and a start-up grant from the Albert Einstein College of Medicine.
Footnotes
In the second boundary condition of the residue-based simulation, the binding interfaces of two proteins are initially placed within the given values of the distance cutoff dc, and the range of packing angles Θc. The same values of distance cutoff and range of packing angles should be used in the rigid-body simulations as criteria for binding in order to pass the calculated value of rass from the higher-resolution model to the lower-resolution model.
To derive the association rate rass for all pairs of subunits in the complex (3.2), the maximal length of each simulation trajectory should be equal the time step of the rigid-body-based simulation. By the definition of rass and ΔtRB, if two molecules that meet the binding criteria, association will occur at the probability of rass×ΔtRB within each time step of rigid-body simulation. To estimate the value of ras, residue-based simulations should be carried out with the same time scale. Consequently, each trajectory of residue-based simulation consists of n steps so that the total length of simulation time for each trajectory satisfies ΔtRB =n×Δt, in which Δt is the time step of residue-based simulation.
As we mentioned in 3.1, if no experimental kon is available for a specific pair of protein subunits, the association rate for this pair of subunits is directly calculated by using the physics-based energy function with the default value of weight constant w. On the other hand, if no experimental dissociation constants is available for a specific pair of protein subunits, computational methods can be used to predict either the absolute values of wild-type binding affinity, such as PPEPred [45]. Other computational methods such as BindProfX [46] can predict the relative changes of binding affinity due to mutations at the binding interfaces.
In current stage of the study, each protein subunit in the lower-resolution simulation is simplified by a spherical rigid body. Therefore, our method will not be able to be applied to protein complexes containing subunits of non-globular shapes. In the future, our method can be improved by using non-spherical rigid bodies. Furthermore, by applying a domain-based representation in which each globular domain is represented by a rigid body, our method can be extended to protein complexes that contain multi-domain protein subunits.
The conformational changes are not considered during our study of complex assembly. Previous studies have illustrated that conformational changes are important in protein complex assembly. Although the effect of conformational flexibility cannot be reflected by the rigid-body model, it can be estimated by our residue-based simulation. For instance, the elastic network model (ENM) [47] has been integrated into the current model of our residue-based simulation so that protein conformations can be changed during association.
Our previous study demonstrated that our residue-based simulation method can capture the effects of single- and double-point mutations on the association rates [39]. Therefore, the framework of our multi-scale model can be used to study how mutations affect the kinetics of protein complex assembly by applying the same procedure to both wild-type protein complex and to its mutant systems.
The concentration of ions around two interacting proteins is an important factor controlling the rate of their association. The ionic strength is an adjustable parameter in our residue-based simulation. Our tests showed that the residue-based model can reproduce the effect of the ionic strength on associations [39]. Therefore, by changing the value of ionic strength, our multi-scale method will also be able to evaluate how protein complex assembly can be regulated by solvation effect.
References
- 1.Ali MH, Imperiali B. Protein oligomerization: how and why. Bioorg Med Chem. 2005;13(17):5013–5020. doi: 10.1016/j.bmc.2005.05.037. [DOI] [PubMed] [Google Scholar]
- 2.Levy ED, Teichmann S. Structural, evolutionary, and assembly principles of protein oligomerization. Prog Mol Biol Transl Sci. 2013;117:25–51. doi: 10.1016/b978-0-12-386931-9.00002-7. [DOI] [PubMed] [Google Scholar]
- 3.Marsh JA, Hernandez H, Hall Z, Ahnert SE, Perica T, Robinson CV, Teichmann SA. Protein complexes are under evolutionary selection to assemble via ordered pathways. Cell. 2013;153(2):461–470. doi: 10.1016/j.cell.2013.02.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Levy ED, Boeri Erba E, Robinson CV, Teichmann SA. Assembly reflects evolution of protein complexes. Nature. 2008;453(7199):1262–1265. doi: 10.1038/nature06942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ellis RJ. Protein misassembly: macromolecular crowding and molecular chaperones. Adv Exp Med Biol. 2007;594:1–13. doi: 10.1007/978-0-387-39975-1_1. [DOI] [PubMed] [Google Scholar]
- 6.Gabdoulline RR, Wade RC. Biomolecular diffusional association. Curr Opin Struct Biol. 2002;12(2):204–213. doi: 10.1016/s0959-440x(02)00311-1. [DOI] [PubMed] [Google Scholar]
- 7.Zhou HX. Rate theories for biologists. Quarterly reviews of biophysics. 2010;43(2):219–293. doi: 10.1017/S0033583510000120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Picco A, Irastorza-Azcarate I, Specht T, Boke D, Pazos I, Rivier-Cordey AS, Devos DP, Kaksonen M, Gallego O. The In Vivo Architecture of the Exocyst Provides Structural Basis for Exocytosis. Cell. 2017;168(3):400–412. e418. doi: 10.1016/j.cell.2017.01.004. [DOI] [PubMed] [Google Scholar]
- 9.Gilmore BL, Winton CE, Demmert AC, Tanner JR, Bowman S, Karageorge V, Patel K, Sheng Z, Kelly DF. A Molecular Toolkit to Visualize Native Protein Assemblies in the Context of Human Disease. Sci Rep. 2015;5:14440. doi: 10.1038/srep14440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Heck AJ. Native mass spectrometry: a bridge between interactomics and structural biology. Nat Methods. 2008;5(11):927–933. doi: 10.1038/nmeth.1265. [DOI] [PubMed] [Google Scholar]
- 11.Wieczorek G, Zielenkiewicz P. Influence of macromolecular crowding on protein-protein association rates--a Brownian dynamics study. Biophysical journal. 2008;95(11):5030–5036. doi: 10.1529/biophysj.108.136291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ermakova E. Lysozyme dimerization: Brownian dynamics simulation. Journal of molecular modeling. 2005;12(1):34–41. doi: 10.1007/s00894-005-0001-2. [DOI] [PubMed] [Google Scholar]
- 13.Forlemu NY, Njabon EN, Carlson KL, Schmidt ES, Waingeh VF, Thomasson KA. Ionic strength dependence of F-actin and glycolytic enzyme associations: a Brownian dynamics simulations approach. Proteins. 2011;79(10):2813–2827. doi: 10.1002/prot.23107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Long H, Chang CH, King PW, Ghirardi ML, Kim K. Brownian dynamics and molecular dynamics study of the association between hydrogenase and ferredoxin from Chlamydomonas reinhardtii. Biophysical journal. 2008;95(8):3753–3766. doi: 10.1529/biophysj.107.127548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Frembgen-Kesner T, Elcock AH. Absolute protein-protein association rate constants from flexible, coarse-grained Brownian dynamics simulations: the role of intermolecular hydrodynamic interactions in barnase-barstar association. Biophys J. 2010;99(9):L75–77. doi: 10.1016/j.bpj.2010.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zimmer MJ, Geyer T. Do we have to explicitly model the ions in brownian dynamics simulations of proteins? The Journal of chemical physics. 2012;136(12):125102. doi: 10.1063/1.3698593. [DOI] [PubMed] [Google Scholar]
- 17.Dlugosz M, Huber GA, McCammon JA, Trylska J. Brownian dynamics study of the association between the 70S ribosome and elongation factor G. Biopolymers. 2011;95(9):616–627. doi: 10.1002/bip.21619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Huber GA, Kim S. Weighted-ensemble Brownian dynamics simulations for protein association reactions. Biophysical journal. 1996;70(1):97–110. doi: 10.1016/S0006-3495(96)79552-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rojnuckarin A, Livesay DR, Subramaniam S. Bimolecular reaction simulation using Weighted Ensemble Brownian dynamics and the University of Houston Brownian Dynamics program. Biophysical journal. 2000;79(2):686–693. doi: 10.1016/S0006-3495(00)76327-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zou G, Skeel RD. Robust biased Brownian dynamics for rate constant calculation. Biophysical journal. 2003;85(4):2147–2157. doi: 10.1016/S0006-3495(03)74641-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhou HX. Brownian dynamics study of the influences of electrostatic interaction and diffusion on protein-protein association kinetics. Biophysical journal. 1993;64(6):1711–1726. doi: 10.1016/S0006-3495(93)81543-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Northrup SH, Erickson HP. Kinetics of protein-protein association explained by Brownian dynamics computer simulation. Proceedings of the National Academy of Sciences of the United States of America. 1992;89(8):3338–3342. doi: 10.1073/pnas.89.8.3338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Merlitz H, Rippe K, Klenin KV, Langowski J. Looping dynamics of linear DNA molecules and the effect of DNA curvature: a study by Brownian dynamics simulation. Biophysical journal. 1998;74(2 Pt 1):773–779. doi: 10.1016/S0006-3495(98)74002-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mereghetti P, Gabdoulline RR, Wade RC. Brownian dynamics simulation of protein solutions: structural and dynamical properties. Biophysical journal. 2010;99(11):3782–3791. doi: 10.1016/j.bpj.2010.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lin J, Beratan DN. Simulation of electron transfer between cytochrome C2 and the bacterial photosynthetic reaction center: Brownian dynamics analysis of the native proteins and double mutants. The journal of physical chemistry B. 2005;109(15):7529–7534. doi: 10.1021/jp045417w. [DOI] [PubMed] [Google Scholar]
- 26.De Rienzo F, Gabdoulline RR, Menziani MC, De Benedetti PG, Wade RC. Electrostatic analysis and Brownian dynamics simulation of the association of plastocyanin and cytochrome f. Biophysical journal. 2001;81(6):3090–3104. doi: 10.1016/S0006-3495(01)75947-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Haddadian EJ, Gross EL. A Brownian dynamics study of the interactions of the luminal domains of the cytochrome b6f complex with plastocyanin and cytochrome c6: the effects of the Rieske FeS protein on the interactions. Biophysical journal. 2006;91(7):2589–2600. doi: 10.1529/biophysj.106.085936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hattne J, Fange D, Elf J. Stochastic reaction-diffusion simulation with MesoRD. Bioinformatics. 2005;21(12):2923–2924. doi: 10.1093/bioinformatics/bti431. [DOI] [PubMed] [Google Scholar]
- 29.Ander M, Beltrao P, Di Ventura B, Ferkinghoff-Borg J, Foglierini M, Kaplan A, Lemerle C, Tomas-Oliveira I, Serrano L. SmartCell, a framework to simulate cellular processes that combines stochastic approximation with diffusion and localisation: analysis of simple networks. Syst Biol (Stevenage) 2004;1(1):129–138. doi: 10.1049/sb:20045017. [DOI] [PubMed] [Google Scholar]
- 30.Rodriguez JV, Kaandorp JA, Dobrzynski M, Blom JG. Spatial stochastic modelling of the phosphoenolpyruvate-dependent phosphotransferase (PTS) pathway in Escherichia coli. Bioinformatics. 2006;22(15):1895–1901. doi: 10.1093/bioinformatics/btl271. [DOI] [PubMed] [Google Scholar]
- 31.Stiles, Bartol TM. Monte Carlo methods for simulating realistic synaptic microphysiology using MCell. Computational Neuroscience. 2001:87–127. [Google Scholar]
- 32.Andrews SS, Bray D. Stochastic simulation of chemical reactions with spatial resolution and single molecule detail. Phys Biol. 2004;1(3–4):137–151. doi: 10.1088/1478-3967/1/3/001. [DOI] [PubMed] [Google Scholar]
- 33.Ridgway D, Broderick G, Lopez-Campistrous A, Ru’aini M, Winter P, Hamilton M, Boulanger P, Kovalenko A, Ellison MJ. Coarse-grained molecular simulation of diffusion and reaction kinetics in a crowded virtual cytoplasm. Biophysical Journal. 2008;94(10):3748–3759. doi: 10.1529/biophysj.107.116053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Frazier Z, Alber F. A Computational Approach to Increase Time Scales in Brownian Dynamics-Based Reaction-Diffusion Modeling. Journal of Computational Biology. 2012;19(6):606–618. doi: 10.1089/cmb.2012.0027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lee B, LeDuc PR, Schwartz R. Stochastic off-lattice modeling of molecular self-assembly in crowded environments by Green’s function reaction dynamics. Physical Review E. 2008;78(3) doi: 10.1103/PhysRevE.78.031911. [DOI] [PubMed] [Google Scholar]
- 36.Xie ZR, Chen J, Wu Y. Multiscale Model for the Assembly Kinetics of Protein Complexes. J Phys Chem B. 2016;120(4):621–632. doi: 10.1021/acs.jpcb.5b08962. [DOI] [PubMed] [Google Scholar]
- 37.Aragon S. A precise boundary element method for macromolecular transport properties. J Comput Chem. 2004;25(9):1191–1205. doi: 10.1002/jcc.20045. [DOI] [PubMed] [Google Scholar]
- 38.Aragon S, Hahn DK. Precise boundary element computation of protein transport properties: Diffusion tensors, specific volume, and hydration. Biophys J. 2006;91(5):1591–1603. doi: 10.1529/biophysj.105.078188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Xie ZR, Chen J, Wu Y. Predicting Protein-protein Association Rates using Coarse-grained Simulation and Machine Learning. Sci Rep. 2017;7:46622. doi: 10.1038/srep46622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hills RD, Jr, Brooks CL., 3rd Insights from coarse-grained Go models for protein folding and dynamics. Int J Mol Sci. 2009;10(3):889–905. doi: 10.3390/ijms10030889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kim YC, Hummer G. Coarse-grained models for simulations of multiprotein complexes: application to ubiquitin binding. Journal of molecular biology. 2008;375(5):1416–1433. doi: 10.1016/j.jmb.2007.11.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ravikumar KM, Huang W, Yang S. Coarse-grained simulations of protein-protein association: an energy landscape perspective. Biophys J. 2012;103(4):837–845. doi: 10.1016/j.bpj.2012.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kyte J, Doolittle RF. A simple method for displaying the hydropathic character of a protein. Journal of molecular biology. 1982;157(1):105–132. doi: 10.1016/0022-2836(82)90515-0. [DOI] [PubMed] [Google Scholar]
- 44.Xie Z-R, Chen J, Wu Y. A coarse-grained model for the simulations of biomolecular interactions in cellular environments. Journal of Chemical Physics. 2014;140:054112. doi: 10.1063/1.4863992. [DOI] [PubMed] [Google Scholar]
- 45.Su Y, Zhou A, Xia X, Li W, Sun Z. Quantitative prediction of protein-protein binding affinity with a potential of mean force considering volume correction. Protein Sci. 2009;18(12):2550–2558. doi: 10.1002/pro.257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Xiong P, Zhang C, Zheng W, Zhang Y. BindProfX: Assessing Mutation-Induced Binding Affinity Change by Protein Interface Profiles with Pseudo-Counts. J Mol Biol. 2017;429(3):426–434. doi: 10.1016/j.jmb.2016.11.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Atilgan AR, Durell SR, Jernigan RL, Demirel MC, Keskin O, Bahar I. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophysical Journal. 2001;80(1):505–515. doi: 10.1016/S0006-3495(01)76033-X. [DOI] [PMC free article] [PubMed] [Google Scholar]