MINFLUX monitors rapid molecular jumps with superior spatiotemporal resolution

Significance

Popular localization of single molecules through calculating the centroid of the diffraction pattern produced by molecular fluorescence on a camera is typically limited to spatiotemporal resolutions of >10 nm per >10 milliseconds. By requiring at least 10–100 times fewer detected photons and being free of bias due to molecular orientation, the localization concept called MINFLUX propels molecular tracking to the hitherto-unachievable regime of single-digit nanometer precision within substantially less than a millisecond. Our experiments herald the feasibility to detect molecular interactions and conformational changes at microsecond timescales.

Abstract

Compared with localization schemes solely based on evaluating patterns of molecular emission, the recently introduced single-molecule localization concept called MINFLUX and the fluorescence nanoscopies derived from it require up to orders of magnitude fewer emissions to attain single-digit nanometer resolution. Here, we demonstrate that the lower number of required fluorescence photons enables MINFLUX to detect molecular movements of a few nanometers at a temporal sampling of well below 1 millisecond. Using fluorophores attached to thermally fluctuating DNA strands as model systems, we demonstrate that measurement times as short as 400 microseconds suffice to localize fluorescent molecules with ∼2-nm precision. Such performance is out of reach for popular camera-based localization by centroid calculation of emission diffraction patterns. Since theoretical limits have not been reached, our results show that emerging MINFLUX nanoscopy bears great potential for dissecting the motions of individual (macro)molecules at hitherto-unattained combinations of spatial and temporal resolution.

Fluorescence nanoscopy methods such as those called stimulated emission depletion (STED)/reversible saturable optical linear fluorescence transitions (RESOLFT) microscopy (1, 2) and photoactivated localization microscopy (PALM)/stochastic optical reconstruction microscopy (STORM) (3–5) routinely achieve 20- to 50-nm spatial resolution (6–8) with recording times down to tens of milliseconds, albeit with the requirements for fast recording and high spatial resolution difficult to reconcile. By synergistically combining the strengths of the two superresolution families, the recent MINFLUX concept is bound to solve this problem.

MINFLUX is based on the insight that, while both STED/RESOLFT and PALM/STORM modulate fluorescence emission to distinguish nearby molecules, they differ at establishing the molecular position (9). Whereas in STED/RESOLFT the position of the molecule is determined by interrogating the sample with a spatially controlled illumination pattern, for example, a doughnut or a standing wave, in PALM/STORM the molecular position is inferred from the pattern of fluorescence light rendered by a single molecule on a pixelated detector, such as a camera (10). Concretely, the molecule’s position is equated with the maximum of the fluorescence diffraction pattern, following backprojection into sample space. The precision of this camera-based “localization” ideally reaches ${\sigma }_{\mathrm{cam}}\ge {\sigma }_{\mathrm{PSF}}/\sqrt{N}$, with ${\sigma }_{\mathrm{PSF}}$ being the SD of the pattern [“point spread function” (PSF)] and $N$ being the number of fluorescence photons making up the pattern (11–13). ${\sigma }_{\mathrm{cam}}$ is thus clearly bounded by the finite fluorescence emission rate, which for currently used fluorophores rarely yields more than a few hundred detections per millisecond (<1 MHz). Moreover, emission is frequently interrupted and eventually ceases due to blinking and bleaching (14, 15).

The need for large photon detection numbers $N$ has spurred the development of related methods, such as confocalized tracking with multiple point detectors (16, 17), detection PSF engineering (18), Gaussian beam scanning schemes (i.e., orbital tracking) (19–24), and multiplexed excitation schemes (25–28). While all these methods provide specific advantages, none of them solved the need for large detection events $N$, keeping the photon emission rate as the limiting factor for the obtainable spatiotemporal resolution. As a result, current state-of-the-art single-molecule tracking performance has remained in the tens of nanometer per several tens of millisecond range.

Drawing on the basic rationale of the coordinate determination employed in STED/RESOLFT microscopy, MINFLUX has addressed these fundamental limitations (29). By localizing individual emitters with an excitation beam featuring an intensity minimum that is spatially precisely controlled, MINFLUX takes advantage of coordinate targeting for single-molecule localization. In a typical 2D MINFLUX implementation, the position of a molecule is obtained by placing the minimum of a doughnut-shaped excitation beam at a known set of spatial coordinates in the molecule’s proximity. These coordinates are within a range L in which the molecule is anticipated (Fig. 1). Probing the number of detected photons for each doughnut minimum coordinate yields the molecular position. It is the position at which the doughnut would produce minimal emission, if the excitation intensity minimum were targeted to it directly. As the intensity minimum is ideally a zero, it is the point at which emission is ideally absent. The precision of the position estimate increases with the square root of the total number of detected photons and, more importantly, by decreasing the range $L$. For small ranges $L$ at which the intensity minimum is approximated by a quadratic function, the localization precision does not depend on any wavelength and, for the case of no background and perfect doughnut control, the precision ${\sigma }_{\mathrm{MF}}$ simply scales with $L/\sqrt{N}$ at the center of the investigated range. In other words, the better the coordinates of the excitation minimum match the position of the molecule, the fewer fluorescence detections are needed to reach a given precision. In the conceptual limit where the excitation minimum coincides with the position of the emitter (i.e., $L=0$), the emitter position is rendered by vanishing fluorescence detection. This is contrary to conventional centroid-based localization where precision improvements are tightly bound to having increasingly larger numbers of detected photons. So far, demonstrations of MINFLUX have achieved (i) localization precisions of ∼1.5 nm utilizing $500$ photons to image organic fluorophores $6$ nm apart (20-fold improvement in photon efficiency with respect to popular centroid-localization) and (ii) localization precisions ${\sigma }_{\mathrm{MF}}$ of $\sim 50$ nm utilizing only $10$ photons for tracking fluorescent proteins with a nonconfocal configuration in living bacteria at a rate of $8$ kHz (fivefold improvement).

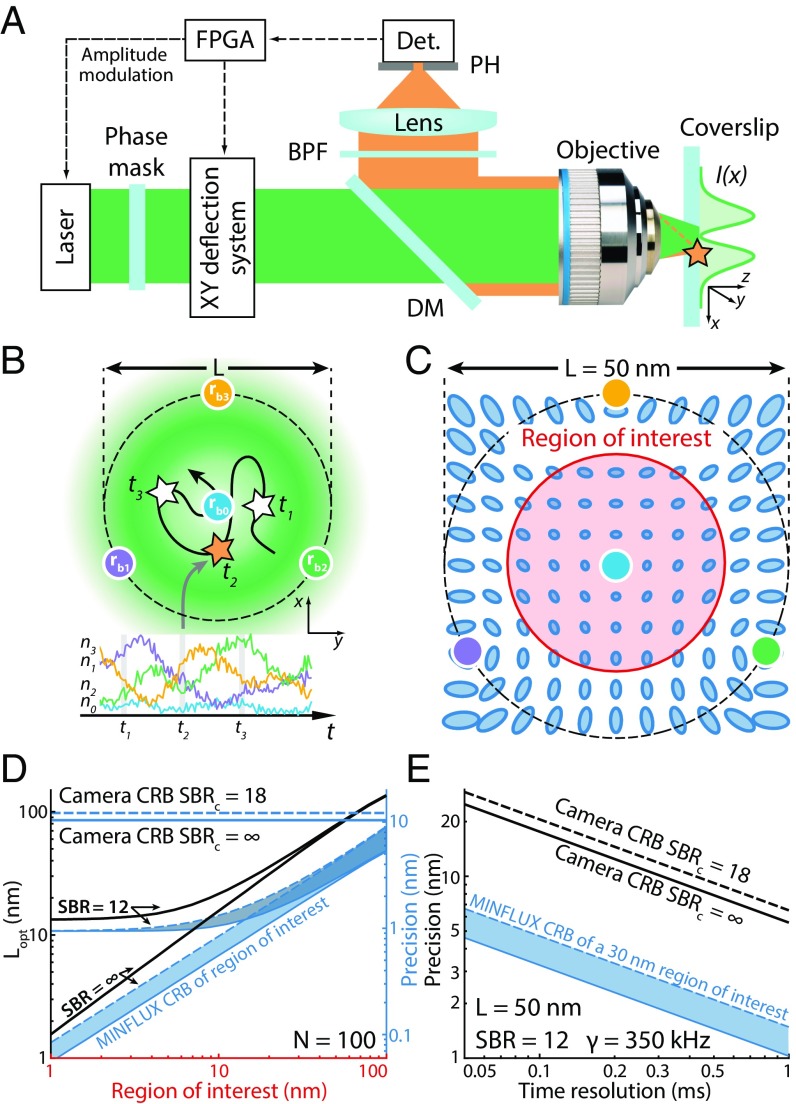
Fig. 1.

MINFLUX probes the position of an emitter with light distributions featuring intensity zeros that are targeted to defined coordinates in sample space. (A) Schematic of the MINFLUX setup used here. A laser beam is structured by a phase mask to obtain a doughnut-shaped excitation profile $I\left(\overline{r}\right)$ at the focal plane of the objective. The emitter fluorescence is collected in backscattering geometry and separated from the excitation beam by a dichroic mirror (DM). After passing a bandpass filter (BPF), the fluorescence photons are focused onto a confocal pinhole (PH) and counted by a detector (Det.). A field-programmable gate array (FPGA) board controls the deflection system, modulates the beam intensity, and processes the detected photons. (B) (Upper) The intensity zero of the doughnut is targeted in quick succession to coordinates ${\overline{r}}_{b0},\dots ,{\overline{r}}_{b3}$ lying within a circle of diameter $L$, defining the set of targeted coordinates. (Lower) Example of a collected photon trace ($n_0,\dots ,n_3$) for a molecule transiting the rapidly retargeted doughnut beams. (C) Visualization of the position-dependent localization uncertainty. The blue ellipses represent the $e^{-1/2}$ contour level of the covariance matrix ${\mathrm{\Sigma }}_{\mathrm{CRB}}\left(\overline{r}\right)$ as a quadratic form, for a total of N = 1,000 photons and $L=50$ nm. The red encircled area defines a region of interest (ROI). (D) Optimal $L$ value $L_{\mathrm{opt}}$ (black) for two SBR values ($\mathrm{SBR}=\infty ,\hspace{0.17em}\mathrm{SB}{\mathrm{R}}_{L=50\mathrm{nm}}^{\overline{r}=\overline{0}}=12$) and corresponding MINFLUX CRB ${\sigma }_{\mathrm{CRB}}$ (blue bands, $L=L_{\mathrm{opt}}$, N = 100 photons) as a function of the diameter of the ROI. A considerable improvement over ideal camera performance is achievable especially for small ROIs. In the presence of background $L_{\mathrm{opt}}$ saturates for small ROI values. (E) Localization precision as a function of time resolution. The MINFLUX CRB ${\sigma }_{\mathrm{CRB}}$ in a 30-nm ROI (blue band, $L=50$ nm, $\gamma =350$ kHz, $\mathrm{SB}{\mathrm{R}}_{L=50\mathrm{nm}}^{\overline{r}=\overline{0}}=12$) is compared with ideal camera performance without background (black) and with realistic background contributions (dashed black, ${\text{SBR}}_{\text{c}}=18$).

Here, we demonstrate nanometer-precision tracking of a single emitter quickly fluctuating within a 20-nm range. We also show that, for attaining a certain precision in a predefined region of interest (ROI), there is an optimal distance $L$, depending on the signal-to-background ratio (SBR) and the ROI size. Establishing the optimal $L$ allowed us to increase the spatiotemporal resolution beyond reported values, as demonstrated by tracking the stochastic movement of a labeled DNA construct with submillisecond resolution and ∼2-nm precision.

Results

Nanometer-scale MINFLUX tracking measurements were carried out with a custom-built laser-scanning fluorescence microscope featuring fast beam deflection and modulation (SI Appendix, Fig. S2A) that followed a previously reported design (29). The excitation beam is doughnut-shaped $I_i\left(\overline{r}\right)=I\left(\overline{r}-{\overline{r}}_{bi}\right)$, with ${\overline{r}}_{b0},\dots ,{\overline{r}}_{b3}$ denoting a set of targeted coordinates (STC) to which the central doughnut minimum is placed in quick succession (SI Appendix, Eq. S1). Concretely, our STC consists of three points that reside on a circle of diameter $L$ and a fourth point at the circle center (Fig. 1B and SI Appendix, Fig. S2B). For each localization measurement, the emitter fluorescence is collected point by point using confocal detection. The set of fluorescence detections $n_0,\dots ,n_3$ resulting from a complete STC cycle yields the emitter position.

Studying nanoscale movements using this stationary STC requires the molecules of interest to be placed proximal to the STC center, because this is where localization precision is highest. The precision deteriorates toward the STC periphery, depending on $L$ (SI Appendix, Fig. S8): small values of $L$ yield high precision in small regions, whereas large $L$ values exhibit poorer precision over a larger area. Thus, this parameter needs to be adapted to the size of the ROI. As a cost function for optimizing $L$, we chose the average localization Cramér-Rao bound (CRB) over the edge of a circular ROI with diameter $d_{\mathrm{ROI}}$ (Fig. 1C). The evaluation was performed numerically for an infinite SBR and also for a typical experimental $\mathrm{SB}{\mathrm{R}}_{L=50\mathrm{nm}}^{\overline{r}=\overline{0}}=12$, which denotes the SBR at the STC center ($\overline{r}=0$) for $L=50$ nm. Note that the SBR depends on the position of the emitter within the particular STC. For small diameters $d_{\mathrm{ROI}}$ and an infinite SBR, a linear relationship emerges between the optimal value $L_{\mathrm{opt}}$ and $d_{\mathrm{ROI}}$ that is given by $L_{\mathrm{opt}}\left(d_{\mathrm{ROI}}\right)\approx 1.57\cdot d_{\mathrm{ROI}}$. However, for values greater than $d_{\mathrm{ROI}}\approx 30$ nm the relationship deviates from linearity (Fig. 1D), due to the quadratic approximation of the doughnut-shaped intensity profile becoming increasingly invalid. For $\mathrm{SB}{\mathrm{R}}_{L=50\mathrm{nm}}^{\overline{r}=\overline{0}}=12$, the optimal $L$ value converges to $L_{\mathrm{opt}}\approx 13$ nm for small ROIs. That is explained by the fact that a reduction of $L$ improves the localization precision only up to a minimal $L$ value in the presence of background (see figure S3D and equation S31 of ref. 29). Further reduction would only deteriorate the localization precision (SI Appendix, Fig. S8B).

This relationship indicates which $L$ to choose for a given ROI. The MINFLUX CRB values inside this region for a total of $N=100$ photons per localization are shown in Fig. 1D. Note that small ROIs yield high precisions compared with the ideal no-background camera performance. However, even under realistic background conditions, the MINFLUX CRB predicts attaining molecular precision ($\approx 1$ nm) using only $100$ photons. To relax the need for centering the target within the STC range in our experiments, we typically chose an $L$ that is slightly bigger than $L_{\mathrm{opt}}$, given that a good localization precision is still provided on a slightly bigger region.

Because MINFLUX requires fewer detected photons, molecules can be localized at higher temporal resolution. For a detection count rate of $\gamma =350$ kHz with a realistic ${\text{SBR}}_{L=50\mathrm{nm}}^{\overline{r}=\overline{0}}=12$, a beam separation $L=50$ nm yields a CRB of ${\sigma }_{\mathrm{CRB}}\left(\overline{0}\right)\approx 1.6$ nm at a time resolution of $\delta t=400$ µs. The ideal no-background camera CRB is ${\sigma }_{\mathrm{cam}}\approx 8.8$ nm (Fig. 1E). Thus, the MINFLUX CRB predicts fivefold improvement of the localization precision under realistic conditions. Also, to reach ${\sigma }_{\mathrm{cam}}=1.6$ nm under the same detection rate, ideal camera-based localization requires 25 times longer recording time.

MINFLUX Performance Evaluation.

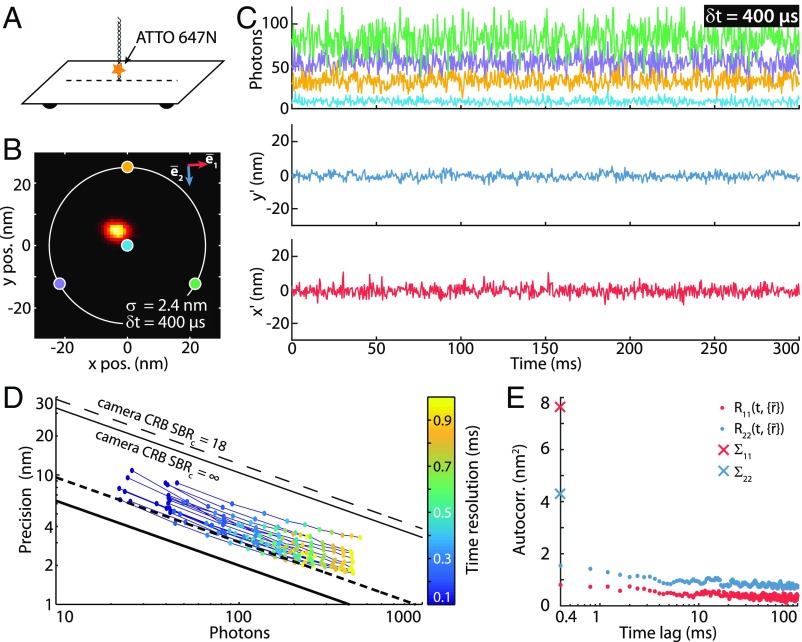
The experimental MINFLUX performance at high temporal resolution was characterized by repeatedly localizing individual immobilized ATTO 647N fluorophores within the ROI (Fig. 1C). Our measurements used $L=50$ nm with a time resolution of $100$ µs per STC cycle. The exposure at each coordinate point lasted $17$ µs (SI Appendix, Fig. S2). In this regime, spontaneous emitter intermittencies (blinking) have to be considered, because blinking within an STC cycle compromises the position estimation result. Therefore, ATTO 647N fluorophores were embedded in a reducing and oxidizing system buffer (30), reducing the average off-time to ${\overline{\tau }}_{\text{off}}=5.7\pm 1.4$ µs (SI Appendix, Fig. S7). To average over the intermittencies, the traces were binned at the expense of temporal resolution (SI Appendix, Segmentation and Binning of the Count Traces). We also considered emission rate saturation of ATTO 647N as a limiting factor which, under our experimental conditions amounted to about $1$ MHz. Therefore, we adjusted the average count rate to $350$ kHz, that is, far enough from saturation.

We first evaluated the experimental MINFLUX localization precision for temporal resolutions of 0.1–$1$ ms, attained by 1- to 10-fold binning of the measured count traces. For a b-fold binning, the detected photons from each of the four exposures of an STC cycle were added to those of the following $(b-1)$ subsequent cycles. Thus, we typically obtained 35–350 photon counts per localization. The emitter position was estimated using the numLMS estimator (SI Appendix, Localization). Prior evaluations have shown that this estimator is well suited for the low photon regime, in contrast to other estimators like the maximum-likelihood estimator, which does not converge to its CRB for photon counts below 100–150 (see figure S9 of ref. 29).

An example of the position estimates for a 300-ms trace extract is shown in Fig. 2C. Evaluation of the resulting localization precision $\sigma$ using all 13,625 localizations of the trace yields ${\sigma }_{\mathrm{MF}}\approx 2.4$ nm at a temporal resolution of $\delta t=400$ µs and an average of $\langle N\rangle \approx 168$ fluorescent photons per localization (Fig. 2B). This corresponds to an approximately $3.9$ times increase in localization precision compared with ideal camera performance with realistic background contributions ($\mathrm{SB}{\mathrm{R}}_{\mathrm{c}}=18$). If the camera was to achieve ${\sigma }_{\mathrm{cam}}\approx 2.4$ nm for the given count rate, the temporal resolution would be $15$ times lower, that is, $\delta t\approx 6$ ms. The same spatiotemporal resolution could, in principle, be achieved by increasing the detection rate 20-fold. However, controlled and stable detection rates of $5.25$ MHz cannot be obtained with ATTO 647N or other existing organic fluorophores.

Fig. 2.

Fluorescence time traces of a single molecule and resulting localization precision at high temporal resolution using MINFLUX. (A) Diagram of the DNA origami construct with a single ATTO 647N fluorophore attached closely to a glass surface. Immobilization was achieved by complementarily pairing a ssDNA linked to an ATTO 647N molecule with a second ssDNA that is attached to a rectangular DNA origami (SI Appendix, Sample Preparation). (B) Histogram of 13,625 MINFLUX localizations of a sample with 1 × 1-nm binning. Time resolution, $\delta t=400$ µs; localization precision, ${\sigma }_{\mathrm{MF}}=2.4$ nm; average counts, $\langle N\rangle =168$ photons. The positions of the doughnut zeros are marked as colored dots with a parameter $L=50$ nm. The ${\overline{e}}_2$ axis (blue arrow) indicates the direction of maximal emitter movement; the red arrow is perpendicular to it (SI Appendix, Autocorrelation Analysis). (C, Upper) A 300-ms excerpt of the detected photon count trace (time resolution of $\delta t=400$ µs per localization). The color coding corresponds to the targeted coordinates shown in B. (C, Lower) Estimated mean-subtracted trajectory $\left\{\widehat{\overline{r}}\right\}$ (rotated coordinate system: $x\prime =\widehat{\overline{r}}\cdot {\overline{e}}_1$, $y\prime =\widehat{\overline{r}}\cdot {\overline{e}}_2$). (D) Colored dots: experimental MINFLUX localization precision ${\sigma }_{\mathrm{MF}}$ as a function of the number of photons for emitters within a ROI of d_ROI = 30 nm. The color coding indicates the time resolution of the measurement. The MINFLUX CRB at the center of the targeted coordinates set (thick black line), the average CRB at the edge of the ROI (thick dashed line), and the ideal camera CRB (thin black lines) are included. (E) Autocorrelation analysis of the trajectory along the principal axes detailed in B with a time resolution of $\delta t=400$ µs. $R_{11}\hspace{0.17em}\left(t,\left\{\overline{r}\right\}\right):$ along axis ${\overline{e}}_1$. $R_{22}\left(t,\left\{\overline{r}\right\}\right)$: along axis ${\overline{e}}_2$. ${\mathrm{\Sigma }}_{11}$ and ${\mathrm{\Sigma }}_{22}$ (crosses) are the variances along these two directions.

Since optimized centering within the STC range is not possible for all emitters (SI Appendix, Data Acquisition), different positions within the ROI provide slightly different precision. However, throughout a ROI with d_ROI = 30 nm and for all temporal resolutions evaluated, the localization precision is improved over that provided by ideal camera localization (Fig. 1E). On the other hand, the measured localization precisions did not fully reach their CRB. The precision of ${\sigma }_{\mathrm{MF}}\approx 2.4$ nm of the trace shown in Fig. 2C did not reach its CRB of ${\sigma }_{\mathrm{CRB}}\approx 1.5$ nm for the given photon number. This deviation can be attributed to system instabilities, emitter blinking, or any relative movement of the emitter with respect to the STC. Emitter movements are manifested in a correlation between temporally adjacent emissions. Indeed, by using a correlation analysis, the magnitude of the emitter movement at $\delta t=400$ µs was found to be up to ${\text{σ}}_{\text{mov},11}\approx 1.3$ nm (Fig. 2E and SI Appendix, Autocorrelation Analysis).

Nanometer-Scale MINFLUX Tracking.

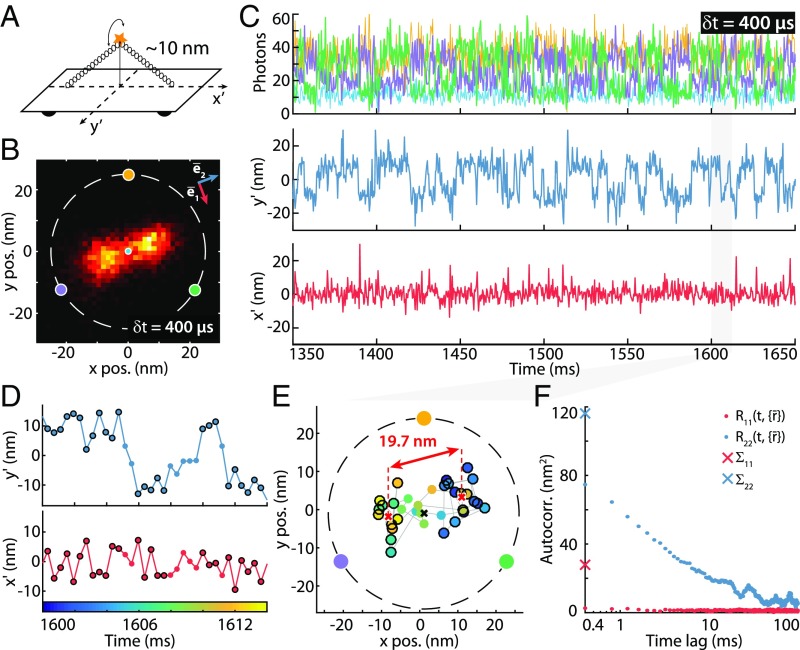
To demonstrate its ability to record fast movements of target molecules with high spatiotemporal resolution, we applied MINFLUX to the detection of rapid movements of a custom-designed DNA origami sample (Fig. 3A). Two extended ssDNA attached to a modified Rothemund rectangle (31) were base paired with a DNA bridge strand. An ATTO 647N emitter was attached approximately at the center of the bridge, resulting in a maximal distance of about $10$ nm from the DNA origami base (SI Appendix, DNA Origami Sample Preparation). This 1D diffuser (1DD bridge) can only move on a half-circle above the DNA origami by design, ideally yielding a 1D movement. For a maximal emitter displacement of $20$ nm, the predicted optimal $L$ value is $L_{\mathrm{opt}}\approx 33$ nm (Fig. 1E). To account for nonperfect placement of the sample to the STC center area, we set $L$= $50$ nm.

Fig. 3.

MINFLUX tracking of rapid movements of a custom-designed DNA origami. (A) Diagram of the DNA origami construct with a single ATTO 647N fluorophore attached at the center of the bridge ($10$ nm from the origami base). By design, the emitter can move on a half-circle above the origami and is thus ideally restricted to a 1D movement. (B) Histogram of 6,118 localizations of the sample in A with δt = 400-µs time resolution and a 1.5 × 1.5-nm binning. The predominant motion is along a single direction (${\overline{e}}_2$). (C, Upper) A 300-ms excerpt of the photon count trace (time resolution δt = 400 µs per localization). The color coding corresponds to the zero positions shown in B. (C, Lower) Mean-subtracted trajectory $\left\{\widehat{\overline{r}}\right\}$ (rotated coordinate system: $x^{\text{'}}=\widehat{\overline{r}}\cdot {\overline{e}}_1$, $y^{\text{'}}=\widehat{\overline{r}}\cdot {\overline{e}}_2$). (D) Excerpt of 14-ms duration of the trace shown in C containing 35 localizations, highlighting the predominant and rather stationary positions (black circles). Transitions between these predominant positions are clearly resolved. (E) Scatter plot of the excerpt shown in D. The color coding of the dots indicates the time (same color bar as in D). The distance of black encircled data points (also marked in D) is displayed. (F) Autocorrelation analysis of the trajectory along the principal axes detailed in B. $R_{22}\hspace{0.17em}(t,\left\{\overline{r}\right\})$: along principal axis ${\overline{e}}_2$. $R_{11}\hspace{0.17em}\left(t,\left\{\overline{r}\right\}\right):$ along secondary axis ${\overline{e}}_1$. ${\mathrm{\Sigma }}_{11}$ and ${\mathrm{\Sigma }}_{22}$ (crosses) are the variances along these two directions. The estimated SD of the emitter movement along these directions are ${\sigma }_{\mathrm{mov},11}\approx 1.7$ nm and ${\sigma }_{\mathrm{mov},22}\approx 9.2$ nm (with a relaxation half-time of 2.1 ms; SI Appendix, Autocorrelation Analysis).

Like for the static DNA construct, a 2D histogram of the localizations (Fig. 3B) and photon counts (Fig. 3C, Upper) together with the trajectory trace excerpt (Fig. 3C, Lower) are shown for the 1DD (Movies S1 and S2). Again, acquisition was performed at $100$ µs per STC cycle and the counts binned to $\delta t=400$ µs for gaining precision and reducing the influence of blinking. As is expected from the possible range of emitter movements, the counts gained for the peripheral STC points are largely anticorrelated. Position estimation using the numLMS estimator allowed us to identify a movement that was predominantly 1D, as expected (Fig. 3C, Middle and Lower and Fig. 3B). The axis ${\overline{e}}_2$ of predominant movement is obtained by autocorrelation analysis (SI Appendix, Autocorrelation Analysis). Note the striking difference to the results obtained for the immobilized emitter (Fig. 2).

For a perfect 1D movement, the localization precision perpendicular to ${\overline{e}}_2$ should ideally reach the CRB, which is however not the case for our 1DD bridge sample. The CRB at the average position of the emitter $\langle \widehat{\overline{r}}\rangle$ is calculated as ${\sigma }_{\mathrm{CRB}}\left(\langle \widehat{\overline{r}}\rangle \right)\approx 2.1$ nm for an average of $\langle N\rangle \approx 94$ photons. Evaluation of the experimental localization precision at $\langle \widehat{\overline{r}}\rangle$ perpendicular to ${\overline{e}}_2$, results in ${\sigma }_{11}\left(\langle \widehat{\overline{r}}\rangle \right)\approx 4.2$ nm. The deviation can be due to system instabilities and emitter blinking, but also to a nonnegligible movement perpendicular to the principal axis. The latter can be due to the flexibility of the emitter with respect to the DNA origami and the DNA origami itself. The estimation of the emitter movement in this direction by an autocorrelation analysis results in a SD of ${\sigma }_{\text{mov},11}\approx 1.7$ nm (Fig. 3F and SI Appendix, Autocorrelation Analysis).

As we measured the projection of a 3D movement on a 2D plane, the result resembles a translocation with two predominant positions on the principal axis. Fig. 3D shows a $14$-ms excerpt containing $35$ localizations in which the transitions between the predominant positions (marked by black circles) are clearly resolved. The distance between these positions is $19.7\pm 0.2$ nm, in full agreement with the sample design (Fig. 3E). However, we also found similarly designed constructs with emitters that were rather immobile, moved randomly in a restricted area, or that displayed smaller movement magnitude. These examples may be due to a nonperfect assembly of the DNA origami and the roughness of the surface to which the DNA origamis are immobilized; a detailed classification of the various cases, together with quantifications of the movement and its relaxation time, can be found in the SI Appendix, Fig. S4.

Discussion and Conclusion

MINFLUX operates by targeting one or more intensity minima of an excitation light pattern to a defined set of positions. Matching the positions closely with that of the emitter reduces the number of fluorescence photons required for localization compared with conventional schemes that extract molecular positions just from emission patterns. Due to this conceptual advantage, MINFLUX has the power to attain higher spatiotemporal resolution, as demonstrated in this study.

As for virtually every fluorescence technique, the presence of background emission and optical aberrations (which affects in turn the contrast and absolute depth of the intensity minima) restrict the performance of MINFLUX, limiting how efficiently the collected photons can be used. Furthermore, the fluorophore saturation sets a bound for the achievable spatiotemporal resolution, and the emission blinking naturally limits the temporal resolution.

While the sub-10-nm scale can also be accessed through near-field interactions using a nanosized tip or Förster resonant energy transfer (FRET), a strength of MINFLUX is that it can investigate the nanometer scale from virtually any distance. Besides, unlike FRET, MINFLUX does not entail a photophysically constrained range of action (32) nor does it require multiple labels. Nevertheless, one can envisage combining MINFLUX with FRET to extract further information about molecules such as short distance interactions, rotations, and translations.

We further showed that in a practical MINFLUX implementation, the presence of background leads to an optimal spatial range $L$ of the set of coordinates used for probing the molecular position. Reducing this range does not improve performance further. By the same token, optimizing our range $L$ allowed us to reach spatial precisions ${\sigma }_{x,y}$ of 1.7–$11$ nm, while maintaining the 1- to 0.1-ms temporal resolution. These performances substantially exceed those from published MINFLUX tracking recordings where precisions of only 40–60 nm were achieved at this same timescale; in terms of photon efficiency, this corresponds to a shift from 5- to 20-fold improvement. Further improvements can be expected, for example, from an adaptive STC reacting on the emitter movement/position or the use of a totally internally reflected excitation beam (i.e., total internal reflection fluorescence doughnut) for reducing the background signal.

The advancement in spatiotemporal resolution was demonstrated through directly observing nanometer molecular movements over extended periods (of $5.9$ s on average), yielding tens of thousands of localizations. The demonstrated performance makes biological applications of MINFLUX foreseeable, especially in a multicolor implementation. For example, MINFLUX should improve the observation of rotations and movements of molecular motors as well as of protein folding. The unique combination of localization precision and recording speed should also enhance our understanding of protein and lipid diffusion in cell membranes. In general, MINFLUX localization should trigger a number of single-molecule–based spatiotemporal investigations that have been so far precluded by the attainable fluorescence flux.

Materials and Methods

A description of the sample preparation, the optical setup, data acquisition, as well as data analysis including the emitter localization can be found in SI Appendix, Materials and Methods. In brief, MINFLUX was implemented in a custom-built confocal laser-scanning microscope with fast beam positioning and modulation capabilities. Electro-optical deflectors achieved rapid beam repositioning on nanometer scales. A scanning tip/tilt mirror was used to scrutinize larger areas of the sample. The doughnut-shaped excitation PSF was generated by a $2\pi$ vortex phase plate. To place the STC as centrally as possible on the emitter, we recorded a faint wide-field image of the origami sample and estimated the positions of the ATTO 647N molecules by a 2D Gaussian fit to the measured intensity profiles. The STC was send to an estimated position and the centering optimized using our MINFLUX tracking routine (SI Appendix, Data Acquisition). Retrieving positions from the measured count traces was accomplished with the numLMS estimator that was shown to converge to its CRB also for low photon detection number (SI Appendix, Localization).