Cross-linkers both drive and brake cytoskeletal remodeling and furrowing in cytokinesis

Abstract

Cell shape changes such as cytokinesis are driven by the actomyosin contractile cytoskeleton. The molecular rearrangements that bring about contractility in nonmuscle cells are currently debated. Specifically, both filament sliding by myosin motors, as well as cytoskeletal cross-linking by myosins and nonmotor cross-linkers, are thought to promote contractility. Here we examined how the abundance of motor and nonmotor cross-linkers affects the speed of cytokinetic furrowing. We built a minimal model to simulate contractile dynamics in the Caenorhabditis elegans zygote cytokinetic ring. This model predicted that intermediate levels of nonmotor cross-linkers are ideal for contractility; in vivo, intermediate levels of the scaffold protein anillin allowed maximal contraction speed. Our model also demonstrated a nonlinear relationship between the abundance of motor ensembles and contraction speed. In vivo, thorough depletion of nonmuscle myosin II delayed furrow initiation, slowed F-actin alignment, and reduced maximum contraction speed, but partial depletion allowed faster-than-expected kinetics. Thus, cytokinetic ring closure is promoted by moderate levels of both motor and nonmotor cross-linkers but attenuated by an over-abundance of motor and nonmotor cross-linkers. Together, our findings extend the growing appreciation for the roles of cross-linkers in cytokinesis and reveal that they not only drive but also brake cytoskeletal remodeling.

INTRODUCTION

The actomyosin cortex powers cell shape change during diverse cellular behaviors including cell migration, tissue morphogenesis, and cell division. The cortex is a heterogeneous meshwork rich in actin filaments (F-actin), cytoskeletal cross-linkers, cytoskeleton–plasma membrane linkers, and myosin motors (Clark et al., 2014). The final step of a mitotic or meiotic cell division is cytokinesis, the physical division of the cell into two. During cytokinesis, cues from the anaphase spindle elicit specialization of the cortical cytoskeleton to form an actomyosin ring at the cell equator. The cytokinetic actomyosin ring is enriched with long unbranched F-actin generated by formin family actin nucleators, active nonmuscle myosin II (NMM-II), and cross-linking proteins, including anillin, α-actinin, the septins, and plastin. Initially, the ring dynamically rearranges from a wide band into a tighter ring and ultimately constricts until completely closed, generating a membrane partition between the daughter cells (Green et al., 2012).

The cytoskeletal rearrangements proposed to generate cytokinetic ring closure include actomyosin filament sliding, F-actin depolymerization, and cytoskeletal cross-linking (Mendes Pinto et al., 2013). Sliding is thought to be driven by the motor activity of myosins including NMM-II; loss of NMM-II function via injection of a blocking antibody, gene knock-out, protein depletion, or pharmaceutical inhibition eliminates furrowing (Schroeder, 1972; Mabuchi and Okuno, 1977; Straight et al., 2003; Matsumura et al., 2011). In some settings, the rate of cell constriction scales with the motor activity of NMM-II (Vasquez et al., 2016). However, an NMM-II mutant that binds, but has an impaired ability to slide, F-actin rescued the reduction of cytokinetic furrowing speed caused by thorough depletion or genetic deletion of NMM-II from animal cells (Ma et al., 2012). In addition, cell biological work with budding yeast and theoretical modeling demonstrated that ring closure can be powered by the thermal ratcheting of nonmotor cross-linkers along depolymerizing F-actin (Mendes Pinto et al., 2012; Oelz et al., 2015). Similarly, in fission yeast, a motor-impaired NMM-II mutant that robustly cross-links F-actin is sufficient for ring assembly (Palani et al., 2017). Collectively, these studies suggest that F-actin cross-linking promotes cytoskeletal remodeling, and thus cytokinetic ring closure, in animal and fungal cells.

As introduced above, several cytoskeletal cross-linkers are abundant in the cytokinetic rings of animal cells, including NMM-II and anillin. NMM-II forms minifilaments, bipolar assemblies containing 16–56 motor subunits, each of which is bound to F-actin for 5–35% of its ATPase cycle (Burridge and Bray, 1975; Niederman and Pollard, 1975; Sinard et al., 1989; Verkhovsky et al., 1995). NMM-II minifilaments are robust F-actin cross-linkers (Vicente-Manzanares et al., 2009). Anillin is a multidomain protein thought to coordinate both structural components of the cytokinetic ring and the regulatory proteins that elicit its formation and constriction. Anillin was first identified as an F-actin bundling protein and has since been shown to bind active NMM-II, septins, the formin mDia2, RhoA, and several other proteins, as well as plasma membrane lipids (Piekny and Maddox, 2010; Liu et al., 2012; Reyes et al., 2014; Sun et al., 2015). Anillin depletion causes cytokinesis failure in cultured mammalian and Drosophila cells but is dispensable for cytokinetic ring closure in the Caenorhabditis elegans zygote (Maddox et al., 2005; Straight et al., 2005; Zhao and Fang, 2005; Hickson and O’Farrell, 2008). Cortexillin cross-links F-actin indirectly to the membrane and is important for the mechanical properties of the cortex and cytokinesis dynamics in the social amoeba Dictyostelium discoideum (Srivastava et al., 2016). Additional cytoskeletal cross-linkers that constitutively reside in the cortex, such as fimbrin/plastin, also contribute to cytokinesis (Ding et al., 2017). In sum, diverse cytoskeletal cross-linkers are abundant in the cytokinetic ring.

Interestingly, before cross-linking was implicated in driving cytokinesis, it was demonstrated that cross-linkers can block ring closure in mammalian cultured cells. The abundance of α-actinin scales inversely with furrowing speed in animal cells, as overexpression slows furrowing while depletion allows faster furrowing (Mukhina et al., 2007). The picture is more complex in fission yeast, where both an intermediate abundance and intermediate F-actin binding affinity of α-actinin are required for proper cytokinetic ring dynamics; thus this cross-linker both drives and blocks cytokinetic ring remodeling (Li et al., 2016). Similarly, in vitro reconstituted and simulated simple actomyosin rings exhibit maximal contraction speed and force generation with an intermediate amount of connectivity (Ennomani et al., 2016). Finally, an experimental increase or decrease of the abundance of plastin/fimbrin slows cytokinetic furrowing in the C. elegans zygote (Ding et al., 2017). Thus, the abundance of cross-linkers has been variously shown to scale with actomyosin ring closure speed positively, negatively, or in a nonmonotonic manner so that speed is maximal at intermediate cross-linker levels. As such, it is currently unresolved whether cytoskeletal cross-linkers drive or attenuate remodeling in the cytokinetic ring.

Here we tested how tuning motor and nonmotor cross-linkers influences cytokinetic ring constriction in animal cells. We used the C. elegans zygote as a model cell type since its stereotyped size, shape, and cell division kinetics, as well as its mechanical isolation make it well suited for quantitative studies of ring-intrinsic factors. To gain insight about tuning cross-linker levels in this contractile system and guide our biological experimentation, we built an agent-based minimal model of the C. elegans zygote cytokinetic ring that depicted fibers representing F-actin, fiber cross-linkers, and motor ensembles representing NMM-II minifilaments. Tuning cross-linker abundance in silico predicted that an intermediate level of nonmotor cross-linker would allow maximal ring closure speed. We then targeted the scaffold protein anillin in vivo and generated a population of cells with a graded abundance of anillin by carrying out RNA interference (RNAi)-mediated depletion over a time course. Partial depletion of anillin allowed faster furrowing than observed in control cells, but in more thoroughly depleted cells, speed was normal. We next used our model to tune the abundance of motor ensembles and found a nonlinear relationship between motor abundance and ring closure speed. In vivo, partial NMM-II depletion allowed faster furrowing than in control cells, while thorough depletion slowed ring closure. Towards defining the mechanism by which NMM-II both drives and brakes furrowing, we examined the kinetics of F-actin organization and found evidence that NMM-II also not only drives but also slows cytoskeletal remodeling. Our work demonstrates that both a motor and a nonmotor cross-linker can both drive and attenuate cytokinesis, extending our current understanding of the roles of cytoskeletal cross-linkers in cortical remodeling.

RESULTS

Simulated actomyosin rings with NMM-II–like motor ensembles close with in vivo kinetics

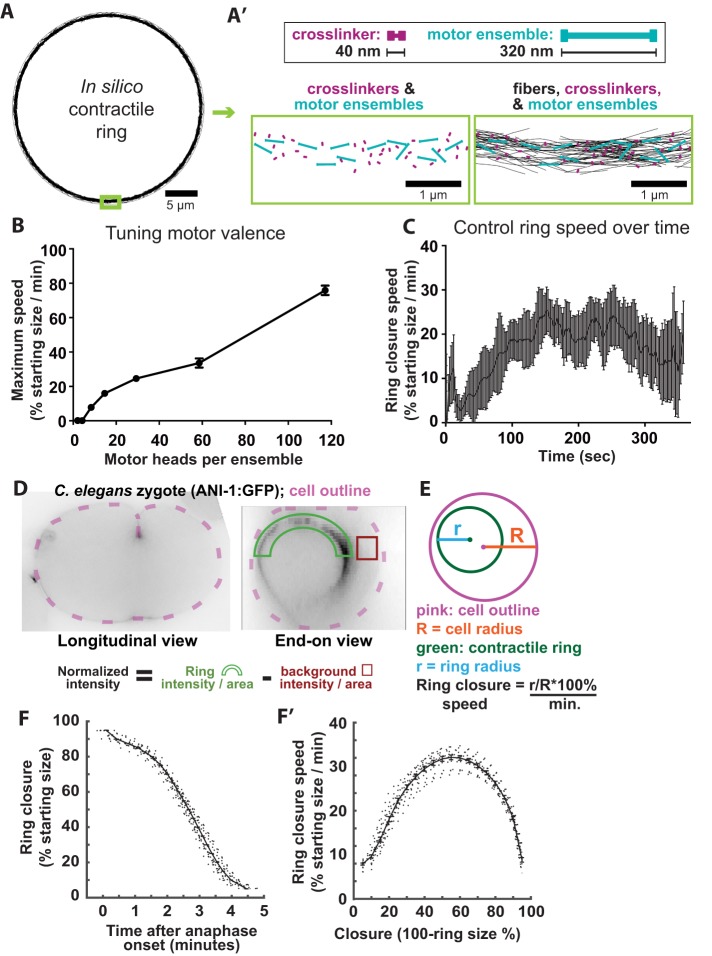
The key elements of the cytokinetic ring are actin filaments, nonmuscle myosin II minifilaments (NMM-II), and cytoskeletal cross-linkers. The collective behavior of a large ensemble of these cytoskeletal elements can be modeled by agent-based simulations, which replicate the physical interactions among molecular components of a cellular process. Agent-based simulation of cytoskeletal dynamics by Cytosim (described under Materials and Methods) was recently used to tune the abundance of motors and nonmotor cross-linkers in actomyosin-like patches and rings with different architectures (Ennomani et al., 2016). While this approach provided the valuable insight that intermediate levels of cross-linkers allow maximal contraction speed, several features of the published models limit their relevance to cytokinesis in vivo. First, they employed motors modeled on myosin VI (a dimeric, pointed end-directed, highly processive motor [ Rock et al., 2001]) or a generic, fast, processive, barbed end-directed motor (Ding et al., 2017). Further, these simulations contained nondynamic fibers of constant length. Here we built on published models to depict NMM-II–like motors (see below), cross-linkers, and dynamic fibers, in a 30-micron-diameter ring representing a two-dimensional slice of the C. elegans zygote cytokinetic ring.

The absolute and relative abundance of components was set according to measurements of the fission yeast cytokinetic ring, scaled to a cross-section of the C. elegans zygote division plane (Figure 1, A, A′, and D [ Wu and Pollard, 2005]; see Materials and Methods). The starting length and treadmilling dynamics of actin-like fibers were based on measurements from molecule counting studies, electron microscopy, as well as previously established parameter ranges (see Supplemental Table 1) (Wu and Pollard, 2005; Kamasaki et al., 2007; Mendes Pinto et al., 2012; Davies et al., 2014; Oelz et al., 2015). While employing these established parameters in our model, we also adapted published models to simulate the behavior of NMM-II minifilaments, modeling motor ensembles as rods with a single motoring actin-binding site (“hand”) at each end (Figure 1A). The behavior of each hand exhibits the collective binding dynamics for a prescribed number of motor heads according to alterations of motor parameters that include binding rate, unbinding rate, and duty ratio (see Supplemental Table 1) (Stam et al., 2015). Since NMM-II can exist as dimers or as minifilaments with as many as 56 motor subunits in vivo (Burridge and Bray, 1975; Niederman and Pollard, 1975; Sinard et al., 1989; Verkhovsky et al., 1995), we kept the number of motor ensembles constant and tested how the speed of in silico ring closure was affected by the number of motor subunits per ensemble (the “valence”). Rings with motor ensembles representing 28 motor subunits closed with the most biologically relevant speeds (Figure 1B), leading us to utilize this valence in our control simulations.

FIGURE 1:

An intermediate abundance of nonmotor cross-linkers allows maximal contractile ring closure speed in silico. (A) In silico contractile ring at time-point 0. (A′) Top: cross-linkers and motor ensembles are composed of a rigid backbone with identical functional units at both ends. In the case of motor ensemble, each unit represents multiple myosin heads. Bottom left: magnified view of cross-linkers and motor ensembles on a ring, while fibers are hidden. Bottom right: same view as left but with fibers shown. (B) Maximum ring closure speed obtained while varying the motor subunit behavior to represent various numbers of myosin heads per motor ensemble (2–112 heads per motor ensemble). Increasing motor ensemble valence increases contractile speed, but above 60 heads, this speed was biologically irrelevant. n = 4 for each condition. (C) Average ± SD closure speed of five control simulations. (D) Transverse and end-on optical sections of C. elegans zygotes expressing fluorescently tagged anillin (mNG∷ANI-1). Green arc and red box represent regions measured for cytokinetic ring fluorescence intensity and background normalization, respectively. (E) Schematic of ring size measurements for calculation of closure speed. (F) Ring closure over time plots for control cells (n = 32). (F′) Furrowing speed over time calculated from control cell data in F.

We then measured the kinetics of simulated ring closure and found that our control in silico rings first accelerated and then maintained a relatively constant speed for much of closure, with maximum ring closure rates occurring 150–250 s after closure initiation, before gradually decelerating (Figure 1C). To compare simulation results with in vivo data, we visualized the cytokinetic ring with a fluorescently tagged ring component expressed in C. elegans zygotes, acquired optical sections through the entire thickness of the embryo, rotated image data sets 90° to observe the entire division plane en face, and used custom Matlab-based software to annotate the position of the cytokinetic ring over time (Figure 1, D and E) (Dorn et al., 2010). As in silico, the ring closed in an average of 5 min, accelerating until approximately half closed, and then decelerating (Figure 1, F and F′) (Bourdages et al., 2014). Thus, simulated control rings and rings visualized in vivo exhibited similar closure dynamics, suggesting that our in silico approach using bipolar motor ensembles faithfully recapitulates some aspects of in vivo ring dynamics.

An intermediate amount of nonmotor cross-linkers allows maximal ring closure speed in silico and in vivo

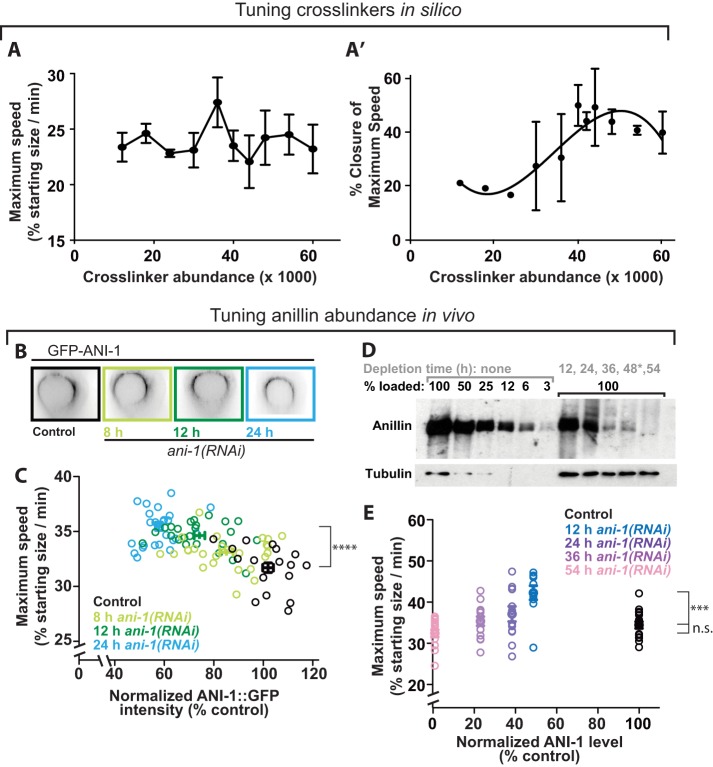
As introduced above, work in several contexts has demonstrated that intermediate levels of cytoskeletal cross-linking maximizes constriction speed. This published work was done with a reconstituted network containing actin and myosin VI, simulated networks of F-actin and dimeric motors, and the fission yeast and C. elegans cytokinetic rings in vivo (Ennomani et al., 2016; Li et al., 2016; Ding et al., 2017). Here we used in silico modeling to test the dependence of ring constriction on nonmotor fiber cross-linkers. We performed simulations by varying the number of cross-linkers around a value based on the collective abundance of two major F-actin cross-linkers (α-actinin and anillin [Mid1]), measured in the fission yeast cytokinetic ring (Wu and Pollard, 2005), scaled up to our 30-micron-diameter ring. Given the 10-fold increase in ring perimeter and assuming similar protein densities, we scaled up the numbers of actin fibers, motor ensembles, and cross-linkers 10-fold. At the starting value (12,000 cross-linkers) set from estimates in fission yeast, rings often fragmented (data not shown). Since ring fragmentation is not observed in control cells in vivo, we reasoned that our starting value of cross-linkers underestimated connectivity, potentially because cytoskeleton–membrane coupling is not accounted for in our minimal model. Therefore, we increased cross-linker abundance from our starting value. Varying the amount of cross-linkers did not reveal a strong effect on the maximum speed attained during closure but suggested that intermediate levels are ideal for maximal speed (Figure 2A). Furthermore, the time at which this maximum was attained was closest to that observed in vivo (∼50%) with intermediate levels of cross-linkers (Figure 2A′). Together these results indicate that intermediate cross-linker levels promote proper constriction dynamics.

FIGURE 2:

Nonmotor cross-linkers both drive and brake cytokinetic ring closure in silico and in vivo. (A) Maximum ring closure speed for simulations varying according to total nonmotor cross-linkers (12,000–60,000). (A′) Closure percentage at which maximum speed occurred on average for each condition plotted in A. Averages ± SEM for n = 4 simulations per condition are plotted for A and A′. (B) mNG::ANI-1 in the cytokinetic ring in representative control cell and those generated by worms depleted of anillin for various amounts of time (hours). (C) Maximum furrowing speed (at 50% closure) plotted against mNG::ANI-1 measured in the cytokinetic ring as in Figure 1E for control cells and those depleted of anillin for between 8 and 24 h via dsRNA feeding. (D) Western blots demonstrate the depletion of anillin over a time course of injection RNAi. Tubulin = loading control. Gray: hours of depletion; black: percentage sample loaded. *: No cell data collected for 48-h depletion. (E) Maximum furrowing speed (at 50% closure) plotted against levels of residual endogenous anillin measured by Western blotting, for control cells and those depleted of anillin for between 12 and 54 h via dsRNA injection. For C and E, bars denote average ± SEM; ****p < 0.0001, ***p = 0.0001, and n.s. denotes p = 0.1 (two-tailed t test).

We next tested the prediction that an intermediate level of nonmotor cross-linkers in vivo also allows maximum speed. The multidomain scaffold protein anillin is implicated in providing mechanical connectivity to the ring. While Drosophila and mammalian cells fail cytokinesis following anillin depletion, C. elegans zygotes’ cytokinesis is robust to thorough depletion of anillin (encoded by the gene ani-1) (Maddox et al., 2005), allowing us to study the effects of depletion on cytokinetic dynamics. To test how the speed of cytokinetic ring constriction scales with the amount of cross-linking in animal cells, we performed a time course of anillin depletion via RNAi to vary anillin levels (Figures 1D and 2, B and C). Depletions were performed in embryos expressing anillin tagged at its endogenous locus with mNeonGreen (mNG∷ANI-1) (Rehain-Bell et al., 2017), and the abundance of residual anillin in the ring, following depletion, was estimated from the fluorescence intensity in the 180° arc closest to the coverslip (Figure 1D). With increasing depletion time, zygotes contained progressively less anillin (Figure 2, B and C). We calculated the maximum furrowing speed (32 ± 0.6% of the starting radius per minute for control cells; Figure 2C), as a metric for cytokinetic ring performance. As the level of anillin was reduced, furrowing reached a significantly higher maximum speed (p < 0.0001; Figure 2C). These results suggest that, while anillin is a highly conserved scaffold protein enriched in the cytokinetic ring and thus presumed to augment ring function, wild-type levels of anillin attenuate ring closure speed.

In cells depleted of anillin beyond ∼50%, furrowing speed could no longer be reliably tracked by visualizing residual mNG∷ANI-1. To test how more thorough anillin depletion changed furrowing speed, we tracked furrowing kinetics in cells expressing functional fluorescently tagged NMM-II heavy chain (NMY-2∷GFP) from an integrated exogenous locus (Nance et al., 2003). We measured residual endogenous anillin levels by immunoblotting extracts made from whole worms depleted of anillin for various lengths of time, which led to a gradual reduction of anillin to 2% control levels (Figure 2D). Similarly to our observation above, partial depletion of anillin to 50% of control levels led to a significant increase in furrowing speed (p = 0.0002; Figure 2E). In contrast, further reduction of anillin levels gradually restored furrowing speed to values statistically indistinguishable from that of control cells (p = 0.10 for comparison of 54 h depletion to control; Figure 2E). Since the faster speeds at intermediate anillin levels could not be explained by an overabundance of NMM-II in the cytokinetic ring (Supplemental Figure S1), our results suggest that for anillin in vivo, as in vitro and in silico for α-actinin (Ennomani et al., 2016) and in vivo for plastin and α-actinin (Li et al., 2016; Ding et al., 2017), an intermediate amount of scaffolding produces maximal contractility. These results support the hypothesis that connectivity not only drives cytokinetic ring closure but also attenuates furrowing speed. Furthermore, our in silico and in vivo results demonstrate that while alteration of cross-linker/scaffold abundance can tune ring closure speed, these systems are robust and can attain a control-level speed even after a dramatic (50-fold) reduction of a major scaffold protein. This is in contrast to the behavior of other simulated contractile networks, which fail to constrict with low cross-linker level and arrest with high cross-linker level (Ennomani et al., 2016; Ding et al., 2017). This difference suggested that our simulated actomyosin network contained another robust cross-linker, namely the bipolar motors that represent NMM-II.

NMM-II both drives cytokinetic ring closure and limits its maximum speed

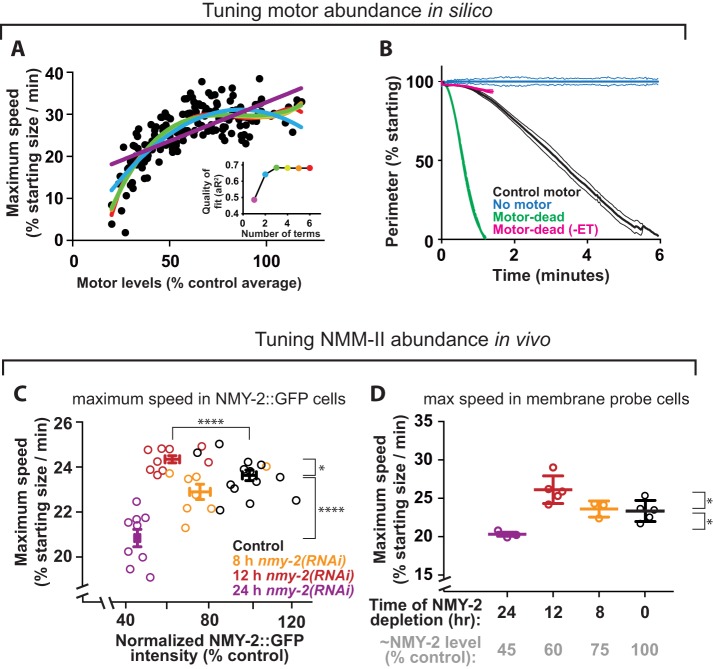
The cross-linking activity of NMM-II has been implicated in driving cytokinetic ring closure (Ma et al., 2012), but the effects of tuning motor cross-linker levels on ingression dynamics has not been explored. To test whether motor cross-linkers can both promote and attenuate ingression speed, as described here for nonmotor cross-linkers, we first used our model to test how tuning the abundance of bipolar motor ensembles affected ring closure speed in silico. To do this, we performed simulations with randomly varied motor abundance between 20 and 120% of the control value (Figure 3A). Reduction of motor levels below 50% of the control value slowed ring closure, in agreement with the idea that motors drive ring closure. Furthermore, rings lacking bipolar motor arrays altogether failed to constrict (Figure 3B). However, over much of the range of motor level (between 50 and 120% control levels), ring closure speed did not appreciably vary (Figure 3A). The observation that adding more motors in silico beyond a certain level does not increase ring closure speed suggests that bipolar motor arrays not only drive, but also attenuate, furrowing.

FIGURE 3:

Furrowing kinetics respond nonlinearly to NMM-II abundance. (A) Maximum ring closure speed in simulations in which bipolar motor abundance was varied randomly between 20 and 120% control levels (n = 167). Colored lines: polynomials of increasing complexity (see inset for color key to number of terms). Inset: adjusted R-squared values are plotted for each color-coded polynomial. (B) Simulated closure kinetics for rings containing control motor ensembles, motor-dead bipolar “motors” capable (“Motor dead”) or incapable of tracking fiber ends (“Motor dead (-EB)”), or lacking bipolar motor ensembles (“No motor”). Bars = SD; n = 5 per condition. (C) Maximum furrowing speed (at 50% closure) plotted against ring NMY-2::GFP for control cells and those depleted of NMY-2 for 8, 12, and 24 h. Two-tailed t tests compare control and 12 h speed: p = 0.020 (*); control and 12 h myosin intensity: p < 0.0001 (****); control vs. 24 h speed: p < 0.0001 (****). (D) Maximum furrowing speed (at 50% closure) in cells expressing a GFP-tagged membrane probe is compared for control cells and those depleted of NMY-2 for 8, 12, or 24 h. Gray column labels indicate approximate remaining NMY-2 levels, according to measurements as in C. Two-tailed t tests to compare control and 12 h: p = 0.025; control vs. 24 h: p = 0.011.

To test how the level of NMM-II affects furrowing speed in vivo, we tuned the abundance of NMM-II in cells by depleting the NMM-II heavy chain (NMY-2) in worms expressing NMY-2::GFP and then measured residual NMY-2 to track ring closure. Reduction of NMY-2 below 50% of control levels significantly slowed ring closure (p < 0.0001), in agreement with the idea that motors drive ring closure in vivo (Figure 3C). However, partial depletion of NMY-2, to ∼60% of control levels, led to a significant increase in maximum ring closure speed (p = 0.02), suggesting that NMY-2 can also attenuate closure speed in vivo (Figure 3C). The same nonmonotonic dependence between myosin level and maximum furrowing speed was also obtained with a different C. elegans strain expressing a GFP-tagged membrane probe (Figure 3D). These in vivo results suggest that myosin not only drives ring closure but also resists cytoskeletal remodeling during furrowing.

Does NMM-II act as a motor, a cross-linker, or both? Our in silico and in vivo data (described above) are consistent with NMM-II having both motoring and cross-linking functions. Some insight into this dichotomy may emerge from our minimal model. If NMM-II were to act only as a motor, then one might expect that the speed of contractile events would scale linearly with NMM-II abundance. If NMM-II were to act only as a cross-linker, then one would expect contractility speed to peak at intermediate NMM-II levels (Ennomani et al., 2016; Li et al., 2016). We reasoned that a combination of the two effects (motor–linear, and cross-linker–quadratic) would result in a complex relationship between NMM-II and contractility. We sought mathematical evidence that NMM-II levels affect speed in a linear, quadratic, or more complex manner (evidence that it acts as a motor, a cross-linker, or both), by fitting our data comparing NMM-II abundance and ring closure speed to polynomial curves of increasing order and monitoring the quality of the fit. Our in silico data were better fitted by higher-order polynomials than by simpler curves, indicating that motor abundance has a complex (nonlinear) relationship with ring closure speed (Figure 3A and inset). The same tests performed on in vivo data indicated that the dependence of ring closure speed on NMM-II abundance was also best fitted by higher-order polynomial curves (Supplemental Figure S3, A, B, and inset). These findings further support the idea that NMM-II functions both as a motor and a cross-linker.

Interestingly, motor-impaired NMM-II is sufficient for cytokinesis in mammalian cells (Ma et al., 2012). To determine whether we could recapitulate this result in silico, we simulated rings in which motor ensembles had a motoring speed of zero. Rings with nontranslocating “motor-dead” motor ensembles constricted faster than simulated rings with control motors (Figure 3B). Importantly, end-tracking of depolymerizing fibers was required for nontranslocating motor ensembles to drive rapid ring closure in silico (Figure 3B), and this feature is enabled in our simulations. These results agree with the concept that cross-linking, in concert with treadmilling actin, can drive ring closure (Mendes Pinto et al., 2012; Oelz et al., 2015) and, furthermore, that motoring can oppose ring closure as a brake. In sum, this in silico work supports the idea that the correct balance of motor and cross-linker activities and abundance is required for optimal ring dynamics.

NMM-II both drives and attenuates cytokinetic furrowing initiation and F-actin organization

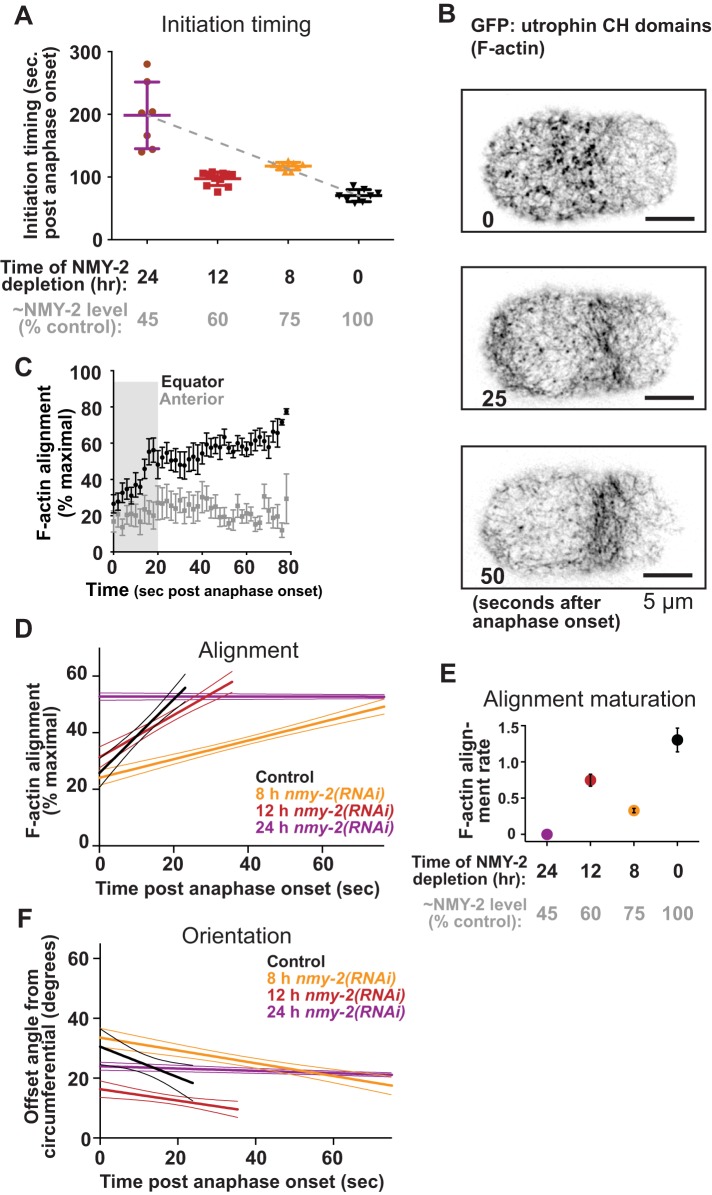
When the cytokinetic ring is at maximum speed, it is a tightly focused, diffraction-limited cytoskeletal cord (Green et al., 2012). In this configuration, cross-linkers could attenuate ring closure by blocking cytoskeletal sliding and remodeling. In contrast, when the cytokinetic ring first forms, cytoskeletal components are sparse, occupying a broad band of cortex (Henson et al., 2017), and cross-linkers could act differently on this network configuration than on the more tightly bundled cytoskeletal cord corresponding to ring morphology at maximum closure speed. Thus, we next examined how NMM-II level relates to the timing of furrow initiation by again depleting NMM-II over a time course and scoring the onset of furrowing, the time when the cortex first began to ingress away from the coverslip, relative to anaphase onset. Over most of the range of depletion time, initiation occurred later in cells more thoroughly depleted of NMM-II (Figure 4A). However, when myosin was partially depleted to the level that elicited higher maximum speeds (Figure 3, C and D; 12 h), ingression initiated earlier than predicted (∼100 s after anaphase onset vs. ∼150 s as predicted by the trend among 0-, 8-, and 24-h depletions [gray line]; Figure 4A). These results suggest that while NMM-II drives furrow initiation, it also attenuates this early cell shape change to some degree.

FIGURE 4:

The kinetics of furrow initiation and circumferential F-actin bundling respond nonlinearly to NMM-II abundance. (A) Furrow initiation timing in cells expressing a GFP-tagged F-actin probe, relative to time of depletion for control cells and those depleted of NMY-2 for 8, 12, and 24 h. Gray column labels indicate approximate remaining NMY-2 levels, according to measurements as in Figure 3C. Bars denote average SEM. (B) Cortical F-actin visualized via GFP-utrophin at three time points with respect to polar cap disappearance. (C) F-actin order in the cell equator and anterior region (negative control); average ± SD are plotted; n = 9. (D) Initial linear increase in F-actin order in the cell equator plotted for control cells and those depleted of NMY-2 for 8, 12, and 24 h. For C and D, thick lines = averages; thin lines = SD. (E) Average ± SD slope of initial linear increase in equatorial F-actin order for control cells and those depleted of NMY-2 for 8, 12, and 24 h. Gray column labels as in A. For C, D, and E, average ± SD are plotted; n > 7 cells per condition. (F) Offset angle during the initial linear increase in F-actin order in the cell equator, plotted for control cells and those depleted of NMY-2 for 8, 12, and 24 h.

Furrow initiation has been attributed to the remodeling of an initially isotropic cytoskeletal meshwork into circumferential bundles (Reymann et al., 2016). The effects of NMM-II levels on furrowing kinetics could relate to NMM-II’s roles in this cytoskeletal organization. NMM-II could drive F-actin bundling and circumferential alignment, and it could limit alignment by stabilizing isotropic cytoskeletal intersections (Henson et al., 2017). To test how these opposing activities affect early cytoskeletal remodeling during furrow initiation, we imaged cells expressing a GFP-tagged probe for F-actin (Jordan et al., 2016), depleted NMY-2 over a time course, and measured the orientation of F-actin features through time. As previously shown (Reymann et al., 2016), in controls, F-actin was initially poorly organized in the cell equator, and local order increased linearly in a process we will call F-actin alignment “maturation” (Figure 4, B and C). This increase in alignment coincided with a circumferential convergence (decrease in offset angle; Figure 4F). We plotted the initial linear rate of maturation for control cells and those depleted of NMY-2 to various extents. The rate of alignment maturation was reduced by the mildest depletion and more strongly reduced by the most severe depletion (Figure 4, D and E). However, at the intermediate NMM-II level at which higher maximum furrowing speed and precocious initiation took place (12-h depletion), the rate of F-actin alignment maturation was higher than what would be predicted based on the maturation rates of control cells and those depleted for 8 or 24 h (Figure 4, D and E). From these results, we conclude that NMM-II not only drives but also attenuates cytoskeletal alignment. This implicates NMM-II not only in cross-linking but specifically in promoting F-actin alignment, potentially by mediating F-actin bundling. In sum, our findings support the idea that cross-linkers not only contribute positively to, but also limit, the cytoskeletal remodeling that underlies cytokinetic ring closure.

DISCUSSION

Speed is of the essence for cytokinesis in early embryos, since cell cycles are short, and a persistent cytoplasmic connection between daughter cells could lead to aneuploidy or defects in cell fate determination. Like other aspects of cell division in the C. elegans zygote, furrowing is exceptionally rapid and appears to have been fully optimized for rapid early development by evolutionary adaptation. Therefore, it is somewhat unexpected that any experimental perturbation can increase furrowing speed. How can a depleted cytokinetic ring function “better” than a control ring? Cross-linkers, including NMM-II, may block cytoskeletal remodeling and therefore furrowing in one or more ways; possibilities include stiffening the cortex by stabilizing interactions, suppressing actin depolymerization, and increasing steric hindrance. One might predict that cross-linkers in excess of the levels that allow maximal furrowing speed are incorporated into the ring to facilitate early remodeling. However, the same intermediate NMM-II depletion that allowed faster maximum speed also resulted in faster-than-expected cytoskeletal organization and furrow initiation (Figures 3, C and D, and 4A). This lack of kinetic advantage in any of the stages we assayed demonstrates that mechanical brakes are part of the cytokinetic ring despite compromising speed and suggests that they offer a distinct advantage, perhaps to make furrowing responsive to inhibitory signals for error correction.

The nature of the cytoskeletal remodeling that drives animal cytokinetic ring closure is still debated. One hypothesis is that filaments slide past one another as in muscle contraction (Schroeder, 1972). Alternatively, the new ends of depolymerizing F-actin may be ratcheted together via dynamic nonmotor cross-linking (Mendes Pinto et al., 2012). Our findings that cross-linkers both drive and attenuate furrowing do not refute this latter model but suggest that the abundance of cross-linker must be delicately balanced to optimally achieve remodeling. Our findings that ring closure speed in silico plateaus over a threshold of motor abundance supports the idea that this complex balance exists. However, contractility in silico may plateau due to a limited availability of shrinking fiber ends to motors and/or ratcheting nonmotor cross-linkers.

Of similar importance is the question of how myosin motors drive constriction. Recent work has demonstrated that dynamic end-tracking cross-linking can drive constriction in the absence of motor activity (Mendes Pinto et al., 2012; Oelz et al., 2015), but a role for motor activity has not been fully discounted (Zumdieck et al., 2007; Oelz et al., 2015; Bidone et al., 2017). Our in silico findings that motor-dead myosin-like ensembles can drive ring closure as long as they can track depolymerizing actin fiber ends (Figure 3B) support the idea that dynamic cross-linking of treadmilling actin drives contraction. However, we also found that motoring activity slows closure of in silico rings, compared with motor-dead myosins, supporting the idea that motoring attenuates actomyosin contractile dynamics (Figure 3B). In sum, our work suggests three contributions from motor ensembles: driving contractility via motoring, driving contractility via cross-linking, and potentially limiting contractility. However, our in silico findings must be considered cautiously since motor-dead NMM-II in vivo could have different biophysical properties than in silico; it may not only lack the power stroke but also bind and unbind F-actin with different kinetics. In addition, our modeling of NMM-II minifilaments may not accurately simulate some aspects of motor ensembles; our calculated multimerization of binding and unbinding dynamics of NMM-II minifilaments could change the effect or magnitude of motoring activity on contractility. Finally, our simplification of motor dynamics may also explain the dependence of our model on a higher abundance of cross-linkers than previous models. As such, a more accurate depiction of minifilament binding, motoring, and end-tracking dynamics may be warranted for future models.

We found that intermediate amounts of anillin and NMM-II allow maximal contraction speed (Figures 2, C and E, and 3, C and D). Similarly, maximal speed is achieved from intermediate amounts of α-actinin in Schizosaccharomyces pombe (Li et al., 2016) and in vitro (Ennomani et al., 2016). Agent-based models of contractile networks containing generic motor dimers (Ding et al., 2017), myosin VI–like dimers (Ennomani et al., 2016), and bipolar motor ensembles that represent NMM-II minifilaments (Figure 1A) also demonstrate that intermediate amounts of cross-linking allows maximal contractility. Continuum theory suggests that this behavior results from an effect on cytoskeletal mesh size and structure (Lenz et al., 2012). Together, these diverse observations suggest that the balance of positive and negative effects of motor and nonmotor cytoskeletal cross-linkers, revealed here for animal cell cytokinesis, is a general principle of actomyosin contractility.

MATERIALS AND METHODS

Strains, growth conditions, and sample preparation

The following strains were used: JJ1473 (zuIs45 [nmy-2::NMY-2::GFP + unc-119(+)] V), OD95 (unc-119(ed3) III; ltIs38 [pAA1; pie-1/GFP::PH(PLC1delta1); unc-119 (+)]; ltIs37 [pAA64;pie-1/mCherry::his-58;unc-119(+)]IV), MDX29(ani-1(mon7[mNeonGreen^3xFlag::ani -1]) III) (Rehain-Bell et al., 2017), MDX40 (ani-1(mon7[mNeonGreen^3xFlag::ani-1], unc-119(ed3) III; nmy-2(cp52[nmy-2::mkate2 + LoxP unc-119(+) LoxP]) I), and JCC719 (mgSi3[tb-unc-119(+) pie-1>gfp:utrophin] II.; unc-119 (+)] III; ltIs37 [pAA64; pie-1/mCherry::his-58; unc-119 (+)] IV) (Jordan et al., 2016). Worms were maintained at 20°C according to standard procedures (Munro et al., 2004). Embryos were dissected from gravid hermaphrodites and mounted on coverslips on 2% agarose pads.

RNA-mediated protein depletions

Depletion of ANI-1, NMY-2, LET-502, and MEL-11 was performed by feeding worms bacteria from the Ahringer collection expressing double-stranded RNAs (dsRNAs) directed against the targets, according to standard procedures (Min et al., 2010). The identity and sequence of all dsRNAs were confirmed by sequencing. Throughout this study, we exclusively examined perturbations that allow cyto­kinesis to succeed, while exhibiting quantitative defects.

C. elegans embryo live cell imaging conditions

Imaging for Figures 2, C–E, 3, C and D, 4A, and 5A and Supplemental Figure S2 was performed on a DeltaVision Elite widefield microscopy system using the software softWoRx (Applied Precision GE-Healthcare), equipped with a CoolSnap HQ2 camera (Photometrics) at 2 × 2 binning and a 60×/1.42 plan Apo objective (Olympus). All image analysis was performed on nondeconvolved data.

Imaging for Figure 2G and Supplemental Figure S1 (NMY-2∷GFP embryos depleted of ANI-1^anillin) was performed with a Nikon TE-2000 inverted microscope equipped with a swept field real-time confocal module (Prairie Instruments) and Coolsnap HQ2 CCD camera (Photometrics). The use of the 70-µm slit, 60× magnification, and a 200-ms exposure time were kept constant.

Imaging of actin alignment during furrow initiation was performed on a Nikon TE300 inverted microscope with a Plan APO 60× 1.4 NA oil objective, a Yokogawa Nipkow spinning disk, Hamamatsu ORCA-ER camera, Prior stage microcontroller, and Melles Griot ion laser power supply. Embryos were dissected as previously described, and imaged prior to the first mitotic division with 2-s intervals between each image acquisition. Images were acquired in a single cortical plane through the maturation of the furrow, which was determined based on the ingression of the contractile ring past the cortical imaging plane. Image sequences were time aligned based on disappearance of the polar concentration of actin and the onset of cortical swirling prior to furrow initiation. To measure actin alignment and offset angle, we used Local Gradient Orientation detection as part of the Directionality plugin for FIJI (ImageJ; https://imagej.net/Directionality), which detects the directionality of objects in an image field. Measurements of local gradient orientation uses a local 5 × 5 Sobel Filter to enhance edges and detect local gradient orientations. The total image histogram of total detected orientations is built from these local orientations, yielding a magnitude of detected orientations for the image. Images with only randomly oriented objects will yield roughly evenly distributed histograms, whereas images with at least partial orientation will reveal histogram peaks at detected orientations.

Measurements of ring closure

Anaphase onset was determined by observing a separation between chromatin masses visible against the background of myosin fluorescence in the spindle. Ring closure was determined using semiautomated custom software cyanRing (for CYtokinesis ANalysis of the RING) as described previously (Dorn et al., 2010; Bourdages et al., 2014). In cyanRing, the equatorial region of the embryo is cropped from the three-dimensional image stack, rotated, and maximum-intensity projected to produce a view of the cytokinetic ring along the spindle axis as viewed from the posterior direction. The user then defines the cell outline as well as the outline of the cytokinetic ring by selecting at least three points, through which best-fit circles are drawn. Radii are calculated from best-fit circles and used to calculate ring closure as a percentage of starting size.

Measurements of cytokinetic ring myosin levels

The intensity of myosin at maximum speed was extracted from cyanRing annotations of ring position. The integrated intensity was calculated for a nine-pixel radius torus encompassing the cytokinetic ring and normalized against a region of background outside the cell. Experimental intensity values were normalized to the average of control cell data acquired on the same day.

Quantitative immunoblotting

L4-stage hermaphrodites were injected with dsRNA directed against ani-1 (Maddox et al., 2005) and incubated at 20°C for 12–54 h. Extracts were prepared from control worms and those depleted of ANI-1^anillin using standard protocols. Extract loaded onto the 100% loading lanes contains ∼10 worms. Immunoblotting was performed using an anti–ANI-1 polyclonal antibody (Maddox et al., 2005) and anti–α-tubulin clone DM1α (Sigma). Protein bands from film were quantified using ImageJ software. Loading was normalized using tubulin as a control. Data presented are the relative anillin amounts as a ratio of anillin in depleted worms relative to that of control worms. The extent of depletion estimated via blotting for endogenous anillin in whole worms likely underestimates levels in embryos, since the target protein is more thoroughly depleted from the germline and embryos than other tissues.

Simulations

The Brownian dynamics of cytoskeletal fibers (Nedelec and Foethke, 2007) was modeled using the open source software Cytosim (www.cytosim.org). The general setup is described in detail in the included simulation file and supplemental table (Supplemental File 1; Supplemental Table 1). Motor head unbinding dynamics are calculated by the Kramer method: k_off = k₀ · exp(F_t/F₀), where k₀ is the unloaded unbinding rate, F₀ is the unbinding force, and F_t is the norm of the force felt by the bound motor at time t. Motoring speed was calculated at each simulation frame by the formula V_t = V₀ · (1 – F_t/F₀), where V₀ is the unloaded motor speed, F₀ is the stall force, and F_t is the component of the force that is tangential to the fiber at time t. Myosin complexes contained two identical actin-binding motoring domains, one attached at either end of a short rod. Each actin-binding motor domain was modeled to simulate the dynamics of multiple myosin motoring heads (between 2 and 28) for total myosin valence of 4–56 motors. Actin-like fibers are modeled as strings of equidistant points, subject to bending elasticity with parameters corresponding to the persistence length of F-actin (∼15 µm; bending rigidity ∼0.06 pN µm²). In brief, the movement of fibers is determined by an overdampened Langevin equation, which has the general form ξdx / dt = f(x, t) + B(t), where the drag coefficient ξ is determined by the Stokes’ radius of the fiber and the system viscosity. On the right-hand side of the equation, B(t) is a random fluctuating noise vector that is calibrated as a function of thermal energy (K_BT). The other term, f(x, t), includes the bending elasticity of the fiber and the forces exerted by all connectors, which are considered as Hookean springs. Finally, x is a vector containing the coordinates of all the fiber points, and the equation is linearized and solved using an implicit integration scheme for improved performance (Nedelec and Foethke, 2007). Actin dynamics were based on previous models (Mendes Pinto et al., 2012; Oelz et al., 2015) and include depolymerization primarily at pointed ends and poly­merization primarily at barbed ends, with a net treadmilling rate of 0.04 µm/s. Early in constriction fibers grow to ∼1.4 microns; however, during the latter half of constriction, fibers shrink due to a force-­dependent reduction in polymerization rate. Cross-linkers were modeled after those of previous work (Ennomani et al., 2016) to represent a cross-linker like α-actinin, bearing a single fiber-binding domain at each end of a small rod. Initially, actin-like fibers were assembled in a tangential orientation to the circular cell space in a radius of ∼14.5 µm with a ring width of 300 nm. After equilibrating in the simulation, cross-linkers and motors were added to the simulation space, and simulations were allowed to run for 400 s of simulated time. Control contractile ring simulation parameters are listed in Supplemental Table 1 and in the attached configuration file. Plots of in silico ring closure kinetics were smoothened with a five time-point rolling average to reduce noise. The code and the configuration files used to run the simulations of this study are made available to ensure full reproducibility.

Stepwise regression analysis

Stepwise regression analysis for our in vivo and in silico myosin depletion speed curves was performed using GraphPad Prism software (GraphPad Software, La Jolla, CA). Data were normalized to control myosin levels (x-axis) and control maximum speed (y-axis). Polynomial regressions were fitted to the normalized experimental data and simulation data, and F-test analysis was performed to generate absolute sum of squares and adjusted R² (aR²) values for each polynomial fit. Optimal fitting was determined based on increase of the aR² to a peak value followed by plateauing or decrease as additional terms are added to the polynomial fit equation.

Abbreviations used:

dsRNA

double-stranded RNA

F-actin

filamentous actin

NMM-II

nonmuscle myosin II

RNAi

RNA-mediated interference (protein depletion).