The effect of sitting posture on the loads at cervico-thoracic and lumbosacral joints

Abstract

BACKGROUND:

The sitting in an awkward posture for a prolonged time may lead to spinal or musculoskeletal disease. It is important to investigate the joint loads at spine while sitting.

OBJECTIVE:

The purpose of this study was to investigate the joint moment and antero-posterior (AP) reaction force at cervico-thoracic and lumbosacral joint for various sitting postures.

METHODS:

Twenty healthy males participated in this study. Six sitting postures were defined from three spinal curvatures (slump, flat, and lordosis) and two arm postures (arms-on-chest and arms-forward). Kinematic and kinetic data were measured in six sitting postures from which joint moment and AP reaction force were calculated by inverse dynamics.

RESULTS:

In the cervico-thoracic joint, joint moment and AP reaction force were greater in slump than the flat and lordosis postures ($p<$ 0.001) and also in arms-forward posture compared to arms-on-chest posture. In the lumbosacral joint, joint moment and AP reaction force were greater in slump than flat and lordotic posture ($p<$ 0.001) but there was no difference between different arm postures. The joint loads (moment and AP reaction force) at the cervico-thoriacic joint were closely related to the head flexion angle ($r>$ 0.86) while those at the lumbosacral joint were correlated to the trunk flexion angle ($r>$ 0.77). In slump posture, the joint moments were close to or over the extreme of the daily life such as sit-to-stand and walking. Consequently, if the slump is continued for a long time, it may cause pain and diseases at the cervico-thoracic and lumbosacral joints.

CONCLUSIONS:

The results of the study indicated that the lordosis or flat would be better spinal postures. Also, keeping arms close to body would be desirable to reduce joint loads.

1. Introduction

It has been reported that people sit more than 8 hours per day [1]. Consequently, more attention has been given to the diseases associated with the extended sitting posture. The pressures within the intervertebral disc at the sitting posture were reported to be approximately twice of the standing posture [2, 3]. Therefore, sitting in an awkward posture for a prolonged time may lead to spinal or musculoskeletal disease [4, 5, 6, 7]. Particularly, 25–51% of office workers, who sit for extended periods, suffer from low back pain (LBP), which is one of the most common musculoskeletal disorders [8, 9]. There have been a lot of studies on postural stability, but most of them were limited to standing or squatting postures [10, 11].

Various studies have evaluated the spinal curvature in the sitting posture. Some studies investigated the lumbar angle in the sagittal plane in various sitting postures by using radiography [12, 13] or skin surface tracking [14]. Radiographic examination in the sagittal plane was used to quantify vertebral curvature and vertebral rotation [12]. However, all these methods do not provide the loading information on vertebrae and vertebral discs, which is a critical limitation.

In-vivo studies were conducted to measure the intradiscal pressure in various sitting posture [2, 3, 15]. However, these invasive methods are hardly performed outside the hospital and may accompany serious side effects such as disk degeneration [16].

Castanharo et al. estimated the lumbar joint moment from the activation of the trunk and abdominal muscles at the lumbar flat and lumbar lordotic postures [17]. However, it was shown to be difficult to predict the joint moment based on muscle activities [18], because muscle activities for the same joint moments show very different patterns among subjects [19]. Additionally, anteroposterior (AP) reaction force, which is closely related to the low back pain, was not examined [20, 21]. Furthermore, even though sitting posture affects other joints such as the cervico-thoracic joint [22], the investigation was limited to the lumbosacral joint [17].

The joint loads can be estimated from the inverse dynamics which is commonly used in the sit-to-stand studies instead of an EMG-driven model with low reliability. The method estimates the joint loads (moment and AP reaction force) by feeding kinematics and the external forces at feet and hip into the skeletal model [23, 24, 25, 26]. The loads can be estimated at various joints such as the cervico-thoracic (CT) and lumbosacral (LS) joints.

Therefore, this study aimed to evaluate the moment and AP reaction force of two joints (i.e., CT and LS joints), which are closely related to the spinal diseases coming from improper sitting posture. To achieve the objective, this study measured all external forces and kinematics at various sitting postures and performed an inverse dynamics analysis by using the 3D skeletal model.

2. Methods

2.1. Subjects

Twenty healthy males participated in this study (age: 24.7 $\pm$ 1.6 yrs, height: 177 $\pm$ 0.1 cm, body mass: 79.0 $\pm$ 9.7 kg). Subjects had no history of musculoskeletal disease and back/neck pain. All subjects provided informed consent and approval was obtained from the institutional human research ethics committee of Konkuk University.

2.2. Task and protocol

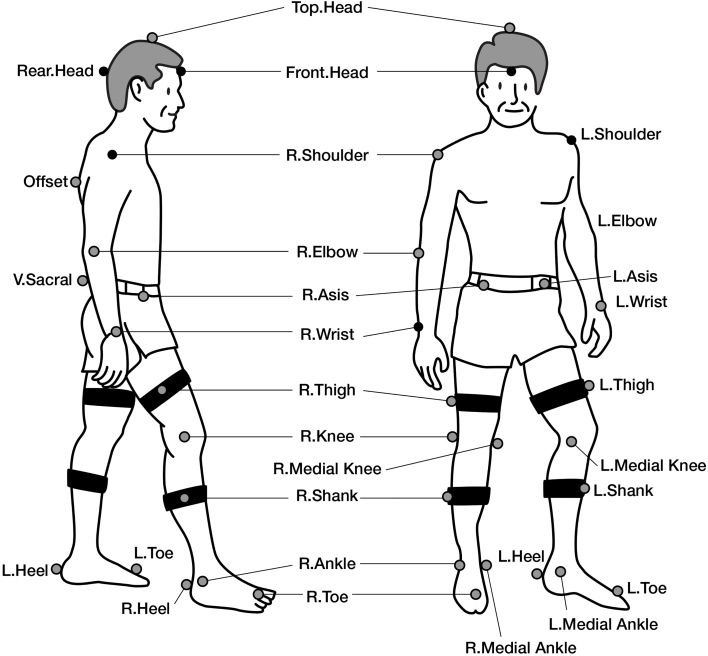
The subjects wore a skinny T-shirt and shorts and remained bare foot throughout the experiment. Thirty three reflective markers (10 mm diameter) were placed according to Helen Hayes marker set (Fig. 1) and additional three markers were attached to the spinous processes of the T5, T10, and L3. Subjects sat on an adjustable chair mounted with a force plate (Accusway dual top, AMTI Inc., MA) to measure the chair reaction force on the buttock [27]. Two force plates (OR6-7, AMTI Inc., MA) were positioned at the floor to measure the ground reaction force on feet. The initial posture was set as the subject’s knees and ankles at approximately 90${}^{\circ }$ and the feet distance equal to each subject’s shoulder width. Office workers do various activities in the sitting posture such as typing, reading, and writing which results in various arm positions. Lifting an arm was shown to affect the joint reaction force [28]. Therefore, the experimental design considered different arm postures as well as spinal curvatures. Spinal curvatures investigated were

Figure 1.

The Helen Hayes marker set.

• •Slump: thoracolumbar and lumbar angle both kyphotic (flexion 10 $\sim$ 20${}^{\circ }$ and 5 $\sim$ 10${}^{\circ }$, respectively)
• •Flat: thoracolumbar and lumbar angle both flat ($-$5 $\sim$ 5${}^{\circ }$)
• •Lordosis: flat thoracolumbar and lordotic lumbar ($-$5$\sim$ 5${}^{\circ }$ and $-$25 $\sim$$-$20${}^{\circ }$, respectively)

Raquel et al. calculated the mean lumbar joint moment while the vertebral curvature changed from the lumbar kyphosis to the lumbar flat or the lumbar lordosis [17]. Therefore, the results of their study did not reflect practical lumbar joint moment at the static posture, which causes low back pain. The subjects of this study were instructed to maintain a sitting posture for one minute to mimic a static posture in daily sitting activities.

Thoracolumbar and lumbar angles were calculated from the lines between markers on the spinous process, i.e., lines of T5-T10 and T10-L3 for thoraco-lumbar angle and lines of T10-L3 and L3-S2 for lumbar angle [14].

For each spinal curvature, two arm postures were tested, i.e., arms-on-chest and arms-forward. The subjects were instructed to flex their arms on the chest (arms-on-chest) and to stretch their arms forward with 90${}^{\circ }$ elbow angle and 30${}^{\circ }$ shoulder flexion (arms-forward). In arms-forward posture, subjects were instructed to hold a sheet of paper with both hands and look at the center of paper as if using a smart phone.

2.3. Data collection and analysis

Three-dimensional coordinates of reflective markers were measured by a motion capture system with six infrared cameras (Eagle, Motion analysis Inc., CA, USA). Kinematic data and chair/ground reaction forces were collected at 120 samples per second and for 1 min per each sitting posture while subject was seated.

Joint moments and AP reaction force at CT and LS joint were calculated by using the Software for Interactive Musculoskeletal Modeling (SIMM, MusculoGraphics Inc., CA, USA), specifically, by feeding the measured reaction forces and marker data into the inverse solution model of ’Fullbody Dynamic Flexible’ built in SIMM. This model regarded the cervical spine as one rigid segment and the lumbar spine as another rigid segment, where C7-T1 junction was defined as CT joint and L5-S1 as LS joint. AP reaction force was normalized by body mass considering that reaction force has a proportional relationship with body mass [29, 30]. Joint moment was also normalized by body mass times height (Nm/(kg*m)) [23, 29, 31]. In the static sitting position, the joint moment and the joint reaction force are greatly influenced by gravity, and the moment is proportional to sin $\theta$ as in Eq. (1). Therefore, the flexion angle was calculated to investigate the effects of gravity on various sitting positions. r is the distance from the joint to the center of gravity, $m$ is the segmental mass, $g$ is the gravitational acceleration, and $\theta$ is the tilted angle of the segment.

$$\text{𝑀𝑜𝑚𝑒𝑛𝑡}=\text{𝑟𝑚𝑔}\sin \theta$$ (1)

The flexion angle of each joint was defined as the segmental angle of the upper segment of the vertical line. From the top head marker to the shoulder marker in the sagittal plane is defined as the head segment, and the trunk segment is defined by the right shoulder marker to the anterior superior iliac spine (ASIS) marker.

2.4. Statistics

The flexion angles and joint loads (joint moment and joint reaction force) analyzed by SIMM were presented as mean and standard deviation of twenty subjects. These variables were evaluated by two-way repeated measures ANOVA, with spinal curvature and arm posture as independent variables. As the post-hoc test of the effect of spinal curvature, one-way ANOVA with repeated measures was performed for pairwise comparisons of spinal curvatures, if any spinal curvature main effects were significant. The post-hoc comparisons (paired t-test) of spinal load between arm postures were performed for each spinal curvature if the interaction was significant. Spearman’s rank order correlation coefficients were calculated using SPSS ver.22 (IBM corp., New York, USA) to assess the relationship between flexion angles (head and trunk) and joint loads (joint moment, AP reaction force). The level of significance was determined as $p<$ 0.001.

3. Result

3.1. Cervico-thoracic joint

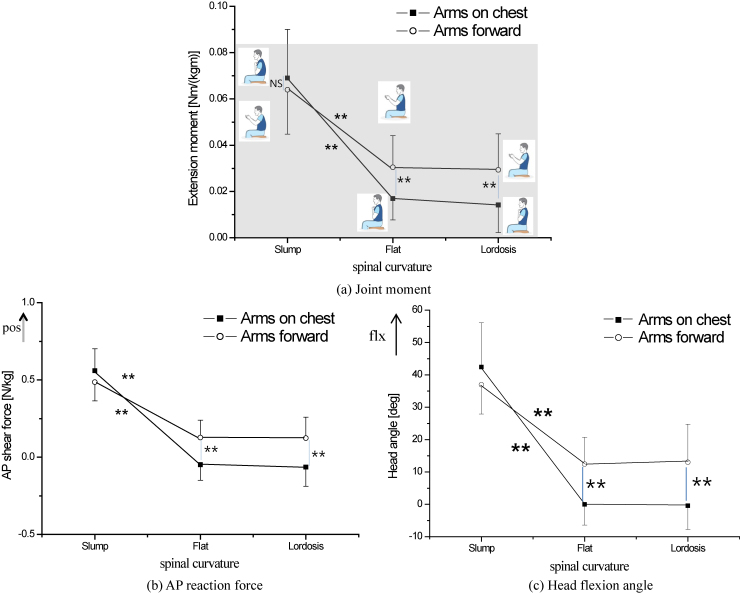
Figure 2a and Table 1 show the joint moment with respect to the three spinal curvatures and two arm postures in CT joint. The joint moment was greater during slump than flat and lordosis ($p<$ 0.001) with no difference between flat and lordosis ($p=$ 0.025).

Figure 2.

The joint loads at cervico-thoracic joint and head flexion angle on various sitting posture (${}^{**}p<$ 0.001, Range of joint moment during the sit-to-stand movement is marked by gray box).

Table 1.

The joint loads and flexion angle on various sitting posture (mean value)

	Moment [Nm/(kg*m)]		AP reaction force [N/kg]		Head flexion angle [deg]
	On chest	Forward	On chest	Forward	On chest	Forward
Cervico-thoracic joint
Slump	0.07	0.06	0.56	0.49	42.44	36.98
Flat	0.02	0.03	$-$0.05	0.13	$-$0.03	12.42
Lordosis	0.01	0.03	$-$0.06	0.12	$-$0.46	13.02
Lumbosacral joint
Slump	0.28	0.30	1.45	1.39	7.38	7.96
Flat	0.09	0.12	0.32	0.25	$-$8.72	$-$8.63
Lordosis	0.09	0.12	0.37	0.27	$-$8.07	$-$8.48

Similar to the joint moment, Fig. 2b shows that the AP reaction force was greatest in the slump ($p<$ 0.001) with no difference between flat and lordosis. Both the joint moment and the AP reaction force were greater for arms-forward than arms-on-chest ($p<$ 0.001) for flat and lordosis postures (Fig. 2a and b).

Head segment was significantly flexed in slump than flat and lordosis (Fig. 2c and Table 1, $p<$ 0.001), with no difference between flat and lordosis posture. In spinal curvature of flat and lordosis, the head segment was more flexed for arms-forward than arms-on-chest ($p<$ 0.001). In CT joint, joint moment and AP reaction force increased with the head flexion angle. The correlation between head flexion angle and joint loads (moment, AP reaction force) was significant (Head-moment: 0.860, Head-AP reaction force: 0.962, $p<$ 0.01).

3.2. Lumbosacral joint

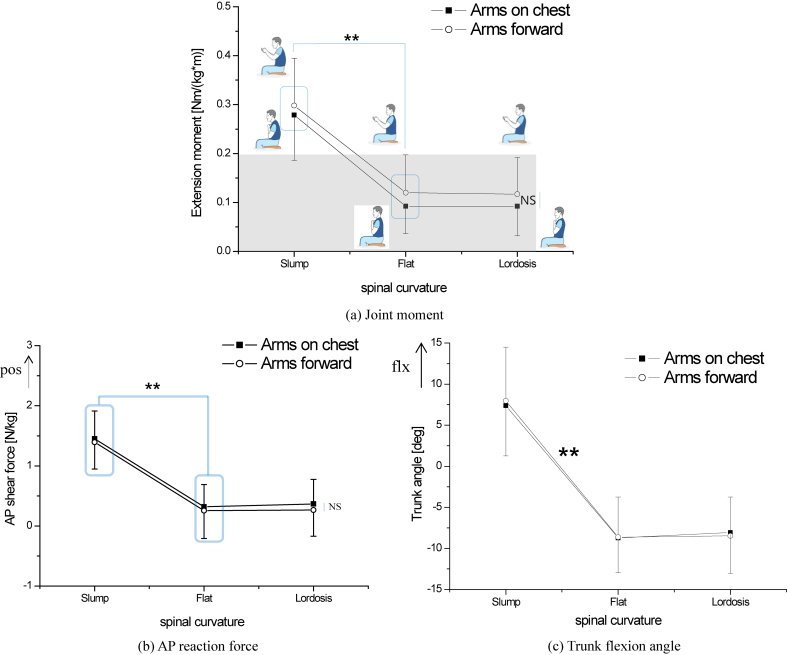
Figure 3a and Table 1 show the joint moment with respect to the three spinal curvatures and two arm postures in LS joint. The joint moment was greater during slump than flat and lordosis ($p<$ 0.001) with no difference between flat and lordosis ($p=$ 0.025).

Figure 3.

The joint loads at lumbosacral joint and trunk flexion angle on various sitting posture (${}^{**}p<$ 0.001, Range of joint moment during normal walking is marked by gray box).

The AP reaction force was greater in slump posture than in flat and lordosis posture (Fig. 3b, $p<$ 0.001), and it was similar between flat and lordosis. There was no effect on the LS joint loads (the joint moment and the AP reaction force) by arm posture (Fig. 3a and b, $p=$ 0.015).

Similar to head flexion angle, trunk flexion angle was significantly greater in slump than flat and lordosis (Fig. 3c and Table 1, $p<$ 0.001), whereas there was no difference in trunk flexion angle in different arm postures. The LS joint loads (moment or AP reaction force) and the trunk flexion angle were highly correlated (Trunk-moment: 0.776, Trunk-AP reaction force: 0.894, $p<$ 0.01).

4. Discussion

This study investigated the loads at the CT and the LS joint in various conditions of the spinal curvature and the arm postures. This study conducted inverse dynamic analysis using the 3D musculoskeletal model in order to calculate the moment and the AP reaction force, that joint moments were estimated from muscle activity which has relatively low reliability in contrast [17].

4.1. Effect of spinal curvatures

Both at the CT and LS joint, the moment and the AP reaction force were the highest in the slump posture. The CT joint moment of slump posture was close to the maximum moment during the sit-to-stand movement (range: $-$0.012 $\sim$ 0.086 [Nm/kg*m]) [23] as in Fig. 2a. The LS moment of slump posture exceeded those of normal walking (0 $\sim$ 0.2 [Nm/kg*m]) [32] as in Fig. 3a. These high moments of CT and LS joint might be related to the neck and low back pain occurring with an extended period of slump posture [21].

Castanharo et al. reported that the mean lumbar joint moment during posture change from slump to lordosis was lower than to flat posture, which disagreed with this study where no difference between flat and lordosis was shown [17]. Difference in the task (Dynamic postural change in Castanharo et al. and static postural maintenance in this study) could be the reason for the disagreement. Workers who maintain the identical sitting posture throughout their working hours were reported to be more vulnerable to LBP than those who change postures [33]. Therefore, when comparing the joint moments for various sitting postures, it would be practical to investigate the moment in static postures than in dynamic postures.

Since the spine is less resistant to reaction force than the compressive force [34, 35, 36], reaction forces have been reported to be associated with spinal injuries [36]. The AP reaction force was the highest in the slump and flat and lordosis were not different (Figs 2b and 3b). Therefore, the slump posture would be more vulnerable to spinal injuries than the other spinal curvatures.

The net joint moment comprises active moment, indicating the net effect of the agonist and antagonist muscles, and passive moment generated by ligament and passive elements such as muscle fascia [37]. When the neck or the truck is flexed, the extension moment is required to maintain a bent posture and the spinal extensors need to be activated. Neck and back pain is closely related to prolonged muscle contraction [38, 39]. Therefore, the active moment generated by the muscle may be related to the neck and back pain. On the other hand, the joint reaction force calculated in this study is the summation the bone-on-bone (BB) force and the muscle force [37]. The BB force is generated by the contact of two bones. Sitting in the slump posture for an extended period may cause joint pain [21] because the normal BB force increases the disc pressure [2, 3] and the BB reaction force can induce inflammation due to friction between bones [40].

4.2. Effect of arm postures

The experiments were performed with two arm postures: the arms-forward, mimicking the posture of using a smart phone and the arms-on-chest, putting arms on the chest. The effect of arm posture on the joint loads was significant at the flat and the lordosis postures for both moment and AP reaction force of CT joint (Fig. 2a and b). The head flexion angle increased significantly in the arms-forward posture as compared to arms-on-chest (Fig. 2c). In the slump posture, arm posture did not affect the head angle (Fig. 2c). It was because subjects were instructed to focus on the center of a paper at hands in arms-forward posture in contrast that they tended to look down in arms-on-chest posture (Fig. 2c). The LS moment and the AP reaction force were not significantly different by two arm postures (Fig. 3a and b). The results indicated that the arms-forward posture applied a little additional load to the LS joint, unlike the elevation of both arms with weight [28].

4.3. Associations of joint loads and segment angle

In the CT and LS joints, the joint moment and the AP reaction force increased with flexion angle of the upper segment. In particular, the correlation coefficients between the head flexion angle and the CT joint loads (moment and AP reaction force) were higher ($r=$ 0.860 and 0.962) than those between the trunk flexion angle and the LS joint loads ($r=$ 0.776 and 0.894). In this study, the head flexion angle was defined as the inclination of the top head marker from the shoulder marker and the trunk flexion angle as the inclination of the shoulder marker from the ASIS marker. The inclination of the upper segment may have affected the joint moment or the AP reaction force through gravity. The lower correlation between the trunk flexion angle and the LS joint load may be due to the displacement of other body segments such as the head and the upper extremity.

4.4. Limitations and further study

This study has some limitations. The six sitting postures were used to imitate daily sitting posture in this study, but study for daily sitting postures such as forward inclined and reclined sitting posture is still insufficient. Also, the model used for the inverse dynamics was a musculoskeletal model provided by SIMM and it regarded the cervical spine as one rigid segment and the lumbar spine as another rigid segment. Therefore, the joint load could be calculated only between C7 and T1 for the cervical joint and between L5 and S1 for the lumbar joint. If more sitting postures are included and a more detailed model optimized for the spine is used in the future, it will contribute to better understanding of the joint loads.

5. Conclusion

The moment and the AP reaction force at both the cervico-thoracic and lumbosacral joint were significantly smaller in the lordosis and the flat postures than the slump posture. Additionally, the cervico-thoracic joint loads decreased in the arms-on chest posture. Consequently, flat or lordotic spinal curvature with arms close to the axial line of the trunk is suggested to be desirable sitting postures.

Conflict of interest

None to report.