Evaluation of the 3dMDface system as a tool for soft tissue analysis

Structured Abstract

Objectives

To evaluate the accuracy of three-dimensional stereophotogrammetry by comparing values obtained from direct anthropometry and the 3dMDface system. To achieve a more comprehensive evaluation of the reliability of 3dMD, both linear and surface measurements were examined.

Setting and Sample Population

UCLA Section of Orthodontics. Mannequin head as model for anthropometric measurements.

Material and Methods

Image acquisition and analysis were carried out on a mannequin head using 16 anthropometric landmarks and 21 measured parameters for linear and surface distances. 3D images using 3dMDface system were made at 0, 1 and 24 hours; 1, 2, 3 and 4 weeks. Error magnitude statistics used include mean absolute difference, standard deviation of error, relative error magnitude and root mean square error. Intra-observer agreement for all measurements was attained.

Results

Overall mean errors were lower than 1.00 mm for both linear and surface parameter measurements, except in 5 of the 21 measurements. The three longest parameter distances showed increased variation compared to shorter distances. No systematic errors were observed for all performed paired t tests (P<.05). Agreement values between two observers ranged from 0.91 to 0.99.

Conclusions

Measurements on a mannequin confirmed the accuracy of all landmarks and parameters analysed in this study using the 3dMDface system. Results indicated that 3dMDface system is an accurate tool for linear and surface measurements, with potentially broad-reaching applications in orthodontics, surgical treatment planning and treatment evaluation.

1 | INTRODUCTION

With the progression of three-dimensional (3D) imaging methods, digital 3D photography, also known as stereophotogrammetry, has become a more robust alternative to traditional orthodontic diagnostic tools such as radiographs, study models and two-dimensional photography. This advancement has sparked a growing interest in facial anthropometry and has had notable implications in orthodontics, oral and maxillofacial surgery, and plastic surgery.^1–5 Paired with 3D cone beam computed tomography (CBCT) technology, stereophotogrammetry offers clinicians a more comprehensive view of the dento-facial complex during the treatment planning and progress.

Digital 3D photography is a non-invasive method that allows users to acquire a 3D representation of the craniofacial complex.⁶ Stereophotogrammetry generates a 3D reconstruction of an object by photographing the object from at least two different planes. This not only provides a means to measure linear distances, but it also considers surface distances, surface areas and volumes. In addition, three-dimensional coordinates can be extrapolated to perform a variety of statistical shape analyses, which can be used for the diagnosis of craniofacial dysmorphology or changes to the craniofacial complex throughout treatment.^7–9 Thus, stereophotogrammetry has the potential to provide a more comprehensive and indepth assessment of a patient’s craniofacial morphology compared to traditional methods.^10–13

Using custom software, the 3D images can be enlarged, rotated and rendered for better analysis. More importantly, multiple 3D images can be superimposed along the whole surface of the face. Software tools align 3D data sets at different time points and allow the clinician to use colour-coded maps to measure longitudinal changes or treatment outcomes of orthodontic and surgical intervention.^14–16 This automated method eliminates the need for observer-dependent techniques to overlap anatomic landmarks and greatly reduces error.¹⁷ In addition, landmarks can be assigned directly onto these 3D images allowing the clinician to collect measurements immediately after data acquisition. With patients who have developmental disabilities, where behaviour and cooperation may be difficult, decreasing the time required of patient interaction improves the accuracy of measurement.¹⁸

Most of the current devices for 3D imaging involve simple visual evaluation or linear and angular measurements between various landmarks, and their accuracy has not been validated independently.^13,19–21 The aims of this study were to evaluate the accuracy of 3D imaging using the stereophotogrammetry technique and to analyse surface measurements.

2 | MATERIALS AND METHODS

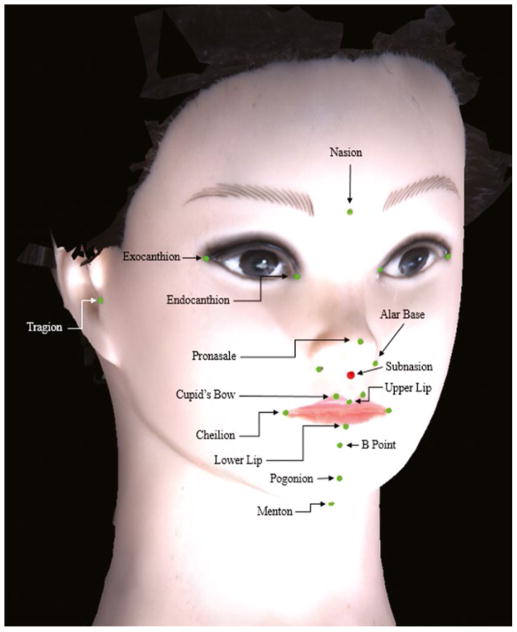
A mannequin head was used in this study as the facial contours do not change when taking images at different time points. Fourteen standard anthropometric surface landmarks were identified and labelled directly on the mannequin head (Figure 1). These landmark markings and tracings remained on the mannequin throughout the duration of the study.

FIGURE 1.

Stereophotogrammetric mannequin model with labelled anatomic landmarks. Fourteen standard anthropometric surface landmarks were identified and labelled directly on a mannequin head, which provides fixed facial contours across different time points

The 3dMDface system (3dMD Inc., Atlanta, GA, USA) photogrammetric device was chosen in this study because it is widely recognized for its precision, with a geometry accuracy of 0.2 mm root mean square (RMS).^12,13 Two modular units of six medical-grade, machine vision cameras with industrial-grade flash systems are each fixed at different angles to simultaneously capture images to produce a 180-degree face capture ear to ear, at a capture speed of 1.5 milliseconds. These images are then combined and processed by the 3dMD software to produce a 3D image. Software algorithms of 3dMDface system combine the images into a single, unified 3D point cloud. To enhance visualization, points comprising the surface are linked by vertices creating a 3D polygonal mesh, and these polygons are filled in to create an “airtight” surface.^22,23 Texture and colour formats are then projected onto the underlying polygonal mesh framework to give a life-like, computer-generated rendering of the object.

Table 1 lists the abbreviations and definitions of the landmarks used in applying this system to the mannequin head. To analyse measurement accuracy, two investigators independently measured the linear and surface measurements 1 week apart. Twenty-one parameters (6 in the vertical dimension, 10 in the anteroposterior dimension and 5 in the transverse dimension) were obtained. Linear measurements were made using a 300 mm digital calliper (Mitutoyo America Co., Aurora, IL, USA) with a ± 0.025 mm accuracy, and surface measurements were made using a conduit measuring tape (Current Tools Inc., Greenville, SC, USA), with both linear and surface measurements constituting the “true” values, which once averaged between the two investigators yields the “True Mean.” Additionally, images using 3dMDface system were made at seven time points (0, 1 hour, 24 hours, 1 week, 2 weeks, 3 weeks and 4 weeks). The different timing follows the protocol conventionally used for patients and serves to eliminate confounding variables. Importantly, before linear and surface measurements were collected from the software images, referred to as “Measured Means,” it was recognized that error may be a function of the landmarks.^24–26 For that reason, two investigators collected landmark data twice at each of the seven time points. Each data collection trial was checked for any significant errors, such as mislabelling of a landmark.

TABLE 1.

Anthropometric Landmarks and Definition of Linear and Surface Distances

Abbreviation	Landmarks (mm)	Definition
Alar Base	Base of Alar	Distance between most lateral points on nasal alae
ExoCD	Exocanthal distance	Distance between right and left outer corners of eye fissure where eyelids meet
InterCD	Intercanthal distance	Distance between right and left inner corners of eye fissure where eyelids meet
N_B	Nasion, b point	Mid-point of nasofrontal suture (N) to most concave point between chin and lower lip point
N_Ll	Nasion, lower lip	N to junction between vermillion and soft tissue of lower lip in midline
N_Me	Nasion, menton	N to most inferior portion of chin on the midline
N_Pg	Nasion, pogonion	N to most projecting median point on the anterior surface of the chin
N_Prn	Nasion, pronasale	N to most protruded point of nasal tip
N_Ul	Nasion, upper lip	N to junction between vermillion and soft tissue of upper lip in midline
RtLtCuspidB	Right to left cupid’s bow	Distance between right and left points of the crest of the philtrum
RtLt_Ch	Right to left cheilion	Distance between outer corners of mouth
Tr_B	Tragion, b point	Notch above the tragus of the ear (Tr) to most concave point between chin and lower lip point
Tr_Ll	Tragion, lower lip	Tr to junction between vermillion and soft tissue of lower lip in midline
Tr_Me	Tragion, menton	Tr to most inferior portion of the chin on the midline
Tr_N	Tragion, nasion	Tr to mid-point of nasofrontal suture
Tr_Pg	Tragion, pogonion	Tr to most projecting median point on the anterior surface of the chin
Tr_Prn	Tragion, pronasale	Tr to most protruded point of nasal tip
Tr_RtCuB	Tragion, right cupid’s bow	Tr to right point on crest of philtrum
Tr_RtCh	Tragion, right cheilion	Tr to right outer corner of mouth
Tr_Sn	Tragion, sella-nasion line	Tr to a line connecting the sella to the nasion
Tr_Ul	Tragion, upper lip	Tr to junction between vermillion and soft tissue of upper lip in midline

Images acquired from the 3dMDface system were saved as .obj files and imported into the 3dMDvultus software system (3dMD Inc., Atlanta, GA, USA). A custom landmark template was created, which contained all 21 landmarks of interest. The 3dMDvultus software allows the user to define the anatomic region of interest, thus creating new XYZ point coordinates, which it then uses to track throughout the sequence on the 3D surface of the 3dMDface system reference frame. The software then generates a coordinate map for this sequence, taking into account the correct temporal context, to generate the linear distance for each parameter of interest. Topographical measurements were also made between the two points on the surface of the 3dMD-face system image using the shortest path along the contour of the surface. Both the generated linear distances and topographical measurements constitute the “measured means,” which uses the distances generated from the 3dMD software system. A comprehensive report including the landmark XYZ positions and surface measurements was saved as an XLS file (.xls).

2.1 | Statistical analysis

For assessing system accuracy, several error magnitude statistics were employed, including mean absolute difference (MAD), standard deviation of the error (SD), relative error magnitude (REM), root mean square error (RMSE) and intraclass correlation coefficient (ICC). Paired student t tests were used to compare the systematic error between measurements obtained from 3dMDvultus with that of the “true” values. P .05 was used to assess statistical significance. MAD is the aver-age of the absolute difference between the “true” values (made using measuring tape and digital calliper) and the “measured” values (generated from 3dMDface system). REM is calculated by dividing the MAD for a given parameter by the measured mean and multiplying the result by 100. Thus, REM is expressed as a percentage and represents an estimate of error magnitude relative to the size of the measurement. RMSE is an error magnitude statistic that incorporates MAD and SD into a single value for ease of comparison:

$$\text{RMSE}=\sqrt{\text{error}{\text{SD}}^2+\text{mean}{\text{difference}}^2}$$

Intraclass correlation coefficient is commonly used in intra- observer studies and is employed to look at error estimates between investigators. Values range from 0 to 1 and represent errors between investigators. A value closer to 0 indicates more measurement error between investigators, while a value closer to 1 indicates less measurement error.²⁷

3 | RESULTS

All measurements obtained in the linear and surface categories were deemed accurate. Of the 21 interlandmark linear measurements, 19 showed an MAD value of less than 1mm with the exception of Tr_Prn (1.35 mm) and Tr_Ul (1.59 mm), while 16 of the 21 interlandmark surface measurements showed an MAD value of less than 1 mm. In Tables 2 and 3, N_Pg (1.64 mm), ExoCD (2.11 mm), Tr_Pg (2.39 mm), N_Me (3.44 mm) and Tr_Me (4.09 mm) had MAD values larger than 1 mm. All 21 parameters for both linear and surface measurements showed that there was no statistical difference between “true” value and measured mean (P<.05).

TABLE 2.

Error Statistics for Linear Measurements

Distances	True mean (mm)	Measured mean (mm)	P values	MAD (mm)	REM (%)	RMSE (mm)
Alar Base	24.80	24.38	.58	0.42	1.20	0.28
ExoCD	102.73	100.62	.41	2.11	0.90	0.85
InterCD	38.44	38.63	.55	0.19	2.50	0.71
N_B	72.60	72.45	.69	0.16	0.50	0.34
N_Ll	63.86	64.05	.42	0.19	1.10	0.60
N_Me	104.54	101.11	.15	3.44	0.20	0.16
N_Pg	86.95	85.31	.25	1.64	0.10	0.05
N_Prn	25.57	25.56	.70	0.02	1.50	0.34
N_Ul	48.45	47.67	.35	0.78	1.70	0.71
RtLtCuspidB	9.57	10.06	.57	0.49	3.60	0.36
RtLt_Ch	44.76	45.60	.61	0.84	1.40	0.52
Tr_B	111.50	111.73	.74	0.23	0.10	0.08
Tr_Ll	108.86	108.13	.85	0.73	0.70	0.70
Tr_Me	112.78	108.69	.12	4.09	0.40	0.46
Tr_N	108.75	109.70	.68	0.95	0.00	0.05
Tr_Pg	112.79	110.41	.27	2.39	0.10	0.16
Tr_Prn	108.04	107.42	.58	0.63	1.30	1.35
Tr_RtCuB	103.06	102.15	.52	0.92	0.20	0.15
Tr_RtCh	80.88	81.06	.44	0.17	0.40	0.36
Tr_Sn	105.56	105.82	.73	0.26	0.70	0.68
Tr_Ul	107.78	108.12	.51	0.34	1.60	1.59

MAD, mean absolute difference; REM, relative error magnitude; RMSE, root mean square error

TABLE 3.

Error Statistics for Surface Measurements

Distances	True mean (mm)	Measured mean (mm)	P values	MAD (mm)	REM (%)
Alar Base	24.38	24.81	.61	0.42	1.70
ExoCD	100.62	102.73	.26	2.11	2.10
InterCD	13.63	38.44	.73	0.19	1.10
N_B	72.45	72.62	.82	0.16	0.60
N_Ll	64.05	63.86	.37	0.19	1.10
N_Me	101.11	104.54	.44	3.44	3.40
N_Pg	85.31	86.95	.31	1.64	1.90
N_Prn	25.56	25.56	.87	0.02	1.60
N_Ul	47.67	48.45	.62	0.78	1.60
RtLtCuspidB	10.06	9.57	.72	0.49	4.90
RtLt_Ch	45.62	44.76	.23	0.84	1.90
Tr_B	111.73	111.52	.79	0.23	0.30
Tr_Ll	108.13	108.86	.84	0.73	0.70
Tr_Me	108.69	112.78	.23	4.09	3.80
Tr_N	109.71	108.75	.61	0.95	0.90
Tr_Pg	110.41	112.79	.73	2.39	2.20
Tr_Prn	107.42	108.04	.27	0.63	0.80
Tr_RtCuB	102.15	103.06	.44	0.92	0.90
Tr_RtCh	81.06	80.88	.23	0.17	0.90
Tr_Sn	105.82	105.56	.87	0.26	0.20
Tr_Ul	108.12	107.78	.52	0.34	0.30

MAD, mean absolute difference; REM, relative error magnitude

Following the Weinberg et al. (2004) method of quantification, REM scores were divided into five categories: < 1% = excellent, 1% to 3.9% = very good, 4% to 6.9% = good, 7% to 9.9% = moderate and > 10% = poor.²⁸ When assessing REM scores for linear measurements, 12 of the 21 were deemed “excellent,” while the other nine were deemed “very good.” At the same time, 7 of the 21 surface measurements were deemed “excellent,” 13 measurements were deemed “very good,” and one measurement (RtLtCupidB) was deemed “good.”

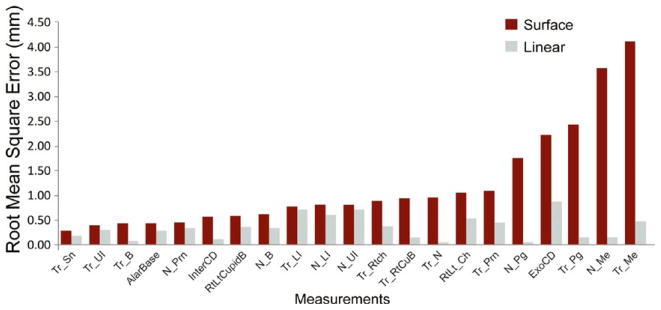
Root mean square error values were obtained and organized in increasing order for both linear and surface measurements. In Figure 2, N_Me and Tr_Me, two of the longest surface measurements of the face, had the largest variability.

FIGURE 2.

Root Mean Square Error (RMSE) values for measurements. RMSE values showed that calliper measurements were more accurate than surface measurements across all 21 parameters. Surface measurements using parameters involving menton (N_Me and Tr_Me) resulted in the greatest deviation from the true value suggesting the least accuracy

4 | DISCUSSION

Precision is critical in craniofacial orthodontics and surgery. Recent technology, including sophisticated 3D imaging devices, has improved the accuracy of measurements made by orthodontists and surgeons as part of the treatment planning and evaluation process.²⁹ As part of our research protocol, it was imperative that we limited all other factors that may contribute to measurement error other than from the stereophotogrammetry software. For this reason, a mannequin head was used and all the landmarks were marked on the facial surface before stereophotogrammetric acquisition.

Accuracy is defined as the degree to which a measurement deviates from its “true” value.³⁰ For this study, the “true” value was obtained by averaging the values recorded by two separate investigators. The stereophotogrammetry technique was accurate in the assessment of all 21 linear distances. Similar measurement errors were noted in previous studies by Gornick, Ort et al., de Menezes et al., and Dindaroglu et al.;^5,18,22,31 therefore, to ensure standardized reliable and repeatable measurements, linear measurement is the method of choice to quantify accuracy with 3D imaging technology. However, linear measurements can only tell us so much about craniofacial changes and takes us back to the same limits that had originally constrained 2D imaging. Therefore, our aims were not only to verify the accuracy of linear measurements, but to also establish a standard protocol to assess accuracy of surface measurements.

In our study, linear measurements had an overall MAD mean and REM mean that were lower than that of surface measurements. However, paired t tests showed that there was no statistical difference between the “true” value and measured value using stereophotogrammetry for both linear and surface measurements. The three longest parameter distances (Tr_Pg, N_Me and Tr_Me) showed the largest variation compared to shorter distances. Areas of great curvature and changes in surface trajectory, such as areas around the eyes (ExoCD), were prone to greater error compared to areas of the mannequin face that were flatter like in Tr_Sn, Tr_Ul, Tr_B, N_Prn. A possible explanation for this discrepancy could be that the surface topology-tracking device used in 3dMDface system creates variable trajectories, especially in long distances that have curvatures.

Three-dimensional technology has immense potential in the field of orthodontics, and this study is an attempt to demonstrate how such technology can be used to acquire reliable measurements, data and surface images that 2D technology is incapable of producing. Despite this, the current study is limited in that the data come from a specific device, namely the 3dMDface system used here. Thus, the results provide a general guideline for future studies when using this software; certain values can be used with minimal error, while other values should be used with caution. Additionally, this study is performed in a controlled setting, so application to clinical practice needs to be further evaluated. With more precise and reliable data and a proper analysis of such data, more effective and efficient treatment plans can be realized and put into practice. The goal of clinicians is to offer patients the best treatment outcome possible, and 3D imaging certainly has the potential to help the clinician deliver more predictable treatment results using the most comprehensive diagnostic means possible. As research continues to demonstrate the accuracy of 3D facial imaging, future studies should explore the utility of these measurements in treatment planning and clinical outcome analysis. Our hope is that this understanding will lead to more predictable and precise treatment outcomes.