Brain-wide electrical spatiotemporal dynamics encode depression vulnerability

Summary

Brain-wide fluctuations in local field potential oscillations reflect emergent network-level signals that mediate behavior. Cracking the code whereby these oscillations coordinate in time and space (spatiotemporal dynamics) to represent complex behaviors would provide fundamental insights into how the brain signals emotional pathology. Using machine learning, we discover a spatiotemporal dynamic network that predicts the emergence of major depressive disorder (MDD)-related behavioral dysfunction in mice subjected to chronic social defeat stress. Activity patterns in this network originate in prefrontal cortex and ventral striatum, relay through amygdala and ventral tegmental area, and converge in ventral hippocampus. This network is increased by acute threat, and it is also enhanced in three independent models of MDD vulnerability. Finally, we demonstrate that this vulnerability network is biologically distinct from the networks that encode dysfunction after stress. Thus, these findings reveal a convergent mechanism through which MDD vulnerability is mediated in the brain.

In Brief

Patterns of brain activity predict vulnerability versus resilience to depression in response to stress

Introduction

MDD is the leading cause of disability in the world (WHO, 2017). While stress contributes to the onset of MDD (Caspi et al., 2003; Kendler et al., 1999), only a fraction of individuals that experience stressful events develop behavioral pathology. Multiple factors including childhood trauma and alterations in several molecular pathways have been shown to increase disease risk (Caspi et al., 2003; Widom et al., 2007); nevertheless, the neural pathways on which these factors converge to yield subthreshold changes that render individuals vulnerable to stress are unknown. Knowledge of these neural pathways would facilitate the development of novel diagnostic technologies that stratify disease risk as well as preventative therapeutics to reverse neural circuit endophenotypes that mediate vulnerability to MDD. To achieve this aim, it is essential to distinguish the neural alterations that confer vulnerability to MDD from those that accompany the emergence of behavioral dysfunction.

Chronic social defeat stress (cSDS) is a widely validated pre-clinical model of MDD (Berton et al., 2006; Chaudhury et al., 2013; Krishnan et al., 2007). In this paradigm, test mice are repeatedly exposed to larger aggressive CD1 strain mice. At the end of these exposures, test mice develop a MDD-like behavioral state characterized by social avoidance, anhedonia- and anxiety-like behavior, and sleep/circadian dysregulation (Berton et al., 2006; Krishnan et al., 2007). Critically, only ~60% of C57 mice subjected to this paradigm exhibit susceptibility to developing this stress-induced syndrome. While the remaining ~40% of mice subjected to cSDS exhibit resilience (Krishnan et al., 2007), susceptible and resilient mice experience the same degree of aggressive encounters. Thus, the cSDS paradigm provides a framework to probe putative basal network vulnerabilities that may exist in stress-vulnerable mice prior to stress exposure.

Multiple regions including subgenual cingulate cortex, amygdala, ventral hippocampus (VHip), nucleus accumbens (NAc), and ventral tegmental area (VTA) have been proposed to contribute to a putative MDD brain network (Bagot et al., 2016; Chaudhury et al., 2013; Hultman et al., 2016; Mayberg et al., 1999; Mayberg et al., 2005; Nestler et al., 2002). Supporting this notion, functional magnetic resonance imaging (fMRI) studies in depressed subjects have discovered distinct functional connectivity alterations involving these brain regions that predict individual behavioral phenotypes and antidepressant treatment responses (i.e., pharmacology, psychotherapy, and transcranial magnetic stimulation) (Drysdale et al., 2017; Dunlop et al., 2017). However, our prior in vivo findings in genetic mouse models of MDD and in mice exposed to cSDS suggest that MDD-like behavioral dysfunction also arises at the level of circuit/network spatiotemporal dynamics, involving altered interactions of neural activity between spatially separated brain regions over time that are not captured by the fMRI timescale (Dzirasa et al., 2013; Hultman et al., 2016; Kumar et al., 2013). We postulated that a signature predicting MDD vulnerability may exist at this dynamic circuit/network-level as well.

To test this hypothesis, we employed a transdisciplinary strategy integrating cSDS in mice, multi-circuit in vivo recordings from a subset of MDD-related regions including prelimbic cortex (PrL_Cx), infralimbic cortex (IL_Cx), NAc, central nucleus of the amygdala (CeA), basolateral amygdala (BLA), VTA, and VHip (Fig. 1A–B), a translational assay of neural circuit reactivity (Fig. 1B; see also Supplemental Movie S1) (Hultman et al., 2016; Kumar et al., 2014), and machine learning (Gallagher et al., 2017; Ulrich et al., 2015). We selected this subset of brain regions since they have each been validated in contributing to MDD-like behavior in multiple human and animal studies across several different research groups, and each region can be reliably targeted in mice using our multi-circuit recording technology (Dzirasa et al., 2013). Our in vivo recording approach quantified both cellular activity and local field potentials (LFPs), which reflect the pooled activity of many neurons located up to 1mm from the electrode tip, their synaptic inputs, and their output signals (Kajikawa and Schroeder, 2011).

Figure 1. Identification of stress-related networks using machine learning.

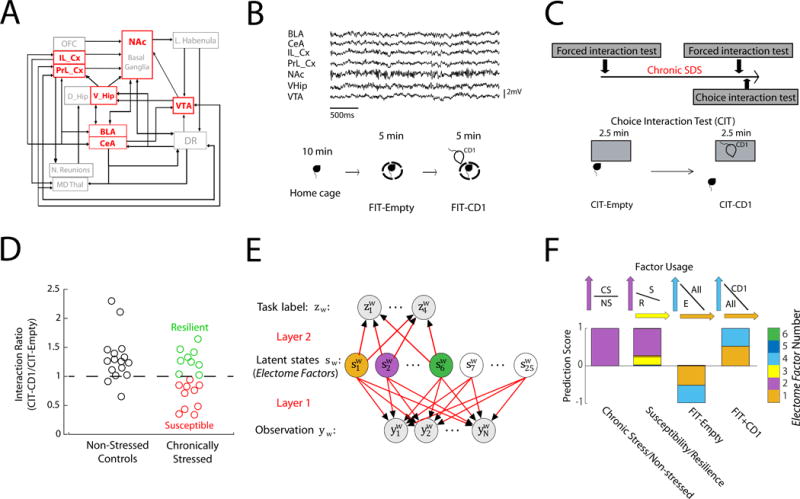
A) Partial structural wiring diagram across MDD related brain regions in mice. We recorded from areas shown in red. B) Sample LFP traces recorded concurrently from seven implanted brain areas (top). Homecage—Forced interaction test (FIT) used to probe brain activity during: homecage, placed inside a small sub-chamber in an empty cage, or inside small sub-chamber in a cage with a CD1 mouse (bottom). C) Experimental timeline (top), and schematic of choice interaction test (CIT) to identify susceptible vs. resilient mice after cSDS (bottom). D) Choice interaction ratios after 10 days of cSDS compared to non-stress controls. E) Cross-spectral factor analysis model where observations are brain features (LFP power, cross-area synchrony, and cross-area phase offsets) that are shared by latent states (networks). These networks coordinate distinct ‘emotional brain states’ represented by a given task label (i.e. susceptibility vs. resilience). We trained 25 descriptive latent networks. Six of these networks were also trained to be predictive F) Four networks/Electome Factors identified using a support vector machine jointly discriminated the stress states (Networks 1, 2, 3, and 4). Example support vectors are shown above.

We uncovered network-level spatiotemporal dynamic signatures that distinguish the neural alterations that confer vulnerability to MDD prior to stress from those that accompany the emergence of behavioral dysfunction after stress. We then utilized three independent mouse models of MDD vulnerability to verify that one spatiotemporal dynamic network represents a convergent network-level vulnerability pathway for MDD-related abnormalities. Finally, we used two distinct antidepressant manipulations to verify that this network underlying MDD vulnerability is biologically distinct from the neural networks underlying the expression of MDD-related behavioral dysfunction after stress exposure.

Results

Neural model of brain network function

To study the relationship between widespread spatiotemporal dynamics and MDD pathology, we developed a probabilistic machine learning approach using LFP activity data recorded from seven brain regions across multiple frequencies. We term this approach “discriminative cross-spectral factor analysis” or dCSFA (see Fig. 1E and supplemental methods for full details of dCSFA model)(Gallagher et al., 2017). Our dCSFA approach yields a descriptive/generative model, such that it discovers LFP patterns across regions that change together over seconds of time. The model is also predictive such that it discriminates the LFP patterns that are specific for several pre-specified behavioral variables. Paralleling classic fMRI models that describe functional connectivity in the human brain, our dCSFA model discovers activity that is correlated across many brain regions over seconds of time. However, in contrast to fMRI models, our approach also enables the analysis of fast oscillatory electrical signals at the millisecond timescale. Indeed, the faster timescale features that contribute to the observed LFP patterns include spectral power (LFP amplitude across frequencies), synchrony (a neural correlate of brain circuit function that quantifies how two LFPs correlate over a millisecond timescale), and phase-directionality (a neural correlate of information transfer, in a statistical forecasting sense, which quantifies which of two synchronous LFPs leads the other), across many brain regions (see supplemental Fig. S1). We therefore refer to these LFP patterns as “Electome Factors” (electrical functional connectome factors/networks). Importantly, our dCSFA model also yields an Electome Factor activity score, which indicates the activity of each Electome Factor during each five second segment of LFP data. A given brain area or circuit can belong to multiple Electome Factors, providing the opportunity for distinct Electome Factors to functionally interact to yield a global brain state (the complete Electome).

Brain-wide neural networks signal MDD vulnerability

Brain activity was recorded while animals were in their home cage and during a forced interaction test (FIT) with an aggressive mouse (Fig. 1B). A subset of the mice was subjected to cSDS, and the post-stress susceptibility of these mice was characterized using the choice interaction test (Fig. 1C), which has been shown to reliably track the expression of the full MDD-like behavioral syndrome (Krishnan et al., 2007). All mice were then subjected to another home cage–FIT recording. We trained our dCSFA model using supervised machine learning to determine the oscillatory signals that are modulated across time and discriminate: 1) all mice subjected to cSDS from non-stressed controls (post-cSDS; N=19 and 16 mice, respectively), 2) susceptible from resilient mice (post-cSDS; N=10 and 9 mice, respectively) and 3) activity recorded during different segments of the homecage—FITbrecordings (Fig. 1B, pre-cSDS and post-cSDS; N=44 total mice, including 9 mice that were only run in the pre-stress condition; see methods)(Hultman et al., 2016; Kumar et al., 2014).

To determine which Electome Factors derived by our dCSFA model discriminated these stress conditions, we learned a multivariate support vector machine classifier as part of the dCSFA model. We found that 4 out of the 25 specified Electome Factors discriminated these various behavioral conditions (Fig. 1F, see STAR Methods for detailed dCSFA model description). For discriminating cSDS exposure, Electome Factor 2 activity was higher in mice subjected to cSDS than in non-stressed controls (Fig. 1F and Fig. 2D). Electome Factor 2 was also higher in stress-susceptible mice compared to the resilient animals (Fig. 1F and 2D). This Electome Factor was defined by co-modulated delta and beta oscillations, and oscillations in this network exhibited directionality largely from NAc to VHip and VTA (Fig. 2A–C). Electome Factor 3 was also higher in stress-susceptible mice compared to the resilient animals (Fig. 1F). This Electome Factor was defined by co-modulated delta oscillations that exhibited directionality from PFC and NAc to BLA (Fig. 2A–C). Finally, Electome Factor 1 activity was enhanced by acute exposure to the CD1 mouse during the FIT both before and after cSDS (Figs. 1F and 2D). Electome Factor 1 was largely defined by 8-20Hz oscillations that exhibit directionality from PFC and NAc to VHip (Fig. 2A–C). Electome Factor 4, defined by local delta (1-4Hz) oscillations in VHip, did not show dramatic changes with behavioral conditions (Fig. 2D), although was nonetheless associated significantly with the FIT (Fig. 1F).

Figure 2. Four Electome Factors signal distinct stress states.

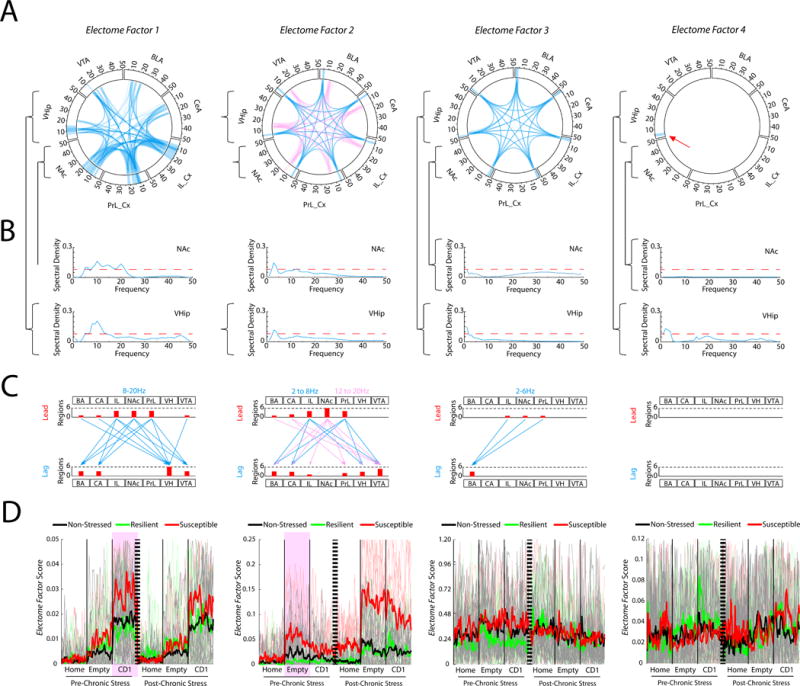
A) Power and coherence measures that compose each network. Brain areas and oscillatory frequency bands ranging from 1 to 50Hz are shown around the rim of the circle plot. The spectral power measures that contribute to each Electome Factor are depicted by the highlights around the rim, and synchrony measures are depicted by the lines connecting the brain regions through the center of the circle. Pink and blue ribbons are used for Electome Factor2 to highlight the two separate frequency bands that compose the factor (Blue, 2-8Hz; Pink, 12-20Hz). B) The NAc and VHip spectral power density plots are shown as examples for each Electome Factor. The red dashed horizontal line identifies the relative spectral density threshold used to depict the Electome Factor plots. C) Phase offset measures that define directionality within each Electome Factor (phase activity is shown at a threshold of 0.1 radians). Histograms quantify the number of lead and lagging circuit interactions for each brain region. D) Electome Factor activation during pre- and post-stress home cage—FIT recordings. The thick colored lines show the average across animals, while the thin lines in the background show the values from individual mice. Two Electome Factors (highlighted by purple) showed test-related statistical differences between susceptible and resilient mice prior to cSDS exposure (P<0.01; n=5–7 mice/group). See also Fig. S1.

Strikingly, two of the Electome Factors signaled vulnerability prior to the cSDS experience in this cohort of mice. During acute exposure to the CD1 mouse (i.e. the second half of the FIT), Electome Factor 1 was higher in stress-naïve mice that later exhibited susceptibility to cSDS than those mice that later exhibited resilience (U=133, P = 0.0057 for comparison of pre-stress Electome Factor 1 activity during the forced interaction with the CD1; Receiver Operating Characteristic AUC=0.86; N=9–10 mice per group; Fig. 2D). In contrast, Electome Factor 2 was higher in stress-naïve mice that later exhibited susceptibility, specifically when they were placed in the interaction chamber during the first half of the FIT (U=138, P=9.7×10⁻⁴ for comparison of pre-stress Electome Factor 2 activity during FIT-Empty; Receiver Operating Characteristic AUC=0.92; N=9–10 mice per group; Fig. 2D). We did not observe significant differences between stress-naive susceptible mice and stress-naïve resilient mice when they were in their home cage, or across any of the other Electome Factors (P>0.05 for all comparisons). Thus, Electome Factors 1 and 2 were putative biomarkers of vulnerability since they distinguished the stress-naïve test mice that would later show behavioral dysfunction after cSDS from the mice that would later exhibit resilience. Electome Factor 2 was also a biomarker of the emergence of MDD-related behavioral dysfunction as activity in this network was increased in the stress-susceptible mice compared to the resilient mice and the non-stress controls.

Electome Factor activity correlates with unit firing

Having identified these putative stress-related signatures, we set out to verify that the Electome Factors were a bona fide representation of biological activity and not simply abstract mathematical constructs. To do this, we tested whether Electome Factor activity demonstrated a relationship to the activity of neurons recorded simultaneously from the seven brain regions, which is a clear reflection of biological function. Specifically, we quantified the activity of each of the 644 single- and multi-units in 5 second bins and compared this activity to the activity of each Electome Factor (Fig. 3A–E). To verify that the degree of correlation of the Electome Factors with cellular firing rates was meaningful and not due to random chance, we compared these results to randomly shuffled firing rates (see supplemental methods). Each of the four Electome Factors exhibited activity that correlated with 10–15% of the recorded cells (N=644 units pooled from all brain areas, Fig. 3F). Many neurons (250/644, 39%) showed activity that correlated with more than one Electome Factor, and 21–51% of the neurons from each individual brain area correlated with at least one of the four Electome Factors (Fig. 3F). These data confirmed that the Electome Factors reflect network-level neural processes that emerge from cellular firing across large spatiotemporal distributions (Carlson et al., 2014).

Figure 3. Electome Factor activity correlates with brain-wide cellular firing.

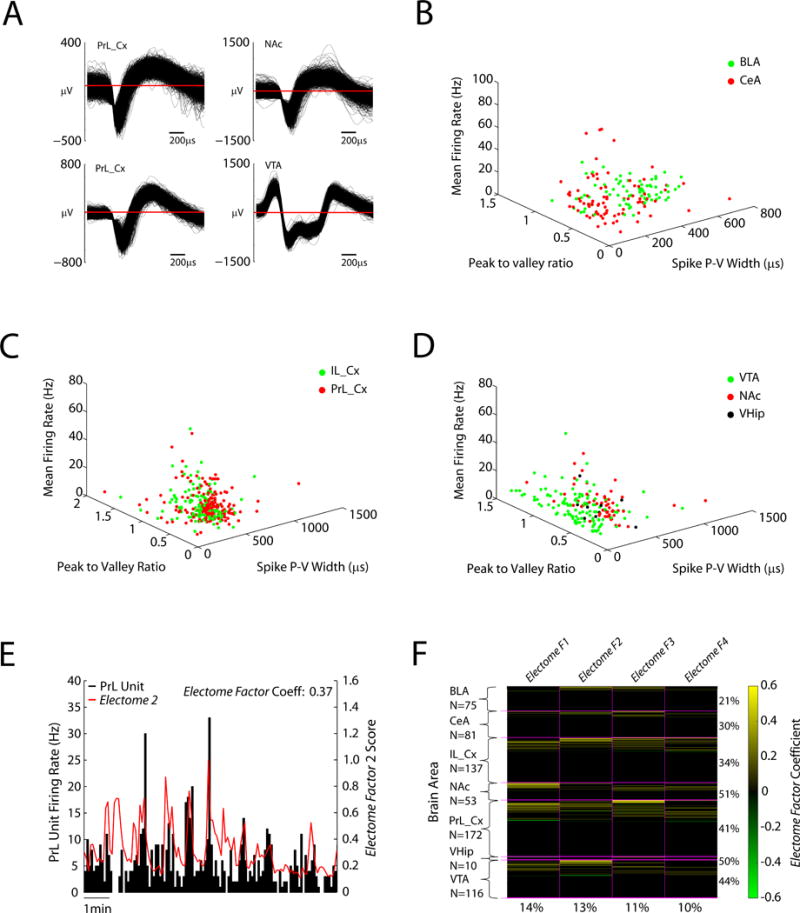
A) Example neuron waveforms. B–D) Mean firing rates are plotted against wave properties (peak to valley ratio and peak to valley width) for amygdala (basolateral and central), prefrontal cortex (prelimbic and infralimbic cortex), VTA, NAc, and ventral hippocampus. E) Example of PFC neuron that showed significant firing relative to Electome Factor 2 activity in the home cage. F) Population firing relative to Electome Factor activity (N = 644 cells). Yellow bars highlight units that showed firing that correlated with Electome Factor activity. Green bars highlight units that showed anti-correlated firing relative to Electome Factor activity. The percentage of units from each area that show firing correlated with one of the four Electome Factors is shown to the right. The percentage of units across the show correlated firing with each Electome Factor (irrespective of recording site) is shown on the bottom.

Enhanced Electome Factor activity signals vulnerability in three independent models

We tested whether Electome Factor 1 and/or Electome Factor 2 indeed reflect a convergent stress-vulnerability pathway that predicts susceptibility to future stress. We reasoned that, if these electrical patterns were truly reflective of general MDD vulnerability mechanisms, then manipulations across many different levels of analysis implicated in MDD vulnerability should also generate these electrical signatures. Thus, we subjected mice to overexpression of a susceptibility hub gene, chronic interferon-alpha (IFNα) treatment, or early life stress (ELS), and directly tested whether these manipulations increased Electome Factor 1 or Electome Factor 2 activity. Notably, we did not train new Electome Factors using these data; rather, the electrophysiological signatures of these mice were projected to the space of the Electome Factors we previously learned using the cDSD data to provide independent validation.

We first exploited a molecular approach to enhance vulnerability in the cSDS model and then quantified the impact of this manipulation on the Electome Factors. Both Electome Factor 1 and Electome Factor 2 exhibited directionality towards VHip. Since we recently found that the Sdk1 gene, which encodes the cell adhesion protein, sidekick 1, plays a central hub role in mediating stress susceptibility in VHip (Bagot et al., 2016), we confirmed that Sdk1 overexpression in VHip increases stress vulnerability (U=328, P=0.0074; N=13–17 mice per group; Fig. 4A). We then tested whether VHip-Sdk1 overexpression influences Electome Factor 1 or Electome Factor 2 activity, using a within-subject design (Fig. 4B). After an initial homecage—FIT recording session, animals were injected intra-VHip with HSV-Sdk1-GFP or an HSV-GFP control vector (Fig. 4C). Two days later, we repeated our neurophysiological recording protocol. By applying these recording data to the Electome model coefficients learned from our initial model in cSDS mice (Fig. 4D), we recovered Electome Factor activity measures for the new testing sessions. Strikingly, VHip-Sdk1 overexpression, in the absence of stress, increased Electome Factor 1 activity during exposure to a CD1 mouse (U=57, P=0.037; N=5–7 mice; Fig. 4E). VHip-Sdk1 overexpression in the absence of chronic stress had no impact on Electome Factor 2 (U=50, P=0.265), nor did it yield the behavioral dysfunction that defines stress-susceptibility as observed previously (F_1,17=1.03, P=0.32 for overexpression effect on social interaction; t_1,15=0.07, P=0.95 for immobility time; see Fig. 4F–G) (Bagot et al., 2016). Thus, this molecular manipulation induced a stress-vulnerability behavioral state and enhanced one of the spatiotemporal dynamic networks that our computational model linked previously to enhanced vulnerability to cSDS in stress-naïve, wildtype mice.

Figure 4. VHip-Sdk1 overexpression selectively increases Electome Factor 1 activity in stress-naïve mice.

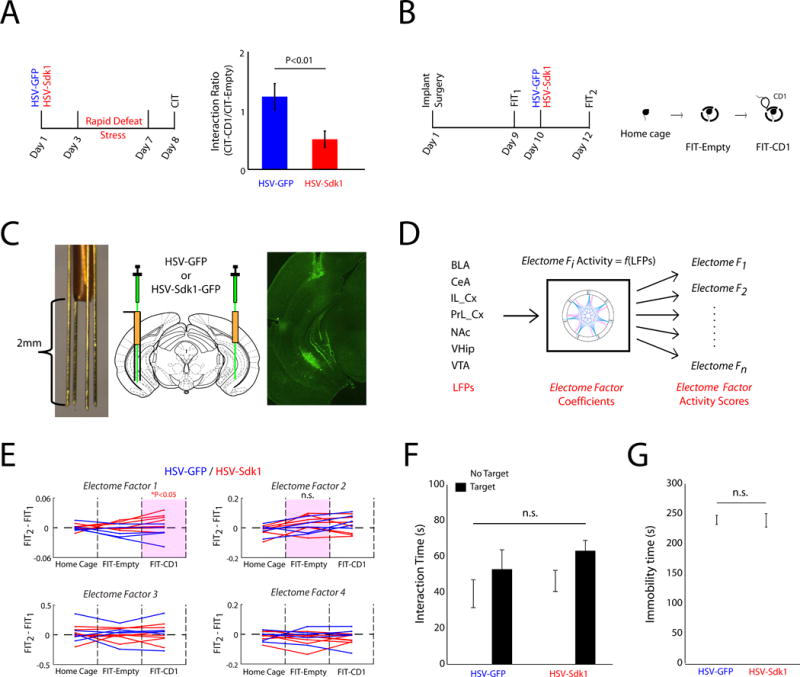
A) Mice were subjected social defeat twice daily for 4 days (i.e. accelerated defeat). The Sdk1 overexpression group exhibited increased susceptibility. B) Experimental schematic for neurophysiological recordings. C) Cannutrode enables site-specific viral injection in chronically implanted mice (left), surgical schematic (middle), and image showing GFP expression in chronically implanted mouse. D) LFPs recorded during the FIT were transformed using the initial dCSFA Electome model/coefficients. E) Sdk1 overexpression in VHip increased Electome Factor 1 activity during the FIT-CD1 (p<0.05 for comparison activity in HSV-Sdk1 and HSV-GFP mice using a one-tailed Wilcoxon rank-sum test). Purple boxes highlight network biomarkers of vulnerability to chronic stress in normal mice (see Fig. 2). F–G) Sdk1 overexpression had no significant effect on F) social interaction or G) immobility during a forced swim test in non-stressed mice. Data are represented as mean ± SEM.

Secondly, we tested whether a physiological manipulation, administration of IFNα, a drug that increases risk for developing a MDD-like phenotype in humans (Bonaccorso et al., 2001), is sufficient to induce Electome Factor activity related to MDD vulnerability (Fig. 5A). Prior studies have also shown that mice chronically treated with IFNα exhibit modest deficits in social behavior and increased immobility in the forced swim assay, partially recapitulating the behaviors induced by cSDS exposure (Zheng et al., 2014). Our IFNα-treated mice continued to exhibit preference for the social stimulus vs. the empty chamber in a three-chamber social interaction test (F_1,18=34.89, P<0.0001; post-hoc paired t-tests t_1,9=4.45, P=0.0016 and t_1,9=4.13, P=0.0026 for PBS and IFNα treated mice, respectively). Though the IFNα-treated mice tended to show reduced interaction time with the social chamber compared to the controls, these results did not reach statistical significance (F_1,18=7.14, P=0.015; post-hoc unpaired t-test t_1,18=2.1, P=0.051 for comparison of social time; N=10 mice per group; Fig. 5B). No differences were observed in distance traveled in the open field (t_1,18=0.599, P=0.56 using an unpaired two-tailed t-test; Fig. 5C). Critically, IFNα treated mice did not show preference for sucrose (t_1,9=2.3, P=0.048 for testing of sucrose effect in Veh treated mice, N=10; t_1,7=0.53, P=0.61 for sucrose effect in IFNα treated mice, N=8; Fig. 5D; see also supplemental Fig. S2). Thus, chronic IFNα induced a MDD-related phenotype, however these mice did not exhibit social avoidance, the key phenotype that defines the full MDD-like behavioral syndrome induced by cSDS (Krishnan et al., 2007).

Figure 5. Enhanced Electome Factor 1 activity in two translational models of MDD vulnerability.

A) Experimental schematic. B) Chronic IFNα administration reduced social behavior in the classic three-chamber test (^P<0.05 for novel-mouse effect using two-way ANOVA, ^#P<0.05 using paired t-test, *P=0.05 using unpaired t-test). C) No locomotor differences were observed in the open field (t_1,18=0.599, P=0.56 using an unpaired two-tailed t-test; N=10 mice per group). D) Sucrose preference test (*P<0.05 using paired t-test). E) Schematic for neurophysiological experiments. F) Chronic IFNα treatment recapitulated the neurophysiological signature of stress vulnerability identified in Electome Factor 1, but not Electome Factor 2. G) Schematic for ELS paradigm and experimental timeline for neurophysiological testing. H) Impact of ELS and cSDS on social behavior (#P<0.05 for ELS × sub-threshold cSDS interaction effect using two-tailed two-way ANOVA; *P<0.05 using unpaired two-tailed t-test). I) Experimental schematic for in vivo recording experiments. J) ELS mice exhibited higher Electome Factor 1 activity during exposure to a CD1 mouse compared to normally reared controls. No difference was observed in Electome Factor 2 activity. Data are represented as mean ± SEM.

We then implanted C57 animals with electrodes and treated them with IFNα or vehicle for 5 weeks. Mice were then subjected to the FIT (Fig. 5E). Chronic IFNα treatment significantly increased Electome Factor 1 activity during CD1 exposure in the FIT (U=51, P=0.041; N=8 mice per group; Fig. 5F). No difference was observed in Electome Factor 2 activity (U=63; P=0.323; Fig. 5F). Thus, IFNα treatment recapitulated the Electome Factor 1 spatiotemporal dynamic network we identified in the cSDS and Sdk1 models of MDD vulnerability (see also supplemental Fig. S3). Notably, a powerful feature of our dCSFA model is that once the original model and coefficients are learned, the same output features (Electome Factor activity) can be determined from new data with LFP activity from only a subset of brain areas (Fig. 5E; see STAR Methods). Thus, these mice were only implanted in the most technically accessible brain areas (PrL_Cx, IL_Cx, NAc, BLA, and CeA).

Thirdly, we sought to determine whether naturally occurring behavioral experiences that increase stress vulnerability also enhance our putative vulnerability network. Childhood trauma is a major risk factor for developing MDD in adulthood (Widom et al., 2007). Thus, we tested whether maternal separation stress (Pena et al., 2017; Sachs et al., 2013) was sufficient to render animals more vulnerable to stress in adulthood (Fig. 5G). ELS mice and their normally reared controls were subjected to a sub-threshold cSDS protocol where the animals were housed independently from the CD1 mice after each defeat. Mice subjected to ELS and sub-threshold cSDS exhibited the social avoidance that defines the stress-susceptible cSDS phenotype (F_1,34=4.23, P=0.048; t₁₃=5.43; P=0.0001 for post-hoc comparison of ELS/cSDS and ELS/non-stressed mice; N=7–8 per group; Fig 5H); However, neither ELS nor the sub-threshold cSDS exposure were sufficient to induce social avoidance on their own (t₁₅=0.81; P=0.43 and t₁₈=0.88; P=0.38, for comparison of normally reared/non-stressed mice to maternally-separated/non-stressed and normally reared/non-stressed, respectively, using t-test; N=10 per group; Fig. 5H). No differences were observed in the interaction time with the non-social stimulus (F_1,34=0.01, P=0.93 for ELS × sub-threshold cSDS interaction effect using two-way ANOVA). Together, these findings verified that ELS increased vulnerability to adult stress.

We then implanted a new cohort of adult ELS mice and normally-reared controls with recording electrodes. After recovery, mice were subjected to the FIT assay (Fig. 5I). By transforming the recorded LFP activity using our initial cSDS dCSFA model and coefficients, we found that ELS increased Electome Factor 1 activity during exposure to the CD1 mouse (U=17; P=0.005 using one-tailed Wilcoxon Rank-sum test; N = 5–7 per group), with no effect on Electome Factor 2 activity (U=29; P=0.318 using one-tailed Wilcoxon Rank-sum test; Fig. 5J). Thus, ELS was sufficient to induce the vulnerability network signature in adult animals. Together, these findings confirmed that three independent molecular, physiological and behavioral manipulations that increase MDD vulnerability in adult animals all converged on the same Electome Factor 1 network. Electome Factor 2 failed our validation testing as a convergent vulnerability signature across the three independent models.

The convergent vulnerability network is distinct from MDD-like behavior networks

Our initial cSDS dCSFA model discovered that a network that signals latent stress vulnerability (Electome Factor 1, prior to stress) was computationally distinct from other putative networks that signal the emergence of the MDD-like behavior state in susceptible mice after cSDS (Electome Factor 2 and Electome Factor 3, post-stress). After validating Electome Factor 1 as a convergent biological marker of MDD vulnerability, we tested whether MDD vulnerability was truly biologically distinct from MDD-related behavioral abnormalities. We reasoned that if the Electome Factor 1 vulnerability signature was indeed mechanistically distinct from the networks underlying the pathological behavior state, biological manipulations that reverse MDD-related behavioral abnormalities would fail to suppress Electome Factor 1 activity during our FIT assay. Thus, we selected two distinct manipulations that have been shown to exert antidepressant effects in both humans and rodent models.

Deep brain stimulation (DBS) of subgenual cingulate cortex (Brodmann area 25, BA25) induces antidepressant effects in select clinical populations with MDD (Mayberg, 2009; Mayberg et al., 2005). Critically, direct stimulation of left IL_Cx (the rodent homologue of BA25) exhibits antidepressant-like effects in the cSDS model as well (Lee et al., 2015). To test the impact of left IL_Cx stimulation on Electome Factor activity, we infected animals with a stabilized step-function opsin (SSFO, AAV-CaMKII-SSFO) in IL_Cx (Fig. 6A). When stimulated by blue light, SSFO induces increased firing of neurons for over 20 minutes (Yizhar et al., 2011). Control animals were infected with a sham virus (AAV-Ef1a-DIO-SSFO), which does not express the opsin (Fig. 6A–B). We then implanted animals with electrodes and recorded their LFP activity in the FIT immediately after blue light stimulation (Fig. 6B–C, see also Supplemental Fig. S4). IL_Cx-DBS stimulation had no impact on Electome Factor 1 activity during exposure to the CD1 mouse (P=0.47 using rank-sum test; N=5–8 mice/group). However, IL_Cx-DBS stimulation did suppress Electome Factor 2 activity, even though the mice were stress-naïve (Fig. 6D, left; F_1,22=6.3, P= 0.029). Electome Factor 3 activity was not suppressed by this manipulation (Fig. 6D, right; F_1,22=0.99, P=0.34). Thus, as anticipated, IL_Cx-DBS stimulation had no impact on our MDD-vulnerability signature.

Figure 6. Biologically distinct mechanism underlies MDD vulnerability.

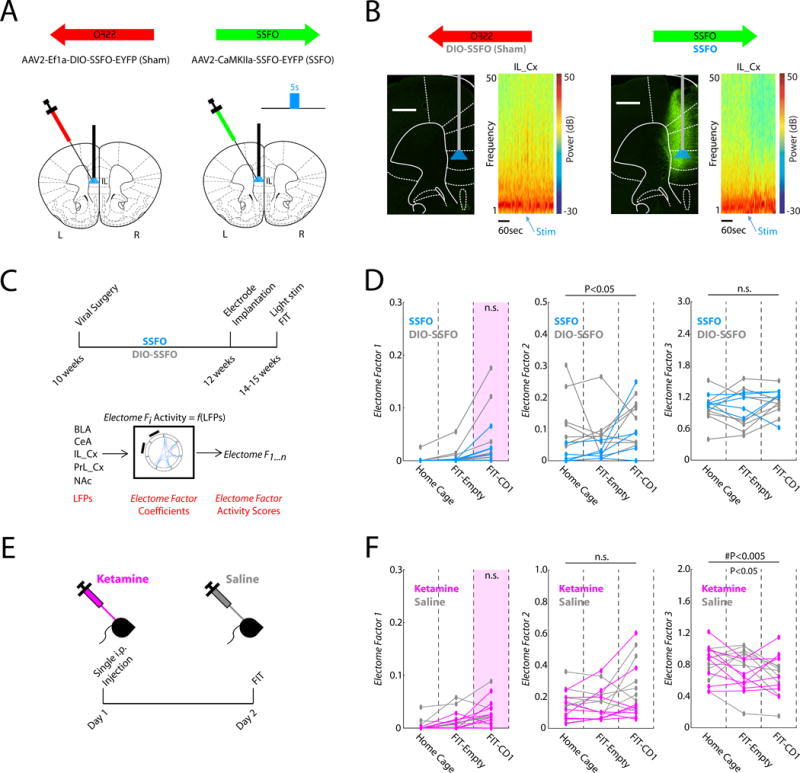
A) IL_Cx infection strategy. B) Prominent suppression of IL_Cx gamma (30-50Hz) oscillations was observed after blue light stimulation in animals expressing SSFO. Representative Prefrontal cortex histological images in SSFO mice and DIO-SSFO controls. Broad EYFP labeling was observed in PrL_Cx and IL_Cx in SSFO mice. The light fiber was implanted at the dorsal IL_Cx border. C) Schematic for SSFO experiments. D) Electome Factor activity in SSFO mice compared to the DIO-SSFO sham controls (N=5–8 mice/group). E) Schematic for Ketamine experiment. F) Electome Factor activity in Ketamine treated mice compared to saline treated controls (n=8 mice/group).

Ketamine is an emerging rapidly-acting antidepressant agent. A single sub-anesthetic dose of ketamine has been shown to ameliorate susceptibility in the cSDS model in C57 mice when it is administered after the last defeat episode but 24 hours prior to behavioral testing (Donahue et al., 2014; Zanos et al., 2016). Thus, we tested whether ketamine, under these same sub-anesthetic conditions, was sufficient to suppress Electome Factor 1 activity, again in stress-naïve mice. Animals were treated with ketamine (20mg/kg, i.p.), and the FIT was performed 24 hours later (Fig. 6E). Applying our initial cSDS Electome model and coefficients to our recorded LFP data, we found that ketamine indeed failed to suppress Electome Factor 1 activity (P=0.41 using rank-sum test; N=8 mice/group). This was consistent with prior findings in C57 mice, which demonstrated that sub-anesthetic ketamine has no impact on behavioral responses to subsequent cSDS (Donahue et al., 2014) or chronic corticosterone administration (Brachman et al., 2016) when it is administered prior to the first stress episode. Taken together with these behavioral observations, our neurophysiological results suggest that ketamine does not target the convergent biological mechanisms underlying vulnerability in C57 mice. Thus, as hypothesized, neither of the manipulations that target post-stress behavioral pathology impacted our stress vulnerability signature, Electome Factor 1, providing clear evidence that neural network mechanisms conferring stress vulnerability are distinct from those mediating a stress-induced MDD-like behavioral state (see supplemental Fig. S5). Interestingly, ketamine did suppress Electome Factor 3 activity (F_2,28=5.61, P=0.009; U=64, P=0.72; U=88, P=0.038; and U=60, P=0.44 using post-hoc rank-sum test for the homecage, FIT-empty, and FIT-CD1 intervals, respectively). Electome Factor 2 was not affected by this manipulation (Fig. 6F; F_1,28= 1.27, P= 0.28).

Discussion

The complex way multiple brain regions coordinate in time and space to effect specific emotional states has been the aim of a number of animal studies correlating neural synchrony at the millisecond timescale with emotional and cognitive behavior (Adhikari et al., 2010; Dzirasa et al., 2013; Jones and Wilson, 2005; Sigurdsson et al., 2010). Behaviorally-relevant manipulations including pharmacology, genetics, and task difficulty have all been shown to impact neural synchrony as well (Brincat and Miller, 2015; Tamura et al., 2016; Wang et al., 2016). While these correlation studies have promoted the causal role of neural synchrony in encoding emotional behavior, they have not generally included measures of brain-wide neural synchrony. As such, it has remained unclear whether observed changes in neural synchrony are restricted to specific brain circuits or reflect more general phenomena that are distributed across larger networks. Additional studies sought to address this question by selectively manipulating cellular activity within specific circuit nodes (Karalis et al., 2016; Schmitt et al., 2017; Spellman et al., 2015). While these circuit-specific manipulations were sufficient to alter emotional behavior, further studies also revealed that manipulating activity within one circuit node was sufficient to alter activity across other brain regions/neural circuits (Hultman et al., 2016; Kumar et al., 2013). Taken together, these findings suggest that emotional behavior arises from the coordinated interaction of many brain circuits rather than individual circuits in isolation. In this network framework, emotions emerge when millisecond interactions across many circuits are coordinated together across a broader timescale. Supporting this model, newer studies in which oscillatory activity was measured from many brain sites concurrently have shown that changes in neural synchrony occur concurrently across many circuits during emotional behaviors (Schaich Borg et al., 2017; Wang et al., 2016).

Machine learning has emerged as a powerful tool in neuroscience for relating large-scale observations in the brain to behavior. While multiple supervised approaches have demonstrated the ability to classify new subjects/animals/trials into specific groups based on complex patterns in large-scale data (i.e. prediction), this has generally occurred at the expense of understanding the way these complex predictive patterns map directly to distinct lower order phenomena in the brain (i.e. interpretability). We developed our two-layer dCSFA approach to address this gap (Fig. 1E). The first layer of our dCSFA approach is based on achieving interpretability (i.e. relating our findings back to specific neural measurements). We built this layer on LFP activity since LFPs 1) can be measured at the temporal resolution of neuronal spiking (i.e. milliseconds), 2) can be reliably obtained from implanted animals, 3) can be stably acquired across testing sessions, and 4) are robust to subtle differences in electrode placement (supplemental Fig. S6). Furthermore, multiple studies by various groups have directly related LFP features including power, synchrony, and directionality to normal emotional and cognitive behavior, and to behavioral dysfunction in disease models, demonstrating that these features are interpretable. This layer of our dCSFA approach describes how the interpretable features in the model change together over time (descriptive/generative). It is analogous to classical approaches like Principal Component Analysis that have been used broadly to identify ‘networks’ in complex data. Since prior work in humans has linked stress-pathology with changes in brain-wide generative networks across seconds of time (Drysdale et al., 2017; Greicius et al., 2007), we built this layer to integrate the time resolution of LFP activity with the time-resolution of human-fMRI (i.e. seconds). As a result, the first layer of the dCSFA model integrates the dynamic activity of many brain regions and their millisecond-timescale neural circuit interactions into a single statistical framework. The second layer of dCSFA is designed to achieve prediction. This layer encourages the model to learn ‘interpretable’ components that separate distinct pre-specified behavioral periods. By integrating these two layers into a single method, our resultant machine learning models achieved prediction and interpretability (Gallagher et al., 2017).

We used this machine learning approach to discover how the activities of many circuits are coordinated into distinct networks to signal normal and pathological emotional states. Not only did our dCSFA model discover an interpretable network that was predictive across a new group of animals (i.e. generalizable, see supplemental Fig. S5B), this network was also predictive across multiple biological contexts related to MDD vulnerability (i.e. convergent). By contrast, the neural correlate of vulnerability we previously discovered in the cSDS model (Kumar et al., 2014)(PFC 2-7 Hz reactivity) failed to predict the increased vulnerability we observed in the translational ELS model (supplemental Fig. S5C). Thus, the dCSFA approach discovered a pattern of coordinated brain-wide activity that signals MDD vulnerability. Each network discovered by the dCSFA model can be composed of as little as one brain area/brain circuit (e.g. Electome Factor 4 was only composed of hippocampal delta activity), and each brain area/circuit can belong to multiple networks. The dCSFA model can also discover both univariate and multivariate features that relate to behavioral states. Thus, when a particular interpretable feature is included within an Electome Factor (network), the model suggests that the behavioral relevance of that feature is dependent upon the activation context of the other circuits within that same Factor (see supplemental Fig. S5D).

Strikingly, we found that three of the behaviorally relevant networks we discovered in the cSDS model (Electome Factors 1, 2, and 3) each involve all of the brain regions we recorded. This coordination of multiple cortical and limbic brain regions sheds light on prior cell and molecular studies, which have found that manipulations of multiple target brain sites across this network can promote or suppress susceptibility in the cSDS model (Bagot et al., 2016; Chaudhury et al., 2013; Hultman et al., 2016). Importantly, these three Electome Factors were only distinguished by their spatiotemporal dynamic features including the frequency of oscillatory synchrony and the directionality of information flow across the regions. Since our machine learning approach facilitates unbiased discovery of the oscillatory frequencies of each brain area/circuit within a network, our results suggest that spatiotemporal dynamics are a central biological mechanism that organizes brain-wide neural activity into behaviorally relevant networks. This importance of spatiotemporal dynamics is consistent with myriad optogenetic studies, which demonstrate that the behavioral output induced by supraphysiological circuit activation is dependent on the frequency at which light stimulation is delivered. Our results extend these findings by discovering the endogenous oscillatory frequencies that guide the function of emotionally-relevant neural circuits. We also show that the coordination of spatiotemporal dynamics across wide-spread neural circuits, and not solely synchrony between pairs of brain regions, is a key neural mechanism underlying MDD pathology.

Two of the spatiotemporal dynamic networks we discovered reflect the emergence of MDD-like behavior in susceptible animals after cSDS (see Fig 2D; Electome Factor 2 and Electome Factor 3). Two distinct antidepressant-like manipulations each suppressed activity in one, but not both, of these Electome Factors (Fig. 6 and Fig. 7). Notably, we did not test whether ketamine nor IL_DBS directly exhibited antidepressant behavioral effects in our study. Nevertheless, since we observed that these manipulations suppressed activity in networks relevant for the emergence of MDD-like behavior, we believe that our findings are consistent with prior work demonstrating that prefrontal cortex stimulation and ketamine both induce antidepressant-like effects in the cSDS model (Donahue et al., 2014; Kumar et al., 2013; Lee et al., 2015; Zanos et al., 2016). Thus, our findings suggest that multiple networks may have to synergize in order to yield a global spatiotemporal dynamic global brain state that mediates MDD. Furthermore, suppressing activity in any one of these networks may be sufficient to reverse MDD pathology (i.e., an Electome Factor two hit model, see Fig. 7). Alternatively, each of the Electome Factors may mediate a different subset of MDD-related behaviors, and suppressing an Electome Factor may only normalize the pathological behaviors that it encodes. Future experiments will be needed to clarify the role of additional MDD-related brain regions in the Electome Factors.

Figure 7. Experimental findings a Electome model of MDD vulnerability.

A) Summary of experimental findings. Arrows indicate direction of change in Electome Factor scores under conditions on left. Results in green indicate confirmation of experimental hypotheses. B) Putative model of MDD vulnerability and behavioral dysfunction based on experimental observations. Experiences such as early life trauma increase Electome Factor 1 activity which promotes vulnerability. Chronic stress in vulnerable animals increases Electome Factor 2 and 3 activities, yielding MDD pathology. Antidepressants suppress Electome Factor 2 and 3 to reverse behavioral pathology. Manipulations that suppress Electome Factor 1 in stress-naïve mice remain to be discovered.

While our current and prior findings provide strong support for human studies that frame MDD as a brain circuit/network disorder based in disrupted spatiotemporal dynamics (Drysdale et al., 2017; Greicius et al., 2007; Hultman et al., 2016), here we discovered a naturally occurring spatiotemporal dynamic network that signals vulnerability to cSDS in stress-naïve mice (Electome Factor 1). To demonstrate the reliability of this network, we applied gold-standard validation based on complete out-of-sample testing. We performed this validation in three independent models of MDD vulnerability (P=6.2×10⁻⁴ using Fisher’s combined probability test) to demonstrate that this network was biologically relevant to MDD vulnerability and not solely the cSDS model. Finally, we demonstrated that this network was not affected by our two antidepressant-like manipulations. These findings thus provide clear evidence that Electome Factor 1 encodes a MDD vulnerability pathway that is convergent across many biological conditions that increase risk for MDD. Furthermore, our studies using well-validated antidepressants indicated that this network pathway is biologically distinct from these pathway that signals MDD-like behavioral dysfunction. Such identification of distinct networks representing different biological states demonstrates that our computational approach allows us to discover the network features that organize state-specific information within individual brains. Importantly, we also show that these network features extrapolate across different animals and biological paradigms, addressing a critical challenge that has limited the utility of machine learning to uncover the fundamental mechanisms whereby the brain encodes emotional pathology at the systems level. Future experiments aimed at determining whether our Electome Framework extends to other emotional disorders are warranted.

Finally, we discovered that Electome Factor 2 was enhanced in the stress-naïve mice that exhibited vulnerability to future cSDS stress (Fig. 2D). While this Electome Factor failed validation testing as a convergent vulnerability biomarker in the other MDD models, future studies are warranted to determine the role of this network in mediating naturally occurring differences in vulnerability to chronic social stress. We also found that IFNα treated mice did not show an increase in Electome Factor 2 and 3 activities (Fig. 5F and Supplemental Fig. S3), the two factors that signaled the emergence of behavioral pathology in the cSDS model. This raises the possibility that the behavioral pathology induced by IFNα may be signaled by an Electome Factor that was not observed in the cSDS model. Future experiments in which a unique Electome is learned in the IFNα may clarify this question.

Overall, the identification and validation of a MDD vulnerability neural network in healthy stress-naïve mice raises the potential that brain spatiotemporal dynamics can be exploited to develop a novel class of therapeutics that prevent the emergence of MDD in vulnerable individuals in response to stressful experiences.

STAR Methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Kafui Dzirasa (kafui.dzirasa@duke.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Animal Care and Use

C57BL/6J (C57) male mice purchased from the Jackson Labs and CD1 male mice purchased from Charles River Laboratory were used for cSDS, Sdk1, and IFNα experiments presented in this study. The C57 male mice used for early life stress studies were bred within the Duke Vivarium. C57 mice were housed 3-5 per cage and separated after surgery, and then singly-housed without enrichment four days prior to social defeat. All CD1 mice were retired male breeders. These mice were singly-housed with environmental enrichment. All animals were maintained on a 12-hour light/dark cycle, in a humidity- and temperature-controlled room with water and food available ad libitum.

Studies were conducted with approved protocols from the Duke University Institutional Animal Care and Use Committee and were in accordance with the NIH guidelines for the Care and Use of Laboratory Animals. Except when noted otherwise for early life stress experiments, these studies were conducted using mice that were 8–16 weeks old.

METHOD DETAILS

Neurophysiological data acquisition

Neuronal activity was sampled at 30kHz using the Cerebus acquisition system (Blackrock Microsystems Inc., UT). Local field potentials (LFPs) were bandpass filtered at 0.5–250Hz and stored at 1000Hz. Neuronal data were referenced online against a wire within the same brain area that did not exhibit a SNR > 3:1. At the end of the recording, cells were sorted again using an offline sorting algorithm (Plexon Inc., TX) to confirm the quality of the recorded cells. Only cellular clusters well-isolated with respect to background noise, defined as a Mahanalobis distance greater than 3 compared to the null point, were used for our unit-Electome Factor correlation analysis. Clusters that exhibited more than 99.5% of their inter-spike-interval distribution above 2ms were defined as single units (53% of recorded neurons). Ultimately, we chose to use both single and multi-units for our analysis since our sole objective was to determine whether the Electome Factor Activity showed temporal dynamics that reflected cellular activity. Neurophysiological recordings were referenced to a ground wire connected to both ground screws.

Electrode implantation surgery

Mice were anesthetized with 1.5% isoflurane, placed in a stereotaxic device, and metal ground screws were secured above the cerebellum and anterior cranium. The recording bundles designed to target amygdala (AMY), NAc, VTA, PFC, and VHip were centered based on stereotaxic coordinates measured from bregma (AMY: −1.6mm AP, 2.75 mm ML, −3.9 mm DV from the dura; NAc: 1.6mm AP, 1.4mm ML, −3.5 mm DV from the dura; PFC: 1.7mm AP, 0mm ML, 2.25mm DV from the dura; VTA: −3.3mm AP, 0.5 mm ML, −4.25 mm DV from the dura; (VHip: −3.7mm AP, 3.0mm ML, −3.5mm DV from the dura). We chose these coordinates to match the coordinates utilized in our prior molecular studies in the cSDS model (Bagot et al., 2016). We targeted PrL and IL using the PFC bundle by building a 0.5mm DV stagger into our electrode bundle. The cSDS cohort of animals was implanted bilaterally in PFC. All other animals were implanted on the left side. We targeted BLA and CeA by building a 0.5mm ML stagger and 0.3mm DV stagger into our AMY electrode bundle. Histological analysis of implantation sites was performed at the conclusion of experiments to confirm recording sites used for neurophysiological analysis.

Homecage recordings

Mice were connected to a headstage (Blackrock Microsystems, UT, USA) without anesthesia, and placed in a new home cage. Recordings were initiated after a 30-min habituation period.

Forced interaction test

The forced interaction test was performed as previously described (Hultman et al., 2016; Kumar et al., 2014). Notably, a homecage recording was always performed immediately prior to the start of the forced interaction test. C57 mice were placed in a 3.25” × 7” Plexiglas cylinder. Following a 5-min recording period during which neurophysiological activity was recorded, a CD1 aggressor mouse was introduced to the cage outside of the cylinder (18” high walls surround the outer cage to prevent escape and a lid is place over the inner chamber to prevent the aggressor from climbing in). Neurophysiological data were then recorded for five additional minutes. Mice used to build the Electome model were subjected to the forced interaction test prior to and after exposure to cSDS. Mice used for the Sdk1 overexpression experiment were subjected to the forced interaction test prior to and after viral infection. Mice used for the IFNα and maternal separation stress experiments were only subjected to the forced interaction test once in adulthood.

Chronic social defeat stress

Mice implanted with electrodes underwent 10 days of cSDS as previously described (Berton et al., 2006; Hultman et al., 2016; Krishnan et al., 2007). Specifically, male retired-breeder CD1 (Charles River) mice were used as resident aggressors for the social defeat and were singly-housed prior to the experiments. C57 mice were then randomly assigned to control or defeat groups such that no entire cage was assigned to the same group. All C57 mice were singly housed prior to being subjected to cSDS. Particularly aggressive CD1s, as defined by demonstrating at least one successful act of aggression toward an intruder C57 male within 60 secs, were selected for use for cSDS. Intruder male C57 mice were introduced to the cage of a novel CD1 aggressor for 5 min daily, and then housed adjacent to the same aggressor for 24 hrs. During this time, mice were separated by a transparent and porous plexiglass barrier to enable constant sensory exposure.

During bouts of exposure to the CD1 mice, hallmark behavioral signs of subordination stress were observed including escape, submissive postures (i.e., defensive upright and supine) and freezing. Following the last 24-hr exposure to a CD1 aggressor mouse, all C57s were housed individually. Mice that exhibited significant injuries during social defeat stress were removed from post-stress analysis (Hultman et al., 2016). Several animals used to construct the initial cSDS Electome model were also used in our prior study (Hultman et al., 2016). Neither the pre-stress data presented in this study nor any neurophysiological activity from VHip were used for any prior analysis.

Choice social interaction test

Mice were placed within a novel arena (46cm × 46cm) with a small cage located at one end, and each mouse’s movement was monitored for 150 seconds. Mice were then removed from the testing chamber, and reintroduced 30 seconds later after a non-aggressive CD1 mouse was placed in the small cage. The time C57 mice spent in the interaction zone was quantified using Ethovision XT 7.1 software (Noldus Information Technology, Wageningen, Netherlands). The interaction ratio was calculated as (Interaction time when CD1 was present)/(Interaction time when CD1 was absent) (Hultman et al., 2016; Kumar et al., 2014).

Discriminative Cross-Spectral Factor Analysis (dCSFA)

Prior to the application of our machine learning framework to the data, there are several preprocessing steps. The raw data consists of multiple electrode channels for each brain region. First, the raw data channels for each region are averaged together. Then the data is notch filtered at 60Hz to remove electrical line noise. The recordings are normalized such that signal from each electrode within each window has a mean of 0 and standard deviation of 1. The data is then subsampled to 200Hz from the original sampling rate of 1000Hz for computational and memory efficiency.

Within each window, the statistical model assumes that the signal is stationary, meaning that relevant dynamics occur at the level of windows. Prior work has shown relative robustness for window sizes between .5 seconds and 10 seconds (Ulrich et al., 2015). Briefly, each time-window includes N observations from R distinct brain regions. N is determined by the sampling rate and the length of time that each window represents. For a 5-sec window subsampled at 200Hz, N is 1000. We represent the matrix of observations from window w by ${\mathit{Y}}^w=\left[{\mathit{y}}_1^w,\dots ,{\mathit{y}}_N^w\right]\in {\mathrm{ℝ}}^{R\times N}$. These observations are located on a uniformly spaced temporal grid, such that each ${\mathit{y}}_n^w$ corresponds to the relative time location $x_n^w$ within the window. The difference between subsequent temporal samples is given by $x_n^w-x_{n-1}^w\triangleq \delta$ where 1/δ represents the sampling rate of the LFP time-series (note that 1/δ = 200 Hz from the sampling rate). The set of time locations sampled in window w is denoted x^w.

These data were processed with a discriminative cross-spectral factor analysis model, where the contribution of each factor to the signal within a window was modeled as a draw from a multi-output Gaussian process. The full set of Gaussian processes, each corresponding to one factor, allow us to capture brain spatiotemporal dynamical features in an integrated brain-wide model. This methodology has been previously published (Gallagher et al., 2017), and we include all key steps below.

To allow the individual factors to discover LFP features that incorporate spectral power, synchrony and phase-directionality between many brain regions, the factors were modeled by a multi-output Gaussian process within a multiple-kernel-learning framework (Gönen and Alpaydın, 2011). Gaussian processes are non-parametric probabilistic descriptions of data that offer a powerful basis for non-linear multivariate regression and classification tasks. They are widely utilized in the machine learning literature. The probabilistic relationship between data are determined by the Gaussian process “kernels” that describe covariance relationships between individual data points. We recently designed a Gaussian process kernel termed the Cross-Spectral Mixture (CSM) kernel, which targets spectral power, synchrony and phase-directionality between many brain regions (Ulrich et al., 2015). In dCSFA, we model our data as contributions from multiple Electome Factors, where each factor is defined by a single CSM kernel. By windowing the data, we track the expressed strength of these factors over time. We model each temporal observation in a window by

$${\mathit{Y}}^w={\displaystyle {\sum }_{\mathrm{\ell }=1}^L{s}_{w\mathrm{\ell }}{\mathit{F}}_w^{\mathrm{\ell }}\left(\mathit{x}\right)}+{\mathit{\epsilon }}^w$$

where ε^w ∈ ℝ ^R × ^N is additive Gaussian noise where each entry is drawn independently with precision (i.e. inverse variance) γ. The parameters s_w = [s_w1,…,s_wL]^T are a vector of factor scores, and are unique to each time window. The factor scores denote how strongly each Electome Factor is expressed in that window, and can be interpreted approximately as the amount of signal variance associated with the corresponding factor. Importantly, the ℓ^th latent function (denoted by ${\mathit{F}}_w^{\mathrm{\ell }}\left(\mathit{x}\right)$) has a different instantiation for every window, and represents the contribution of the ℓ^th factor to that window. For all windows, ${\mathit{F}}_w^{\mathrm{\ell }}\left(\mathit{x}\right)$ is independently drawn from the same distribution. These functions are not directly shared across time windows; rather, the underlying cross-spectral content (power and phase synchrony) of the signals is shared and implied by the distribution. To obtain this effect, a distribution over the latent functions is used to encode the full cross-spectrum, given by a multi-output Gaussian process (A. et al., 2011; Rasmussen and Williams, 2006).

$${\mathit{F}}_w^{\mathrm{\ell }}\left(\mathit{x}\right)\sim \mathcal{G}\mathrm{P}\left(\mathbf{0},{\mathit{K}}_{\text{CSM}}\left(\cdot ,\cdot ;{\mathit{\theta }}_{\mathrm{\ell }}\right)\right),$$

where the covariance kernel K_CSM(x, x′; θ_ℓ) establishes the Gaussian covariance structure between all latent function values ${\mathit{F}}_w^{\mathrm{\ell }}=\left[{\mathit{f}}_w^{\mathrm{\ell }}\left(x_1^w\right),\dots ,{\mathit{f}}_w^{\mathrm{\ell }}\left(x_N^w\right)\right]$. Mathematically, ${\left({\mathit{K}}_{\text{CSM}}\left(x,x^{\prime };{\mathit{\theta }}_{\mathrm{\ell }}\right)\right)}_{ij}\triangleq \mathrm{cov}\left(f_{wi}^{\mathrm{\ell }}\left(x\right),f_{wj}^{\mathrm{\ell }}\left(x^{\prime }\right)\right)$; in words, this defines how the function ${\mathit{F}}_w^{\mathrm{\ell }}$ at time x in region i covaries with the same function at time x′ in region j. The multi-output Gaussian process structure models the signal as a multivariate normal. Specifically,

$$\text{vec}\left({\mathit{F}}_w^{\mathrm{\ell }}\right)\sim N\left(\mathbf{0},\sum \right),$$

where “vec” denotes the vectorization of the matrix, and Σ denotes a covariance matrix constructed by evaluating the covariance kernel at the appropriate points x^w. The CSM covariance kernel represents the cross-spectra between the R regions as the real part of a complex mixture of Q Gaussians defined in the frequency domain (Ulrich et al., 2015; Wilson and Adams, 2013).

$${\mathit{K}}_{\text{CSM}}\left(x,x^{\prime };{\mathit{\theta }}_{\mathrm{\ell }}\right)=\mathrm{Re}\left\{{\displaystyle \sum _{q=1}^Q{\mathit{B}}_q^{\mathrm{\ell }}{k}_{sg}\left(x,x^{\prime };{\mu }_q^{\mathrm{\ell }},{\nu }_q^{\mathrm{\ell }}\right)}\right\},$$

where ${\mathit{B}}_q^{\mathrm{\ell }}\in {\mathrm{ℂ}}^{R\times R}$ is the coregionalization matrix, and k_sg is a spectral Gaussian kernel. The covariance kernel parameters are given as ${\mathit{\theta }}_{\mathrm{\ell }}=\left\{{\mathit{B}}_q^{\mathrm{\ell }},{\mu }_q^{\mathrm{\ell }},{\nu }_q^{\mathrm{\ell }}\right\}$, defining a unique stationary CSM kernel (Ulrich et al., 2015). These parameters θ_ℓ directly map to power and phase coherence.

$$k_{sg}\left(x,x^{\prime };{\mu }_q^{\mathrm{\ell }},{\nu }_q^{\mathrm{\ell }}\right)=\exp \left(-\frac{1}{2}{\nu }_q^{\mathrm{\ell }}{\left(x-x^{\prime }\right)}^2+j{\mu }_q^{\mathrm{\ell }}\left(x-x^{\prime }\right)\right),$$

where j. represents $\sqrt{-1}$. The spectral Gaussian kernel gives a covariance structure that is equivalent to a power spectral density that is a Gaussian distribution in the frequency domain centered at frequency ${\mu }_q^{\mathrm{\ell }}$ and with variance ${\nu }_q^{\mathrm{\ell }}$. The coregionalization matrix ${\mathit{B}}_q^{\mathrm{\ell }}$ applies a relative scale and phase-shift to the corresponding spectral Gaussian kernel for spectral density that we wish to model. We model a spectral density for each area and pair of areas, with the diagonal entries of ${\mathit{B}}_q^{\mathrm{\ell }}$ corresponding to the power-spectral densities for individual areas and non-diagonal entries corresponding to cross-spectral densities for every pair of areas. The coregionalization matrix is also limited to a rank-R structure, which reduces the total number of parameters in the model and reduces overfitting. This is constrained by using the parameterization ${\mathit{B}}_q^{\mathrm{\ell }}={\stackrel{\sim }{B}}_q^{\mathrm{\ell }}{({\stackrel{\sim }{B}}_q^{\mathrm{\ell }})}^{†}$, where ${\stackrel{\sim }{B}}_q^{\mathrm{\ell }}\in {\mathrm{ℂ}}^{C\times \mathrm{R}}$ is in the complex domain and † is the conjugate transpose. ${\stackrel{\sim }{B}}_q^{\mathrm{\ell }}$ is then learned from the data instead of learning ${\mathit{B}}_q^{\mathrm{\ell }}$ directly. For identifiability in the factor model, the CSM kernels are restricted to a correlation function such that max(diag(K_CSM(0,0;θ_ℓ))) = 1 for all ℓ

During inference, all latent functions are marginalized out and gradient-based optimization is used to obtain the set of parameters $\mathbf{\Theta }=\{{\left\{{\mathit{\theta }}_{\mathrm{\ell }}\right\}}_{\mathrm{\ell }=1}^L,{\left\{{\mathit{s}}_w\right\}}_{w=1}^W\}$ that maximize the log marginal likelihood, ln p (Y|Θ) (Rasmussen and Williams, 2006). We choose the iRprop-learning algorithms for optimization (Igel and Husken, 2003). The model parameters are learned over iterative steps until the model has reached the convergence criterion, indicating that further steps will not produce significant improvement of the model. The convergence criterion is considered to have occurred if the average relative change over all parameters was less than a chosen threshold χ for 10 consecutive learning iterations. For training the initial model, we let χ be 0.001.

The approach described above is completely unsupervised (does not use label/task/behavioral information); however, it is often beneficial to uncover data-fitting latent structure while also inheriting strong predictive power pertaining to recorded side information (e.g., task condition or whether an animal was subject to chronic social defeat stress). In the discriminative CSFA (dCSFA) model, a supervised max-margin formulation (Zhu et al., 2009) influences factor score learning such that the scores s_w and the CSM kernels are more predictive of this side information, thereby encouraging the model to extract latent features relevant to the electrophysiological signatures of these conditions.

Each window is provided a binary class label z_w ∈ {−1,1}. Denoting a ∘ b as the elementwise vector product, we desire the squared factor scores ${\stackrel{\sim }{s}}_w={\mathit{s}}_w\circ {\mathit{s}}_w\in {\mathrm{ℝ}}^L$ to be predictive of the class label z_w for each window w. Max-margin optimization problems attempt to find the optimal hyperplane that separates the two classes (Cortes and Vapnik, 1995). In particular, classification parameters Ψ are introduced, and a linear discriminant function is defined by $g\left({\stackrel{\sim }{s}}_w;\mathbf{\Psi }\right)={\mathit{\beta }}^T{\stackrel{\sim }{s}}_w+b$, with Ψ = {β, b}. The classification rule ${\widehat{z}}_w=\text{sign}\left(g\left({\stackrel{\sim }{s}}_w;\mathbf{\Psi }\right)\right)$ is used to form a prediction of the class label. The optimization problem is then set up as a composite objective function consisting of the original CSFA objective and the classification objective,

$$\underset{\mathbf{\Theta },\mathbf{\Psi }}{\arg min}{\displaystyle \sum _{w=1}^W-\log p\left({\mathit{Y}}^w|\mathbf{\Theta }\right)}+\lambda {\left(1-z_{w}g\left({\stackrel{\sim }{s}}_w;\mathbf{\Psi }\right)\right)}_{+}+\frac{1}{2}{\Vert \mathit{\beta }\Vert }^2.$$

The second term of the previous equation enforces maximum separation between classes by penalizing on the hinge loss function ${(1-z_{w}g({\stackrel{\sim }{s}}_w;\mathbf{\Psi }))}_{+}=0$ for all windows, where (x)₊ = max(0, x), An ℓ₂ - regularization penalty is placed on β for identifiability. The algorithm setting of λ controls the relative emphasis of the classifier during learning, as compared to the log-likelihood term. A gradient method is used to jointly optimize the factor analysis parameters Θ. To increase the interpretability of the approach, the classifier is typically limited to use only a subset of the learned factors for class prediction.

We note a few unique aspects of this approach. 1) While prediction is often performed in a downstream processing component (e.g., first fit a latent factor model, then train an SVM independently on the factor scores), the ability to jointly infer model parameters with a max-margin model improves predictive power while simultaneously uncovering latent structure (Zhu et al., 2009). 2) The factor scores in the Gaussian process factor model are a non-linear embedding of the multi-channel time-series observations; this embedding is analogous to a non-linear version of supervised dictionary learning (Mairal et al., 2010) and to interpretable descriptive neural networks (Pu et al., 2015) with imposed structure on cross-spectral density estimation.

Projecting new data into the ‘Factor Space’

After the network has been trained, the learned feature representation can be applied to novel data by ‘projecting’ the new data onto the original set of factors. Given a new window ${\mathit{Y}}^{w^{\ast }}$, then the electome factor parameters are fixed and only the factor scores are learned with the objective of minimizing the negative log likelihood

$$\begin{array}{c}\arg min\\ {\mathbf{s}}_{w^{\ast }}\end{array}-\log p({\mathit{Y}}^{w^{\ast }}|{\mathbf{s}}_{w^{\ast }},{\left\{{\mathit{\theta }}_{\mathrm{\ell }}\right\}}_{\mathrm{\ell }=1}^L).$$

This optimization is calculated via the same gradient iterative methods described above. For fitting all of the non-training datasets in this work, we let the convergence threshold χ be 0.01.

In some cases, the set of recorded brain regions in a new window does not match the set of regions that the CSFA model was trained on. Because the latent factor analysis is a generative model, this data can be still projected to the original factor set by removing the unobserved channels from the log-likelihood calculation under a Missing Completely at Random (MCAR) assumption. Because of the Gaussian formulation, the mathematical form is analytic. Specifically, the missing channels can be marginalized out of the covariance kernel for each factor. The resulting likelihood can then be used to learn the feature scores with the same gradient methods as above. Therefore, datasets with different measured brain regions can be projected and compared in the same space.

Hyper-parameter selection

Our objective in training was to learn four predictive features (±chronic stress, susceptibility/resilience, the empty segment of the forced interaction test, and the CD1 segment of the forced interaction test). The hyperparameter settings for the model were chosen as follows: We chose to use 25 total factors based on a leave-one-animal-out cross-validation scheme. We chose to include 6 predictive factors to allow for model flexibility in solving the predictive learning task. Predictions on the classification task were limited to those six factors to force a compact, scientifically testable and statistically friendly hypothesis space. For learning the initial model, the noise precision (γ) was chosen to be 200, the number of spectral Gaussians kernels per factor (Q) was chosen to be 20, and the rank of ${\mathit{B}}_q^{\mathrm{\ell }}\left(R\right)$ was chosen to be 2, all based on previous work (Ulrich et al., 2015). The objective ratio parameter (λ) was chosen to be 50. For projecting new datasets into the factor space from the initial model, γ was chosen to be 0.1.

Data sets

We used a total of 44 C57 mice for our dCSFA analysis. We used 19 mice subjected to cSDS and 16 non-stressed controls in the post-stress data. All 35 of these mice were also used in the pre-stress data group. Data from 9 additional mice were included in the pre-stress, but not post-stress, data set. Adding these 9 mice assured that the predictive factors learned for the home cage—forced interaction test segments did not contain mouse specific signals that yielded incidental putative vulnerability signatures in the pre-stress data set.

The initial cSDS training data was split into a training dataset and a testing data set. Specifically, 30% of the data windows were held out from training to serve as a test set. Note that datasets collected after the initial model was trained were not used to choose model parameters and can be treated as a true validation or hold-out set. This includes datasets collected for the sdk1, IFNα, ELS, ketamine, and SSFO experiments.

Spike-Electome Factor activity correlation

Data acquired during the ‘post-stress’ forced interaction test were used for this analysis. Unit firing activity was averaged within 5-sec non-overlapping windows for the 20-min recording period (10 min home cage, 10 min forced interaction test). A Rho_Raw was calculated for each spike and Electome Factor correlation using the spearman rank test. We then randomly shuffled the bins of spike activity within the homecage and each segment of the forced interaction test, and recalculated the spearman rank to yield a Rho_Rand. We repeated this shuffling procedure 10,000 times to yield a distribution of correlation values expected by chance between each unit and Electome Factor and ranked the resulting Rho_Rand values. The Electome Factor coefficient score for a unit was then defined as Rho_Raw-Σ(Rho_Rand)/10,000. Electome Factor-Spike coefficient was considered significant for Rho_Raw values less than the 62^nd lowest Rho_Rand or higher than the 9,937^th highest Rho_Rand value of the chance distribution (corresponding to an α=0.05 with Bonferroni correction for the 4 Electome Factors tested).

Sdk1 viral surgery for accelerated defeat

Mice were anaesthetized with ketamine (100mg/kg) and xylazine (10mg/kg) and placed in a small-animal stereotaxic instrument (Kopf Instruments). HSV virus (0.5μL of either HSV-Sdk1 or HSV-GFP) was bilaterally infused using 33-gauge syringe needles (Hamilton) into the vHIP (bregma coordinates: anterior/posterior, −3.7 mm; medial/lateral, 3 mm; dorsal/ventral, −4.8 mm; 0° angle; targeting ventral subiculum). Two days after viral infusion, the animals underwent an accelerated defeat protocol in which they were subjected to social defeat stress twice daily for 10 min over four days.

Sdk1 viral surgery for neurophysiological recordings

We developed the “cannutrode” system to infuse virus into previously implanted animals and thereby quantify the effect of VHip-Sdk1 overexpression using a within-subject design. For in vivo recording experiments, animals were implanted with recording electrodes as specified above. A cannula was built into the microwire bundle targeting left VHip. Additionally, a 360μm diameter cannula (MicroLumen, Oldsman, FL) was implanted above right VHip, both of the cannulas were implanted to a depth of 1mm. After the initial forced interaction test experiment, mice were anesthetized with 1.5% isoflurane, and a 33-gauge Hamilton syringe was used to bilaterally infuse 0.5 μl HSV vector at a rate of 0.1 μl/min through the cannula into VHip.

This cannutrode system was critical for using HSV viruses to interrogate the impact of molecular pathways on Electome Factor activity, since our mice required 10–14 days to recover from electrode implantation, and HSV transgene expression is limited to 1–5 days after infection.

Viral histology

Animals were perfused with 4% paraformaldehyde and brains were harvested and stored for 24 hrs in PFA. Brains were cryoprotected with sucrose and frozen in OCT compound and stored at −80C. Brains were sliced at 35μm and stained using anti-GFP (ThermoFisher, Waltham, MA) and Alexa488-anti-rabbit (ThermoFisher, Waltham, MA) antibodies using standard methods. Images were obtained using a Nikon Eclipse fluorescence microscope at 4x and 10x magnifications.

IFNα dosing

We utilized an IFNα administration protocol that has been previously shown to induce MDD-like behavior in mice (Zheng et al., 2014). Briefly, mice were assigned by cage to control and experimental groups randomly. Mice were then injected with either mouse IFNα (4×10⁵IU/kg i.p; Miltenyi Biotec, Auburn, CA) diluted in phosphate-buffered saline (PBS) or a PBS vehicle for 5 weeks. Implanted animals were tested in the sucrose preference test and forced interaction test. Non-implanted animals were tested in the social interaction test and open field. Animals continued to receive daily injections throughout the course of the study.

Three chamber social interaction test

A plexiglass box 60.7cm × 43.2cm × 21.6cm with four clear outside walls and a double-sided mirror base was used. Infrared video recordings were collected from beneath. Two plastic cages were put on each side of the box one empty and the other containing the social target, a male C57 of the same age. The mice were habituated four times prior to testing by: placing the mouse in the arena with each of the plastic cages empty (i.e., no novel object or social target) and allowed free exploration for 10 minutes. Testing trials lasted 10 minutes where each mouse was allowed to freely explore the chambers.

Maternal separation and social defeat stress

Maternal separation was performed as described previously(Sachs et al., 2013). Briefly, the experimental pups were separated from their dams for three hours each day on post-natal days (PNDs) 1–14, and control pups were reared under standard conditions. Litters were assigned to control and experimental groups in random pairs, such that each experimental litter has an aged-matched control. During the separation period, the pups were placed on a heating pad and remained in contact with their littermates. Animals were weaned on day 21.

For behavioral experiments, males were subjected to SDS starting when they were eight-ten weeks old (or were left as controls). For the SDS paradigm, experimental mice were introduced into the home cage of a singly housed resident CD1 male for five minutes a day for ten days. These mice were then introduced into the home cage of a new CD1 male mouse each day. On day 11, mice were tested for social avoidance behavior. For in vivo physiology experiments, animals were implanted at 14–16 weeks, and the forced interaction test was performed after a 2-wk recovery period.

SSFO experiments

Mice were anesthetized with 1.5% isoflurane and placed in a stereotaxic device. A 33-gauge Hamilton syringe was used to infuse 0.5 μl of AAV2-CaMKIIa-SSFO-EYFP vector at a rate of 0.1 μl/min into left IL_Cx (1.7mm AP, 0.25mm ML, 2mm DV from the dura). An AAV2-Ef1a-DIO-SSFO-EYFP vector was used a non-expressing control. CaMKII and DIO surgeries were conducted alternately such that animals’ experimental recording timeline was distributed randomly. Two weeks after viral surgeries, mice were anesthetized again, and recording electrodes will implanted as described above. A fiberoptic cannula was built into the IL_Cx/PrL_Cx bundle (Hultman et al., 2016; Kumar et al., 2013). The tip of the 100μm diameter fiberoptic (Doric Lenses) was situated 250μm above the tip of the IL recording microwires (i.e., targeting the dorsal IL_Cx border). In vivo recordings and stimulations were conducted after 2 weeks of recovery. Light stimulation was delivered at 1.5 mW (473nm wavelength, CrystaLaser, CL473-025-O), and the laser output was verified using a Power meter (Thorlabs, PM100D). SSFO expression was confirmed histologically in IL_Cx in 6 out of the 8 animals. Five of the six SSFO mice showed a strong suppression of IL_Cx gamma activity immediately following blue light stimulation. None of the DIO-SSFO mice exhibited this physiological response, thus the one SSFO mouse that did not demonstrate IL_Cx gamma suppression was removed from subsequent analysis in the IL_Cx-DBS study.

Ketamine experiments

Mice used for SSFO experiments were used for ketamine experiments after a 1 week “washout” period to return to baseline. Mice were pseudorandomized to the ketamine or saline group such that half of the mice in each group were infected with SSFO, and the other half were infected with DIO-SSFO. This pseudo randomization was performed in order to avoid any confounds that may have resulted from prior IL_Cx-DBS. Mice were injected with ketamine (20mg/kg, i.p.) twenty-four hours prior to the forced interaction test. Critically, while prophylactic administration of ketamine (20mg/kg, i.p.) has been shown to prevent the subsequent emergence of behavioral dysfunction in 129S6/SvEv strain mice subjected to cSDS (Brachman et al., 2016), this ketamine administration strategy is not effective is preventing stress induced behavioral dysfunction in C57 mice (Brachman et al., 2016; Donahue et al., 2014). Ketamine (Ketathesia®, Henry Schein, 100mg/mL) was diluted in saline to a concentration of 5mg/mL prior to administration.

QUANTIFICATION AND STATISTICAL ANALYSIS

Statistical analysis was performed using MATLab software R2016a (Mathworks). We used machine learning to define behaviorally relevant Electome Factors. Post-hoc testing was not performed on the across-group differences observed post-stress since this was a learned feature of our dCSFA model. The stress-susceptibility/resilience identities of animals was not utilized to supervise training of the pre-stress neural data. Thus, pre-stress differences in Electome Factor activity could be quantified. This was accomplished using a two-tailed Wilcoxon rank-sum test at α=0.05, and the area under of the curve of the receiver operating characteristic. We did not correct for multiple comparisons in this analysis since our chosen strategy was to validate all of the significant Electome Factor differences using complete out-of-sample testing. Our a priori hypothesis for this subsequent validation testing was that other MDD vulnerability models would show the same Electome Factor differences identified in the vulnerable mice prior to cSDS. All out-of-sample testing to validate Electome Factor 1 and Electome Factor 2 as signatures of stress-vulnerability (sdk1, IFNα, and ELS) was performed using a one-tailed Wilcoxon rank-sum test. Using this one-tailed testing strategy allowed us to constrain the number of animals needed per group while retaining statistical power. Finally, we combined the p-values for the three independent validations sets using a Fisher’s combined probability test. With this approach, we were able to increase the number of independent validation paradigms (5 total independent validation experiments for the study, with 6–8 animals per manipulation or control group for each experiment). The correlation between unit firing and Electome Factor activity was tested using a Spearman Regression with bootstrapping. A Bonferroni correction was applied to account for the 4 Electome Factors tested.

For testing aimed at validating MDD-related behavior inducing effect of the previously published sdk1 model, we used a two-tailed Wilcoxon rank-sum test to compare the post-stress social interaction ratio of mice that overexpressed sdk1 versus controls. We used a Two-way ANOVA to test whether sdk1 overexpression impacted normal social behavior, and a two-tailed un-paired t-test to test whether this manipulation impacted immobility time in the forced swim test. To test the impact of IFNα on social behavior, we used a Mixed Model ANOVA. We determined both the Group effect (between subject) and the Social effect (within subject) for the IFNα and vehicle treated animals. Post-hoc testing was performed with a paired two-tailed t-test for the within subject analysis, and an un-paired two-tailed t-test for the between subject analysis. For the sucrose preference experiment, we first established the paradigm in an independent cohort of C57 mice (see supplemental Figure S1). This initial analysis was performed using a two-tailed paired t-test. We then tested our a priori hypothesis that mice chronically treated with IFNα would show a disruption in sucrose preference while mice treated with a vehicle would not. This was achieved with two-tailed paired t-tests. For testing establishing MDD-related behavior in the ELS-vulnerability model for which there was no prior literature, our statistical analysis was performed using a Two-way ANOVA. All post-hoc testing was performed using un-paired two-tailed t-tests.

Our a priori hypothesis for the anti-depressant manipulation validation studies was that anti-depressive therapeutics (IL-DBS or ketamine) would fail to suppress Electome Factor 1 activity. We used a one-tailed Wilcoxon rank-sum test for this analysis. Using this one-tailed testing strategy allowed us to constrain the number of animals needed per group while retaining statistical power. We also tested the effect of these manipulations on Electome Factor 2 and 3 activity. Electome Factor 2 and 3 activity was increased in the mice that exhibited MDD-like behavioral dysfunction after cSDS. Nevertheless, since our experiments were performed in stress-naïve mice, our a priori hypothesis was that these antidepressant manipulations would have no impact on Electome Factor 2 or 3. We used a mixed-model-ANOVA (with Box—Cox Transformation) for this analysis. Post-hoc testing was performed with a two-tailed Wilcoxon rank-sum test.

DATA AND SOFTWARE AVAILABILITY

Code base for dCSFA analysis can be found at: https://github.com/neil-gallagher/CSFA

KEY RESOURCES TABLE

The table highlights the genetically modified organisms and strains, cell lines, reagents, software, and source data essential to reproduce results presented in the manuscript. Depending on the nature of the study, this may include standard laboratory materials (i.e., food chow for metabolism studies), but the Table is not meant to be comprehensive list of all materials and resources used (e.g., essential chemicals such as SDS, sucrose, or standard culture media don’t need to be listed in the Table). Items in the Table must also be reported in the Method Details section within the context of their use. The number of primers and RNA sequences that may be listed in the Table is restricted to no more than ten each. If there are more than ten primers or RNA sequences to report, please provide this information as a supplementary document and reference this file (e.g., See Table S1 for XX) in the Key Resources Table.

Please note that ALL references cited in the Key Resources Table must be included in the References list. Please report the information as follows:

• REAGENT or RESOURCE: Provide full descriptive name of the item so that it can be identified and linked with its description in the manuscript (e.g., provide version number for software, host source for antibody, strain name). In the Experimental Models section, please include all models used in the paper and describe each line/strain as: model organism: name used for strain/line in paper: genotype. (i.e., Mouse: OXTR^fl/fl: B6.129(SJL)-Oxtr^tm1.1Wsy/J). In the Biological Samples section, please list all samples obtained from commercial sources or biological repositories. Please note that software mentioned in the Methods Details or Data and Software Availability section needs to be also included in the table. See the sample Table at the end of this document for examples of how to report reagents.

• SOURCE: Report the company, manufacturer, or individual that provided the item or where the item can obtained (e.g., stock center or repository). For materials distributed by Addgene, please cite the article describing the plasmid and include “Addgene” as part of the identifier. If an item is from another lab, please include the name of the principal investigator and a citation if it has been previously published. If the material is being reported for the first time in the current paper, please indicate as “this paper.” For software, please provide the company name if it is commercially available or cite the paper in which it has been initially described.

• IDENTIFIER: Include catalog numbers (entered in the column as “Cat#” followed by the number, e.g., Cat#3879S). Where available, please include unique entities such as RRIDs, Model Organism Database numbers, accession numbers, and PDB or CAS IDs. For antibodies, if applicable and available, please also include the lot number or clone identity. For software or data resources, please include the URL where the resource can be downloaded. Please ensure accuracy of the identifiers, as they are essential for generation of hyperlinks to external sources when available. Please see the Elsevier list of Data Repositories with automated bidirectional linking for details. When listing more than one identifier for the same item, use semicolons to separate them (e.g. Cat#3879S; RRID: AB_2255011). If an identifier is not available, please enter “N/A” in the column.

  • ○A NOTE ABOUT RRIDs: We highly recommend using RRIDs as the identifier (in particular for antibodies and organisms, but also for software tools and databases). For more details on how to obtain or generate an RRID for existing or newly generated resources, please visit the RII or search for RRIDs.

Please use the empty table that follows to organize the information in the sections defined by the subheading, skipping sections not relevant to your study. Please do not add subheadings. To add a row, place the cursor at the end of the row above where you would like to add the row, just outside the right border of the table. Then press the ENTER key to add the row. Please delete empty rows. Each entry must be on a separate row; do not list multiple items in a single table cell. Please see the sample table at the end of this document for examples of how reagents should be cited.

TABLE FOR AUTHOR TO COMPLETE

Please upload the completed table as a separate document. Please do not add subheadings to the Key Resources Table. If you wish to make an entry that does not fall into one of the subheadings below, please contact your handling editor. (NOTE: For authors publishing in Current Biology, please note that references within the KRT should be in numbered style, rather than Harvard.)

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Anti-GFP (polyclonal)	ThermoFisher	A-11122
Bacterial and Virus Strains
AAV2-CaMKIIa—hChR2 (C128S/D156A)-eYFP	Duke Viral Vector Core, Durham, NC	Collection no. 134
HSV-Sdk1-GFP	Laboratory of Rachael Neve, Massachusetts Institute of Technology, Cambridge, MA	N/A
HSV-GFP	Laboratory of Rachael Neve, Massachusetts Institute of Technology, Cambridge, MA	N/A
AAV2-Ef1a-DIO- hChR2 (C128S/D156A) eYFP	Duke Viral Vector Core, Durham, NC	Collection no. 136
AAV2-CaMKIIa-eYFP	Duke Viral Vector Core, Durham, NC	Collection no. 10
Biological Samples
Chemicals, Peptides, and Recombinant Proteins
buspirone	Sigma	Cat no. B7148-5G
ketamine	Ketathesia®, Henry Schein	Reorder # 056344
IFNα	Miltenyi Biotec	Cat no. 130-093-130
NeuroTrace 500/525 Green Fluorescent Nissl Stain	ThermoFisher Scientific	Cat no. N21480
Critical Commercial Assays
Deposited Data
Experimental Models: Cell Lines
Experimental Models: Organisms/Strains
Mouse: C57BL/6J	Jackson Labs	RRID:IMSR_JAX:000 664
Mouse: CD1	Charles River Laboratories	RRID:IMSR_CRL:22
Oligonucleotides
Recombinant DNA
Software and Algorithms
MATLab R2016a	Mathworks	https://www.mathworks.com/
Ethovision XT 7.1	Noldus	http://www.noldus.com/animal-behavior-research/products/ethovision-xt
dCSFA code	This Paper	https://github.com/neil-gallagher/CSFA
Other

Supplementary Material

1

Supplemental Figure S1: Example of autocorrelation and cross-correlation functions that define an Electome Factor, related to Fig. 2. Brain areas are shown to the top and the left (red) identifying auto-correlation and cross-correlation density functions for Electome Factor 1. Amplitude values reflect the relative LFP spectral energy observed at each frequency, where each Electome Factor is normalized to the total energy observed across all of the 25 factors. Phase offsets for each cross-correlation density functions are also shown in purple (i.e. directionality; axis scale to the right). Positive phase offsets correspond to frequencies at which the area listed along the left leads the area listed on the top. Negative phase offsets correspond to the frequencies at which the area listed on the top leads the area listed on the left. The circular plot depicts the frequencies for power (outer rim) and coherence (curved lines connecting two regions) above an amplitude threshold of 0.08. As a representative example, the power measures for infralimbic cortex (IL_Cx) are highlighted in bright green in both the circular and correlation plots; coherence between IL_Cx and basolateral amygdala (BLA) are highlighted in magenta.

Supplemental Figure S2: Establishment of sucrose preference assay in C57 mice, related to Fig. 5. C57 mice were placed in the testing chamber for one hour on two consecutive days. Preference for sucrose was observed across the population on the second, but not first testing day (t₉=0.86 and P=0.41; t₉= 2.7 and P=0.026 for Day 1 and Day 2, respectively, using two-tailed paired t-test. n=10 mice). Data are represented as mean ± SEM.

Supplemental Figure S3: Electome Factor 3 activity tends to be increased in one translational model of MDD vulnerability, related to Fig. 5. Electome Factor 3 Activity was averaged and plotted for each phase of the homecage–FIT. Treatment with IFNα failed to increase Electome Factor 3 activity (F_1,28=0.05, P=0.41 for group effect). Early life stress tended to increase Electome Factor 3 activity, though these differences did not reach statistical significance (F_1,20=2.8, P=0.06 for group effect).

Supplemental Figure S4: Spectral plots showing LFP activity in NAc and BLA prior to and following IL_Cx light stimulation, related to Fig. 6. A) Our IL_Cx-DBS protocol suppressed Electome Factor 2 activity. The suppression did not solely reflect stimulation induced changes in local IL_Cx oscillatory activity. B) No stimulation effects were observed in a mouse infected with an AAV2-CaMKIIa-EYFP vector in IL.

Supplemental Figure S5: Validation of Electome Factor 1 encoding distinct emotional states, related to Fig. 1 and 2. A) Treatment with the anxiolytic agent, Buspirone, does not impact the Electome Factor 1 vulnerability biomarker. We treated eight implanted mice with saline and subjected them to our home cage—FIT protocol. Three days later, we treated these mice with saline (n=4) or Buspirone (1.5mg/kg, i.p; n=4), and repeated the FIT. Treatment with Buspirone had no impact on Electome Factor 1 activity during the FIT-CD1 period (P =0.69 using Wilcoxon rank-sum test). These mice were implanted in PrL_Cx, IL_Cx, NAc, BLA, and CeA. B) Validation of Electome Factor 1 activity coding for the homecage—FIT periods. Electome Factor 1 activity measured during the homecage—FIT test was pooled across the control animals used for the IFN (n=8), ELS (n=5), and SSFO experiments (n=5), and all data measured during the first session of the sdk1 experiment (N =12 animal). Electome Factor 1 activity significantly increased during each subsequent interval of the homecage—FIT test, validating the findings from the pre-stress model that was discovered for the cSDS mice (Friedman’s Χ²=26.68, df=2, N=30, P=1.6×10⁻⁶; P<0.05 for Bonferroni-corrected post-hoc testing using sign-rank test). Receiver operating characteristic area under the curve for FIT-CD1 vs. All (Home and FIT-Empty) = 0.74. C) Vulnerability prediction scores from PFC reactivity correlate fails to predict vulnerability in the ELS model. Our previously published neural correlate of cSDS vulnerability (PFC 2-7Hz reactivity in the FIT)(Kumar et al., 2014) failed to predict increased vulnerability in the ELS model, whereas Electome Factor 1 activity in the same animals successfully predicted increased vulnerability as shown in the main text. D) Predictive performance of univariate features composing Electome Factor 1. We tested whether the univariate components (seven power measures and two coherence measures) of Electome Factor 1 also predicted vulnerability to future stress. Activity was measured during the FIT-CD1 segment in the pre-stress cSDS cohort. The predicted vulnerability rank is plotted for each mouse based on each brain activity measure (N=19 mice; bottom). Mice that exhibited susceptibility after stress are highlighted in red, and mice that exhibited resilience after stress are highlighted in green. The area under the curve (AUC) for the receiver operating characteristic (ROC) is shown above (black). Electome Factor 1 (identified by blue circle on AUC plot) outperformed each of the univariate features we tested.

Supplemental Figure S6: Intra-area synchrony, related to Fig. 1. Coherence was calculated from each microwire LFP pair implanted in the same brain area using magnitude-squared coherence:

$$C_{AB}\left(f\right)=\frac{{\left|Ps{d}_{AB}\left(f\right)\right|}^2}{Ps{d}_{AA}\left(f\right)Ps{d}_{BB}\left(f\right)}$$

where coherence is a function of the power spectral densities (Psd) of A and B, and their cross-spectral densities. Results obtained for the ‘pre-stress’ recording in the cSDS cohort were averaged across animals for each interval of the homecage-FIT recording (N=44 mice). We found high coherence across the wires implanted within PrL_Cx and IL_Cx (>0.6), and very high coherence across wires implanted within the other brain regions (>0.8). Data were shown as the 95% confidence interval averaged across the 44 mice. Thus, the Electome Factors are stable (at least up to 50Hz) to minor difference in electrode placement, because the measured spatiotemporal dynamics are largely redundant across individual microwires.

Supplemental Figure S7: Histological confirmation of electrode placements, related to Fig. 1 and 2. Electrode bundles were centered within the red boxes shown for each target brain area (left). The initial cSDS cohort was also implanted in right PFC, which is highlighted by the light blue box. Representative histological images are shown the right. Red arrows highlight electrode tracks. White scalebars indicate 500um.

Supplemental Table S1: Extended Author Contributions, related to STAR Methods.

Supplemental Movie S1: Homecage and Forced Interaction Test (FIT) neurophysiological recording paradigm, related to Fig. 1.

Highlights.

• Brain-wide electrical spatiotemporal dynamic map of stress states

• Hippocampally-directed network signals stress-vulnerability in stress-naïve animals

• Early life stress increases activity in stress-vulnerability network

• Stress-vulnerability network is mechanistically distinct from pathology networks