Electro-optic deflectors deliver advantages over acousto-optical deflectors in a high resolution, ultra-fast force-clamp optical trap

Abstract

We characterized experimental artifacts arising from the non-linear response of acousto-optical deflectors (AODs) in an ultra-fast force-clamp optical trap and have shown that using electro-optical deflectors (EODs) instead eliminates these artifacts. We give an example of the effects of these artifacts in our ultra-fast force clamp studies of the interaction of myosin with actin filaments. The experimental setup, based on the concept of Capitanio et al. [Nat. Methods 9, 1013–1019 (2012)] utilizes a bead-actin-bead dumbbell held in two force-clamped optical traps which apply a load to the dumbbell to move it at a constant velocity. When myosin binds to actin, the filament motion stops quickly as the total force from the optical traps is transferred to the actomyosin attachment. We found that in our setup, AODs were unsuitable for beam steering due to non-linear variations in beam intensity and deflection angle as a function of driving frequency, likely caused by low-amplitude standing acoustic waves in the deflectors. These aberrations caused instability in the force feedback loops leading to artifactual jumps in the trap position. We demonstrate that beam steering with EODs improves the performance of our instrument. Combining the superior beam-steering capability of the EODs, force acquisition via back-focal-plane interferometry, and dual high-speed FPGA-based feedback loops, we apply precise and constant loads to study the dynamics of interactions between actin and myosin. The same concept applies to studies of other biomolecular interactions.

1. Introduction

1.1 Applications of optical trapping and force-clamp experiments

Optical trapping techniques have been widely used for studying a variety of biological processes, including the stepping of single kinesin [1] and myosin motors [2], breaking of intermolecular bonds [3], the replication of DNA [4], and many more. Optical traps, also called laser tweezers, can trap and exert forces on a dielectric particle, such as a micron-sized polymer bead, as a focused laser beam passes through the object [5]. These forces act to pull the particle toward the beam center with a spring-like force proportional to displacement from the trap center. It is possible to measure forces acting on the particle in the piconewton range using back-focal plane detection [6] and calibration methods that determine the stiffness of the trap’s potential energy profile [7]. When the bead is coupled to a molecule of interest, such as a molecular motor capable of exerting force as it moves along a biological polymer track, the changes in force and position produced by the molecule can be accurately recorded. Since the force developed and the bead position follow a linear relationship when the bead is close to the trap center, it is often useful to use a feedback mechanism to isolate the effects of force and movement on the instrument and the biological system [8–11]. Such feedback systems operate to hold (clamp) the force or bead position constant [8,11,12].

In force-clamp experiments, the motion of a molecule can be studied as an explicit function of applied load, and relationships such as a force-velocity curve can be calculated [11]. For molecular motors which are non-processive (they take only one step before dissociating from their substrate), the two-trap, three-bead geometry is commonly used to examine the interaction between the motor molecule and its substrate [13,14]. This arrangement is described in more detail below [Fig. 1]. In the case of non-processive motors, the time the molecule interacts with its track may be too short (<50 ms) to engage a feedback loop in response to an interaction, thereby preventing determination of the load dependence of interactions. To overcome this obstacle, a technique known as the ultra-fast force-clamp (described below) has been developed which can apply a specified load to a molecule within ~10-30 µs of its first interaction with its substrate [15]. This technique relies on a very rapid and robust feedback system to observe displacements of the track during interactions. We have attempted to utilize this system for the study of cardiac myosin and have found non-linearities from acousto-optical deflectors (AODs) make them unusable for such precise force-clamp systems. We have characterized these deficiencies and show how electro optical deflectors allow the system to perform as necessary. This finding applies not only to this specialized application, but to other feedback-based systems utilizing AODs for beam steering.

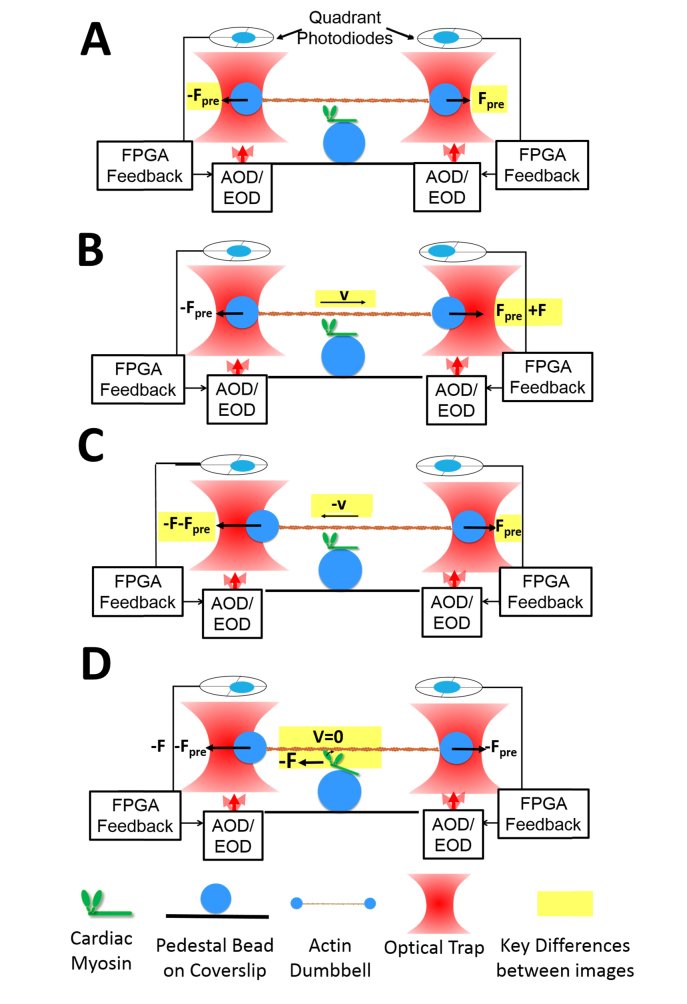
Fig. 1.

Illustration of the sequence of events in the ultra-fast force clamp method. Changes between each frame are highlighted in yellow. A) An actin dumbbell is held under pretension load by two optical traps which can be independently controlled via force-feedback loops and beam steering devices (either AODs or EODs). B). The setpoint of the feedback loop for one bead (right) is increased by F, which causes a force to be exerted to the right, resulting in the motion of the dumbbell at a constant velocity (v) which creates hydrodynamic drag on the dumbbell that matches the applied force, F. The feedback loops work to maintain a constant force on both beads during the dumbbell’s motion. C) After a set excursion distance, the force setpoints are changed for both beads, with the applied force, F, now being applied to the left bead in the opposite direction. This results in motion of the dumbbell in the opposite direction. D)This cycle repeats until the myosin interacts with the actin filament, at which point the force is quickly transferred from hydrodynamic drag to the myosin molecule and the dumbbell’s motion stops within ~30-50 microseconds. This allows precise detection of the attachment time and the ability to study myosin under set loads from the beginning of its interaction with actin.

1.2 Myosin: a biomolecule which rapidly generates force and displacement

Myosins are a class of molecular motor proteins responsible for powering contraction of muscle and other motile and contractile processes in biology [16]. A single myosin molecule utilizes the energy from the hydrolysis of adenosine triphosphate (ATP), to cause a displacement of its filamentous substrate, actin. In skeletal and cardiac muscle, arrays of thousands of myosins interact with actin filaments arranged in highly ordered structures known as sarcomeres, to cause shortening of the muscle cells which leads to contraction of the entire tissue. Each interaction between actin and myosin lasts less than 20 ms on average under physiological conditions, and the displacement of the actin filament is thought to occur in less than 1-5 ms after binding [15,17,18]. This displacement step is necessary for force production in muscles, and is expected to be modulated by force on the muscle, metabolite concentrations, and various drugs [15,19,20]. Because this displacement follows attachment so quickly, previous single-molecule studies have been unable to study its dynamics under load [15].

2. Ultra-fast force-clamp optical trapping

We have implemented an ultra-fast, force-clamp, three-bead optical trap feedback system which can detect the timing, amplitude, and force dependence of the myosin power stroke with sub-millisecond time resolution under constant, programmable load.

2.1 Ultra-fast force-clamp concept

In the three-bead assay the motor (myosin) is sparsely attached to a 2.5 μm silica sphere, termed a pedestal bead, on the coverslip surface. An assembly of an actin filament suspended between two 500 nm polystyrene beads is termed an actin dumbbell. A dual beam, force-clamp optical trapping system, as described by Capitanio et al. [15], independently maintains a constant force on each dumbbell bead while their positions change within a spatial range of several hundred nanometers. The system adjusts the positions of the traps to maintain a constant force on each bead as detected by back-focal-plane detection of the trapping laser light scattered by the beads. This system has previously been applied to the study of myosin [15], DNA-binding proteins [21], and microtubule binding proteins [22].

During an experiment, an actin dumbbell under approximately 5 pN of tension is brought close to a myosin molecule on the surface of a pedestal bead affixed to a glass coverslip [Fig. 1(a)]. The feedback system is activated and the force setpoint for the right bead is changed to apply a force, F [Fig. 1(b)]. This results in an unbalanced force on the dumbbell assembly, causing it to move rightward at a constant velocity such that the excess force applied to the right bead is balanced by hydrodynamic drag on the moving dumbbell. The dumbbell travels at this constant velocity until the traps have moved a specified distance (~100 nm) at which point the setpoint for each bead is triggered to change the direction of the forces [Fig. 1(c)], leading to the dumbbell moving in the opposite direction. The applied force and direction of motion continue to alternate back and forth until the myosin interacts with the actin filament, at which point, the force balanced by hydrodynamic drag is quickly (within 50 µs) transferred to the myosin molecule [15], which becomes loaded with the applied force. This transfer of force abruptly stops the dumbbell’s motion, while the total forces on both beads are maintained constant by the feedback system [Fig. 1(d)]. While the myosin interacts with actin, the force applied to it is held constant, and the motion of the actin filament is recorded from the position of the two traps. Thus, the displacement of the power stroke can be observed under various pre-determined loads. When the myosin dissociates from actin, the dumbbell continues its earlier motion, and the applied force is transferred back to hydrodynamic drag. In a single 30 s long recording, the actin dumbbell switches its direction of travel thousands of times and myosin attaches to actin in dozens of interactions, depending on the particular myosin isoform and various experimental parameters.

2.2 Ultra-fast force-clamp optical trapping implementation

To implement the ultra-fast force-clamp method, four key components are required: 1) a stable dual beam optical trap setup, 2) high bandwidth force detection electronics, 3) a high-speed feedback control system, and 4) low-latency, high precision beam steering.

The response time of the force-clamp feedback loop must be very rapid (≤ 10 µs) to investigate processes such as the myosin power stroke, as it must maintain constant forces on both beads while the actin dumbbell is in motion. To stably maintain the mean force on the beads to within 5% of the set points under these conditions, we found it necessary to keep the feedback loop update rate less than 10 µs. This includes the time to 1) detect the instantaneous force on the beads, 2) perform the feedback calculations, and 3) update the position of the trapping beam. We optimized each of these three components of the setup to reach the 10 µs loop time.

The force on each bead is monitored by back-focal plane interferometry of the 1064 nm trapping laser on two silicon quadrant photodiodes (QPDs, JQ-50P, Electro Optical Components Inc.) which can achieve a rise time for the force detection system of ~2 µs.

We utilize a National Instruments Multifunction I/O module (PXI-7851) equipped with a Field Programable Gate Array (FPGA) to perform the feedback calculations, based on the QPD signals and the force setpoint, to update the control signal for the beam deflectors. The feedback calculations are performed at the same rate as the data acquisition rate, 250 kHz, leading to the update time for the feedback loop of 4 µs.

The control signal from the feedback calculations must move the position of the beam in the sample chamber precisely and rapidly. Acousto-optical deflectors (AODs) were initially used in our setup because of their fast response time (< 10 µs), and moderate deflection angle, e.g. 30 mrad (1.7 degrees) [23]. We found, however, that the AODs introduced distortions to the laser beams which had highly detrimental consequences for the feedback loops (as explained below). This led us to attempt the experiments with electro-optical deflectors (EODs), which did not exhibit such effects and allowed the system to respond more reliably. EODs offer a smaller deflection range of only 3 mrad (0.17 degrees), but afford greater transmission and more uniform modulation of the beam along with a faster response time (2 µs) [23,24]. Each of these deflector systems was optimized to reposition the beam in less than 4 µs from the command signal input, allowing us to achieve the required 10 µs loop time (2 µs force detection + 4 µs feedback calculation + 4 µs beam steering).

This loop time is much faster than the trapped bead’s response time in solution (~160 µs), as indicated from the power spectrum of bead displacement, which has a corner frequency near 2 kHz. While it has previously been shown that a position-clamp feedback loop running faster than the time response of the bead can increase the effective trap stiffness [25], our feedback loop operates in the force-clamp mode. This causes a decrease in the effective stiffness of the trap (since the trap follows the bead rather than restraining it). The (reduced) effectiveness stiffness in solution is not highly relevant to the experiments as the primary interest is the dynamics of the actin filament during interactions with myosin. In this situation, the effective stiffness of the entire system becomes much greater than that of the trap, mostly due to the myosin’s stiffness on the order of 1 pN/nm. Previous calculations have shown that this ultrafast system is capable of detecting halting of the actin within 50 µs of myosin attachment under the conditions of our experiments [15] and subsequent displacements of the actin filament can also be resolved within ~50 µs.

3. Acousto-optical deflectors

3.1 Basic principle and response time limits

AODs contain a transparent crystal with a piezo-element at its end that produces radio frequency (RF), ultrasonic acoustic waves that travel across the crystal nearly perpendicular to the incident optical beam. As laser light interacts with the compressions and rarefactions of the acoustic waves, a portion of the beam energy (typically ~50-70%) is diffracted into a deflected beam, where the wavelength of the ultrasonic waves sets the diffraction angle [9,23,26]. Thus, the RF signal frequency modulates the diffraction angle of the beam.

The response time of the beam deflection after the RF signal changes depends primarily on the speed of sound in the crystal and the size and position of the incident beam relative to the piezo element. With proper optimization, our AOD’s (45035-3-6.5DEG-1.06 Gooch and Housego/NEOS) have a total response time of 3 µs.

3.2 Observed artifacts in feedback experiments

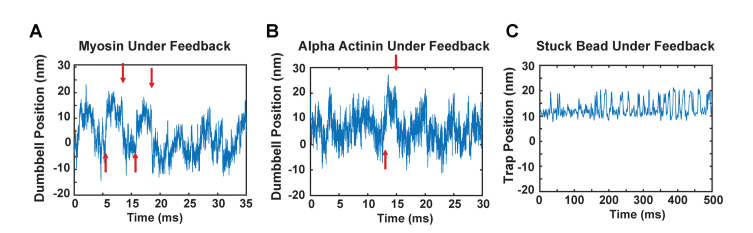
While performing force-clamp experiments on myosin, we observed very rapid (<1 ms) “jumps” in the trap position of 10 - 20 nm while the myosin was interacting with the actin filament [Fig. 2(a)]. These jumps often were reversible, with the trap position alternating between two positions many times during a single interaction lasting 10 to 100 ms. The sizes of the jumps varied between each interaction and experiment, but within one actin-myosin binding event they were relatively constant in size and frequency. To test whether these motions were an artifact caused by the feedback system, we performed a control experiment replacing the myosin in the assay with alpha-actinin, a non-catalytic actin binding protein that should not displace actin during its interaction. In these experiments, we also observed jumps in our trap position [Fig. 2(b)] with a similar 10 - 20 nm deflection, strongly suggesting these were experimental artifacts. As an additional control, we centered the laser over a large 2.5 µm diameter pedestal bead firmly attached by nitrocellulose to the surface of the coverslip. We engaged the force-clamp and observed the trap position. Figure 2(c) shows similar fluctuations of the trap position that were observed depending on the initial AOD deflection. Such fluctuations severely compromise measuring the 5 - 10 nm actin displacements expected from myosin, as it becomes impossible to distinguish the myosin displacements from the fluctuations.

Fig. 2.

A) Example of artifactual ~20 nm jumps in the dumbbell position during an interaction between myosin and the actin filament while the force-clamp is engaged using AOD beam steering. Jumps are marked by red arrows. B) A control experiment replacing myosin with alpha-actinin, which interacts with actin but is not expected to cause displacements. Similar jumps of 15 nm are marked (red arrows). C) Another control experiment placed the trapping laser over a pedestal bead stuck firmly to the surface and engaged the force-clamp feedback. Although the time scale of the feedback loop was different here, artifactual ~10 nm jumps of the trap position were observed.

3.3 Non-uniformities in AOD beam deflection due to standing acoustic waves

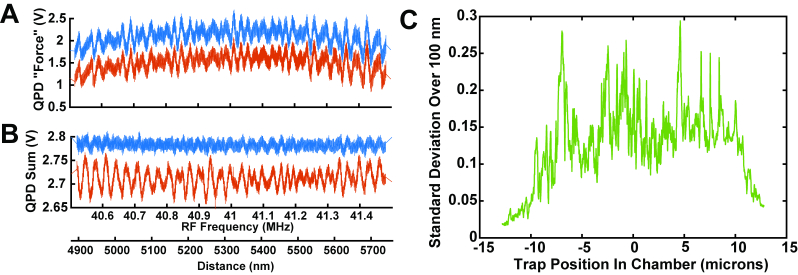
We determined that the source of the artifactual jumps in trap position were due to non-uniform deflection of the beam by the AODs. It was reported previously that beams deflected by AODs can exhibit “wiggles”, which were shown to cause the position of a trapped bead, as measured by an independent tracking laser, to move with quasi-periodic variations from a linear path when the AOD RF frequency was linearly swept [9]. In our setup the force is directly measured via scattering of the trapping laser [6] in contrast to the previous work which used an independent position-tracking beam. This difference in detection method causes these non-linear effects to present differently. We measured the non-uniform deflection by sweeping the beam position in the chamber, without a bead present, and monitored the differential QPD signal that usually indicates the force in the sweeping direction. This signal should remain quite constant as the beam position is swept due to the design of the system. Figure 3(a) shows periodic fluctuations in the QPD signals (red) as the beam was swept. The period of the fluctuations corresponds to a ~20 nm period at the sample. This distance corresponds to a change of ~30 kHz in frequency of the AOD RF signal input. Similar fluctuations in the total beam intensity were also observed [Fig. 3(b), red]. When we damped the intensity variation by a feedback system controlling the RF signal amplitude [Fig. 3(b), blue], the fluctuations in the QPD “force” signal remained [Fig. 3(a), blue]. Over the entire 25 μm range of the AOD’s beam deflection at the sample, certain positions/RF frequencies exhibited smaller or larger variations [Fig. 3(c)].

Fig. 3.

A) Example of variations in the force signal observed with the AOD beam steering system as a function of beam position. The y-axis shows the differential voltage from the QPD as the trap position was scanned in the chamber without any trapped bead. Similar variations were seen when the bead was present but were visually masked by Brownian motions. The variations are shown without (red) and with (blue) intensity-maintaining feedback. The two signals overlay nearly perfectly and are displayed with an offset for clarity. The two x-axis scales below panel B apply both to panels A and B. B) The total intensity of the light reaching the QPD also varies with a similar periodicity. Using an independent feedback loop to maintain a constant total QPD illumination (B, blue), did not eliminate the variations in force signals. C) The standard deviations of the fluctuations over a 100 nm window were calculated over the entire 25 μm deflection range of the AOD. Some positions (corresponding to particular RF frequencies) exhibited much larger variations in the recorded force signal than the average. The y-axis scale in C corresponds approximately to pN using typical experimental calibrations.

We also used a lateral effect photodiode (LEPD, Pacific Silicon Sensor DL100-7-PCBA3) for force detection to determine whether these signal variations arose from the movement of fringes across the discrete quadrant boundaries of the QPD. The lateral effect photodiode effectively returns the first moment of the intensity distribution along each axis and should be less sensitive to fringes. However, we found variations with the same periodicity and similar amplitudes when using the LEPD (data not shown).

The periodicity of the fluctuations in Fig. 3 matches that expected from standing waves in the crystal. Such a standing wave can arise from partial reflection of the acoustic wave from the far face of the crystal which constructively and destructively interferes with the original wave, leading to a small amplitude of non-propagating nodes and internodes. The crystal is thus a weak resonator (low quality factor, Q) with resonant peaks at frequencies giving integral numbers of wavelengths in the crystal. The round-trip time of the acoustic wave in the crystal is approximately 32.2 µs, giving an expected periodicity of 31 kHz for the applied RF signal, closely matching our observations. When the input RF frequency was swept across 20 kHz of RF variation at a very high rate (1 sweep per ms or faster), the pattern of the force signal variations was disrupted. At such fast RF update rates, the frequency of the acoustic wave in the crystal does not remain constant long enough for the reflected wave to interfere coherently and produce the standing wave.

Besides previously published reports of these deflection variations occurring in several brands of AODs [9], we have also tested four brands of AODs of various models and ages and have found that such non-linearities exist in all of them. Their magnitude and spacing seemed to depend on many factors such as the model and service age of the deflector.

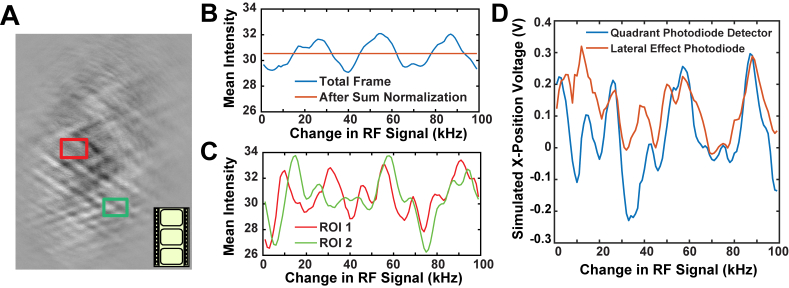
The effects of the standing waves could be visualized by imaging the beam at the AOD crystal [26]. We projected an image of the 1064 nm light at the AOD crystal through neutral density filters onto a CCD camera. The beam profile was recorded while linearly sweeping the applied RF frequency 100 kHz over a period of 10 s, acquiring images at 10 frames per second (Visualization 1 ^{(1.7MB, mov)} ). We flattened the image and enhanced the contrast to better visualize changes in the beam during the sweep. Large variations in the overall intensity of the beam as well as localized fluctuations were detected. Figure 4(b) shows that the overall fluctuations varied with a periodicity of ~30 kHz, in agreement with the total QPD voltage fluctuations. Wave-like variations are apparent that slowly move across the beam path as the RF frequency changes, supporting the idea that standing waves are present (the ~35 MHz acoustic wave itself is not visible). If the intensity of each frame is scaled, so that the total intensity of each frame is normalized (as in Visualization 1 ^{(1.7MB, mov)} ), there are still local variations in the intensity of the beam [Fig. 4(c)]. These fluctuations likely give rise to the artifactual force signals we observed even when the total intensity of the beam was held constant by a feedback loop [Fig. 3(c)]. Variations in both the global and local intensities are observed whether or not the images were flattened and contrast enhanced.

Fig. 4.

A) Snapshot from video of a 1064 nm wavelength beam at the face of the AOD crystal (Visualization 1 ^{(1.7MB, mov)} ). The applied RF signal was swept over a range of 100 kHz in a 10 second period, corresponding to about 75 nm of displacement at the microscope stage. The video rate is 10 frames per second. The intensity of each frame has been normalized. Two regions of interest (ROIs) were selected, shown in red (ROI 1) and green (ROI 2). B) The original mean frame intensity (blue) from the video of panel A shows an approximate periodicity of 25 kHz, corresponding to 20 nm at the sample. The intensity-normalized video (orange) has a constant mean intensity, as expected. This normalized video was used for analysis in panels C and D. C) The mean intensity in each ROI in the normalized video shows pseudo-periodic fluctuations in its localized intensity with a similar period (25 kHz). The fluctuations in the different regions vary in amplitude and phase. D) The signal that would be created from projecting the recorded images onto either a Quadrant Photodiode (QPD, blue) or a lateral effect photodiode (LEP, red) were calculated. The force signal varied for both types of detectors with similar periodicity but with somewhat different secondary characteristics.

We analyzed each frame of the video to approximate the signal that would be generated by projecting the intensity-normalized image onto quadrant photodiodes. The plane of the AOD is conjugate to the QPD, so this signal mimics the conditions of Fig. 3. Calculation of the estimated QPD output was performed by dividing each frame horizontally in half, summing the total intensity from each half, and subtracting the two sums. The resulting signals show that the detected force signal (red) fluctuates due to the regional variations in the light intensity at an overall periodicity of 30 kHz, consistent with actual QPD recordings [Fig. 4(d)]. Secondary, apparently random variations in the calculated force signal are superimposed. To investigate whether the observed variations are due to the movement of fringes across the centerline of the image (corresponding to the quadrant boundary of the QPD), we also calculated the first moment of the image in the x dimension (blue), approximating the signal from a lateral effect photodiode, which reports the mean beam position more faithfully than a QPD. The overall variations remained, with only the smaller, secondary deflections differing. This is consistent with observations, mentioned above, using an actual lateral effect photodiode in the experimental system that gave results very similar to the QPD.

3.4 Effect of distortions from AODs on the feedback system’s response

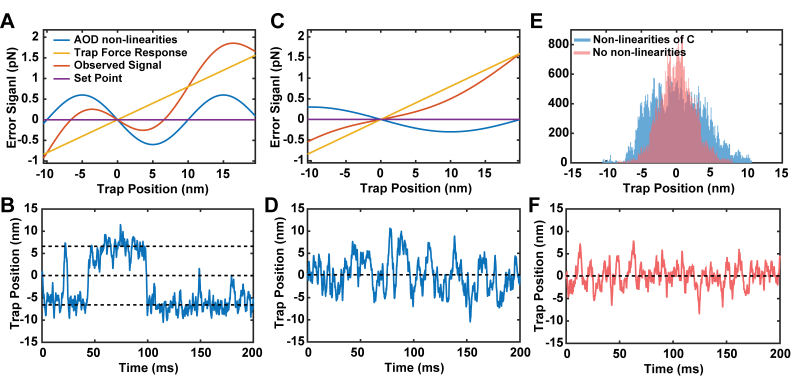
To better understand how these variations in the detected force signal influence force-clamp experiments, we performed Monte-Carlo simulations of a feedback system acting to keep a constant force on a tethered bead undergoing Brownian motion. The detected error signal of the system was simulated by adding the error signal arising from moving the trap relative to a fixed bead (the linear force response of the trap [Figs. 5(a) and 5(c), yellow]), to the error signal arising solely from the non-linearities of the AOD (blue), modeled as a sinusoid. The simulations were set to maintain zero load on the bead (set point, purple lines). Visualizing the observed error signal of the system as a function of trap position under conditions similar to an experiment (the sum of the yellow and blue curves [Figs. 5(a) and 5(c), red]) shows that there are multiple trap positions where the setpoint force would be observed (the intersections of red and purple lines [Figs. 5(a) and 5(c)]). Brownian motions would cause the trap to visit each of these positions while the feedback loop attempts to maintain a constant force. The trap position is not stable at 0 nm, due to the reversed slope of the error signal. However, the trap positions at −7 nm and + 7 nm are stabilized by the feedback loop. This was observed in the simulations of the trap position over time, shown in Fig. 5(b), where rapid jumps between these stable positions were observed.

Fig. 5.

A) Simulated error signals for a trapped bead undergoing Brownian motion. The total measured error signal as a function of trap position (red) includes the Hookean (linear) trap force (yellow) and the imposed variations from the AOD (blue) modeled as a sinusoidal curve. Due to the influence of the AOD force variations, there are two possible trap positions (−7 nm and + 7 nm) where the force will be stabilized at the set point (zero error signal, purple). B) Simulated trap positions for the potential in A using parameters similar to our experiments. The trap position quickly jumps between the values where the total measured force is equal to the set point (horizontal dashed lines show intercepts of red and purple curves from A. C) A reduction in the amplitude of the variations and doubling of their spacing changes the profile of the measured error response (red), effectively reducing the loop gain. D) Simulated trap positions from the profiles in C show that large jumps are no longer observed, but the small AOD variations introduce added noise. E) A comparison of the simulated trap positions with the low levels of non-linearity shown in Panel C (blue histogram) compared with simulated positions without non-linearities (pink histogram). F) Simulated trap positions under feedback when only the trap’s potential is present and non-linearities are absent.

The probability, timing, and size of these jumps depend on many of the simulation parameters, including the relative position between the bead and the peaks of the force variations. This situation, combined with the fact that the real non-linearities vary considerably in their positions and amplitude across the AOD deflection range, explains why the size and frequency of the jumps we observed in the experiments varied widely among myosin binding events. We simulated a “better” AOD in Fig. 5(c) and 5(d), where the variations had half the amplitude and twice the spacing as found in our system. This combination did not exhibit the drastic jumps in position because the observed error signal (red) crossed zero only once, but its sensitivity became lower, effectively reducing the loop gain and leading to increased noise in the trap position, as compared to a simulation without any superimposed AOD non-linearities [Fig. 5(d) and (e)]. The latter situation is probably closer to what we observed in a previously described setup [15] where the periodic variation of amplitude and force signals are both smaller and exhibit a larger period (data not shown).

4. Electro-optical deflectors

4.1 Principles, time response, and previous use of electro-optical deflectors

An electro-optical crystal generates a linear refractive index gradient proportional to an applied electric field. This gradient causes light propagating in it to be deflected from its straight path through the crystal. When zero voltage is applied, the beam passes straight through the device, simplifying alignment, and when the field is applied, all of the light (except for small portions that are reflected or scattered) is deflected the same amount. Because there is no traveling acoustic wave as is in an AOD, the response time of an EOD is mainly limited by the driver applying the high voltage signal to the device, which acts as a capacitive load. Our EODs (LTA-4 crystal, Conoptics) and high voltage driver (Model 412, Conoptics) have a combined response time of about 1 µs, well within the 4 µs requirement to maintain a total loop time <10 µs. This same EOD system has previously been shown to work well in optical trap feedback systems, and not to exhibit the non-linearities in deflection that are found in AODs [9].

4.2 Implementation of ultra-fast force clamp with EODs

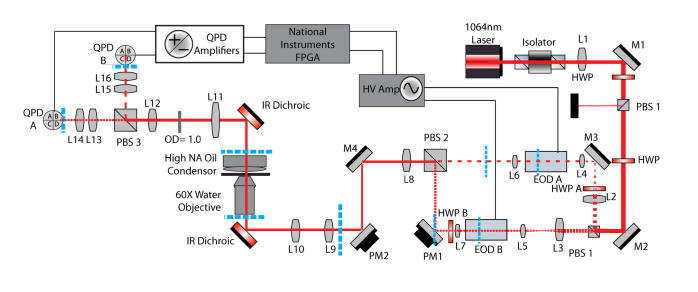
The reduced angular displacement of the EODs and the location of the effective center of the deflection within the EOD device required special consideration in the optical path design. EODs can deflect the beam up to 3 milliradians peak-to-peak, which is ~10-fold less than the AODs. In our system this corresponds to several hundred nanometers of trap translation at the sample, which is sufficient for our feedback experiments. However, to form actin dumbbells from filaments of various lengths that are pre-tensioned to 5 pN, >3 µm of beam travel is required. This is accomplished via a remote-controlled gimbal mounted mirror (PM1 in Fig. 6) placed at another position conjugate to the back focal plane (BFP) of the objective. Angular changes at this mirror produce displacement at the sample. The center of deflection of the EOD, which also needs to be conjugate to the BFP of the objective, is located approximately 2 centimeters inside the 10 cm EOD device, as measured from the exit aperture. To ensure both this center of deflection and the mirror are conjugate to each other, a short focal length relay lens is used to image the center of rotation of the EOD onto the mirror as a 4f relay system. While only one of the traps is manipulated by this conjugate mirror, both traps contain corresponding relay lenses (L6 and L7 in Fig. 6) to produce similar beam characteristics once they are recombined.

Fig. 6.

A) Schematic of the optical trap setup including EODs. Dashed blue lines indicate conjugate planes. L7 is necessary to create a conjugate plane at Picomotor Mirror 1 (PM1) to properly control the position of EOD B’s beam relative to EOD A’s beam. A similar lens is included after EOD A to maintain the optical characteristics between the two beam paths. HWP A (Half Wave Plate) is necessary to rotate the polarization of the incoming light to horizontal as required for deflection. A pair of lenses in front of each EOD (L2-L4, and L3-L5) acts to reduce the beam diameter during transit through the EOD crystals. The layout used with the AOD was similar to that shown, however without the lenses described above and slightly different positions of half waveplates and other lenses. PBS1 allows the total intensity of both traps to be simultaneous controlled by diverting energy into a beam block (black box). PBS: Polarizing Beam Splitter, M: Mirror, L: Lens, HV Amp: High voltage amplifier.

4.3 Visualizing the myosin power stroke with EOD based feedback

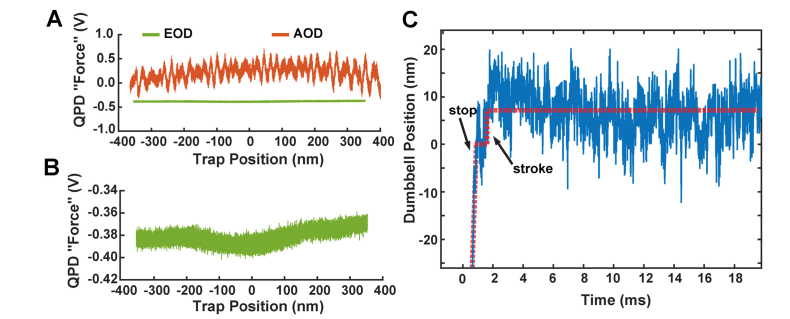
When the beam is carefully aligned inside the EODs, and all the conjugate planes are properly positioned, the response of the QPD force signals as the beam position is moved over a range of 700 nm is smooth [Fig. 7(a)]. The EODs do not exhibit the variations and non-linearities detected from the AODs. It should be noted that in our case, when the beam was larger or slightly misaligned so that even a small amount of its power (1% - 5%) struck the edges of the 2 mm diameter crystals and/or their electrodes, the effective position of beam imaged at the QPD was unstable.

Fig. 7.

A) Characterization of the deflection of the EODs as a function of trap position (green) shows a uniform detected force signal on the QPD. The corresponding signal using AODs from Fig. 3 is shown offset at the same scale. B) An enlarged view of the EOD data from Panel A shows that there are no detectable “wiggles” in the deflection of the beam by the EOD. C) The actin dumbbell’s position is shown for the beginning of a single interaction between cardiac myosin and actin using the EOD-based force-clamp system. Red dashed lines guide the eye to the dumbbell’s motions. The dumbbell is traveling at a constant velocity under feedback before it quickly stops at t = 1 ms. There is one clear displacement of ~10 nm at 2 ms and no other large fluctuations. A similar figure for the AOD-based system is shown in Fig. 2A without the initial motion of the filament at a constant velocity.

The improvements in beam steering from the EODs enable experiments on myosin to be accomplished without the artifactual jumps which had previously foiled analyzing myosin’s power stroke. When we use the force clamp system with EODs, we can observe the position of the actin dumbbell smoothing traveling under the feedback system and coming to an abrupt and precise stop when the myosin interacts with actin. A representative trace shown in Fig. 7(c), clearly exhibits a single ~10 nm displacement of the actin filament within a few milliseconds of binding, as expected for the cardiac myosin isoform under study. The position of the dumbbell does not exhibit the fluctuations seen in Fig. 2(a), and thus the power stroke of the myosin can be properly characterized. This will allow elucidation of the amplitude and kinetics of the power stroke under defined mechanical loads and biochemical conditions.

5. Conclusions

We have shown that using AODs for beam steering in a force clamp optical trap system, where force is directly measured by deflections of the trapping laser, can cause substantial artifacts in the output signals. This builds on a previous report [9] of a similar effect in a system using a separate position tracking laser. While it was not initially obvious how the quasi-periodic variations in the deflected beam would cause jumps in the feedback control signals, a combination of control experiments and simulations showed that they are the cause. The simulations emphasize that key parameters such as the spacing and amplitude of the force non-linearities and the stiffness of the trap have considerable qualitative and quantitative effects on a force feedback system.

Thus, for some researchers using feedback systems with AODs, it is possible such variations may introduce spurious and difficult to trace noise into their experimental data. AOD devices are designed to reduce standing waves by including an absorptive material or out of plane angle on the crystal face opposite to the piezo element, but it seems that the specific design of the device and its service age may influence the amount of reflection [26]. For high precision force feedback experiments, researchers are recommended to check that deflection variations from standing waves do not lead to artifacts such as shown here. Even if the effects do not manifest as large jumps in trap positions, smaller non-linearities may be adding additional noise to a system, as shown in Fig. 5. If such effects are present, changes to experimental or device parameters, or the use of EODs for beam steering, may be advisable.

We have found that using EODs for beam steering reduced the noise and spurious jumps in our feedback signals which were masking the myosin power stroke phenomenon we set out to study. Although their deflection range is smaller than AODs, their faster time response and uniform deflection response makes EODs more reliable for high speed, high precision experiments requiring precise beam control.

Funding

This work was funded by NIH grants R01-GM086352, R35-GM118139, P01-GM087253, R01-HL133863, a NSF Graduate Research Fellowship to MSW, the European Union's Horizon 2020 grant 654148 Laserlab-Europe, the Italian FIRB grant RBFR13V4M2, and by Ente Cassa di Risparmio di Firenze.

Disclosures

The authors declare that there are no conflicts of interest related to this article.