Oscillating dispersed-phase co-flow microfluidic droplet generation: Multi-droplet size effect

Abstract

Controllable generation of microdroplets at desired sizes and throughputs is important in many applications. Many biological assays require size-optimized droplets for effective encapsulation of analytes and reagents. To perform size optimization, different-size droplets must be generated from identical sources of samples to prevent potential cross-sample variations or other sources of error. In this paper, we introduce a novel alteration of the co-flow droplet generation technique to achieve multi-size generation of monodispersed droplets. Using a custom-made mechanism, we oscillate the disperse-phase (d-phase) flow nozzle perpendicular to the continuous phase (c-phase) flow in a co-flow channel. Oscillation of the d-phase nozzle introduces an additional lateral drag force to the growing droplets while exposing them to various levels of axial drag owing to the parabolic velocity distribution of the c-phase flow. Superimposing both effects results in simultaneous and repeatable generation of monodispersed droplets with different sizes. The effect of nozzle oscillation frequency (f = 0–15 Hz) on droplet generation at different d-phase (Q_d = 0.05, 0.10, and 0.50 ml/min) and c-phase (Q_c = 2, 5, and 10 ml/min) flow rates was studied. A wide range of monodispersed droplets (4nl–4 μl) were generated using this method. Droplet sizes were directly proportional to the We number and inversely proportional to the Ca number and oscillation frequency. Our technique is promising for applications such as aqueous two-phase systems, where due to inherently low interfacial tension, the d-phase flow forms a long stable jet which can be broken into droplets using the additional oscillatory drag in our device.

I. INTRODUCTION

During the past two decades, droplet-based microfluidic systems have drawn considerable attention as high throughput platforms for biological, pharmaceutical, and chemical analyses.¹ Sub-microliter volumes of droplets offer a low reagent consumption rate due to their small sizes and enhanced heat and mass transfer characteristics due to their high surface-area-to-volume ratios, both resulting in reduced assay times in microenvironments. Moreover, droplets hold good encapsulation efficiency due to their high surface tension and thus minimize the risk of contamination in highly sensitive biochemical assays. Generating microdroplets in a wide range of sizes has found applications in drug delivery,² optical screening of protein crystallization,^3,4 nanoparticle synthesis,^5,6 and encapsulation and cultivation of cells,^7–9 bacteria,^10–12 and model organisms such as Caenorhabditis elegans.^13,14

Microfluidic-based droplet generation techniques are divided into active and passive methods. In active methods, external sources of energy such as electric fields,¹⁵ magnetic fields,¹⁶ mechanical vibration,¹⁷ and acoustic waves¹⁸ are used to intensify the surface instability and rupture the liquid-liquid interfaces into droplets. In passive methods, the dispersed-phase (d-phase) and continuous phase (c-phase) channels are arranged in various angles to intensify interface instabilities and accomplish the breakup. Co-flow^19,20 (two parallel channels), flow focusing²¹ (parallel channels with a contraction in the c-phase channel), and cross junction (T-junction²² and Y-junction²³) methods are amongst the most widely used channel arrangements in passive droplet generation techniques.

The above microfluidic droplet generation techniques have been used to achieve high levels of droplet throughput and monodispersity.^24,25 However, these devices could not generate more than one droplet size at a time in a continuous, high-throughput, and monodispersed manner. Modern chemical and biological applications require size-optimized droplets for effective encapsulation of analytes and reagents. To perform size optimization, different-size droplets must be generated from identical sources of samples to prevent potential cross-sample variations or other sources of error. Droplet-based Polymerase Chain Reaction (PCR), a widely used technique in genetic studies, is one of the biological applications that require droplet size optimization especially when dealing with very low reagent concentrations.²⁶ Multi-sized monodispersed droplets are also highly demanded in colloidal bead assembly fabrication which are extensively used in multiplex bioassay applications.^27,28

The size of beads could be well controlled by changing the suspension concentration or the diameter of droplets through adjustment of the flow rate of the water and oil phases.

To the best of our knowledge, few researchers have addressed the need for continuous generation of multi-size monodisperse droplets in microfluidic devices. To generate multiple droplets at a time, a few integrated microfluidic devices have been developed which consist of several simple geometries (e.g., flow focusing or T-junction channels) with different channel dimensions. Li et al.²⁹ fabricated an integrated flow focusing device (FFD) with four parallel channels of various dimensions. The results revealed that generation of droplets in one unit was affected by other units especially in FFDs with identical channel dimensions. Hashimoto et al.³⁰ also studied parallel bubble and droplet formation in integrated FFDs composed of single, double, and quadruple flow focusing units. Zhou et al.³¹ used 16 Y-junctions in parallel to increase the droplet generation throughput of water-in-oil. They investigated the effect of parallelization, flow rate ratio, and physical properties of different c-phase liquids on high-throughput, monodisperse emulsification with low energy consumption.

In the aforementioned multi-droplet generation devices, the droplet diameter can be manipulated by two methods: (1) modifying the physical properties of liquids which is not desired or applicable in many conditions and (2) tuning the c- and d-phase flow rates which is limited by the pressure durability of microfluidic devices. Moreover, the diameters of generated droplets are generally larger than the d-phase nozzle dimension, which restrains the size range of droplets in these methods. Thus, an important gap in the field of droplet microfluidics is the development of dynamically tunable devices capable of spontaneous generation of multi-size monodisperse droplets in a wide range of diameters, especially with sizes smaller than the d-phase nozzle.

This paper presents a new technique for multi-size, monodisperse droplet generation in a conventional co-flow geometry. In this method, the dispersion nozzle is oscillated inside the c-phase fluid channel to generate an additional lateral drag force on the droplets. The combined effects of the axial and lateral drag forces counteracting the interfacial forces lead to generation of multi-sized droplets with a wide range of sizes smaller than the nozzle. We believe that this novel technique will assist researchers in target encapsulation in low-concentration samples, which requires size optimization processes. Moreover, this technique can enhance the droplet breakup by providing extra drag force where shear rates are not sufficient for d-phase disintegration (e.g., aqueous two-phase systems³²).

II. WORKING PRINCIPLE

Understanding the physics of the droplet breakup and the interaction of dominant forces is a priority in characterizing droplet generators. The preliminary steps to study instability wave motion on interfaces and liquid column disintegration into droplets were taken by Plateau³³ and Lord Rayleigh.^34,35 Many researchers have performed experiments to understand interfacial breakup dynamics that has been extensively reviewed in the literature.^36–38 By injecting a d-phase fluid via a nozzle into a flowing c-phase fluid, interfacial forces assist the penetrated d-phase to form a growing droplet at the tip of the nozzle, while the viscous drag force imposed by the c-phase flow seeks to detach the growing droplet. The drag force increases by droplet growth up to the point that breakup-assisting forces overcome the breakup-resisting forces. At this point, while the diameter of the d-phase column decreases to zero, the radial curvature (inversed radius of the column) increases to infinity. This leads to occurrence of finite time singularities in the droplet breakup. Right after this point, surface tension encloses the interface to minimize the surface energy and form a droplet.^39,40

As stated above, the droplet breakup is a result of competition between inertial and viscous forces interacting against interfacial forces. Therefore, two important non-dimensional numbers used to analyze droplet generation in the literature are the Weber (We) and Capillary (Ca) numbers. The We number in Eq. (1) represents the relative effect of inertial to interfacial forces, while the Ca number in Eq. (2) expresses the ratio between viscous and interfacial forces

$${We}_d=\frac{{\rho }_d{D}_d{V}_d^2}{\gamma },$$ (1)

$${Ca}_c=\frac{{\mu }_c{V}_c}{\gamma },$$ (2)

where $\mathrm{\rho }$ [kg/m³] is the density, D [m] is the characteristic length scale (e.g., nozzle diameter), V [m/s] is the velocity, $\gamma$ [N/m] is the interfacial tension, $\mu$ [Pa s] is the viscosity, and subscripts d and c refer to the dispersed and continuous phases, respectively.

In the case of constant physical properties of the immiscible phases, conventional co-flow devices are only capable of generating single-sized droplets at constant We-Ca numbers. To achieve simultaneous generation of multi-size, monodisperse droplets at constant We-Ca conditions, a consistent gradient of viscous forces is required to establish breakup points at different volumes of the growing interface. The growing droplet at the tip of the nozzle experiences an axial drag force imposed by the c-phase stream with a parabolic velocity distribution. If the dispensing nozzle is repositioned across the width of the channel, the growing interface will experience different shear rates at each lateral position. Moreover, if the nozzle is oscillated inside the channel, an additional transverse drag force induced by the relative velocity of the flow and needle's tip will be added to the axial drag. We have investigated the above-mentioned technique in this paper to achieve multi-size monodispersed droplets at constant We-Ca conditions.

III. EXPERIMENTAL

A. Materials

A thoroughly mixed polydimethylsiloxane (PDMS) (Sylgard 184 kit, Dow Corning, USA) pre-polymer with a 10:1 ratio of monomer to curing agent was prepared. The degasified mixture was cast on a replication mold for fabrication of a mini-channel for co-flow droplet generation. The external fluidic network was established using flexible silicon tubing (Masterflex, Cole-Parmer Instruments CO, USA). Blunt stainless steel needles (Gauge 27, ID = 0.008 in, OD = 0.016 in, McMaster-Carr, USA) with Luer-Lock connection were used as a d-phase dispensing nozzle. Needles were embedded in borosilicate capillaries (OD: 1.0 mm, 1B100–4, World Precision Instruments, USA) to be centered inside the mini-channel. Deionized (DI) water droplets (Milli-Q, Millipore Ltd., Canada) were generated inside a c-phase stream of corn oil (Mazola, ACH Food Companies Inc., USA). Methylene blue dye was dissolved in the d-phase fluid to improve the edge detection quality in the image analysis process. All experiments were performed at an ambient temperature of T_amb = 20 °C in which corn oil viscosity, DI-water density, and interfacial tension between the two liquids are reported to be ${\mu }_o=86.4\hspace{0.17em}[\text{mPa}\hspace{0.17em}\hspace{0.17em}\mathrm{s}]$,⁴¹ ${\rho }_w=998\hspace{0.17em}[\mathrm{k}\mathrm{g}/{\mathrm{m}}^3]$,⁴² and ${\gamma }_{w/o}=26.3\times {10}^{-3}[\mathrm{N}/\mathrm{m}]$,⁴³ respectively.

B. Experimental setup

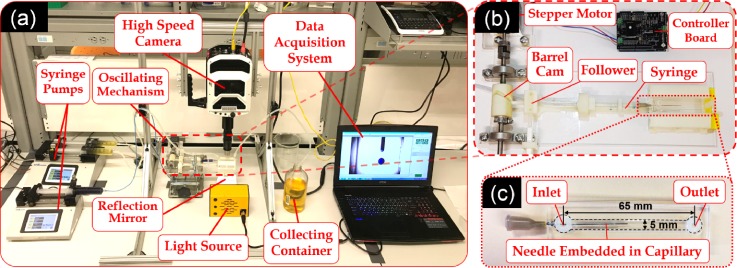
The experimental setup shown in Fig. 1(a) comprised a custom-built fixture, a high speed camera (Phantom V1611, Vision Research, USA), two syringe pumps (LEGATO 110 and 210, KD Scientific, USA), a data acquisition system, a collecting container, an oscillation mechanism (Sec. 1 and Fig. S1 in the supplementary material), a light source, reflection mirror, and a co-flow droplet generation device (Sec. III C). To minimize the effects of photothermal heating on the test section, an oblique mirror (45° angled) was used to reflect the light indirectly onto the device. Oscillation of the needle inside the channel (Video 1 in the supplementary material) was achieved by a 1:1 rotation-to-oscillation conversion mechanism, shown in Figs. 1(b) and S2, driven by a high-torque stepper motor which was controlled using an Arduino controller chip. The motion conversion mechanism was 3D-printed and composed of a barrel cam and a follower component (Figs. S1 and S2). To achieve different oscillation frequencies with precision (Fig. S3 in the supplementary material), a 150∼550 mA current was supplied to the stepper motor through a motor driver board (Rugged motor driver, Rugged Circuits, USA) by a direct current sourcemeter (Keithley 2410, Tektronix, USA). The mechanism was designed in a way that in each oscillation, the needle tip swiped 60% of the channel width to prevent the contact with the side walls.

FIG. 1.

Oscillatory co-flow droplet generation system. (a) Experimental setup consisting of a fluidic device with a channel and an embedded coaxial droplet dispersion needle, a high speed (HS) camera, two syringe pumps, a power supplier, a data acquisition system, a collecting container, an oscillation mechanism, a light source, and reflection mirror. (b) The custom-built rotation-to-oscillation conversion mechanism composed of a barrel cam and a follower. (c) The fluidic device with the needle inserted through a v-shaped groove into the channel with a height of 1.1 mm. The width and the length of the channel were 5 and 65 mm, respectively. The edges are overlapped by dashed lines for better display and visualization of the channel.

C. Device design and fabrication

The co-flow droplet generation device, shown in Fig. 1(c), consisted of a blunt needle (embedded inside a capillary) inserted into a PDMS mini-channel with one inlet and one outlet. The channel was 65 mm long with a rectangular cross section of 5 × 1.1 mm². A 0.1 mm gap between the outer diameter of the capillary and channel's upper and lower walls was implemented for frictionless oscillatory motion of the needle inside the channel. C-phase and d-phase fluids were infused at desirable flow rates via silicon tubes into the channel through the channel and needle inlets, respectively. The width of the channel was designed large enough to prevent any wall contact and unwanted blockage in a full 3 mm range of motion of the needle tip. A V-shaped groove was designed at the needle insertion point to seal the gap while providing sufficient room for needle oscillation.

A standard soft lithography technique⁴⁴ was used to fabricate the fluidic device. A PDMS pre-polymer was cast into a master replication mold designed with SolidWorks 2015 (SolidWorks Co., USA) and fabricated using a 3D-printer (Connex 3 Objet 260, Stratasys Ltd., USA) at high resolution (30 μm with glassy surface finish). After fixing the inlet and outlet silicon tubes at their pre-determined reservoir positions, the degasified PDMS pre-polymer was poured into the replication mold and heated at 70 °C for 3 h. The cured PDMS layer was carefully peeled off the mold and bonded to a microscope glass slide using an oxygen plasma bonding machine (Harrick Plasma, PDC-001, USA) at 45 W for 30 s, followed by a post-bonding heat treatment at 70 °C for 10 min to enhance the bonding quality. To avoid the wall contact in the channel, the needle was fixed inside a larger glass capillary and inserted through the V-shaped groove into the channel, as shown in Fig. 1(c). Then, the fluidic device was mounted onto the experimental setup shown in Figs. 1(a) and 1(b) to conduct the oscillation-based drop generation experiments.

D. Experimental procedure

Experiments were executed at three d-phase (Q_d = 0.05, 0.10 and 0.50 ml/min) and three c-phase (Q_c = 2, 5 and 10 ml/min) flow rates at five oscillation frequencies (f = 0, 1, 3, 7, and 15 Hz). We and Ca numbers were calculated based on Eqs. (1) and (2) as summarized in Table I for different d- and c-phase flow rates.

TABLE I.

Dimensionless We and Ca numbers at different d- and c-phase flow rates.

Dispersed phase		Continuous Phase
Qd [ml/min]	We	Qc [ml/min]	Ca
0.05	0.010	2	0.020
0.10	0.041	5	0.051
0.50	1.021	10	0.102

In each set of experiments, d- and c-phase flow rates were set on the syringe pumps. At each We-Ca combination, first the needle was precisely located at the center of the channel and droplet generation in a stationary co-flow mode was recorded. Then, the oscillation frequency was gradually increased using the Arduino controller program, and the oscillatory-mode droplet generation was studied. A high-speed video (150–400 frames per second) of the droplet generation process was recorded (see Video 2 in the supplementary material) for further quantitative studies. The accuracy of needle oscillation was examined before each experiment by comparing the input oscillation frequency with the needle tip transverse motion rate, obtained by video analysis, to ensure the needle oscillated at the desired frequency (see Sec. 1 of the supplementary material).

E. Data analysis and statistics

Images with repeatable patterns of multiple size droplets were extracted from the recorded videos at minimum six different time segments and analyzed by the open-source image processing software, ImageJ.⁴⁵ In each set of experiments, after length scale calibration, the automatic particle counting and measurement module was used to determine the generated droplet sizes. After subtracting the background values and converting the image into grayscale (8-bit), an empirical threshold value was adopted by comparing the results of the automatic edge detection technique to manually measured sizes. Droplet diameters were calculated based on the projected area assuming a spherical droplet shape. If the calculated diameter was larger than the channel height (H), then droplets were approximated to be cylindrical plugs rather than spherical droplets, and the apparent average diameter was calculated based on volume ($\bar{V}$) of the plug as shown in Eq. (3).

$$d=\left\{\begin{array}{ll}{d}_{av}& \left(d_{av}<H\right)\\ {\left(6\bar{V}/\pi \right)}^{1/3}& \left(d_{av}>H\right).\end{array}\right.$$ (3)

Droplet diameters were categorized into different independent size groups (called clusters) using the k-means clustering method with MATLAB (R2011a, Mathworks Inc., USA). In order to seek the optimal number of clusters, an intuitively heuristic approach⁴⁶ was applied as elaborately discussed in Sec. 2 in the supplementary material. Finally, droplet sizes in each We-Ca condition were converted into dimensionless diameters (d/d₀) using the ratio of generated droplet diameters in the oscillating mode (d) to that of the stationary mode (d₀) at the same We-Ca condition.

All statistical analyses were performed using Microsoft Excel (Microsoft Corp., WA, USA). Droplet sizes were reported as the average of dimensionless diameter ± standard deviation (d/d₀ ± SD). One-tailed unpaired Student's t-test with assumption of unequal variances was selected as the statistical method to identify any significant differences between two groups of data. Power analysis was performed to estimate the required sample sizes by maintaining the upper threshold of the significance level at 0.05 and the power at 90%.

IV. RESULTS

A. Effect of frequency on oscillating co-flow droplet generation

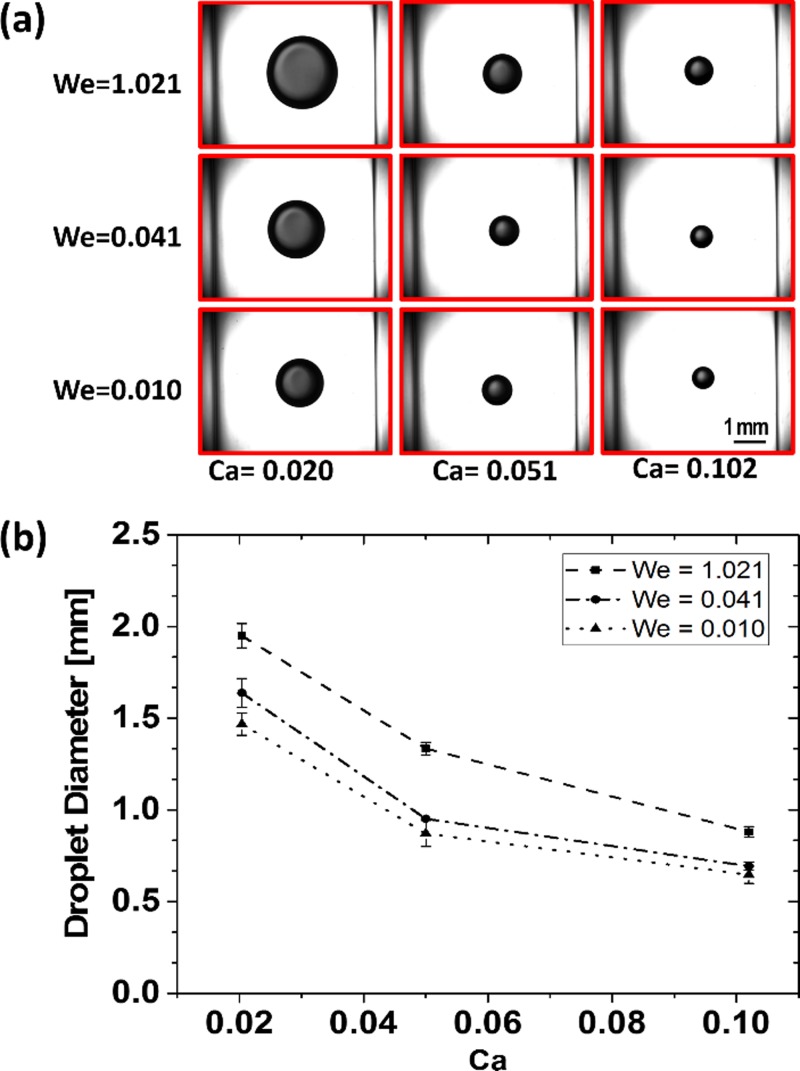
It is well understood that c- and d-phase flow rates represented by Ca and We numbers, respectively, are two important parameters in co-flow droplet generation systems. We first verified the correct performance of our system (Fig. 1) in the stationary d-phase nozzle mode (i.e., f = 0 Hz). The c- and d-phase flow rates in the ranges of 2–10 ml/min and 0.05–0.50 ml/min were used, respectively, and the real-time images of the generated droplets were acquired using a lens-equipped high-speed camera [Fig. 2(a)]. The average droplet diameters in the stationary mode were then calculated at various Ca-We conditions, as shown in Fig. 2(b). As expected, upon increasing the We number and due to the increased level of inertial forces, more d-phase liquid was injected into the growing droplet before the interfacial instabilities managed to disintegrate the interface. Therefore, droplets grew larger as the We number was increased. On the contrary, increasing the Ca number elevated the axial viscous drag force that counteracted the droplet growth and subsequently yielded a reduction in the size of droplets.

FIG. 2.

Stationary mode (f = 0 Hz) co-flow droplet generation. (a) Images of droplets generated at various We-Ca conditions. (b) Effect of We and Ca numbers on the droplet size in the stationary mode. The droplet size was directly proportional to the d-phase flow rate (We) and inversely proportional to the c-phase flow rate (Ca).

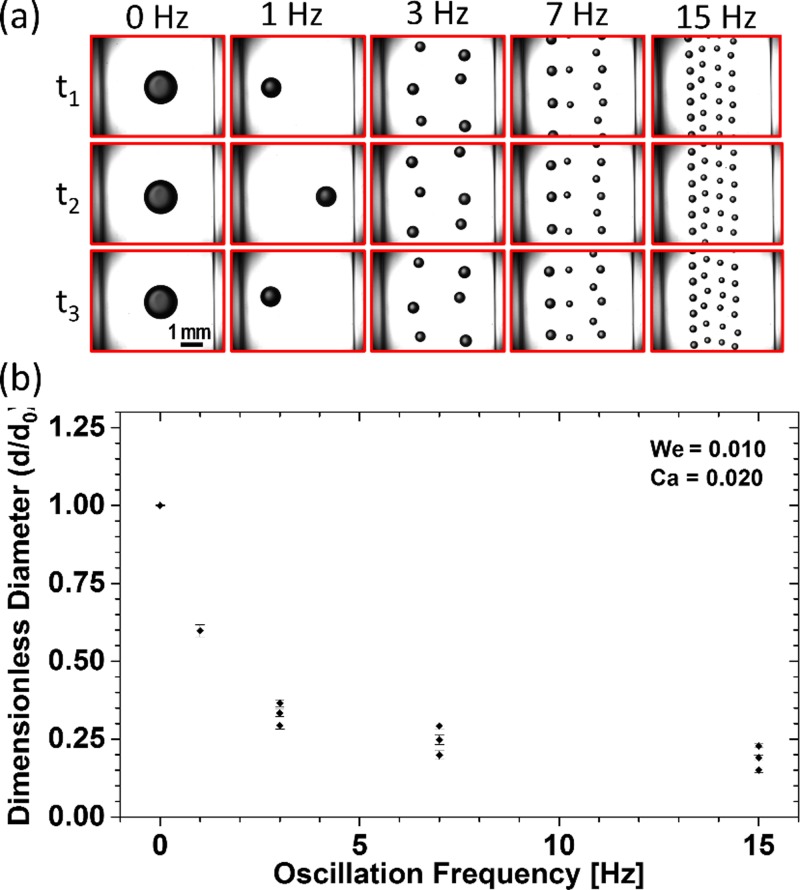
After establishing the stationary-mode framework for our system, the effects of nozzle oscillation and its frequency on water-in-oil droplet generation at different c- and d-phase flow rates were examined. Representing experimental images of droplets and their dimensionless diameters at different oscillation frequencies, when the lowest We = 0.010 and Ca = 0.020 were used, are shown in Figs. 3(a) and 3(b), respectively. The effects of nozzle oscillation on the number of generated droplets and their sizes are clearly observed in this figure.

FIG. 3.

Oscillatory mode (f = 1–15 Hz) co-flow droplet generation at the lowest flow rate levels with We = 0.010 and Ca = 0.020. (a) Droplet images at different oscillation frequencies with repeatable patterns. (b) Effect of oscillation frequency on the number of generated droplets and their dimensionless diameter (d/d_o). Upon increasing the oscillation frequency, transverse drag increased and subsequently led to an overall droplet size reduction. Meanwhile, the lateral motion of the nozzle exposed the growing droplet to a variable axial drag, and the droplet breakup occurred at different sizes at different locations.

We used our clustering method, described in Sec. 2 of the supplementary material to identify the number of independent droplet size clusters in the experiments above. As shown in Figs. 3(a) and 3(b), by increasing the oscillation frequency, the number of generated droplets increased from one set at 0 and 1 Hz to three statistically independent sizes (one-tailed unequal variance t-test, p-values <0.001) at the frequencies of 3, 7, and 15 Hz. Moreover, the average droplet size decreased by 84.9% of the stationary droplet size as the oscillation frequency was increased to 15 Hz, and droplets smaller than the stationary mode could be generated by oscillation.

More elaborate and detailed data about the overall effect of oscillation frequency on the number, dimensionless diameter, and monodispersity (via the coefficient of variance, CV%²⁹) of generated droplets at different We-Ca conditions of Table I can be found in Sec. 3 of the supplementary material. The general trends were similar in all conditions, but generation of some droplet clusters that were slightly larger than the stationary mode droplets was also observed at the high We-Ca levels. In these conditions, at the initial low-frequency stages of oscillation and regardless of the additional transverse drag effect, the dimensionless size of generated droplets increased with frequency. However, by a further increase in the oscillation frequency, the dimensionless size dropped below unity for all We-Ca conditions.

B. Effect of the d-phase flow rate (We) on oscillating co-flow droplet generation

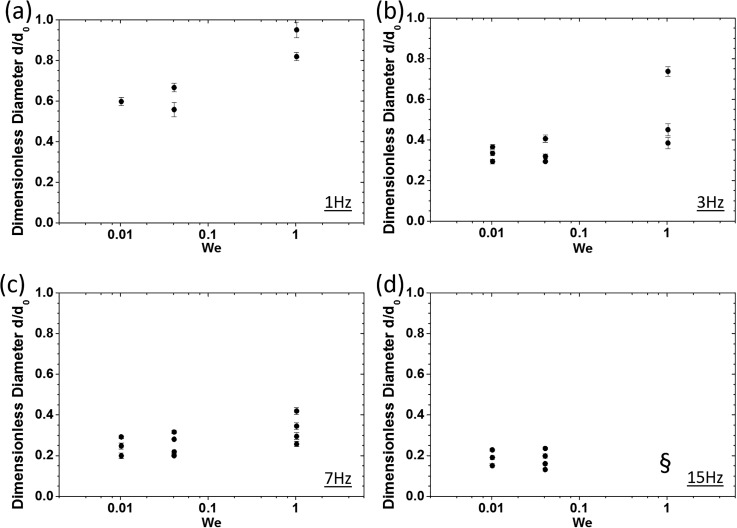
To study the effect of d-phase flow rate on the number of generated droplets and their corresponding dimensionless diameters in our system, we conducted a series of experiments similar to Sec. IV A. Dimensionless droplet sizes obtained at various We numbers of 0.010, 0.041, and 1.021 and a constant Ca number of 0.020 for different oscillation frequencies are shown in Fig. 4.

FIG. 4.

Effect of the d-phase flow rate (We number) on dimensionless size and the number of generated droplets at a constant c-phase flow rate (Ca = 0.02) and at various oscillation frequencies of (a) 1 Hz, (b) 3 Hz, (c) 7 Hz, and (d) 15 Hz. The symbol § in (d) indicates a condition under which the generated droplets overlapped due to increased throughput (see supplementary material), and image processing-based edge detection and size assessment were not feasible.

As shown in Fig. 4, by increasing the oscillation frequency, droplet sizes decreased as discussed earlier in Sec. IV A. Moreover, at each oscillation frequency, increasing the We number led to an elevated number of generated droplets with an overall increase in their sizes. At f = 1 Hz, the sizes of generated droplets were closer to the sizes obtained in the stationary mode. By increasing the oscillation frequency, a reduction trend in dimensionless droplet size was observed, and at the highest oscillation frequency of f = 15 Hz, the sizes of generated droplets were almost independent of the We number.

C. Effect of the c-phase flow rate (Ca) on oscillating co-flow droplet generation

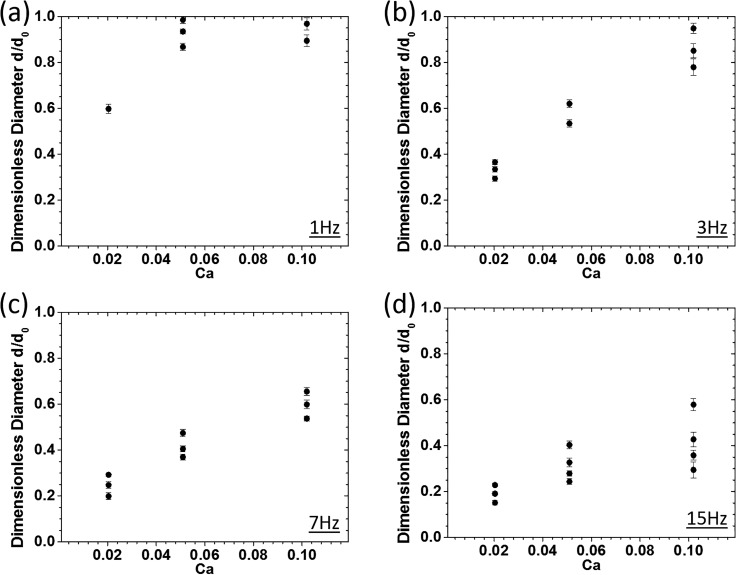
As stated earlier, the Ca number which shows the ratio of viscous to interfacial forces is a representative for the c-phase flow rate. Dimensionless diameters of water-in-oil droplets at various Ca numbers of 0.020, 0.051, and 0.102 and a constant We number of 0.010 for different oscillation frequencies are shown in Fig. 5.

FIG. 5.

Effect of the c-phase flow rate (Ca number) on dimensionless size and the number of generated droplets at a constant d-phase flow rate (We = 0.010) and at various oscillation frequencies of (a) 1 Hz, (b) 3 Hz, (c) 7 Hz, and (d) 15 Hz.

Our results revealed increasing trends in the number of generated droplets and their dimensionless diameters upon increasing the Ca number at fixed oscillation frequencies. Moreover, increasing the oscillation frequency yielded an overall decrease in droplet sizes as mentioned earlier in Sec. IV. At low oscillation frequencies, the generated droplets at high c-phase flow rates became similar in size and almost equal to the stationary droplets. By increasing the oscillation frequency, the dimensionless diameter of droplets scaled down compared to the size of the static mode droplets while retaining the increasing trend upon increasing the Ca number.

V. DISCUSSION

As shown in Fig. 3, the transverse oscillation of the d-phase needle inside the channel, perpendicular to the c-phase stream, had two important effects on the droplets. Most importantly, an extra lateral drag was added to the existing axial drag, assisting the breakup to happen at smaller droplet diameters, especially at high-frequency levels. Accordingly, by increasing the oscillation frequency, the lateral drag force was intensified, and the overall sizes of generated droplets decreased. Moreover, the transverse motion also exposed the growing droplets to a varying axial drag due to the parabolic profile of the c-phase flow velocity and the varying rate of deformation across the width of the channel. This effect is more dominant at lower frequency levels. Altogether, we observed that the oscillatory motion of the d-phase fluid leads to a droplet breakup at different lateral locations in the channel and a frequency-dependent generation of multiple droplets with a general decrease in the diameter (see Fig. S9 of the supplementary material for more supporting data).

The increase in the number of generated droplets at higher We numbers in Fig. 4 can be attributed to the situation where the total drag force (i.e., axial and transverse drag) equates the interfacial force during oscillation. The axial drag force varies with the lateral displacement of the d-phase nozzle and the size of the growing droplet. The transverse drag force is relatively constant at a constant oscillation frequency and only increases upon droplet growth. When the We number is increased, droplet growth happens faster at a constant frequency and the Ca number. Therefore, droplets reach their breakup diameters faster, and droplet generation happens more often at higher We levels, leading to generation of more clusters of droplets.

The overall droplet size increase at higher We levels in Fig. 4 can be described by the increased inertial effects that were also discussed for the stationary droplets. As shown in Figs. 4(a)–4(c), at lower oscillation frequencies where the inertial effect was dominant, an increase in the We number resulted in a dominant increase in the dimensionless droplet sizes. However, by increasing the frequency, the effect of total drag force became dominant over the inertial effects, and as shown in Fig. 4(d), the generated droplets were approximately the same size at various We numbers.

An increase in the axial drag force at the same lateral positions in the channel was predicted upon increasing the Ca number. Therefore, the droplet breakup was expected to occur at smaller sizes. As shown in Fig. 5, the dimensionless diameter of droplets increased by increasing the Ca number, which may seem controversial. However, by referring to the actual droplet diameters, we observed that the droplets generated at higher Ca numbers were indeed smaller. Increasing trends in the dimensionless droplet size at higher We number levels were also observed upon increasing the Ca number as shown in Sec. 4 in the supplementary material. Moreover, at low frequencies [Figs. 5(a) and 5(b)], axial drag was dominant over transverse drag, and the generated droplets were approximately the same size or smaller than those generated at the stationary mode (conventional co-flow device). However, at higher frequencies [7 and 15 Hz in Figs. 5(c) and 5(d)], lateral drag became more than or as effective as the axial drag, and the dimensionless size of droplets in all Ca numbers scaled down (due to the effect of increased transverse shear) by retaining the same increasing trend observed in low-frequency modes. An order of magnitude analysis for lateral and axial drag forces was performed (Sec. 5 in the supplementary material), and the results were in good agreement with observations above.

In the stationary mode, where the needle is centered in the channel, axial and transverse drags are at their maximum and minimum (zero) levels, respectively. In the low We-Ca oscillating modes, due to the dominant impact of the transverse drag, the sizes of generated droplets were always equal to or smaller than the droplets in the pure axial drag mode (i.e., stationary mode). Interestingly, at elevated We-Ca conditions, upon increasing the oscillation frequency, an atypical behavior was observed. Generation of oscillatory-mode droplets larger than their stationary-mode counterparts at higher We-Ca conditions can be attributed to the counteraction of the total drag force components (axial and transverse drag), in the presence of increased levels of inertia. At lower oscillation frequencies where transverse drag was insignificant, due to higher injection rates, dimensionless sizes of generated droplets were larger than unity at increased Ca levels. However, by increasing the oscillation frequency, transverse drag became significant, and consequently, dimensionless diameters at higher injection rates dropped below unity in all flow conditions.

It is possible that multiple modes of operation can be identified to offer various empirical correlations or even theoretical predictions. However, we focused on demonstrating the proof of concept in this paper while more experiments covering a wider range and higher-resolution set of flow rates, fluid properties and oscillation frequencies are required to develop a comprehensive map and propose an analytical model for droplet size estimation.

The large size of the nozzle, back-needle leakage, and pressure-related burst problems at higher flow rates and mechanism seizure at increased frequencies were the main challenges constraining the generation of droplets with smaller sizes. These parameters will be optimized in our future work.

VI. CONCLUSION

The effects of oscillating the d-phase nozzle on the number of droplets and their sizes were investigated in a co-flow device at different flow rates and oscillation frequencies. First, performance of the system in the stationary d-phase nozzle mode (i.e., f = 0 Hz) was investigated to establish the framework for nozzle oscillation studies. Then, the effect of oscillation-induced drag force on the size of generated droplets was studied at different frequencies (f = 1–15 Hz). Unlike other conventional passive methods, the oscillating d-phase nozzle technique was able to simultaneously produce a wide range of monodispersed droplets (4 nl up to 4 μl) at constant c- and d-phase flow rates with no modification in the physical properties of liquids. Increasing the We number, the Ca number and oscillation frequency yielded a general increase in the number of generated droplets. Increasing the oscillation frequency generally resulted in droplet size reduction due to the dominant effect of the transverse drag. Upon increasing the We number, due to the higher injection rate of d-phase fluid, a general increase in the size of droplets was observed. By increasing the Ca number, the effect of axial drag became dominant over the transverse drag. Thus, droplets were mostly generated with smaller sizes but not very distant from the stationery mode. This technique is of interest in co-flow applications where droplet size reduction is desired but not with the increasing rate of d- or c-phase fluids. It also may find applications in aqueous two-phase systems³² (ATPS), where due to inherently low interfacial tension, the d-phase flow forms a long stable jet which can be broken up into droplets using the additional oscillatory drag in our device.

SUPPLEMENTARY MATERIAL

See supplementary material for more details on the oscillation mechanism, k-means clustering algorithm, figures for size and monodispersity of all experimental conditions, and order of magnitude analysis for lateral and axial drag forces. Movies 1 and 2 show real time videos of the oscillation mechanism and the generated droplet trains at different oscillation frequencies for one of the We-Ca conditions.