Changes in Effective Playing Space when Considering Sub-Groups of 3 to 10 Players in Professional Soccer Matches

Abstract

Success in soccer is much dependent on how players and teams create and restrict space and time. In match situations, players constitute small sub-groups to improve their collective synchronization and achievement of specific goals. This study aimed to identify changes in the effective playing space (EPS, defined as the smallest polygonal area delimited by the peripheral outfield players) when considering sub-groups of 3 to 10 players. Twenty outfield professional players participated in this study. The EPS, its regularity pattern (measured by the approximate entropy), coefficient of variation and players’ mean speed were calculated for sub-groups of 3, 4, 5, 6, 7, 8, 9 and 10 players, considering the smallest inter-player distance as the criterion. The EPS presented a most likely increase with a higher number of players, especially considering the transition from 3 to 4 players (~440% of variation, very large). As the EPS increased with the number of players, the correspondent regularity presented a trend of a most likely increase (from EPS3 vs. EPS4: ~25%, very large; to EPS9 vs. EPS10: ~11%, moderate). The mean speed results suggest that players may achieve different states of collective coordination, mainly between ~6 to 8 km.h-1. Overall, three different match scenarios should require additional attention when aiming to design more match transferable tasks: i) transition from EPS3 to EPS4; ii) transition from EPS4 up to EPS8; and iii) transition from EPS8 to EPS9. These results help to understand match self-organized behaviours and, consequently, allow to optimize task characteristics in practice sessions.

Introduction

The study of collective behaviour has contributed to an understanding of how individuals, in their natural environment are constrained by the influence of others’ decisions (Vicsek and Zafeiris, 2012). In team sports, players use local information sources, such as teammates positioning, to achieve dynamic self-organized behaviours (Duarte et al., 2012; Leite et al., 2014). In order to achieve high-level performances with these behaviours, team members organize themselves into different sized sub-groups. The interactions of these sub-systems must then become a basis of information throughout various shared networks for a successful system (Grehaigne and Godbout, 2013; Grehaigne et al., 1997).

In soccer, an understanding of emergent behavioural patterns relies upon the use of player positioning in interaction with teammates and opponents (Davids et al., 2003; McGarry et al., 2002; Moura et al., 2015). With this approach, players’ pitch coordinates permit researchers to link positioning decisions and actions with team strategy and tactics, maintaining proper attention to situational and sequential match characteristics. Thus, research to date has focused on developing pitch-positioning performance indicators, treating team organization as a consequence of functional constraints of the environment scale (Araujo et al., 2006; Duarte et al., 2013). Consequently, the daily challenge for the coaches’ intervention is to identify and replicate the essential informational input of performance environments within simulated scenarios (Dicks et al., 2009). It is intended that practice may promote the emergence of specific behaviours and how this knowledge can optimize transferability of players’ behaviour between training drills and competition (Travassos et al., 2012).

Team sports performance should be understood in terms of space-time interaction dynamics that are mediated by environmental information (Folgado et al., 2014). Accordingly, the assessment of collective behavioural trends should be related to match dynamics, where the players’ interactions are guided by space, time and speed. For example, players are likely to increase their movement synchronization and game pace when the available space increased, whereas the opposite happens when the available space is limited (Gonçalves et al., 2017). Moreover, when players’ roles are similar and their pitch distances are smaller, their synchronization is probably facilitated (Gonçalves et al., 2014). Therefore, the manipulation of simple boundary conditions, such as available playing space, can foster team engagement in adaptive behaviour and improve performance. Based on the information perceived by the players, different teams’ structures will emerge, which can be measured by the teams’ effective playing space (EPS). The EPS is defined as the smallest polygonal area delimited by the peripheral outfield players that provides information about the surface area that is being effectively covered. Concomitantly, the number of players involved in the task will demand continuous team-related behaviour so that a higher number of players demands higher positional organization (Aguiar et al., 2015). Accordingly, organization of the optimal position requires players to use different displacement speeds in both competition (Folgado et al., 2014, 2015) and training scenarios (Sampaio et al., 2014). These dynamic positioning behaviours lead to different time dependent configurations that reflect team specific tactical concepts (Jager and Schollhorn, 2012). Moreover, a better understanding of these sub-units’ behaviour may be achieved when the variability in their structures is considered, which can be measured through the coefficient of variation (CV) and the regularity level of the EPS. These variables may represent the adaptability of collective behaviour according to the number of players involved in the different sub-units (Gonçalves et al., 2017; Travassos et al., 2012). Thus, collectively considering how player displacements are coupled with those of neighbouring teammates, based on spatiotemporal dependence and different levels of interaction, may improve the understanding of the effect on varying numbers of interacting players within team behaviours. Accordingly, this study aimed to identify changes in the effective playing space (EPS) when considering sub-groups of 3-10 players during soccer matches. More specifically, we calculated the EPS of different sub-groups, measured in absolute values (m²), considering a progressively larger number of nearby players. The CV and regularity level of the EPS were compared among various sized subgroups. Finally, the mean speed displacement from each sub-group and corresponding CV were also compared. Although prior expectations suggested that a higher number of players would result in higher EPS values, the magnitude of changes in EPS and the optimal number of players in proximal interaction are unknown and remain to be explored.

Methods

Participants

Twenty outfield soccer players from a Portuguese first league team participated in this study (age, 24.8 ± 3.9 y; professional playing experience, 7.1 ± 4.0 y). The club technical staff provided a formal authorization and all players were instructed about the protocol and informed that they could withdraw from the study at any time. All players expressed verbal consent to participate. The investigation was approved by the local Institutional Research Ethics Committee and conformed to the recommendations of the Declaration of Helsinki.

Design and Procedures

The study was carried in the preseason period and all players were frequently substituted at half time. Thus, to ensure a constant team formation between the analysed matches (GK-4-4- 2), only the first half of each match was used in the analysis. During the collected first halves no player was substituted. The sample was constituted by a total of six matches, played on official-size natural turf pitches, following the official soccer rules. The positional data from each outfield player were collected using a 5 Hz nondifferential GPS device (SPI Pro, GPSports, Canberra, Australia). The raw data, i.e. latitude and longitude coordinates, were exported from the GPS units and computed using dedicated routines in Matlab® software (The MathWorks, Inc., Massachusetts, United States) (for complete data filter guidelines, see Folgado et al. (2014)). During data collection, the number of satellites connected with each device was 8.4 ± 0.8.

Positional variables and processing techniques

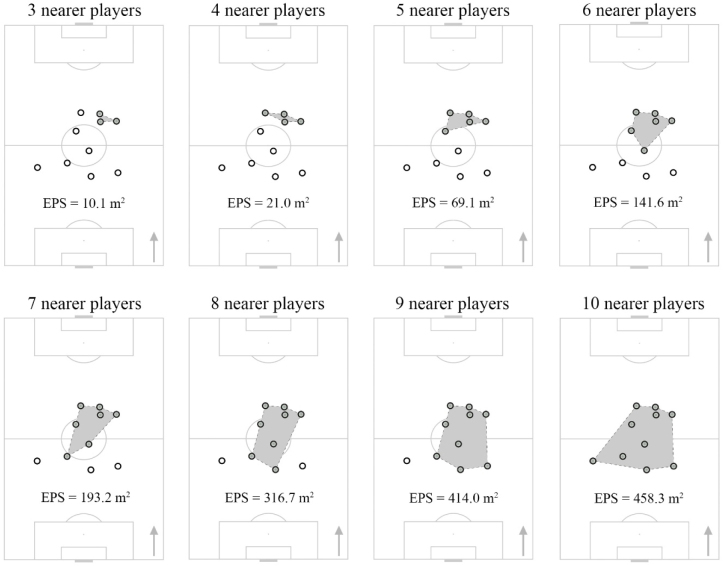
For each match, the EPS (defined by the smallest polygonal area delimited by the peripheral players) was dynamically calculated for sub-groups of 3, 4, 5, 6, 7, 8, 9 and 10 players, using the smallest inter-player distance as the selection criterion. For example, the EPS from the sub-group of 3 players was constituted by the smallest polygonal area delimited by the 3 players who were nearer to each other (see Figure 1 for a visual representation). The results from these partial EPS situations were calculated in absolute values (area: m²) and also considered the amount of regularity (measured by the approximate entropy, ApEn). Mean displacement speed (km·h^–1) of the players who formed each partial EPS was also dynamically calculated. The coefficient of variation (CV) was calculated for each match, for absolute values of EPS and mean displacement speed.

Figure 1.

Frame example of the smallest polygonal areas delimited by outfield players who were nearer to each other, considering 3, 4, 5, 6, 7, 8, 9 and 10 players.

The grey arrow means the team’s attack direction. Abbreviations:

EPS = effective playing space.

The ApEn technique is a non-linear procedure that has been used in several studies to identify the amount of uncertainty regarding the order of an output signal (i.e. regularity in players’ movement patterns). Imputed values of a vector’s length (m) was 2 and the tolerance (r) was 0.2 standard deviations (Pincus, 1991; Yentes et al., 2013). The outcome values range between 0 and 2 (arbitrary units) and lower values represent more repeatable, regular, predictable and less chaotic sequences of data points. From a processing approach, ApEn expresses the regularity that the configuration of one segment of data in a time series will allow the prediction of the configuration of another segment of the time series a certain distance apart (Harbourne and Stergiou, 2009; Pincus et al., 1991). From a practical understanding, this technique permits to identify if players’ displacement trajectories express a regular and predictable pattern which may, in turn, provide information regarding their tactical behaviour (Gonçalves et al., 2014; Sampaio et al., 2014; Silva et al., 2016). For instance, an EPS time-series with lower ApEn values may suggest a higher regular variation over time in the occupied area. All processing techniques were computed using dedicated routines in Matlab® software (The MathWorks, Inc., Massachusetts, United States).

Statistical Analysis

Magnitude-based inferences and precision of estimation were used to analyse the data (Batterham and Hopkins, 2006; Buchheit, 2016). Prior to the comparisons, all processed variables were log-transformed to reduce the nonuniformity of error. A descriptive analysis was performed using mean and standard deviations for the EPS variables, i.e. absolute values, ApEn and mean speed displacements (the presented mean is the back-transformed mean of the log transform). Differences between sub-groups (EPS3 vs. EPS4; EPS4 vs. EPS5; EPS5 vs. EPS6; EPS6 vs. EPS7; EPS7 vs. EPS8; EPS8 vs. EPS9; EPS9 vs. EPS10) were expressed in percentage units with 95% confidence limits. Smallest worthwhile differences were estimated from the standardized units multiplied by 0.2. Uncertainty in the true differences of the scenarios was assessed using non-clinical magnitude-based inferences (Hopkins et al., 2009). Also, the sub-group comparisons were assessed via standardized mean differences and respective 95% confidence intervals. Thresholds for effect sizes statistics were 0.2, trivial; 0.6, small; 1.2, moderate; 2.0, large; and >2.0, very large (Cumming, 2012; Hopkins et al., 2009; Maszczyk, et al. 2014).

Results

Tables 1 and 2 present both descriptive and statistical analysis of the partial EPS and the sub-group comparisons (percentage of variation, uncertainty in the true differences and standardized Cohen units). The EPS (absolute values) presented a most likely increase with an increasing number of players. These differences ranged from 442% (95% confidence intervals: 412 to 472%) in EPS3 vs. EPS4 to 35% (33 to 37%) in EPS9 vs. EPS10. The CV results presented a most likely decrease across comparison (from EPS3 vs. EPS4: difference: -36% (-37 to -35%); to EPS9 vs. EPS10: -9% (-10 to 8%)) with magnitudes ranging from moderate to very large. The EPS10 was 897.3 ± 60.5 m² (mean ± SD) with 0.39 ± 0.05 of the CV. There were two different trends in this variable: the transition from 3 to 4 players presented a very large decrease in the CV values, -36.0% (-37 to - 31%); and the transition from 8 to 9 and 9 to 10 players presented an increase in % variation from the previous trend. In other words, the variability in the surface area occupied by the players decreased more when considering more than 8 players (since CV presented an increase in % variation).

Table 1.

Descriptive analysis for sub-group comparisons.

Variables	EPS3	EPS4	EPS5	EPS6	EPS7	EPS8	EPS9	EPS10
Absolute values
Mean ± SD (m2)	11.6 ± 0.8	62.9 ± 4.9	136.3 ± 11.0	232.0 ± 17.1	348.9 ± 25.4	488.0 ± 39.3	664.7 ± 53.2	897.3 ± 60.5
Pitch % of free space	99.8%	99.1%	98.1%	96.8%	95.1%	93.2%	90.7%	87.4%
CV ± SD	1.06 ± 0.06	0.68 ± 0.04	0.58 ± 0.04	0.53 ± 0.04	0.50 ± 0.05	0.46 ± 0.05	0.43 ± 0.05	0.39 ± 0.05
Regularity(ApEn)
Mean ± SD (a.u.)	0.37 ± 0.05	0.28 ± 0.04	0.22 ± 0.03	0.18 ± 0.03	0.16 ± 0.02	0.13 ± 0.02	0.12 ± 0.02	0.10 ± 0.02
Mean speed displacements
Mean ± SD (a.u.)	7.1 ± 0.2	7.1 ± 0.3	7.1 ± 0.2	7.0 ± 0.3	7.0 ± 0.4	7.0 ± 0.2	6.8 ± 0.2	6.8 ± 0.4
CV ± SD	0.63 ± 0.04	0.59 ± 0.04	0.57 ± 0.04	0.55 ± 0.04	0.53 ± 0.04	0.52 ± 0.05	0.52 ± 0.04	0.51 ± 0.04

Note: Abbreviations and symbols: EPS = effective playing space;

ApEn = approximate entropy; CV = coefficient of variation

Table 2.

Descriptive statistics for sub-group comparisons.

Variables	EPS3 Vs EPS4	EPS4 vs EPS5	EPS5 Vs EPS6	EPS6 vs EPS7	EPS7 vs EPS8	EPS8 vs EPS9	EPS9 vs EPS10
Absolute values
Mean ± SD (m2)
Sub-group comparisons	441.8; ±30.0 Most likely↑	116.8; ±1.8 Most likely↑	70.2; ±1.5 Most likely↑	50.4; ±1.3 Most likely↑	39.8; ±1.2 Most likely↑	36.2; ±0.7 Most likely↑	35.1; ±2.0 Most likely↑
Standardized units	18.93; ±0.62 Very large	8.67; ±0.09 Very large	5.96; ±0.10 Very large	4.58; ±0.10 Very large	3.76; ±0.10 Very large	3.46; ±0.06 Very large	3.37; ±0.16 Very large
CV ± SD
Sub-group comparisons	-36.0; ±1.1 Most likely↓	-13.7; ±2.3 Most likely↓	-8.9; ±1.3 Most likely↓	-7.0; ±1.9 Most likely↓	-6.4; ±0.6 Most likely↓	-6.7; ±2.4 Most likely↓	-9.2; ±0.9 Most likely↓
Standardized units	-4.17; ±0.17 Very large	-1.38; ±0.25 Large	-0.87; ±0.13 Moderate	-0.68; ±0.19 Moderate	-0.62; ±0.06 Moderate	-0.64; ±0.24 Moderate	-0.9; ±0.1 Moderate
Regularity (ApEn)
Mean ± SD (a.u.)
Sub-group comparisons	-25.5; ±3.9 Most likely↑	-21.1; ±2.8 Most likely↑	-17.1; ±2.3 Most likely↑	-14.6; ±3.9 Most likely↑	-14.9; ±2.8 Most likely↑	-13.1; ±1.5 Most likely↑	-11.0; ±3.1 Most likely↑
Standardized units	-1.76; ±0.31 Large	-1.42; ±0.21 Large	-1.12; ±0.16 Moderate	-0.94; ±0.27 Moderate	-0.96; ±0.19 Moderate	-0.84; ±0.10 Moderate	-0.7; ±0.2 Moderate
Mean speed displacements
Mean ± SD (a.u.)
Sub-group comparisons	0.9; ±1.0 Possibly↑	-0.5; ±0.6 Possibly↓	-0.6; ±0.7 Possibly ↓	-0.5; ±0.5 Likely trivial	-0.8; ±0.7 Possibly ↓	-2.9; ±0.7 Most likely↓	0.4; ±0.9 Likely trivial
Standardized units	0.21; ±0.24 Small	-0.13; ±0.15 Trivial	-0.15; ±0.16 Trivial	-0.13; ±0.13 Trivial	-0.19; ±0.16 Trivial	-0.71; ±0.18 Moderate	0.10; ±0.21 Small
CV ± SD
Sub-group comparisons	-6.4; ±2.4 Most likely↓	-3.8; ±1.3 Most likely↓	-3.4; ±1.8 Very likely↓	-3.1; ±1.5 Very likely↓	-1.9; ±07 Likely↓	-0.3; ±1.7 Likely trivial	-2.2; ±2.2 Possible↓
Standardized units	-0.70; ±0.27 Moderate	-0.41; ±0.14 Small	-0.37; ±0.20 Small	-0.33; ±0.17 Small	-0.19; ±0.07 Trivial	-0.03; ±0.18 Trivial	-0.19; ±0.18 Trivial

Abbreviations and symbols: EPS = effective playing space; ApEn = approximate entropy; CV = coefficient of variation; Sub-group comparisons are expressed in %; ±95% confidence limits and respective standardized differences are expressed in Cohen d; ±95% confidence limits.

^↑increase

^↓decrease

As the EPS increased with the number of players, the ApEn presented a most likely decreasing trend (from EPS3 vs. EPS4: difference: -25% (-29 to -21%), very large magnitude; to EPS9 vs. EPS10:-11% (-14 to -8%), moderate magnitude), i.e. the occupied surface area became more regular (Tables 1 and 2).

The mean displacement speed for each sub-group showed trivial/small differences from EPS3 vs. EPS4 to EPS7 vs. EPS8 sub-group comparison (from EPS3: 7.1 ± 0.2 km.h^–1; to EPS8: 7.0 ± 0.2 km.h^–1). However, when considering EPS8 vs. EPS9 comparison, the results presented a most likely -3% (-4 to -2%) decrease, with a moderate magnitude effect. When considering 10 players (EPS9 vs. EPS10), a likely trivial difference was identified. The correspondent CV results showed a most likely moderate -6% (-9 to -4%) decrease from EPS3 to EPS4, and small/trivial effect in the remaining comparisons (Tables 1 and 2).

Figure 2 presents a graphical overview of the analysed variables for each of the six matches. The corresponding results showed strong intermatch stability in performance across all matches. The results show an increase in absolute EPS values with an increase in the number of players (Figure 2a), a decrease in the correspondent ApEn values (i.e. increasing regularity) (Figure 2b) and the mean displacement speed ranging from ~6-8 km·h^–1 (Figure 2c).

Figure 2.

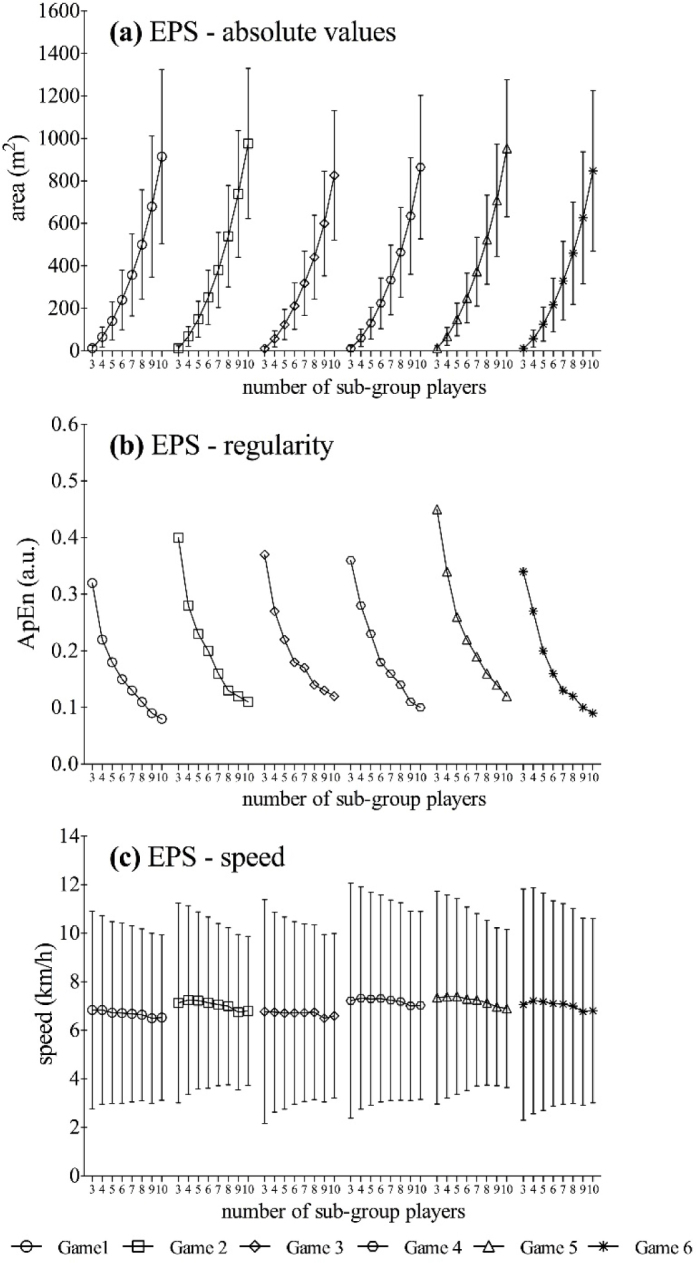
Graphical descriptive overview from each of the six-preseason match variables.

Abbreviations: EPS = effective playing space; ApEn = approximate entropy.

Error bars indicate the standard deviation for each value.

Discussion

This study aimed to identify changes in the effective playing space (EPS) when considering sub-groups of 3 to 10 players in soccer matches. As expected, the results showed that increasing the number of players leads to a higher EPS. However, additional findings allowed to identify that the transitions from 3 to 4 and 8 to 9 players were particularly different from other EPS situations. In the EPS10 that considers all outfield players, the covered area was ~900 m². The mean speed results showed that players might achieve different states of collective coordination. Furthermore, there were very tenuous match-to-match changes in all variables.

The players’ movements and actions generate local information which ultimately influences the teammates and opponents behaviour (Passos et al., 2013). These spatiotemporal relationships are presented as essential-on-field constraints for coupling their behaviours and achieving functional coordination patterns (Duarte et al., 2013; Gonçalves et al., 2014). However, knowledge about key variables that determine this optimal coordination during competition is still very scarce, especially when considering team players based on nearest relationships. Therefore, findings of the current study can provide valuable clues for training optimization, specifically for designing more transferable tasks to competition (Travassos et al., 2012, 2013). In this sense, the current results confirmed that a higher number of players resulted in higher EPS values. It is interesting and unknown that the transition from 3 to 4 sub-group presented a higher variation in EPS differences (around ~440%) and this was also the sub-group with a higher CV. In addition, despite the ApEn values decreased with the increase of the number of players, the EPS3 vs. EPS4 comparison showed higher magnitude values (very large). Analysing match relationships from a geometrical perspective and considering the EPS constituted by 3 nearest teammates, each individual displacement will necessarily change the absolute values of the occupied space and will promote higher variability. In terms of the EPS constituted by more than 3 nearer teammates (e.g. see Figure 1, 8 nearer players), it may occur that individual displacement from the players inside of the formed area would not influence the EPS.

Accordingly, recent research showed that 3-a-side small-sided games could be used to improve the unpredictability of behaviour as these scenarios presented higher irregularity of players’ positional behaviour (Aguiar et al., 2015). Another possibility is linked with the positioning of the 3 nearest players. Given the fact that in the current study there is a limitation of not having measured the ball location, it may be possible, although hypothetical, that the 3 nearest players were the players closer to the ball. In these situations, the teams aim to maintain stability in local subsystems while defending and creating instability during the offensive process (Vilar et al., 2013). Thus, this higher variation could be linked with the different aims in offensive and defensive match situations. That is, the defending teams aim to maintain stability in local sub-systems, as opposed to desired high-variability in positioning during the offensive phase. For coaching applications, it may be suggested that field dimensions should be optimized to enable players to attune their behaviour with environmental cues. For example, a ~12 m² effective field space seems to enhance players’ perceptions for action when involving 3 teammates. Also, coaches should vary this field dimension, considering that within this configuration, EPS might vary ~100% (CV = 1.06 ± 0.06). Thus, coaches should promote training situations that control players’ positioning while defending, and free them when regaining ball possession.

An additional key result is the potential value from the absolute EPS, which may add meaningful information to increase transference from training tasks to competition. In fact, several studies have designed specific practice protocols where space available for players to develop their behaviours is proportional to the full-sized match (for review see Hill-Haas et al. (2011)). For example, Fradua and colleagues (2012) recommended individual playing areas ranging from 65 to 110 m² for training tactical aspects when the aim was to increase full-size representative demands. On the other side, a recent study demonstrated how field dimensions and skill level constrained the covered EPS when playing 4-a-side small-sided game (Silva et al., 2014). The results showed that the EPS (from national-level players) ranged from 121.16 ± 24.55m² in a small field to 251.2 ± 46.33 m² in a large field. However, an EPS of 4 players captured during a SSG might be very different from the EPS of 4 players captured during an 11-a-side match. For instance, in the current study, the EPS formed by the 4 nearest teammates was ~60 m². Apparently, players used higher EPS values during SSG when compared to official matches, which strongly highlights how player’s behaviour is constrained by all the remaining teammates and opponents. Another interesting finding is related to the EPS10 since it was showed that players normally used a small part of the pitch, ~900 m² (with ~0.40 CV), that represented ~13% of the official 105 x 68 m pitch dimensions (pitch % of free space based on EPS mean values = ~87%, Table 1). Using the full-pitch size as the reference to the individual playing area may lead to a decrease in the training effect of tactical aspects of the match, especially in the spatiotemporal information perceived by teammates.

A consistent trend in the obtained performance profiles was identified across the six analysed matches, either in the positioning variables or in the mean speed. It has been argued that a complementary relationship between players’ displacement speed and their movement direction would provide useful insights for coaches (Folgado et al., 2014; Sampaio et al., 2014; Travassos et al., 2014). This approach may optimize coaches’ external instructions, aiming to constraint the environmental task and players’ performance. From the present approach, there was a trivial variation in mean displacement speed identified from 3 to 8 players’ sub-groups. This outcome should be well interpreted, since players’ displacement presented a range of variability in displacement speed when they still maintained synchronization behaviours (specially in EPS3). However, this trend slightly changed when the sub-group was constituted by more than 8 players. From this point, the mean displacement speed presented a most likely decrease and this outcome was complemented by the decrease in variability from the surface area when considering more than 8 players. The decreasing influences of the 9th and 10th players in the behavioural variables (ApEn and Speed) may be related to the lower activity involvement within match strategy due to the longer distance to the ball and a lower activity profile. Nonetheless, players’ displacement speed around ~6 to 8 km·h^–1 (CV = ~0.5 a.u.) is required to promote collective functional behaviours. However, coaches should increase speed variability to promote widely adaptive and representative dynamical environments, for example, by using external instructions imposed to the task (Sampaio et al., 2014).

Conclusion

The current study allowed the identification of how the increase in the number of players influenced both regularity and absolute EPS areas. Players’ communication during soccer matches requires the development of specific space and time interactions. Thus, results of this study highlight three match scenarios that seem to be very different and should require additional attention in designing competition-transferable tasks: i) transition from EPS3 to EPS4; ii) transition from EPS4 up to EPS8; and iii) transition from EPS8 to EPS9. For example, different spaces should be used when considering tasks with a lower level of interactions (e.g. teams with 3 and 4 players) due to a higher variation in EPS. Conversely, tactical tasks using more players (teams with 8 to 10 players) should contemplate more stable spaces (lower EPS variation). In addition, mean speed results suggest that players achieved different states of collective coordination when the value reached the level of ~6 to 8 km·h^–1. These results help to understand match selforganized behaviours and, consequently, facilitate the optimization of task characteristics in practice sessions.